A Dual Approach

For

Federated Optimization

Zhenan Fan

Department of Computer Science

Collaborators:

Huang Fang, Michael Friedlander

Federated Optimization

\mathop{min}\limits_{w \in \mathbb{R}^d}\enspace F(\red{w}) \coloneqq \sum\limits_{i=1}^\blue{N} f_i(w) \enspace\text{with}\enspace f_i(w) \coloneqq \frac{1}{|\mathcal{D}_i|} \sum\limits_{(x, y) \in \green{\mathcal{D}_i} } \purple{\ell}(w; x, y)

model

number of clients

local dataset

loss function

Primal problem

Dual problem

\mathop{min}\limits_{y_1, \dots, y_N \in \mathbb{R}^d}\enspace G(\mathbf{y}) \coloneqq \sum\limits_{i=1}^N \red{f_i^*}(y_i) \enspace\text{subject to}\enspace \sum_{i=1}^N \blue{y_i} = \mathbf{0}

conjugate function

local dual model

Primal-based Algorithm

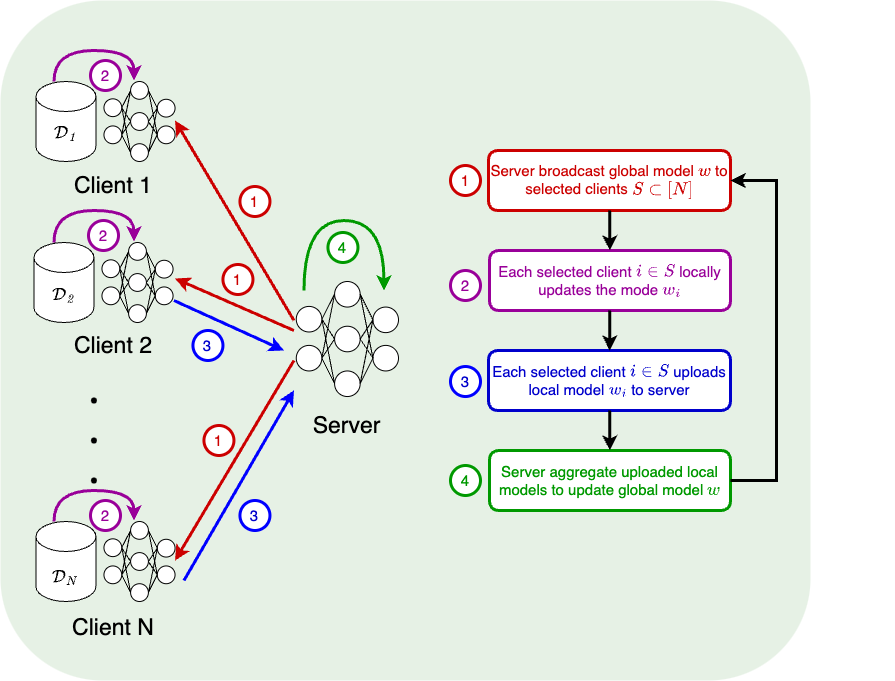
FedAvg [McMahan et al.'17]

w_i \leftarrow w_i - \eta \tilde \nabla f_i(w_i) \quad (K \text{ times})

w \leftarrow \frac{1}{|S|}\sum_{i \in S} w_i

SCAFFOLD [Karimireddy et al.'20]

w_i \leftarrow w_i - \eta (\tilde \nabla f_i(w_i) - c_i + c) \quad (K \text{ times})

c_i \leftarrow \tilde \nabla f_i(w), \enspace c \leftarrow \frac{1}{|S|}\sum_{i \in S} c_i, \enspace w \leftarrow \frac{1}{|S|}\sum_{i \in S} w_i

FedDCD

A extension of [Necoara et al.'17]

w_i = \nabla f_i^*(y_i) \coloneqq \mathop{argmin}\limits_{w\in \mathbb{R}^d} \{ f_i(w) - \langle w, y_i \rangle \}

\{\hat w_i\}_{i \in S} = \mathop{Proj}_{\mathcal{C}}(\{w_i\}_{i \in S}) \enspace\text{where}\enspace \mathcal{C} = \{ \{v_i \in \mathbb{R}^d\}_{i \in S} \mid \sum_{i \in S} v_i = \mathbf{0}\}

y_i \leftarrow y_i - \eta \hat w_i

Each selected client computes dual gradient and upload to server

Server adjusts the gradients (to keep feasibility) and broadcasts to selected clients

Each selected client locally updates the dual model

Convergence Rate

Strong convexity

f_i(x) \geq f_i(y) + \langle \nabla f_i(y), x-y \rangle + \frac{\alpha}{2}\|x-y\|^2 \quad \forall i, x, y

Smoothness

f_i(x) \leq f_i(y) + \langle \nabla f_i(y), x-y \rangle + \frac{\beta}{2}\|x-y\|^2 \quad \forall i,x,y

Data heterogeneity

\|\nabla f_i(w^*)\| \leq \zeta \quad \forall i

Theorem

\mathbb{E}[ G(y^T) - G(y^*) ] \leq (1 - \frac{\tau - 1}{N - 1}\frac{\alpha}{\beta})^T (G(y^0) - G(y^*))

[Necoara et al.'17]

and

\mathbb{E}[ \|w^T - w^*\|^2 ] \leq \frac{1}{\alpha^2}(1 - \frac{\tau - 1}{N - 1}\frac{\alpha}{\beta})^T \zeta^2

[Fan et al.'22]

Inexact FedDCE

w_i^t \red{\approx} \nabla f_i^*(y_i^t) \coloneqq \mathop{argmin}\limits_{w\in \mathbb{R}^d} \{ f_i(w) - \langle w, y_i^t \rangle \}

Each selected client approximately computes dual gradient and upload to server

\red{ \mathbb{E}[ \|w_i^t - \nabla f_i(y_i^t)\| ] \leq \delta \|w_i^{t-1} - \nabla f_i(y_i^t)\| }

Theorem

\mathbb{E}[ G(y^T) - G(y^*) ] \leq (1 - \kappa)^T (G(y^0) - G(y^*))

and

\mathbb{E}[ \|w^T - w^*\|^2 ] \leq \frac{20}{3\alpha^2}(1 - \kappa)^T \zeta^2

[Fan et al.'22]

\kappa = \frac{\alpha(\tau - 1)}{32\beta(N-1)}, \quad \delta = \frac{1-\kappa}{4}

with

Accelerated FedDCD

Random coordinate descent with Nesterov's acceleration has been widely studied [Nestrov'12; Lee & Sidford'13; Allen Zhu et al.'16; Lu et al.'18]

Only applied for unconstrained problem. We extend [Lu et al.'18] to linear constrained problem.

Theorem

\mathbb{E}[ G(y^T) - G(y^*) ] \leq (1 - \kappa)^T (G(y^0) - G(y^*))

and

\mathbb{E}[ \|w^T - w^*\|^2 ] \leq \frac{1}{\alpha^2}(1 - \kappa)^T \zeta^2

[Fan et al.'22]

\kappa = \frac{\sqrt{\alpha / \beta}}{(N-1)/(\tau - 1) + \sqrt{\alpha / \beta}}

with

Comparasion

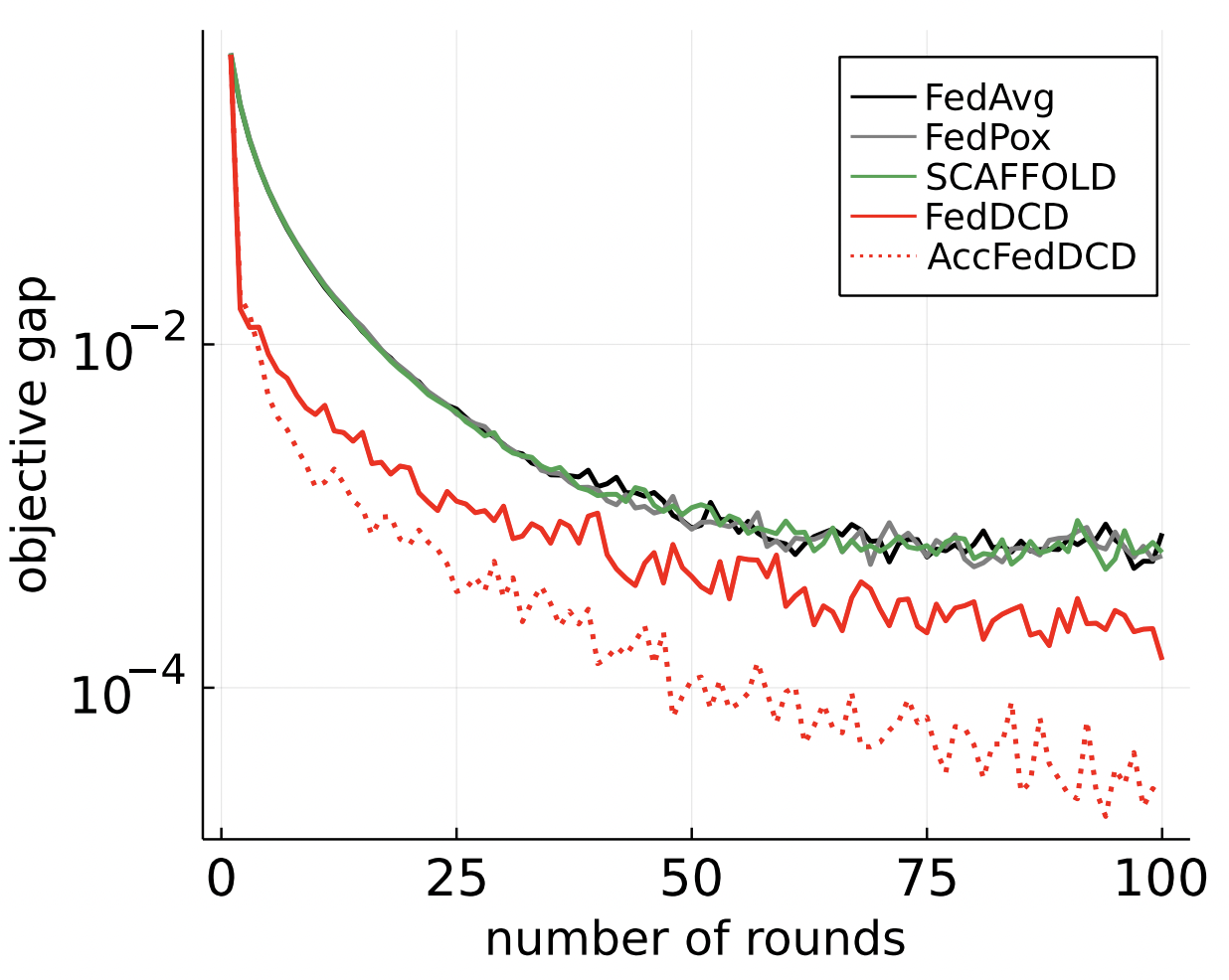
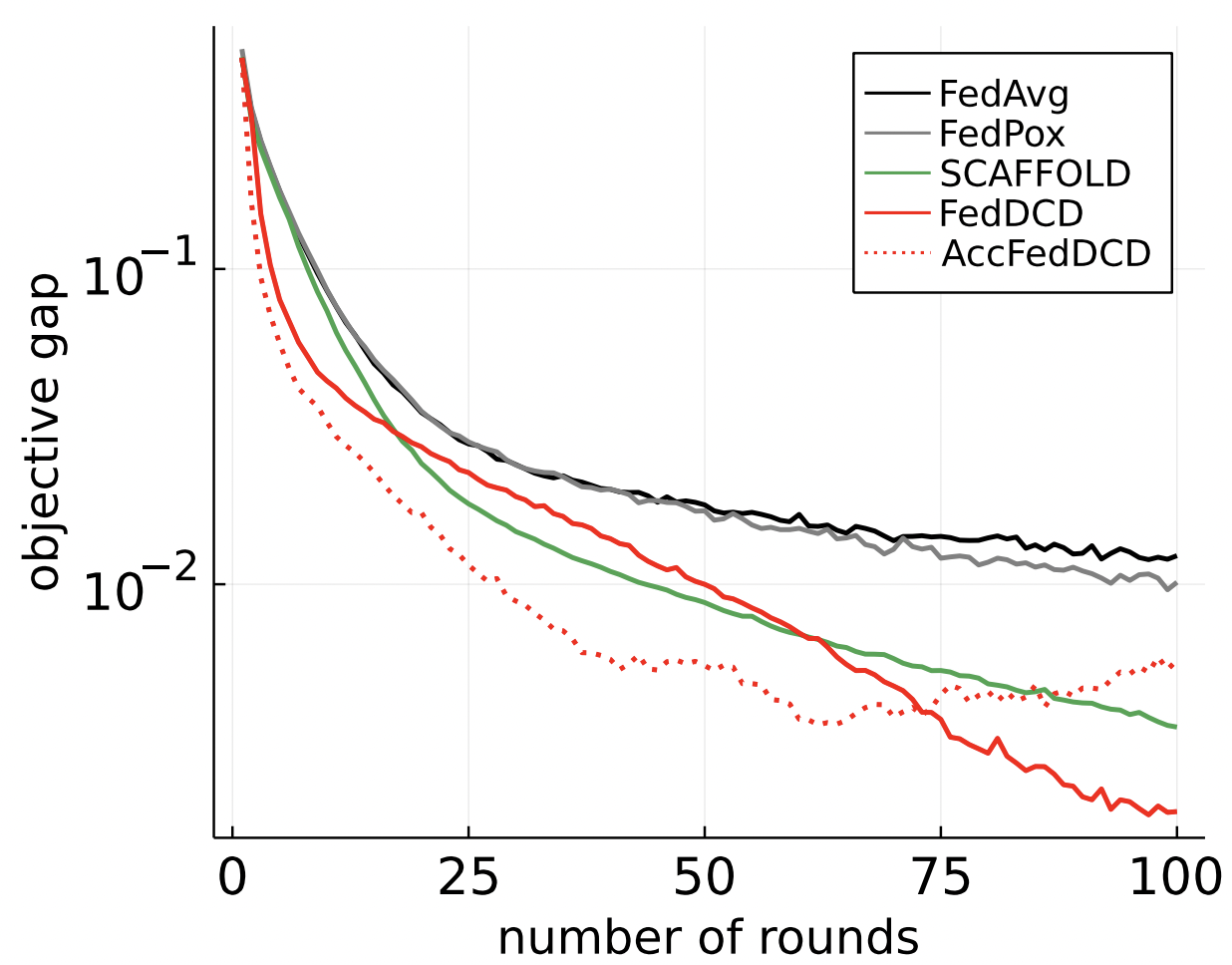
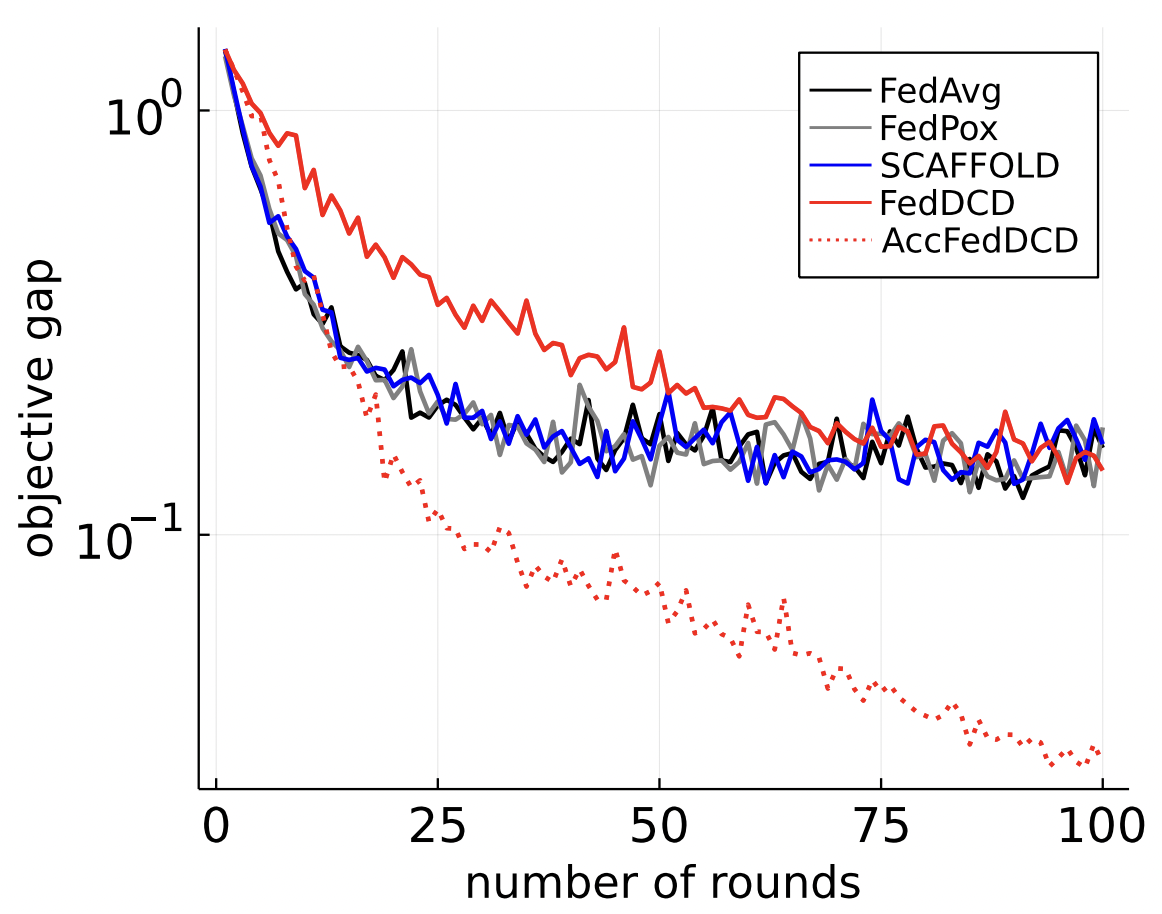
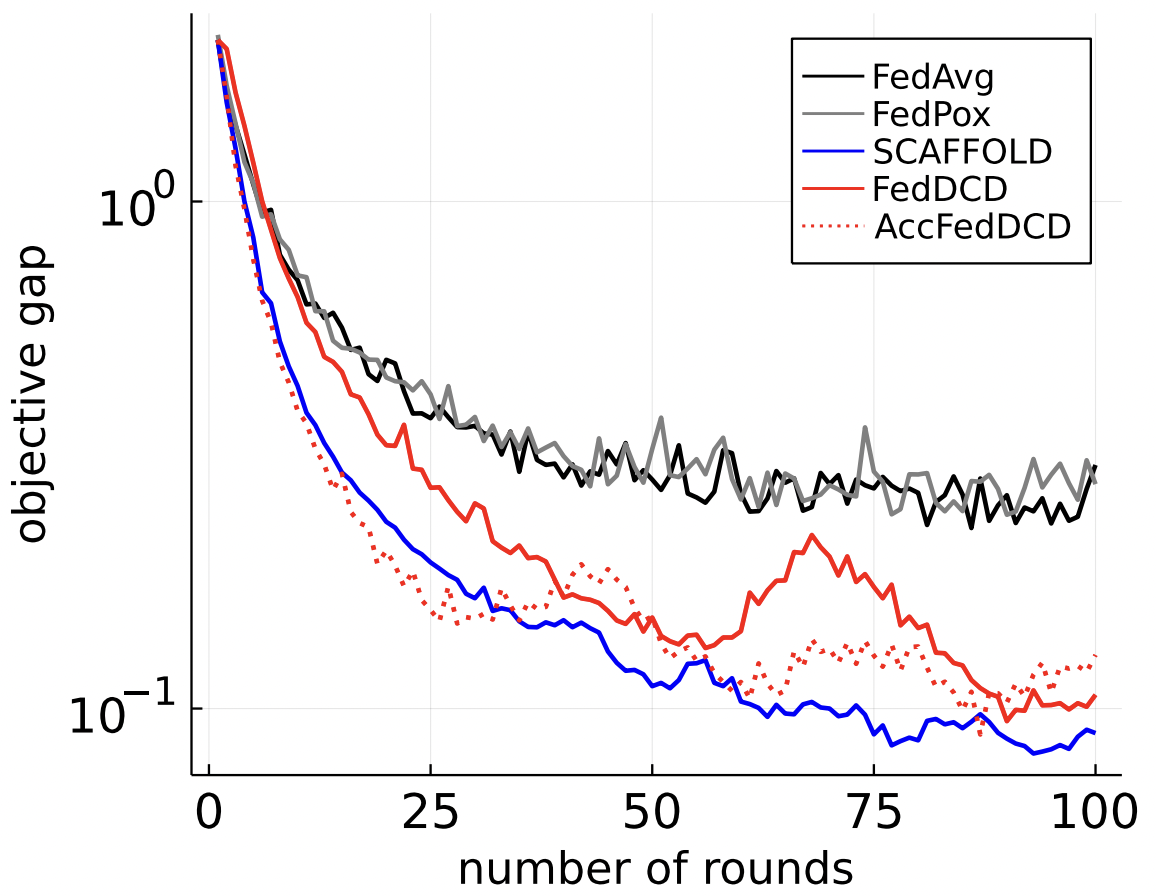
i.i.d

non-i.i.d