Polar Alignment
and
Primal Retrieval
Zhenan Fan
Department of Computer Science
Collaborators:
Huang Fang, Yifan Sun, Halyun Jeong, Michael Friedlander

Atomic Decomposition
[Chen, Donoho & Sauders'01; Chandrasekaran et al.'12]
- sparse n-vectors
-
low-rank matrices
x = \sum_j c_j e_j \quad \mathcal{A} = \{\pm e_1, \dots, \pm e_n\}
X = \sum_j c_ju_jv_j^T \quad \mathcal{A} = \{uv^T \mid \|u\| = \|v\| = 1\}
How do we identify the support of a vector x with respect to an arbitrary atomic set A?
cardinality
x = \sum\limits_{j=1}^\purple{\large r} \blue{c_j} a_j, \quad \green{a_j} \in \red{\mathcal{A}}
atomic set
weight
atom

Gauge and Support Functions
Gauge function
\gamma_{\mathcal{A}}(x) =
\inf\left\{ \sum\limits_{a\in\mathcal{A}}c_a ~\big\vert~ x = \sum\limits_{a\in\mathcal{A}} c_a a, c_a \geq 0 \right\}
Support function
\sigma_{\mathcal{A}}(z) =
\sup\left\{ \langle a, z \rangle ~\big\vert~ a \in \mathcal{A} \right\}
\mathop{epi} \gamma_\mathcal{A} = \mathop{cone}( \mathcal{A} \times \{1\})
\mathop{epi} \sigma_\mathcal{A} = \mathop{cone}( \mathcal{A}^\circ \times \{1\})

Polar Alignment
Polar inequality
\langle x, z \rangle \leq \gamma_\mathcal{A}(x) \cdot \sigma_\mathcal{A}(z)
\quad
\forall (x, z) \in \mathop{dom}\gamma_\mathcal{A} \times \mathop{dom}\sigma_\mathcal{A}
Alignment
(x, z) \enspace\text{is}\enspace \mathcal{A}-\text{aligned}
\iff
\langle x, z \rangle = \gamma_\mathcal{A}(x) \cdot \sigma_\mathcal{A}(z)
(x, z) \enspace\text{is}\enspace \mathcal{A}-\text{aligned} \Rightarrow
\underbrace{ \mathop{supp}(\mathcal{A}, x) }_{\red{ \{a \in \mathcal{A} ~\mid~ a \text{ exists in the decomposition of } x\}}}
\subseteq
\underbrace{ \mathop{face}(\mathcal{A}, z)}_{\red{ \{a \in \mathcal{A} ~\mid~ \langle a, z \rangle = \sigma_\mathcal{A}(z)\}}}
Theorem

Examples
\mathcal{A} = \{\pm e_1, \dots, \pm e_n\}
\mathop{face}(\mathcal{A}, z) = \{ \mathop{sgn}(z_i)\cdot e_i ~\mid~ |z_i| = \max_j |z_j| \}
\mathop{supp}(\mathcal{A}, x) = \{ \mathop{sgn}(x_i)\cdot e_i ~\mid~ x_i \neq 0 \}
Sparse vector
Low-rank Matrix
\mathcal{A} = \{uv^T \mid \|u\| = \|v\| = 1\}
\mathop{supp}(\mathcal{A}, X) = \{ u_1v_1^T, \dots, u_rv_r^T \}
X has rank r
\mathop{face}(\mathcal{A}, Z) = \{ u_1v_1^T, \dots, u_dv_d^T \}
largest singular value of Z has multiplicity d

Alignment in Structured Optimization
\min\limits_x \enspace f(Mx) + \rho\gamma_\mathcal{A}(x)
\min\limits_x \enspace f(Mx)
\enspace\text{subject to}\enspace
\gamma_\mathcal{A}(x) \leq \tau
\min\limits_x \enspace \gamma_\mathcal{A}(x)
\enspace\text{subject to}\enspace
f(Mx) \leq \alpha
(P1)
(P2)
(P3)
Theorem
(x^*, M^Ty^*) \enspace\text{is}\enspace \mathcal{A}-\text{aligned}
\quad\text{where}\quad
y^* = \nabla f(Mx^*)
(y* is same as optimal dual variable up to proper scaling.)

Extension to Sum of Sets
Theorem
\mathcal{A} = \sum\limits_{i=1}^k \mathcal{A}_i
\enspace\text{and}\enspace
\{x_i^*\}_{i=1}^k \in \argmin\limits_{x_1,\dots,x_k}\left\{ \max\limits_{i=1,\dots,k} \gamma_{\mathcal{A}_i}(x_i) \mid \sum\limits_{i=1}^k x_i = x^*\right\}
\Rightarrow
(x_i^*, M^Ty^*) \enspace\text{is}\enspace \mathcal{A}_i-\text{aligned}
\min\limits_x \enspace f(Mx) + \rho\gamma_\mathcal{A}(x)
\min\limits_x \enspace f(Mx)
\enspace\text{subject to}\enspace
\gamma_\mathcal{A}(x) \leq \tau
\min\limits_x \enspace \gamma_\mathcal{A}(x)
\enspace\text{subject to}\enspace
f(Mx) \leq \alpha
(P1)
(P2)
(P3)

Cardinality-Constrained Data-Fitting
Assumption
x^* \in \argmin\limits_x \enspace \gamma_\mathcal{A}(x)
\enspace\text{subject to}\enspace
\|Mx - b\| \leq \alpha
\text{Find}\enspace x \in \mathcal{X}
\enspace\text{such that}\enspace
\red{ \mathop{card}(\mathcal{A}, x) } \leq k
\enspace\text{and}\enspace
\|Mx - b\| \leq \alpha
(P)
is feasible to (P)
\red{ \inf\{ \mathop{nnz}(c) \mid x = \sum_{a \in \mathcal{A}} c_a a, \enspace c_a \geq 0\} }
Dual problem
\mathop{min}\limits_{\tau \in \mathbb{R}_+, y \in \mathcal{Y}}\enspace
\tau \enspace\text{s.t.}\enspace
(y, \tau) \in \mathop{cone}(M\mathcal{A} \times \{1\})
\enspace\text{and}\enspace y \in \mathbb{B}_2(b, \alpha)
Goal retrieve a primal variable near-feasible to (P) from a near-optimal dual variable

Primal Retrieval
Essential Cone of Atoms
\mathop{EssCone}_{\mathcal{A}, k}(M^*y) \in \{x \mid \mathop{card}(\mathcal{A}, x) \leq k\}
Primal retrieval
x_y \in \argmin\limits_{x} \|Mx - b\|
\enspace\text{subject to}\enspace
x \in \mathop{EssCone}_{\mathcal{A}, k}(M^*y)
(PR)
Key Idea
\mathop{card}(\mathcal{A}, x_y) \leq k
(PR) is easy to solve when k is small
x_{y^*}
is feasible to (P)

Polyhedral Atomic Set
\mathop{EssCone}_{\mathcal{A}, k}(M^*y) = \mathop{cone} \red{ \mathcal{A}_k }
\red{
\mathcal{A}_k = \{a_i\}_{i=1}^k \subseteq \mathcal{A}
\enspace\text{such that}\enspace
\langle M^*y, a_i \rangle \geq \langle M^*y, a \rangle
\enspace \forall a \in \mathcal{A} \setminus \{a_i\}_{i=1}^k
}
x_y = \sum\limits_{i=1}^k \hat c_i a_i
\enspace\text{with}\enspace
\hat c \in \argmin\limits_{\red{ c \geq 0 }}\enspace \|M\sum_{i=1}^k c_ia_i - b \|
(PR)
can be removed when A is symmetric
Theorem
Suppose the primal problem is non-degenerate
\red{ ( a \in \mathop{supp}(\mathcal{A}, x^*)
\enspace\text{or}\enspace
\langle a, M^*y^* \rangle \leq \sigma_\mathcal{A}(M^*y^*) - \delta) }
\red{\epsilon_y} \in \mathcal{O}(\sqrt{\delta})
\Rightarrow
\mathop{card}(\mathcal{A}, x) \leq k
\enspace\text{and}\enspace
\|Mx - b\| \leq \alpha
(duality gap)

Experiment: Basis Pursuit Denoise
\text{Find}\enspace x \in \mathbb{R}^n
\enspace\text{such that}\enspace
\mathop{nnz}(x) \leq k
\enspace\text{and}\enspace
\|Mx - b\| \leq \alpha
(P)
Test problems from Sparco [van den Berg et al.'09]


Spectral Atomic Set
\mathcal{A} = \{uv^T \mid \|u\| = \|v\| = 1\}
\enspace\text{and}\enspace
M^*(Y) =
\begin{bmatrix}
U_k & U_{-k}
\end{bmatrix}
\begin{bmatrix}
\Sigma_k & \\
& \Sigma_{-k}
\end{bmatrix}
\begin{bmatrix}
V_k^T \\
V_{-k}^T
\end{bmatrix}
\mathop{EssCone}_{\mathcal{A}, k}(M^*y) = \mathop{cone} \red{ \mathcal{A}_k } = \{U_k C V_k^T \mid C \in \mathbb{R}^{k\times k}\}
\red{
\mathcal{A}_k = \{ uv^T | u\in\mathop{range}(U_k),\ v\in\mathop{range}(V_k),\ \|u\| =\|v\| =1 \} \subset \mathcal{A}
}
X_Y = U_k \hat C V_k^T
\enspace\text{with}\enspace
\hat C \in \argmin\limits_{C \in \mathbb{R}^{k\times k}}\enspace \|M( U_k C V_k^T) - b \|
(PR)
Theorem
\mathop{rank}(X_Y) \leq k
\enspace\text{and}\enspace
\|M(X_Y) - b\| \leq \alpha + \mathcal{O}(\sqrt{\epsilon_Y})

Experimet: Low-Rank Matrix Completion
\text{Find}\enspace X \in \mathbb{R}^{m\times n}
\enspace\text{such that}\enspace
\mathop{rank}(x) \leq k
\enspace\text{and}\enspace
\sum\limits_{(i,j)\in\Omega} \frac{1}{2}(X_{i,j} - B_{i,j})^2 \leq \alpha
(P)
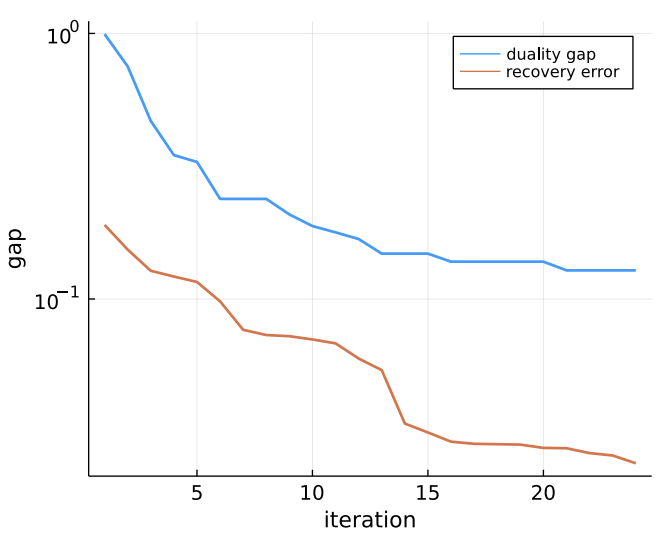
Simiar experiment as in [Candès & Plan'10]
X^\natural \in \mathbb{R}^{6798\times 366}
( from National Centers for Environmental Information)
X^\natural
is approximately low-rank
We subsample 50% of
X^\natural