Duality in
Structured and Federated Optimization
Zhenan Fan
Department of Computer Science
Supervisor: Michael P. Friedlander
September 14th, 2022
Outline
1
Duality
in
Optimization
Structured
Optimization
Federated
Learning
2
3
Duality in Optimization
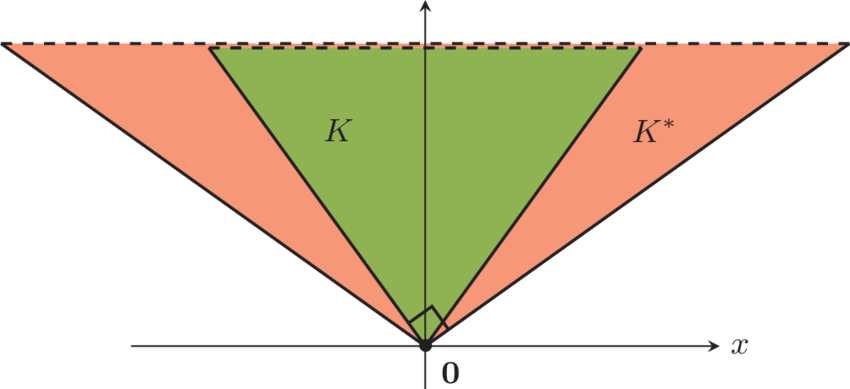
Primal and Dual
Optimization is everywhere
-
machine learning
-
signal processing
-
data mining
p^* = \mathop{min}\limits_{x \in \mathcal{X}}\enspace f(x)
Primal problem
Dual problem
d^* = \max\limits_{y \in \mathcal{Y}} \enspace g(y)
Weak duality
p^* \geq d^*
(always hold)
Strong duality
p^* = d^*
(Under some domain qualification)
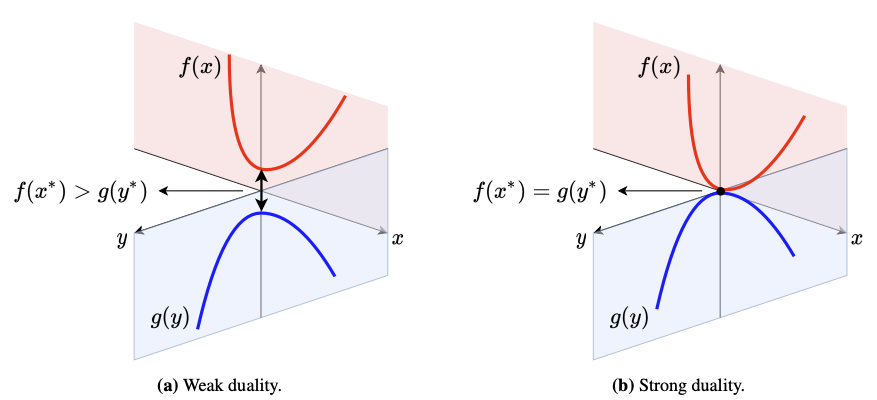
Dual Optimization
Possible advantages
-
parallelizable [Boyd et al.'11] -
better convergence rate [Shalev-Shwartz & Zhang.'13] -
smaller dimension [Friedlander & Macêdo'16]
Possible dual formulations
-
Fenchel-Rockafellar dual [Rockafellar'70] -
Lagrangian dual [Boyd & Vandenberghe'04] -
Gauge dual [Friedlander, Macêdo & Pong'04]
(All these different dual formulations can be intepreted using the perturbation framework proposed by [Rockafellar & Wets'98])
Structured Optimization
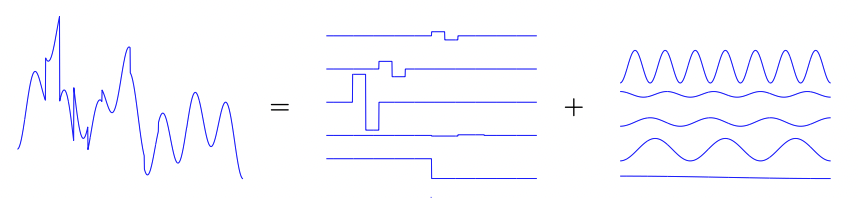
Structured Data-Fitting
Atomic decomposition: mathematical modelling for structure
[Chen, Donoho & Sauders'01; Chandrasekaran et al.'12]
\text{Find}\enspace \purple{x_1,\dots,x_k} \in \mathcal{X} \enspace\text{such that}\enspace \red{M}(\sum_{i=1}^k x_i)
\approx \blue{b} \enspace\text{and}\enspace
x_i \text{ is \green{structured} }\enspace \forall i
linear map
observation
sparse low-rank smooth
variables
x = \sum\limits_{j=1}^\purple{\large r} \blue{c_j} a_j, \quad \green{a_j} \in \red{\mathcal{A}}
cardinality
weight
atom
atomic set
- sparse n-vectors
-
low-rank matrices
x = \sum_j c_j e_j \quad \mathcal{A} = \{\pm e_1, \dots, \pm e_n\}
X = \sum_j c_ju_jv_j^T \quad \mathcal{A} = \{uv^T \mid \|u\| = \|v\| = 1\}
\green{
x_i \text{ is sparse with respect to } \mathcal{A}_i
}
Example: Separating Stars and Galaxy
b
x_1
x_2
\mathcal{A}_1 = \{\pm e_ie_j^T \}
\mathcal{A}_2 = \{ \mathop{DCT}(\pm e_ie_j^T) \}
[Chen, Donoho & Sauders'98; Donoho & Huo'01]
Example: Separating Chessboard and Chess
b
x_1
x_2
\mathcal{A}_1 = \{\pm e_ie_j^T \}
\mathcal{A}_2 = \{uv^T \mid \|u\| = \|v\| = 1\}
[Chandrasekaran et al.'09; Candès et al.'09]
Example: Multiscale Low-rank Decomposition
b
x_1
x_2
x_3
x_4
\mathcal{A}_i = \{uv^T \mid u, v \in \mathbb{R}^{4^{i-1}}, \|u\| = \|v\| = 1\}
[Ong & Lustig'16]
Roadmap
Convex relaxation with guarantee
Primal-dual relationship and dual-based algorithm
Efficient primal-retrieval strategy
Fan, Z., Jeong, H., Joshi, B., & Friedlander, M. P. Polar Deconvolution of Mixed Signals. IEEE Transactions on Signal Processing (2021).
Fan, Z., Jeong, H., Sun, Y., & Friedlander, M. P. Atomic decomposition via polar alignment: The geometry of structured optimization. Foundations and Trends® in Optimization (2020).
Fan, Z., Fang, H. & Friedlander, M. P. Cardinality-constrained structured data-fitting problems. Submitted (2022).
Convex Relaxation
Gauge function: sparsity-inducing regularizer [Chandrasekaran et al.'12]
\gamma_{\mathcal{A}}(x) =
\inf\left\{ \sum\limits_{a\in\mathcal{A}}c_a ~\big\vert~ x = \sum\limits_{a\in\mathcal{A}} c_a a, c_a \geq 0 \right\}
Examples
- sparse n-vectors
-
low-rank matrices
\mathcal{A} = \{\pm e_1, \dots, \pm e_n\} \quad \gamma_{\mathcal{A}}(x) = \|x\|_1
\mathcal{A} = \{uv^T \mid \|u\| = \|v\| = 1\} \quad \gamma_{\mathcal{A}}(X) = \|X\|_*
Structured convex optimization [FJJF, IEEE-TSP'21]
\{x_i^*\}_{i=1}^k \in \mathop{argmin}\limits_{x_1, \dots, x_k}
\left\{ \red{ \max\limits_{i=1,\dots,k} \frac{1}{\lambda_i}\gamma_{\mathcal{A}_i}(x_i) }
~\big\vert~ \blue{ \|M(\sum_{i=1}^k x_i) - b\| \leq \alpha} \right\}
Minimizing gauge function can promote atomic sparsity!
structure assumption
data-fitting constraint
Recovery Guarantee
b = M(\sum_{i=1}^k x_i^\natural) + \eta \in \mathcal{Y}, \quad
x_i^\natural \enspace\text{is}\enspace \mathcal{A}_i-\text{sparse}, \quad
\|\eta\| \leq \alpha, \quad
\lambda_i = \gamma_{\mathcal{A}_1}(x_1^\natural)/\gamma_{\mathcal{A}_i}(x_i^\natural)
Theorem [FJJF, IEEE-TSP'21]
If the ground-truth signals are incoherent and the measurement are gaussian, then with high probability
\|x_i^* - x_i^\natural\| \leq 4\alpha[\sqrt{\mathop{dim}(\mathcal{Y})} - \Delta], \quad \forall i = 1,\dots,k
Primal-dual Correspondence
Primal problem
\mathop{min}\limits_{x_1, \dots, x_k \in \mathcal{X}}\enspace
\max\limits_{i=1,\dots,k} \gamma_{\lambda_i\mathcal{A}_i}(x_i)
\enspace\text{s.t.}\enspace \|M(\sum_{i=1}^k x_i) - b\| \leq \alpha
\mathcal{O}(k\cdot\mathop{dim}(\mathcal{X})) \enspace\text{storage}
Dual problem
\mathop{min}\limits_{\tau \in \mathbb{R}_+, y \in \mathcal{Y}}\enspace
\tau \enspace\text{s.t.}\enspace
(y, \tau) \in \mathop{cone}(M\mathcal{A} \times \{1\})
\enspace\text{and}\enspace y \in \mathbb{B}_2(b, \alpha)
\enspace\text{with}\enspace \mathcal{A} = \sum_{i=1}^k \lambda_i\mathcal{A}_i
\mathcal{O}(\mathop{dim}(\mathcal{Y})) \enspace\text{storage}
Theorem [FSJF, FNT-OPT'21]
Let
\{x_i^*\}_{i=1}^k
y^*
and
denote optimal primal and dual solutions. Under mild assumptions,
\underbrace{ \mathop{supp}(\mathcal{A}_i, x_i^*) }_{\red{ \{a \in \mathcal{A}_i ~\mid~ a \text{ exists in the decomposition of } x_i^*\}}}
\subseteq
\underbrace{ \mathop{face}(\mathcal{A}_i, z^* \coloneqq M^*(b - y^*))}_{\red{ \{a \in \mathcal{A}_i ~\mid~ \langle a, z^* \rangle \geq \langle \hat a, z^* \rangle \enspace \forall \hat a \in \mathcal{A}_i\}}}
Dual-based Algorithm
y^{k+1} \leftarrow \mathop{Proj}_{\tau^kM\mathcal{A}}(y^k)
\tau^{k+1} \leftarrow \tau^{k} + \frac{\|y^{k+1} - b\| - \alpha}{\sigma_{M\mathcal{A}}(y^{k+1})}
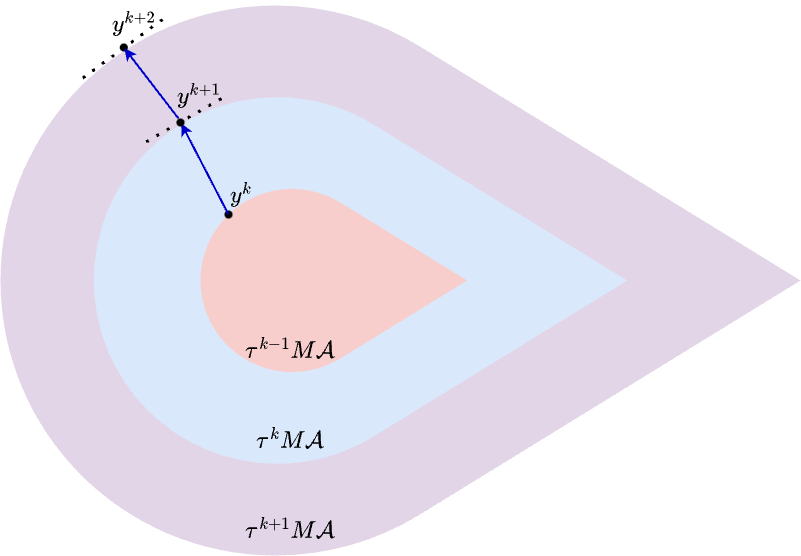
(Projection can be computed approximately using Frank-Wolfe.)
Complexity
\mathcal{O}(\log(1 / \epsilon))
projection steps
or
\mathcal{O}(\log(1 / \epsilon) / \epsilon)
Frank-Wolfe steps
A variant of the level-set method developed by [Aravkin et al.'18]
Primal-retrieval Strategy
Can we retrieve primal variables from near-optimal dual variable?
\{\hat x_i\}_{i=1}^k \in \mathop{argmin}\limits_{x_1, \dots, x_k \in \mathcal{X}}
\left\{
\|M(\sum_{i=1}^k x_i) - b\|
~\big\vert~
\mathop{supp}(\mathcal{A}_i; x_i) \in \mathop{face}(\mathcal{A}_i, M^*y)
\right\}
Theorem [FFF, Submitted'22]
\epsilon
Let
denote the duality gap. Under mild assumptions,
\mathop{cardinality}(\mathcal{A}_i; \hat x_i) \approx \mathop{cardinality}(\mathcal{A}_i; x_i^*) \enspace \forall i
\enspace\text{and}\enspace
\|M(\sum_{i=1}^k \hat x_i) - b\| \leq \alpha + \mathcal{O}(\sqrt{\epsilon})
Open-source Package https://github.com/MPF-Optimization-Laboratory/AtomicOpt.jl
(equivalent to unconstrained least square when atomic sets are symmetric)
Federated Learning
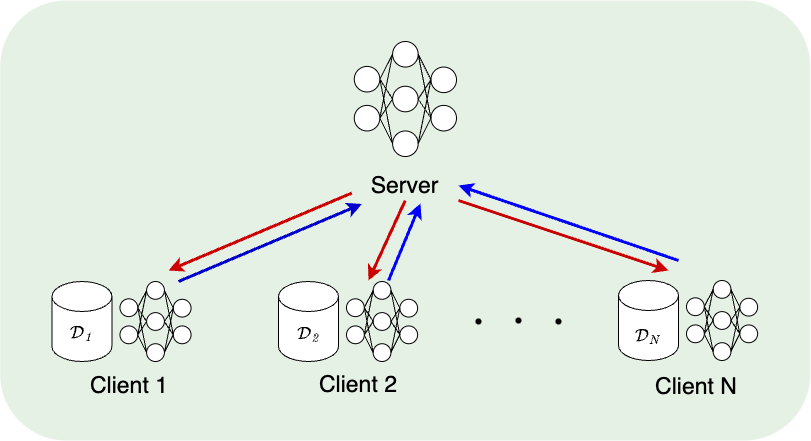
Motivation
Setting
Definition
Federated learning is a collaborative learning framework that can keep data sets private.
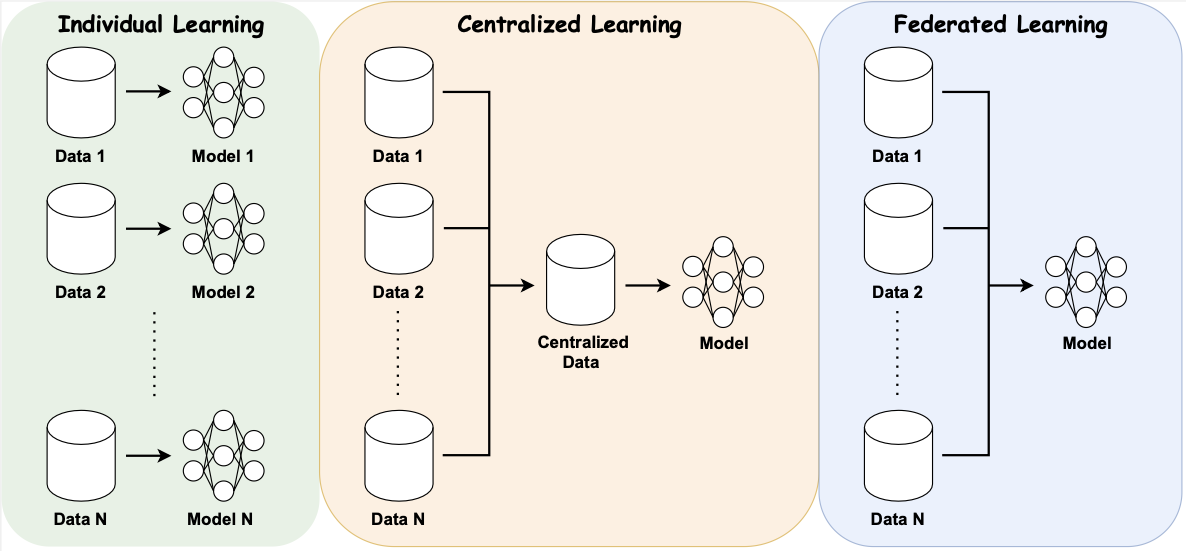
Decentralized data sets, privacy concerns
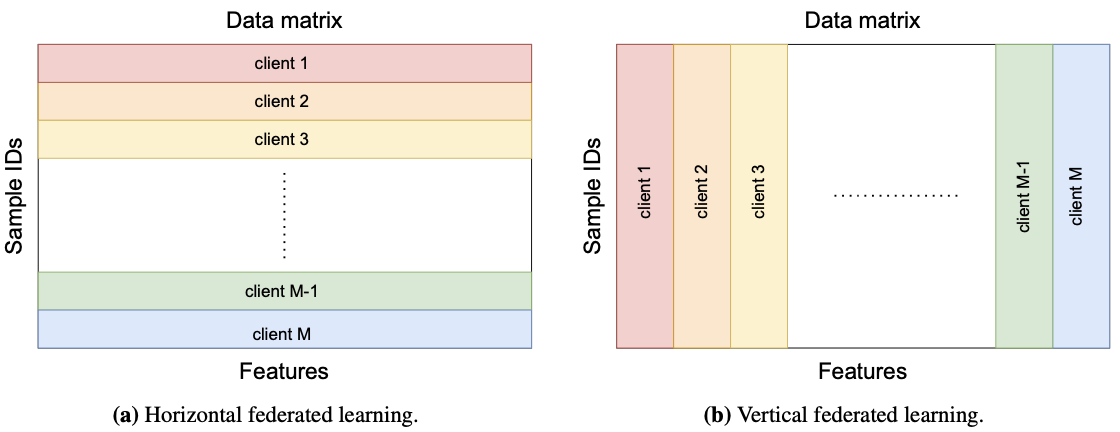
Horizontal and Vertical Federated Learning
Roadmap
Dual-based algorithm for federated optimization
Contribution valuation in federated learning
Fan, Z., Fang, H., Zhou, Z., Pei, J., Friedlander, M. P., Liu, C., & Zhang, Y. Improving Fairness for Data Valuation in Horizontal Federated Learning. IEEE International Conference on Data Engineering (ICDE 2022).
Fan, Z., Fang, H., Zhou, Z., Pei, J., Friedlander, M. P., & Zhang, Y. Fair and efficient contribution valuation for vertical federated learning. Submitted (2022).
Fan, Z., Fang, H. & Friedlander, M. P. FedDCD: A Dual Approach for Federated Learning. Submitted (2022).
Federated Optimization
Important features of federated optimization
-
communication efficiency
-
data privacy
-
data heterogeneity
-
computational constraints
\mathop{min}\limits_{w \in \mathbb{R}^d}\enspace F(\red{w}) \coloneqq \sum\limits_{i=1}^\blue{N} f_i(w)
\enspace\text{with}\enspace
f_i(w) \coloneqq \frac{1}{|\mathcal{D}_i|} \sum\limits_{(x, y) \in \green{\mathcal{D}_i} } \purple{\ell}(w; x, y)
model
number of clients
local dataset
loss function
Primal-based Algorithm
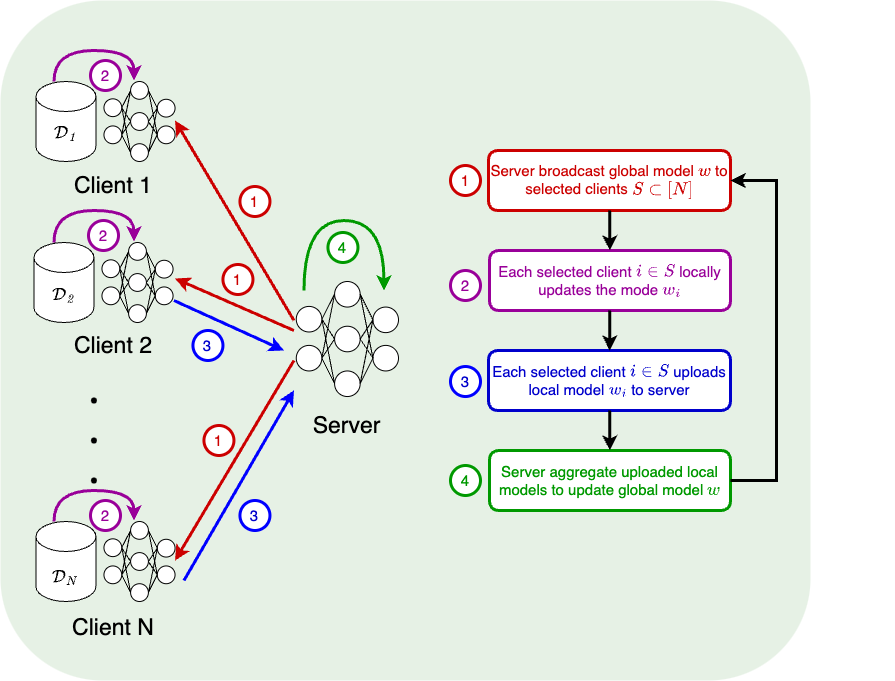
FedAvg [McMahan et al.'17]
w_i \leftarrow w_i - \eta \tilde \nabla f_i(w_i) \quad (K \text{ times})
w \leftarrow \frac{1}{|S|}\sum_{i \in S} w_i
SCAFFOLD [Karimireddy et al.'20]
w_i \leftarrow w_i - \eta (\tilde \nabla f_i(w_i) - c_i + c) \quad (K \text{ times})
c_i \leftarrow \tilde \nabla f_i(w), \enspace
c \leftarrow \frac{1}{|S|}\sum_{i \in S} c_i, \enspace
w \leftarrow \frac{1}{|S|}\sum_{i \in S} w_i
Dual-based Algorithm
\mathop{min}\limits_{y_1, \dots, y_N \in \mathbb{R}^d}\enspace G(\mathbf{y}) \coloneqq \sum\limits_{i=1}^N \red{f_i^*}(y_i)
\enspace\text{subject to}\enspace
\sum_{i=1}^N \blue{y_i} = \mathbf{0}
Federated dual coordinate descent (FedDCD) [FFF, Submitted'22]
w_i \approx \nabla f_i^*(y_i) \coloneqq \mathop{argmin}\limits_{w\in \mathbb{R}^d} \{ f_i(w) - \langle w, y_i \rangle \}
\{\hat w_i\}_{i \in S} = \mathop{Proj}_{\mathcal{C}}(\{w_i\}_{i \in S})
\enspace\text{where}\enspace \mathcal{C} = \{ \{v_i \in \mathbb{R}^d\}_{i \in S} \mid \sum_{i \in S} v_i = \mathbf{0}\}
y_i \leftarrow y_i - \eta \hat w_i
Each selected client approximately compute dual gradient and upload to server
Server adjusts the gradients (to keep feasibility) and broadcasts to selected clients
Each selected client locally updates the dual model
(A extension of [Necoara et al.'17]: inexact gradient, acceleration)
conjugate function
local dual model
Communication Rounds
Setting
\alpha-\text{strongly convex}, ~\beta-\text{smooth}, ~\zeta-\text{data heterogeneous}, ~\sigma-\text{gradient variance}
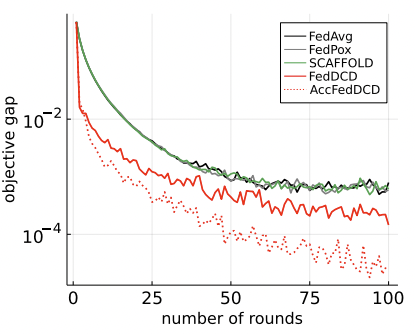
Open-source Package https://github.com/ZhenanFanUBC/FedDCD.jl
Contribution Valuation
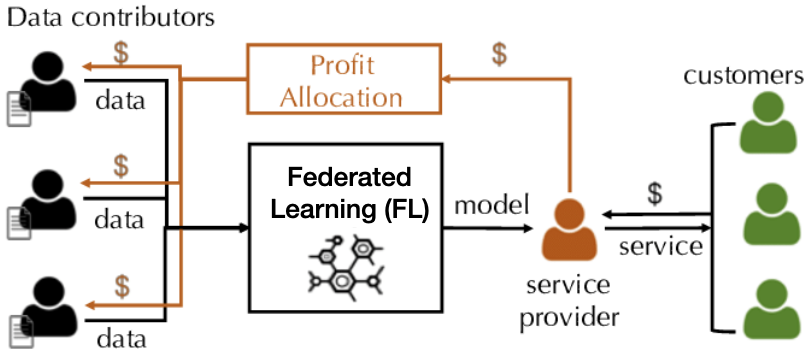
Key requirement
1. Data owners with similar data should receive similar valuation. 2. Data owners with unrelated data should receive low valuation.
Shapley Value
Shapley value is a measure for players' contribution in a game.
v(\red{i}) = \frac{1}{N} \sum\limits_{S \subseteq [N] \setminus \{i\}} \frac{1}{ N-1 \choose |S|}
[U(S \cup \{i\}) - \blue{U(S)}]
Advantage
It satisfies many desired fairness axioms.
Drawback
Computing utilities requires retraining the model.
Previous work
[Wang et al.'20] propose to compute Shapley value in each communication round, which eliminates the requirement of retraining the model.
New drawback
Random selection will cause potential unfairness.
player i
utility created by players in S
marginal utility gain
Our Contribution
[FFZPFLZ, ICDE'22]
We propose a method to improve the fairness. The key idea is to complete a matrix consisting of all the possible contributions by different subsets of the data owners.
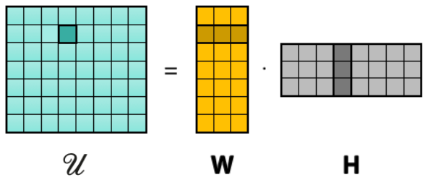
[FFZPFZ, Submitted'22]
We extend this framework to vertical federated learning. (can also be used to determine feature importance)
These two works are partly done during my internship at Huawei Canada. Our code is publicly available at Huawei AI Gallery.
Acknowledgement
Supervisor
University Examiners
External Examiner
Supervisory Committee
Collaborators
