Duality in
Structured and Federated Optimization
Zhenan Fan
Microsoft Research Asia
November 22th, 2022
Outline
1
Duality
in
Optimization
Structured
Optimization
Federated
Learning
2
3
Duality in Optimization
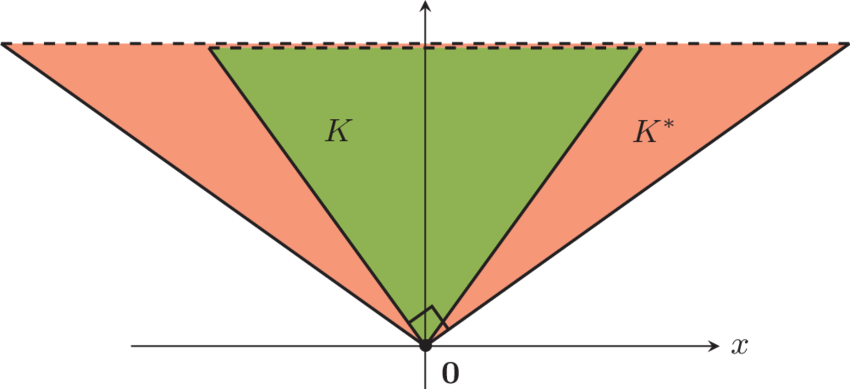
Primal and Dual
Optimization is everywhere
-
machine learning
-
signal processing
-
data mining
p^* = \mathop{min}\limits_{x \in \mathcal{X}}\enspace f(x)
Primal problem
Dual problem
d^* = \max\limits_{y \in \mathcal{Y}} \enspace g(y)
Weak duality
p^* \geq d^*
(always hold)
Strong duality
p^* = d^*
(Under some domain qualification)
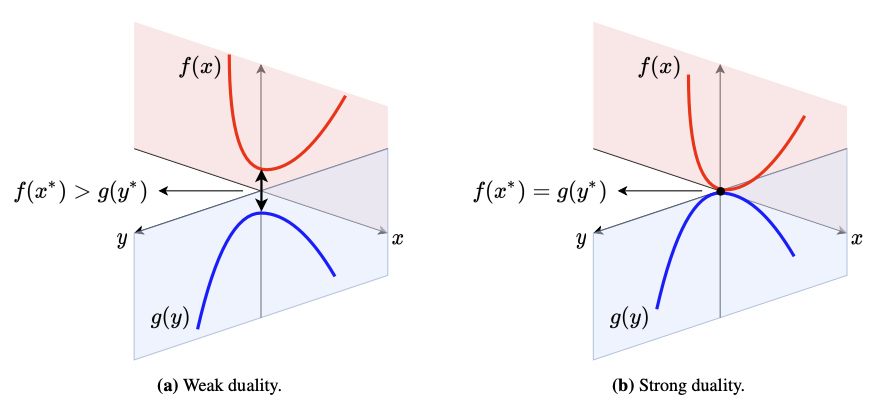
Dual Optimization
Possible advantages
-
parallelizable [Boyd et al.'11] -
better convergence rate [Shalev-Shwartz & Zhang.'13] -
smaller dimension [Friedlander & Macêdo'16]
Possible dual formulations
-
Fenchel-Rockafellar dual [Rockafellar'70] -
Lagrangian dual [Boyd & Vandenberghe'04] -
Gauge dual [Friedlander, Macêdo & Pong'04]
(All these different dual formulations can be intepreted using the perturbation framework proposed by [Rockafellar & Wets'98])
Structured Optimization
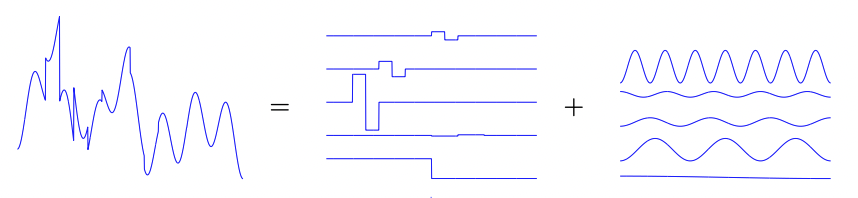
Structured Data-Fitting
Atomic decomposition: mathematical modelling for structure
[Chen, Donoho & Sauders'01; Chandrasekaran et al.'12]
\text{Find}\enspace \purple{x_1,\dots,x_k} \in \mathcal{X} \enspace\text{such that}\enspace \red{M}(\sum_{i=1}^k x_i)
\approx \blue{b} \enspace\text{and}\enspace
x_i \text{ is \green{structured} }\enspace \forall i
linear map
observation
sparse low-rank smooth
variables
x = \sum\limits_{j=1}^\purple{\large r} \blue{c_j} a_j, \quad \green{a_j} \in \red{\mathcal{A}}
cardinality
weight
atom
atomic set
- sparse n-vectors
-
low-rank matrices
x = \sum_j c_j e_j \quad \mathcal{A} = \{\pm e_1, \dots, \pm e_n\}
X = \sum_j c_ju_jv_j^T \quad \mathcal{A} = \{uv^T \mid \|u\| = \|v\| = 1\}
\green{
x_i \text{ is sparse with respect to } \mathcal{A}_i
}
Example: Separating Stars and Galaxy
b
x_1
x_2
\mathcal{A}_1 = \{\pm e_ie_j^T \}
\mathcal{A}_2 = \{ \mathop{DCT}(\pm e_ie_j^T) \}
[Chen, Donoho & Sauders'98; Donoho & Huo'01]
Example: Separating Chessboard and Chess
b
x_1
x_2
\mathcal{A}_1 = \{\pm e_ie_j^T \}
\mathcal{A}_2 = \{uv^T \mid \|u\| = \|v\| = 1\}
[Chandrasekaran et al.'09; Candès et al.'09]
Example: Multiscale Low-rank Decomposition
b
x_1
x_2
x_3
x_4
\mathcal{A}_i = \{uv^T \mid u, v \in \mathbb{R}^{4^{i-1}}, \|u\| = \|v\| = 1\}
[Ong & Lustig'16]
Roadmap
Convex relaxation with guarantee
Primal-dual relationship and dual-based algorithm
Efficient primal-retrieval strategy
Fan, Z., Jeong, H., Joshi, B., & Friedlander, M. P. Polar Deconvolution of Mixed Signals. IEEE Transactions on Signal Processing (2021).
Fan, Z., Jeong, H., Sun, Y., & Friedlander, M. P. Atomic decomposition via polar alignment: The geometry of structured optimization. Foundations and Trends® in Optimization (2020).
Fan, Z., Fang, H. & Friedlander, M. P. Cardinality-constrained structured data-fitting problems. To appear in Open Journal of Mathematical Optimization (2022).
Convex Relaxation
Gauge function: sparsity-inducing regularizer [Chandrasekaran et al.'12]
\gamma_{\mathcal{A}}(x) =
\inf\left\{ \sum\limits_{a\in\mathcal{A}}c_a ~\big\vert~ x = \sum\limits_{a\in\mathcal{A}} c_a a, c_a \geq 0 \right\}
Examples
- sparse n-vectors
-
low-rank matrices
\mathcal{A} = \{\pm e_1, \dots, \pm e_n\} \quad \gamma_{\mathcal{A}}(x) = \|x\|_1
\mathcal{A} = \{uv^T \mid \|u\| = \|v\| = 1\} \quad \gamma_{\mathcal{A}}(X) = \|X\|_*
Structured convex optimization [FJJF, IEEE-TSP'21]
\{x_i^*\}_{i=1}^k \in \mathop{argmin}\limits_{x_1, \dots, x_k}
\left\{ \red{ \max\limits_{i=1,\dots,k} \frac{1}{\lambda_i}\gamma_{\mathcal{A}_i}(x_i) }
~\big\vert~ \blue{ \|M(\sum_{i=1}^k x_i) - b\| \leq \alpha} \right\}
Minimizing gauge function can promote atomic sparsity!
structure assumption
data-fitting constraint
Recovery Guarantee
b = M(\sum_{i=1}^k x_i^\natural) + \eta \in \mathcal{Y}, \quad
x_i^\natural \enspace\text{is}\enspace \mathcal{A}_i-\text{sparse}, \quad
\|\eta\| \leq \alpha, \quad
\lambda_i = \gamma_{\mathcal{A}_1}(x_1^\natural)/\gamma_{\mathcal{A}_i}(x_i^\natural)
Theorem [FJJF, IEEE-TSP'21]
If the ground-truth signals are incoherent and the measurement are gaussian, then with high probability
\|x_i^* - x_i^\natural\| \leq 4\alpha[\sqrt{\mathop{dim}(\mathcal{Y})} - \Delta], \quad \forall i = 1,\dots,k
Primal-dual Correspondence
Primal problem
\mathop{min}\limits_{x_1, \dots, x_k \in \mathcal{X}}\enspace
\max\limits_{i=1,\dots,k} \gamma_{\lambda_i\mathcal{A}_i}(x_i)
\enspace\text{s.t.}\enspace \|M(\sum_{i=1}^k x_i) - b\| \leq \alpha
\mathcal{O}(k\cdot\mathop{dim}(\mathcal{X})) \enspace\text{storage}
Dual problem
\mathop{min}\limits_{\tau \in \mathbb{R}_+, y \in \mathcal{Y}}\enspace
\tau \enspace\text{s.t.}\enspace
(y, \tau) \in \mathop{cone}(M\mathcal{A} \times \{1\})
\enspace\text{and}\enspace y \in \mathbb{B}_2(b, \alpha)
\enspace\text{with}\enspace \mathcal{A} = \sum_{i=1}^k \lambda_i\mathcal{A}_i
\mathcal{O}(\mathop{dim}(\mathcal{Y})) \enspace\text{storage}
Theorem [FSJF, FNT-OPT'21]
Let
\{x_i^*\}_{i=1}^k
y^*
and
denote optimal primal and dual solutions. Under mild assumptions,
\underbrace{ \mathop{supp}(\mathcal{A}_i, x_i^*) }_{\red{ \{a \in \mathcal{A}_i ~\mid~ a \text{ exists in the decomposition of } x_i^*\}}}
\subseteq
\underbrace{ \mathop{face}(\mathcal{A}_i, z^* \coloneqq M^*(b - y^*))}_{\red{ \{a \in \mathcal{A}_i ~\mid~ \langle a, z^* \rangle \geq \langle \hat a, z^* \rangle \enspace \forall \hat a \in \mathcal{A}_i\}}}
Dual-based Algorithm
y^{k+1} \leftarrow \mathop{Proj}_{\tau^kM\mathcal{A}}(y^k)
\tau^{k+1} \leftarrow \tau^{k} + \frac{\|y^{k+1} - b\| - \alpha}{\sigma_{M\mathcal{A}}(y^{k+1})}
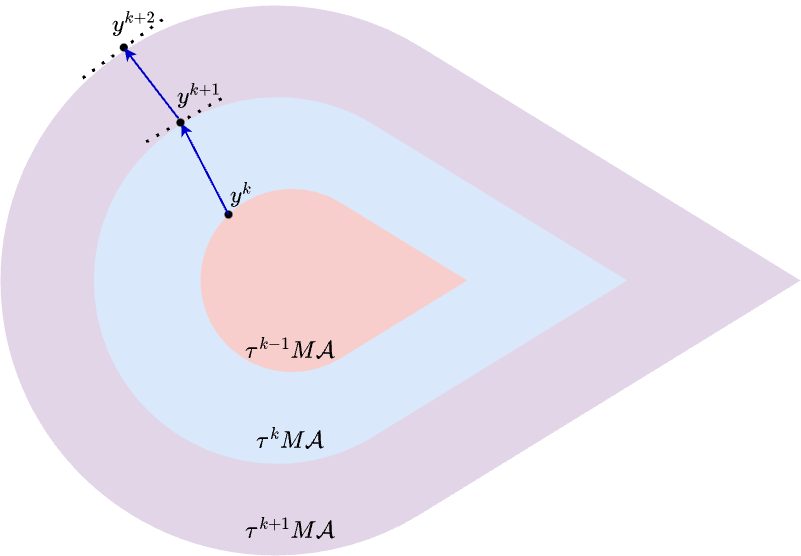
(Projection can be computed approximately using Frank-Wolfe.)
Complexity
\mathcal{O}(\log(1 / \epsilon))
projection steps
or
\mathcal{O}(\log(1 / \epsilon) / \epsilon)
Frank-Wolfe steps
A variant of the level-set method developed by [Aravkin et al.'18]
Primal-retrieval Strategy
Can we retrieve primal variables from near-optimal dual variable?
\{\hat x_i\}_{i=1}^k \in \mathop{argmin}\limits_{x_1, \dots, x_k \in \mathcal{X}}
\left\{
\|M(\sum_{i=1}^k x_i) - b\|
~\big\vert~
\mathop{supp}(\mathcal{A}_i; x_i) \in \mathop{face}(\mathcal{A}_i, M^*y)
\right\}
Theorem [FFF, Submitted'22]
\epsilon
Let
denote the duality gap. Under mild assumptions,
\mathop{cardinality}(\mathcal{A}_i; \hat x_i) \approx \mathop{cardinality}(\mathcal{A}_i; x_i^*) \enspace \forall i
\enspace\text{and}\enspace
\|M(\sum_{i=1}^k \hat x_i) - b\| \leq \alpha + \mathcal{O}(\sqrt{\epsilon})
Open-source Package https://github.com/MPF-Optimization-Laboratory/AtomicOpt.jl
(equivalent to unconstrained least square when atomic sets are symmetric)
Federated Learning
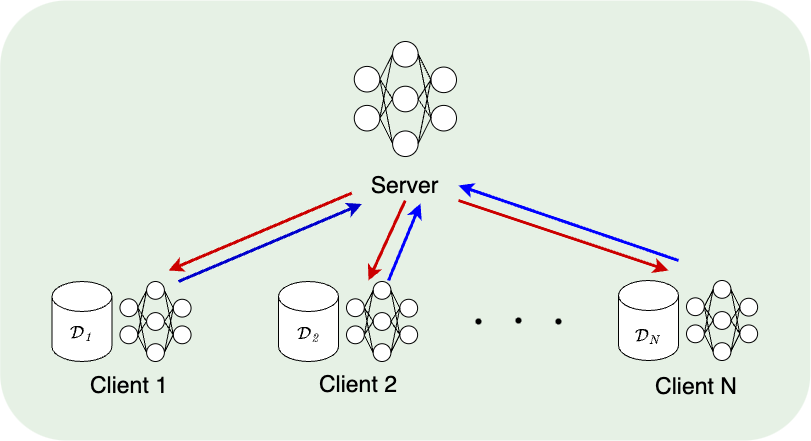
Motivation
Setting
Definition
Federated learning is a collaborative learning framework that can keep data sets private.
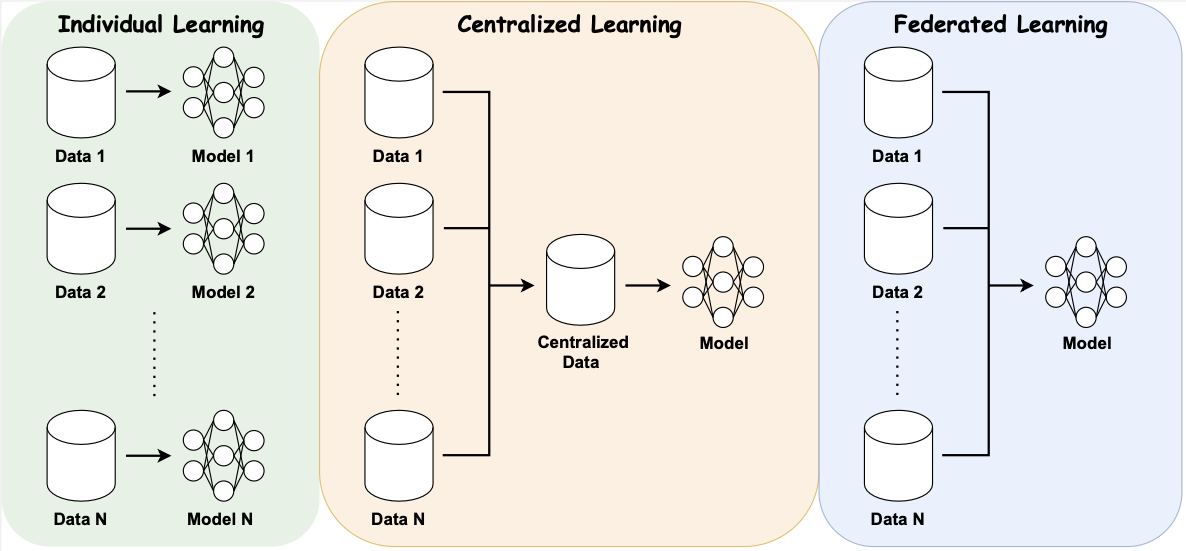
Decentralized data sets, privacy concerns
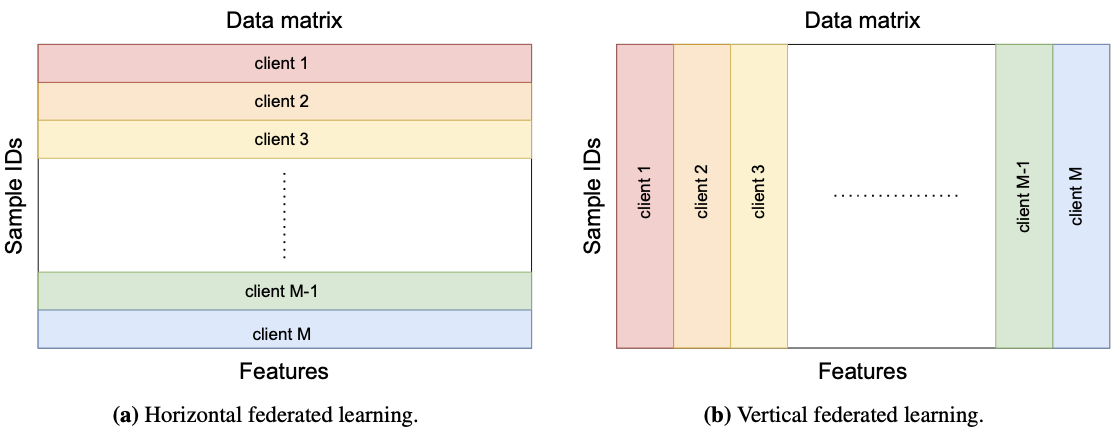
Horizontal and Vertical Federated Learning
Roadmap
Federated optimization
Fan, Z., Fang, H. & Friedlander, M. P. FedDCD: A Dual Approach for Federated Learning. Submitted (2022).
Knowledge-injected federated learning
Fan, Z., Zhou, Z., Pei, J., Friedlander, M. P., Hu, J., Li, C. & Zhang, Y. Knowledge-Injected Federated Learning. Submitted (2022).
Contribution valuation in federated learning
Fan, Z., Fang, H., Zhou, Z., Pei, J., Friedlander, M. P., Liu, C., & Zhang, Y. Improving Fairness for Data Valuation in Horizontal Federated Learning. IEEE International Conference on Data Engineering (ICDE 2022).
Fan, Z., Fang, H., Zhou, Z., Pei, J., Friedlander, M. P., & Zhang, Y. Fair and efficient contribution valuation for vertical federated learning. Submitted (2022).
Federated Optimization
Important features of federated optimization
-
communication efficiency
-
data privacy
-
data heterogeneity
-
computational constraints
\mathop{min}\limits_{w \in \mathbb{R}^d}\enspace F(\red{w}) \coloneqq \sum\limits_{i=1}^\blue{N} f_i(w)
\enspace\text{with}\enspace
f_i(w) \coloneqq \frac{1}{|\mathcal{D}_i|} \sum\limits_{(x, y) \in \green{\mathcal{D}_i} } \purple{\ell}(w; x, y)
model
number of clients
local dataset
loss function
Primal-based Algorithm
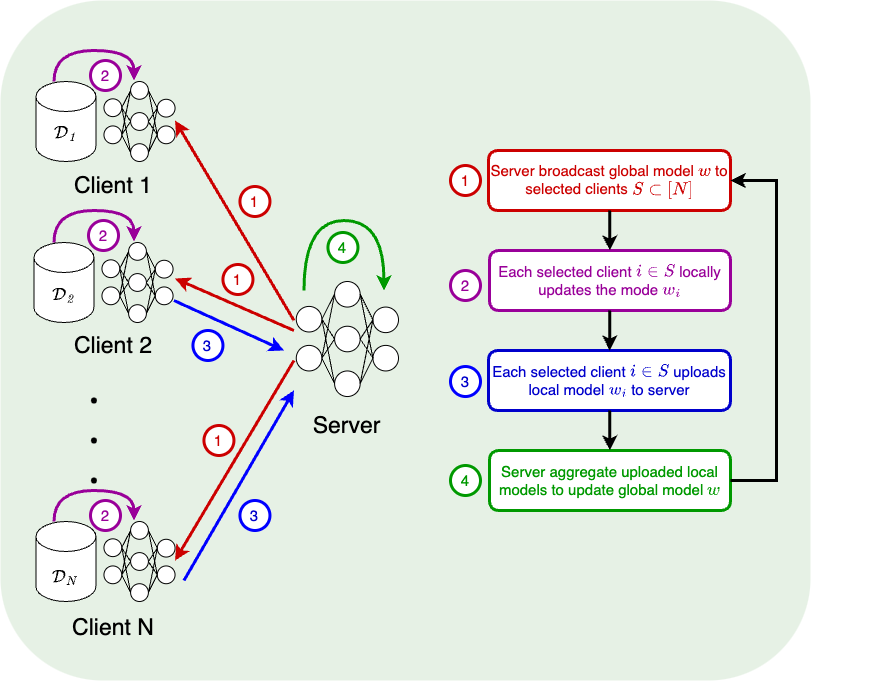
FedAvg [McMahan et al.'17]
w_i \leftarrow w_i - \eta \tilde \nabla f_i(w_i) \quad (K \text{ times})
w \leftarrow \frac{1}{|S|}\sum_{i \in S} w_i
SCAFFOLD [Karimireddy et al.'20]
w_i \leftarrow w_i - \eta (\tilde \nabla f_i(w_i) - c_i + c) \quad (K \text{ times})
c_i \leftarrow \tilde \nabla f_i(w), \enspace
c \leftarrow \frac{1}{|S|}\sum_{i \in S} c_i, \enspace
w \leftarrow \frac{1}{|S|}\sum_{i \in S} w_i
Dual-based Algorithm
\mathop{min}\limits_{y_1, \dots, y_N \in \mathbb{R}^d}\enspace G(\mathbf{y}) \coloneqq \sum\limits_{i=1}^N \red{f_i^*}(y_i)
\enspace\text{subject to}\enspace
\sum_{i=1}^N \blue{y_i} = \mathbf{0}
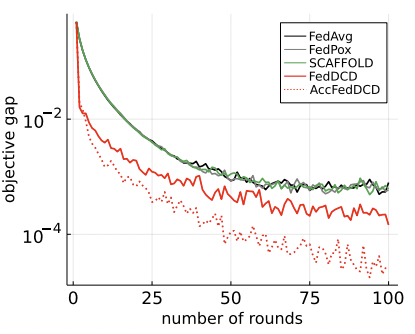
Federated dual coordinate descent (FedDCD) [FFF, Submitted'22]
w_i \approx \nabla f_i^*(y_i) \coloneqq \mathop{argmin}\limits_{w\in \mathbb{R}^d} \{ f_i(w) - \langle w, y_i \rangle \}
\{\hat w_i\}_{i \in S} = \mathop{Proj}_{\mathcal{C}}(\{w_i\}_{i \in S})
\enspace\text{where}\enspace \mathcal{C} = \{ \{v_i \in \mathbb{R}^d\}_{i \in S} \mid \sum_{i \in S} v_i = \mathbf{0}\}
y_i \leftarrow y_i - \eta \hat w_i
Each selected client approximately compute dual gradient and upload to server
Server adjusts the gradients (to keep feasibility) and broadcasts to selected clients
Each selected client locally updates the dual model
(A extension of [Necoara et al.'17]: inexact gradient, acceleration)
conjugate function
local dual model
Communication Rounds
Setting
\alpha-\text{strongly convex}, ~\beta-\text{smooth}, ~\zeta-\text{data heterogeneous}, ~\sigma-\text{gradient variance}
Open-source Package https://github.com/ZhenanFanUBC/FedDCD.jl
Knoledge-Injected Federated Learning
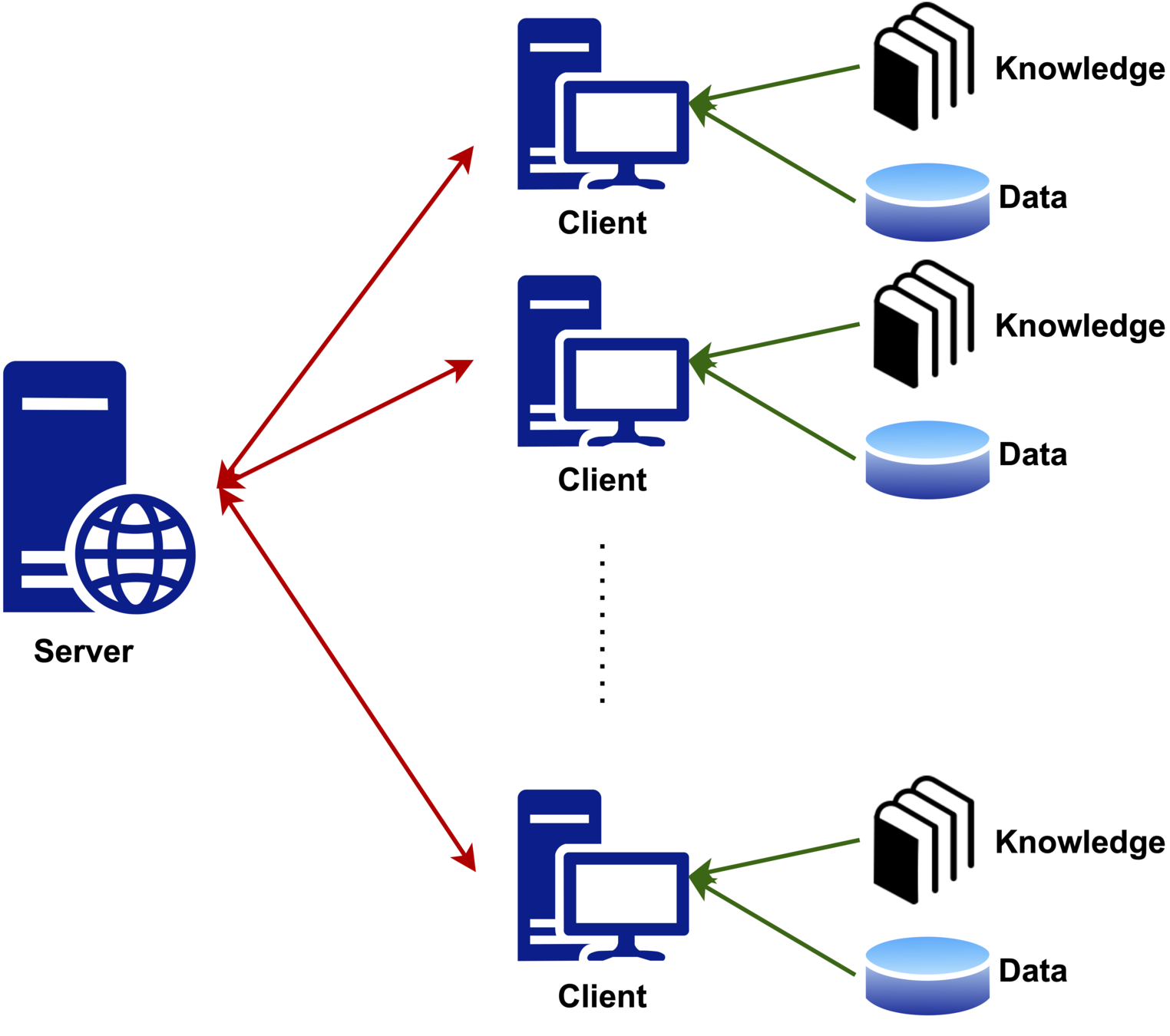
Coal-Mixing in Coking Process
Challenging as no direct formula
Based on experience and knowledge
largely affects cost
Task Description
Goal: improve the expert's prediction model with machine learning
Data scarcity: collecting data is expensive and time consuming
We unite 4 coking industries to collaboratively work on this task
Challeges
local datasets have different distributions
industries have different expert(knowledge) models
privacy of local datasets and knowledge models has to be preserved
Multiclass Classification
\red{\mathcal{D}} = \left\{(\blue{x^{(i)}}, \green{y^{(i)}}\right\}_{i=1}^N \subset \blue{\mathcal{X}} \times \green{\{1,\dots,k\}} \sim \purple{\mathcal{F}}
training set
data instance
(features of raw coal)
feature space
label
(quality of the final coke)
label space
data distribution
Task
\text{Find}\enspace
f: \mathcal{X} \to \{1,\dots,k\}
\enspace\text{such that}\enspace
\mathop{\mathbb{E}}_{(x,y)\sim\mathcal{F}}[f(x) \neq y]
\enspace\text{is small.}
Setting
\enspace\text{or}\enspace
\mathop{\mathbb{E}}_{(x,y)\sim\mathcal{D}}[f(x) \neq y]
\enspace\text{is small.}
Knowledge-based Models
Prediction-type Knowledge Model (P-KM)
g_p: \mathcal{X} \to \{1,\dots,k\}
\enspace\text{such that}\enspace
g_p(x)
\enspace\text{is a point estimation for}\enspace
y
\enspace\forall (x,y) \sim \mathcal{F}
Range-type Knowledge Model (R-KM)
g_r: \mathcal{X} \to 2^{\{1,\dots,k\}}
\enspace\text{such that}\enspace
y \subseteq g_r(x)
\enspace\forall (x,y) \sim \mathcal{F}
Eg. Mechanistic prediction models, such as an differential equation that describes the underlying physical process.
Eg. Can be derived from the causality of the input-output relationship.
\red{(k = 3,\enspace g_p(x) = 2)}
\red{(k = 3,\enspace g_r(x) = \{2, 3\})}
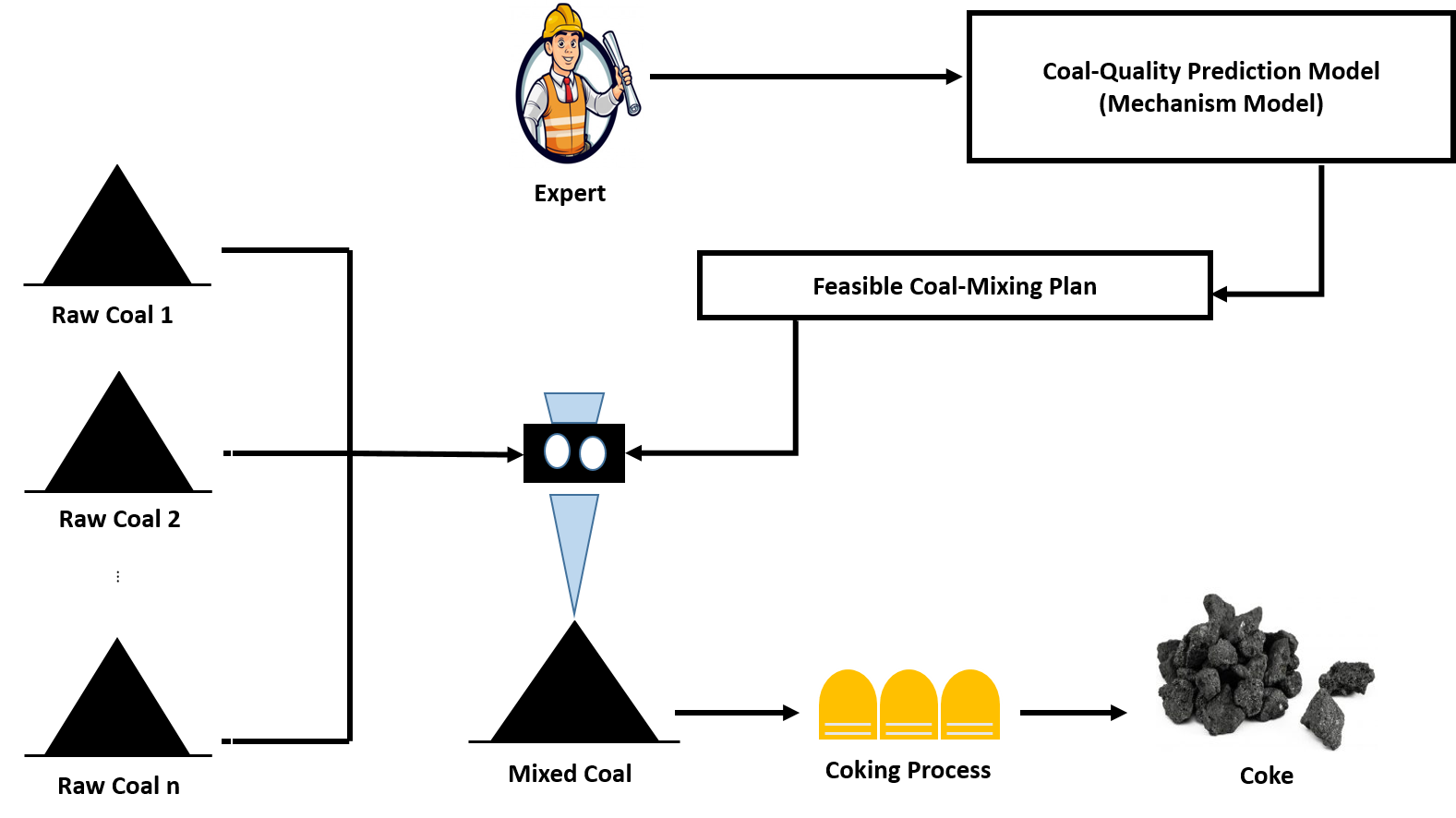
Federated Learning with Knowledge-based Models
M clients and a central server.
\text{training set}\enspace
\mathcal{D}^m \sim \purple{\mathcal{F}^m}
conditional data distribution depending on
\text{P-KM}\enspace
g_p^m
\enspace\text{for distribution}\enspace
\mathcal{F}^m
\text{R-KM}\enspace
g_r^m
\enspace\text{for distribution}\enspace
\mathcal{F}^m
\purple{\mathcal{F}}
Each client m has
g_p^m
\enspace\text{agrees with}\enspace
g_r^m
\enspace \red{(g_p^m(x) \in g_r^m(x) \enspace \forall x)}
Task Description
each client m obatins a personalized predictive model
f^m: \mathcal{X} \to \Delta^k \coloneqq \{p \in \mathbb{R}^k \mid \sum p_i = 1\}
f^m \enspace\text{utilize the local P-KM}\enspace g^m_p \enspace\text{with controllable trust level}
f^m \enspace\text{agrees with local R-KM}\enspace g^m_p
\enspace\text{i.e.}\enspace
\{i \mid f^m(x)_i > 0\} \subseteq g^m_r(x)\enspace
\forall x \in \mathcal{X}
Design a federated learning framework such that
clients can benefit from others' datasets and knowledge
privacy of local datasets and local KMs needs to be protected
Direct Formulation Invokes Infinitely Many Constraints
Simple setting
\text{Single client with}\enspace \mathcal{X} = \mathbb{R}^d
\text{Logistic model}\enspace f(\theta; x) = \blue{\mathop{softmax}}(\theta^T x) \enspace\text{with}\enspace \theta\in\mathbb{R}^{d\times k}
\blue{
\mathop{softmax}(z \in \mathbb{R}^k)_i = \dfrac{\exp(z_i)}{\sum_j \exp(z_j)}
}
\red{(f(\theta; \cdot): \mathbb{R}^d \to \Delta^k)}
\text{Loss function}\enspace \mathcal{L}(\theta) = \frac{1}{|\mathcal{D}|} \sum\limits_{(x,y) \in \mathcal{D}}
\blue{\mathop{crossentropy}}(f(\theta; x), y)
\blue{
\mathop{crossentropy}(p\in\Delta^k, y\in\{1,\dots,k\}) = -\log(p_y)
}
Challenging optimization problem
\min\limits_{\theta \in \mathbb{R}^{d\times k}} \enspace
\mathcal{L}(\theta)
\enspace\text{s.t.}\enspace
\{i \mid f(\theta; x)_i > 0\} \subseteq g_r(x)
\enspace \forall x \in \mathbb{R}^d
\red{(\text{infinitely many constraints})}
Architecture Design
The server provides a general deep learning model
f(\red{\theta}; \cdot): \mathcal{X} \to \mathbb{R}^k
learnable model parameters
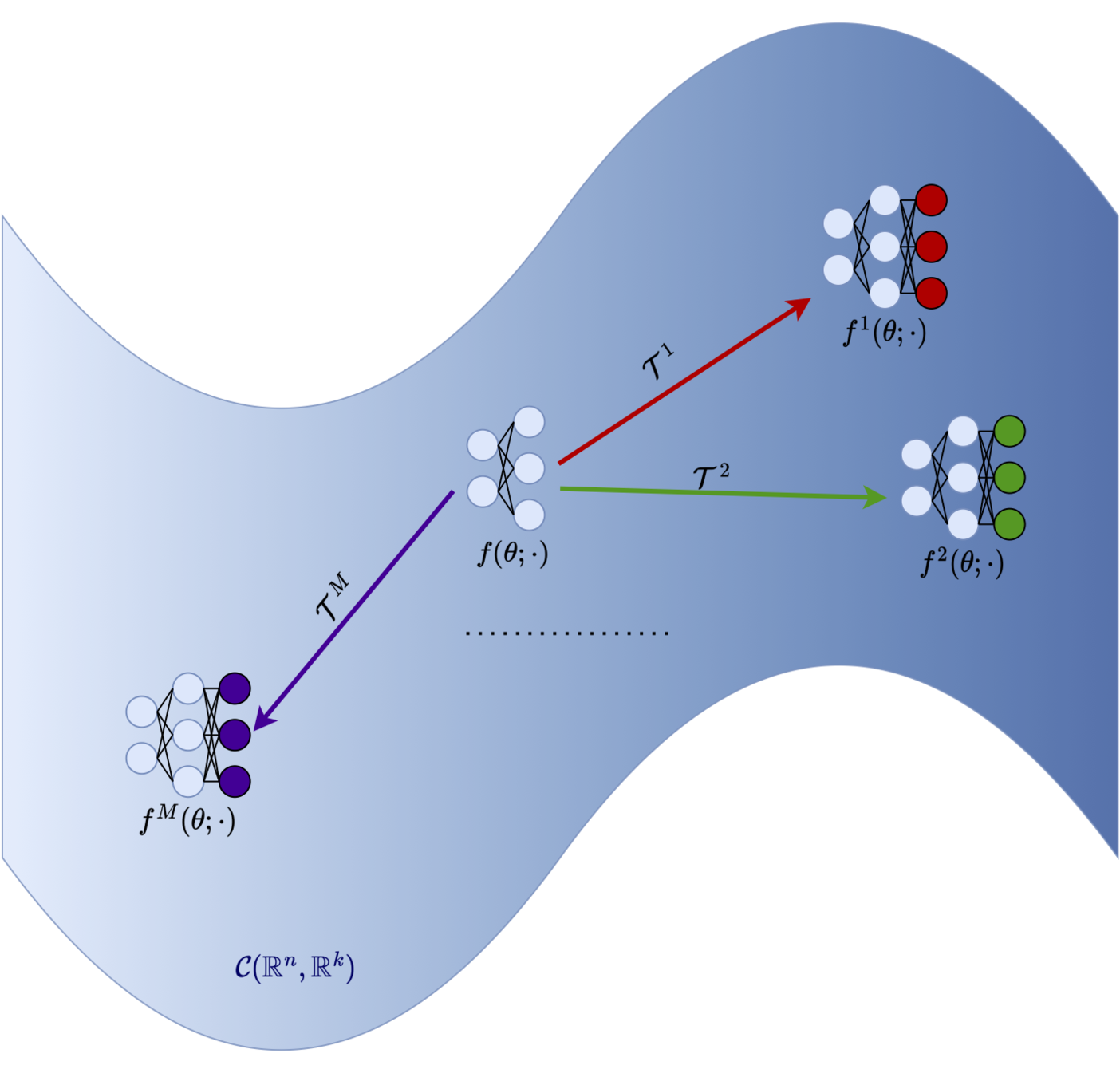
Function transformation
\mathcal{T}_{\lambda, g_p, g_r}(f)(x) =
(1-\lambda)\mathop{softmax}(f(x) + z_r) + \lambda z_p
where
(z_r)_i =
\begin{cases}
0 &\text{if}\enspace i \in g_r(x)\\
-\infty &\text{otherwise}
\end{cases}
\enspace\text{and}\enspace
(z_p)_i =
\begin{cases}
1 &\text{if}\enspace i = g_p(x)\\
0 &\text{otherwise}
\end{cases}
Personalized model
f^m(\red{\theta}; \cdot) \coloneqq \mathcal{T}_{\lambda^m, g_p^m, g_r^m}(f(\red{\theta}; \cdot))
Properties of Personalized Model
f^m(\theta; \cdot)
\enspace\text{is a valid predictive model, i.e.,}\enspace
f^m(\theta; x) \in \Delta^k \enspace \forall x \in \mathcal{X}
\lambda^m \in [0,1]
\enspace\text{controls the trust-level of the local P-KM}\enspace
g^m_p
\langle f^m(\theta; x), g^m_p(x) \rangle \geq \lambda^m \enspace \forall x \in \mathcal{X}
\text{If}\enspace \lambda^m > 0.5
\enspace\text{then}\enspace
f^m
\enspace\text{coincides with}\enspace
g^m_p
\argmax_i f^m(\theta; x) = g_p^m(x)
f^m(\theta; \cdot)
\enspace\text{agrees with local R-KM}\enspace
g^m_r
\{i \mid f^m(x)_i > 0\} \subseteq g^m_r(x)\enspace
\forall x \in \mathcal{X}
Optimization
Optimization problem
\min\limits_{\theta}\enspace\red{\mathcal{L}}(\theta) \coloneqq \sum\limits_{i=1}^M \red{\mathcal{L}^m}(\theta)
\enspace\text{with}\enspace
\mathcal{L}^m(\theta) = \frac{1}{|\mathcal{D}^m|}\sum\limits_{(x,y) \in \mathcal{D}^m} \mathop{crossentropy}(f^m(\theta; x), y)
Eg. FedAvg [McMahan et al.'17]
global loss
local loss
Most existing horizontal federated learning algorithms can be applied to solve this optimization problem!
Numerical Results (Case-study)
Test accuracy
\text{TA} = \frac{1}{|\mathcal{D}^m_{\text{test}}|} \sum\limits_{(x,y) \in \mathcal{D}^m_{\text{test}}} \mathbb{I}(\{f^m(\theta; x) = y\})
Percentage of violation
\text{POV} = \frac{1}{|\mathcal{D}^m_{\text{test}}|} \sum\limits_{(x,y) \in \mathcal{D}^m_{\text{test}}}
\mathbb{I}(\{f^m(\theta; x) \notin g_r^m(x)\})
Open-source Package https: //github.com/ZhenanFanUBC/FedMech.jl
Contribution Valuation in Federated Learning
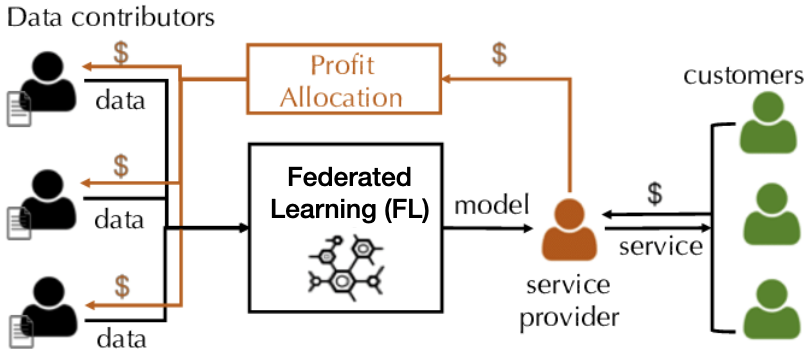
Key requirement
1. Data owners with similar data should receive similar valuation. 2. Data owners with unrelated data should receive low valuation.
Shapley Value
Shapley value is a measure for players' contribution in a game.
Advantage
It satisfies many desired fairness axioms.
Drawback
Computing utilities requires retraining the model.
performance of the model
v(\red{i}) = \frac{1}{N} \sum\limits_{S \subseteq [N] \setminus \{i\}} \frac{1}{ N-1 \choose |S|}
[U(S \cup \{i\}) - \blue{U(S)}]
player i
utility created by players in S
marginal utility gain
Horizontal Federated Learning
\mathop{min}\limits_{w \in \mathbb{R}^d}\enspace F(\red{w}) \coloneqq \sum\limits_{i=1}^\blue{M} f_i(w)
\enspace\text{with}\enspace
f_i(w) \coloneqq \frac{1}{|\mathcal{D}_i|} \sum\limits_{(x, y) \in \green{\mathcal{D}_i} } \purple{\ell}(w; x, y)
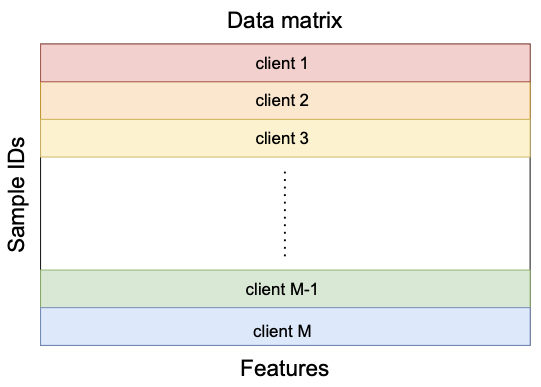
model
number of clients
local dataset
loss function
Federated Shapley Value
[Wang et al.'20] propose to compute Shapley value in each communication round, which eliminates the requirement of retraining the model.
v_t(i) = \frac{1}{M} \sum\limits_{S \subseteq [M] \setminus \{i\}} \frac{1}{ M-1 \choose |S|}
[U_t(S \cup \{i\}) - U_t(S)]
v(i) = \sum\limits_{t=1}^T v_t(i)
Fairness
Symmetry
U_t(S\cup\{i\}) = U_t(S\cup\{j\}) \quad \forall t, S
\Rightarrow
v(i) = v(j)
Zero contribution
U_t(S\cup\{i\}) = U_t(S) \quad \forall t, S
\Rightarrow
v(i) = 0
Addivity
U_t = U^1_t + U^2_t
\Rightarrow
v(i) = v^1(i) + v^2(i)
Utility Function
Test data set (server)
\mathcal{D}_c
U_t(S) = \sum\limits_{(x, y) \in \mathcal{D}_c} \left[ \ell(w^t; x,y) - \ell(w_S^{t+1}; x,y) \right]
\enspace\text{where}\enspace
w_S^{t+1} = \frac{1}{|S|} \sum\limits_{i \in S} w_i^{t+1}
v_t(i) =
\begin{cases}
\frac{1}{|S^t|} \sum\limits_{S \subseteq S^t \setminus\{i\}} \frac{1}{\binom{|S^t|-1}{|S|}} \left[U_t(S\cup\{i\}) - U_t(S)\right] & i \in S^t \\
0 & i \notin S^t
\end{cases}
Problem: In round t, the server only has
\{w_i^{t+1}\}_{i \in S^t}
[Wang et al.'20]
Possible Unfairness
Clients with identical local datasets may receive very different valuations.
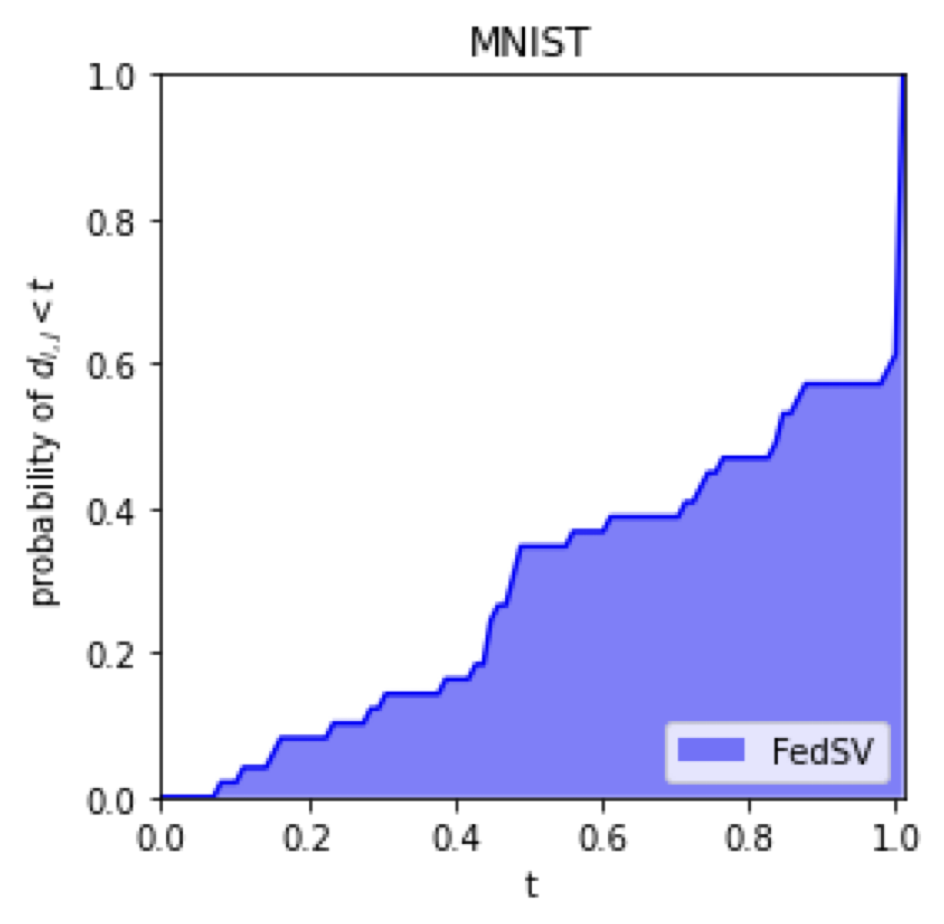
Same local datasets
\mathcal{D}_i = \mathcal{D}_j
Relative difference
d_{i,j} = \frac{|v(i) - v(j)|}{\max\{v(i), v(j)\}}
Empirical probability
\mathbb{P}( d_{i,j} > 0.5) > 65\% \quad \red{\text{unfair!}}
Low Rank Utility Matrix
Utility matrix
\mathcal{U} \in \mathbb{R}^{T \times 2^M} \enspace\text{with}\enspace \mathcal{U}_{t, S} = U_t(S)
This matrix is only partially observed and we can do fair valuation if we can recover the missing values.
Theorem
If the loss function is smooth and strong convex, then
\red{\mathop{rank}_\epsilon}(\mathcal{U}) \in \mathcal{O}(\frac{\log(T)}{\epsilon})
[Fan et al.'22]
\red{ \mathop{rank}_\epsilon(X) = \min\{\mathop{rank}(Z) \mid \|Z - X\|_{\max} \leq \epsilon\} }
[Udell & Townsend'19]
Empirical Results: Singular Value Decomposition
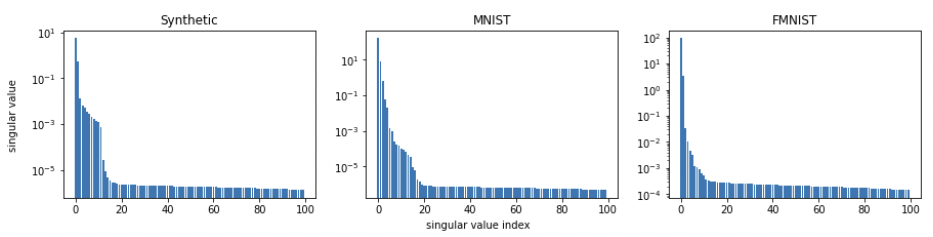
Matrix Completion
\min\limits_{\substack{W \in \mathbb{R}^{T \times r}\\ H \in \mathbb{R}^{2^N \times r}}} \enspace \sum_{t=1}^T\sum_{S\subseteq S^t} (\mathcal{U}_{t,S} - w_t^Th_{S})^2 +
\lambda(\|W\|_F^2 + \|H\|_F^2)
Same local datasets
\mathcal{D}_i = \mathcal{D}_j
Relative difference
d_{i,j} = \frac{|v(i) - v(j)|}{\max\{v(i), v(j)\}}
Empirical CDF
\mathbb{P}( d_{i,j} < t)
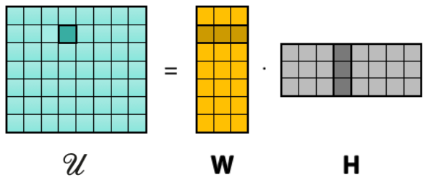
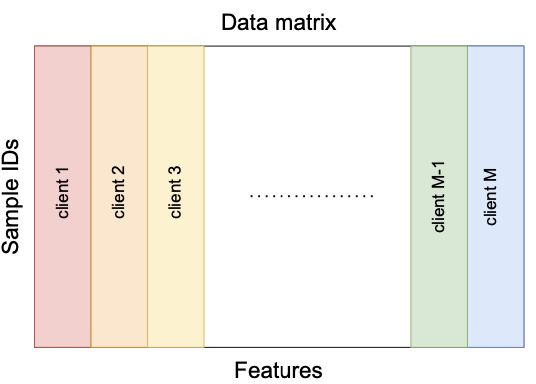
Vertical Federated Learning
\mathop{min}\limits_{\theta_1, \dots, \theta_M}\enspace F(\red{\theta_1, \dots, \theta_M}) \coloneqq
\frac{1}{N}\sum\limits_{i=1}^N \ell(\sum_{m=1}^M h^m_i; y_i)
\enspace\text{with}\enspace
\blue{h^m_i} = \langle \theta_m, x_i^m \rangle
local models
local embeddings
Only embeddings will be communicated between server and clients.
FedBCD
[Liu et al.'22]
Server selects a mini-batch
B^t \subseteq [N]
Each client m compute local embeddings
\{ (h_i^m)^t = \langle \theta_m^t, x_i^m \rangle \mid i \in B^t \}
Server computes gradient
\{g_i^t = \frac{\partial \ell(h_i^t; y_i)}{\partial h_i^t} \mid i \in B^t\}
Each client m updates local model
\theta_m^{t+1} \leftarrow \theta_m^t - \frac{\eta^t}{|B^t|} \sum\limits_{i \in B^t} g_i^t x_i^m
Utility Function
U_t(S) = \frac{1}{N}\sum\limits_{i=1}^N \ell\bigg(\sum\limits_{m=1}^M (h^m_i)^{t-1}; y_i\bigg)
- \frac{1}{N}\sum\limits_{i=1}^N \ell\bigg(\sum\limits_{m\in S} (h^m_i)^{t} + \sum\limits_{m\notin S} (h^m_i)^{t-1}; y_i\bigg)
Problem: In round t, the server only has
\{ (h_i^m)^t \mid i \in B^t \}
Embedding matrix
\mathcal{H}^m \in \mathbb{R}^{T \times N} \enspace\text{with}\enspace \mathcal{H}^m_{t, i} = (h_i^m)^t
Theorem
If the loss function is smooth, then
\mathop{rank}_\epsilon(\mathcal{H}^m) \in \mathcal{O}(\frac{\log(T)}{\epsilon})
[Fan et al.'22]
Empirical Results: Approximate Rank
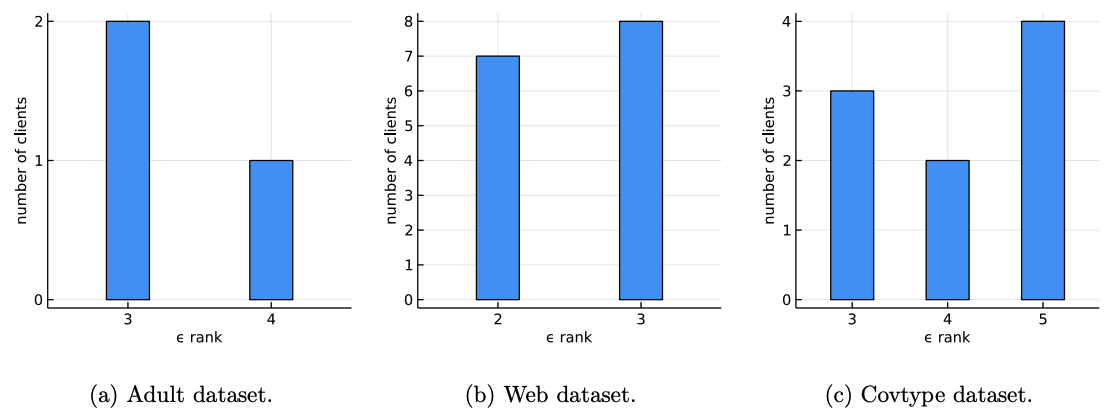
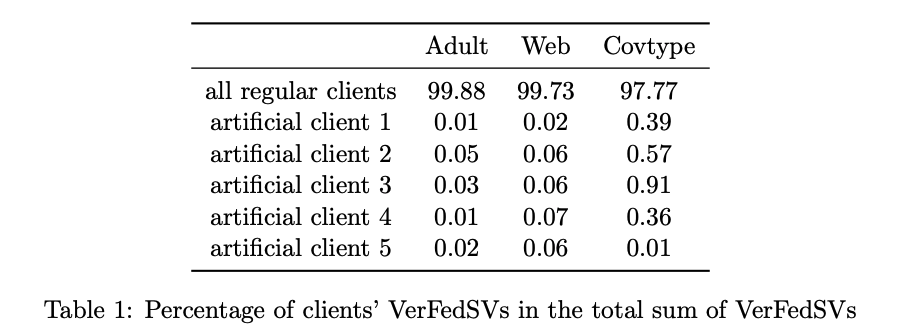
Experiment: Detection of Artificial Clients
These two works are partly done during my internship at Huawei Canada. Our code is publicly available at Huawei AI Gallery.
