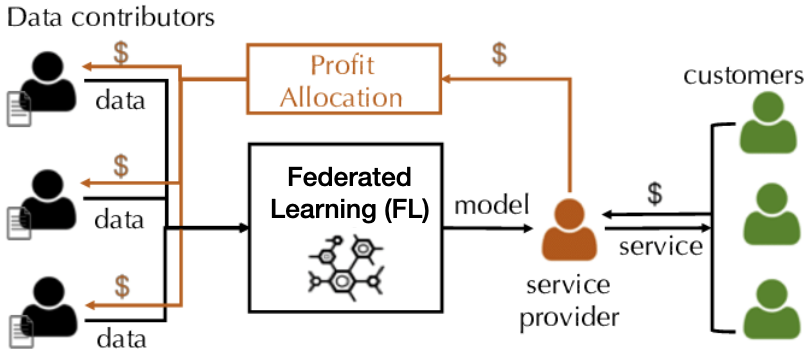
Contribution Valuation

In

Federated Learning

Zhenan Fan

Department of Computer Science

Collaborators:

Huang Fang, Zirui Zhou, Yong Zhang, Jian Pei, Michael Friedlander

Contribution Valuation

Key requirement

1. Data owners with similar data should receive similar valuation.
2. Data owners with unrelated data should receive low valuation.

Shapley Value

Shapley value is a measure for players' contribution in a game.

Advantage

It satisfies many desired fairness axioms.

Drawback

Computing utilities requires retraining the model.

performance of the model

v(\red{i}) = \frac{1}{N} \sum\limits_{S \subseteq [N] \setminus \{i\}} \frac{1}{ N-1 \choose |S|} [U(S \cup \{i\}) - \blue{U(S)}]

player i

utility created by players in S

marginal utility gain

Federated Shapley Value

[Wang et al.'20] propose to compute Shapley value in each communication round, which eliminates the requirement of retraining the model.

v_t(i) = \frac{1}{M} \sum\limits_{S \subseteq [M] \setminus \{i\}} \frac{1}{ M-1 \choose |S|} [U_t(S \cup \{i\}) - U_t(S)]

v(i) = \sum\limits_{t=1}^T v_t(i)

Fairness

Symmetry

U_t(S\cup\{i\}) = U_t(S\cup\{j\}) \quad \forall t, S \Rightarrow v(i) = v(j)

Zero contribution

U_t(S\cup\{i\}) = U_t(S) \quad \forall t, S \Rightarrow v(i) = 0

Addivity

U_t = U^1_t + U^2_t \Rightarrow v(i) = v^1(i) + v^2(i)

Horizontal Federated Learning

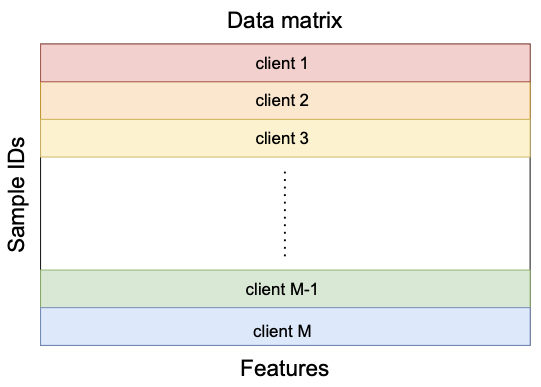
\mathop{min}\limits_{w \in \mathbb{R}^d}\enspace F(\red{w}) \coloneqq \sum\limits_{i=1}^\blue{M} f_i(w) \enspace\text{with}\enspace f_i(w) \coloneqq \frac{1}{|\mathcal{D}_i|} \sum\limits_{(x, y) \in \green{\mathcal{D}_i} } \purple{\ell}(w; x, y)

model

number of clients

local dataset

loss function

FedAvg

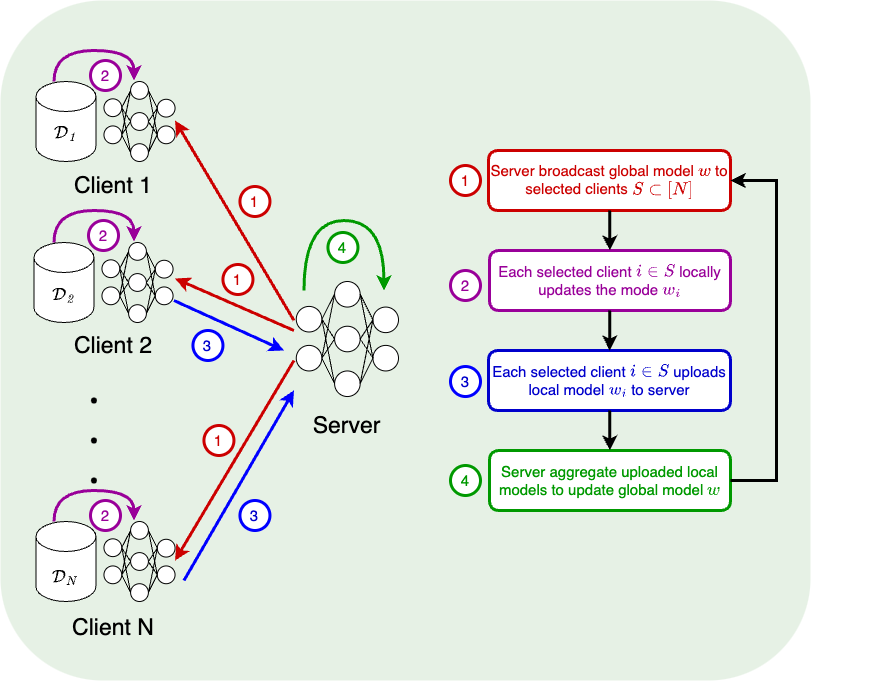
[McMahan et al.'17]

w_i^{t+1} \leftarrow w_i^t - \eta \tilde \nabla f_i(w_i^t) \quad (K \text{ times})

w^{t+1} \leftarrow \frac{1}{|S^t|}\sum_{i \in S^t} w_i^{t+1}

Utility Function

Test data set (server)

\mathcal{D}_c

U_t(S) = \sum\limits_{(x, y) \in \mathcal{D}_c} \left[ \ell(w^t; x,y) - \ell(w_S^{t+1}; x,y) \right] \enspace\text{where}\enspace w_S^{t+1} = \frac{1}{|S|} \sum\limits_{i \in S} w_i^{t+1}

v_t(i) = \begin{cases} \frac{1}{|S^t|} \sum\limits_{S \subseteq S^t \setminus\{i\}} \frac{1}{\binom{|S^t|-1}{|S|}} \left[U_t(S\cup\{i\}) - U_t(S)\right] & i \in S^t \\ 0 & i \notin S^t \end{cases}

Problem: In round t, the server only has

\{w_i^{t+1}\}_{i \in S^t}

[Wang et al.'20]

Possible Unfairness

Clients with identical local datasets may receive very different valuations.

Same local datasets

\mathcal{D}_i = \mathcal{D}_j

Relative difference

d_{i,j} = \frac{|v(i) - v(j)|}{\max\{v(i), v(j)\}}

Empirical probability

\mathbb{P}( d_{i,j} > 0.5) > 65\% \quad \red{\text{unfair!}}

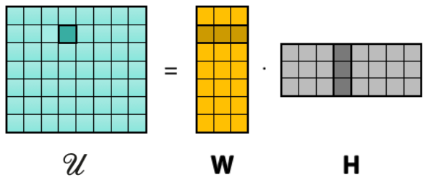
Low Rank Utility Matrix

Utility matrix

\mathcal{U} \in \mathbb{R}^{T \times 2^M} \enspace\text{with}\enspace \mathcal{U}_{t, S} = U_t(S)

This matrix is only partially observed and we can do fair valuation if we can recover the missing values.

Theorem

If the loss function is smooth and strong convex, then

\red{\mathop{rank}_\epsilon}(\mathcal{U}) \in \mathcal{O}(\frac{\log(T)}{\epsilon})

[Fan et al.'22]

\red{ \mathop{rank}_\epsilon(X) = \min\{\mathop{rank}(Z) \mid \|Z - X\|_{\max} \leq \epsilon\} }

[Udell & Townsend'19]

Empirical Results: Singular Value Decomposition

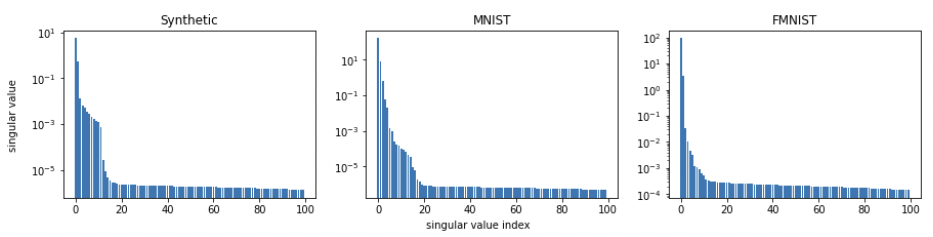
Matrix Completion

\min\limits_{\substack{W \in \mathbb{R}^{T \times r}\\ H \in \mathbb{R}^{2^N \times r}}} \enspace \sum_{t=1}^T\sum_{S\subseteq S^t} (\mathcal{U}_{t,S} - w_t^Th_{S})^2 + \lambda(\|W\|_F^2 + \|H\|_F^2)

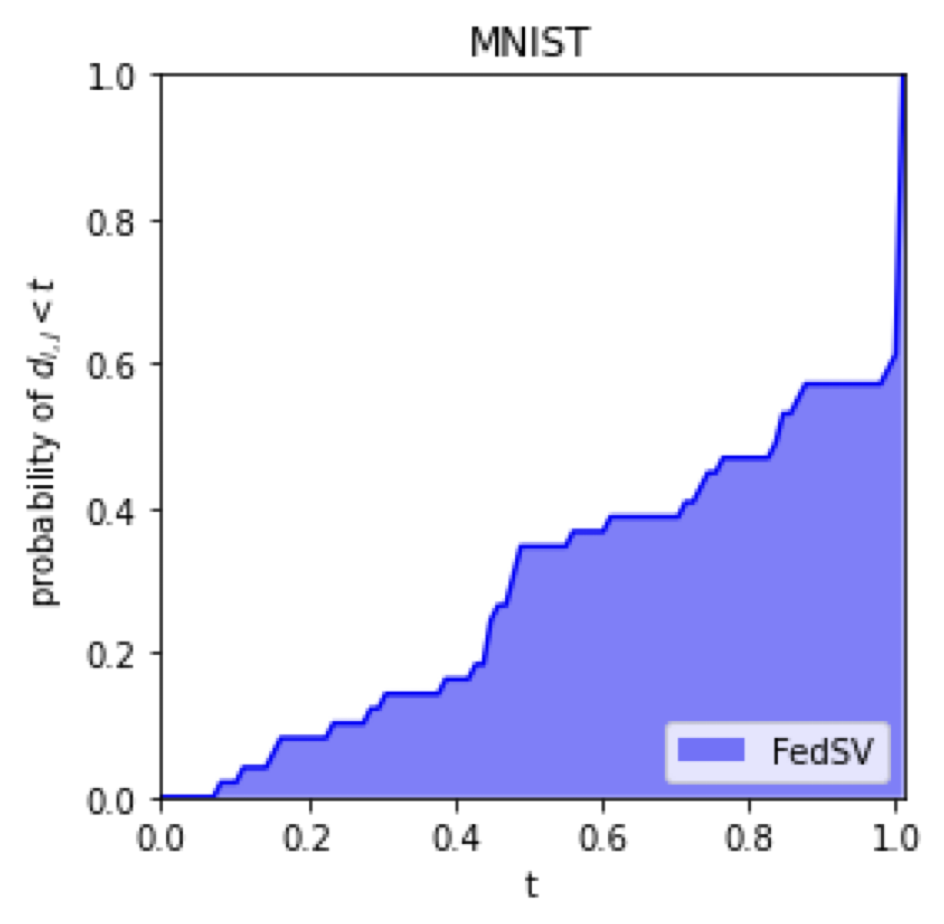
Same local datasets

\mathcal{D}_i = \mathcal{D}_j

Relative difference

d_{i,j} = \frac{|v(i) - v(j)|}{\max\{v(i), v(j)\}}

Empirical CDF

\mathbb{P}( d_{i,j} < t)

\mathop{min}\limits_{\theta_1, \dots, \theta_M}\enspace F(\red{\theta_1, \dots, \theta_M}) \coloneqq \frac{1}{N}\sum\limits_{i=1}^{\red{N}} \ell(\sum_{m=1}^M h^m_i; y_i) \enspace\text{with}\enspace \blue{h^m_i} = \langle \theta_m, x_i^m \rangle

local models

local embeddings

number of training samples

Only embeddings will be communicated between server and clients.

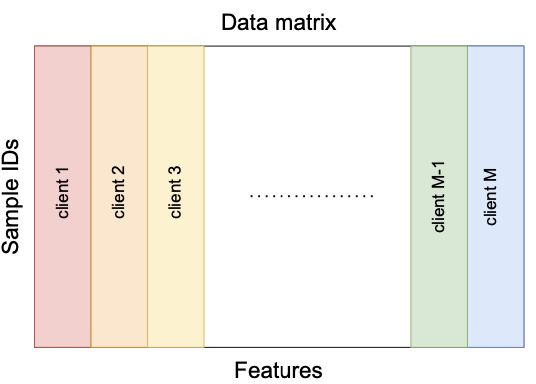
FedBCD

[Liu et al.'22]

Server selects a mini-batch

B^t \subseteq [N]

Each client m compute local embeddings

\{ (h_i^m)^t = \langle \theta_m^t, x_i^m \rangle \mid i \in B^t \}

Server computes gradient

\{g_i^t = \frac{\partial \ell(h_i^t; y_i)}{\partial h_i^t} \mid i \in B^t\}

Each client m updates local model

\theta_m^{t+1} \leftarrow \theta_m^t - \frac{\eta^t}{|B^t|} \sum\limits_{i \in B^t} g_i^t x_i^m

Utility Function

U_t(S) = \frac{1}{N}\sum\limits_{i=1}^N \ell\bigg(\sum\limits_{m=1}^M (h^m_i)^{t-1}; y_i\bigg) - \frac{1}{N}\sum\limits_{i=1}^N \ell\bigg(\sum\limits_{m\in S} (h^m_i)^{t} + \sum\limits_{m\notin S} (h^m_i)^{t-1}; y_i\bigg)

Problem: In round t, the server only has

\{ (h_i^m)^t \mid i \in B^t \}

Embedding matrix

\mathcal{H}^m \in \mathbb{R}^{T \times N} \enspace\text{with}\enspace \mathcal{H}^m_{t, i} = (h_i^m)^t

Theorem

If the loss function is smooth, then

\mathop{rank}_\epsilon(\mathcal{H}^m) \in \mathcal{O}(\frac{\log(T)}{\epsilon})

[Fan et al.'22]