From Susceptibility Imaging

To Principled Learned Proximal Operators

Zhenghan Fang

November 21, 2023

Measure

Inversion

x
y
A
y=Ax+v

Inverse Problems

  • \(A\): Linear forward operator
  • ill-posed

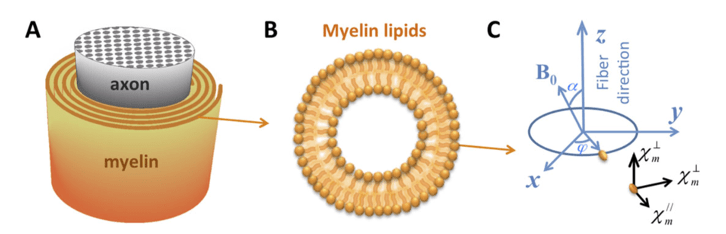
Susceptibility Tensor Imaging

Magnetic Susceptibility

M = {\color{green} \chi} H
  • Degree to which a material is magnetized in an external magnetic field

Susceptibility Anisotropy

  • Fiber tracking
  • Disease characterization
\begin{bmatrix} \chi_{11} & \chi_{12} & \chi_{13} \\ \chi_{12} & \chi_{22} & \chi_{23} \\ \chi_{13} & \chi_{23} & \chi_{33} \end{bmatrix}

Susceptibility Tensor Imaging

Mean

Anisotropy

PEV

Time-consuming data acquisition

☹

Dipole Convolution

Dipole Inversion

x
y
A
y=Ax+v

Inverse Problem in STI

  • \(A\): depends on number of orientations, angles
  • Number of orientations < 6: ill-posed

Phase measurements at different angles

DeepSTI: Learned Proximal Method

  • Unrolling/unfolding
  • \(\hat{x} = \hat{x}_K\), for a fixed \(K\)
  • Use information of physics model
  • Adaptive to \(A\)
\min_x \|y - Ax \|_2^2 + R(x)

Regularizer

Classical Method

  • Not sufficient for few orientations

Learned Proximal

\hat{x}_{k+1} = \mathrm{prox}_{\eta R}(\hat{x}_k - \eta A^H(A\hat{x}_k - y))

Proximal Operator

\hat{x}_{k+1} = {\color{orange} f_\theta}(\hat{x}_k - \eta A^H(A\hat{x}_k - y)) \\

Train \(f: X \to Y \) on \(\mathcal{D} = (x_i, y_i)_{i=1}^N\)

Vanilla Neural Network

  • Not Adaptable to \(A\)

\(\hat{x} = {\color{orange} f_\theta}(y)\)

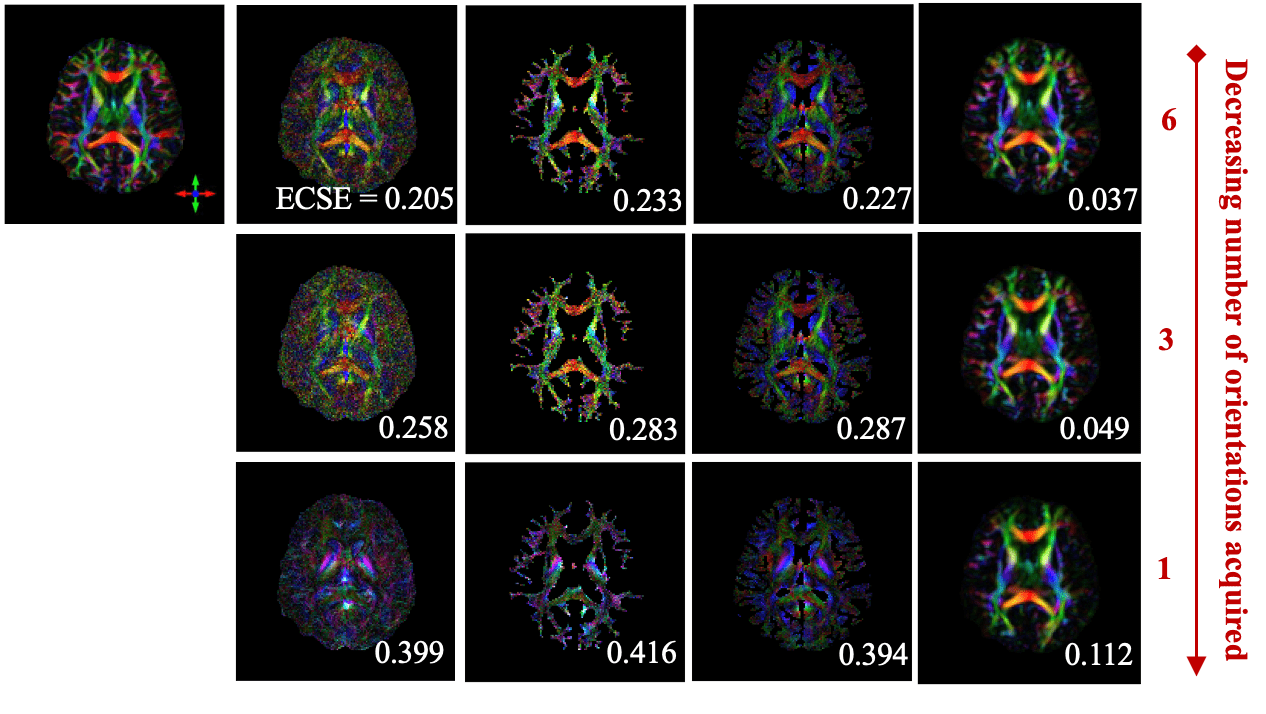
Ground-Truth

STIimag

[Li et al.]

MMSR

[Li and Van Zijl]

aSTI+

[Shi et al.]

DeepSTI

(ours)

[1] Li et al, NMRB 2017; [2] Li and van Zijl, MRM, 2014;

[3] Cao et al., MRM, 2021; [4] Shi et al., IEEE JBHI, 2022

[5] Fang et al. Medical Image Analysis, 2023

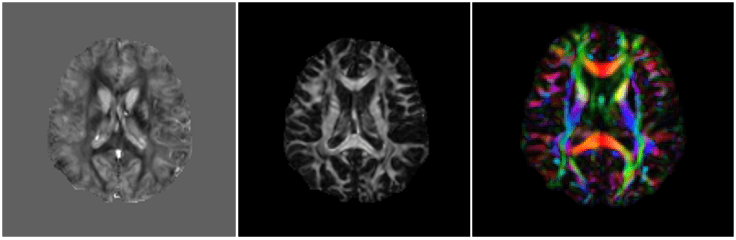
Simulation Results

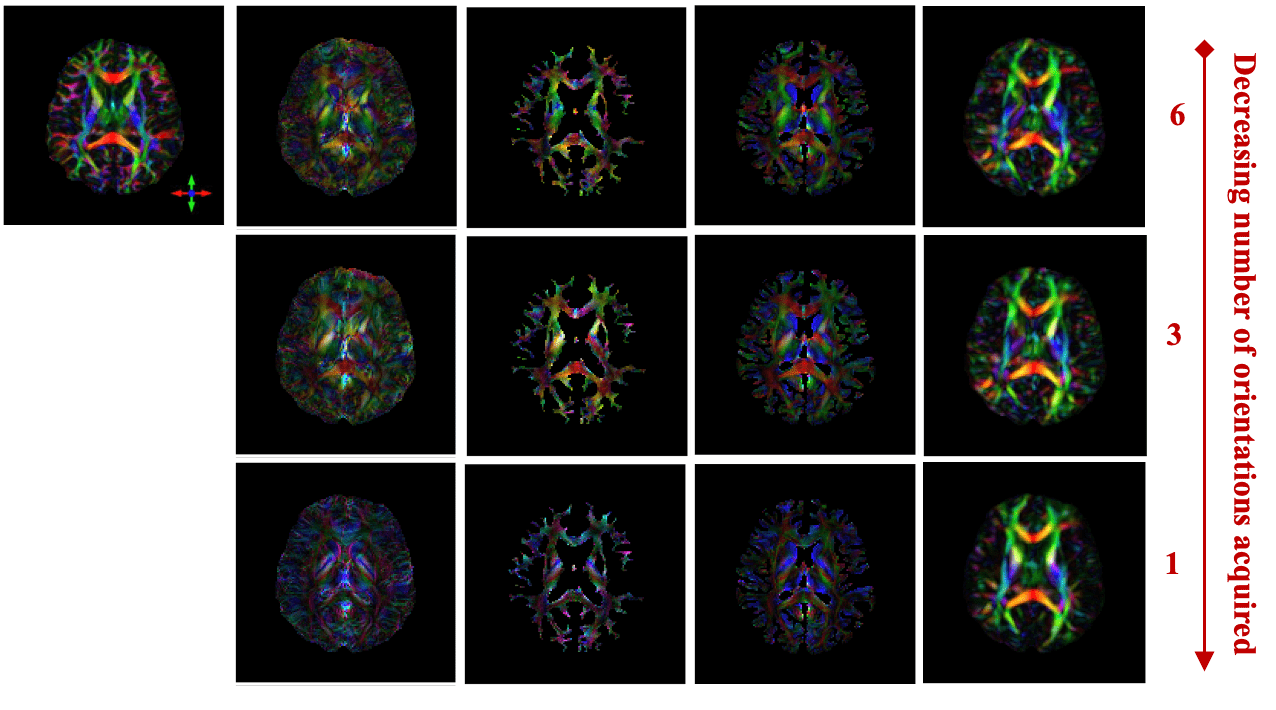
In Vivo Results

DTI

STIimag

[Li et al.]

MMSR

[Li and Van Zijl]

aSTI+

[Shi et al.]

DeepSTI

(ours)

[1] Li et al, NMRB 2017; [2] Li and van Zijl, MRM, 2014;

[3] Cao et al., MRM, 2021; [4] Shi et al., IEEE JBHI, 2022

[5] Fang et al. Medical Image Analysis, 2023

  • Is \(f_\theta\) actually the proximal operator of some function \(R_\theta\)?
  • What is the learned regularizer \(R_\theta(x)\)?
\hat{x}_{k+1} = {\color{orange} f_\theta}(\hat{x}_k - \eta A^H(A\hat{x}_k - y)) \\

Towards Principled and Interpretable Learned Proximal Operator 👉

Characterization of proximal operators [Gribonval and Nikolova, 2020]

Let \(f : \mathcal{Y} \rightarrow \R^n\) be a continuous function.

\(f\) is a proximal operator of a function \(R:\R^n \rightarrow \R \cup \{+\infty\}\)

if and only if

there exists a convex differentiable function \(\psi\) such that \(f(y) = \nabla \psi(y)\).

  • Proximal operators are gradients of convex functions

Background

Input Convex Neural Networks [Amos et al.]

Nonnegative

Learned Proximal Networks

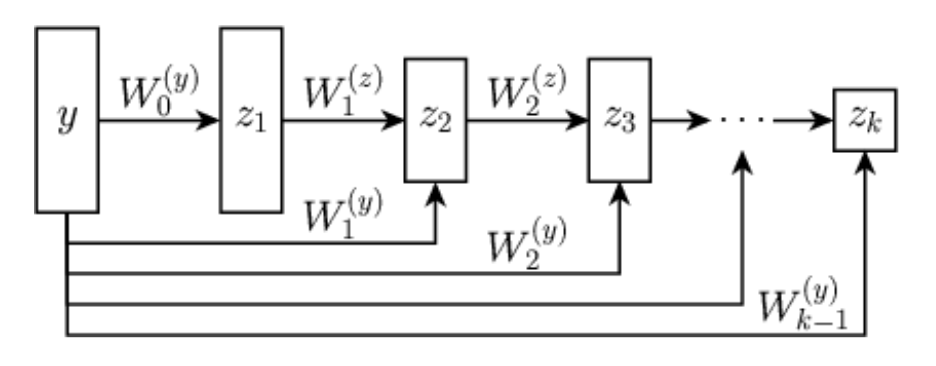
Proposition. Let \(\psi_\theta: \R^{n} \rightarrow \R\) be defined by \[z_{1} = g( \mathbf H_1 y + b_1), \quad z_{k} = g(\mathbf W_k  z_{k-1} + \mathbf H_k y + b_k), \quad \psi_\theta(y) = \mathbf w^T z_{K} + b\]

with

\(g\) a convex, non-decreasing nonlinear activation,

and

all \(\mathbf W_k\) and \(\mathbf w\) non-negative.

 

 

 

Let \(f_\theta = \nabla \psi_{\theta}\).

Then, there exists a function \(R_\theta\) such that  \(f_\theta(y) = \mathrm{prox}_{R_\theta}(y)\).

LPN: Uncovering the Prior

Given \(f_\theta\), how can we evaluate \(R_\theta\)?

\(R(x) = \langle x, f^{-1}(x) \rangle - \frac{1}{2} \|x|_2^2 - \psi(f^{-1}(x))\)

\[\min_y \psi_{\theta}(y) - \langle x, y \rangle\]

Optimality condition: \(\nabla \psi_\theta(y^*) = x\)

[Gribonval and Nikolova]

The minimizer satisfies \(f_\theta(y^*) = x\)

How to invert \(f\)? 🤔

LPN: Proximal Matching Training

\(\mathrm{prox}_{-\log p_x} (y)\)

Ideally, \(R = -\log p_x\)    (MAP estimate) 

\min_x \frac{1}{2}\|y - Ax \|_2^2 + R(x)

How to learn? ☹ \(p_x\) is unknown

LPN: Proximal Matching Training

\(\mathrm{prox}_{-\log p_x} (y)\)

Ideally, \(R = -\log p_x\)    (MAP estimate) 

\min_x \frac{1}{2}\|y - Ax \|_2^2 + R(x)

\(=\arg\max p(x \mid y)\)

\(= \arg\min_z \frac{1}{2}\|y - z \|_2^2 -\log p_x (z)\)

\(x \sim p_x,    v \sim \mathcal{N}(0, \mathbf{I}),    y = x + \sigma v\)

Prox is a MAP denoiser

Learn a MAP denoiser for data

LPN: Proximal Matching Training

\(x \sim p_x,    v \sim \mathcal{N}(0, \mathbf{I}),    y = x + \sigma v\)

\(\ell2\) \(\to\) E[x|y], MMSE

\(\ell1 \to\) Median[x|y]

argmax[x|y]  ?

\(\min_{f} \mathbb{E}_{x,y} \mathcal{L}(f(y),  x) \)

Train a denoiser \(f\):

LPN: Proximal Matching Training

\(x \sim p_x,    v \sim \mathcal{N}(0, \mathbf{I}),    y = x + \sigma v\)

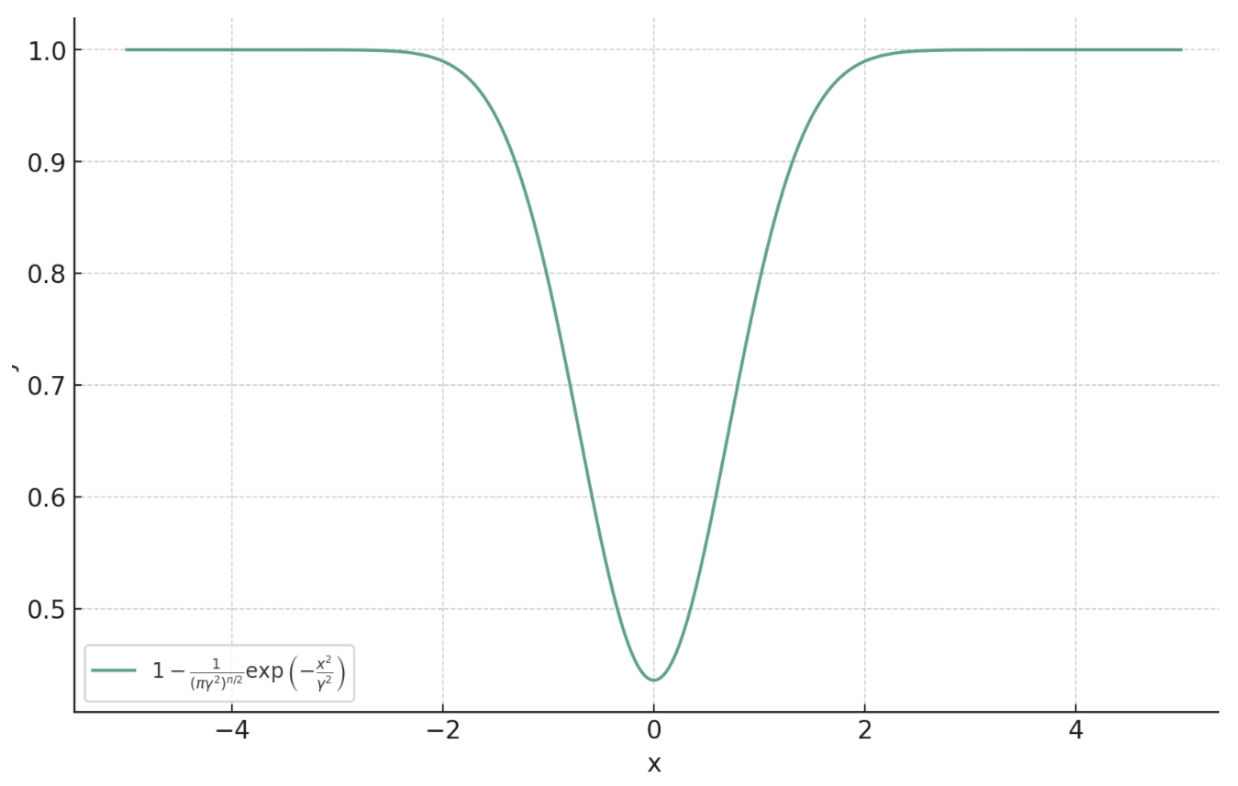
\(\ell2\) \(\to\) E[x|y], MMSE

\(\ell1 \to\) Median[x|y]

Theorem (informal). Let
\[f^* = \argmin_{f} \lim_{\gamma \searrow 0} \mathbb{E}_{x,y} \left[ m_\gamma \left( \|f(y) - x\|_2 \right)  \right].\]

Then, almost surely (for almost all \(y\)),

\[f^*(y) = \argmax_{c} p_{x \mid y}(c) = \mathrm{prox}_{-\sigma^2\log p_x}(y).\]

\(m_{\gamma}(x) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{x^2}{\gamma^2}\right)\)

Prox Matching Loss

Train a denoiser \(f\):

\(\min_{f} \mathbb{E}_{x,y} \mathcal{L}(f(y),  x) \)

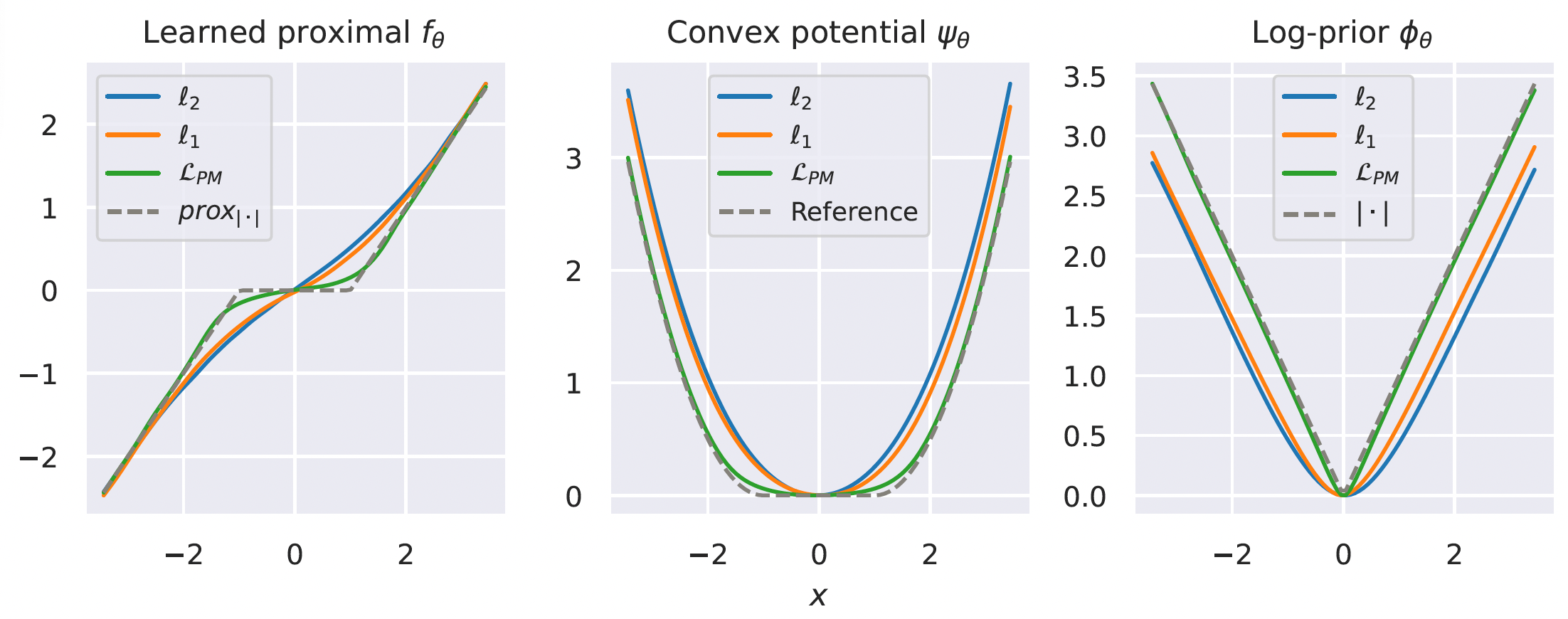
Learning a Prox for the Laplacian

Proximal matching is essential for learning the correct prox/prior

Learning a Prior for Hand-Written Digits

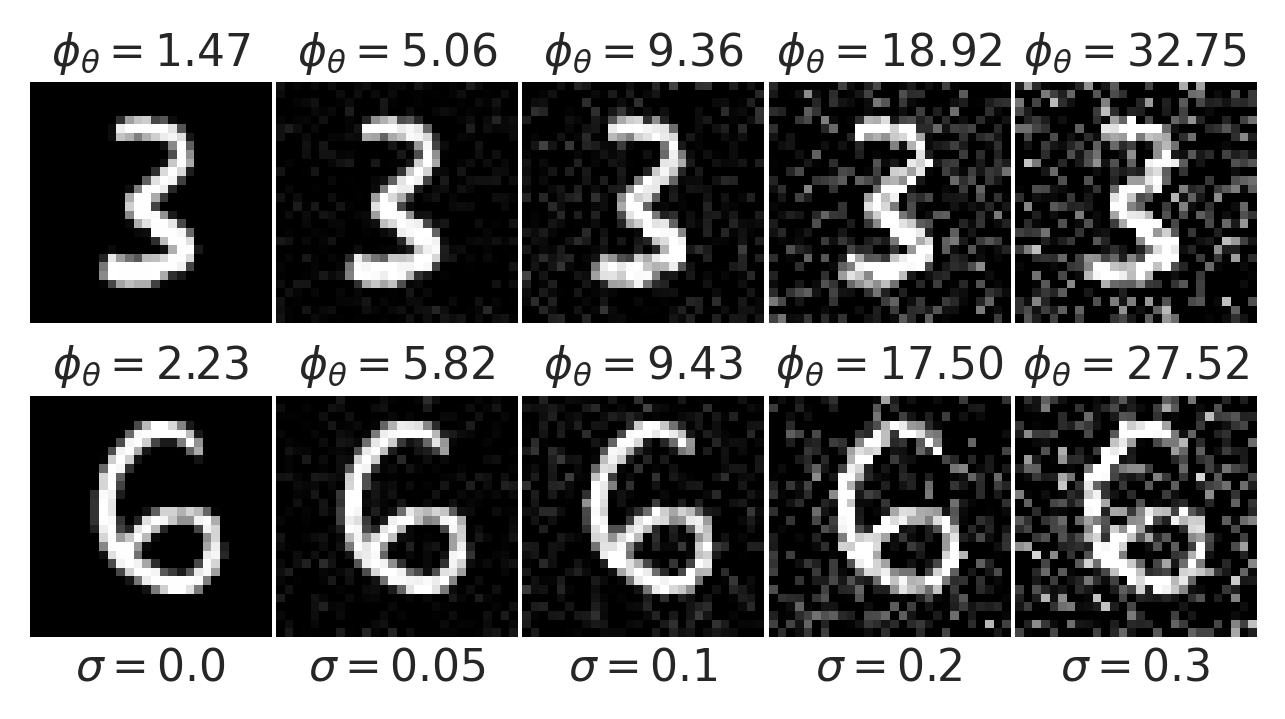
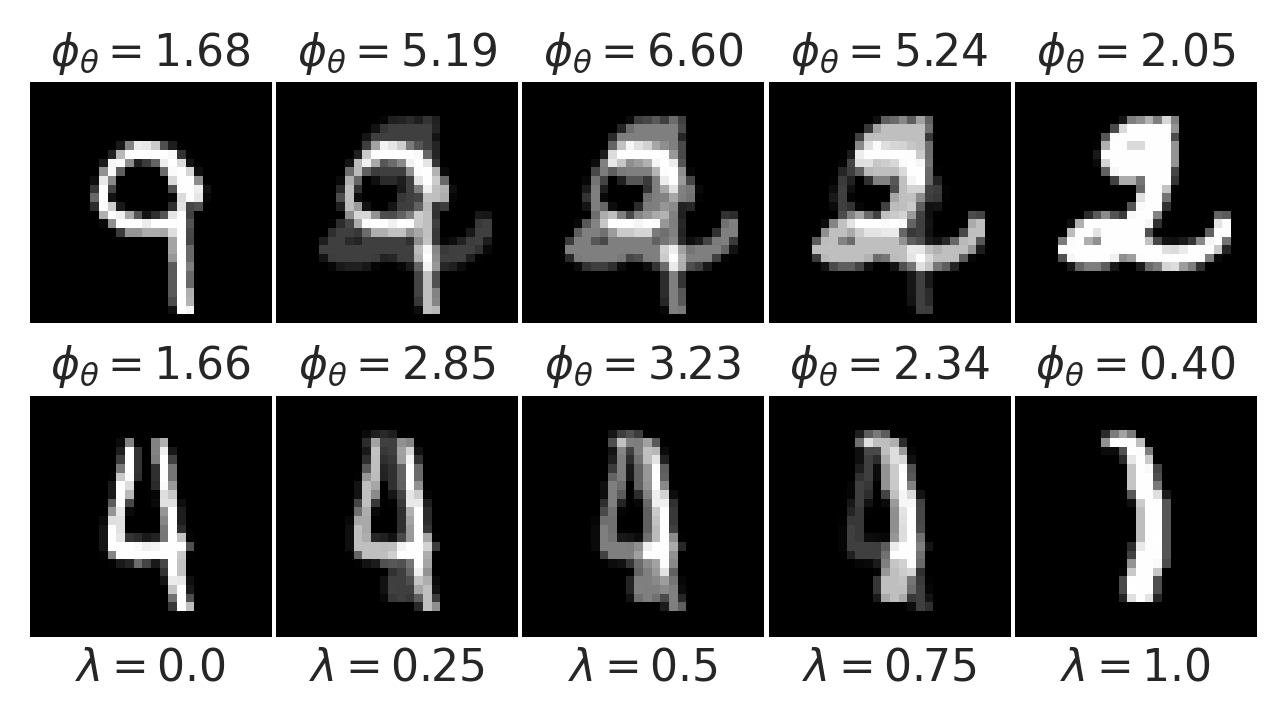
Gaussian noise

Convex interpolation

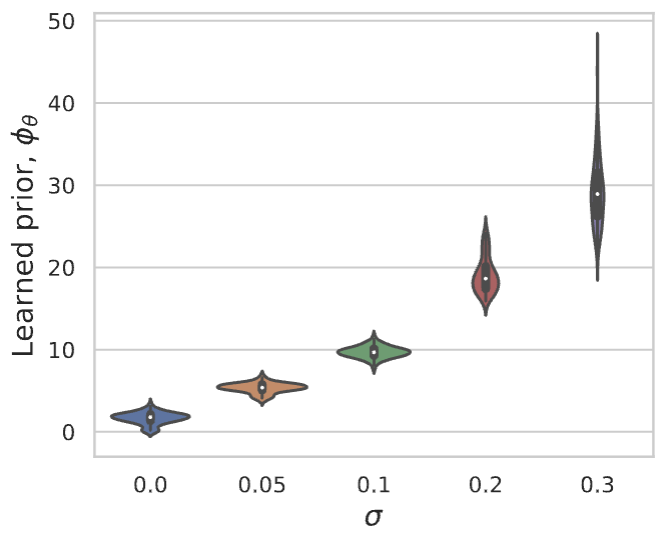
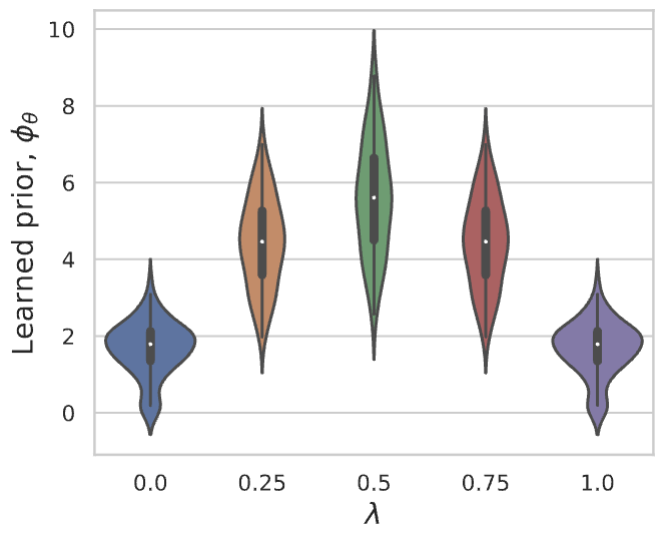
LPN faithfully captures distribution of natural images

Solving Inverse Problems

Summary

  • DeepSTI achives susceptibility tensor reconstruction using fewer orientations via data-driven prior

 

  • Learned proximal networks presents a principled and interpretable algorithm for inverse problems

Future Directions

  • Improve susceptibility imaging for MS characterization
  • Accelerate diffusion models by LPN
  • Unsupervised learning on large-scale dataset
  • Quantify uncertainty in data-driven predictions

Acknowledgements

  • NIH NIBIB (P41EB031771)
  • Distinguished Graduate Student Fellows program of the KAVLI Neuroscience Discovery Institute
Made with Slides.com