Zhenghan Fang*, Sam Buchanan*, Jeremias Sulam

ICLR 2024

Poster session: Fri 10 May 10:45 a.m.

*Equal contribution.

What's in a Prior?

Learned Proximal Networks for Inverse Problems

Sam Buchanan

TTIC

Jeremias Sulam

JHU

Shoutout to Collaborators

Inverse Problems

x
y
  • Super-resolution
  • Denoising
  • Inpainting
  • Medical imaging
  • Compressed sensing
  • ...

Measure

Inversion

y=Ax+v

Inverse Problems

y=Ax+v
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + R(x)

MAP estimate

Inverse Problems

y=Ax+v
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + {\color{darkorange} R}(x)

MAP estimate

\[{\color{darkorange}\mathrm{prox}_{R}} (z) = \argmin_u \tfrac{1}{2} \|u-z\|_2^2 + R(u)\]

x_{k+1} = {\color{darkorange}\mathrm{prox}_{\eta R}}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = {\color{darkorange} \mathrm{prox}_{R/\rho}}(u_{k+1} + x_{k+1})

Proximal Gradient Descent

ADMM

MAP denoiser

Plug-and-Play: replace \({\color{darkorange} \mathrm{prox}_{R}}\) by off-the-shelf denoisers

 Cited by 1047

{\color{darkorange} R} = -\log p_x

Inverse Problems

y=Ax+v
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + R(x)

MAP estimate

Plug-and-Play: replace \({\color{darkorange} \mathrm{prox}_{R}}\) by off-the-shelf denoisers

 Cited by 1047

x_{k+1} = {\color{red}f_{\theta}}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = {\color{red} f_\theta }(u_{k+1} + x_{k+1})

PnP-PGD

PnP-ADMM

SOTA Neural Network based Denoisers...

Inverse Problems

y=Ax+v
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + R(x)

MAP estimate

x_{k+1} = {\color{red}f_{\theta}}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = {\color{red} f_\theta }(u_{k+1} + x_{k+1})

PnP-PGD

PnP-ADMM

SOTA Neural Network based Denoisers...

  1. When is a neural network \(f_\theta\) a proximal operator?
  2. What's the prior \(R\) in the neural network \(f_\theta\)?

Questions

Learned Proximal Networks

Proposition (Learned Proximal Networks, LPN).

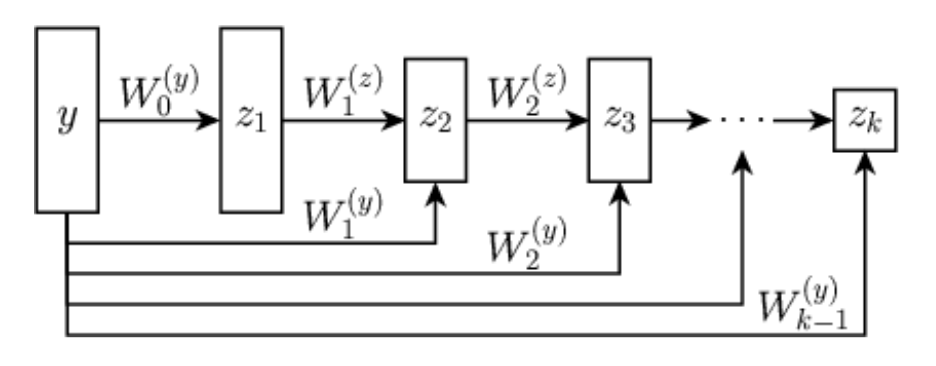
Let \(\psi_\theta: \R^{n} \rightarrow \R\) be defined by \[z_{1} = g( \mathbf H_1 y + b_1), \quad z_{k} = g(\mathbf W_k  z_{k-1} + \mathbf H_k y + b_k), \quad \psi_\theta(y) = \mathbf w^T z_{K} + b\]

with \(g\) convex, non-decreasing, and all \(\mathbf W_k\) and \(\mathbf w\) non-negative.

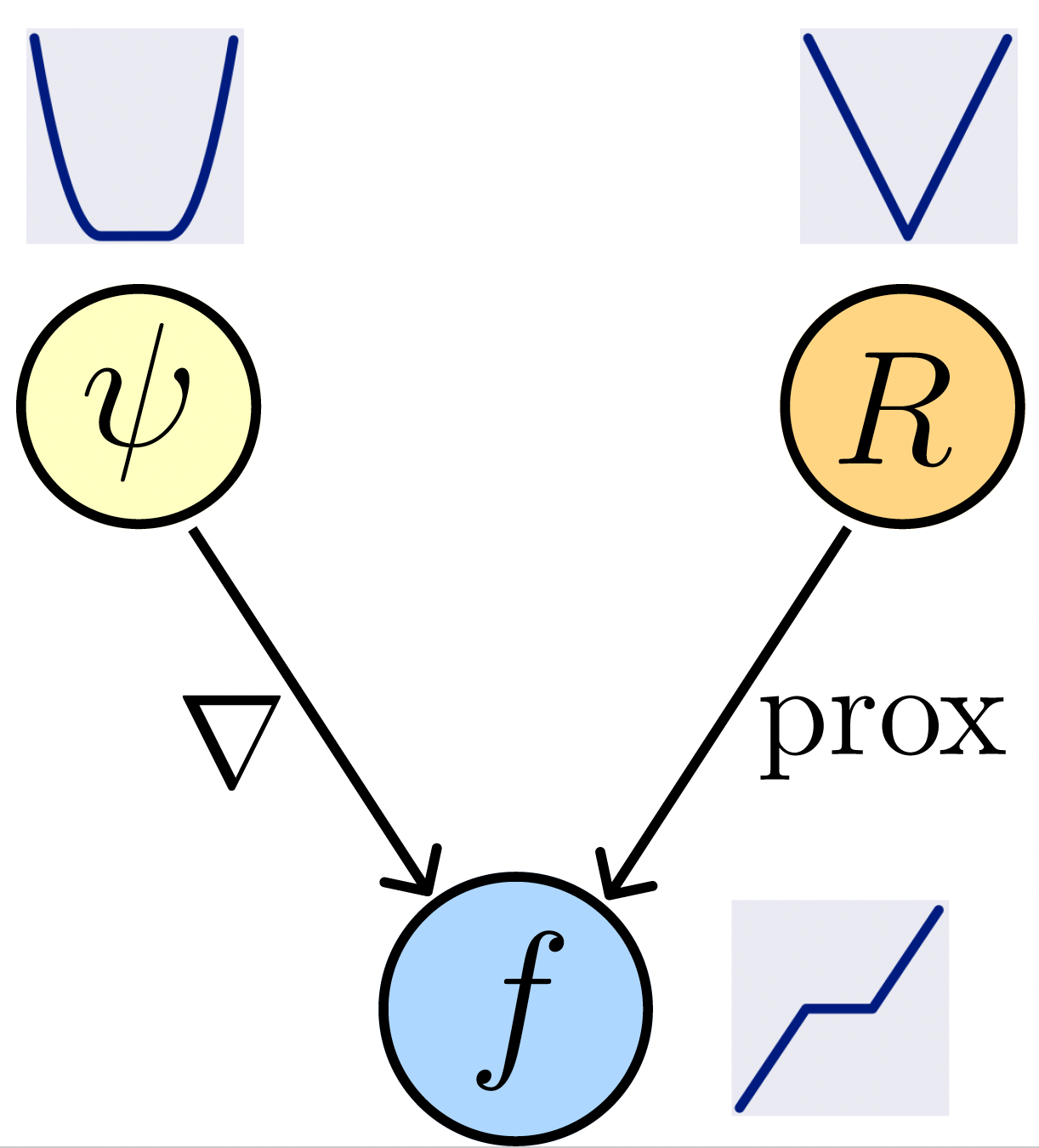
Let \(f_\theta = \nabla \psi_{\theta}\). Then, there exists a function \(R_\theta\) such that  \(f_\theta(y) = \mathrm{prox}_{R_\theta}(y)\).

Neural networks that guarantee to parameterize proximal operators

Proximal Matching

\(\ell_2\) loss \(\implies\) E[x|y], MMSE denoiser

\(\ell_1\) loss \(\implies\) Median[x|y]

Can we learn the proximal operator of an unknown prior?

\(f_\theta = \mathrm{prox}_{-\log p_x}\)

\(R_\theta = -\log p_x\)

But we want...

\(\mathrm{prox}_{-\log p_x} = \) Mode[x|y],  MAP denoiser

Conventional losses do not suffice!

Prox Matching Loss

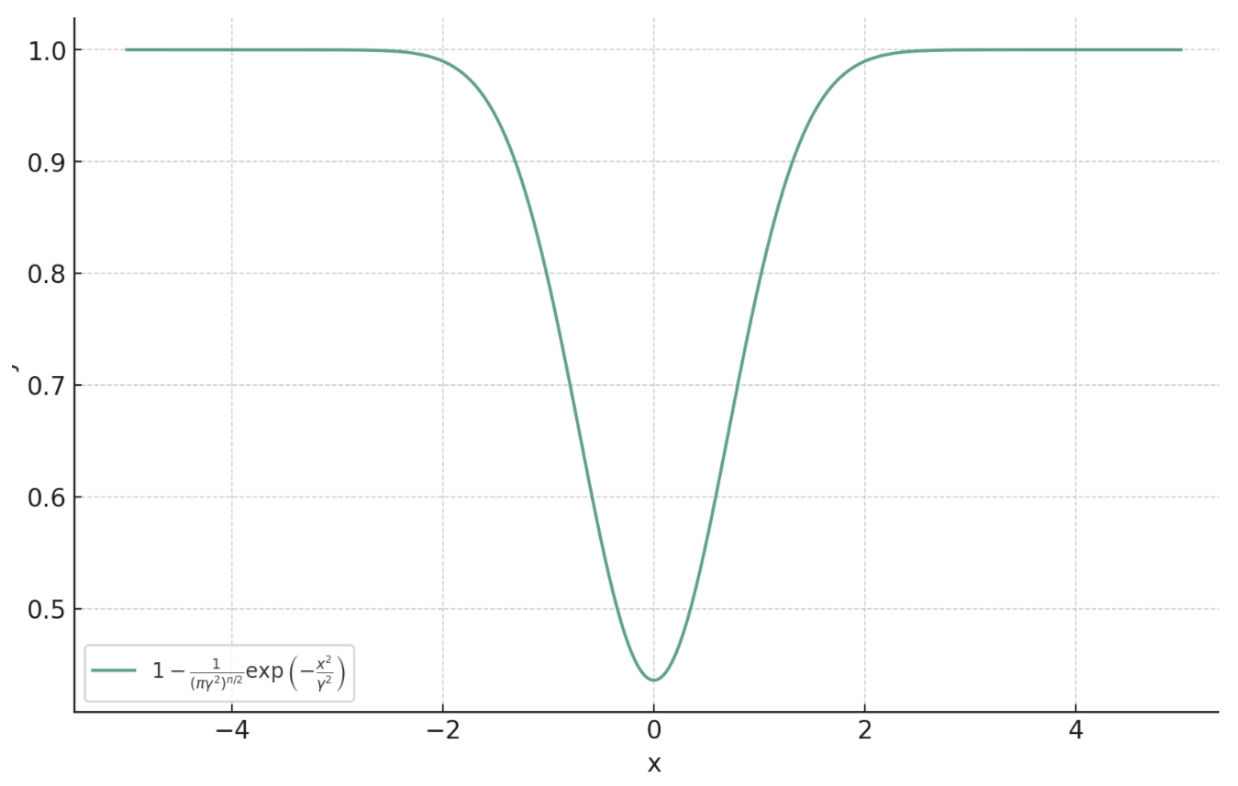
\[\ell_{\text{PM}, \gamma}(x, y) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{\|f_\theta(y) - x\|_2^2}{ \gamma^2}\right)\]

\gamma

Theorem (Prox Matching, informal).

Let
\[f^* = \argmin_{f} \lim_{\gamma \searrow 0} \mathbb{E}_{x,y} \left[ \ell_{\text{PM}, \gamma} \left( x, y \right)\right].\]

Then, almost surely (for almost all \(y\)),

\[f^*(y) = \argmax_{c} p_{x \mid y}(c) = \mathrm{prox}_{-\alpha\log p_x}(y).\]

Proximal Matching

\(\ell_2\) loss \(\implies\) E[x|y], MMSE denoiser

\(\ell_1\) loss \(\implies\) Median[x|y]

Can we learn the proximal operator of an unknown prior?

\(f_\theta = \mathrm{prox}_{-\log p_x}\)

\(R_\theta = -\log p_x\)

But we want...

\(\mathrm{prox}_{-\log p_x} = \) Mode[x|y],  MAP denoiser

Conventional losses do not suffice!

Prox Matching Loss

\[\ell_{\text{PM}, \gamma}(x, y) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{\|f_\theta(y) - x\|_2^2}{ \gamma^2}\right)\]

\gamma

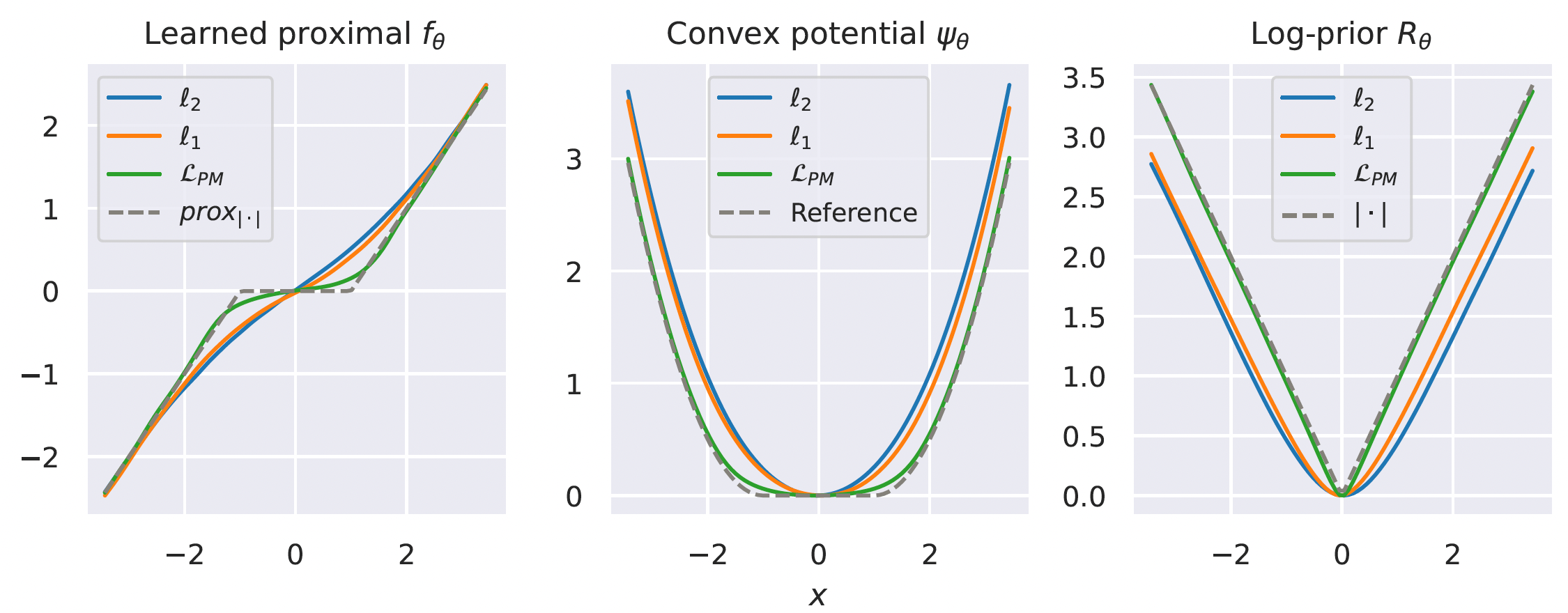
Learning the prox of a Laplacian distribution

Learned Proximal Networks

LPN provides convergence guarantees for PnP algorithms under mild assumptions.

Theorem (Convergence of PnP-ADMM with LPN, informal)

Consider running LPN with Plug-and-Play and ADMM with a linear forward operator \(A\). Assume the ADMM penalty parameter satisfies \(\rho > \|A^TA\|\). Then, the sequence of iterates converges to a fixed point of the algorithm.

Solve Inverse Problems with LPN

Sparse View Tomographic Reconstruction

Compressed Sensing

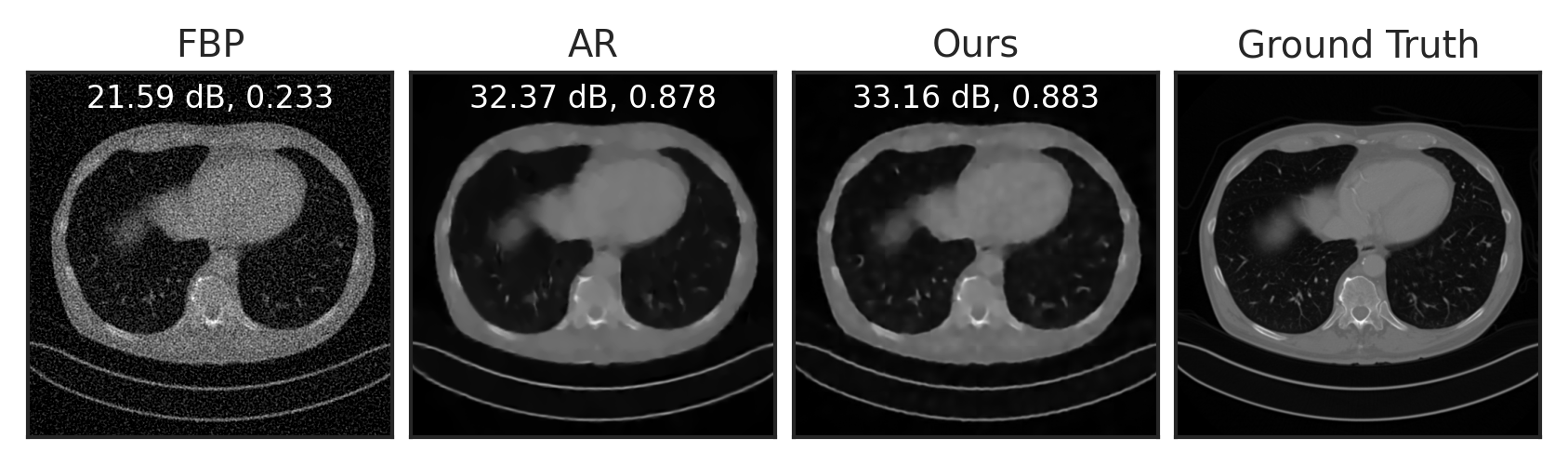
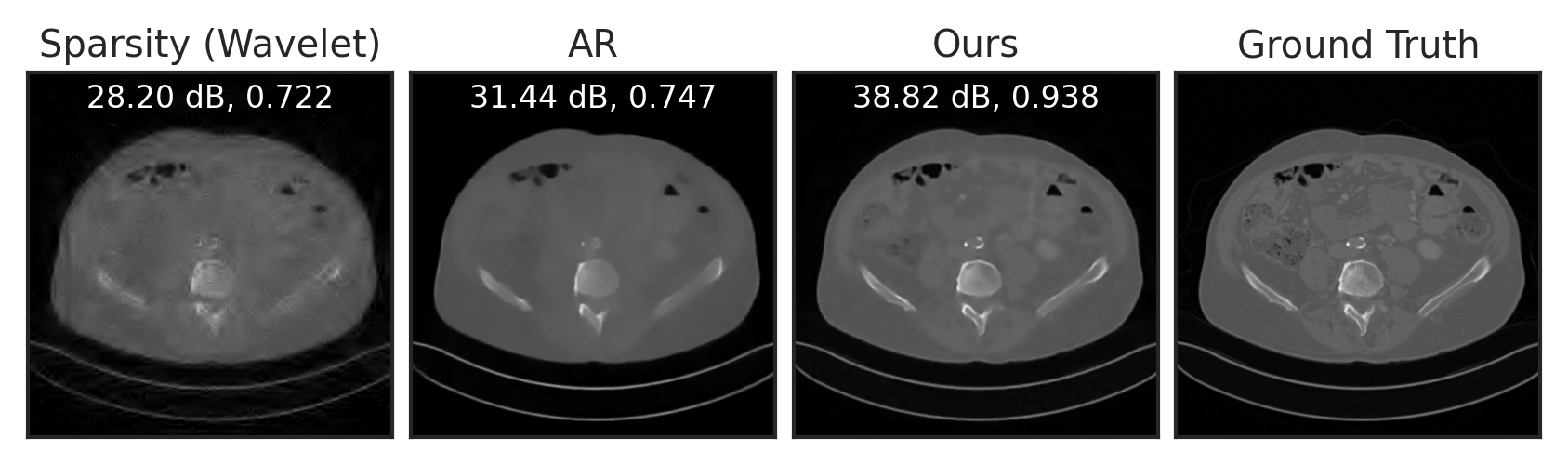
Deblurring

Summary

  • Learned proximal networks parameterize proximal operators, by construction
  • Proximal matching: learn the proximal of an unknown prior
  • Interpretable priors for inverse problem
  • Convergent PnP with LPN

Poster session: Fri 10 May 10:45 a.m.

Fang, Buchanan, Sulam.
What's in a Prior? Learned Proximal Networks for Inverse Problems.
ICLR 2024

Inverse Problems

\min_x \|y - Ax \|_2^2 + R(x)

MAP estimate

Many optimization algorithms uses the proximal operator of \(R\)...

x_{k+1} = \mathrm{prox}_{\eta R}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = \mathrm{prox}_{R/\rho}(u_{k+1} + x_{k+1})

Proximal Gradient Descent

ADMM

\[\mathrm{prox}_{R} (z) = \argmin_u \tfrac{1}{2} \|u-z\|_2^2 + R(u)\]

Plug-and-Play: Plug-in off-the-shelf denoisers for \(\mathrm{prox}_{R}\)

Learned Proximal Networks

Proposition (Learned Proximal Networks). Let \(\psi_\theta: \R^{n} \rightarrow \R\) be an input convex neural network.

Let \(f_\theta = \nabla \psi_{\theta}\). Then, there exists a function \(R_\theta\) such that  \(f_\theta(y) = \mathrm{prox}_{R_\theta}(y)\).

Neural networks that guarantee to parameterize proximal operators

f = \mathrm{prox}_R \iff \exists \psi \text{ convex}, f = \nabla \psi

\(W_i^{(z)}\) nonnegative

Learned Proximal Networks

Can we recover the prior \(R_\theta\) for an LPN \(f_\theta=\mathrm{prox}_{R_\theta}\)?

\(R(x) = \langle x, f^{-1}(x) \rangle - \frac{1}{2} \|x\|_2^2 - \psi(f^{-1}(x))\)

[Gribonval and Nikolova]

\(f_\theta\) can be inverted by solving \(\min_y \psi_{\theta}(y) - \langle x, y\rangle\).

LPN provides convergence guarantees for PnP algorithms under mild assumptions.

Theorem (Convergence of PnP-ADMM with LPN)

Consider running LPN with Plug-and-Play and ADMM with a linear forward operator \(A\). Assume the ADMM penalty parameter satisfies \(\rho > \|A^TA\|\). Then, the sequence of iterates converges to a fixed point of the algorithm.

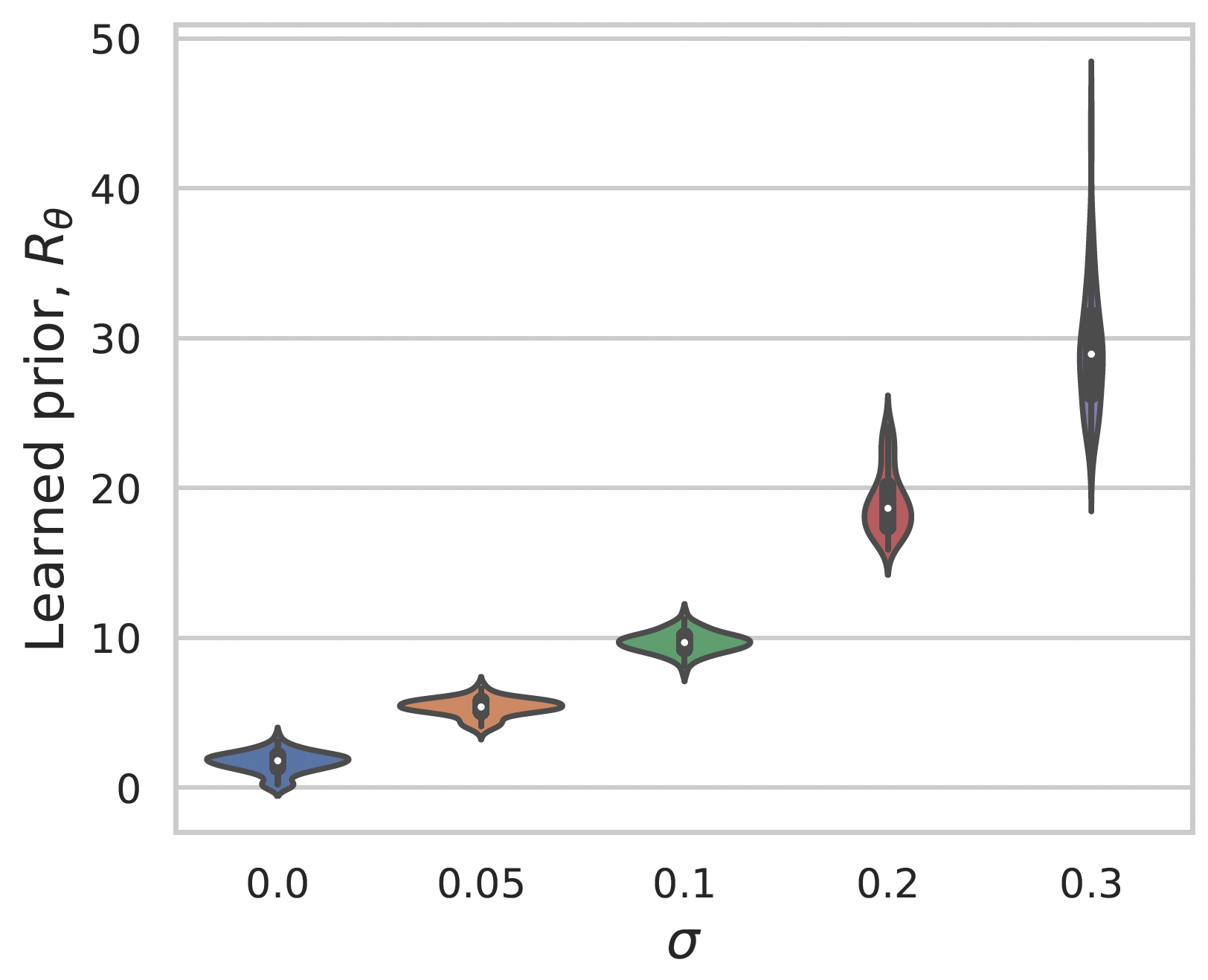
Learning a prior for MNIST images

Gaussian noise

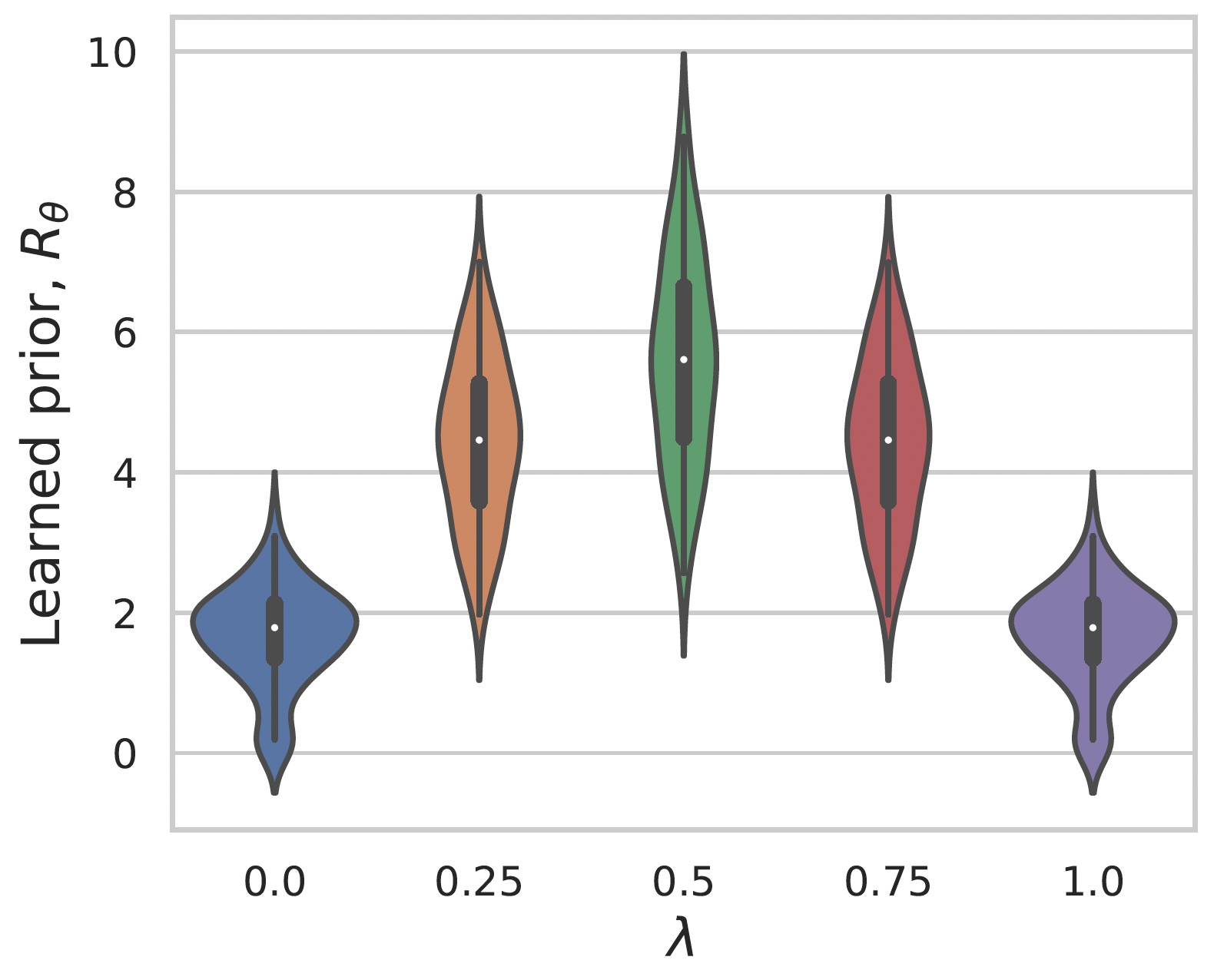
Convex interpolation

Made with Slides.com