Zhenghan Fang*, Sam Buchanan*, Jeremias Sulam

IMSI Computational Imaging Workshop

Wed, 7 Aug, 2024

*Equal contribution.

What's in a Prior?

Learned Proximal Networks for Inverse Problems

Inverse Problems

x
y
  • Computational imaging

Measure

Inversion

y=Ax+v

Inverse Problems

MAP estimate

\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + {\color{darkorange} R}(x)
{\color{darkorange} R} = -\log p_x

Prox. Grad. Desc.

x_{k+1} = {\color{darkorange}\mathrm{prox}_{\eta R}}(x_k - \eta A^H(A x_k - y))

Deep neural networks

{\color{darkorange}\mathrm{prox}_{R}} (z) = \argmin_u \tfrac{1}{2} \|u-z\|_2^2 + R(u)

Proximal Operator

x_{k+1} = \quad {\color{red}f_{\theta}} \quad \ (x_k - \eta A^H(A x_k - y))

Plug-n-Play

Questions and Contributions

1. When is a neural network \(f_\theta\) a proximal operator?

2. What's the prior \(R\) learned by the neural network \(f_\theta\)?

3. How can we learn the prox of the true prior?

4. Convergence guarantees for PnP

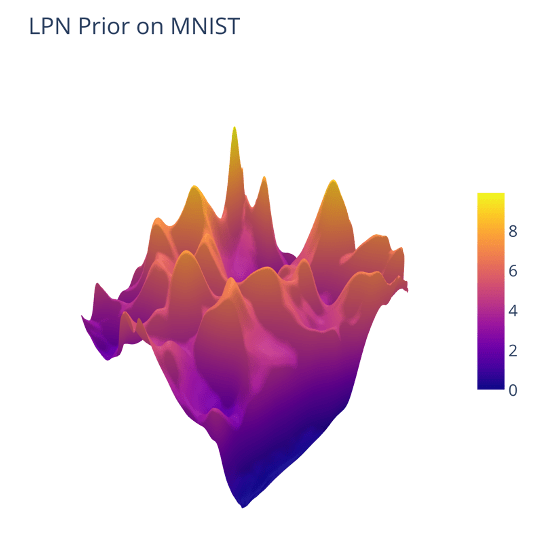
Prior Landscape

Proximal Matching Loss

Learned proximal networks (LPN)

neural networks for prox. operators

Questions and Contributions

1. When is a neural network \(f_\theta\) a proximal operator?

2. What's the prior \(R\) learned by the neural network \(f_\theta\)?

3. How can we learn the prox of the true prior?

4. Convergence guarantees for PnP

Prior Landscape

Proximal Matching Loss

Learned proximal networks (LPN)

neural networks for prox. operators

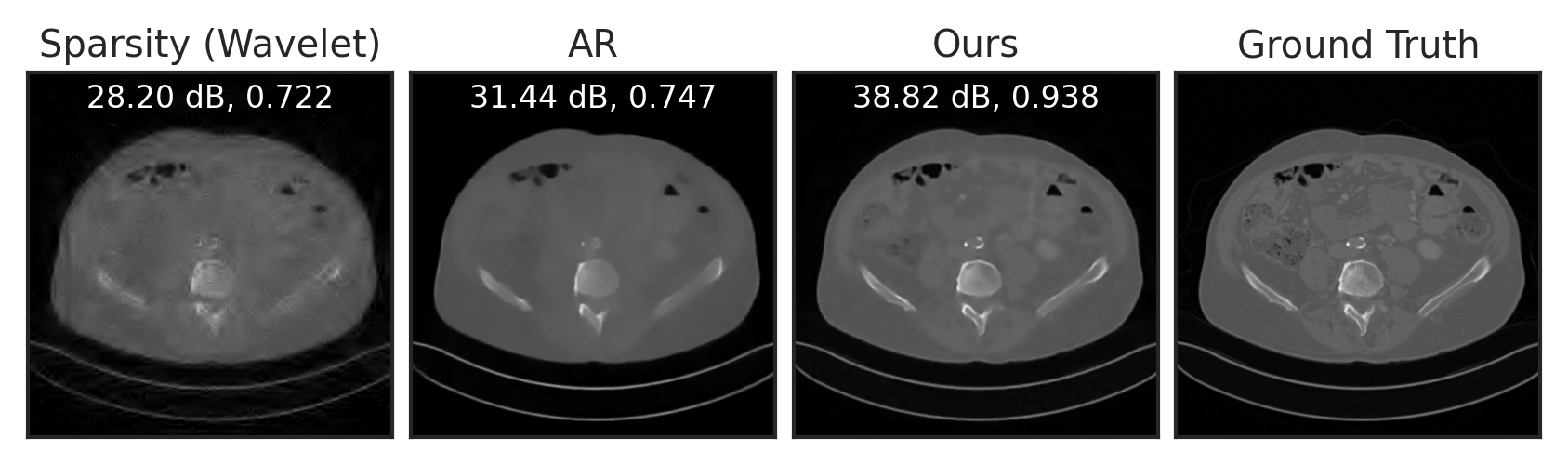
Compressed Sensing

Acknowledgements and References

Fang, Buchanan, Sulam. What's in a Prior? Learned Proximal Networks for Inverse Problems. ICLR 2024.

Sam Buchanan

TTIC

Jeremias Sulam

JHU

Inverse Problems

y=Ax+v
\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + {\color{darkorange} R}(x)

MAP estimate

x_{k+1} = {\color{darkorange}\mathrm{prox}_{\eta R}}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = {\color{darkorange} \mathrm{prox}_{R/\rho}}(u_{k+1} + x_{k+1})

Proximal Gradient Descent

ADMM

{\color{darkorange} R} = -\log p_x

\[{\color{darkorange}\mathrm{prox}_{R}} (z) = \argmin_u \tfrac{1}{2} \|u-z\|_2^2 + R(u)\]

MAP denoiser

Prox Operator

Plug-and-Play: replace \({\color{darkorange} \mathrm{prox}_{R}}\) by off-the-shelf denoisers

 Cited by 1047

Inverse Problems

y=Ax+v

MAP estimate

  1. When is a neural network \(f_\theta\) a proximal operator?
  2. What's the prior \(R\) in the neural network \(f_\theta\)?

Questions

x_{k+1} = {\color{red}f_{\theta}}(x_k - \eta A^H(A x_k - y))
x_{k+1} = \argmin_x\tfrac{1}{2} \| y - Ax \|_2^2 + \tfrac{\rho}{2} \|z_k - u_k - x\|_2^2
u_{k+1} = u_k + x_{k+1} - z_k
z_{k+1} = {\color{red} f_\theta }(u_{k+1} + x_{k+1})

PnP-PGD

PnP-ADMM

SOTA Neural Network based Denoisers...

\min_x \tfrac{1}{2}\|y - Ax \|_2^2 + {\color{darkorange} R}(x)
{\color{darkorange} R} = -\log p_x

Proximal Matching

\(\ell_2\) loss \(\implies\) E[x|y], MMSE denoiser

\(\ell_1\) loss \(\implies\) Median[x|y]

Can we learn the proximal operator of an unknown prior?

\(f_\theta = \mathrm{prox}_{-\log p_x}\)

\(R_\theta = -\log p_x\)

But we want...

\(\mathrm{prox}_{-\log p_x} = \) Mode[x|y],  MAP denoiser

Conventional losses do not suffice!

Prox Matching Loss

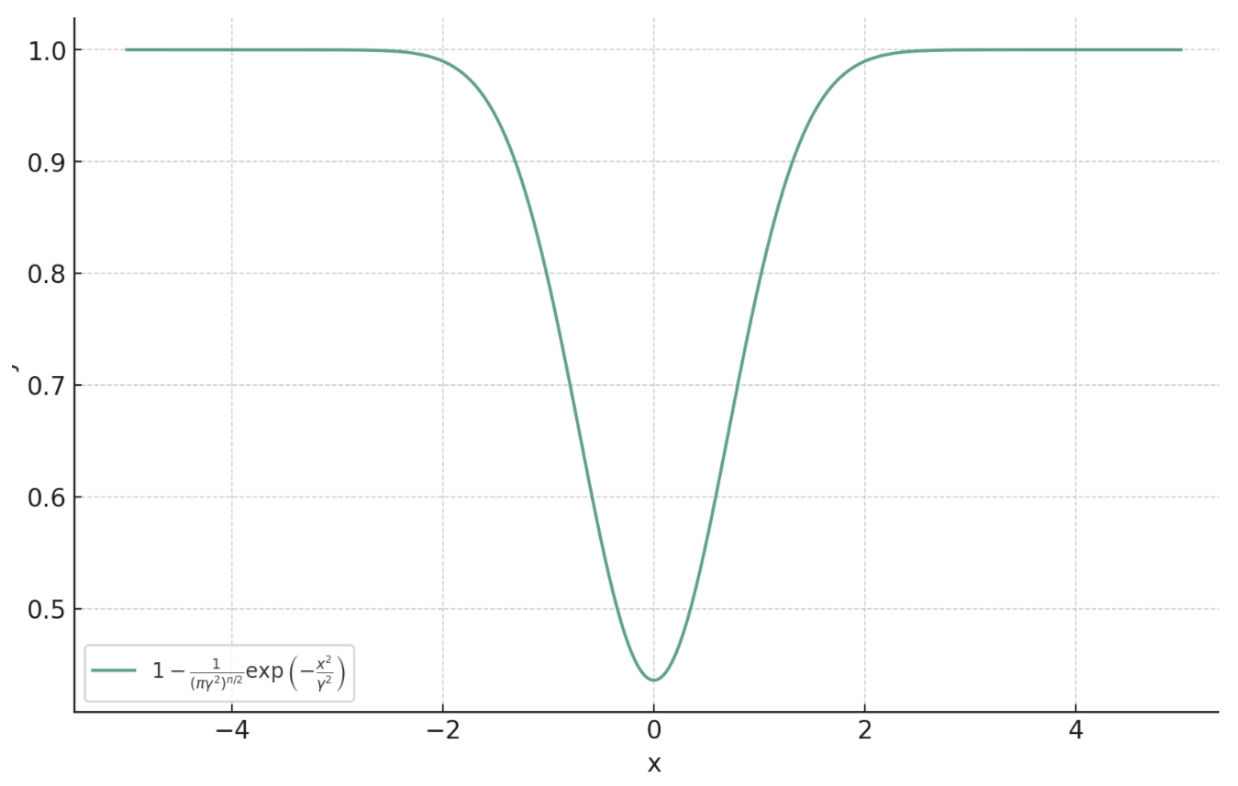
\[\ell_{\text{PM}, \gamma}(x, y) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{\|f_\theta(y) - x\|_2^2}{ \gamma^2}\right)\]

\gamma

Learning the prox of a Laplacian distribution

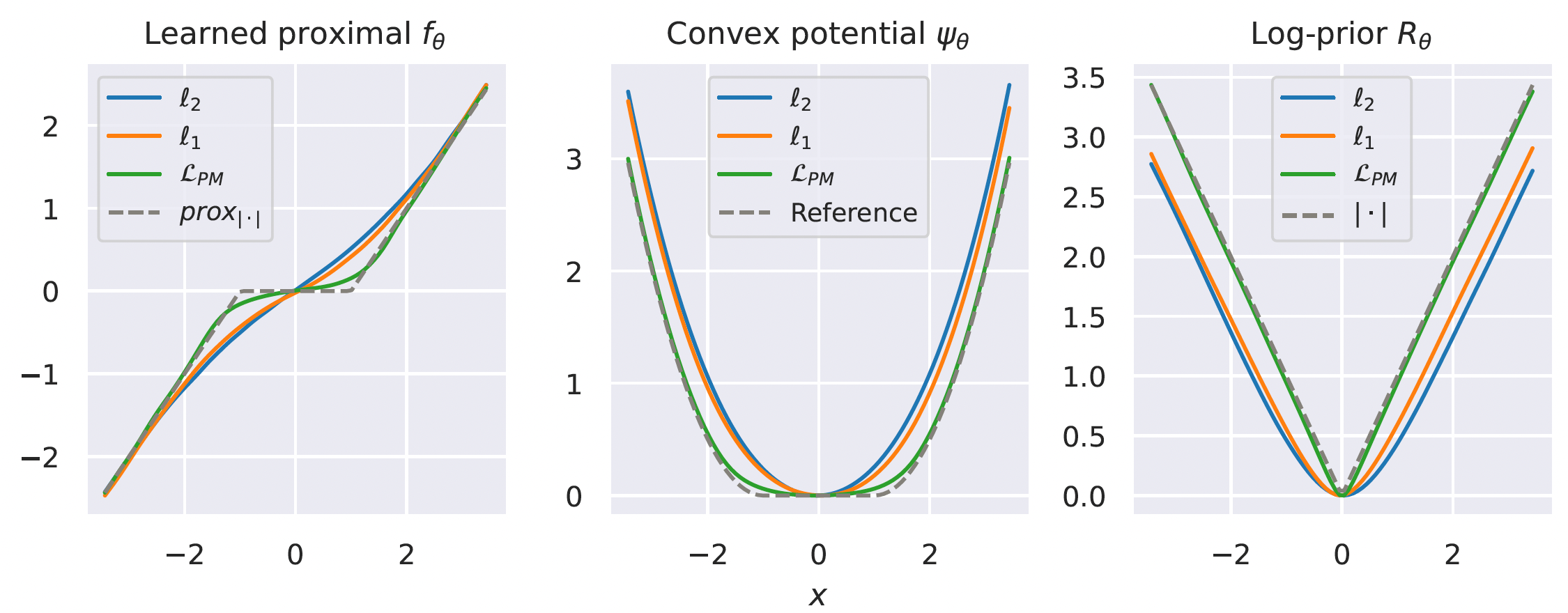
Learned Proximal Networks

Proposition (Learned Proximal Networks, LPN).

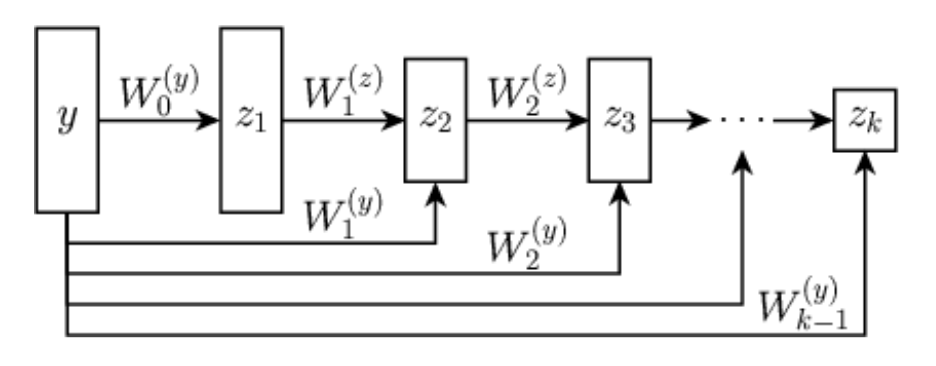
Let \(\psi_\theta: \R^{n} \rightarrow \R\) be defined by \[z_{1} = g( \mathbf H_1 y + b_1), \quad z_{k} = g(\mathbf W_k  z_{k-1} + \mathbf H_k y + b_k), \quad \psi_\theta(y) = \mathbf w^T z_{K} + b\]

with \(g\) convex, non-decreasing, and all \(\mathbf W_k\) and \(\mathbf w\) non-negative.

Let \(f_\theta = \nabla \psi_{\theta}\). Then, there exists a function \(R_\theta\) such that  \(f_\theta(y) = \mathrm{prox}_{R_\theta}(y)\).

Neural networks that guarantee to parameterize proximal operators

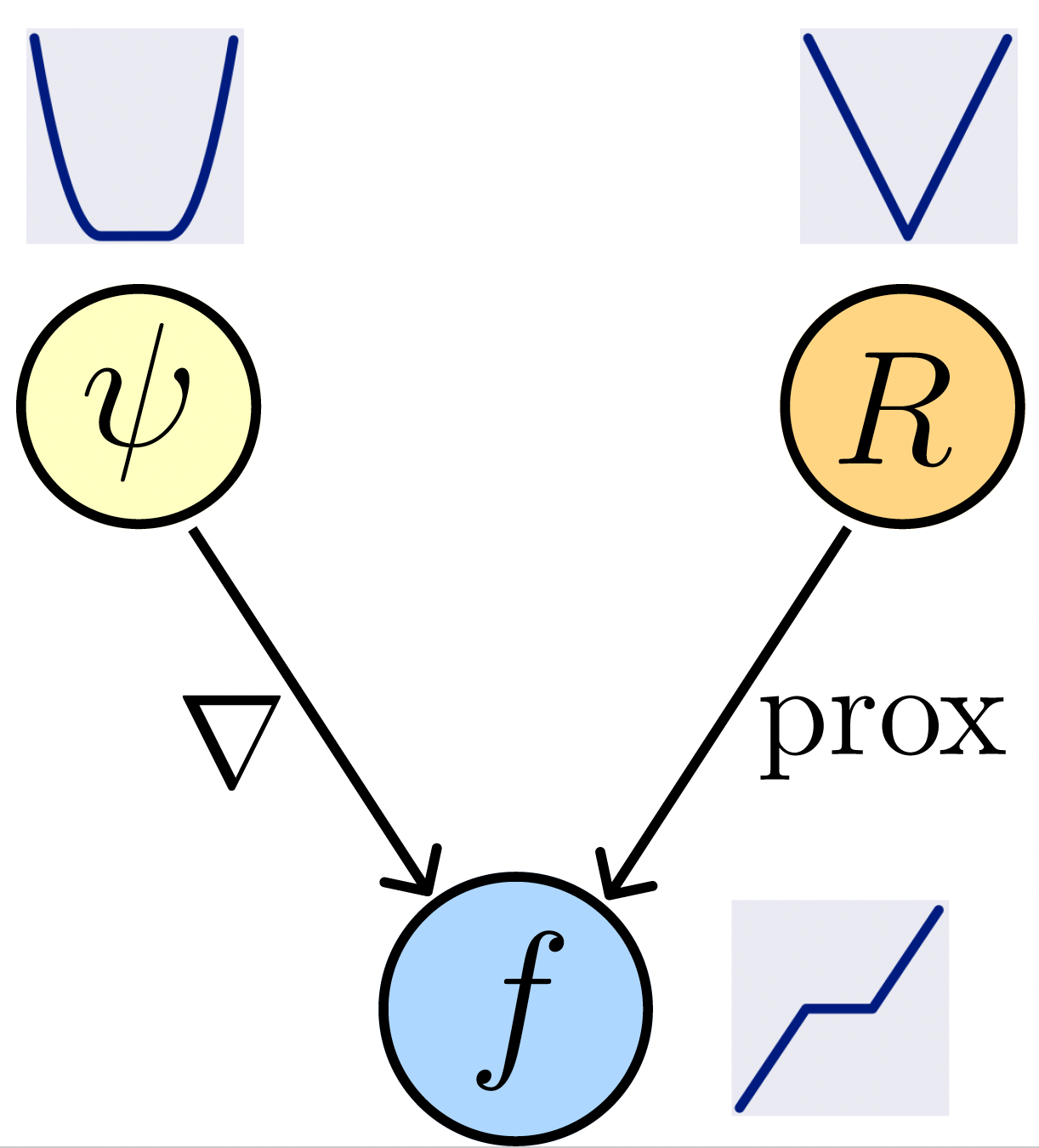
Proximal Matching

\(\ell_2\) loss \(\implies\) E[x|y], MMSE denoiser

\(\ell_1\) loss \(\implies\) Median[x|y]

Can we learn the proximal operator of an unknown prior?

\(f_\theta = \mathrm{prox}_{-\log p_x}\)

\(R_\theta = -\log p_x\)

Conventional losses do not suffice!

Prox Matching Loss

\[\ell_{\text{PM}, \gamma}(x, y) = 1 - \frac{1}{(\pi\gamma^2)^{n/2}}\exp\left(-\frac{\|f_\theta(y) - x\|_2^2}{ \gamma^2}\right)\]

\gamma

Theorem (Prox Matching, informal).

Let
\[f^* = \argmin_{f} \lim_{\gamma \searrow 0} \mathbb{E}_{x,y} \left[ \ell_{\text{PM}, \gamma} \left( x, y \right)\right].\]

Then, almost surely (for almost all \(y\)),

\[f^*(y) = \argmax_{c} p_{x \mid y}(c) = \mathrm{prox}_{-\alpha\log p_x}(y).\]

But we want...

\(\mathrm{prox}_{-\log p_x} = \) Mode[x|y],  MAP denoiser

Learned Proximal Networks

LPN provides convergence guarantees for PnP algorithms under mild assumptions.

Theorem (Convergence of PnP-ADMM with LPN, informal)

Consider running LPN with Plug-and-Play and ADMM with a linear forward operator \(A\). Assume the ADMM penalty parameter satisfies \(\rho > \|A^TA\|\). Then, the sequence of iterates converges to a fixed point of the algorithm.

Learning a prior for MNIST images

Gaussian noise

Convex interpolation

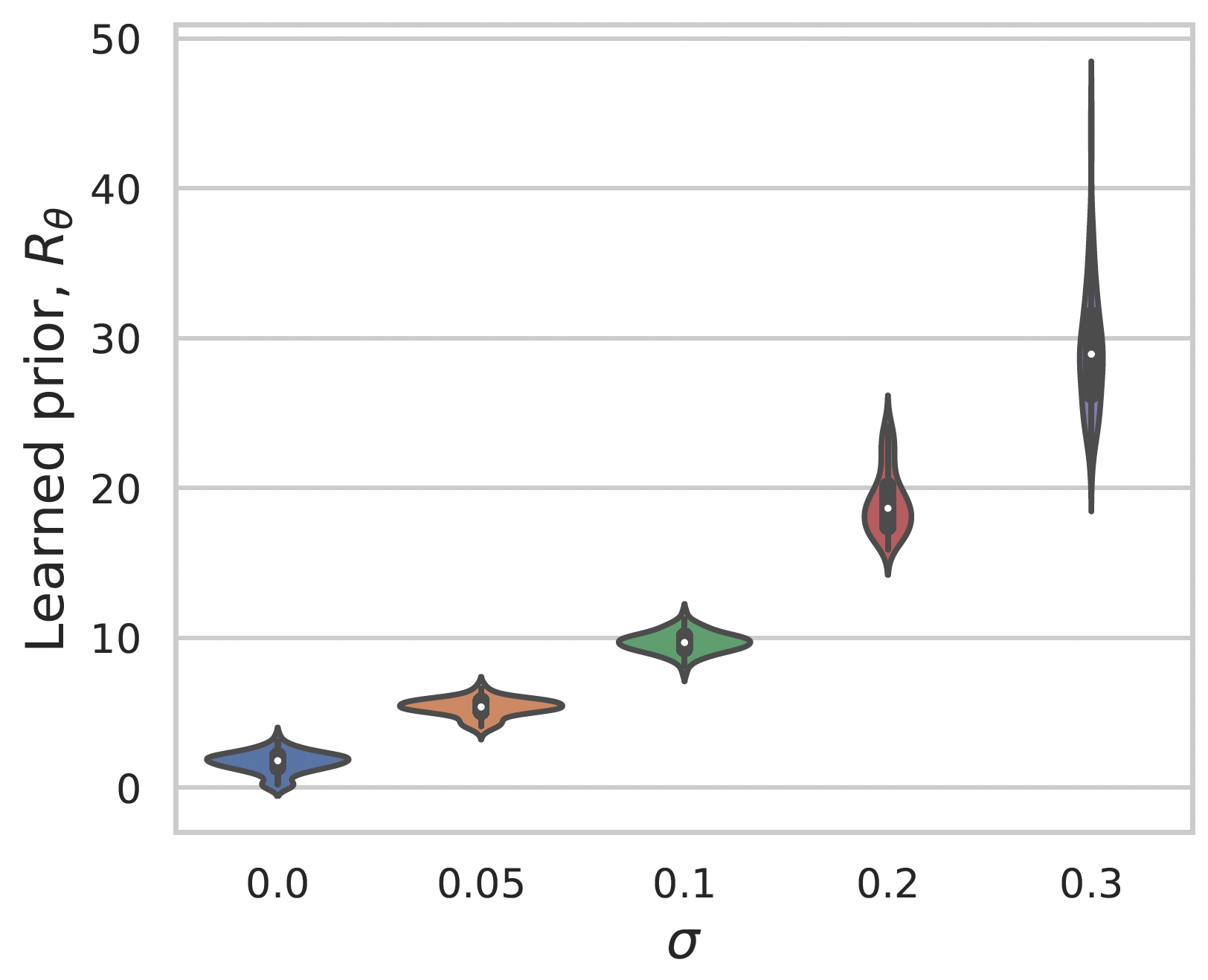
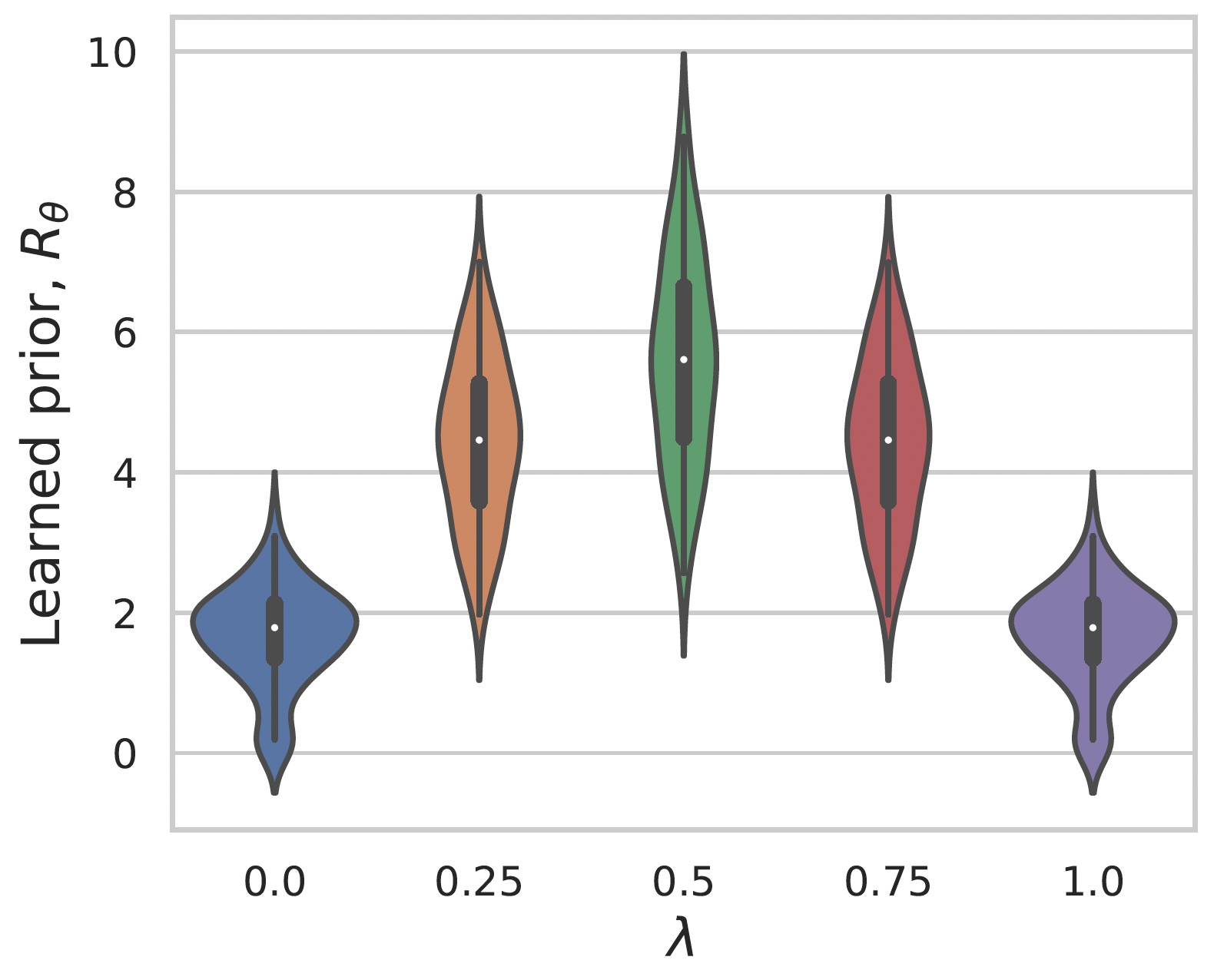
Summary

  • Learned proximal networks parameterize proximal operators, by construction
  • Proximal matching: learn the proximal of an unknown prior
  • Interpretable priors for inverse problem
  • Convergent PnP with LPN

Fang, Buchanan, Sulam. What's in a Prior? Learned Proximal Networks for Inverse Problems. ICLR 2024.

Sam Buchanan

TTIC

Jeremias Sulam

JHU

Made with Slides.com