Downloading many-body continuous variable entanglement to qubits

Zhihua Han, Kero Lau

Simon Fraser University

December 6, 2024

Outline

  1. Background and Motivation
    • Qubit and CV quantum computation
    • Cluster states
  2. Entanglement Download Protocol
    • The Displaced GKP basis
  3. Understanding noise
    • Equivalent Circuit Model
    • Finite squeezing and thermalization
  4. Suppressing noise
    • Multiple-qubits-per site
    • Weak conditional displacement
    • Physical Implementations

Imagine I have some qubits:

|+\rangle

Qubit cluster state

and now I entangle the edges with the (qubit) CZ gate.

|+\rangle

Qubit cluster state

\hat{C}_Z = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 &-1 \end{bmatrix}
\hat{C}_Z

For this talk, I will define a entanglement gate as a two-qubit/qumode gate.

and now I entangle the edges with the (qubit) CZ gate.

|+\rangle

Qubit cluster state

\hat{C}_Z

In the circuit model, it looks like this:

|+\rangle

Qubit cluster state

Adjacency matrix

\mathbf{A} = \begin{bmatrix} 0 & 1 & 0 \\1 & 0 & 1\\ 0 & 1 & 0\end{bmatrix}

\(A_{ij} = 1 \) if \(i\) and \(j\) have an edge

\begin{aligned} &= |G\rangle \end{aligned}

The quantum state specified by \(G\) is called a qubit cluster state.

\begin{aligned} &= |G\rangle\\ &= \hat{\mathbf{C}}_{Z}(\mathbf{A}) |+\rangle^{\otimes N} \end{aligned}
\hat{C}_Z
|+\rangle

Qubit cluster state

Bold CZ means apply according to the graph structure.

Qubit cluster state

+

Single qubit measurements

Fault tolerant universal quantum computation

(Raussendorf 2001)

Why we need qubit cluster state

|+\rangle

First entangle 1 and 2, then entangle 2 and 3

"Bottom up approach"

How to make qubit cluster states?

|+\rangle

Two qubit gates are typically the noisiest gate in hardware

"Bottom up approach"

How to make qubit cluster states?

Superconducting qubits: 51

Photonic qubits: 14

Trapped ion: 32

How to make qubit cluster states?

Qubit cluster state

+

Single qubit measurements

Fault tolerant universal quantum computation

  • "Want to replace circuit model because two qubit gates have too much noise"
  • "Need better two qubit gates to replace the circuit model"

How to make qubit cluster states?

Qubit cluster state

Why we need qubit cluster state

Goal: Make many body entanglement in physical qubits

How do we make scalable qubit cluster states?

"Downloading entanglement from a CV cluster state"

Continuous variable (CV) cluster state

Physical qubits

\hat{S}(r)|\mathrm{vac}\rangle
\hat{C}_Z^\mathrm{CV}

Entanglement Download Protocol

How do we make scalable qubit cluster states?

Entanglement Download Protocol

Continuous variable (CV) cluster state

Qubit cluster state

\hat{S}(r)|\mathrm{vac}\rangle
\hat{C}_Z^\mathrm{CV}

Entanglement Download Protocol

"Top down approach"

Now if I have some qumodes:

\hat{S}(r)|\mathrm{vac}\rangle

CV cluster state

Squeezed vacuum state

and entangle them with CV CZ gate:

\hat{S}(r)|\mathrm{vac}\rangle
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}

CV cluster state

We say it is a CV cluster state.

\hat{S}(r)|\mathrm{vac}\rangle
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}
\begin{aligned} &= |G\rangle^\mathrm{CV} \end{aligned}
\begin{aligned} &= |G\rangle^\mathrm{CV}\\ &= \hat{\mathbf{C}}_{Z}^\mathrm{CV}(\mathbf{A}) (\hat{S}(r)|\mathrm{vac}\rangle )^{\otimes N} \end{aligned}

CV cluster state

\(r\) is the squeezing of the squeezed state. 

\hat{S}(r)|\mathrm{vac}\rangle

When \(r \to \infty\), the CV cluster state is an ideal CV cluster state.

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle

Finite vs Ideal CV cluster state

\(r\) is the squeezing of the squeezed state.

\hat{S}(r)|\mathrm{vac}\rangle

\(p\)

|0\rangle_p

Finite vs Ideal CV cluster state

When \(r \to \infty\), the CV cluster state is an ideal CV cluster state.

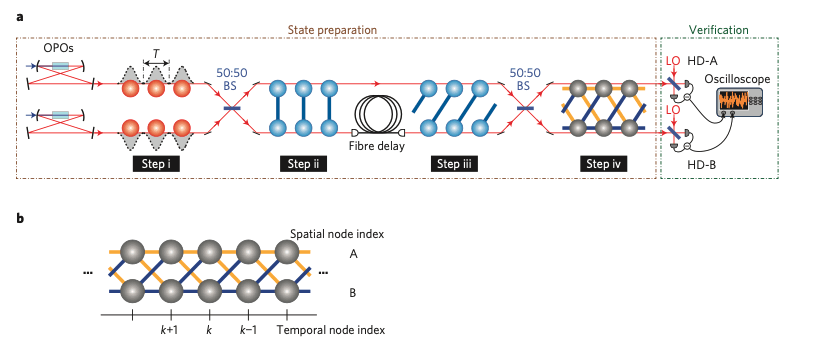
10000 modes! 1D, (Furusawa 2013)

How to make CV cluster state

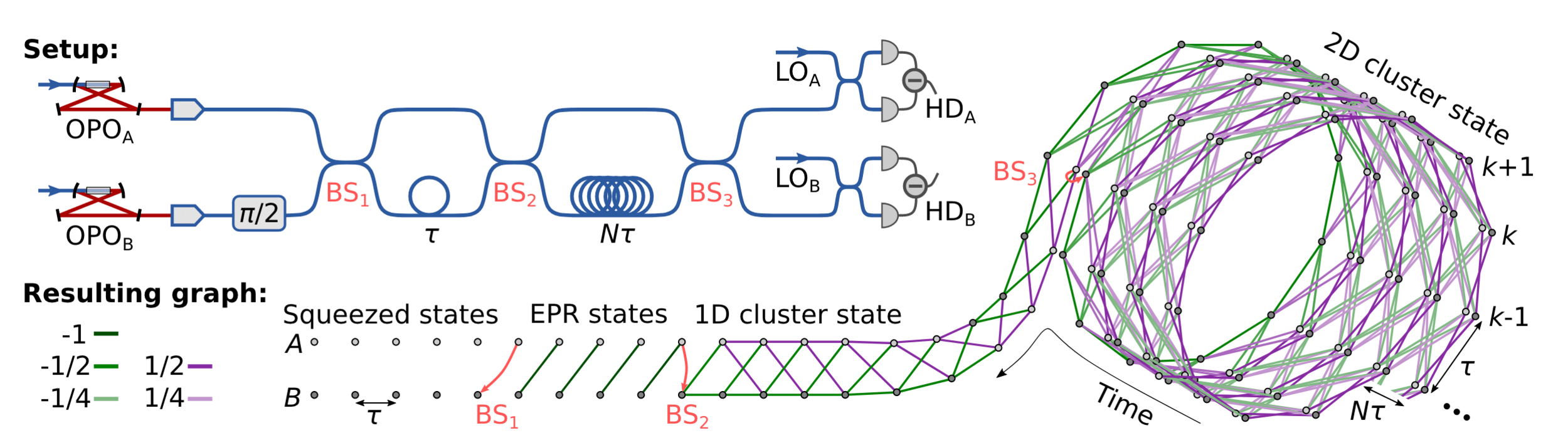
1 million modes, 1D, (Furusawa 2016)

How to make CV cluster state

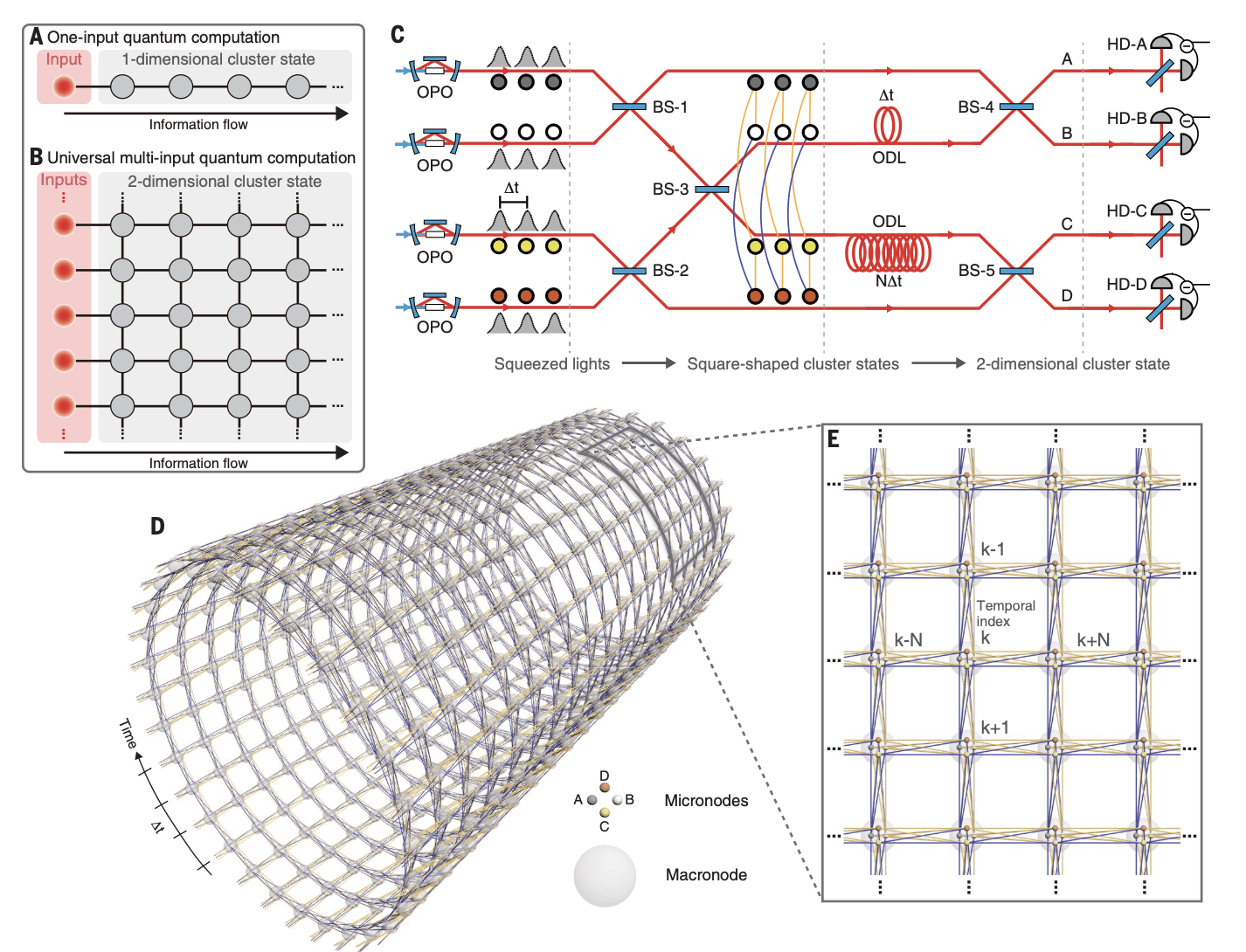
 5x1240 modes, 2D, (Furusawa 2019)

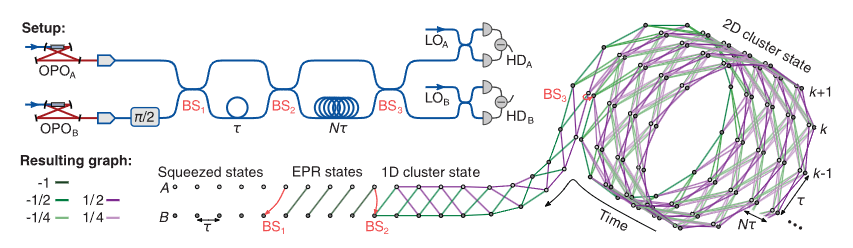
24x1250, 2D (Andersen 2019)

How to make CV cluster state

Can generate CV cluster state with engineered dissipation

Ideal CV cluster state

|G\rangle^\mathrm{CV} = \hat{\mathbf{C}}_{Z}^\mathrm{CV}(\mathbf{A}) |0\rangle_p^{\otimes N}
|0\rangle_p
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}

Qubit cluster state

\begin{aligned} |G\rangle= \hat{\mathbf{C}}_{Z}(\mathbf{A}) |+\rangle^{\otimes N} \end{aligned}
|+\rangle
\hat{C}_Z = \text{diag}(1, 1, 1, -1)

CV vs qubit cluster state

Continuous variable (CV) cluster state

Physical qubits

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

How to perform entanglement transfer?

\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}
\hat{C}_Z = \text{diag}(1, 1, 1, -1)

Entanglement download protocol

How to perform entanglement transfer?

Continuous variable (CV) cluster state

Qubit cluster state

|0\rangle_p
\hat{C}_Z
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}
\hat{C}_Z = \text{diag}(1, 1, 1, -1)

Entanglement download protocol

 We need: 

  • A CV cluster state*
  • \(\hat{q}\) quadrature homodyne detection
  • Conditional displacement gate \( \hat{C}_D\)
\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})

How to perform entanglement transfer?

Entanglement download protocol

1. Initialize all qubits to \(|+\rangle\).

(These are physical qubits)

|+\rangle

Entanglement Download Protocol

Step 2: Prepare a CV cluster state.

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

Entanglement Download Protocol

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

Entanglement Download Protocol

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

\hat{C}_D

Entanglement Download Protocol

Step 4. Measure \(q\) quadrature.

Entanglement Download Protocol

1. Initialize all qubits to \(|+\rangle\).

|+\rangle

Entanglement Download Protocol

|+\rangle

Entanglement Download Protocol

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

2. Prepare a CV cluster state.

Entanglement Download Protocol

|+\rangle
|0\rangle_p

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

Entanglement Download Protocol

|+\rangle
|0\rangle_p
\hat{C}_D

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

Entanglement Download Protocol

Step 4. Measure the \(q\) quadrature and correct phases.

|+\rangle
|0\rangle_p

You now have a qubit cluster state!

But why does it work?

Entanglement Download Protocol

We show there is a hidden qubit cluster state inside a CV cluster state! 

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

\(q\)

\(q\)

\(q\)

\(q\)

CV cluster state

Qubit cluster inside CV cluster

Logical qubit cluster state!

|0^\mathrm{GKP}\rangle = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

Gottesman-Kitaev-Preskill (GKP state)

\(q\)

\(|2n\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

GKP Background

|1^\mathrm{GKP}\rangle = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\hat{X}^{\mathrm{GKP}} = e^{-i \sqrt \pi \hat p} = \hat{D}_q(\sqrt{\pi})

GKP Background

|1^\mathrm{GKP}\rangle = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\(|2n\sqrt{\pi}\rangle\)

|0^\mathrm{GKP}\rangle = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

GKP Background

|+^\mathrm{GKP}\rangle = \sum_{n=-\infty}^{\infty} |n\sqrt{\pi}\rangle_q = \frac{1}{\sqrt{2}}(|0^\mathrm{GKP}\rangle + |1^\mathrm{GKP}\rangle)

\(|2n\sqrt{\pi}\rangle\)

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

GKP Background

\(p\)

|0\rangle_p

Node of ideal CV cluster

\(q\)

|0\rangle_p

Node of ideal CV cluster

\(q\)

|0\rangle_p
|+^\mathrm{GKP}\rangle

GKP state

Node of ideal CV cluster

\(q\)

|0\rangle_p

\(\mu_q\)

\mu_q \in [-\frac{\sqrt{\pi}}{2}, -\frac{\sqrt{\pi}}{2})
\hat{D}_q(\mu_q)|+^\mathrm{GKP}\rangle

Displaced GKP state

|+^\mathrm{GKP}_{\mu_q, 0} \rangle \equiv \hat{D}_q(\mu_q)|+^\mathrm{GKP}\rangle

(Glancy 2006)

Displaced GKP

\(q\)

|0\rangle_p
|+^\mathrm{GKP}_{\mu_q, 0} \rangle \equiv \hat{D}_q(\mu_q)\hat{D}_p(0)|+^\mathrm{GKP}\rangle

So if we integrate over \(\mu_q\), we form an ideal \(|0\rangle_p\) state with \(\mu_p = 0\).

Node of ideal CV cluster is superposition of displaced GKP

Displaced GKP Basis

 

(Glancy 2006)

\(\mu_q\) displacement is color coded

\(q\)

|0\rangle_p
+
+
+
+
= \int d\mu_q

Node of ideal CV cluster is superposition of displaced GKP

=

Displaced GKP Basis

CV Basis

A single zero momentum state is a superposition of displaced GKP states.

\(q\)

|0\rangle_p
= \int d\mu_q

Node of ideal CV cluster is superposition of displaced GKP

=

Displaced GKP Basis

CV Basis

A single zero momentum state is a superposition of displaced GKP states.

\(q\)

= \int d\bm{\mu_q }

Node of ideal CV cluster is superposition of displaced GKP

Multiple zero momentum states is multiple integrals of displaced GKP states.

\(q\)

\(q\)

\(q\)

\pmb{\mu_q} = \begin{bmatrix} \mu_{q_1} \\ \vdots\\ \mu_{q_N}\\ \end{bmatrix}
\ket{+^{\mathrm{GKP}}_{\pmb{\mu_q, 0}}}^{\otimes N}
\pmb{\mu_q} = \begin{bmatrix} \mu_{q_1} \\ \vdots\\ \mu_{q_N}\\ \end{bmatrix}

To keep track of displaced GKP states, we define the pair \((\bm{\mu_q}, \bm{\mu_p})\), where

Node of ideal CV cluster is superposition of displaced GKP

\pmb{\mu_p} = \begin{bmatrix} \mu_{p_1} \\ \vdots\\ \mu_{p_N}\\ \end{bmatrix}

Ideal zero momentum eigenstates: \(\bm{\mu_p} = 0\)

\(q\)

|0\rangle_p
= \int d\mu_q

Node of ideal CV cluster is superposition of displaced GKP

=

Displaced GKP Basis

CV Basis

\(q\)

Node of ideal CV cluster is superposition of displaced GKP

The next step as per the protocol is applying CV CZ.

\int d\bm{\mu_q}\ket{+^{\mathrm{GKP}}_{\pmb{\mu_q, 0}}}^{\otimes N}

Let's translate these gates into the displaced GKP basis , which will reveal the mystery.

Edge of ideal CV cluster is logical CZ

= \frac{1}{2}(|00\rangle_\mathrm{GKP} + |01\rangle_\mathrm{GKP} + |10\rangle_\mathrm{GKP} -|11\rangle_\mathrm{GKP})
\hat{C}_Z^\mathrm{CV} \ket{++}_{\mathrm{GKP}}

Logical qubit CZ gate on GKP states!

= \sum_{n_1, n_2}e^{i \pi n_1 n_2} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q
\equiv \hat{C}_Z^\mathrm{GKP} \ket{++}_{\mathrm{GKP}}
\hat{C}_Z^\mathrm{CV}

CV CZ applied to a (non-displaced) GKP state

Edge of ideal CV cluster is logical CZ

The generalization is much more involved, but it can be written in a single line.

\hat{\mathbf{C}}_{Z}^\mathrm{CV}(\mathbf{A}) \ket{+_{\bm{\mu_q}, \bm{0}}}^{\otimes N}_{\mathrm{GKP}} = \hat{\mathbf{C}}_{Z}^\mathrm{GKP}(\mathbf{A}) \ket{+_{\bm{\mu_q}, \mathbf{A}\bm{\mu_q}}}^{\otimes N}_{\mathrm{GKP}}

(Global phase omitted)

\(q\)

|0\rangle_p

Edges of ideal CV cluster

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
=

\(q\)

|0\rangle_p

Edges of ideal CV cluster

+
+
+
+
+
+
+
+

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
=
=

\(q\)

|0\rangle_p
+
+
+
+
+
+
+
+

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
= \iint d \mu_{q_1} d \mu_{q_2}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}

Edges of ideal CV cluster

\hat{C}_Z^\mathrm{CV}

Displaced GKP Basis

CV Basis

\(q\)

|0\rangle_p
+
+
+
+
+
+
+
+

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}

Edges of ideal CV cluster

= \iint d \mu_{q_1} d \mu_{q_2}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}

Edge of ideal CV cluster is logical CZ

\hat{\mathbf{C}}_{Z}^\mathrm{CV}(\mathbf{A}) \ket{+_{\bm{\mu_q}, \bm{0}}}^{\otimes N}_{\mathrm{GKP}} = \hat{\mathbf{C}}_{Z}^\mathrm{GKP}(\mathbf{A}) \ket{+_{\bm{\mu_q}, \mathbf{A}\bm{\mu_q}}}^{\otimes N}_{\mathrm{GKP}}

(Global phase omitted)

A CV CZ gate is a logical CZ gate, but it changes the displacement in \(\bm{\mu_p}\).

An ideal CV cluster state: \(\bm{\mu_p} = \mathbf{A} \bm{\mu_q}\).

Edge of ideal CV cluster is logical CZ

\hat{C}_D(\sqrt{\pi})|+\rangle|L_{\mu_q, \mu_p}^{\mathrm{GKP}}\rangle = |0\rangle|L_{\mu_q, \mu_p}^{\mathrm{GKP}}\rangle + e^{-i\mu_p\sqrt{\pi}}|1\rangle|(L+1)_{\mu_q, \mu_p}^{\mathrm{GKP}} \rangle

Next is conditional displacement, which acts as a logical X gate + a phase shift on the qubit.

From the last slide, an ideal CV cluster state has \(\bm{\mu_p} = \mathbf{A} \bm{\mu_q}\).

Edge of ideal CV cluster is logical CZ

Next is conditional displacement, which acts as a logical X gate + a phase shift on the qubit.

\hat{C}_D(\sqrt{\pi})|+\rangle|L_{\mu_q, \mu_p}^{\mathrm{GKP}}\rangle = |0\rangle|L_{\mu_q, \mu_p}^{\mathrm{GKP}}\rangle + e^{-i\mu_p\sqrt{\pi}}|1\rangle|(L+1)_{\mu_q, \mu_p}^{\mathrm{GKP}} \rangle
=

\(q\)

|0\rangle_p

\(\mu_q\)

\mu_q \in [-\frac{\sqrt{\pi}}{2}, -\frac{\sqrt{\pi}}{2})
q = (2n+L)\sqrt\pi + \mu_q

Finally, if we measure the \(q\) quadrature of the displaced GKP state, we can infer the \(\mu_q\) displacement and the logical value \(L\)!

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\(|2n\sqrt{\pi}\rangle\)

qubit 

qubit 

qubit 

One bit teleportation

For qubits, the one-bit teleportation circuit is 

qubit 

qubit 

qubit 

One bit teleportation

One bit teleportation

We can add in a rotation by \(\theta\) without changing the end result.

One bit teleportation

Hybrid one-bit teleportation

Normally, we can't do much since we don't know \(\mu_p\)...

One bit teleportation

If this state was part of an ideal CV cluster state, \(\bm{\mu_p} = \mathbf{A} \bm{\mu_q}\).

This means for an ideal CV cluster state we can download whatever logical information is in the displaced GKP state, i.e. the entanglement!

The final thing is to match the post-processing.

If we use the identity \(\hat{X}^L\ket{+} = \ket{+}\) and:

 

Our protocol is equivalent to hybrid quantum teleportation.

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

Displaced GKP cluster inside a CV cluster

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
= \int \ldots
+
+

Displaced GKP cluster inside a CV cluster

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^{\mathrm{GKP}}

Displaced GKP cluster inside a CV cluster

= \int \ldots
\ket{+^{\mathrm{GKP}}_{\bm{\mu_q}, \mathbf{A}\bm{\mu_q}}}^{\otimes N}
\hat{\mathbf{C}}_{Z}^\mathrm{GKP}(\mathbf{A})

Interpret the GKP cluster as a qubit cluster.

We perform qubit-qubit quantum teleportation.

Displaced GKP cluster to qubit cluster

\hat{C}_Z^{\mathrm{GKP}} = \text{diag}(1, 1, 1, -1)

Interpret the GKP cluster as a qubit cluster.

We perform qubit-qubit quantum teleportation.

\hat{C}_Z = \text{diag}(1, 1, 1, -1)
\ket+

Displaced GKP cluster to qubit cluster

|0\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

Gottesman-Kitaev-Preskill (GKP state)

\(q\)

\(|2n\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

GKP-qubit one bit teleportation: X gate

|1\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\hat{X}^{\mathrm{GKP}} = e^{-i \sqrt \pi \hat p} = \hat{D}_q(\sqrt{\pi})

GKP-qubit one bit teleportation: X gate

|0\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

Gottesman-Kitaev-Preskill (GKP state)

\(q\)

\(|2n\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

GKP-qubit one bit teleportation: \(\mu_q, \mu_p\)

|1\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\(|2n\sqrt{\pi}+\mu_q\rangle\)

\(\mu_q\): Rotational X gate

\(\mu_p\): Rotational Z gate

\(\mu_q, \mu_p\) as rotational X, Z

= \int \ldots
q = (2n+L)\sqrt\pi + \mu_q
|0\rangle_p
\hat{C}_Z^\mathrm{CV}
+
+

Homodyne detection collapses the GKP cluster

However, we can have mode preparation noise.

\(q\)

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle

We need to prepare the zero momentum eigenstate, which requires infinite squeezing and is physically impossible.

However, we can have mode preparation noise.

We need to prepare the zero momentum eigenstate, which requires infinite squeezing and is physically impossible.

\(q\)

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle

Finite squeezing noise.

Another possibility is that the mode is not in the ground state before squeezing.

However, we can have mode preparation noise.

Another possibility is that the mode is not in the ground state before squeezing.

\(q\)

\(p\)

\rho(\bar{n})

A thermal state is a statistical mixture of these coherent states, so effectively the variance is larger. 

However, we can have mode preparation noise.

Another possibility is that the mode is not in the ground state before squeezing.

\(q\)

\(p\)

\hat{S}(r)\rho(\bar{n})\hat{S}^\dagger(r)

A thermal state is a statistical mixture of these coherent states, so effectively the variance is larger. 

And a general qumode will have \(\mu_p \neq 0\) in the displaced GKP basis:

\ket{\psi} = \int_{-\sqrt{\pi}/2}^{\sqrt{\pi}/2} \int_{-\sqrt{\pi}/2}^{\sqrt{\pi}/2} \, d\mu_q d\mu_p \, a_0(\mu_q, \mu_p) \ket{0_{\mu_q, \mu_p}^\mathrm{GKP}}+ \,a_1(\mu_q, \mu_p) \ket{1_{\mu_q, \mu_p}^\mathrm{GKP}}
\ket{0}_p = \frac{1}{\sqrt{\pi}}\int_{-\sqrt{\pi}/2}^{\sqrt{\pi}/2} d\mu_q \ket{+_{\mu_q, 0}^\mathrm{GKP}}.

Infinite squeezing is not physically possible:

😵‍💫

Displaced GKP basis cannot describe mixed states!

However, it turns out that CV CZ can be converted to a qubit CZ gate at the operator level, before we even specify what the state is:

\bra{\bm{q}} \hat{\mathbf{C}}_D \hat{\mathbf{C}}_Z^\mathrm{CV}(\mathbf{A}) = \hat{\mathbf{R}}_Z^\dagger(\bm{\phi}) \hat{\mathbf{C}}_Z(\mathbf{A}) \bra{\bm{q}} \hat{\mathbf{C}}_D

CV CZ

Qubit CZ

Phase shifts

Equivalent circuit model

=
\ket{\Psi(q)}

Mode preparation error = single qubit preparation error

  • We can now handle all the mode preparation errors, including thermalization errors and finite squeezing!

Finite squeezing:

\(p\)

\hat{S}(r)\ket{\mathrm{vac}}

Loss: Finite Squeezing

\(q\)

\hat{S}(r)\ket{\mathrm{vac}}

Finite squeezing:

Loss: Finite Squeezing

\(q\)

\hat{D}_q(\sqrt{\pi})\hat{S}(r)\ket{\mathrm{vac}} \ket{1}^{\mathrm{Qubit}}

After conditional displacement:

\hat{S}(r)\ket{\mathrm{vac}} \ket{0}^{\mathrm{Qubit}}

Loss: Finite Squeezing

\(q\)

\hat{D}_q(\sqrt{\pi})|0, \sigma_p \rangle_p \ket{1}^{\mathrm{Qubit}}

Now, the probability of measuring \(q\):

|0, \sigma_p \rangle_p \ket{0}^{\mathrm{Qubit}}

Loss: Finite Squeezing

\(q\)

After measuring \(q\):

Loss: Finite Squeezing

\(q\)

After measuring \(q\):

Loss: Finite Squeezing

\(q\)

After measuring \(q\):

\ket{0} + \, \, \ket 1

Amplitude imbalance error

The qubit is:

Loss: Finite Squeezing

\ket{0} + \, \, \ket 1

Amplitude imbalance error

The qubit is:

We can correct the qubit by performing weak measurement POVMs \(M_0, M_1\), which commute with qubit CZ.

Failure:

\ket{1}
\ket{0} + \, \, \ket 1

Success:

Loss: Finite Squeezing

\ket{0} + \, \, \ket 1

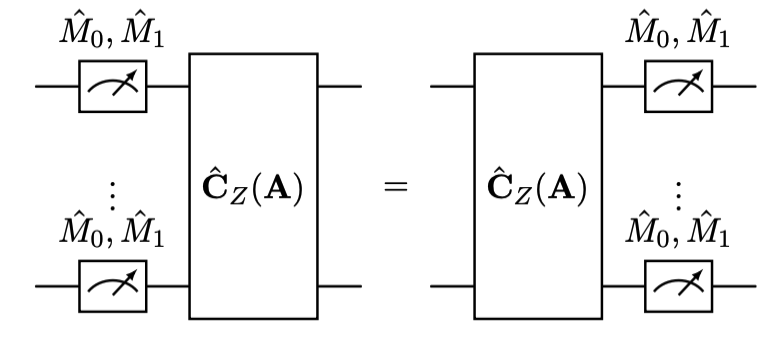
Amplitude imbalance error

The qubit is:

We can correct the qubit by performing weak measurement POVMs \(M_0, M_1\).

Failure: \(p\)

\ket{1}
\ket{0} + \, \, \ket 1

Success: \(1-p\)

\hat M_0
\hat M_1

Loss: Finite Squeezing

Finitely squeezed CV cluster state

Loss: Finite Squeezing

Loss: Finite Squeezing

Amplitude imbalance error!

After weak measurement:

Loss: Finite Squeezing

Failure: \(p\)

Can convert initial squeezing error to deletion error!

Loss: Finite Squeezing

How much squeezing do we need?

Loss: Finite Squeezing

Failure: \(p\)

(Stace 2009)

(Barrett and Stace 2010)

11.9 dB

5.4 dB

Loss: Finite Squeezing

5.4 dB: Loss-tolerant Quantum computation

Loss: Finite Squeezing

5.4 dB: Loss-tolerant Quantum computation

Loss: Finite Squeezing

5.4 dB: Robust quantum memory

Loss: Finite Squeezing

11.9 dB: Fault-tolerant quantum computation

Loss: Finite Squeezing

11.9 dB: Fault-tolerant quantum computation

Loss: Finite Squeezing

Can we suppress the deletion probability?

Loss: Finite Squeezing

Loss: Finite Squeezing

After weak measurement, qubits 1 and 3 are no longer entangled.

Loss: Finite Squeezing

Site 1

Site 2

Site 3

Loss: Finite Squeezing

Loss: Finite Squeezing

After weak measurement:

Loss: Finite Squeezing

Dual rail encoding (n=2)

Loss: Finite Squeezing

In order to break entanglement between site 1 and 3 both qubits has to be deleted.

Dual rail encoding (n=2)

Loss: Finite Squeezing

Deletion probability of a site: \(p^n\)

What happens to the qubit if you send in a squeezed thermal state?

\(q\)

\(p\)

\rho^{\mathrm{thermal}}
= \rho

\(q\)

\(p\)

|0, \sigma_p \rangle_p
\hat{D}_p(p_0)

Squeezed thermal state

Loss: Channel and detector loss

What happens to the qubit if you send in a squeezed thermal state?

\(q\)

\(p\)

\rho^{\mathrm{thermal}}
= \rho

\(q\)

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle
\hat{D}_p(p_0)

Mixture of displaced squeezed states

Squeezed thermal state

=

Loss: Channel and detector loss

What happens to the qubit if you send in a squeezed thermal state?

Loss: Channel and detector loss

\(q\)

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle
\hat{D}_p(p_0)
\hat{S}(r)|\mathrm{vac}\rangle
\hat{D}_p(p_0)

Displaced squeezed state

What happens to the qubit if you send in a squeezed thermal state?

Loss: Channel and detector loss

\(q\)

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle
\hat{D}_p(p_0)
\hat{D}_p(p_0)
\ket{\Psi(q)}

Amplitude imbalance

Displaced squeezed state

What happens to the qubit if you send in a squeezed thermal state?

Loss: Channel and detector loss

\(q\)

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle
\hat{D}_p(p_0)
\hat{R}_Z(-p_0\sqrt{\pi})
\ket{\Psi(q)}

Amplitude imbalance + Phase shift

What happens to the qubit if you send in a squeezed thermal state?

Loss: Channel and detector loss

\(q\)

\(p\)

\hat{S}(r)|\mathrm{vac}\rangle
\hat{D}_p(p_0)
\hat{R}_Z(-p_0\sqrt{\pi})
\ket{\Psi(q)}

Amplitude imbalance + Phase shift

Infinite squeezing:

Same result as displaced GKP basis

What happens to the qubit if you send in a squeezed thermal state?

Loss: Channel and detector loss

\hat{R}_Z(-p_0\sqrt{\pi})
\ket{\Psi(q)}
\int_{-\infty}^{\infty} dp_0 \cdot f(p_0, \sigma_{p_0}^2)

What happens to the qubit if you send in a squeezed thermal state?

Loss: Channel and detector loss

(1-s)\ket{\Psi(q)}\bra{\Psi(q)}+ s\hat{Z} \ket{\Psi(q)}\bra{\Psi(q)} \hat{Z}

The qubit becomes mixed and dephases

In experiment, conditional displacement interaction can be weak, or reduced by a factor of \(\sqrt{R}\).

Weak conditional displacement

\hat C_D(\sqrt{\pi/R}) = \ket 0 \bra 0 \otimes I + \ket 1 \bra 1 \otimes \hat D_q (\sqrt {\pi / R})

We now introduce a scheme to address this.

Suppose \(\hat{C}_D\) is \(R = 3\) times weaker

Weak conditional displacement

Weak conditional displacement

Suppose \(\hat{C}_D\) is \(R = 3\) times weaker

Weak conditional displacement

Suppose \(\hat{C}_D\) is \(R = 3\) times weaker

Weak conditional displacement

Suppose \(\hat{C}_D\) is \(R = 3\) times weaker

Only one round of weak measurement correction.

Suppose \(\hat{C}_D\) is 3 times weaker

Weak conditional displacement

The noise introduced by preparing \(R\) fresh CV cluster states and performing conditional displacement \(R\) times at strength \(\sqrt{\pi/R}\) has the same noise as preparing 1 CV cluster state and 1 round of CD at \(\sqrt \pi\).

Weak conditional displacement

Noise occurs at the middle of the circuit!

Optical loss

Detection inefficiency

Mode preparation error

Optical loss:

Optical loss:

  • Absorbed by the material
  • Scattering loss
  • Reflection loss
  • Bending / misalignment / manufacturing defects
  • Loss of signal / energy / intensity / power / photons

Intensity is reduced

Optical loss:

\ket{\mathrm{vac}}

Optical loss is modelled as a beam splitter:

\hat{a}_1 \to \hat{a}_1 \sqrt{\eta} + \hat{a}_2 \sqrt{1 - \eta}.

(\(\eta \to 1\) is no optical loss)

Bob can amplify the signal (either digitally or using an optical parametric amplifier)

Amplifier

Bob can amplify the signal (either digitally or using an optical parametric amplifier)

Amplifier

Bob can amplify the signal (either digitally or using an optical parametric amplifier)

Amplifier

This (phase insensitive) amplification process is a transformation on phase space, which increases the variance of the Gaussian state.

\(q\)

\(p\)

Amplitude 

\(q\)

\(p\)

Amplitude 

This (phase insensitive) amplification process is a transformation on phase space, which increases the variance of the Gaussian state.

This (phase insensitive) amplification process is a transformation on phase space, which increases the variance of the Gaussian state.

Optical parametric amplification using

Spontaneous parametric down conversion

\(q\)

\(p\)

Digital amplification

\hat{a}_1 \to \frac{1}{\sqrt{\eta}}\hat{a}_1- \sqrt{\frac{1 - \eta}{\eta}} \hat{a}_3^\dagger

Real life photodetectors do not perfectly absorb photons:

Amplifier

  • Absorption inefficiency
  • Shot noise
  • Loss on the electronics level e.g. temperature

Detector inefficiency is modelled as optical loss + amplification before a perfect detection.

\hat{a}_1 \to \hat{a}_1 + \sqrt{\frac{1 - \eta}{\eta}}(\hat{a}_2 + \hat{a}^\dagger_3)

added noise

\hat{a}_1 \to \hat{a}_1 + \sqrt{\frac{1 - \eta}{\eta}}(\hat{a}_2 + \hat{a}^\dagger_3)

added noise

\(q\)

\(p\)

Detector inefficiency is modelled as optical loss + amplification before a perfect detection.

\hat{a}_1 \to \hat{a}_1 + \sqrt{\frac{1 - \eta}{\eta}}(\hat{a}_2 + \hat{a}^\dagger_3)

added noise

\(q\)

\(p\)

Detector inefficiency is modelled as optical loss + amplification before a perfect detection.

Returning to the entanglement download protocol, channel loss and detector inefficiency complicate the protocol.

\hat{a}_1 \to \hat{a}_1 \sqrt{\eta} + \hat{a}_2 \sqrt{1 - \eta}.

Channel loss

\hat{a}_1 \to \hat{a}_1 + \sqrt{\frac{1 - \eta}{\eta}}(\hat{a}_2 + \hat{a}^\dagger_3)

Detector inefficiency

Beginning with detector inefficiency, we expand the Gaussian random noise in terms of a circuit.

Beginning with detector inefficiency, we expand the Gaussian random noise in terms of a circuit.

After tracing out mode 3, we have only Gaussian random noise in the \(q\) quadrature, and all loss is lumped together.

The CV cluster state is entangled before optical loss:

Thus, we cannot have independent errors, and the errors must be correlated.

However, we can add a beam splitter before entangling all modes to ensure the modes are uncorrelated after loss.

The properties of the input modes, beam splitter, and squeezing depend on the adjacency matrix \(\mathbf{A}\).

Implementation details:

  1. A scalable CV cluster state,
  2. A qubit platform, 
  3. Conditional displacement gate,
  4. Measurement of the \(q\) quadrature.

Three possible implementations:

  1. Cavity QED
  2. Circuit QED
  3. Free electron qubits

Possible implementations: Cavity QED

CV cluster: Furusawa protocol

|\alpha\rangle

Cavity QED system with Jaynes-Cumming interaction

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

|\alpha\rangle

Controlled Rotation gate

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

Cat state coupled to qubit

Free photons generated from Furusawa protocol

\eta \to 1

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

\eta \to 1

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

Free photons generated from Furusawa protocol

\eta \to 1

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

Free photons generated from Furusawa protocol

Apply X gate to qubit

Reroute entangled pulse back to cavity

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

Free photons generated from Furusawa protocol

Apply another X gate

Disentangle with

controlled phase

Net result: Conditional displacement 

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

(Dhara, Jiang, and Guha 2024)

Possible implementations: Cavity QED

Free photons generated from Furusawa protocol

(Dhara, Jiang, and Guha 2024)

Homodyne detection

Possible implementations: Cavity QED

Homodyne detection

Homodyne detection in optics

Coherent state

as a reference mode

State we are interested in measuring

I_1
I_2
|\alpha\rangle

Homodyne detection

Homodyne detection in optics

Coherent state

as a reference

mode

State we are interested in measuring

I_1
I_2
I_1 - I_2 \propto |I_1 I_2| \cos(\phi_1 - \phi_2)
|\alpha\rangle

Possible implementations: Free electron qubits

CV cluster: Furusawa protocol

Possible implementations: Free electron qubits

Free electron qubits

(Reinhardt 2021)

CV cluster: Furusawa protocol

\ket{0} = \sum_n \ket{2n\hbar \omega}
\ket{1} = \sum_n \ket{(2n+1)\hbar \omega}

Possible implementations: Free electron qubits

Free electron qubits

(Reinhardt 2021)

\ket{0} = \sum_n \ket{2n\hbar \omega}
\ket{1} = \sum_n \ket{(2n+1)\hbar \omega}

photon-induced nearfield electron
microscopy (PINEM)

Possible implementations: Free electron qubits

Free electron qubits

(Reinhardt 2021)

\ket{0} = \sum_n \ket{2n\hbar \omega}
\ket{1} = \sum_n \ket{(2n+1)\hbar \omega}

Possible implementations: Free electron qubits

Electron-photon scattering can be used as a CD gate 

(Baranes 2023)

Possible implementations: Free electron qubits

(Baranes 2023)

Possible implementations: Free electron qubits

S = \exp(g\hat{b} \hat{a}^\dagger - g^* \hat{b}^\dagger \hat{a})

Free electron-photon scattering (Dahan 2021):

\(\hat b^\dagger = \hat b = \sigma_x \) are Fermionic operators

PINEM: when the mode \(\hat a\) is a coherent state

General mode \(\hat a\) implements a conditional displacement

(Baranes 2023)

Possible implementations: Free electron qubits

Prepare free electrons as qubits using PINEM and coherent laser pulses

Prepare CV cluster state using the Furusawa protocol

S = \exp(g\hat{b} \hat{a}^\dagger - g^* \hat{b}^\dagger \hat{a})

Electron-photon coupling:

CD gate

Homodyne detection

Use free electrons as qubits or couple to other qubits

Possible implementations: Superconducting qubits

CV cluster: Frequency comb in microwave resonator

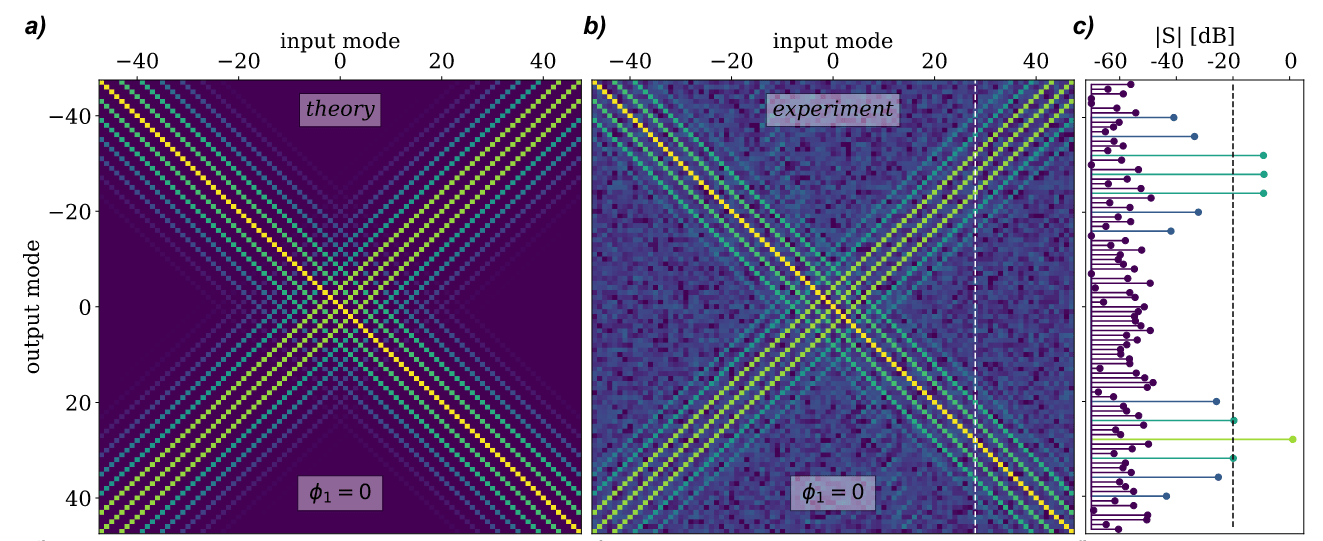
95 mode CV cluster state

(Hernández 2024)

Possible implementations: Superconducting qubits

CV cluster: Frequency comb in microwave resonator

Josephson Parametric Amplifier

Vacuum fluctuations

CV cluster state

Time varying flux to modulate the signal

Possible implementations: Superconducting qubits

Transmon qubit

CV cluster state: Frequency comb in microwave resonator

Jaynes-Cummings interaction with dispersive coupling 

\(H_I = \chi \sigma_z \hat{a}^\dagger \hat{a} \)

Conditional rotation

Possible implementations: Superconducting qubits

Transmon

Echoed conditional displacement gate

(A. Eickbusch 2018)

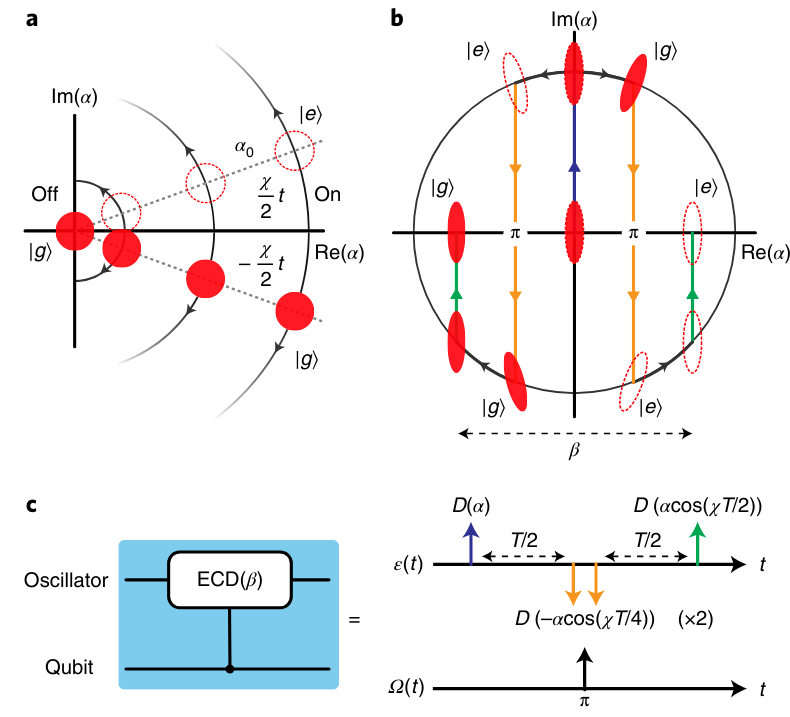
Possible implementations: Superconducting qubits

Transmon

How to measure \(q\) quadrature?

Possible implementations: Superconducting qubits

Transmon

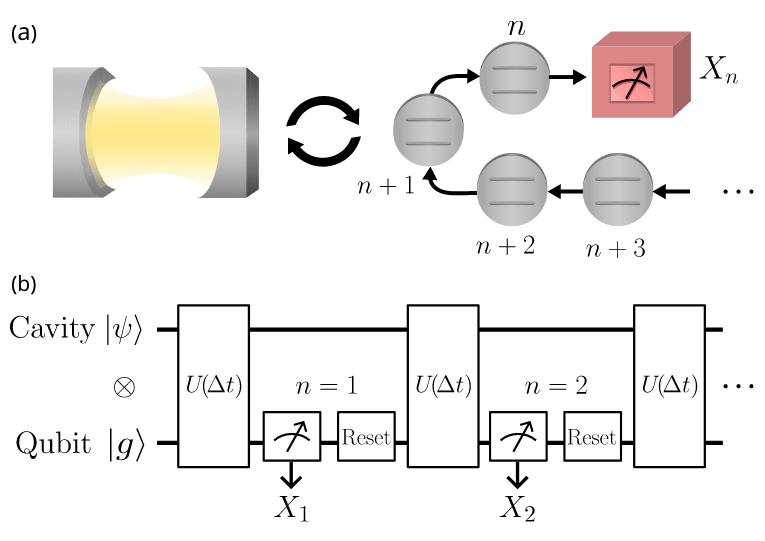
1. Qubitdyne detection

(Strandberg 2023)

Ancilla qubit for measuring

Jaynes-Cumming interaction:

\(H_I = \hat{a} \sigma_+ + \hat{a}^\dagger \sigma_-\)

Possible implementations: Superconducting qubits

Transmon

1. Qubitdyne detection

(Strandberg 2023)

Jaynes-Cumming interaction:

\(H_I = \hat{a} \sigma_+ + \hat{a}^\dagger \sigma_-\)

Ancilla qubit for measuring

Possible implementations: Superconducting qubits

Transmon

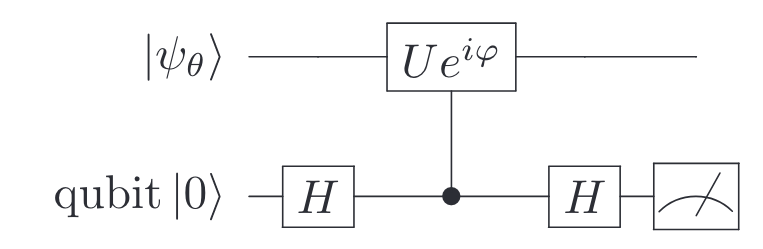
2. Quantum Phase Estimation (Terhal and Weigand 2016)

ECD gate + dispersive coupling

\(H_I = \sigma_z (\alpha \hat{a}^\dagger - \alpha^* \hat{a})\)

Ancilla qubit for measuring

Conditional displacement \(U = (\hat{X}^{\mathrm{GKP}})^2\)

Possible implementations: Superconducting qubits

Transmon

Ancilla oscillator for measuring

Optomechanical coupling:

\(H_I = g\hat{b}^\dagger\hat{b} (\hat a + \hat a^\dagger)\)

\hat{q} \propto (\hat{a} + \hat{a}^\dagger )

3. Photon-pressure coupling (Terhal and Weigand 2020)

Waveguide

Circuit QED Free electron qubits Cavity QED
CV cluster state Frequency comb in cavity  Furusawa protocol Furusawa protocol
Conditional displacement Echoed conditional displacement gate (ECD gate) Electron-photon coupling Mediated interaction with coherent state
q quadrature measurement 1. Quantum phase estimation
2. Qubitdyne detection
3. Photon-pressure coupling		 Homodyne detection Homodyne detection
Qubit Transmon Free electrons Atom in cavity

Possible implementations: Summary

Downloading many-body continuous variable entanglement to qubits

  • We can make many body entanglement in qubits!
  • Entanglement transfer from CV cluster state to qubit cluster state is possible
  • Quality of the qubit cluster state depends on initial CV cluster
  • Weak measurement / qubit deletion protocol can reduce requirements
  • ​6dB squeezing for robust quantum memory
  • 12dB squeezing for fault tolerant quantum computing
  • No generation of GKP states is needed
  • arXiV in progress
  • This research was sponsored by the QuantumBC CREATE Program.

Zhihua Han: zhi_han@sfu.ca

References

[1] W. Asavanant et al., Generation of Time-Domain-Multiplexed Two-Dimensional Cluster State, Science 366, 373 (2019).

[2] S. Takeda and A. Furusawa, Toward Large-Scale Fault-Tolerant Universal Photonic Quantum Computing, APL Photonics 4, 060902 (2019).

[3] J. Yoshikawa, S. Yokoyama, T. Kaji, C. Sornphiphatphong, Y. Shiozawa, K. Makino, and A. Furusawa, Invited Article: Generation of One-Million-Mode Continuous-Variable Cluster State by Unlimited Time-Domain Multiplexing, APL Photonics 1, 060801 (2016).

[4] Nicolas C. Menicucci, Peter van Loock, Mile Gu, Christian Weedbrook, Timothy C. Ralph, and Michael A. Nielsen, Universal Quantum Computation with Continuous-Variable Cluster States, Phys. Rev. Lett. 97, 110501 (2006).

[5] Shota Yokoyama et al., Ultra-large-scale continuous-variable cluster states multiplexed in the time domain, Nat. Photonics 7, 5 (2013).

[6] J. Yoshikawa, S. Yokoyama, T. Kaji, C. Sornphiphatphong, Y. Shiozawa, K. Makino, and A. Furusawa, Invited Article: Generation of One-Million-Mode Continuous-Variable Cluster State by Unlimited Time-Domain Multiplexing, APL Photonics 1, 060801 (2016).

[7] T. Monz, P. Schindler, J. T. Barreiro, M. Chwalla, D. Nigg, W. A. Coish, M. Harlander, W. Hänsel, M. Hennrich, and R. Blatt, 14-Qubit Entanglement: Creation and Coherence, Phys. Rev. Lett. 106, 130506 (2011).

[8] C. Song et al., Generation of Multicomponent Atomic Schrödinger Cat States of up to 20 Qubits, Science 365, 574 (2019).

[9] X.-L. Wang et al., Experimental Ten-Photon Entanglement, Phys. Rev. Lett. 117, 210502 (2016).

[10] R. Raussendorf, D. E. Browne, and H. J. Briegel, Measurement-Based Quantum Computation with Cluster States, Phys. Rev. A 68, 022312 (2003).


References

[11] D. Gottesman, A. Kitaev, and J. Preskill, Encoding a Qubit in an Oscillator, Phys. Rev. A 64, 012310 (2001).

[12] J. E. Bourassa et al., Blueprint for a Scalable Photonic Fault-Tolerant Quantum Computer, Quantum 5, 392 (2021).

[13] S. Glancy and E. Knill, Error Analysis for Encoding a Qubit in an Oscillator, Phys. Rev. A 73, 012325 (2006).

[14] A. Botero and B. Reznik, Modewise Entanglement of Gaussian States, Phys. Rev. A 67, 052311 (2003).

[15] C. Weedbrook, S. Pirandola, R. Garcia-Patron, N. J. Cerf, T. C. Ralph, J. H. Shapiro, and S. Lloyd, Gaussian Quantum Information, Rev. Mod. Phys. 84, 621 (2012).

[16] S. L. Braunstein and P. van Loock, Quantum Information with Continuous Variables, Quantum Information with Continuous Variables 77, 65 (2005).

[17] S. Takeda and A. Furusawa, Toward Large-Scale Fault-Tolerant Universal Photonic Quantum Computing, APL Photonics 4, 060902 (2019).

[18] R. Raussendorf, D. E. Browne, and H. J. Briegel, Measurement-Based Quantum Computation with Cluster States, Phys. Rev. A 68, 022312 (2003).

[19] M. V. Larsen, X. Guo, C. R. Breum, J. S. Neergaard-Nielsen, and U. L. Andersen, Deterministic Generation of a Two-Dimensional Cluster State, Science 366, 369 (2019).

[20] B. M. Terhal and D. Weigand, Encoding a Qubit into a Cavity Mode in Circuit QED Using Phase Estimation, Phys. Rev. A 93, 012315 (2016).

References

[21] O. Reinhardt, C. Mechel, M. Lynch, and I. Kaminer, Free-Electron Qubits, Annalen Der Physik 533, 2000254 (2021).

[22] G. Baranes, S. Even-Haim, R. Ruimy, A. Gorlach, R. Dahan, A. A. Diringer, S. Hacohen-Gourgy, and I. Kaminer, Free-Electron Interactions with Photonic GKP States: Universal Control and Quantum Error Correction, Phys. Rev. Res. 5, 043271 (2023).

[23] R. Dahan, G. Baranes, A. Gorlach, R. Ruimy, N. Rivera, and I. Kaminer, Creation of Optical Cat and GKP States Using Shaped Free Electrons, Phys. Rev. X 13, 031001 (2023).

[24] B. Hacker, S. Welte, S. Daiss, A. Shaukat, S. Ritter, L. Li, and G. Rempe, Deterministic Creation of Entangled Atom–Light Schrödinger-Cat States, Nature Photon 13, 110 (2019).

[25] I. Strandberg, A. Eriksson, B. Royer, M. Kervinen, and S. Gasparinetti, Digital Homodyne and Heterodyne Detection for Stationary Bosonic Modes, arXiv:2312.14720.

[26] A. Eickbusch, V. Sivak, A. Z. Ding, S. S. Elder, S. R. Jha, J. Venkatraman, B. Royer, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, Fast Universal Control of an Oscillator with Weak Dispersive Coupling to a Qubit, Nat. Phys. 18, 1464 (2022).

[27] B. Wang and L.-M. Duan, Engineering Superpositions of Coherent States in Coherent Optical Pulses through Cavity-Assisted Interaction, Phys. Rev. A 72, 022320 (2005).

[28] S. Kono, K. Koshino, Y. Tabuchi, A. Noguchi, and Y. Nakamura, Quantum Non-Demolition Detection of an Itinerant Microwave Photon, Nature Phys 14, 546 (2018).

[29] J. Hastrup and U. L. Andersen, Protocol for Generating Optical Gottesman-Kitaev-Preskill States with Cavity QED, Phys. Rev. Lett. 128, 170503 (2022).

[30] A. Reiserer, S. Ritter, and G. Rempe, Nondestructive Detection of an Optical Photon, Science 342, 1349 (2013).

[31] J. C. R. Hernández, F. Lingua, S. W. Jolin, and D. B. Haviland, Control of Multi-Modal Scattering in a Microwave Frequency Comb, arXiv:2402.09068.

[32] S. W. Jolin, G. Andersson, J. C. R. Hernández, I. Strandberg, F. Quijandría, J. Aumentado, R. Borgani, M. O. Tholén, and D. B. Haviland, Multipartite Entanglement in a Microwave Frequency Comb, Phys. Rev. Lett. 130, 120601 (2023).

bonus slides