Superconducting Qubits in 1 hour
Based off the CMC Superconducting Qubits Workshop
Zhi Han
Overview
- Review of superconductivity
- The LC Circuit
- The Josephson effect
- Transmons
- Jaynes-Cumming Hamiltonian
- SQUIDs
Main goal is give an overview to superconductors and provide reference
What is a superconductor?
- Meissner effect
- Zero resistivity under \(Tc\)
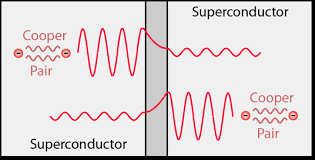
- Cooper pairs
- One macroscopic wavefunction


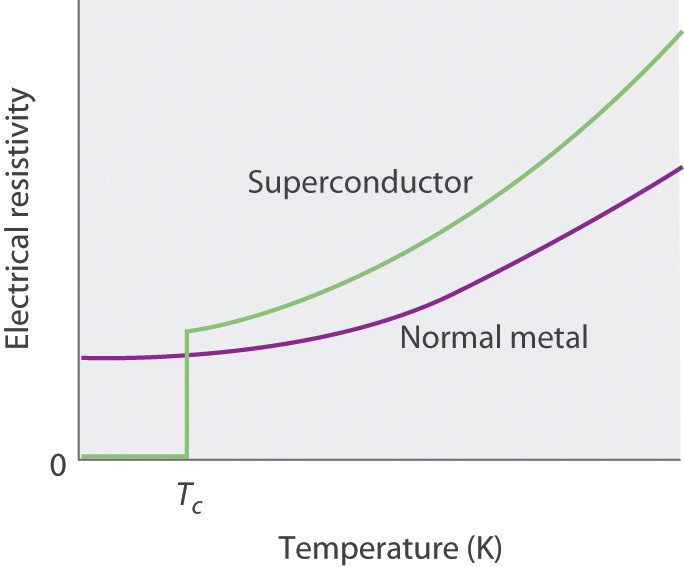
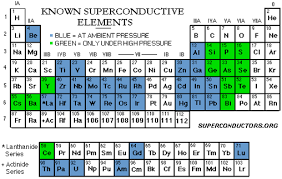
Image: Reddit
Cooper pairs
- Electrons pair up to form cooper pairs.
- These cooper pairs behave as bosons rather than photons.
- Bosons do not obey the Pauli exclusion principle.
- Therefore, all the cooper pairs can simultaneously occupy the ground state, and behave as one wavefunction.
- We will make this ansatz later: \[ \psi = \sqrt{n}e^{i\varphi}\]
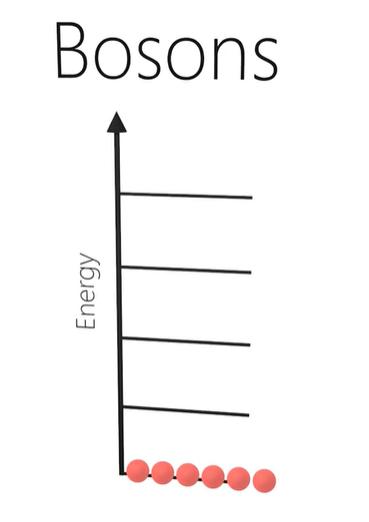
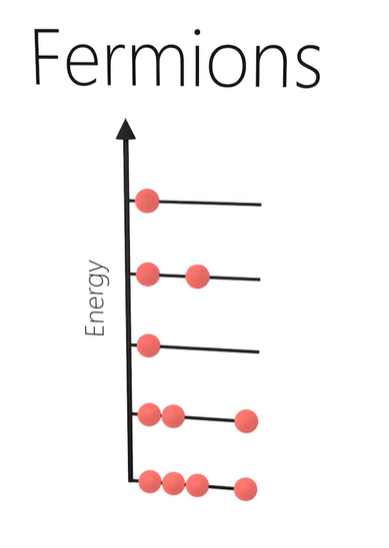
Image: Higgsino Physics
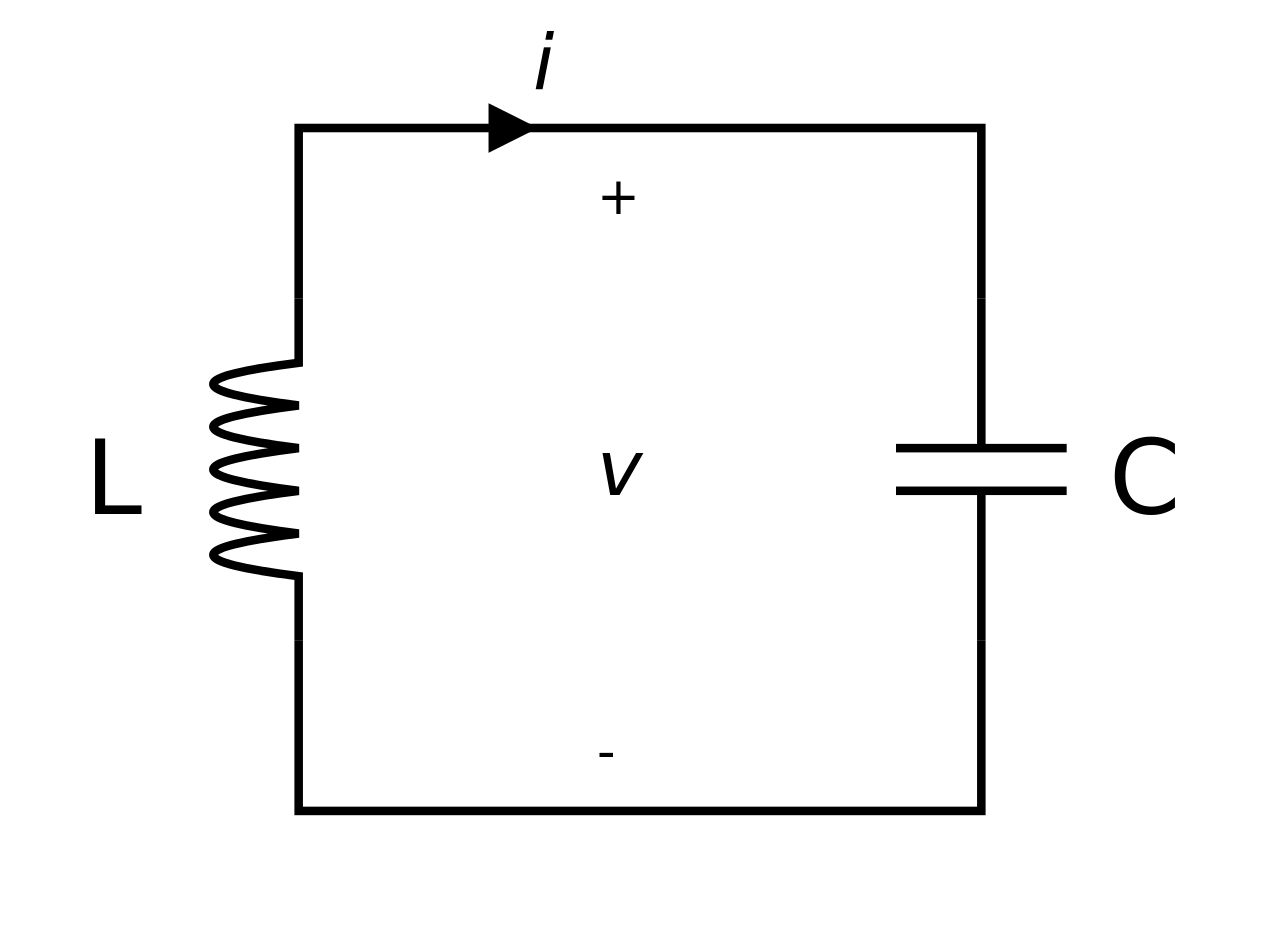
LC Circuit

Looks like SHO:
\[E=\frac{1}{2}m\omega^2x^2 + \frac{1}{2}m\dot{x}^2\]
Total energy:
\[ E_m + E_e = \frac{1}{2}C\omega_r^2\Phi^2(t) + \frac{1}{2}C\dot{\Phi}^2(t)\]
LC Circuit
Image: Wikipedia - LC Circuit
Electric and Magnetic Energy
Lagrangian Formulation
Solution
Euler Lagrange Equations
Equation of motion
Conjugate momentum
to flux is charge
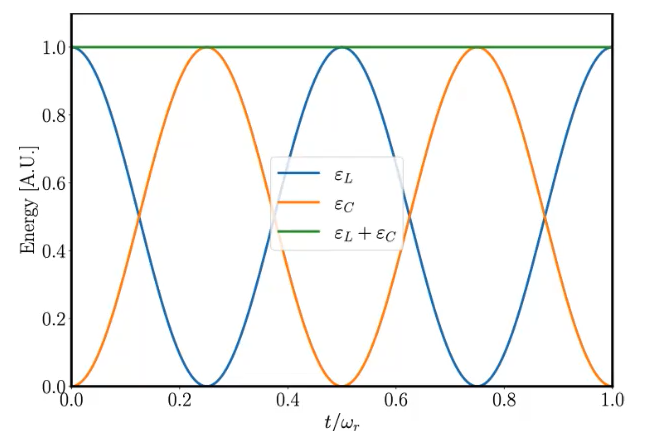
Oscillating between electric and magnetic
LC Hamiltonian
Promote flux and charge to quantum operators (canonical/dirac quantization)
Since flux and charge are already canonical coordinates we just promote
LC Hamiltonian
Original Hamiltonian
Raising/lowering operators
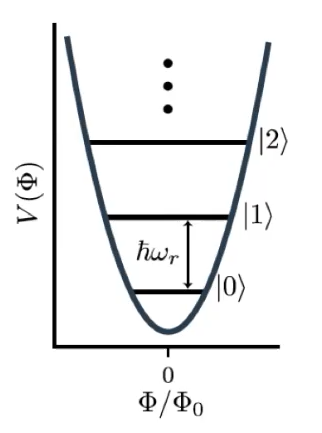
LC circuit as QHO
- Eigenstates of LC circuit satisfies \( a^\dagger a | n \rangle = n |n\rangle \)
- \(a^\dagger \) creates a quantized excitation of flux and charge. In other words, a photon of frequency \( \omega_r\) is created.
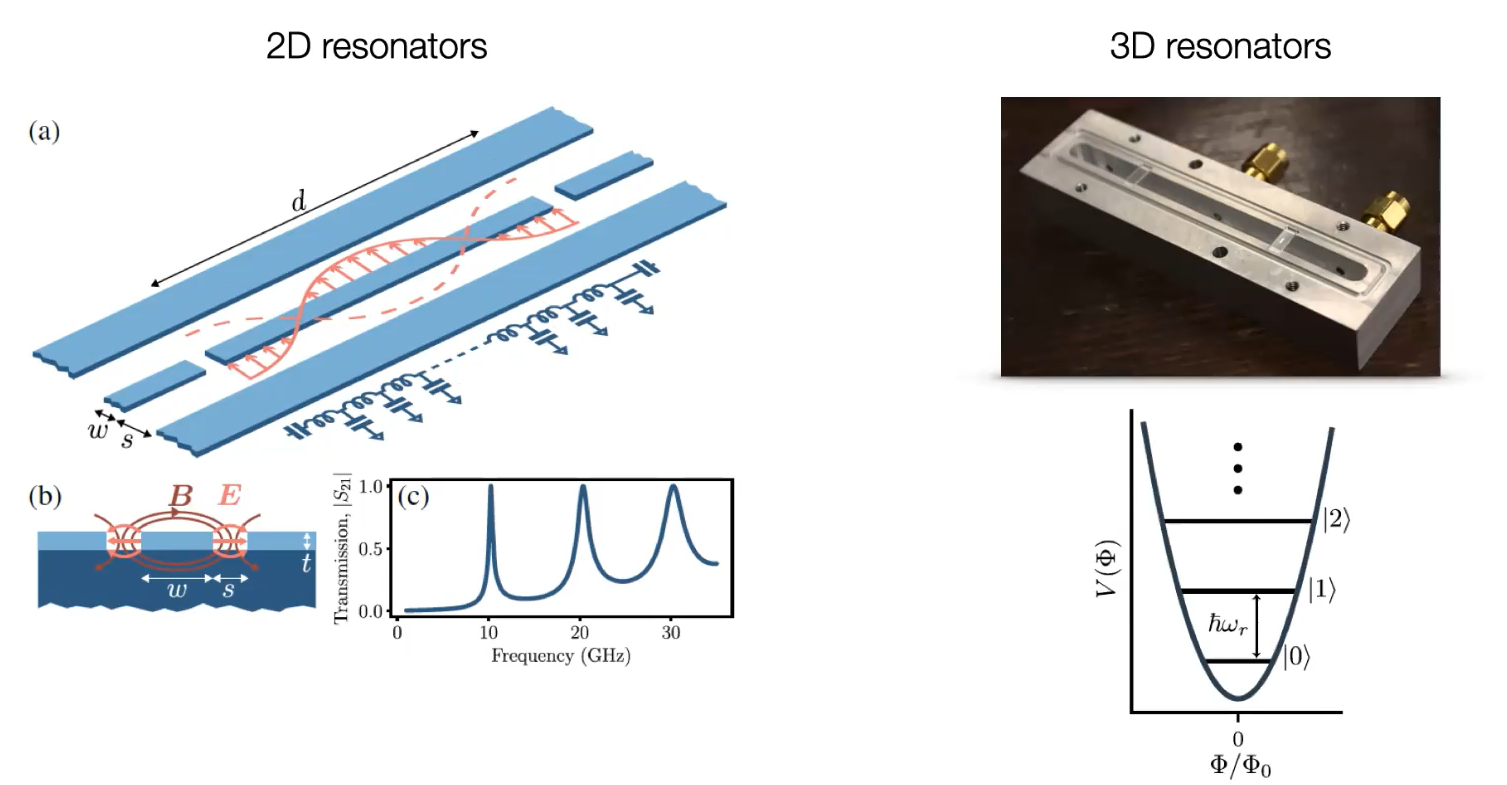
Coplanar waveguide
Resonant Modes
Transmission line LC circuit

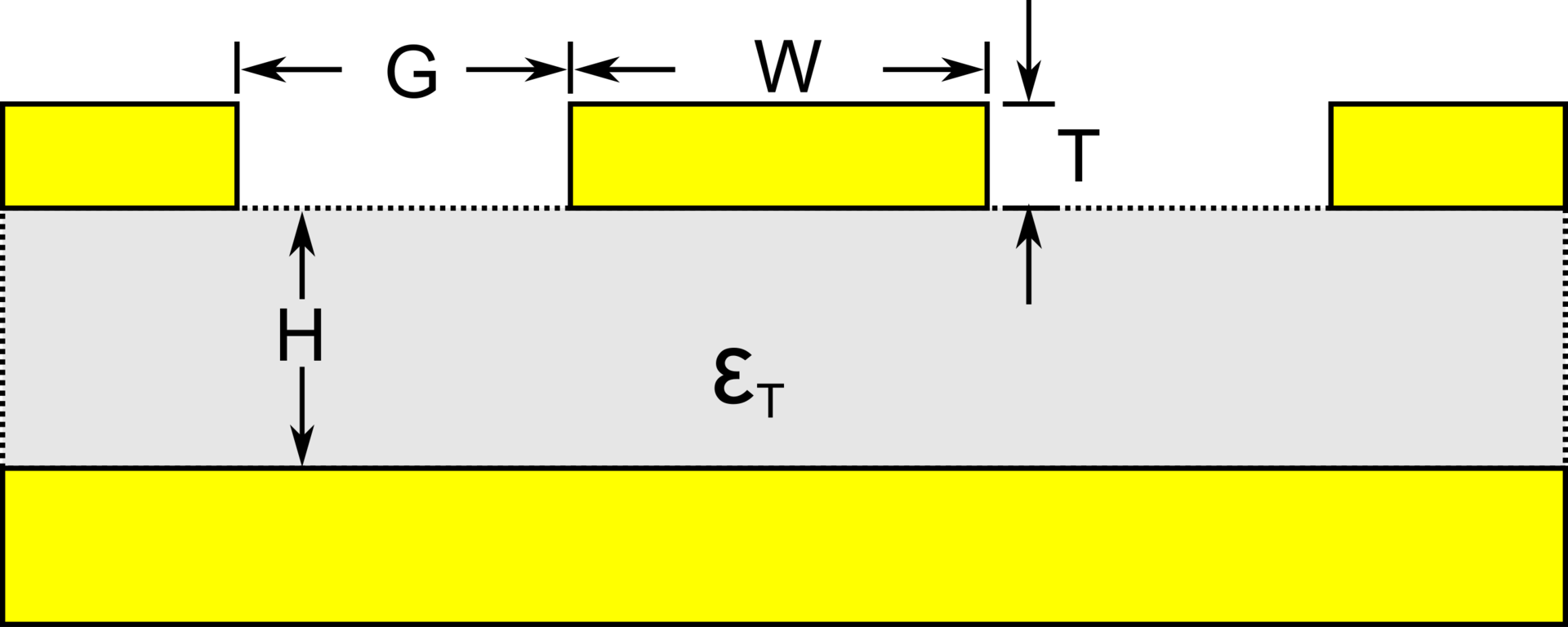
Conductors
Dielectric
Coplanar Waveguides

- Transmission line.
- Behave as coupled LC circuits.
- The solution for a chain of 1d harmonic oscillators is given by a wave equation.
- Described by the Telegrapher's equations.
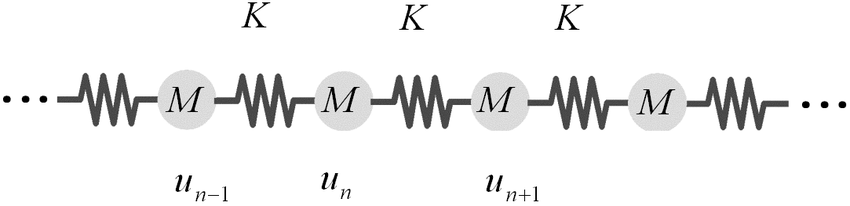
Images: Wikipedia
| SC Device | Physics | Function in SC circuit |
|---|---|---|
| LC circuit/Resonator | Quantum Harmonic Oscillator | Readout, control, couple qubits. |
| Coplanar Waveguide | Telegrapher's Equations | Transmission of qubits as photons |
| Josephson Junction | Josephson's Equations | Nonlinear inductor |
| SQUID | Josephson's Equations, Two state system | Qubit (Magnetic flux) |
| Transmon | Two state system | Qubit (Charge) |
| Transmon with LC circuit | Jaynes-Cumming Hamiltonian | Qubit (Charge) |
Josephson Junctions
- LC circuit is a linear device that cannot be used for a qubit. But it is used for readout, control, and couple qubits.
- Non-linearity is needed to process and encode quantum information.
- Superconducting qubits and quantum parametric amplifiers are possible only with a non linear element.

Josephson Relations
- Obtained by solving the Schrodinger equation with the ansatz \[ \psi = \sqrt{n}e^{i\phi}\] on both sides of the junction.
Josephson Phase
Quantum flux
Worth memorizing!!!!
Josephson current equation
Non-linear inductor
Linear inductor
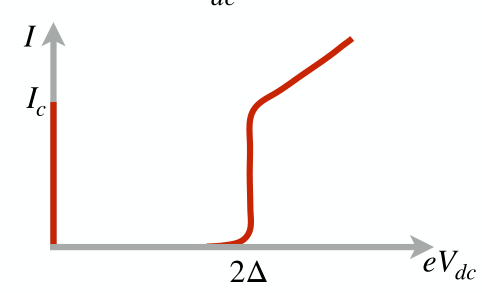
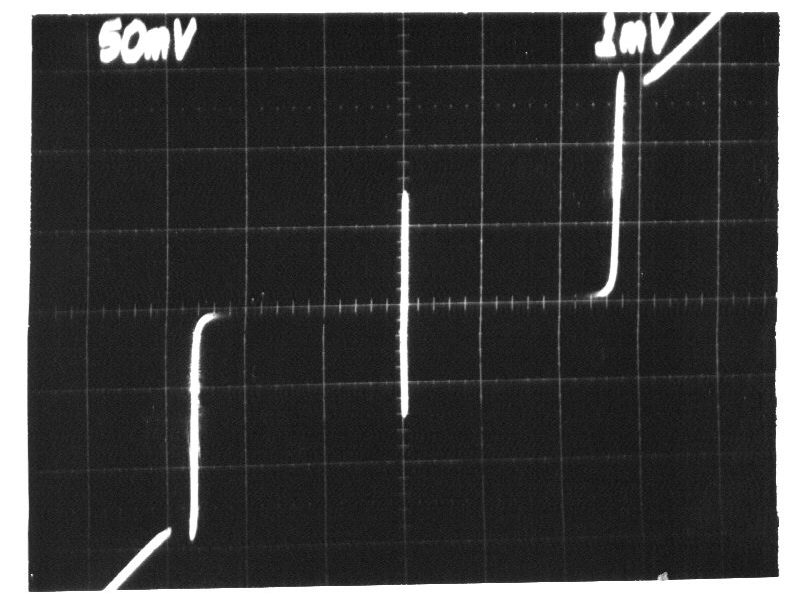
Energy of a Josephson Junction
Archetype 1:
Transmon Qubit
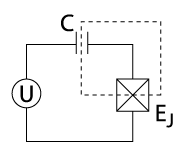
Transmon Qubit
- Replace linear inductor with a Josephson Junction.

Quantization
Hamiltonian of a Transmon
Transmon Qubit
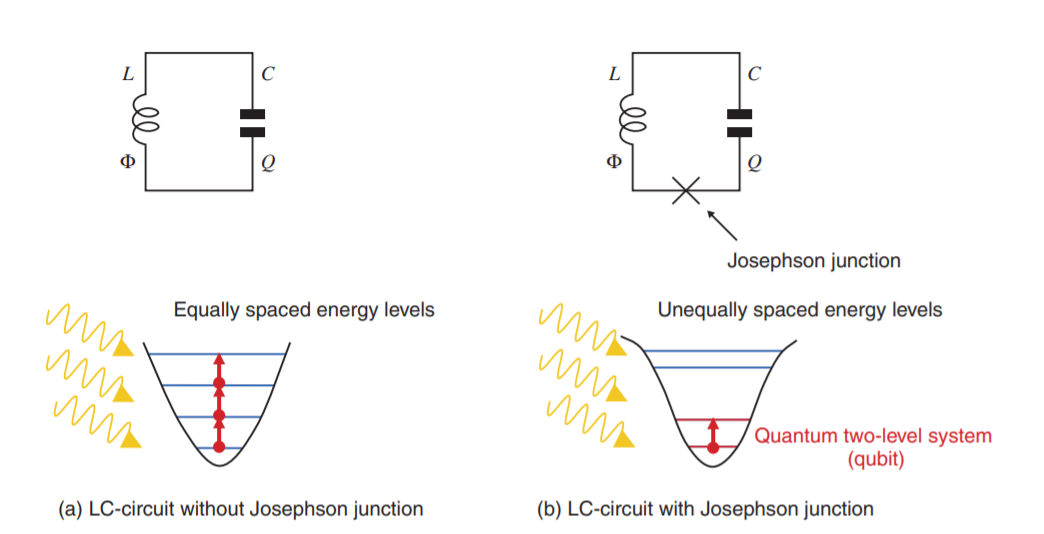

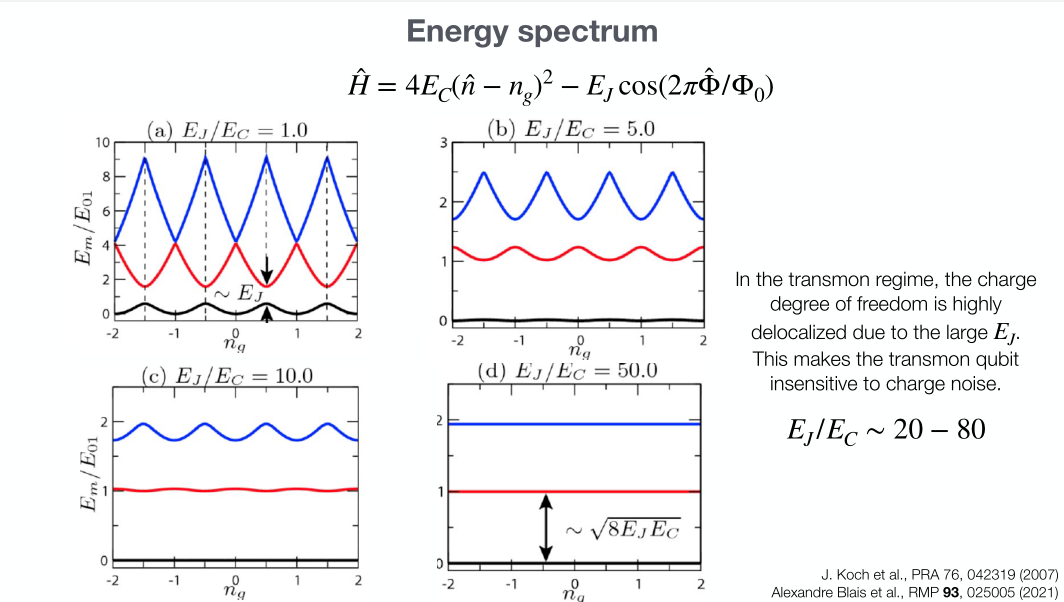

LC-Transmon Hamiltonian
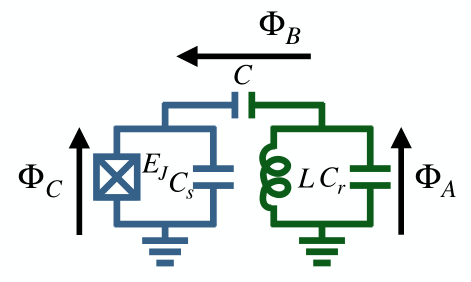
- Transmon coupled with LC circuit.
- Solving this circuit results in the Jaynes-Cumming Hamiltonian.
- Qubit readout commutes with the Hamiltonian, so we don't disturb the state.
- Interaction is mediated by virtual photons.
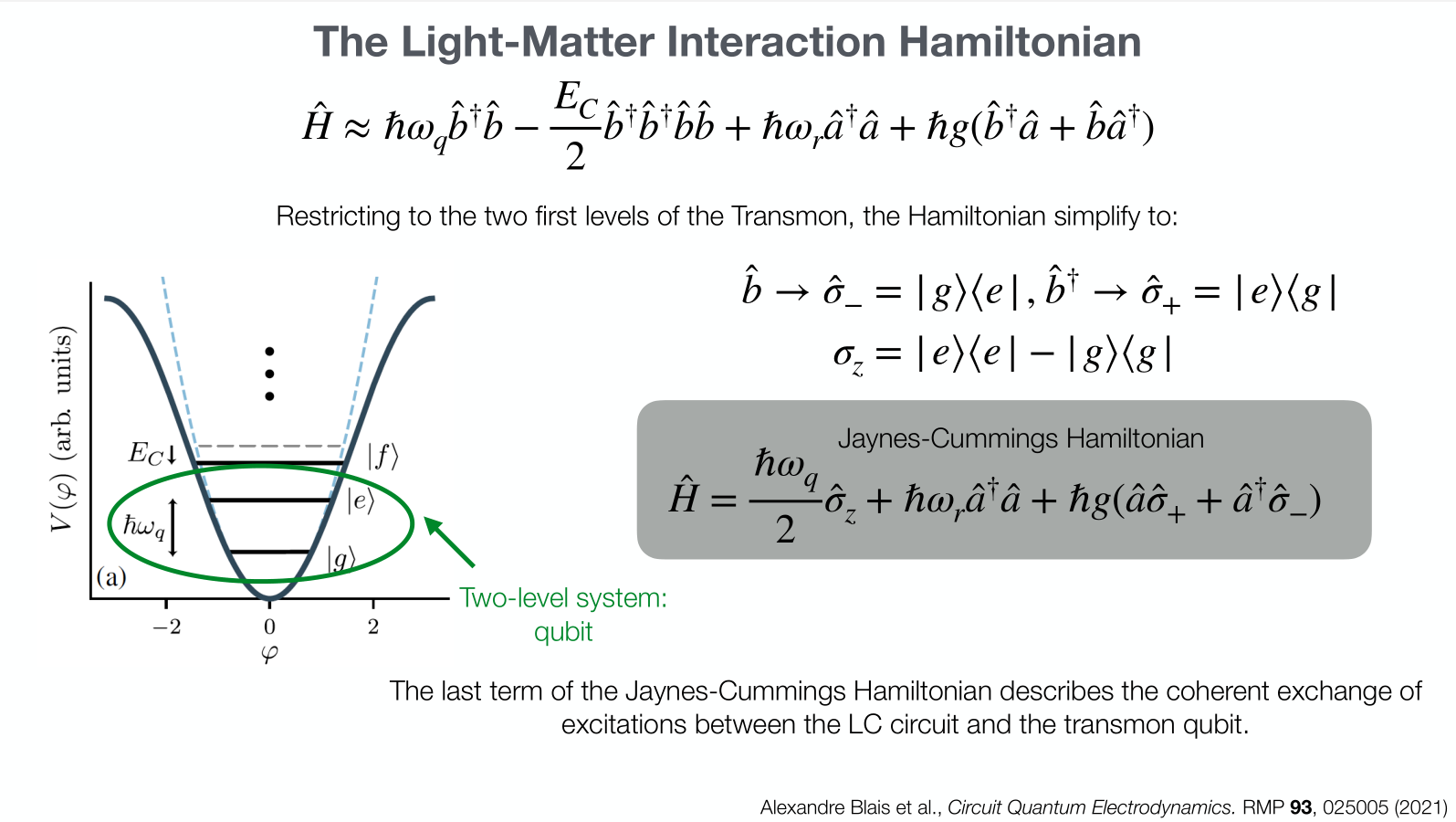
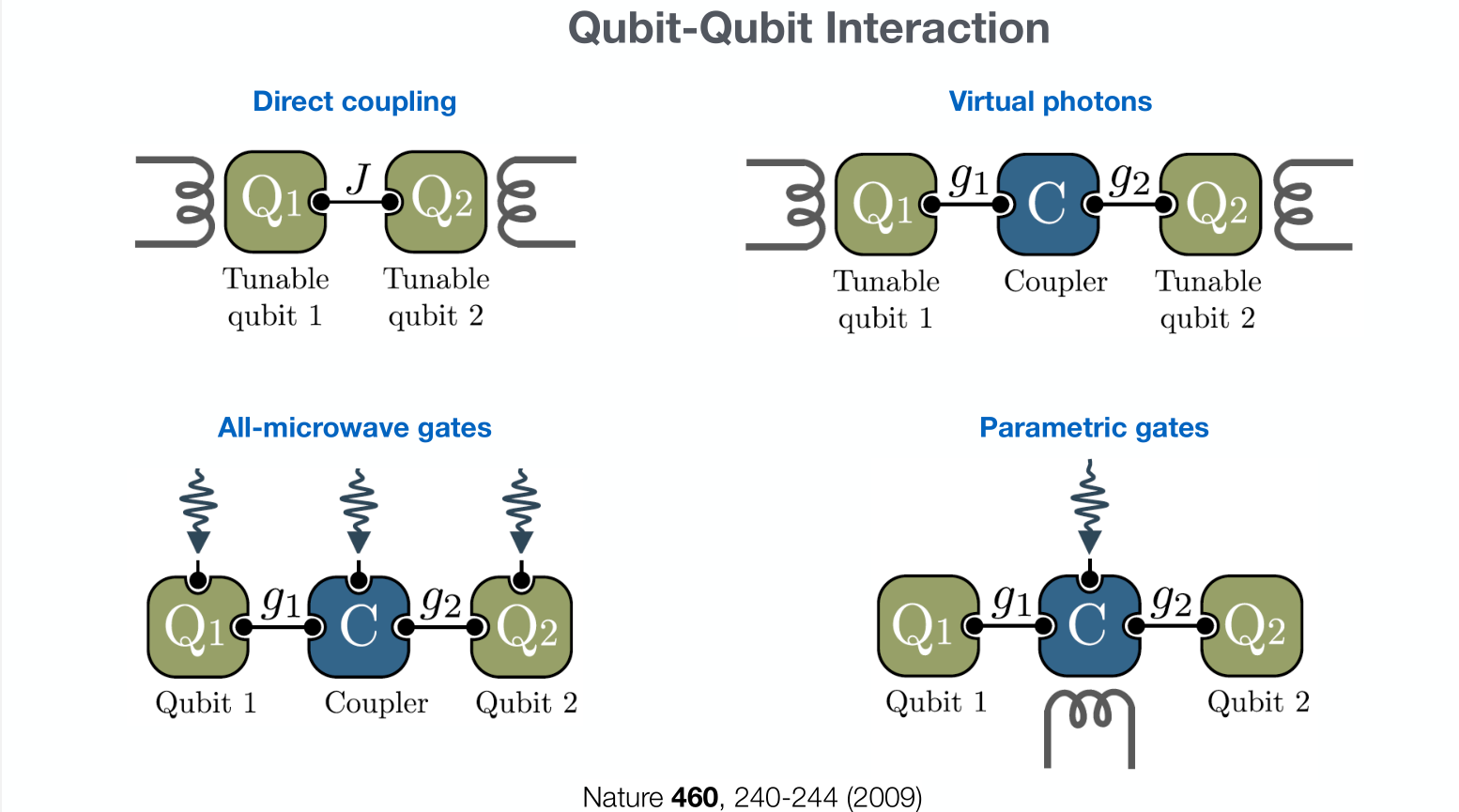
Archetype 2: SQUID Qubits

| SC Device | Physics | Function in SC circuit |
|---|---|---|
| LC circuit/Resonator | Quantum Harmonic Oscillator | Readout, control, couple qubits. |
| Coplanar Waveguide | Telegrapher's Equations | Transmission of qubits as photons |
| Josephson Junction | Josephson's Equations | Nonlinear inductor |
| SQUID | Josephson's Equations, Two state system | Qubit (Magnetic flux) |
| Transmon | Two state system | Qubit (Charge) |
| Transmon with LC circuit | Jaynes-Cumming Hamiltonian | Qubit (Charge) |
Superconducting loop
Ginzburg-Landau
Internal flux
External flux
Source: Wikipedia
Superconducting loop
Periodic boundary conditions
Flux is quantized
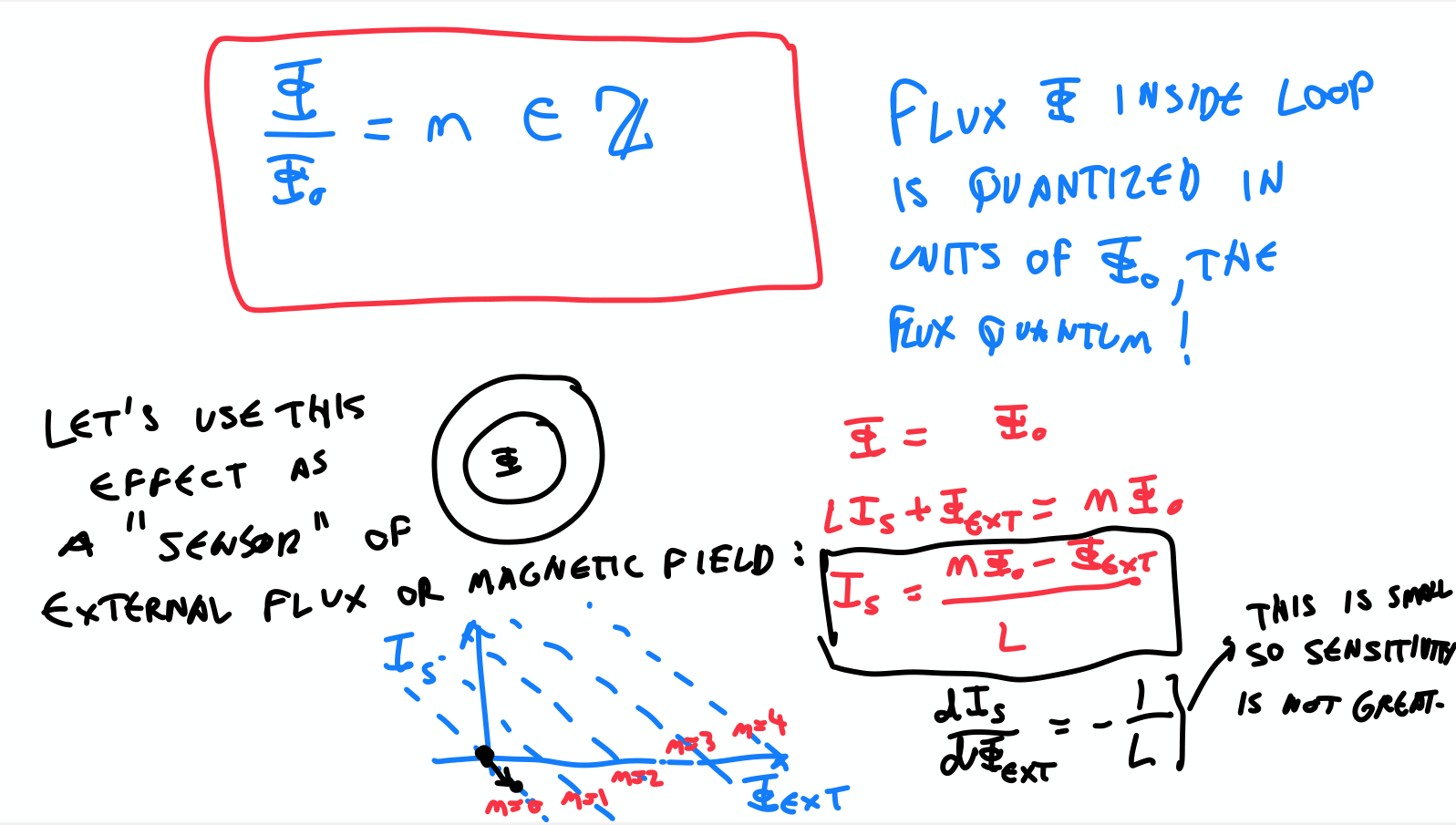
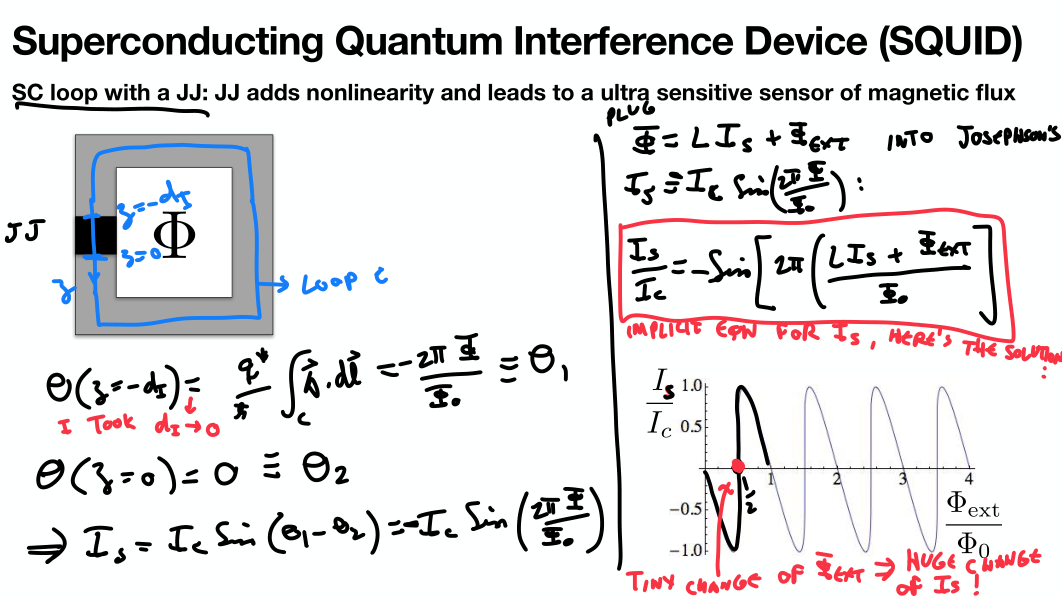

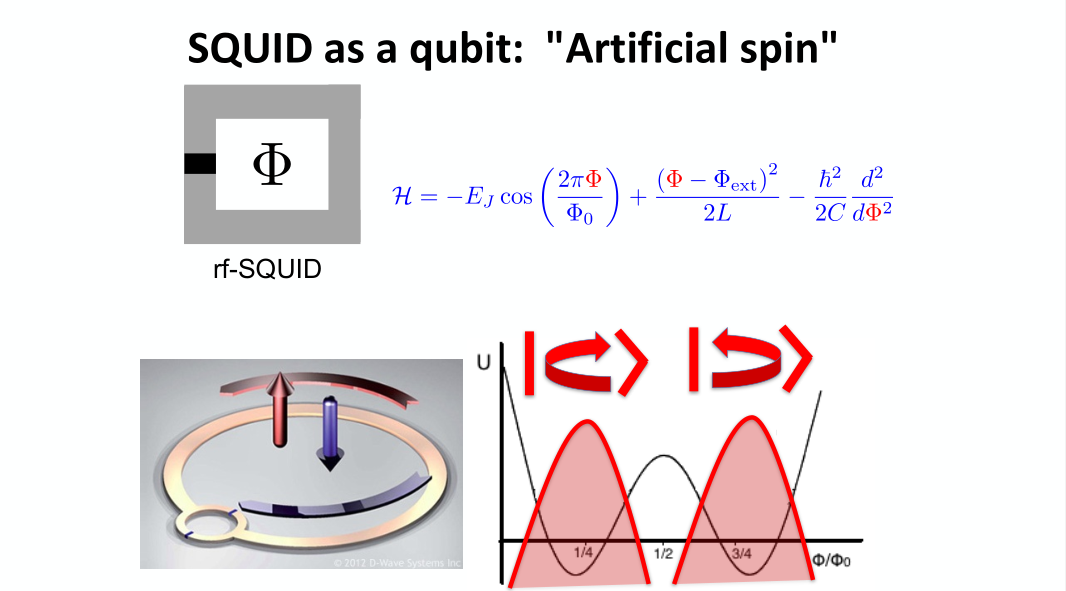
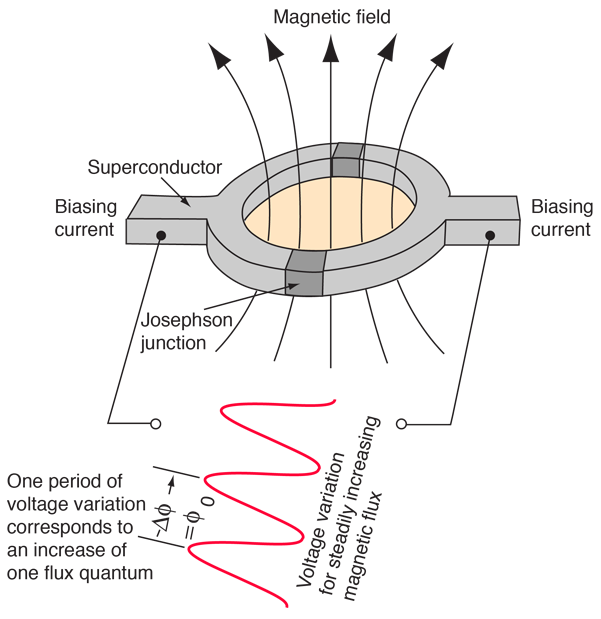
- A small change in the external magnetic field changes the current.
- Used as qubit or quantum sensor.
- Based on the idea that flux is quantized.
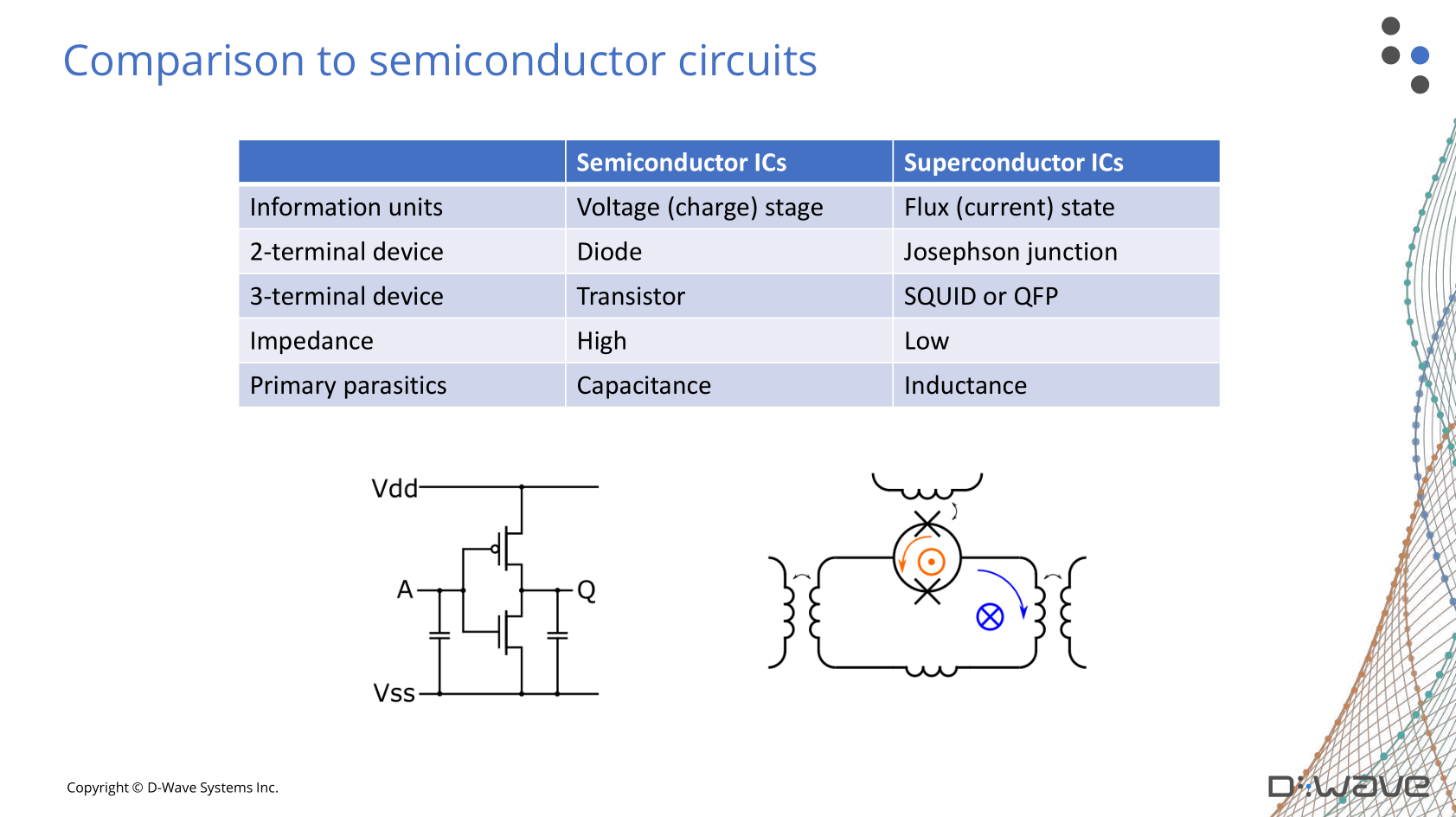
(D-Wave slides)
Further Reading on Transmons
- Circuit Quantum Electrodynamics, Alexander Blais
- arXiv:2005.12667 [quant-ph]
- Udson C. Mendes slides from Cornerstones of Quantum Computing Workshop
