4/27
自我介紹

提問!
Yes or NO
我現在想吃甚麼水果?

動物

換我猜!
Quiz
- 我的英文名字是甚麼?
- How are you?
早安
晚安
I'm fabulous.
尾聲
- 建議
- 想學的東西?
作業
- 下次跟我分享一件好事
5/11
好事!
複習
英文-重組單字
- iogrmnn
- tihgn
英文-對話
- How are you?
- 午安
- 問別人名字
遊戲
- 再來玩看看
遊戲-必勝策略
假設目標是數到\(n\)就贏
首先算出\(n\)除以 的餘數
一開始就先拿那麼多個
接下來每回合如果別人拿\(x\)個,我就拿 個
\(4\)
\(4-x\)
遊戲-問題
如果\(n\)除以\(4\)的餘數是\(0\)怎麼辦?
如果每個人變成可以數1~4個數字怎麼辦?
English Time
數學?
因數與倍數
有12顆蘋果,可以平均分給多少人?
\(12=1 \times 12 = 2\times 6 = 3\times 4\)
12有6個因數
質數
只有兩個因數的數
難以平分的蘋果
哪些是質數?
1,2,3,4,5
2,3,5,7,11,13,15,17
質因數分解
\(12 = 2 \times 2 \times 3\)
練習遊戲:wallprime
5/18
好事!
複習
英文-單字



pencil
school bag
Computer
英文-問候語
隨便說出兩個用來打招呼的句子!
數學-因數、倍數
複習小遊戲
兩個人輪流數數-目標數到50!
(1)數到有2的數字或是2的倍數要用拍手代替
(2)數到有7的數字或是7的倍數要用拍手代替
數學
質數、質因數
請對24做質因數分解
為甚麼要質因數分解?
\(2\times 2\) 可以整除 \(3 \times 3 \times 5 \times 7\)嗎?
\(3\times 7\) 可以整除 \(3 \times 3 \times 5 \times 7\)嗎?
\(3\times 5 \times 5\) 可以整除 \(3 \times 3 \times 5 \times 7\)嗎?
English Time
未來想做甚麼呢?
5/25
好事
複習
質因數分解小遊戲
英文-問問題
(1) 你幾歲?
(2)你叫甚麼名字?
英文-單字

school bag
年齡
age

eraser
公因數與公倍數
六個蘋果、八個梨子,可以平均分給幾個人?














一年級有4個人,二年級有6個人,要為給每年級幾顆蘋果,才能讓每年即每個人分到一樣多?
一年級




二年級






公因數
兩個數字共同的因數,稱為公因數
像1,2就是6跟8的公因數
公倍數
兩個數字共同的倍數,稱為公倍數
像12,24,36,...就是6跟4的公倍數
最大公因數
兩個數字共同的因數中最大的,稱為最大公因數
像2就是6跟8的最大公因數
最小公倍數
兩個數字共同的倍數中最小的,稱為最小公倍數
像12就是6跟4的最小公倍數
| 2跟10 | 18跟12 | |
| 最大公因數 | ||
| 最小公倍數 |
2
10
6
36
怎麼求?
質因數分解法
\(18 = 2 \times 3 \times 3\)
\(12 = 2 \times 2 \times 3\)
最大公因數\(= 2 \times 3\)
最小公倍數\(= 2 \times 2 \times 3 \times 3\)
質因數分解法
16跟10的最小公倍數、最大公因數?
English time
6/1
好事
看影片!
問題
1. 錢薇娟為甚麼會想打籃球?
2. 錢薇娟做了哪些努力?
復習
英文單字



book
ruler
computer
英文句型
你好嗎?
How are you?
因數、公因數
20的因數:
1
2
4
5
10
20
16的因數:
1
2
4
8
16
20跟16的公因數:
1
2
4
20跟16的最大公因數:
4
English time
train
picture


故事接龍
6/8
好事!
複習
英文單字




cake
plane
elephant
pencil
picture
Is it a doll?

倍數、公倍數
10的倍數:
10
20
30
40
50
60
16的倍數:
16
32
48
64
80
10跟16的公倍數:
80
160
240
10跟16的最小公倍數:
80
70
80
90
100
96
112
English time
- 梅雨大概是甚麼時後會下?
- 為甚麼它要叫做梅雨?
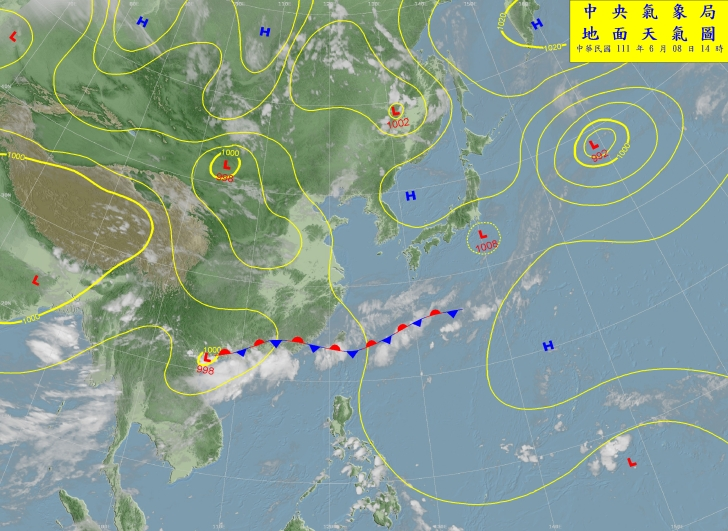
想想看!
3
3
4
4
4
2
5
3
3
3
故事接龍
6/17
好事!
學校在教甚麼?
下次休息一次!
複習
英文單字



clown
yo-yo
puzzle
英文句型

What do you have?
I have a doll, a robot, and a yo-yo.
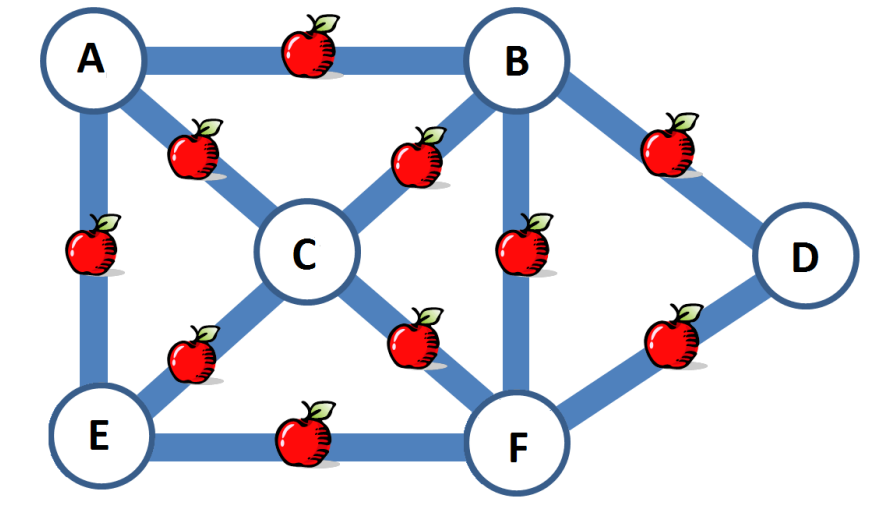
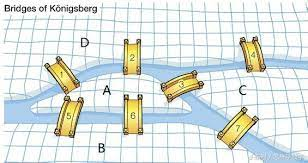
一筆畫問題
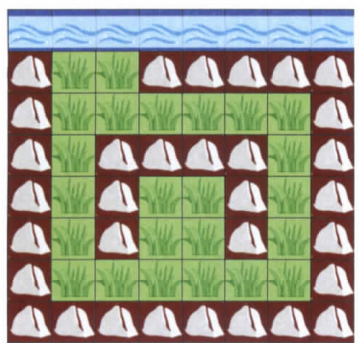
動動腦
多久之後,所有草地都會被水淹到?
故事接龍
- 聲音怎麼產生?
- 人怎麼聽到聲音?
- 為甚麼聲音有高有低?
Kolmogorov Complexity and the Incompressibility Method
What's the next number?
\(1,2,4,8,16,\)
What's the next number?
\(1,2,4,8,16,\)
\(7122\)?
\(32\)?
What is randomness?
\(1,2,4,8,16,7122\)
\(1,2,4,8,16,32\)
k = 1
for i in range(5):
print(k)
k *= 2k = 1
for i in range(4):
print(k)
k *= 2
print(7122)A = [1,2,4,8,16,7122]
for i in range(5):
print(A[i])Kolmogorov Complexity
\(C(x) = \min\{l(p):p \text{ is an encoding/program of }x\}\)
Think of \(x,p\) as binary strings(or natural numbers).
Kolmogorov Complexity
\(C(x) = \min\{l(p):p \text{ is an encoding/program of }x\}\)
Think of \(x,p\) as binary strings(or natural numbers).
A more formal definition
\(C_f(x) = \min\{l(p):f(p) = x\}\)
Where \(f\) is some (partial) function.
Kolmogorov Complexity
\(C(x) = \min\{l(p):p \text{ is an encoding/program of }x\}\)
Think of \(x,p\) as binary strings(or natural numbers).
A more formal definition
\(C_f(x) = \min\{l(p):f(p) = x\}\)
Where \(f\) is some (partial) function.
How should we choose \(f\)? (C++, python, Eric Xiao, ...?)
Kolmogorov Complexity
Maybe \(f\) should be the "minimal" (additively optimal) function:
\(\forall g,x, C_f(x) \leq C_g(x) + c_g\)
Kolmogorov Complexity
Such \(f\) doesn't exist:
Let \(g(i) = x_i\), where \(C_f(x_i) \geq i\)
Maybe \(f\) should be the "minimal" (additively optimal) function:
\(\forall g,x, C_f(x) \leq C_g(x) + c_g\)
Kolmogorov Complexity
Perhaps we should not consider all functions.