DP優化
先說一下:今天說的都是求最大最小值的DP,等一下的max也可以是min
單調隊列優化
長相(通常):
\(dp[i] = \max\limits_{j + k < i}( g(i) + f(j))\)
\(dp[i] = g(i) + \max\limits_{j + k < i} f(j)\)
其中\(k\)固定
考慮
給長度為\(N\)的序列\(A\)和一個數字\(k\),求長度為\(N - k + 1\)的序列\(B\),使得
\(B_i = \max\limits_{j+k-1 < i} A_j\)
Input: N=6, k=3
A: 9 5 3 6 2 8
B: 9 6 6 8
有人會做ㄇ
這裡讓我偷一下
回來看:
\(dp[i] = g(i) + \max_{j + k < i} f(j)\)
其中\(k\)固定
根本跟剛剛一樣?
deque做到O(N)!
其實不只這樣?
1.k可以遞減,不用固定
2. 不一定是index距離小於一個東西
斜率優化
長相(通常):
\(dp[i] = \max\limits_{j < i} (g(i) + a(j) \times f(i) + b(j))\)
\(dp[i] = g(i) + \max\limits_{j < i}( a(j) \times f(i) + b(j))\)
一樣轉換問題
請你支援兩種操作:
1.加入一條直線\(y = a_i \times x + b_i\)
2.詢問一個\(x\)對應到的所有那些直線中y最大的值
我也不會QQ
例題是理解的試金石
狀態
dp[i]代表分好前i個人之後的最大值
轉移
\(dp[i] = \max\limits_{j < i}( dp[j] + a \times (s_i - s_j)^2 + b \times (s_i-s_j) + c)\)
怎麼變成
\(dp[i] = g(i) + \max_{j < i} a(j) \times f(i) + b(j)\)
轉換成功!可是到底怎麼做?
注意這些直線的斜率是\((-2a \times s_j)\),因為原序列是正整數,所以斜率會遞增!而且我們每次都是要查\(s_i\),這東西也會遞增!
斜率、查詢遞增的斜率優化
用deque照斜率遞增維護直線
1
2
3
查詢
插入直線
O(N)
YA!
斜率不單調
用multiset往後殺往前(被)殺
直接當模板ㄅ
方法一
李超線段樹
方法二
二分搜
wqs
我也不太懂啦QQ
作法
二分搜一個mid,把每個白邊的權重都加上mid(也就是指選每個白邊的代價),然後做最小生成樹,若用太多白邊就增加代價,否則減少代價。最後答案就是最小生成樹權重減need*mid。
使用白邊的數量
最小生成樹權重
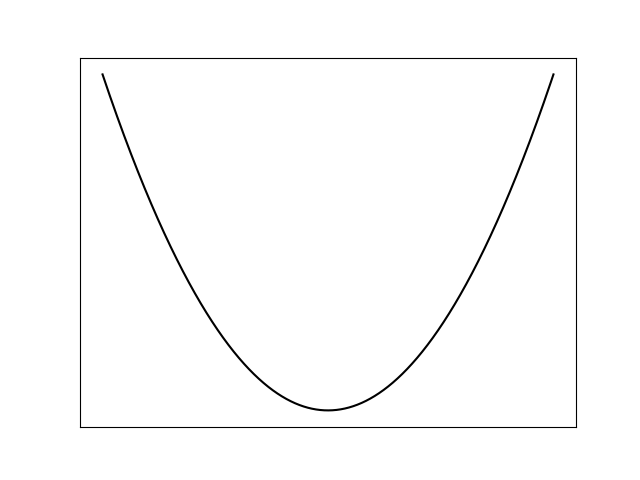
\(need\)
\(f(need)\)
等等,他為啥是凸的?
我就爛QQ
根據經驗
顯然
寫完之後AC
感覺
別人說
使用白邊的數量
最小生成樹權重

\(need\)
\(f(need)\)
???
\(min\)
\(f(min)\)
OK!
使用白邊的數量
最小生成樹權重
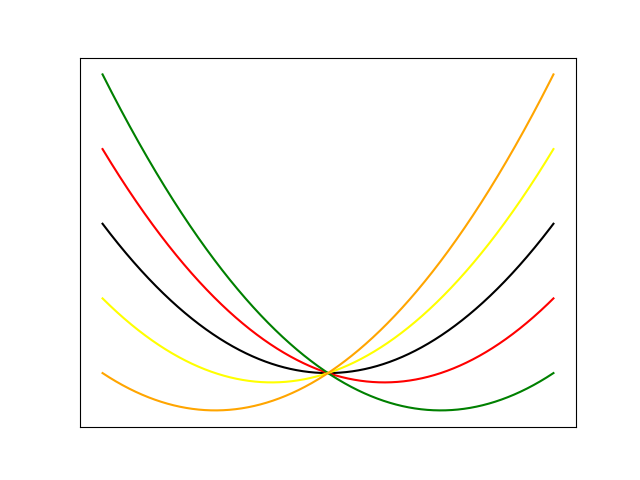
\(f(x)\)
\(f(x)-x\)
\(f(x)-2x\)
\(f(x)+x\)
\(f(x)+2x\)
need
\(f(need)\)
\(f(need)-need\times2\)
YA!
aliens 優化
就是把wqs二分搜套到DP上
例題是理解的試金石
狀態
\(dp[i][j][0]\):考慮前\(i\)天,交易了\(j\)次,而現在手上沒有東西的最大價值
\(dp[i][j][1]\):考考慮前\(i\)天,交易了\(j\)次,而現在手上有東西的最大價值
轉移
\(dp[i][j][0] = \max(dp[i-1][j][0],dp[i-1][j][1] +v[i])\)
\(dp[i][j][1] = \max(dp[i-1][j][1],dp[i-1][j-1][0] -v[i])\)
凸性誰來救
我噁噁的code(不要學)
關於aliens的一些事
1. 你覺得一題是aliens,不是因為他的函數是凸的(除非you mean wall),個人認為有兩個東西比較好看出:
(1)他限制了某個東西的次數
(2)你列出DP式,把不必要的東西去掉後,狀態還是多到就算轉移是O(1)也跑不完
關於aliens的一些事
2. 倘若那個凸函數的值域是整數,就不用小數二分搜
3. 有時候那個函數是不嚴格凸的,所以不一定二分搜的到剛好用了\(k\)次的時候,這時候就讓你的dp在答案一樣的時候盡量用比較少次,再直接把二分搜所加上的權重\(w\)拿去dp,然後你就輸出dp的答案\(-w*k\)就好了
4.二分搜的上下界自己搞清楚或是問@casperwang
現在有時間的話寫寫看這題
四邊形優化
溫馨提醒:為了延續蕭電的風格,就先暫時放下自己的強迫症好了
-- by 忍不住想排版的03t

為什麼叫四邊形?
pD/qD DP
大家應該都知道這是甚麼鬼東西了吧
凸?
若對於任意的\(i < i^′, j < j^′\):
如果\(F(j, i)\geq F(j^′, i)\) 成立的話,必可以保證\(F(j, i^′)\geq F(j^′, i^′)\)。
這是什麼鬼
凸?
若對於任意的\(i < i^′, j < j^′\):
如果\(F(j, i)\geq F(j^′, i)\) 成立的話,必可以保證\(F(j, i^′)\geq F(j^′, i^′)\)。
多米諾效應:
我現在比你多,未來一定比你多
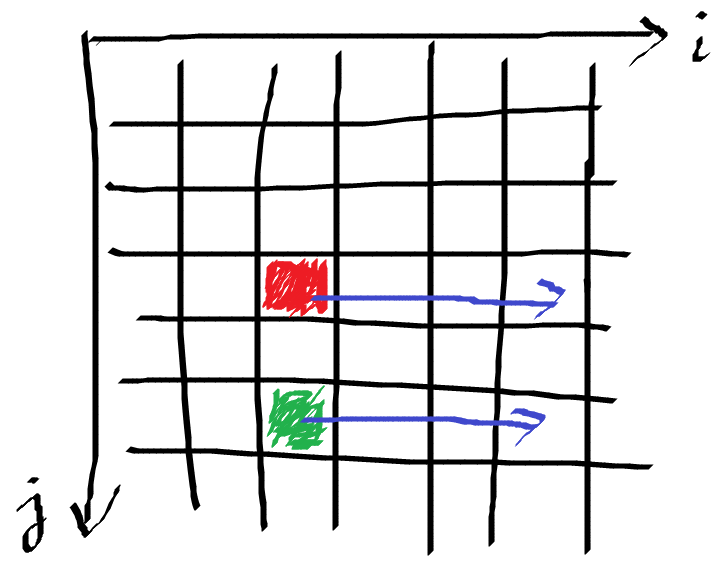
凹?
若對於任意的\(i < i^′, j < j^′\):
如果\(F(j, i)\leq F(j^′, i)\) 成立的話,必可以保證\(F(j, i^′)\leq F(j^′, i^′)\)。
應該懂了(?
小測驗
判斷以下函數是否有凹四邊形單調性
\(F(x, y) = xy\)
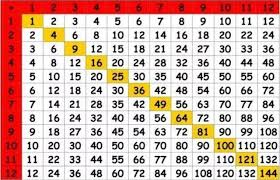
\(F(x, y) = (x-y)^2\)
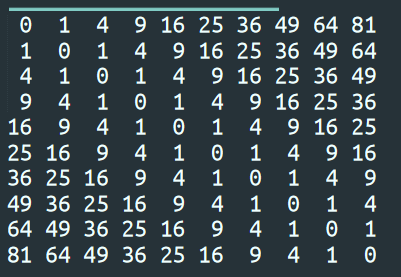
\(F(x, y) = s_x + t_y\)
\(s, t\) 是遞增數列
\(F(x, y) = aA(x, y) + bB(x, y)\)
\(a, b \geq 0\)
A, B 有凹四邊形單調性
四邊形不等式(交叉與包含)
如果對於任何\(i < i^′ \leq j < j^′\)
都有\(F(j, i) + F(j^′, i^′)\leq F(j, i^′) + F(j^′, i)\)
則 F 滿足凸四邊形單調性。
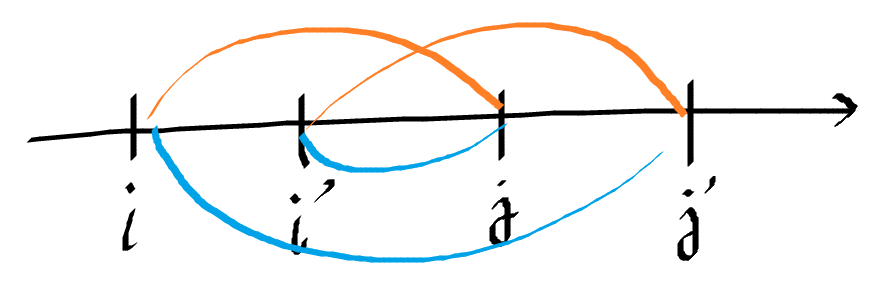
舉一隅以一隅反
如果對於任何\(i < i^′ \leq j < j^′\)
都有\(F(j, i) + F(j^′, i^′)\geq F(j, i^′) + F(j^′, i)\)
則 F 滿足凹四邊形單調性。
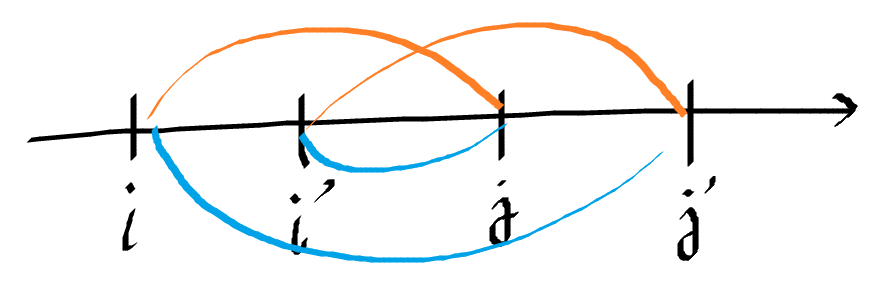
還有
判斷以下函數是否有凹四邊形單調性
C 是正整數數列,K 是正整數
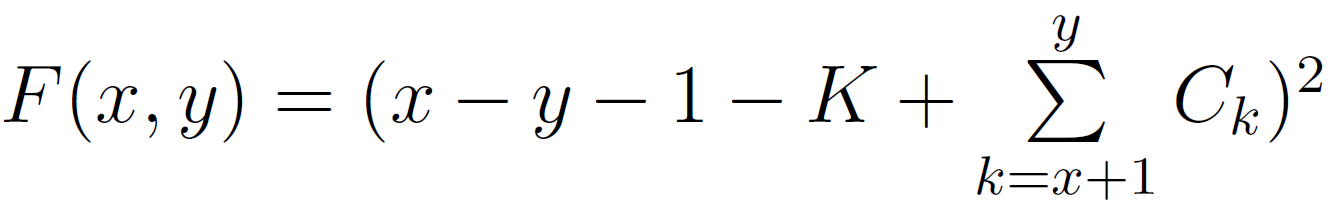
我也不知道答案
[HNOI 2008] 玩具裝箱
它也可以斜率優化
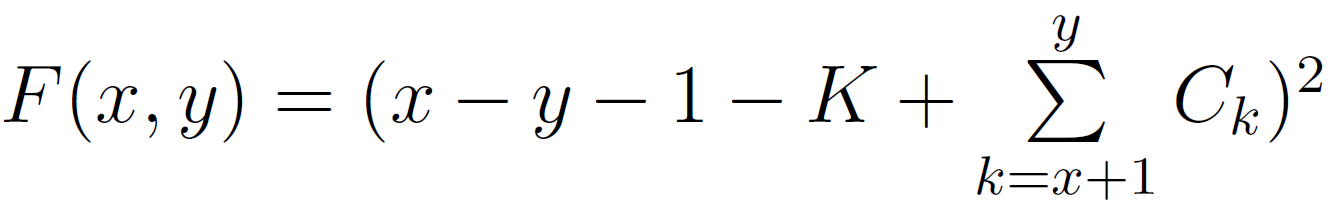
[POI 2011]Lightning Conductor
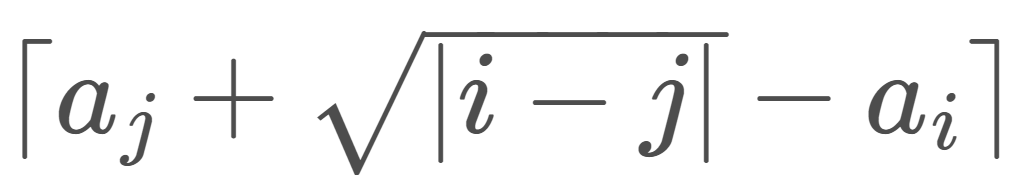
\(F(i, j) = \)
反芻
凹
凸
四邊形不等式
凹跟凸有什麼用
四邊形單調性
2D/1D四邊形優化
長相(通常):
\(dp[i][j] = \min\limits_{i\leq k\leq j}\{dp[i][k] + dp[k][j] + w(i, j)\}\)
從夾在裡面的東西轉移
尋找蘿莉第二彈
額,先別管題敘
算了還是看一下好了
這是建中校內賽題
尋找蘿莉第二彈
\(dp[l][r]=\min\limits_{l≤k≤r}\{dp[l][k]+dp[k][r] + sum(l, r)\}\)

尋找蘿莉第二彈
\(dp[l][r]=\min\limits_{l≤k≤r}\{dp[l][k]+dp[k][r] + sum(l, r)\}\)
凸??
好啦通常w凸dp就凸 QQ 然後這就凸凸的
重要定理
設\(p_{i,j}\) 是dp[i][j] 在轉移時所找到的最佳轉移點,且dp 滿足凸四邊形不等式,則:
\(p_{i,j−1} \leq p_{i,j} \leq p_{i+1, j}\)
打無限個星號 考翻了
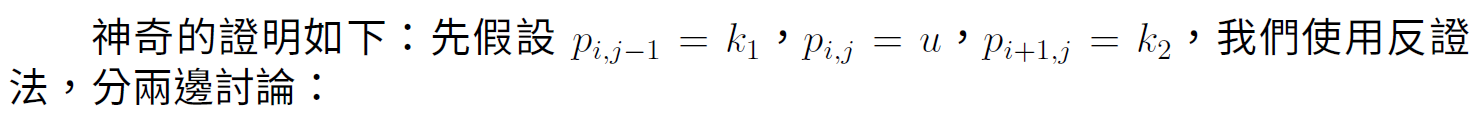

2D/1D凸四邊形優化
\(dp[i][j] = \min\limits_{i\leq k\leq j}\{dp[i][k] + dp[k][j] + w(i, j)\}\)
\(dp[i][j] = \min\limits_{p_{i, j-1}\leq k\leq p_{i+1, j}}\{dp[i][k] + dp[k][j] + w(i, j)\}\)
紀錄好轉移來源

for(int len = 2; len <= n; len++){ // 枚舉區間長度 (i - j)
for(int i = 1, r = len; j <= n; i++, j++){
// 枚舉長度為 len 的所有區間
dp[i][j] = INF;
for (int k = p[i][j-1]; k <= p[i+1][j]; k++) {
if (dp[i][j] > dp[i][k] + dp[k+1][j] + w(i, j)) {
// 更新 dp 陣列
dp[i][j] = dp[i][k] + dp[k+1][j] + w(i, j);
p[i][j] = k; // 記錄(最小)轉移來源
}
}
}
}核心代碼
這題其實有很多種等價的題序,讓我們來看看吧!
其實也有\(O(nlogn)\)的做法
1.石子合併
2.OBST
2D/1D凸四邊形優化
使用時機
1. DP式是2D/1D的
2. 滿足四邊形不等式
3. 至少w要凸
2D/1D凹沒有好性質
所以只能枚舉\(i\),讓dp狀態變成一維
用N次的1D/1D 解決
時間複雜度\(N^2 \log N\)。
1D/1D四邊形優化
a.k.a. 決策單調性優化
長相(通常):
\(dp[i] = \min\limits_{0\leq j < i}\{dp[j] + w(i, j)\}\)
\(dp[i] = \min\limits_{0\leq j < i}\{w(i, j)\}\)
枚舉前面的點轉移
Lightning Conductor
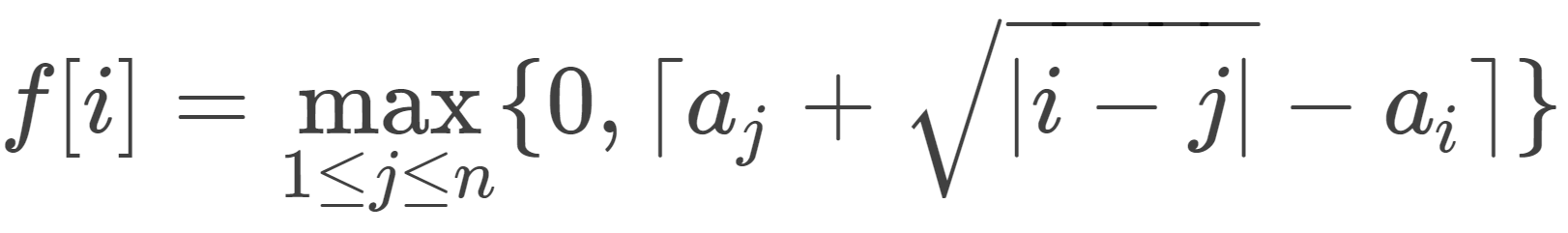
a 是正整數序列,對於每個i求f[i]
Lightning Conductor
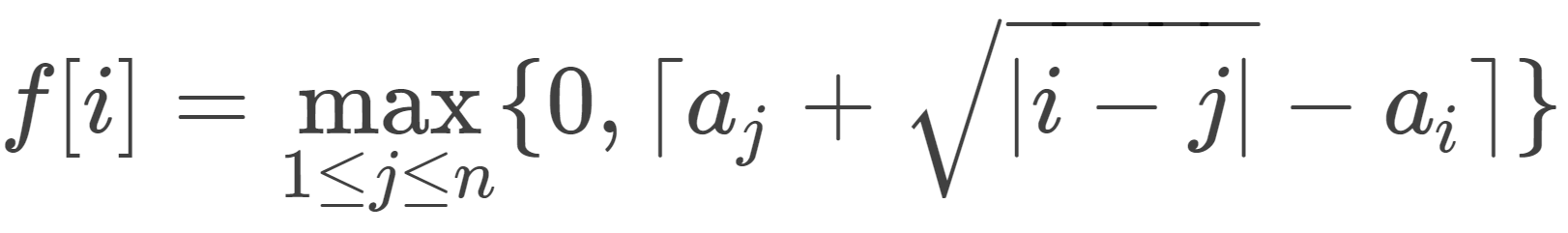
先假設\(i > j\) 把絕對值拆掉
Lightning Conductor
凸?
Lightning Conductor
證明四邊形不等式
\(w(a, d) + w(b, c) \leq w(a, c) + w(b, d)\)
兩邊消掉一些東西
\(\sqrt{d - a} + \sqrt{c - b} \geq \sqrt{c - a} + \sqrt{d - b}\)
兩邊平方,排序不等式
\(bd + ac \geq bc + da\)
Lightning Conductor
有單調性了 XD
多米諾效應:
我現在比你差,未來一定比你差

1D/1D凸四邊形優化
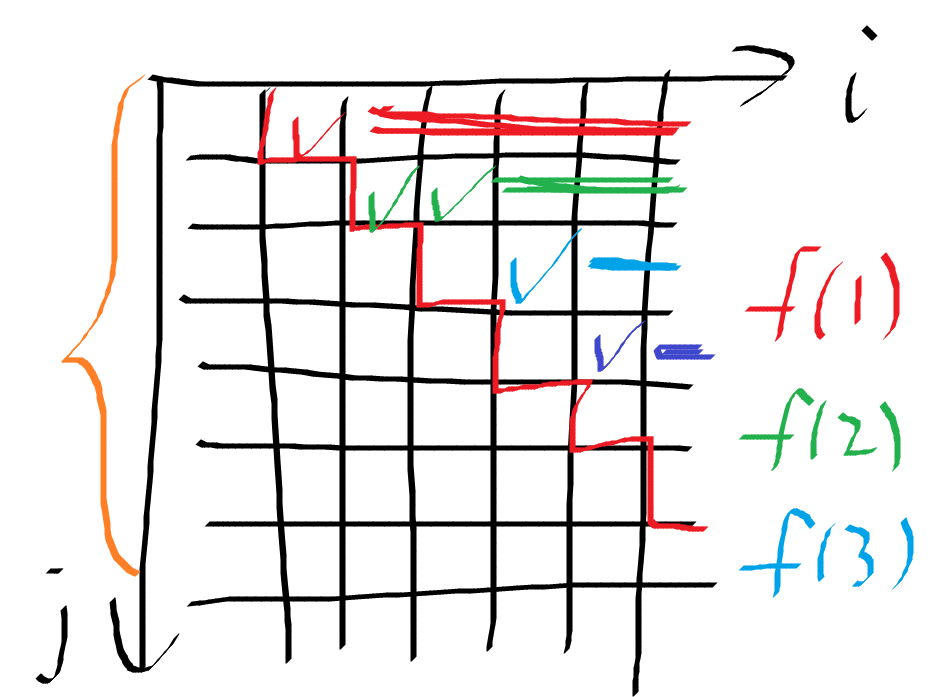

:
struct seg{int p,l,r;};
deque<seg> deq;
void solve() {
deq.push_back(seg{0,1,n});
for(int i=1; i<n; i++) {
// 計算dp[i]
while(deq.front().r <= i) deq.pop_front();
dp[i] = f(deq.front().p, i);
// 更新以 i 作為轉移來源的區間
while(deq.size() && f(i, deq.back().l) < f(deq.back().p, deq.back().l))
deq.pop_back();
seg new_seg = seg{i, i+1, n};
if(deq.size()) { // 有可能全部被 pop 掉
int c = binary_search(deq.back().p, i);
// c 是滿足 f(i, k) < f(deq.back().i, k) 的最小 k
deq.back().r = new_seg.l = c;
}
if(new_seg.l < n) deq.push_back(new_seg);
}
}核心代碼
1D/1D凸四邊形優化
使用時機
1. DP式是1D/1D的
2. 滿足四邊形單調性
3. 至少w要凸
1D/1D的也可以是凹
可是好像沒什麼必要用QQ
分治優化
同一題
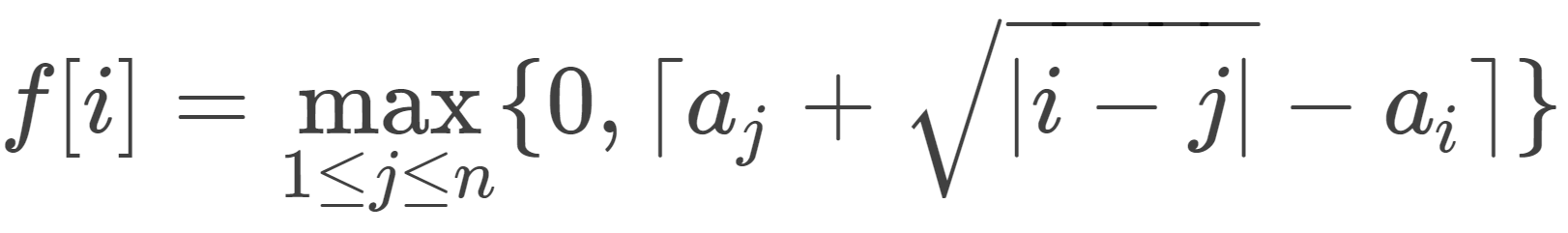
a 是正整數序列,對於每個i求f[i]
分治做法
哈哈 其實這題有輕鬆的做法
solve(L, R, ll, rr)
計算區間[L, R)且轉移點限制在[ll, rr)內的答案
分治做法
solve(L, R, ll, rr)
暴力算mid的答案與轉移來源p
ㄈsolve(l,mid-1,ll,dim)分治解決solve(l, mid, ll, p) 和
solve(mid+1, r, p, rr)即可
核心代碼
void solve(int l,int r,int ll,int rr) {
if(l > r) return;
int mid = (l+r)/2, p = 0;
for(int i=ll; i<=min(mid,rr); i++) {
if(num[i] - num[mid] + sqrt(abs(mid-i)) > dp[mid]) {
dp[mid] = num[i] - num[mid] + sqrt(abs(mid-i));
p = i;
}
}
solve(l, mid, ll, p), solve(mid+1, r, p, rr);
}注意:dp数组要开成 doubledouble ,决策时也要用 doubledouble ,只有输出时才取整,这样才是符合题意的,不能过程中直接取整=。=(不要问我为什么要说这个)
-- 崩潰的大陸人
分治優化使用時機
1. 還是要有決策單調性
2. 不限定計算順序 (轉移式不含dp項)
一堆題目
狀態
\(dp[i][0]\):考慮前\(i\)天,第i天不吃拉麵的最高分
\(dp[i][1]\):考慮前\(i\)天,第i天吃拉麵的最高分
轉移
\(dp[i][0] = \max(dp[i-1][0],dp[i-1][1])\)
\(dp[i][1] = \max\limits_{i-k \leq j < i}(dp[j][0] + S[i] - S[j])\)
1D/1D四邊形優化經典題
\(ans[i] = \max\limits_{j < i} \{A(j, i)\}\)
\(A(j, i)\)是以第j條線為下界,第i條橫線為下界的最大矩形面積
可以證明轉移點遞增
再用1D/1D凸或分治解決
倒過來考慮
狀態
\(dp[i]\)代表放完前\(i\)個東西後的最大值
轉移
\(dp[i] = \max\limits_{i-k\leq j < i}(dp[j]+S_j - (i-j)^2)\)
小心處理過期
狀態
\(dp[i]\)表示買進第\(i\)台機器時,擁有的最多錢數
轉移
\(dp[i] = \max\limits_{j < i,dp[j]\geq0}(dp[j]+(D_i - D_j)^2*G_j+R_j-Pi)\)
狀態
\(dp[i][j]\)表示考慮前\(i\)個房子,蓋了\(j\)座郵局的最短距離和
\(w[i][j]\)表示在第\(i\)個房子和第\(j\)個房子中,只蓋一座郵局的最短距離和
轉移
\(dp[i][j] = \min\limits_{k < i}(dp[k][j-1]+w[k+1][i])\)
狀態
\(dp[i][j]\)表示考慮前\(i\)個洞,放入前\(j\)隻老鼠
\(w[i][j]\)代表前\(j\)隻老鼠都跑到第\(i\)個洞所需的花費
轉移
\(dp[i][j] = \min\limits_{k+c[i] > j}(dp[i-1][k] + w[i][j] - w[i][k+1])\)
狀態
\(dp[i][j]\)表示考慮前\(i\)個洞,放入前\(j\)隻老鼠
\(w[i][j]\)代表前\(j\)隻老鼠都跑到第\(i\)個洞所需的花費
轉移
\(dp[j] = \min\limits_{k+c > j}(dp1[k] + w[j] - w[k+1])\)
狀態:
\(dp[i][j][k]\)代表考慮前\(i\)隻pokemon,用了\(j\)個紅球、\(k\)個黑球的隻數最大期望值
轉移:
\(dp[i][j][k] = \max(dp[i-1][j][k],dp[i-1][j-1][k] + p_i,dp[i-1][j][k-1] + u_i,dp[i-1][j-1][k-1] + u_i+p_i-p_i\times u_i)\)
狀態:
\(dp[i][j][0]\)代表前\(i\)組,取了\(j\)組,第\(i\)組不取
\(dp[i][j][1]\)代表前\(i\)組,取了\(j\)組,第\(i\)組要取
轉移:
\(dp[i][j][0] = \min(dp[i-1][j][1],dp[i-1][j][0])\)
\(dp[i][j][1] = dp[i-1][j-1][0] + 1\)
狀態
\(dp[i][j]\)表示考慮前\(i\)個房子,蓋了\(j\)座郵局的最短距離和
\(w[i][j]\)表示在第\(i\)個房子和第\(j\)個房子中,只蓋一座郵局的最短距離和
轉移
\(dp[i][j] = \min\limits_{k < j}(dp[k][j-1]+w[k+1][j])\)
狀態
\(dp[i][j]\)表示考慮前\(i\)個房子,蓋了\(j\)座郵局的最短距離和
\(w[i][j]\)表示在第\(i\)個房子和第\(j\)個房子中,只蓋一座郵局的最短距離和
轉移
\(dp[i] = \min\limits_{k < i}(dp[k]+w[k+1][i] + cost)\)