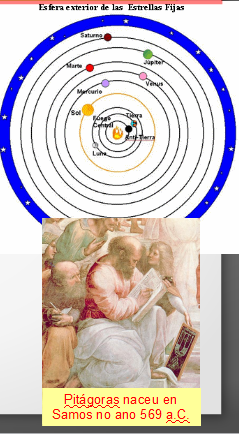
A CONCEPCIÓN PITAGÓRICA DO UNIVERSO

A escola pitagórica explicou a estrutura do universo en termos matemáticos
O gran lume central, orixe de todo, relacionábase co Un, orixe dos números
Ao seu redor xirarían a Terra, a Lúa, o Sol e os planetas
O periodo de revolución da Terra en torno ao lume central era de 24 horas, a quen lle ofrecía sempre a súa cara oculta
Os períodos da Lúa e o Sol eran un mes e un ano respectivamente
O universo concluiría nunha esfera celeste de estrelas fixas, e máis aló atopábase o Olimpo
O número de corpos que formaban o universo era de 10 (obsesión polos números)
Como só observaban nove, supoñían que o décimo estaba situado entre a Terra e o gran lume, ao que chamaron Antiterra
Pitágoras naceu en Samos no ano 569 a.C.

O MODELO DE ARISTÓTELES

O universo estaba constituído por dúas rexións esféricas, separadas e concéntricas
A Terra que ocupaba o centro do universo, era a rexión dos elementos, lume, aire, auga e terra
Máis aló da esfera lunar atopábase a rexión etérea dos ceos, cuxo único elemento era a incorruptible quinta esencia
Os movementos de todos os astros situados en esferas concéntricas coa Terra eran perfectos.
O universo concluía coa esfera das estrelas fixas .

O xeocentrismo de Ptolomeo

Viviu en Alexandría no século II e foi o máis soado astrónomo da antigüidade

As causas máis importantes dos modelos xeocéntricos fronte aos heliocéntricos foron:

- A falta de cálculos e predicións cuantitativas sobre as traxectorias dos planetas

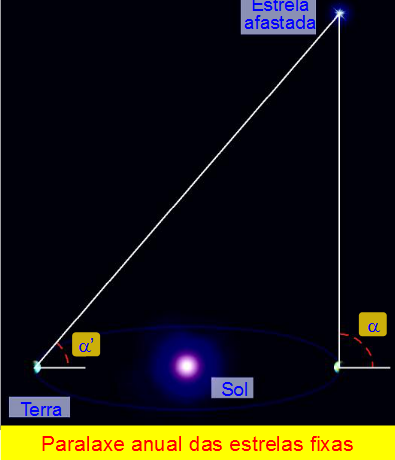
- Si a Terra non fose o centro do universo, ao longo do seu percorrido habería estrelas que terían que verse baixo distintos ángulos. Este fenómeno denomínase paralaxe das estrelas fixas

Ptolomeo xustificou o seu modelo calculando os movementos planetarios e prediciendo eclipses de Sol e de Lúa

O modelo de Ptolomeo: Os epiciclos

Nicolas Copérnico

O modelo Heliocéntrico

Desde a Terra apreciábase que planetas como Mercurio e Venus, que están máis próximos ao Sol, tiñan un brillo variable ao longo do ano, o que parecía indicar que as distancias con respecto á Terra variaban e polo tanto non podían xirar ao redor desta; chegouse á conclusión que todos os planetas tiñan que xirar ao redor do Sol

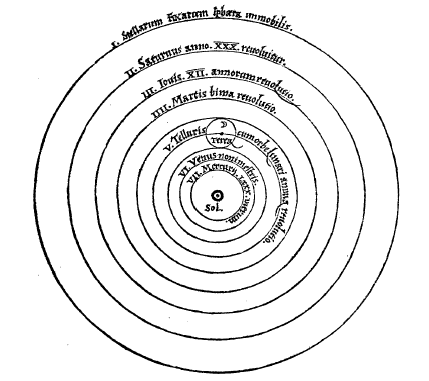
Nicolas Copérnico

O modelo Heliocéntrico

Actividades

Con frecuencia afírmase que Colón sabía que a Terra era redonda, pero que ninguén lle cría. Discute a corrección da proposición.
Cal é a explicación de que o Sol non produza sombra en Asuán ao mediodía do solsticio de verán?
Explica por que o sistema xeocéntrico tamén se chama sistema ptolemaico.
Por que dicimos que no vello sistema xeocéntrico do mundo había dúas mecánicas diferentes?
Explica en que consiste a paralaxe. Por que as estrelas aparentemente non mostran paralaxe?
Razoa sobre a validez desta proposición: «A mecánica celeste de Copérnico baseábase en principios diferentes aos dos antigos gregos».

Newton a Lei de Gravitación Universal

Newton unificou e ampliou as leis de Kepler baixo unha única lei: a chama lei de gravitación universal:

\vec{F} = -G \frac{Mm}{r^2} \vec{u_r}

\vec{F} = -G \frac{Mm}{r^2} \vec{u_r}

Conservación do momento angular e cálculo

Por integración

e substitución de variables

Usando conceptos como o de forza centrípeta...

1ª Lei (ampliada), ecuación dunha cónica

2ª Lei (áreas)

3ª Lei

r= \frac{l}{1+ecos\theta}

r= \frac{l}{1+ecos\theta}

\frac{dA}{dt}= \frac{L}{2m}=ctte

\frac{dA}{dt}= \frac{L}{2m}=ctte

\frac{r^3}{T^2}= \frac{GM}{4{\pi}^2}=ctte

\frac{r^3}{T^2}= \frac{GM}{4{\pi}^2}=ctte

Newton a Lei de Gravitación Universal

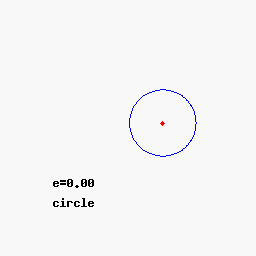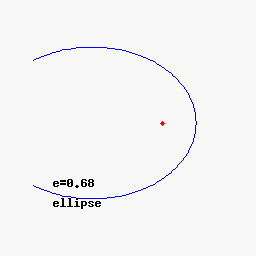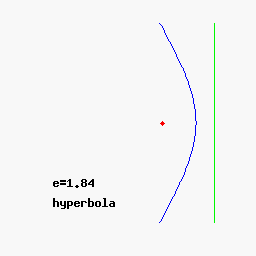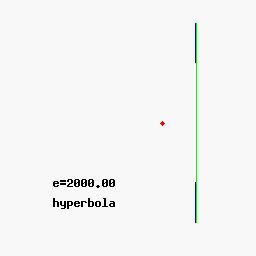
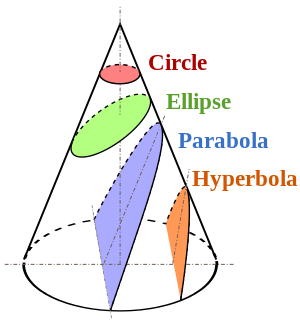
Chámase excentricidade a $e$ , para $e = 0$ , temos un círculo, para $0 < e < 1$ obtemos unha elipse, para $e = 1$ unha parábola, e para $e > 1$ unha hipérbola.

r= \frac{l}{1+ecos\theta}

r= \frac{l}{1+ecos\theta}

Actividades

Cantas voltas ao redor do Sol dá Mercurio nun ano? A distancia media Mercurio-Sol é 0,39 veces a distancia Terra-Sol
Calcula a excentricidade dunha elipse na que o eixe maior duplica ao eixe menor.
Demostra, a partir da lei das áreas, que nunha órbita circular a rapidez do planeta é uniforme.
Un asteroide segue unha órbita circular que completa en 820 días. Canto mide o raio da súa órbita, comparado co da Terra?

Actividades

Sabendo que a distancia do centro da Terra ao centro da Lúa é unhas sesenta veces o raio da Terra, estima a aceleración centrípeta da Lúa.
Razoa si é correcta a seguinte proposición: «Newton descubriu a forza da gravidade».
Comparamos dous satélites artificiais en órbita circular de igual radio, un en Marte e outro na Terra. Moveranse á mesma velocidade? Depende da masa dos satélites?
Calcula con que forza se atraen mutuamente o Sol e a Terra, supoñendo que a órbita da Terra é circular e de raio 150 · 10 ⁶ km. Datos: MSol = 2.0 · 10 ³⁰ kg; MTerra = 6.0 · 10 ²⁴ kg.
Por que a pleamar e a baixamar se alternan cada seis horas, aproximadamente?
Cal debe ser a masa de dúas masas idénticas que a 1 m de distancia se atraian cunha forza de 1 μN?

Actividades

Unha masa puntual móvese en liña recta con velocidade uniforme. Demostra que o seu momento angular é constante respecto de calquera punto.
O cometa Ale-Bopp ten unha órbita moi excéntrica (e = 0,997). Razoa en que punto desta: a) Móvese máis rápido. b) O seu momento angular é maior. c) Ten menor momento lineal. d) Presenta maior velocidade areolar.
Calcula a velocidade areolar de Venus dividindo a área da súa órbita circular polo tempo que tarda en percorrela. Obtense o mesmo resultado que no exercicio resolto? Por que? Que sucedería cun planeta que tivese órbita elíptica?
É correcto dicir que a velocidade dun planeta en órbita elíptica varía de forma inversamente proporcional á súa distancia ao Sol

Actividades do fin da unidade

Campo Gravitatorio

Tipos de forzas e concepto de campo

Forzas de contacto
Forzas a distancia
O Concepto de Campo

Activividades

Enumera as catro interaccións fundamentais da natureza.
Explica por que dicimos que o campo de forzas é vectorial. Inflúe na lei da gravitación de Newton a velocidade dos corpos ou estes atráense igual en movemento que en repouso?
Paréceche aceptable que a gravidade se propague de forma instantánea ou é máis razoable que teña unha velocidade finita de propagación?

Intensidade do campo gravitatorio

A intensidade do campo gravitatorio nun punto é a forza por unidade de masa situada en devandito punto

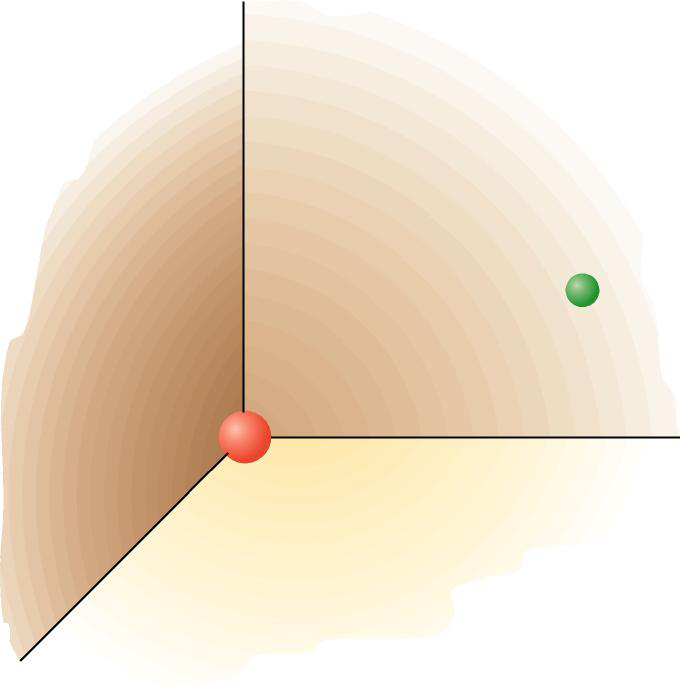
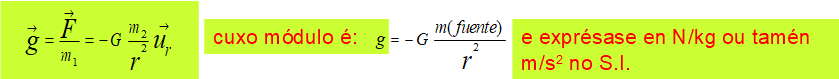
Intensidade do campo gravitatorio

Cando se trata de corpos extensos, suponse a masa concentrada no centro de masas, e ademais considérase para as distancias que r = RT + h

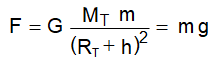
Variación da intensidade de campo terrestre

Coa altura

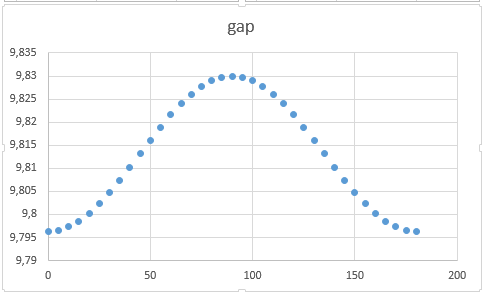
Coa latitude

Concepto de peso aparente

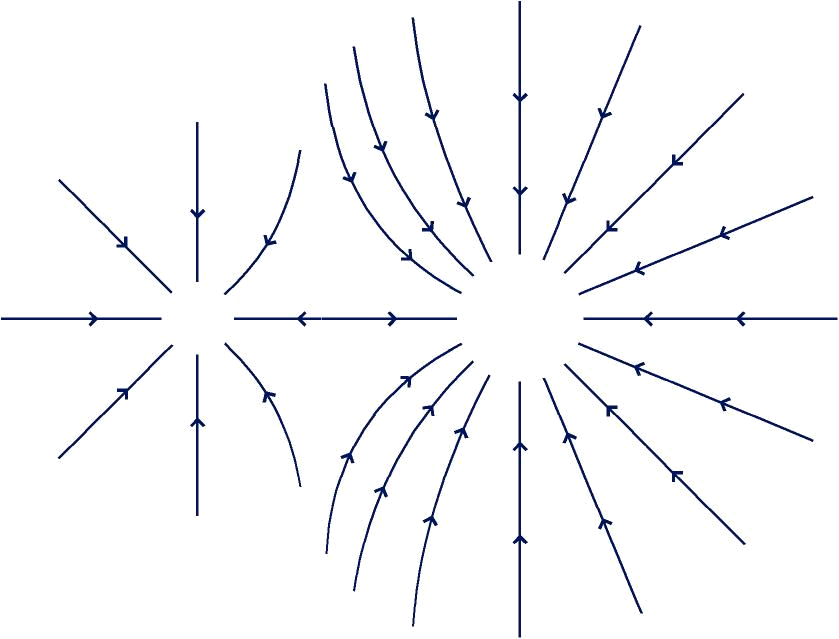
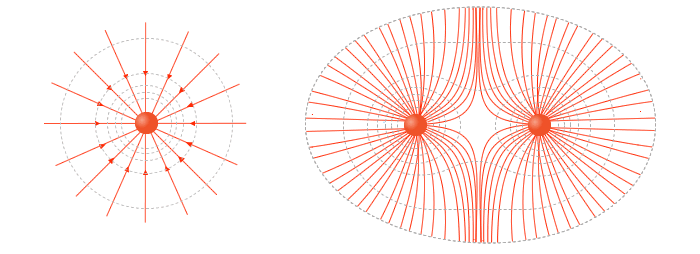
Liñas de forza do campo gravitatorio

Os campos de forzas represéntanse mediante liñas de campo
No campo gravitatorio, as liñas de campo, como é un campo atractivo, diríxense cara ás fontes do campo

Características:

As liñas nacen no infinito e entran nas masas.
A dirección do campo nun punto é a tangente á liña en devandito punto.
O sentido vén indicado pola frecha, e é o que seguiría a unidade de masa colocada en repouso na devandita liña por efecto das forzas do campo

Principio de superposición

A intensidade do campo nun punto P, creado por un conxunto de masas puntuales, obtense calculando a intensidade de campo creada por cada unha das partículas e sumando os resultados parciais.

\vec g_T=\Sigma \vec g_i

\vec g_T=\Sigma \vec g_i

\vec F_T=\Sigma \vec F_i

\vec F_T=\Sigma \vec F_i

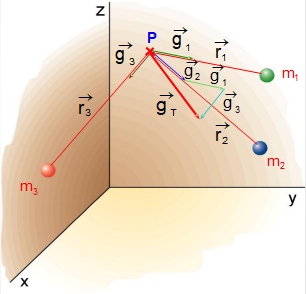
Tamén, loxicamente se pode aplicar ao cálculo dunha forza:

Actividades

Dúas masas diferentes están separadas 1 m. É igual o valor da forza que cada unha realiza sobre a outra? E o valor do campo que cada unha crea na posición da outra?
En que punto da liña que une dúas masas, unha tripla que a outra, se anula o campo gravitatorio total?
Obtén o vector forza que corresponde a unha masa de 25 kg situada nun punto onde o campo vale
Determina o campo total que crean na orixe tres masas de 100 kg situadas nas posicións A (5, 0), B (0, 2) e C (–1, –4), expresadas en metros.

\vec g = 5.4 \vec j \: m\cdot s^{-2}

\vec g = 5.4 \vec j \: m\cdot s^{-2}

CAMPOS DE FORZAS CONSERVATIVOS

Campos de forzas conservativos son aqueles nos que o traballo realizado pola forza depende só dos puntos inicial e final, e non do camiño seguido

W_{A,C1}^B = \int_A^B \vec F \vec {dr} = W_{A,C2 }^B

W_{A,C1}^B = \int_A^B \vec F \vec {dr} = W_{A,C2 }^B

W_{ciclo}= \oint \vec F \vec {dr} = 0

W_{ciclo}= \oint \vec F \vec {dr} = 0

W_A^B = - \Delta E_p

W_A^B = - \Delta E_p

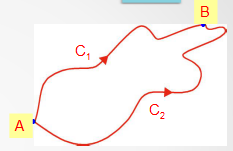
O CAMPO GRAVITATORIO É UN CAMPO CONSERVATIVO

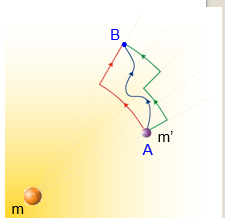
As forzas gravitatorias creadas por unha partícula m que actúan sobre a partícula m’, son radiales e con sentido cara a m

Calquera camiño da ata B descomponse en suma de arcos circulares centrados en m e de desprazamentos radiais

O traballo polo arco circular é nulo, por ser a forza perpendicular ao desprazamento

O traballo polo camiño radial, é igual para todos os camiños que se elixan entre A e B

Defínese circulación dunha magnitude vectorial ao longo dunha liña L á integral definida entre os límites de devandita liña

ENERXÍA POTENCIAL

Unha característica dos campos conservativos é que pode definirse unha magnitude denominada enerxía potencial.

Os cambios producidos na enerxía potencial, indican o traballo realizado polas forzas do campo.

Teorema da enerxía potencial: Nun campo conservativo o traballo realizado polas forzas do campo é igual á variación da enerxía potencial cambiada de signo.

W_A^B = - \Delta E_p

W_A^B = - \Delta E_p

Actividades

9.Calcula a enerxía potencial que adquire unha masa de 8 kg colocada no centro dun cadrado de 1 m de lado en cuxos vértices hai masas puntuales de 200 kg cada unha.

10.Explica por que dicimos que a forza e a enerxía potencial non son magnitudes características exclusivas do campo gravitatorio.

W_A^B = - \Delta E_p

W_A^B = - \Delta E_p

O potencial gravitatorio

Por ser o campo gravitatorio conservativo, pódese definir unha magnitude que depende únicamente do corpo m1 que crea o campo e non do m2 que se coloca como proba no punto P2

Esta magnitude denominase potencial V e obtense así se queremos determinar o potencial que m1 xera no punto P2, a partir da enerxía potencial de interacción entre m1 e m2:

V=\displaystyle\lim_{m_2 \rightarrow 0} \frac{Ep_{1,2}}{m_2}=-G \frac {m_1}{r}

V=\displaystyle\lim_{m_2 \rightarrow 0} \frac{Ep_{1,2}}{m_2}=-G \frac {m_1}{r}

A súa unidade no SI será, loxicamente o J/kg

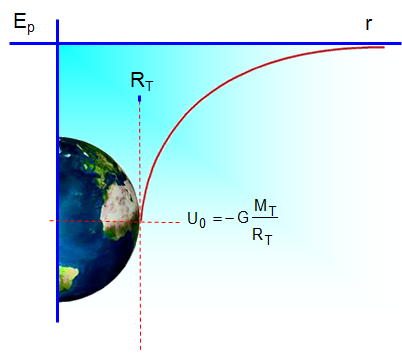
Variación do potencial gravitatorio terrestre

Como era de esperar, a variación do potencial terrestre coa altura é semellante á variación da enerxía potencial dunha masa situada no campo gravitatorio terrestre.

V=-G \frac {M_{Terra}}{r}=-G \frac {M_{Terra}}{R_T+h}

V=-G \frac {M_{Terra}}{r}=-G \frac {M_{Terra}}{R_T+h}

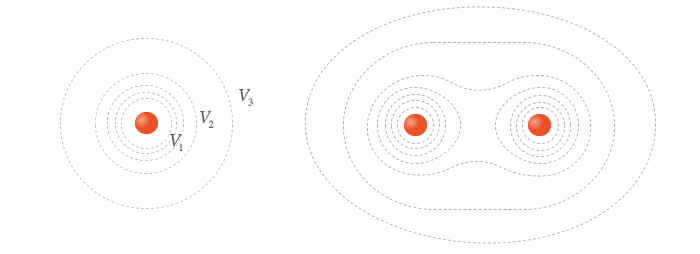
As superficies equipotenciais

Xa vimos unha maneira de representar graficamente o campo gravitatorio, mediante as liñas de forza. Tamén podemos facer unha representación gráfica mediante as chamadas superficies equipotenciais.

As superficies equipotenciais son o conxunto de puntos do espazo que posúen o mesmo potencial

As superficies equipotenciais

Relación campo-potencial

As liñas de forza son perpendiculares en todos os puntos ás superficies equipotenciais:

Xa que:

-dV = \vec g \bullet \vec{dr}

-dV = \vec g \bullet \vec{dr}

Se nos movemos nunha superficie equipotencial:

0 = \vec g \bullet \vec{dr}

0 = \vec g \bullet \vec{dr}

Que implica que g e dr son perpendiculares.

Actividades

11. Que potencial existe a 10 m do centro dunha masa de 8000 kg?

12. A velocidade dun corpo de 40 kg é 60 m/s nun punto cun potencial de –30 J/kg. Cal será a súa velocidade si, movéndose libremente a través do campo, chega a un punto con potencial de –50 J/kg?

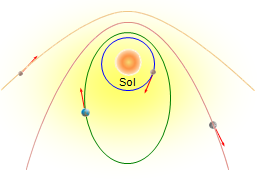
Forma das traxectorias

Xa vimos que, a partir da ecuación da gravitación universal de Newton, era posible calquera traxectoria cónica cando dous corpos se enfrontaban, sendo un deles de gran masa comparado co outro.

Existe unha relación entre as posibles traxectorias e a enerxía total do corpo pequeno:

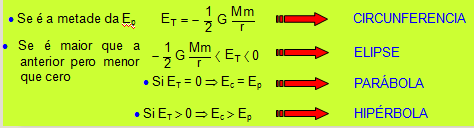
Forma das traxectorias

Existe unha relación entre as posibles traxectorias e a enerxía total do corpo pequeno:

SATÉLITES ARTIFICIAIS: ENERXÍA TOTAL E ENERXÍA DE SATELIZACIÓN

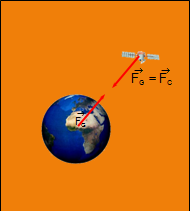
Velocidade de escape

Actividades

13. Por que é algo menor a intensidade do campo gravitatorio no ecuador que nos polos?

14. Determina a gravidade para unha altura igual ao radio terrestre.

15. Compara a gravidade na superficie da Terra coa doutro planeta que teña o mesmo raio, pero cuxa densidade sexa a metade.

16. Con que aceleración cae un corpo de 100 kg? E si é de 1 kg? Explica os resultados.

Actividades

17. Determina a velocidade de escape da superficie solar cos seguintes datos: MSol = 2.0·1030 kg; RSol = 695000 km.

Sol: 619,6 km/s

18. Acha a diferenza de enerxía potencial que se produce cando unha masa de 5 kg se levanta 10 m. Efectúa o cálculo coa fórmula exacta e coa aproximada, Ep = m g0 h. É apreciable a diferenza?

19. Razoa si é correcta a proposición seguinte: « Para dous planetas de igual masa, a velocidade de escape é maior no que ten a densidade máis baixa ».

20. Obtén a enerxía mecánica dun corpo de 800 kg de masa que se move a 4.5 km/s nun punto onde o potencial gravitatorio vale

-5 \cdot10^6 J/kg

-5 \cdot10^6 J/kg

2,0 \cdot10^{30}kg

2,0 \cdot10^{30}kg

Actividades

21. Determina o traballo de escape dun satélite de 1500 kg de masa que segue unha órbita circular en torno á Terra a unha altura igual ao raio medio terrestre.

22. A enerxía cinética dun satélite en órbita circular en torno a Marte é 8,2 · 1010 J. Obtén as súas enerxías potencial gravitatoria e mecánica total.

23. Razoa si é correcta a proposición seguinte: «En órbita elíptica, o momento lineal do satélite é maior no apoxeo que no perixeo».

24. É posible que un satélite de 1000 kg xire en órbita circular terrestre a unha altura de 500 km cunha velocidade de 8 km/s? E si cambiamos a masa do satélite?

25. Calcula o momento angular dun satélite de 2200 kg de masa que xira en órbita circular en torno a Venus cunha frecuencia de 4 voltas por día, si a masa de Venus é MV = 4.87 · 1024 kg.

8,2\cdot10^{10} J.

8,2\cdot10^{10} J.

4,87\cdot10^{24} kg.

4,87\cdot10^{24} kg.

Actividades

26. Como é o traballo exterior non gravitatorio que debemos realizar sobre un satélite para que pase a unha órbita de menor tamaño? É preciso acelerar ou frear ao satélite?

27. Explica por que é favorable instalar cerca do ecuador as bases de lanzamento espacial. En que dirección deberían lanzarse os foguetes?

28. Calcula a enerxía extra que debemos aportar a un satélite de 2400 kg para que pase dunha órbita circular terrestre a 400 km de altura a outra a 1000 km de altura.

29. Determina o traballo necesario para poñer un satélite de 850 kg en órbita circular lunar de radio dobre que o da Lúa.

Datos: ML = 7,35 · 10 kg; RL = 1738 km.

10^{22}

10^{22}

Actividades

26. Como é o traballo exterior non gravitatorio que debemos realizar sobre un satélite para que pase a unha órbita de menor tamaño? É preciso acelerar ou frear ao satélite?

27. Explica por que é favorable instalar cerca do ecuador as bases de lanzamento espacial. En que dirección deberían lanzarse os foguetes?

28. Calcula a enerxía extra que debemos aportar a un satélite de 2400 kg para que pase dunha órbita circular terrestre a 400 km de altura a outra a 1000 km de altura.

29. Determina o traballo necesario para poñer un satélite de 850 kg en órbita circular lunar de radio dobre que o da Lúa.

Datos: ML = 7,35 · 10 kg; RL = 1738 km.

10^{22}

10^{22}

Actividades

30. Explica de forma gráfica por que non pode haber satélites xeoestacionarios sobre o ceo de España.

31. Calcula o radio orbital dun satélite cuxo período sexa a metade do período de rotación da Terra.

32. Determina os parámetros orbitais dun satélite selenoestacionario cos seguintes datos da Lúa: ML = 7.35 · 10 kg; TL = 27 días, 7 horas e 43.2 minutos.

33. Poden ter órbita polar os satélites xeosíncronos? E os xeoestacionarios?

10^{22}

10^{22}

CAMPO GRAVITATORIO

A CONCEPCIÓN PITAGÓRICA DO UNIVERSO

O MODELO DE ARISTÓTELES

O xeocentrismo de Ptolomeo

O modelo de Ptolomeo: Os epiciclos

Nicolas Copérnico

O modelo Heliocéntrico

Nicolas Copérnico

O modelo Heliocéntrico

Actividades

Tycho Brahe e as leis de Kepler

Newton a Lei de Gravitación Universal

Newton a Lei de Gravitación Universal

Actividades

Actividades

Actividades

Actividades do fin da unidade

Actividades do fin da unidade

Campo Gravitatorio

Subtitle

Campo Gravitatorio

Forzas de contacto Forzas a distancia O Concepto de Campo

Activividades

Intensidade do campo gravitatorio

Intensidade do campo gravitatorio

Variación da intensidade de campo terrestre

Liñas de forza do campo gravitatorio

Principio de superposición

Actividades

CAMPOS DE FORZAS CONSERVATIVOS

O CAMPO GRAVITATORIO É UN CAMPO CONSERVATIVO

ENERXÍA POTENCIAL

Actividades

O potencial gravitatorio

Variación do potencial gravitatorio terrestre

As superficies equipotenciais

As superficies equipotenciais

Relación campo-potencial

Actividades

Forma das traxectorias

Forma das traxectorias

SATÉLITES ARTIFICIAIS: ENERXÍA TOTAL E ENERXÍA DE SATELIZACIÓN

Velocidade de escape

Actividades

Actividades

Actividades

Actividades

Actividades

Actividades

Actividades do fin da unidade

Campo
Gravitatorio

Forzas de contacto
Forzas a distancia
O Concepto de Campo