Orixe e evolución dos compoñentes do Universo I
Relator: Enric Ripoll Mira. 2019

Explicación rápida del profesor de:
Modelo atómico de Dalton
Modelo atómico de Thomson
Modelo atómico de Rutherford




1. Estrutura da materia. Hipótese de Planck
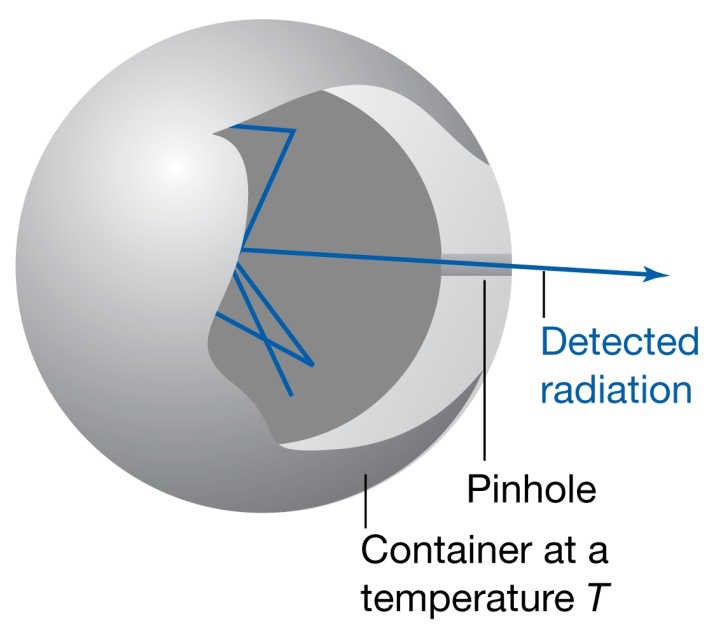
Variación da intensidade da radiación emitida coa lonxitude de onda da radiación e coa temperatura do corpo quente (negro)
Hipótese de Planck:
Os átomos compórtanse como osciladores que vibran todos a un mesma frecuencia, f
A enerxía destes osciladores non pode ser continua senón discreta (cuantizada) E=nhf n=0,1,2,...
A enerxía só se pode intercambiar en forma de “cuantos”. A enerxía dun “cuanto” = hf
Radiación do corpo negro
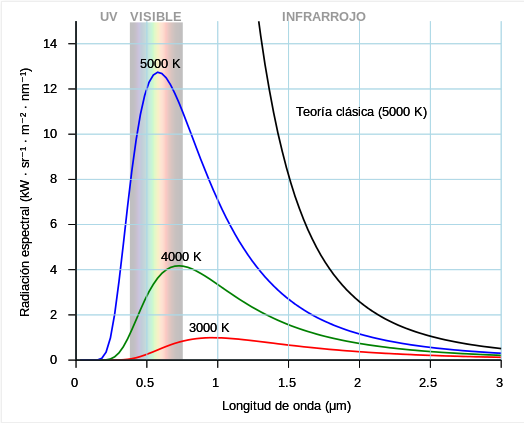
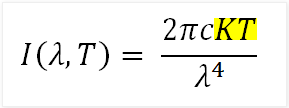
Ley de Rayleigh y Jeans
1. Estrutura da materia. Hipótese de Planck

Variación da intensidade da radiación emitida coa lonxitude de onda da radiación e coa temperatura do corpo quente (negro)
Hipótese de Planck:
Os átomos compórtanse como osciladores que vibran todos a un mesma frecuencia, f
A enerxía destes osciladores non pode ser continua senón discreta (cuantizada) E=nhf n=0,1,2,...
A enerxía só se pode intercambiar en forma de “cuantos”. A enerxía dun “cuanto” = hf
Radiación do corpo negro
Modelo atómico de Bohr



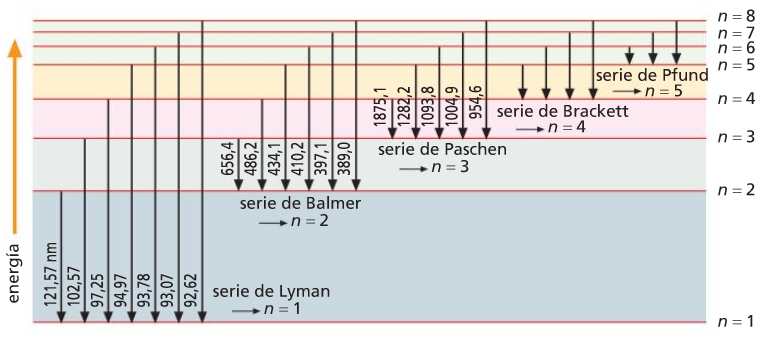
Modelo atómico de Bohr (fórmula de Rydberg)
Serie de Balmer (visible) do espectro de emisión do hidróxeno atómico
Fórmula de Rydberg:
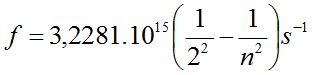
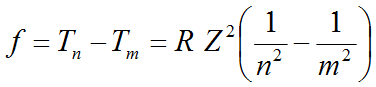
Térmos espectrais, Tn = R Z/n2 ; R =constante de Rydberg, depende do átomo. Só para átomos hidroxenoideos:

Modelo atómico de Bohr
O modelo atómico de Rutherford levaba a unhas conclusións que se contradicían claramente cos datos experimentais. Para evitar isto, Bohr suscitou uns postulados que non estaban demostrados en principio, pero que despois levaban a unhas conclusións que si eran coherentes cos datos experimentais; é dicir, a xustificación experimental deste modelo é a posteriori.
Primeiro postulado
O electrón xira ao redor do núcleo en órbitas circulares sen emitir enerxía radiante.
Segundo postulado
Só son posibles aquelas órbitas nas que o electrón ten un momento angular que é múltiplo enteiro de h/(2 ·π).
Posto que o momento angular defínese como L = mvr, teremos:
mvr = n · h/(2 · π ) —> r = a0 · n2
Modelo atómico de Bohr
Terceiro Postulado
A enerxía liberada ao caer o electrón desde unha órbita a outra de menor enerxía emítese en forma de fotón, cuxa frecuencia vén dada pola ecuación de Planck:
Ea - Eb = h · f
Así, cando o átomo absorbe (ou emite) unha radiación, o electrón pasa a unha órbita de maior (ou menor) enerxía, e a diferenza entre ambas órbitas corresponderase cunha liña do espectro de absorción (ou de emisión).

Modelo atómico de Bohr

Efecto fotoeléctrico
10. Que significa que un espectro de emisión é continuo?
11. Calcula a lonxitude de onda da primeira liña da serie de Balmer.
12. Utilizando a figura 7, asocia unha cor á primeira liña da serie de Balmer.
Actividades
Modelo atómico de Bohr. Actividades
13. Se se quenta un átomo de hidróxeno, que lle ocorre ao seu electrón? Como se chama o nivel enerxético no que se pode atopar?
14. Determina o número máximo de liñas no espectro de emisión que pode orixinar o electrón do átomo de hidróxeno si ocupa o nivel n = 3.
15. Un electrón promociona do seu nivel enerxético fundamental ao segundo nivel enerxético excitado. Absorberá ou emitirá radiación? Calcula:
a) A frecuencia da radiación.
Modelo atómico de Bohr. Actividades
16. A lonxitude de onda dunha das liñas da serie de Balmer é 410.2 nm. En que nivel de enerxía se atopa o electrón nos átomos excitados que orixinan esta liña?
17. En que contradín o modelo de Bohr á física clásica?
18. Como introduce Bohr a hipótese de Planck?
Modelo atómico de Bohr. Correccións
No modelo orixinal de Bohr, precísase un único parámetro (o número cuántico principal, n), que se relaciona co raio da órbita circular que o electrón realiza ao redor do núcleo, e tamén coa enerxía total do electrón. Os valores que pode tomar este número cuántico son os enteiros positivos: 1, 2, 3...
Con todo, pronto foi necesario modificar o modelo para adaptalo aos novos datos experimentais, co que se introduciron outros tres números cuánticos para caracterizar ao electrón:
número cuántico secundario ou azimutal (l)
número cuántico magnético (m)
número cuántico de espín (s)

Modelo atómico de Bohr-Sommerfeld
Unha elipse vén definida por dúas parámetros, que son os valores dos seus semiexes maior e menor. No caso de que ambos semiexes sexan iguais, a elipse convértese nunha circunferencia.
Así, introducimos o número cuántico secundario ou azimutal (l), cuxos valores permitidos son: l = 0, 1, 2, ..., n - 1
Por exemplo, si n = 3, os valores que pode tomar l serán: 0, 1, 2

Número cuántico secundario ou azimutal (l): corrección de Sommerfeld.
En 1916, Sommerfeld modificou o modelo de Bohr considerando que as órbitas do electrón non eran necesariamente circulares, senón que tamén eran posibles órbitas elípticas; esta modificación esixe dispoñer de dúas parámetros para caracterizar ao electrón.
Modelo atómico de Bohr-Sommerfeld
Por exemplo, si o número cuántico secundario vale l = 2, os valores permitidos para m serán: -2, -1, 0, 1, 2
O efecto Zeemann débese a que calquera carga eléctrica en movemento crea un campo magnético; polo tanto, tamén o electrón o crea, así que deberá sufrir a influencia de calquera campo magnético externo que se lle aplique.

Número cuántico magnético (m).
Indica as posibles orientacións no espazo que pode adoptar a órbita do electrón cando este é sometido a un campo magnético externo (efecto Zeemann).
Valores permitidos: - l, ..., 0, ..., + l
Modelo atómico de Bohr-Sommerfeld: o espín
George Uhlenbeck, Hendrik Kramers e Samuel Goudsmit. (Ann Arbor, circa 1928.)
Número cuántico de espín (s).
Indica o sentido de xiro do electrón en torno ao seu propio eixe. Pode tomar só dous valores: +1/2, -1/2.

Modelo atómico de Bohr-Sommerfeld: o espín
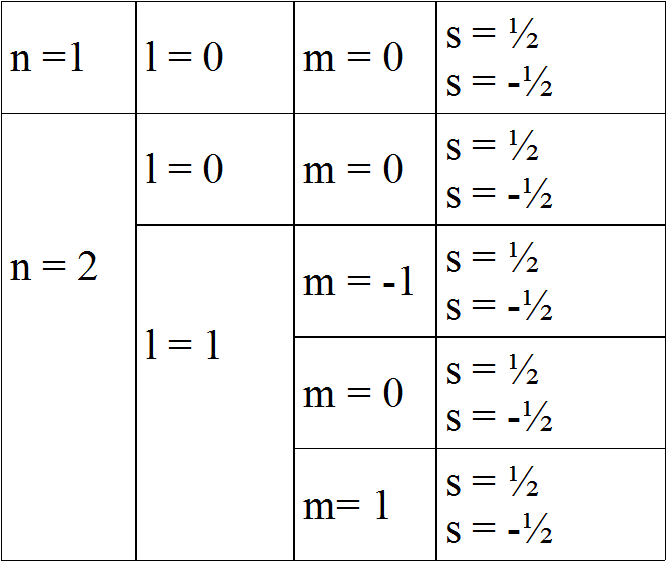
Enerxía da órbita
Forma da órbita
Orientación da órbita
Xiro do electrón sobre ele mesmo
O átomo mecanocuántico
Fallos do modelo de Bohr
O modelo de Böhr permitiu explicar adecuadamente o espectro do átomo de hidróxeno e dos hidroxenoideos, pero fallaba ao intentar aplicalo a átomos polielectrónicos e ao intentar xustificar o enlace químico.
Ademais, os postulados de Bohr supuñan unha mestura un tanto confusa de mecánica clásica e mecánica cuántica.
Dualidad onda corpúsculo de la luz
O átomo mecanocuántico
Efecto fotoeléctrico
O átomo mecanocuántico
Efecto fotoeléctrico
O átomo mecanocuántico
Entre 1925 e 1926 púxose en marcha unha nova teoría da Física que superou a teoría cuántica antiga que crearan Planck, Einstein e Bohr. Esta nova teoría, aínda vixente, denominouse mecánica cuántica. Neste tema só se mencionará a versión denominada mecánica ondulatoria, que foi elaborada por Schrödinger.
O átomo mecanocuántico: A hipótese de De Broglie
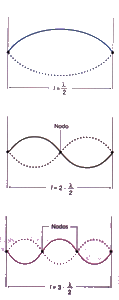
Tradicionalmente, os electróns consideráronse como partículas, e xa que un feixe de electróns sería algo claramente distinto dunha onda. Louis de Broglie propuxo (1923) eliminar esta distinción: un feixe de partículas e unha onda son esencialmente o mesmo fenómeno; simplemente, dependendo do experimento que realicemos, observaremos un feixe de partículas ou observaremos unha onda. Así, o electrón posúe unha lonxitude de onda (que é un parámetro totalmente característico das ondas) que vén dada por:
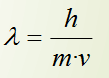

O átomo mecanocuántico: Principio de incerteza de Heisenberg
Establece que é imposible coñecer simultáneamente a posición e a velocidade do electrón, e xa que logo é imposible determinar a súa traxectoria. Canto maior sexa a exactitude con que se coñeza a posición, maior será o erro na velocidade, e viceversa. Soamente é posible determinar a probabilidade de que o electrón atópese nunha rexión determinada.
Podemos entender mellor este Principio si pensamos no que sería a medida da posición e velocidade dun electrón: para realizar a medida (para poder "ver" dalgún modo o electrón) é necesario que un fotón de luz choque co electrón, co cal está modificando a súa posición e velocidade; é dicir, polo mesmo feito de realizar a medida, o experimentador modifica os datos dalgún modo, introducindo un erro que é imposible de reducir a cero, por moi perfectos que sexan os nosos instrumentos.
O átomo mecanocuántico: Principio de incerteza de Heisenberg
Este Principio, enunciado en 1927, supón un cambio básico na nosa forma de estudar a Natureza, xa que se pasa dun coñecemento teoricamente exacto (ou polo menos, que en teoría podería chegar a ser exacto co tempo) a un coñecemento baseado só en probabilidades e na imposibilidade teórica de superar nunca un certo nivel de erro.

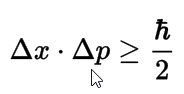
O átomo mecanocuántico: A ecuación de Schrödinger
A Mecánica Cuántica (1927) engloba a hipótese de Louis de Broglie e o Principio de indeterminación de Heisenberg. O carácter ondulatorio do electrón aplícase definindo unha función de ondas, Ψ, e utilizando unha ecuación de ondas, que matematicamente é unha ecuación diferencial de segundo grado, é dicir, unha ecuación na cal interveñen derivadas segundas da función Ψ:

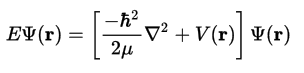
O átomo mecanocuántico: A ecuación de Schrödinger
Ao resolver a ecuación diferencial, obtense que a función e depende dunha serie de parámetros, que se corresponden cos números cuánticos, tal e como se definiron no modelo de Böhr. A ecuación só se cumprirá cando eses parámetros tomen determinados valores permitidos (os mesmos valores que se indicaron antes para o modelo de Böhr).
O cadrado da función de ondas, Ψ2, corresponde á probabilidade de atopar ao electrón nunha rexión determinada, co cal estase introducindo no modelo o Principio de Heisenberg. Por iso, neste modelo aparece o concepto de orbital: rexión do espazo na que hai unha máxima probabilidade de atopar ao electrón.
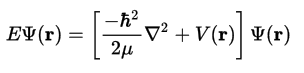
O átomo mecanocuántico: A ecuación de Schrödinger, os orbitais atómicos
(Non debe confundirse o concepto de orbital co de órbita, que corresponde ao modelo de Bohr: unha órbita é unha traxectoria perfectamente definida que segue o electrón, e polo tanto é un concepto moi afastado da mecánica probabilística.)
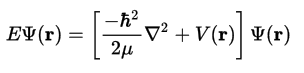
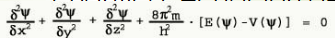
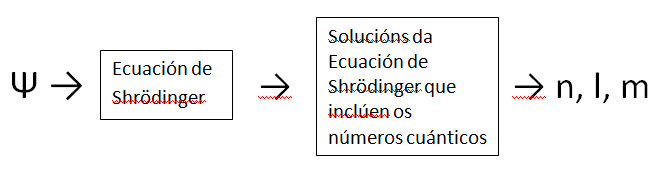
O átomo mecanocuántico: A ecuación de Schrödinger, os números cuánticos
Neste modelo atómico, utilízanse os mesmos números cuánticos que no modelo de Bohr e cos mesmos valores permitidos, pero cambia o seu significado físico, posto que agora hai que utilizar o concepto de orbital:
O átomo mecanocuántico: A ecuación de Schrödinger, os números cuánticos
|
Números cuánticos |
Significado físico |
Valores permitidos |
|---|---|---|
| principal (n) | Enerxía total do electrón (nivel enerxético no que se encontra o electrón) | 1, 2, 3.... |
|
secundario ou azimutal (l) |
Forma do orbital: Subnivel enerxético en onde está o electrón, dentro do nivel determinado por n. |
l = 0: orbital s (esférico) l = 1: orbital p (bilobulado) (un orbital p na dirección de cada eixe coordenado: px, py, pz) l = 2: orbital d 0, 1, 2, ..., n-1 |
|
magnético (m) |
Orientación do orbital cando se aplica un campo magnético externo. | -l, ..., 0, ..., + l |
|
espín (s) |
Campo magnético propio do electrón. |
± 1/2 |
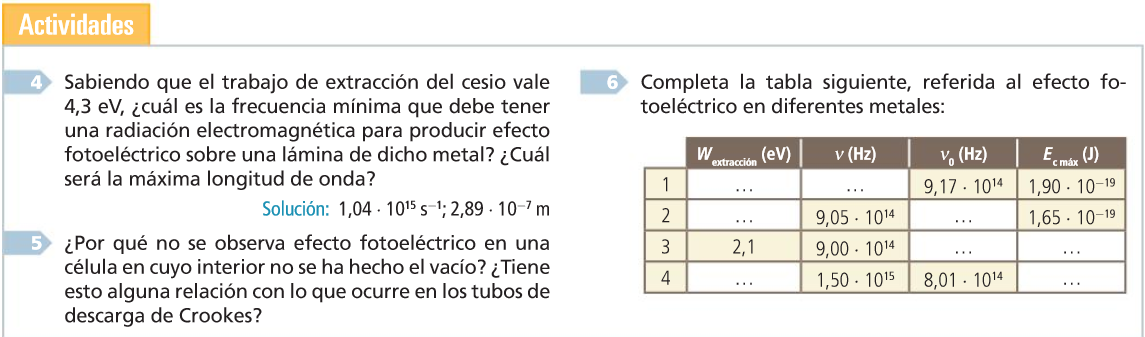
Actividades
Tubo de Crookes
Actividades
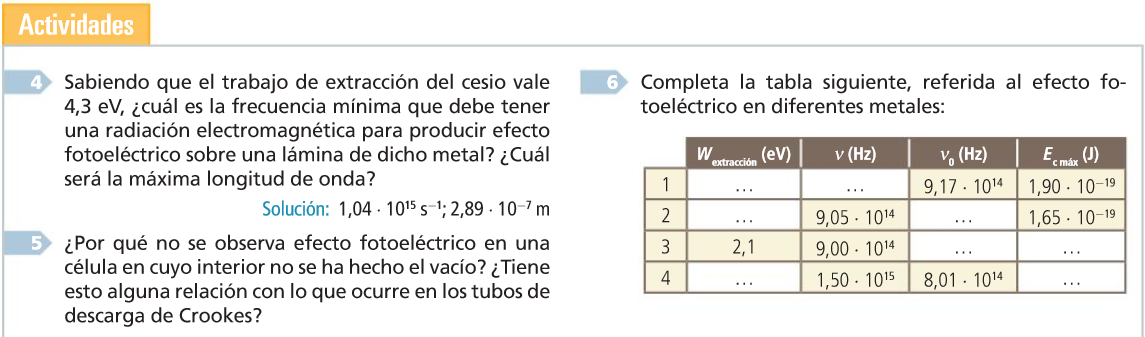
Actividades

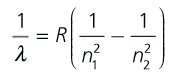
Ley experimental para el átomo de hidrógeno, deducible
a partir del modelo de Bohr
Efotón=h·f
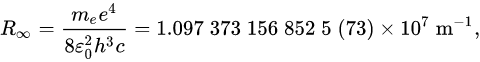
Actividades

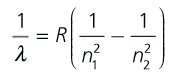
Efotón=h·f

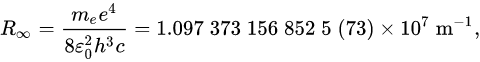
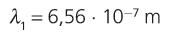
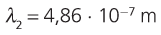
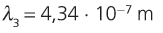
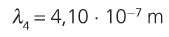


Actividades

Actividades

Actividades

Actividades


Actividades do fin da unidade
Partículas subatómicas
No ano 1913, Moseley confirma a existencia de protóns no átomo. Ao número de protóns dun átomo, Moseley chámalle número atómico, que se simboliza coa letra Z e indícase na parte inferior do símbolo do elemento.
No ano 1932, Chadwik descobre o neutrón, cunha masa semellante á do protón. Como o electrón ten unha masa moi pequena comparada co protón ou o neutrón, á suma destas dúas partículas sele chamou número másico que se simboliza cunha A e indícase na parte superior do símbolo do elemento:
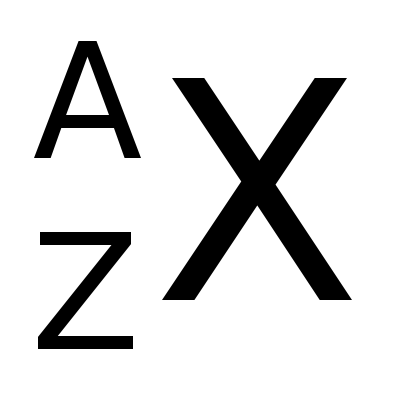
Partículas subnucleares
Partículas constituintes
•Mesóns, un quark e un antiquark
•Barións, tres quarks
•Leptóns (electrón, neutrino). Son partículas elementais.
• Fotóns
Partículas intermediarias
• Gravitóns
•Fotóns
•Bosóns (W e Z, portadores interación débil)
• Gluóns (portador da interación forte)