3ESO. A actividade científica

Aspectos a tratar

  • B1.1. Método científico: etapas.
  • B1.2. Utilización das tecnoloxías da información e da comunicación.
  • B1.3. Aplicacións da ciencia á vida cotiá e á sociedade.
  • B1.4. Medida de magnitudes. Sistema Internacional de Unidades. Notación científica.
  • B1.5. Erros.
  • B1.6. Traballo no laboratorio.
  • B1.8. Proxecto de investigación.

Vídeo

Un mapa conceptual es una herramienta de estudio poderosísima y a lo largo del curso vais a tener que hacer un mapa conceptual cada vez que acabamos un tema.

Un mapa conceptual no es un esquema, ni un mapa mental ni tampoco una tormenta de ideas.

No tiene ningún interés que os lo copiéis de un compañero, no serviría de nada. Hacedlo siguiendo las instrucciones del profesor.

Actividades Método científico

1.En 1792, A. Volta observó que, al colocar la lengua entre una hoja de estaño y una moneda de plata que estaban en contacto, experimentaba una sensación de picor. ¿A qué descubrimiento condujo esta observación?


2.En ocasiones, los científicos descubren algo que no estaban buscando mientras investigan un hecho diferente. ¿A qué descubrimientos llevaron estas observaciones?
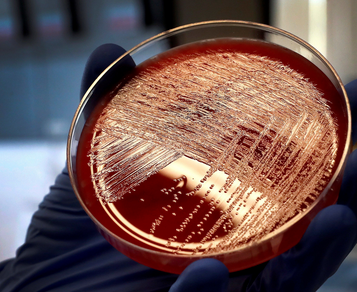
* A. Fleming observó que un hongo que había crecido en una placa de cultivo de bacterias había eliminado alas que estaban en contactocon él.
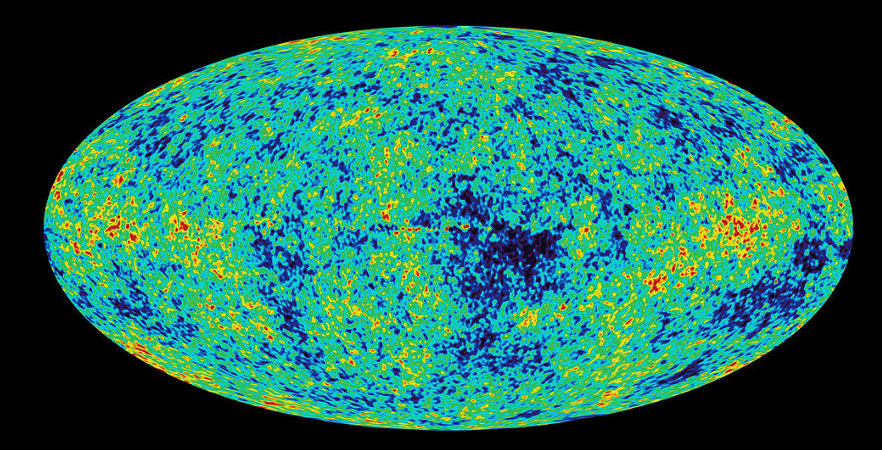
* A. Penzias y R. Wilson ponían a punto una gigantesca antena cuando captaron inesperadamente unas microondas procedentes de todas las direcciones del cielo que persistían durante todo el día y la noche

Actividades Método científico

Actividades Método científico

1.En 1792, A. Volta observó que, al colocar la lengua entre una hoja de estaño y una moneda de plata que estaban en con-tacto, experimentaba una sensación de picor. ¿A qué descubrimiento condujo esta observación?
2.En ocasiones, los científicos descubren algo que no estaban buscando mientras investigan un hecho diferente. ¿A qué descubrimientos llevaron estas observaciones?
* A. Fleming observó que un hongo que había crecido en una placa de cultivo de bacterias había eliminado alas que estaban en contactocon él.
* A. Penzias y R. Wilson ponían a punto una gigantesca antena cuando captaron inesperadamente unas microondas procedentes de todas las direcciones del cielo que persistían durante todo el día y la noche

Actividades

1.2. El planteamiento de hipótesis

3. Plantea el problema y formula una hipótesis en estas situaciones:
a) Observas que una goma elástica se alarga cuando tiras de sus
extremos, y te planteas si existe algún tipo de relación entre la fuerza aplicada y el alargamiento de la goma.
b) Observas que el agua de un recipiente se evapora transcurrido
cierto tiempo, y quieres averiguar qué relación existe entre la superficie del recipiente, la temperatura de la habitación y el tiempo de evaporación.

Actividades

1.2. El experimento

5. ¿Qué diferencias crees que existen entre una observación y un experimento?


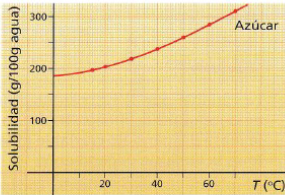
6. ¿Cuál es la solubilidad del azúcar en agua a 20ºC? ¿Y a 50ºC?

1.4. El análisis de los resultados

Las tablas

Las tablas

Las gráficas

Actividades

7. ¿Qué cantidad de azúcar se disuelve en 100 g de agua a 45ºC?


8. ¿A qué temperatura se disuelven 275 g de azúcar en 100 g de agua?

Variable independiente y dependiente

1.4.1. Las gráficas. Establecimiento de leyes

\ a=\frac {y_2-y_1} {x_2-x_1}

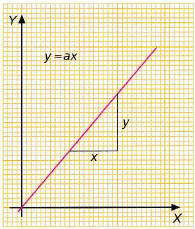
Proporcionalidad directa

1.4.1. Las gráficas. Establecimiento de leyes

\ a=\frac {y_2-y_1} {x_2-x_1}

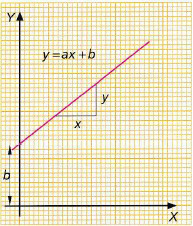
1.4.1. Las gráficas. Establecimiento de leyes

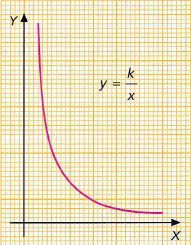
La hipérbola

Proporcionalidad inversa

1.4.1. Las gráficas. Establecimiento de leyes

La parábola

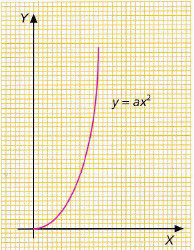
Actividades

9. Pregunta a tu profesor cuál es la ley del péndulo y contesta:
¿Cuánto vale el periodo del péndulo si su longitud es de 0,80 m?
10. ¿Qué longitud ha de tener un péndulo para que su período sea de 1,5 s?


11. Tras realizar diferentes experimentos, se comprueba que las relaciones entre las respectivas variables dependientes e independientes son:
a) y = 5x
b) y=5x+2
c) y=10/x
d) y = 2x2
¿Qué tipo de gráfica corresponde a cada una deestas relaciones?

El péndulo

La formulación de leyes y teorías

Actividad

12. Realizamos una gráfica con los datos obtenidos en un experimento y obtenemos una hipérbola.
Indica cuál de estas dos conclusiones es la correcta:
a) La variable dependiente y la independiente son directamente proporcionales.
b) La variable dependiente y la independiente son inversamente proporcionales.

Para acabar

Actividad

13. ¿Qué diferencia hay entre una ley y una hipótesis?
¿Y entre una ley y una teoría científica?

14. Haz un esquema en tu libreta que muestre los pasos del método científico.

La medida

¿Qué es una magnitud?

Actividad

15. La masa de un paquete de arroz es 1 kg.
Identifica el objeto, la magnitud, la medida y la unidad.

¿Qué es medir?

¿Qué es una unidad?

La medida

2.1. El sistema internacional de unidades

2.1.1. Magnitudes fundamentales y derivadas

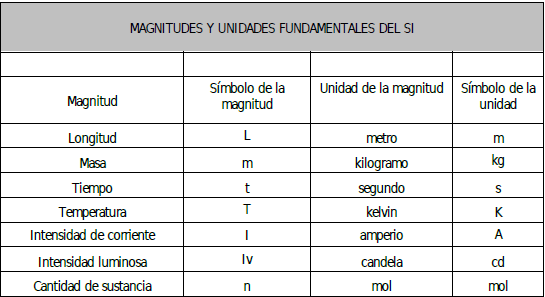
La medida

2.1. El sistema internacional de unidades

2.1.1. Magnitudes fundamentales y derivadas

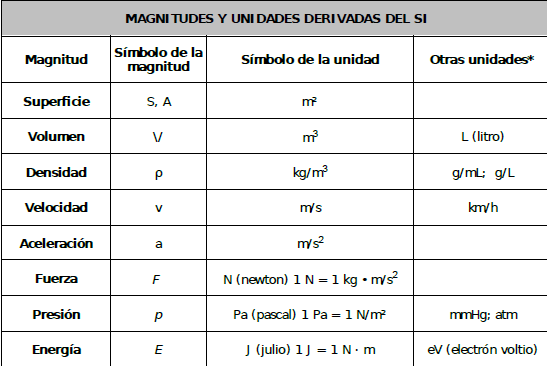
La medida

Actividades

16. Indica qué unidades utilizarías para medir estas magnitudes:
a) Una longitud
b) Un período de tiempo
c) Una masa
d) Una superficie
e) Una intensidad de corriente

Factores de conversión

Actividades

17. Transforma las velocidades en las unidades indicadas:
a) En m/s: 72 km/h, 100 km/h y 120 km/h.
b) En km/h: 12 m/s, 340 m/s y 0,36 m/s.

18. La densidad del agua es 1000 kg/m3. Exprésala en g/cm3.

La notación científica

Actividades

19. La masa de la Tierra es:
6000000000000000000000000 kg
La masa de la Luna es:
73500000000000000000000 kg
La distancia entre la Tierra y la Luna es: 384400000 m

Expresa estas cantidades en notación científica.

20. Expresa estas cantidades en notación científica. ¿Cuál de ellas es mayor: 1600 g, 1,5 kg, 1450 mm ó 1,3 m, 320 s ó 5 min?
21. Expresa las siguientes medidas en las unidades fundamentales
del SI utilizando la notación científica: 76 km, 3 g, 5 dam, 25 cm, 32 mm, 325 ms y 82 g.

22. Escribe las siguientes cantidades en notación científica:
a) 0,00005 g, b) 0,000052 g, c) 2 000000 m, d) 25 000000 m, e) 3010000 s, f) 0,000205 A

2.3. Múltiplos y submúltiplos de unidades

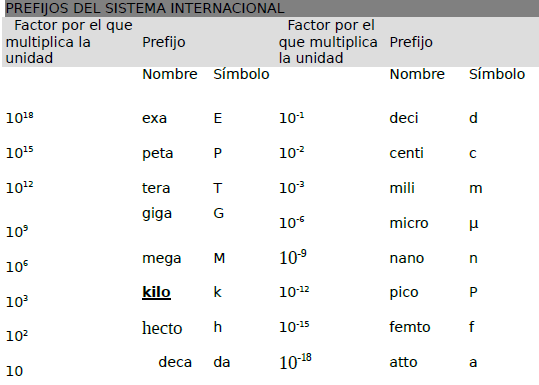
3. LOS INSTRUMENTOS DE MEDIDA

Exactitud

Sensibilidad

Precisión

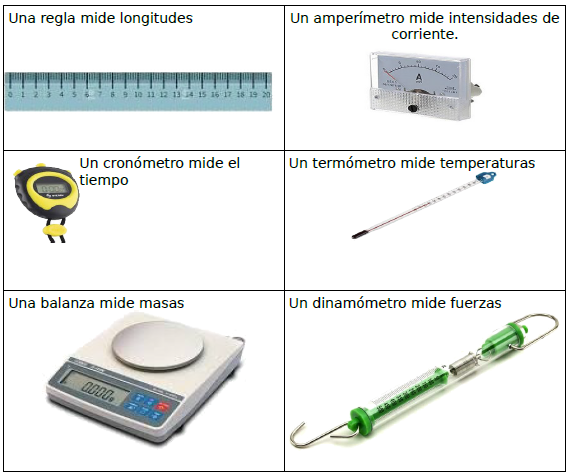
3. LOS INSTRUMENTOS DE MEDIDA

23. ¿Qué es más preciso,u n reloj de pulsera analógico o un cronómetro digital?
¿Cuál es la precisión de tu reloj?

Cifras significativas

¿Qué son?
 

24. Indica el número de cifras significativas de estas medidas:
a) 3,540 km
b) 2,04 kg
c) 8.0 s
d) 0,226 A
e) 0,0032 g
f) 3200 K

El redondeo

25. Redondea los siguientes números hasta la centésima:
a) 1,345
b) 2,355
c) 4,354
d) 14,567
e) 7,385
f) 0,725

3.3. Errores en la medida

  • Accidental
  • Sistemático

¿Cómo lo minimizamos?

¿Cómo lo expresamos?

3.3. Errores en la medida

26. Expresa estas medidas
correctamente:
a) 1,345±0,02
b) 2,355±0,1
c) 4,354±1
d) 14,567±0,0001
e) 7,385±0,2
f) 0,725±0,2


27. Se han realizado tres medidas del tiempo que tarda una piedra en caer desde cierta altura y los resultados fueron: 4 s, 3,9 s y 3,8 s.
Expresa correctamente la medida.

4. ESTRUCTURA DE UN INFORME CIENTÍFICO

1. Portada. En ella figuran el titulo, el autor o los autores del informe y la fecha. El título debe ser corto e indicar de forma clara la investigación que se ha desarrollado
2. Introducción. Contiene la descripción del propósito de la  investigación.
3. Metodología. Se indican con todo detalle los instrumentos empleados y los procedimientos seguidos.
4. Resultados. La exposición se puede acompañar con gráficos y tablas. Es conveniente numerar unos y otras y realizarlos en una hoja de cálculo u otros programas específicos para gráficas científicas.
5. Discusión de los resultados. Contiene el análisis cuantitativo de los resultados un comentario sobre los mismos. En los trabajos bibliográficos se puede sustituir por un comentario personal.
6. Resumen. Su extensión debe

5. El trabajo en el laboratorio

5. El trabajo en el laboratorio

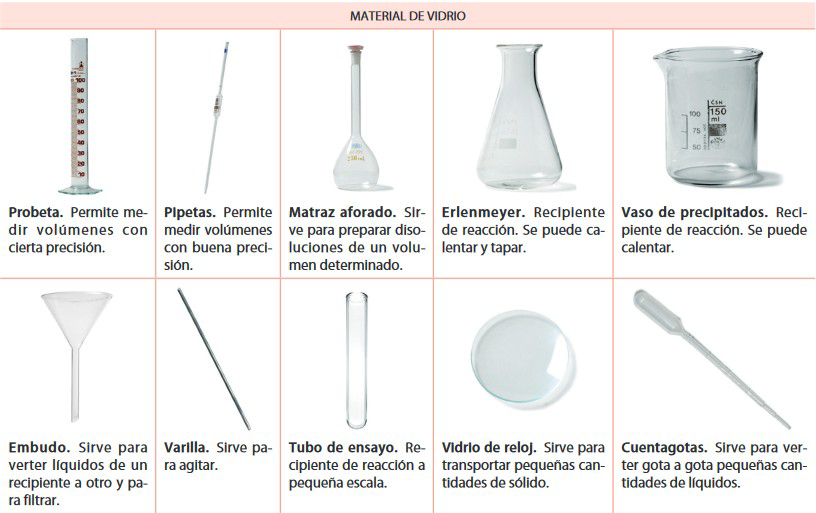
5. El trabajo en el laboratorio

5. El trabajo en el laboratorio. La seguridad

Actividades del fin de la unidad

Estratexias necesarias na actividade científica: O método científico

O método científico

Actividades

1. Suscita dous problemas, un que se poida investigar cientificamente e outro que non poida serdo. Para o primeiro deles, enuncia algunhas hipóteses cientificas.

2. No seguinte relato, identifica as etapas do método científico: No último terzo do século xviii se sabia que cando os metais quentábanse (calcinábanse), no proceso gañábase peso. Por que ocorría isto? En 1774, Lavoisier abordou o fenómeno o supoñendo que na calcinación dos metais estes reaccionaban con algún compoñente do aire, e a iso atribuíu o aumento de peso. Para comprobalo, quentou mercurio nun recipiente pechado e comprobou que o peso total non cambiou durante o proceso. Xurdiu así a «lei de conservación da masa».

3. Deseña un experimento, diferente ao de Galileo, para comprobar que a rapidez de caída dos corpos non depende do seu peso. Realiza unha procura en Internet titulada «Experimento pluma martillo Lúa»; unha vez que atopes o video dunha experiencia que se realizou na superficie da Lúa explica, dun modo crítico, que se podería concluír dela.

Magnitudes físicas. 

  • Unha magnitud física é calquera propiedade da materia que se pode medir de forma obxectiva
    • Unha unidade física é calquera cantidade arbitraria que se adopta como patrón de unha magnitude

    Sistema Internacional de unidades

     

    Actividades

    4. Pon dous exemplos de propiedades que sexan magnitudes físicas, e outros dous que non o sexan. Para cada unha das primeiras, enumera polo menos tres unidades, unha delas a do Sl.
    5. No último párrafo do apartado 2.4 incluíronse algúns exemplos de unidades que non pertencen ao Sistema Internacional de Unidades. Con que magnitudes están relacionadas? Busca a equivalencia entre estas unidades e as correspondentes do SI.

    Actividades

    6. Expresa a túa idade en anos, días, minutos, e na unidade de tempo do SI.
    7. Inventa unha unidade de lonxitude, e expresa nela a túa altura.

    Ao comezo deste tema falouse de que o fracaso do proxecto da Mars Climate Orbiter debeuse a que non todos os equipos utilizaron o mesmo sistema de unidades. Indaga en Internet cal foi, exactamente, o erro cometido. Na túa indagación, segue o esquema simplificado do método científico mostrado o epígrafe anterior.

    A análise dimensional

    A análise dimensional é unha ferramenta que permite simplificar o estudo de calquera fenómeno no que estean involucradas moitas magnitudes físicas.

    Actividades

    8. A lei da gravitación universal de Newton establece que a forza coa que dous corpos se atraen é directamente proporcional ao produto das súas masas e inversamente proporcional ao cadrado da distancia que as separa:

    onde G é a constante universal da gravitación. Determina a ecuación dimensional desta constante e, a partir dela, a súa unidade do SI

    Actividades

    9. Un péndulo simple é un dispositivo formada por un corpo que oscila suxeito no extremo inferior dun fío inextensible de lonxitude l e masa despreciable. Pódese utilizar para mediria aceleración da gravidade (g) nun lugar determinado, calculándoa a partir da medida do tiemp que tarda en dar unha oscilación completa (período, T). Xustifica que ecuación lle corresponde:

    A medida

    Medir é unha operación que consiste en determinar a cantidade dunha magnitude ao comparala coa súa unidade.

    Instrumentos de medida

    Para medir úsanse instrumentos, algunhas calidades destes son:

    • Cotas máxima e mínima
    • Sensibilidade
    • Fiabilidade

    Medidas directas e indirectas

    Actividades

    10. Non sempre as magnitudes fundamentais se miden de forma directa, e as derivadas, de forma directa. Pensa nun exemplo de cada tipo no que isto non ocorra.
     
    11. Realízanse medidas cunha balanza de cota máxima 100 g e limiar de resolución 0,1 g. Indica razonadamente que valores non poden ser obtidos con ela a) 32,4g. b) 0,43. c) 110,8 g
     
    12. Indica con que instrumentos podemos medir a lonxitude, a intensidade de corrente, a velocidade e a forza.
    En www.anayaeducacion.es atópase unha animación interactiva que che axudará a utilizar correctamente o calibre. Pensa en como medirías o grosor dunha folla de papel, de forma directa e de forma indirecta.

    Erros nas medidas

    • Tipos de erros
      • Accidentais
      • Sistemáticos
    • Precisión
      • Similitude nas medidas realizadas
    • Exactitude
      • Proximidade entre medidas realizadas e valor real
    • Erro absoluto e relativo
    • Cálculo de erros nas medidas indirectas
    • Notación científica
    • Expresión da medida: 10±3 cm
    • Interpretación de gráficas, dedución de leis

    Mútiplos e submúltiplos no SI



    Múltiplos
    Factor
    Prefixo
    Símbolo
    1015
    P
    1012
    T
    109
    G
    106
    M
    103
    k
    102
    h
    101
    da
    100
    unidad
    Submúltiplos
    Factor
    Prefixo
    Símbolo
    100
    unidad
    10−1
    d
    10−2
    c
    10−3
    m
    10−6
    µ
    10−9
    n
    10−12
    p
    10−15
    f

    Actividades

    13. Pode ser unha medida precisa pero inexacta? E o contrario? Propón algún exemplo para apoiar o teu razoamento.

     

    14. Cando se mira a hora nun reloxo que atrasa, estase cometendo un erro sistemático ou aleatorio?

     

    15. Se mides a túa altura cunha cinta métrica, e o erro absoluto da medida é de 1 cm, cal é o erro relativo? Exprésao mediante valor numérico e porcentual.

     

    16.  Explica a diferenza entre exactitude e precisión.

     

    Actividades

    17. Realízanse cinco medidas da lonxitude da mesa do laboratorio cunha cinta métrica, obtendo estes valores, en cm:

    120,6     120,4     120,5     120,4     120,3.

    Cal sería o valor da medida? E os erros, absoluto e relativo?

    18. Cando se miden as dimensións dun obxecto plano rectangular obtense: a = 40,05 ± 0,01 cm e b = 120,1 ± 0,1 cm. Determina a superficie e o erro absoluto da medida.

    19. Expresa estas cantidades en notación científica:
    a) 75 600 000 g
    b) 0,000 000 025 V
    c) 149 800 000 km

    20. Selecciona en cada parella a cantidade superior:
    a) 0,0055 m3 e 5,5 mL. b) 612 cg e 0,0612 kg.

     

    Actividades

    19. Expresa correctamente as medidas das actividades 17 e 18 da páxina anterior.

    20. Para medir a celeridade dun móbil procédese a medir o espazo que percorre e o tempo que tarda en facelo. Realízanse tres medidas de cada magnitude, obtendo os seguintes valores:

    e1= 49,9 cm      e2=49,9cm      e3=50,0 cm
    t1=1,47s             t2=1,51s           t3=1,50 s

    a) Determina o limiar de resolución dos instrumentos de medida utilizados.
    b) Cal é a celeridade?
    c) E o erro relativo?

     

    Actividades

    21. Que podes concluír das diferenzas entre as cantidades numéricas 2,0: 2,00: 2,000, procedentes da medida experimental dunha magnitude física?

     

    22. Sería correcto dicir que unha medida de tempo dá como resultado t = 1,35±0,15 s.  Por que?

     

    23. Móstranse a continuación parellas de datos tempo (s)-distancia (cm) medidos nun movemento: (1, 3.9); (2, 8.2); (3, 11.7); (4, 16.0); (5, 19.9). Preséntaos nunha táboa de datos e a partir da súa representación gráfica, determina relación entre as dúas magnitudes físicas.

    Actividades

    24. Estuda as relacións de proporcionalidade na ecuación d=m/V, onde d é a densidade, m é a masa, e V o volume.

     

    25. Propón dous exemplos de pares de magnitudes independentes.

    Actividade resolta

    18. Cando se miden as dimensións dun obxecto plano rectangular obtense: a = 40,05 ± 0,01 cm e b = 120,1 ± 0,1 cm. Determina a superficie e o erro absoluto da medida.

    Tecnoloxías da información e da comunicación no traballo científico

    • As follas de cálculo

    Proxecto de investigación

    Title

    Made with Slides.com