動態規劃 從入門到放棄

Intro to Dynamic Programming

Arvin Liu

前言

DP 很難很難，學不來

所以要記得多複習喔~

DP 大概是整個 APCS 最難懂的章節

複習遞迴 - N!

Factorial of N

求出 N!

給你一個數字 N，請輸出 N!

 

 

N!=∏i=1Ni=1×2×...×(N−1)×NN! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N
N! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N

那還不簡單？

不就是基礎 for 迴圈嗎？

來想想看有沒有其他寫法！

int factorial(int N) {
  int ans = 1;
  for (int i=1; i<=N; i++)
    ans *= i;
  return ans;
}

C++

def factorial(N):
  ans = 1
  for i in range(1, N):
    ans *= i
  return ans

Python

求出 N!

假設現在有一個函數：

f(n)=n!f(n) = n!
f(n) = n!

如果不用 "!" 該怎麼寫？

f(n)=n×(1×2...×(n−1))f(n) = n \times(1 \times 2 ... \times (n-1)) \\
f(n) = n \times(1 \times 2 ... \times (n-1)) \\
=n×(n−1)!=n×f(n−1)= n \times (n-1)! \\ = n \times f(n-1)
= n \times (n-1)! \\ = n \times f(n-1)

給你一個數字 N，請輸出 N!

 

 

N!=∏i=1Ni=1×2×...×(N−1)×NN! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N
N! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N

求出 N!

f(n)=n×f(n−1)f(n) = n \times f(n-1)
f(n) = n \times f(n-1)

直接把它轉成程式？

跑跑看！

int factorial(int N) {
  return N * factorial(N-1);
}
def factorial(N):
  return N * factorial(N-1)

C++

Python

給你一個數字 N，請輸出 N!

 

 

N!=∏i=1Ni=1×2×...×(N−1)×NN! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N
N! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N

求出 N!

輸出結果 :

4
3
2
1
0
-1
-2
....

跑不完！

這裡就該停了!

#include <stdio.h>
int factorial(int N) {
  printf("%d\n", N);
  return N * factorial(N-1);
}

int main() {
    printf("%d", factorial(4));
}
def factorial(N):
  print(N)
  return N * factorial(N-1)


print(factorial(4))

C++

Python

求出 N!

f(n)=  n×f(n−1)f(n) = \, \, n \times f(n-1)
f(n) = \, \, n \times f(n-1)
{1,if n = 0\begin{cases} \\ 1, \text{if n = 0} \end{cases}
\begin{cases} \\ 1, \text{if n = 0} \end{cases}

這樣就可以了！

int factorial(int N) {
  if (N == 0) return 1;
  return N * factorial(N-1);
}
def factorial(N):
  if N == 0: return 1
  return N * factorial(N-1)

C++

Python

給你一個數字 N，請輸出 N!

 

 

N!=∏i=1Ni=1×2×...×(N−1)×NN! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N
N! = \prod_{i=1}^{N} i = 1 \times 2 \times ... \times (N-1) \times N

遞迴總結

Recursion - Review

怎麼寫遞迴？

  1. 定義遞迴函式要做什麼？ 等於什麼？
    • f(n) = n! 的數值
  2. 觀察如何將大函式用小函式完成？
    • f(n) 跟 f(n-1) 有點關係
  3. 記得寫終止條件 (Base Case)
    • f(0) = 1
  • 思考的時候，不要從一開始往上推，例如 n=0 怎麼樣，n=1怎麼樣...
  • 通常情況下，要逆向思考，習慣倒推。
    • 例如 n 要怎麼用n-1表示，或者n-2表示..

記得寫終止條件！

N!遞迴的逐步過程

f(n)={1if n=0n×f(n−1)otherwisef(n) = \begin{cases} 1 & \text{if } n=0\\ n \times f(n-1) & \text{otherwise} \\ \end{cases}
f(n) = \begin{cases} 1 & \text{if } n=0\\ n \times f(n-1) & \text{otherwise} \\ \end{cases}

以           作為舉例

f(3)f(3)
f(3)
f(3)=3×f(2)f(3) = 3 \times f(2)
f(3) = 3 \times f(2)
f(2)=2×f(1)f(2) = 2 \times f(1)
f(2) = 2 \times f(1)
f(1)=1×f(0)f(1) = 1 \times f(0)
f(1) = 1 \times f(0)
f(0)=1f(0) = 1
f(0) = 1

呼叫

呼叫

呼叫

=1×1=1= 1 \times 1 = 1
= 1 \times 1 = 1
=2×1=2= 2 \times 1 = 2
= 2 \times 1 = 2
=3×2=6= 3 \times 2 = 6
= 3 \times 2 = 6

回傳

回傳

回傳

回傳

實際例子可以參考另一個投影片

什麼是動態規劃?

Dynamic Programming

什麼是動態規劃?

就是有技巧的暴搜

技巧? 暴搜?

有技巧的暴搜

怎麼暴力搜尋?

 

暴搜比較好理解的其中一個方法就是遞迴。

技巧? 別急，我們慢慢來。

為什麼叫做動態規劃?

Dynamic Programming

為什麼叫做動態規劃?

Dynamic Programming

這是一個關於發明者Bellman的有趣故事...

*你在圖論會學到以他為名的演算法

Fibonacci Sequence

爬樓梯問題

爬樓梯問題 (zj d212, leetcode 70)

🐦

🐦

3 階有 3 種走法

4 階有 5 種走法

1+1+1

2+1

1+2

有點難？想想看遞迴的三個步驟！

1+1+1+1

1+2+1

2+1+1

1+1+2

2+2

舉例來說：

東東爬階梯每次可以走一或兩階。

假設階梯有 n 階，那有幾種走法?

爬樓梯問題 (zj d212, leetcode 70)

有點難？想想看遞迴的三個步驟！

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
  1. 函式定義：

在簡單的 DP 中，函式定義高機率是裸定。

裸定？那就是 f(題目給的) = 題目要的

假設階梯有 n 階，那有幾種走法?

所以這題的裸定就是：f(n) = 走 n 階的可能數

東東爬階梯每次可以走一或兩階。

假設階梯有 n 階，那有幾種走法?

  1. 函式定義：
  2. 如何拆解：

f(n) = 走 n 階的可能數

爬樓梯問題 (zj d212, leetcode 70)

東東爬階梯每次可以走一或兩階。

假設階梯有 n 階，那有幾種走法?

  1.  
  2. 如何拆解：

如何拆解 DP？

第一步：想一個規則可以把 f(n) 的所有可能拆碎

什麼意思呢？

回憶一下你小時候玩的大風吹...

回憶一下你小時候玩
的大風吹...

拆解 DP 第一步：

那就是想一個規則可以把 f(n) 的所有可能拆碎

大風吹後面會帶一個規則，
可以將所有人分成兩半
(要起來跟沒起來的)

DP 同理，你只要想得出任何一個規則能把所有可能拆碎，那麼它就是一個可行的拆解。

用例子想想看吧！

(不一定要分成兩半，可以分成很多半)

1+1+1+1

1+2+1

2+1+1

1+1+2

2+2

n = 4 的所有可能

爬樓梯問題 (zj d212, leetcode 70)

拆解 DP：

  1. 那就是想一個規則可以把 f(n) 的所有可能拆碎
  2. 想想看每個被拆出來的可能跟遞迴的關係

規則：

最後一步走1

這樣就可以拆碎所有可能了！

最後一步走幾步？

  • 函式定義：f(n) = 走 n 階的可能數
  • 如何拆解：f(n) = f(n-1) + f(n-2)

走到 n 階，但最後一定走 1 的可能數 = ?

最後一步走2

= 走 n-1 階的可能數 = f(n-1)

走到 n 階，但最後一定走 2 的可能數 = ?

= 走到 n-2 階的可能數 = f(n-2)

(第一步也可以)

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

f(n) = 走 n 階的可能數

⭕

❌

❌

爬樓梯問題 (zj d212, leetcode 70)

東東爬階梯每次可以走一或兩階。

假設階梯有 n 階，那有幾種走法?

f(n)=f(n−1)+f(n−2)f(n) = f(n-1) + f(n-2)
f(n) = f(n-1) + f(n-2)
f(1)=1,f(2)=2f(1) = 1, f(2) = 2
f(1) = 1, f(2) = 2

比較簡單的 Base Case 想法：

  1. 想想看函式的定義域
    • ​​階梯至少 1 階起跳，所以 n 為大於等於 1 的正整數。
  2. 想想看哪些參數是無法用遞迴得出來的 (下步遞迴還在值域)​​
    • f(1) 可以用遞迴算出嗎？
    • f(2) 可以用遞迴算出嗎？
    • f(3) 可以用遞迴算出嗎？
  3. 那麼這些參數就別遞迴，直接 return 它該要的答案。
  1.  
  2.  
  3. Base Case：
int fib(int N) {
  if (N == 1) return 1;
  if (N == 2) return 2;
  return fib(N-1) + fib(N-2);
}
def fib(N):
  if N == 1: return 1
  if N == 2: return 2
  return fib(N-1) + fib(N-2)

C++

Python

爬樓梯問題 (zj d212, leetcode 70)

東東爬階梯每次可以走一或兩階。

假設階梯有 n 階，那有幾種走法?

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

f(n) = 走 n 階的可能數

f(n)=f(n−1)+f(n−2)f(n) = f(n-1) + f(n-2)
f(n) = f(n-1) + f(n-2)
f(1)=1,f(2)=2f(1) = 1, f(2) = 2
f(1) = 1, f(2) = 2

簡單的程式碼：

爬樓梯問題與費波那契數列

f(n)={1if n=12if n=2f(n−1)+f(n−2)otherwisef(n) = \begin{cases} 1 & \text{if } n = 1 \\ 2 & \text{if } n = 2 \\ f(n-1) + f(n-2) & \text{otherwise} \end{cases}
f(n) = \begin{cases} 1 & \text{if } n = 1 \\ 2 & \text{if } n = 2 \\ f(n-1) + f(n-2) & \text{otherwise} \end{cases}

這就是鼎鼎大名的費波那契數列

fibonacci

  • f(0) = 1

費波那契數列的遞迴過程

f(n)={1if n=12if n=2f(n−1)+f(n−2)otherwisef(n) = \begin{cases} 1 & \text{if } n = 1 \\ 2 & \text{if } n = 2 \\ f(n-1) + f(n-2) & \text{otherwise} \end{cases}
f(n) = \begin{cases} 1 & \text{if } n = 1 \\ 2 & \text{if } n = 2 \\ f(n-1) + f(n-2) & \text{otherwise} \end{cases}
f(4)=f(3)+f(2)f(4) = f(3) + f(2)
f(4) = f(3) + f(2)

以           作為舉例

f(4)f(4)
f(4)
f(3)=f(2)+f(1)f(3) = f(2) + f(1)
f(3) = f(2) + f(1)
f(2)=2f(2) = 2
f(2) = 2
f(2)=2f(2) = 2
f(2) = 2
f(1)=1f(1) = 1
f(1) = 1

2

1

3

2

=3= 3
= 3
=5= 5
= 5

練習題！

  1. 如果題目改成東東每次可以走 1, 2, 3 階，遞迴會怎麼寫？
  2. 你會用迴圈寫這題嗎？
  3. 你覺得
    1. 遞迴版本的時間複雜度多少？
    2. 迴圈版本的時間複雜度多少？
  4. 如果題目改成東東每次可以走 k 階，遞迴會怎麼寫？
    • Naive O(NK) Hint: 遞迴裡面會帶 for
    • O(N) Hint: 區間和
  5. 這題其實有更快的做法 O(log N)，你會怎麼做？
    • 方法1: 拆半討論 + 用 unordered_map / dict 記憶化
    • 方法2: 矩陣轉移 + 快速冪次，可以參考後面投影片

DP 的思考三步驟

DP 的思考三步驟

1. 狀態定義

2. 如何拆解

3. Base Case

  1. 看到題目先嘗試裸定義題目。
    • 也就是 f(題目給的) = 題目要的。

1. 狀態定義

2. 如何拆解

3. Base Case

  1. 看到題目先嘗試裸定義題目。
    • 也就是 f(題目給的) = 題目要的。
  2. 找出一個規則可以拆碎所有可能
    • ​​通常都跟最後操作有關，例如爬樓梯的規則就是判斷最後一步。
  3. 找出被拆出來的可能群跟遞迴的關係
    • 找不到？那就表示狀態有問題

DP 的思考三步驟

  1. 看到題目先嘗試裸定義題目。
    • 也就是 f(題目給的) = 題目要的。
  2. 找出一個規則可以拆碎所有可能
    • ​​通常都跟最後操作有關，例如爬樓梯的規則就是判斷最後一步。
  3. 找出被拆出來的可能群跟遞迴的關係
    • 找不到？那就表示狀態有問題
    • 通常是因為狀態定義的資訊太少，不足以用遞迴定義表示。
      • 試試其他定義，或把缺少的資訊加上去

1. 狀態定義

2. 如何拆解

3. Base Case

DP 的思考三步驟

  1. 看到題目先嘗試裸定義題目。
  2. 找出一個規則可以拆碎所有可能​
  3. 找出被拆出來的可能群跟遞迴的關係
  4. 想想看 Base Case
    1. 思考傳入哪些參數是在定義域內，但不能往下遞迴。
    2. 把這些參數寫成 rule-based。
    3. 可以考慮往回推幾個步驟。
      • 舉例來說：爬樓梯原本定義
        f(1) = 1, f(2) = 2，
        也可以定義成 f(0) = f(1) = 1。
        因為 f(2) = f(1) + f(0)，所以 f(0) 才設成 1。

1. 狀態定義

2. 如何拆解

3. Base Case

DP 的思考三步驟

也有一種解釋方法是 f(0) = 什麼都不做也是一種可能，看你要怎麼解讀。

組合數

CmnC^n_m
C^n_m

Combination

00369 - Combinations (zj d134)

請問從 n 顆不同的球裡，
有幾種取出 m 顆球的方法？

有 4 顆相異的球

如果取三顆，共 4 種取法

如果取兩顆，共 6 種取法

00369 - Combinations (zj d134)

有 4 顆相異的球

如果取三顆，共 4 種取法

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

這個也好難....

C(n, m) = n 取 m 的可能數

想想看可不可以跟

爬樓梯一樣拆Case！

請問從 n 顆不同的球裡，
有幾種取出 m 顆球的方法？

00369 - Combinations (zj d134)

有 4 顆相異的球

如果取三顆，共 4 種取法

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
}\begin{rcases} \\ \\ \end{rcases}
\begin{rcases} \\ \\ \end{rcases}
}\begin{rcases} \end{rcases}
\begin{rcases} \end{rcases}

取了最
後的球

沒取最
後的球

取了      後

需要再從三顆中取兩顆

放棄      後

需要再從三顆中取三顆

C(n, m) = n 取 m 的可能數

❌

請問從 n 顆不同的球裡，
有幾種取出 m 顆球的方法？

*你會發現拆法會與最後一個動作有關

00369 - Combinations (zj d134)

請問從 n 顆不同的球裡，
有幾種取出 m 顆球的方法？

有 n 顆相異的球

想要取 m 顆

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

取了最
後的球

沒取最
後的球

❌

...

{\begin{cases} \\ \\ \\ \end{cases}
\begin{cases} \\ \\ \\ \end{cases}
{\begin{cases} \\ \\ \end{cases}
\begin{cases} \\ \\ \end{cases}

還剩m顆要選

還剩m-1顆要選

C(n-1, m)

C(n-1, m-1)

+

C(n, m) = n 取 m 的可能數

放棄      後

需要再從n-1顆中取m顆

取了      後

需要再從n-1顆中取m-1顆

00369 - Combinations (zj d134)

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

C(n-1, m)

C(n-1, m-1)

+

C(3, 2)

C(2, 1)

C(2, 2)

C(1, 0)

C(1, 1)

  1. m = 0 的時候，​表示不取，答案為1
  2. m = n 的時候，表示全取，答案為1
  1. n 跟 m 的範圍是什麼，數值才合理？
  2. n 跟 m 減到哪裡該停？

想想看 C(3, 2) 的例子吧!

m = 0 或者 n = m 時為1

C(n, m) = n 取 m 的可能數

請問從 n 顆不同的球裡，
有幾種取出 m 顆球的方法？

00369 - Combinations (zj d134)

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

C(n-1, m)

C(n-1, m-1)

+

m = 0 或者 n = m 時為1

一個看似複雜的題目，遞迴程式卻非常少！

這就是遞迴的魅力之處 (？)

int C(int n, int m){
	if (m == 0 || m == n) return 1;
    return C(n-1, m-1) + C(n-1, m);
}
def C(n, m):
  if m == 0 or m == n: return 1
  return C(n-1, m) + C(n-1, m-1)

C++

Python

請問從 n 顆不同的球裡，
有幾種取出 m 顆球的方法？

C(n, m) = n 取 m 的可能數

練習題！

  1. C(n, m) 其實是有公式的 (題目有給你)。
     

    •  
    • 使用這個公式如果直接在 C++ 用 for 實作，其實會有些問題在，你知道為什麼嗎？
  2. 如果犧牲一些時間複雜度 (裸套公式是 O(N))，
    你還是可以使用公式找答案。
    不過你要怎麼繞過問題呢？
  3. 其實稍微變形一下，還是可以在不 overflow 的情況做到線性複雜度。
    • Hint: C(n-1, m-1) 跟 C(n-1, m) 是有關係的
Cmn=n!m!×(n−m)!C^n_m = \frac{n!}{m! \times (n-m)!}
C^n_m = \frac{n!}{m! \times (n-m)!}

線性時間找 C(n, m)

Cmn=Cm−1n−1+Cmn−1C^n_m = C^{n-1}_{m-1} + C^{n-1}_m
C^n_m = C^{n-1}_{m-1} + C^{n-1}_m
Cm−1n−1=(n−1)!(m−1)!(n−1−(m−1)!)=(n−1)!(m−1)!(n−m)!C^{n-1}_{m-1} = \frac{(n-1)!}{(m-1)! (n-1 - (m-1)!)} = \frac{(n-1)!}{(m-1)!(n-m)!}
C^{n-1}_{m-1} = \frac{(n-1)!}{(m-1)! (n-1 - (m-1)!)} = \frac{(n-1)!}{(m-1)!(n-m)!}
Cmn−1=(n−1)!m!(n−1−(m)!)=(n−1)!m!(n−m−1)!C^{n-1}_{m} = \frac{(n-1)!}{m! (n-1 - (m)!)} = \frac{(n-1)!}{m! (n-m-1)!}
C^{n-1}_{m} = \frac{(n-1)!}{m! (n-1 - (m)!)} = \frac{(n-1)!}{m! (n-m-1)!}
Cmn−1=Cm−1n−1n−mmC^{n-1}_{m} = C^{n-1}_{m-1} \frac{n-m}{m}
C^{n-1}_{m} = C^{n-1}_{m-1} \frac{n-m}{m}

n-m 跟 m 用 GCD 處理後直接除就可以保證 數值不會 Overflow 了

0/1 背包問題

0/1 Knapsack Problem

祖靈好孝順 ˋˇˊ (zj a587)

給你 N 個物品和物品的重量和價值，以及祖靈的背包的重量限制。

請問祖靈最多可以帶價值東西回家?

拿走什麼? 總重 價值
G+C+S 15kg $8
Y+C+S+B 8kg $15
... ... ...

C

B

Y

G

S

祖靈好孝順 ˋˇˊ (zj a587)

給你 N 個物品和物品的重量和價值，以及祖靈的背包的重量限制。

問祖靈可以帶走的最高價值？

  1. 函式定義：

f(n, W) = 前 n 個物品中，
限重 W 的情況下的最大價值

有點複雜... 試試看裸套題目定義

f(2, 5): 如果可以拿0~2號的物品，

背包限重為5，回傳所有可能中的最大價值。

f(7, 10): 如果可以拿0~7號的物品，

背包限重為10，回傳所有可能中的最大價值。

祖靈好孝順 ˋˇˊ (zj a587)

  1. 函式定義：
     
  2. 如何拆解：

又卡住了 :( ...

其實背包問題跟 C(n, m) 很像！

都是 n 個物品裡面挑幾個東西出來

  • C(n, m) 的限制是只能挑 m 個
  • 背包問題的限制是挑出來的物品限重不能超過 W

f(n, W) = 前 n 個物品中，
限重 W 的情況下的最大價值

給你 N 個物品和物品的重量和價值，以及祖靈的背包的重量限制。

問祖靈可以帶走的最高價值？

祖靈好孝順 ˋˇˊ (zj a587)

  1. 函式定義：
     
  2. 如何拆解：

又卡住了 :( ...

f(n, W) = 前 n 個物品中，
限重 W 的情況下的最大價值

有 n 顆相異的物品，

限重 W

取了最
後的

沒取最
後的

❌

...

💎

👑

📿

💎

💎

0/1 背包問題

有 n 顆相異的球

想要取 m 顆

取了最
後的球

沒取最
後的球

❌

...

C(n, m) 問題

給你 N 個物品和物品的重量和價值，以及祖靈的背包的重量限制。

問祖靈可以帶走的最高價值？

祖靈好孝順 ˋˇˊ (zj a587)

  1. 函式定義：
     
  2. 如何拆解：

有 n 顆相異的物品，

限重 W

取了最
後的

沒取最
後的

❌

...

💎

👑

📿

💎

💎

放棄第 n 個物品，
當它不存在。

可以裝的重量少

w💎w_{_💎}
w_{_💎}

但多了價值

v💎v_{_💎}
v_{_💎}
=f(n−1,W)= f(n-1, W)
= f(n-1, W)
=f(n−1,W−w💎)+v💎= f(n-1, W-w_{_💎}) \\ + v_{_💎}
= f(n-1, W-w_{_💎}) \\ + v_{_💎}

f(n, W) = 前 n 個物品中，
限重 W 的情況下的最大價值

背包還剩

背包還剩        

WW
W
W−w💎W-w_{_💎}
W-w_{_💎}

給你 N 個物品和物品的重量和價值，以及祖靈的背包的重量限制。

問祖靈可以帶走的最高價值？

祖靈好孝順 ˋˇˊ (zj a587)

  1. 函式定義：
     
  2. 如何拆解：

取了最
後的

💎

可以裝的重量少

w💎w_{_💎}
w_{_💎}

但多了價值

v💎v_{_💎}
v_{_💎}
=f(n−1,W−w💎)+v💎= f(n-1, W-w_{_💎}) + v_{_💎}
= f(n-1, W-w_{_💎}) + v_{_💎}

f(n, W) = 前 n 個物品中，
限重 W 的情況下的最大價值

背包還剩        

W−w💎W-w_{_💎}
W-w_{_💎}

你的背包 W

💎

背包剩下 W - w💎

那麼橘色的部分怎麼放才可以
最大化總價值呢？

不知道，所以我們用 f 遞迴來問。

給你 N 個物品和物品的重量和價值，以及祖靈的背包的重量限制。

問祖靈可以帶走的最高價值？

祖靈好孝順 ˋˇˊ (zj a587)

  1. 函式定義：
     
  2. 如何拆解：


     
  3. Base Case :  
f(n−1,W)f(n-1, W)
f(n-1, W)
f(n−1,W−wn)+vnf(n-1, W-w_n) + v_n
f(n-1, W-w_n) + v_n

f(n, W) = 前 n 個物品中，
限重 W 的情況下的最大價值

                                                ⏟max⁡\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}_{\max}
\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}_{\max}

n 會一直往下減... 考慮第零號物品！

f(0,W)={0if W<w0v0otherwisef(0, W) = \begin{cases} 0 & \text{if } W < w_0 \\ v_0 & \text{otherwise} \end{cases}
f(0, W) = \begin{cases} 0 & \text{if } W < w_0 \\ v_0 & \text{otherwise} \end{cases}

給你 N 個物品和物品的重量和價值，以及祖靈的背包的重量限制。

問祖靈可以帶走的最高價值？

祖靈好孝順 ˋˇˊ (zj a587)

  1. 函式定義：
     
  2. 如何拆解：

     
  3. Base Case :  

f(n, W) = 前 n 個物品中，限重 W 的情況下的最大價值

f(n,W)=max⁡{f(n−1,W),f(n−1,W−wn)+vn)if W≥wnf(n, W) = \max \begin{cases} f(n-1, W), \\ f(n-1, W-w_n) + v_n) & \text{if } W \ge w_n \end{cases}
f(n, W) = \max \begin{cases} f(n-1, W), \\ f(n-1, W-w_n) + v_n) & \text{if } W \ge w_n \end{cases}
f(0,W)={0if W<w0v0otherwisef(0, W) = \begin{cases} 0 & \text{if } W < w_0 \\ v_0 & \text{otherwise} \end{cases}
f(0, W) = \begin{cases} 0 & \text{if } W < w_0 \\ v_0 & \text{otherwise} \end{cases}
int f(int n, int w) {
  if (n == 0)
    return w >= W[n] ? V[n] : 0;
  if (w >= W[n])
    return max(
      f(n-1, w), 
      f(n-1, w - W[n]) + V[n]
    );
  return f(n-1, w);
}
def f(n, w):
  if n == 0: 
    return V[n] if w >= W[n] else 0
  if w >= W[n]:
    return max(
      f(n-1, w),
      f(n-1, w-W[n]) + V[n]
    );
  return f(n-1, w);

C++

Python

思考看看

  1. Base Case 其實有很多種寫法，有個更簡單大家更常寫的方法，想想看
  2. 假設定義函數 f(n, V) ：n個物品裡面選價值為V的最低重量
    例如 f(n,10)=3 表示選到價值為10的物品時，重量最低為3 )
    • 請問 DP 式該怎麼寫？
  3. 如何使用上題函數定義解決 0/1 背包問題？
  4. (無限背包問題) 如果每個物品都可以拿無限次，如何改遞迴式？
  5. (有限背包問題) 如果每個物品有其個數限制 Ci，如何改遞迴式？
    • 有 Naive O(NWC) -> 二進位拆解 O(NWlogC) -> 需要一點數學 + 單調對解 O(NW) 

記憶化

Memoization

記憶化 Memoization

剛剛的所有code

你知道嗎？

全都會TLE!

(其實是WA 因為我沒開long long)

DP是有技巧的暴搜

怎麼暴力搜尋?

 

暴搜比較好理解的其中一個方法就是遞迴。

 

  • 技巧? 同樣的問題不算第二遍
  • 這稱為 記憶化 Memoization

記憶化 Memoization

重複算有差嗎？我們以爬樓梯的題目來看

fib(3)一樣
卻會重算！

fib(4)

fib(3)

fib(2)

fib(2)

fib(1)

fib(5)

fib(3)

fib(2)

fib(1)

記憶化 Memoization

如何避免重算？

想像有個函數...

ff
f

輸入 A

輸入 B

輸入 A

第一次碰到！

算出f(A)

第一次碰到！

算出f(B)

算過 A 了！

拿出之前算過的答案

你必須在第一次碰到的時候記錄起來！

記憶化 Memoization

  • 如果沒算過，就算出答案，記錄起來。
  • 如果有算過，就直接從記憶裡撈出來。

用一個方法可以記錄 「問題」 -> 「答案」

例如 陣列、unordered_map、dict 等等

long long dp[1000];
long long fib(int n){
	if (n == 0 || n == 1)
    	return 1;
    if (!dp[n])
    	dp[n] = fib(n-1) + fib(n-2);
    return dp[n];
}
dp = {}
def fib(n):
  if n == 0 or n == 1 :
    return 1
  if n not in dp:
    dp[n] = fib(n-1) + fib(n-2)
  return dp[n]

C++

Python

因為 fib 都會 > 0，所以我們可以用

dp[n] 是不是 0 來決定有沒有算過。

記憶化 Memoization

重複算有差嗎？我們以爬樓梯的題目來看

重複計算 (原本的code)

不重複計算 (記憶化)

f(n) = f(n-1) + f(n-2)

"大概"每多一個n，
就會多算一倍

O(2n)O(2^n)
O(2^n)

算完 f(n-1) 時，

f(n-2) 已經算過了，不用重算

O(n)O(n)
O(n)

差超多

記憶化 Memoization

long long dp[1000];
long long f(int n){
	if (n == 0 || n == 1)
    	return 1;
    if (!dp[n])
    	dp[n] = f(n-1) + f(n-2);
    return dp[n];
}

來用人腦跑一次看看吧！如果呼叫 f(4)...

n 0 1 2 3 4
dp[n] 1 1 ? ? ?
- f(1) f(2) f(3)
- f(0) f(1) f(2)

1

1

2

2

1

3

3

2

5

f(2) 不用再重新遞迴一次 f(1) 跟 f(0) 了！

東東爬樓梯 (zj d212) AC code 

#include <stdio.h>
long long dp[1000];
long long f(int n){
	if (n == 0 || n == 1)
    	return 1;
    if (!dp[n])
    	dp[n] = f(n-1) + f(n-2);
    return dp[n];
}
int main() {
    int n;
    while(~scanf("%d", &n)) {
        printf("%lld\n", f(n));
    }
}

00369 - Combinations (zj d134) AC code 

#include <stdio.h>
unsigned long long dp[101][101];
unsigned long long C(int n, int m){
	if (m == 0 || m == n) return 1;
    if (!dp[n][m])
        dp[n][m] = C(n-1, m-1) + C(n-1, m);
    return dp[n][m];
}

int main() {
    int n, m;
    while(~scanf("%d%d", &n, &m) && n != 0 && m != 0) {
        printf("%d things taken %d at a time is %llu exactly.\n", n, m, C(n, m));
    }
}

如果問題有兩個參數呢？ 像是 C(n, m) ?

那記憶化表格就開兩維！

那麼時間複雜度呢？

最多有 O(nm) 的狀態，算出每個狀態需要  O(1)

(轉移複雜度)

總複雜度 : O(nm) * O(1) = O(nm)!

祖靈好孝順 ˋˇˊ (zj a587) AC Code 

#include <stdio.h>
#include <memory.h>
#include <algorithm>
int dp[101][10001];
int W[101], V[101];
int f(int n, int w) {
    if (n == 0)
        return 0;
    if (!dp[n][w]) {
        if (w >= W[n])
            dp[n][w] = std::max(f(n-1, w - W[n]) + V[n], f(n-1, w));
        else
            dp[n][w] = f(n-1, w);
    }
    return dp[n][w];
}
int main() {
    int n, w;
    while(~scanf("%d", &n)) {
        // 將dp陣列全部清空
        memset(dp, 0, sizeof(dp));
        for (int i=1; i<=n; i++)
            scanf("%d%d", &W[i], &V[i]);
        scanf("%d", &w);
        printf("%d\n", f(n, w));
    }
}

記憶化 Memoization

思考看看

  1. 請問背包問題 (祖靈好孝順 ˋˇˊ) 經過記憶化後的時間複雜度是多少？

     

  2. 我們確信問題的答案都大於零，所以才可以使用 !dp[n] 來表示沒有算過。

    那麼如果答案可能是 0 怎麼辦？
     
  3. 如果參數的範圍很大，大到無法開陣列，但問題的種類數量很小 (DP為稀疏陣列)，那怎麼使用記憶化？

    (例如 dp[n] 的 n 有可能超大，但 dp[n] 不為0的值其實沒有那麼多，那要怎麼節省空間？)

Python 的 Built-in 記憶化

from functools import lru_cache

1. 先 import lru_cache

2. 對你的遞迴函式前面加上這行

@lru_cache(None)

那麼你接下來的東西都會被記憶化。

  • 但有個限制：你的參數必須要是 Hashable。(常見的不是Hashable 就是 List)
@lru_cache(None)
def C(n, m):
  if m == 0 or m == n: return 1
  return C(n-1, m) + C(n-1, m-1)

像這樣：

Stack Overflow

棧溢出 / 堆疊溢出

什麼是 Stack Overflow?

在函式裡宣告的變數都會在stack空間。 (包括main)

當你呼叫非常非常非常多的函式...

stack
警戒線

超出stack警戒線就會導致程式執行錯誤。

(所以是Runtime Error)

解決Stack Overflow - C++

stack
警戒線

  • 不要用遞迴寫 (這在幹話?)
    • 如果可以，用for迴圈寫。
      (例如fib可直接用for。)
       
  • 如果不行
    • 使用全域變數或heap空間，用別的方法模擬遞迴 (詳見圖論投影片-bfs/dfs)
    • C++ 黑魔法 - 內嵌組合語言強制遞迴用heap空間

C++ 黑魔法 - 強制調用heap空間

extern int main2(void) __asm__ ("main2"); 
 
int main2() { 
    run();
    exit(0); 
} 
 
int main() { 
    // 跟heap借256MB
    int size = 256 << 20;
    char *p = (char *)malloc(size) + size; 
    __asm__ __volatile__( 
        "movq  %0, %%rsp\n" 
        "pushq $exit\n"  
        "jmp main2\n" 
        :: "r"(p)); 
}
  1. 要
  2. 把你原本程式的main改名成run。
  3. 把上面這份code貼在你的程式的最下面。
#include <cstdlib>

解決Stack Overflow - Python

Python 在要求 Stack 空間的次數
本身就有限制 (預設1000次)

1. 調開這個限制

import sys
sys.setrecursionlimit(10000000)

但這個時候有可能會 RE，
因為記憶體要求過高。

這個時候你就必須要：

2. 先從小 Case 開始跑，提前記憶化。

這樣子就不會一次遞迴過深了。

解決Stack Overflow - Python

2. 先從小 Case 開始跑，提前記憶化。

這樣子就不會一次遞迴過深了。

def fib(N):
  if N == 1: return 1
  if N == 2: return 2
  return fib(N-1) + fib(N-2)

呼叫 f(1000) ? 這樣一次遞迴的深度就會是 1000

以 fib() 做舉例：

f(1000)→f(999)→f(998)→...→f(1)f(1000) \rightarrow f(999) \rightarrow f(998) \rightarrow ... \rightarrow f(1)
f(1000) \rightarrow f(999) \rightarrow f(998) \rightarrow ... \rightarrow f(1)

但是 ... 如果我們先呼叫 f(500)，再呼叫 f(1000)

f(1000)→f(999)→f(998)→...→f(500)‾f(1000) \rightarrow f(999) \rightarrow f(998) \rightarrow ... \rightarrow \underline{f(500)}
f(1000) \rightarrow f(999) \rightarrow f(998) \rightarrow ... \rightarrow \underline{f(500)}

f(500) 不會繼續遞迴，

因為已經被你記憶化了。

DP兩流派

Top-down vs. Bottom-up 

DP是有技巧的暴搜

怎麼暴力搜尋?

 

暴搜比較好理解的其中一個方法就是遞迴。

我遞迴苦手 :(
有沒有不是遞迴的方法？

東東爬樓梯 (zj d212)

東東爬階梯可以一次走一或兩階。

假設階梯有n階，那東東有幾種走法?

第n階答案 = 第n-1階答案 + 第n-2階答案

  • 終止條件 / Base case: f(0) = 1, f(1) = 1

所以 ...

  • f(2) = f(1) + f(0) = 2
  • f(3) = f(2) + f(1) = 3
  • f(4) = f(3) + f(2) = 5

好像可以用迴圈寫ㄟ？

東東爬樓梯 (zj d212)

東東爬階梯可以一次走一或兩階。

假設階梯有n階，那東東有幾種走法?

第n階答案 = 第n-1階答案 + 第n-2階答案

  • 終止條件 / Base case: f(0) = 1, f(1) = 1

所以 ...

  • f(2) = f(1) + f(0) = 2
  • f(3) = f(2) + f(1) = 3
  • f(4) = f(3) + f(2) = 5

好像可以用迴圈寫ㄟ？

#include <stdio.h>
int main() {
    int n;
    long long dp[100] = {0, 1};
    for (int i=2; i<100; i++) {
        dp[i] = dp[i-1] + dp[i-2];
    }
    while(~scanf("%d", &n)) {
        printf("%lld\n", dp[n]);
    }
}

Top-down & Buttom-up

DP主要兩大實作方法

Top-down

將大問題切成小問題，再將小問題切到 Base case。 

Bottom-up

將 Base case 堆成小答案，再將小答案慢慢堆成大答案。

通常比較直觀。
(遞迴寫出來就結束了)

有可能不太直觀，還需要考慮堆答案的順序。

優化困難。

比較可以優化。

比較慢。(呼叫函數比較慢)

比較快。

基本上你可以把 Bottom-up 想成
「小問題全都已經被記憶化」的 Top-down

Top-down & Buttom-up

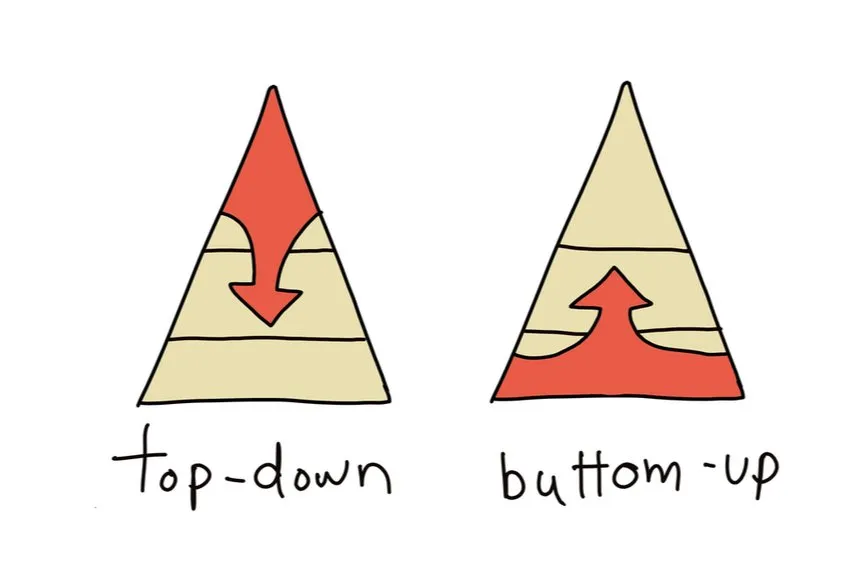
Buttom-up 怎麼寫?

#include <stdio.h>
int main() {
    int n;
    long long dp[100] = {0, 1};
    for (int i=2; i<100; i++) {
        dp[i] = dp[i-1] + dp[i-2];
    }
    while(~scanf("%d", &n)) {
        printf("%lld\n", dp[n]);
    }
}

以東東爬階梯為例子

  1. 在用迴圈寫DP前，先寫好 base case。
    • 也可以直接寫在定義式上，也就是迴圈內
       
  2. 決定迴圈的順序，以及開頭結尾等等...
    • 必須確保你的小答案都已經被算出來。
       
  3. 在內部寫上DP的定義式
    (這叫做 DP 轉移式)

把 Bottom-up 想成
「小問題全都已經被記憶化」
的 Top-down

00369 - Combinations (zj d134)

請問從 N 顆不同的球裡，
有幾種取出 M 顆球的方法？

(假設編號為1...n)

unsigned long long dp[101][101];
unsigned long long C(int n, int m){
	if (m == 0 || m == n) return 1;
    if (!dp[n][m])
        dp[n][m] = C(n-1, m-1) + C(n-1, m);
    return dp[n][m];
}
unsigned long long dp[101][101];
for (int n=1; n<101; n++) {
	for (int m=0; m<=n; m++) {
		if (m == 0 || n == m)
			dp[n][m] = 1;
		else
			dp[n][m] = dp[n-1][m-1] + dp[n-1][m];
    }
}

Top-down

Bottom-up

00369 - Combinations (zj d134)

請問從 N 顆不同的球裡，
有幾種取出 M 顆球的方法？

(假設編號為1...n)

unsigned long long dp[101][101];
for (int n=1; n<101; n++) {
	for (int m=0; m<=n; m++) {
		if (m == 0 || n == m)
			dp[n][m] = 1;
		else
			dp[n][m] = dp[n-1][m-1] + dp[n-1][m];
    }
}

思考看看填表格的順序吧！

0

1

2

3

4

1

2

3

4

5

1

1

1

2

1

1

3

3

1

4

6

1

5

10

1

4

1

5

5

1

10

int f(int n, int w) {
  if (n == 0)
    return 0;
  if (!dp[n][w]) {
    if (w >= W[n])
      dp[n][w] = max(f(n-1, w - W[n]) + V[n], f(n-1, w));
    else
      dp[n][w] = f(n-1, w);
  }
  return dp[n][w];
}
for (int i=1; i<=n; i++) {
  for (int j=0; j<=w; j++) {
    if (j >= W[i])
      dp[i][j] = max(dp[i-1][j-W[i]]+V[i], dp[i-1][j]);
    else
      dp[i][j] = dp[i-1][j];
  }
}

祖靈好孝順 ˋˇˊ (zj a587)

給出 N 個物品和物品的重量和價值。

給出祖靈的背包的重量限制。

請問祖靈最多可以帶價值東西回家?

(假設編號為1...n)

Top-
down

Bottom-
up

* base case寫在memset裡面

祖靈好孝順 ˋˇˊ (zj a587)

編號 1 2 3 4
重量 2 1 3 2
價值 3 2 4 2
N \ W 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 2 3 5 5 5
3 0 2 3 5 6 7
4 0 2 3 5 6 7
DPn,W=max⁡(DPn−1,W,DPn−1,W−wn+Vn)DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)
DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)

怕你沒辦法 Get 到，所以放個表給你 Get 一下

更細的 Bottom-up 區別

認真說起來的話，其實 Bottom-up 也有
區分成 pull / push。

我們基本上都使用 Pull Method。

for (int i=2; i<=n; i++) {
   dp[i] = dp[i-1] + dp[i-2];
}

Fibonacci (Pull)

for (int i=2; i<=n; i++) {
   dp[i] = dp[i-1] + dp[i-2];
}
for (int i=2; i<=n; i++) {
   dp[i] = dp[i-1] + dp[i-2];
}

Fibonacci (Push)

for (int i=0; i<=n-1; i++) {
   dp[i+1] += dp[i];
   dp[i+2] += dp[i];
}
dpi−1dp_{i-1}
dp_{i-1}
dpi−2dp_{i-2}
dp_{i-2}
dpidp_{i}
dp_{i}
dpidp_{i}
dp_{i}
dpi+1dp_{i+1}
dp_{i+1}
dpi+2dp_{i+2}
dp_{i+2}

不過你用 Push 寫出來也可以。

而我也推薦你

更細的 Top-down 區別

認真說起來的話，其實 Top-down 也有
區分成兩種想法: DP-style / dfs-style

for (int i=2; i<=n; i++) {
   dp[i] = dp[i-1] + dp[i-2];
}

Fibonacci (DP style)

int f(int n) {
  if (n == 0 || n == 1)
  	return 1;
  if (dp[n])
    return dp[n]
  return dp[n] = f(n-1) + f(n-2);
}
for (int i=2; i<=n; i++) {
   dp[i] = dp[i-1] + dp[i-2];
}

Fibonacci (dfs style)

int f(int cur, int n) {
  if (cur == n)
    return 1;
  if (cur > n)
    return 0;
  if (dp[cur])
    return dp[cur]
  return dp[cur] = f(cur+1, n) + f(cur+2, n);
}

將所有可能拆成兩個 Case：最後一步是 1 還是 2

從 0 開始走，枚舉下一步要走 1 還是 2，直到 n 或超過 n。

我們基本上接下來的投影片都是 DP style，
但也有一些題目要用 dfs style 會比較簡單。

你也可以想成 DP 是考慮最後一步，dfs 是考慮第一步。

空間優化 - 滾動法 I

Rolling Optimization

滾動法 Rolling

我們來觀察一下用 Bottom-up 解決 0/1 背包問題的時候，DP表的狀態。

編號 1 2 3 4
重量 2 1 3 2
價值 3 2 4 2
N \ W 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 2 3 5 5 5
3 0 2 3 5 6 7
4 0 2 3 5 6 7
DPn,w=max⁡(DP(n−1,W),DP(n−1,W−wn)+Vn)DP_{n, w} = \max (DP_{(n-1, W)}, DP_{(n-1, W-w_n)} + V_n)
DP_{n, w} = \max (DP_{(n-1, W)}, DP_{(n-1, W-w_n)} + V_n)

滾動法 Rolling

N \ W 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 2 3 5 5 5
3 0 2 3 5 6 7
4 0 2 3 5 6 7

我們每次算第 n 列，只會需要第 n-1 列的答案。
n-2 以前都用不到了，不覺得很浪費嗎？

我們來觀察一下用 Bottom-up 解決 0/1 背包問題的時候，DP表的狀態。

滾動法 Rolling

如果我們計算某一列，我們只需要他的前一列的答案。

N \ W 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 2 3 5 5 5
3 0 2 3 5 6 7
4 0 2 3 5 6 7

這個"某一列"，可以利用前兩列的空間來存。

0

0

1

我們可以使用 n % 2 來判斷現在是哪一列。

滾動法 Rolling

int pst=0, cur=1;
for (int i=1; i<=n; i++) {
	for (int j=0; j<=w; j++) {
		if (j >= W[i])
			dp[cur][j] = std::max(dp[pst][j-W[i]]+V[i], dp[pst][j]);
		else
			dp[cur][j] = dp[pst][j];
		}
	cur = 1-cur;
	pst = 1-pst;
}

或者用兩個變數輪替交換。這樣只需要開兩排空間!

x = 1 - x 這個式子：
如果 x == 0，那麼 x = 1。

如果 x == 1，那麼 x = 0。

這樣每一排做完的時候，0/1 就會交換。

*也可以用 x ^= 1，你開心就好

思考看看

  1. 如果第n排的答案需要參照第n-1排以及第n-2排，這使得你必須滾動三排，那麼你該怎麼滾？
    • 舉例來說，東東如果可以爬 1~3 階，你有辦法只開
      O(1) 空間嗎？
  2. 在原本的背包問題是，兩層 for 迴圈是可以交換的。
    那麼如果使用滾動法，這兩層還可以交換嗎？

空間優化 - 滾動法 II

Rolling Optimization II

滾動法 Rolling

我們再觀察一下，當你填某一格答案的時候，你只需要左上角一排的答案。

編號 1 2 3 4
重量 2 1 3 2
價值 3 2 4 2
N \ W 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 2 3 5 5 5
3 0 2 3 5 6 7
4 0 2 3 5 6 7
DPn,W=max⁡(DPn−1,W,DPn−1,W−wn+Vn)DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)
DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)

有沒有一種走訪順序，可以讓空間只開 W 就好呢？

先由右往左，再由上往下。

滾動法 Rolling

  1. 考慮原本的滾動 (只存兩排)。
  2. 每算一個需要前一排的左邊。
  3. 前一排的右邊用不到。
  4. 所以只需要存上排的左邊以及這排的右邊。
編號 1 2 3
重量 2 1 3
價值 3 2 4
N \ W 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 2 3 5 5 5
3 0 2 3 5 6 7
DPn,w=max⁡(DPn−1,W,DPn−1,W−wn+Vn)DP_{n, w} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)
DP_{n, w} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)

不用存，用不到

先由右往左，在由上往下。

你會發現綠色的可以被壓成一排。

那麼陣列會長怎麼樣呢？

滾動法 Rolling

DPn,W=max⁡(DPn−1,W,DPn−1,W−wn+Vn)DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)
DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)

先由右往左，在由上往下。

你會發現綠色的可以被壓成一排。

那麼陣列會長怎麼樣呢？

DP[0] DP[1] DP[2] ... DP[W-1] DP[W]
f(n-1, 0) f(n-1, 1) f(n-1, 2) ... f(n-1, W-1) f(n-1, W)
...

f(n, W)

f(n, W-1)

f(n, 2)

f(n, 0)

f(n, 1)

滾動法 Rolling - 0/1 背包問題

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
    int n, w;
    while(~scanf("%d", &n)) {
        vector<int> W(n), V(n);
        for (int i=0; i<n; i++)
            scanf("%d%d", &W[i], &V[i]);
        scanf("%d", &w);
        vector<int> DP(w+1, 0);
        for (int i=0; i<n; i++) {
            for (int j=w; j>=W[i]; j--) {
                DP[j] = max(DP[j], DP[j-W[i]]+V[i]);
            }
        }
        printf("%d\n", *max_element(DP.begin(), DP.end()));
    }
    return 0;
}

C++

  • 如果 j < W[i]，那麼就不用動。
    所以第二層迴圈跑到 W[i] 就可以了。
import sys
def main():
    def line_generator():
        for word in sys.stdin.read().split():
            yield int(word)
    G = line_generator()

    for N in G:
        items = [(next(G), next(G)) for _ in range(N)]
        W = next(G)
        DP = [0] * (W+1)
        for w, v in items:
            for cur_W in range(W, w-1, -1):
                DP[cur_W] = max(DP[cur_W], DP[cur_W - w]+v)
        print(max(DP))

main()

Python

滾動法 Rolling - 0/1 背包問題

  • 如果 j < W[i]，那麼就不用動。
    所以第二層迴圈跑到 W[i] 就可以了。
  • 這題 Python 解不了 (時間問題)，所以看到 TLE (18s) 沒有 WA 就差不多了。

滾動法 Rolling - 重新思考

背包問題是一個典型的選擇類找最佳解問題。

這就代表著順序是沒有關係的。

你可以改成這樣思考：

加上一個物品後，最佳解可以怎麼轉換？

這樣就不用從
top-down -> bottom-up -> 滾動 這樣思考了。

前 n-1 個東西的最佳解

DP[0] = rec(n-1, 0)

DP[1] = rec(n-1, 1)

DP[2] = rec(n-1, 2)

....

前 n 個東西的最佳解

DP[0] = rec(n, 0)

DP[1] = rec(n, 1)

DP[2] = rec(n, 2)

....

滾動法 Rolling - 無限背包問題

在 0/1 背包問題中，轉移式子是這樣的：

DPn,W=max⁡(DPn−1,W,DPn−1,W−wn+Vn)DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)
DP_{n, W} = \max (DP_{n-1, W}, DP_{n-1, W-w_n} + V_n)

在無限背包問題中，轉移式子是這樣的：

DPn,W=max⁡(DPn−1,W,DPn,W−wn+Vn)DP_{n, W} = \max (DP_{n-1, W}, DP_{n, W-w_n} + V_n)
DP_{n, W} = \max (DP_{n-1, W}, DP_{n, W-w_n} + V_n)

也就是你算 (n, W) 的時候，你需要兩個東西：

  • n-1, W，上一排的同個位置
  • n, W-wn，這一排的左邊位置

無限背包怎麼壓成一維呢？

DP 還原解答

DP Answer Recovery

DP 還原解答

在 0/1 背包問題中...

我們是求出限重 W 的最高價值

但我們卻不知道怎麼取才有這個最高價值。

編號 1 2 3 4
重量 2 1 3 2
價值 3 2 4 2

我們根據之前的算法可以得出：

W=5，最高價值為 7。

但是要怎麼選才可以到達7呢？

DP 還原解答

編號 1 2 3 4
重量 2 1 3 2
價值 3 2 4 2
N \ W 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 2 3 5 5 5
3 0 2 3 5 6 7
4 0 2 3 5 6 7

答案為 DP[4][5]，那麼其實你知道 DP[4][5] 是怎麼被算出來的。

觀察一下答案是怎麼被 max 出來的？接著依序往回走

4號

2號

1號

3號

1號

解答選法

DP 還原解答

// 正常解背包問題
vector<int> W(n+1), V(n+1);
for (int i=1; i<=n; i++)
    scanf("%d%d", &W[i], &V[i]);
scanf("%d", &w);
for (int i=1; i<=n; i++) {
    for (int j=0; j<=w; j++) {
        if (j >= W[i])
            DP[i][j] = max(DP[i-1][j], DP[i-1][j-W[i]]+V[i]);
        else
            DP[i][j] = DP[i-1][j];
    }
}
printf("%d\n", DP[n][w]);
//  還原解答
int cur_i = n, cur_j = w;
do {
    if (DP[cur_i][cur_j] == 
    	DP[cur_i-1][cur_j-W[cur_i]] + V[cur_i]) {
        printf("Choose %d Item\n", cur_i);
        cur_j -= W[cur_i];
    }
    cur_i -= 1;
} while (cur_i != 0);

C++

  • 開一個位置慢慢回溯。

DP 還原解答

Python

DP = [[0] * (W+1) for _ in range(N)]
for i, (w, v) in enumerate(items):
    for cur_W in range(W+1):
        if cur_W >= w:
            DP[i][cur_W] = max(DP[i-1][cur_W], DP[i-1][cur_W-w]+v)
        else:
            DP[i][cur_W] = DP[i-1][cur_W]
print(DP[-1][-1])

cur_i, cur_j = N-1, W
while cur_i != -1:
    w, v = items[cur_i]
    if DP[cur_i][cur_j] == DP[cur_i-1][cur_j-w]+v:
        print(f"Select Item {cur_i}")
        cur_j -= w
    cur_i -= 1
  • 開一個位置慢慢回溯。

想想看

以背包問題做舉例：

  • 請問背包問題的「最佳解有幾種可能」？
    • 舉例來說，這個範例最佳解有兩種可能。




       
    • 提示：這也是一個 DP 題目。
  • 如果你要還原解答，是不是代表你不能滾動？
    • 滾動的意思就代表著你空間複雜度是 O(W)
  • 有沒有辦法在把時間複雜度的換取空間複雜度的狀況下，讓你可以又滾動又還原解答？
    • 提示：將 n 個物品拆成一半各自解決 (分治法)
編號 1 2 3 4
重量 2 1 3 2
價值 3 2 4 2

經典 1D 轉移問題

找硬幣問題 Coin Change (leetcode 322)

Coin Change (leetcode 322)

舉例來說：

  • 台灣有 [1, 5, 10, 50, 100, 500, 1000]​
    • 如果你要找給別人 261 塊你會怎麼做？
      • 100 + 100 + 50 + 10 + 1
    • 貪心策略：優先使用大面額

給定某個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

Coin Change (leetcode 322)

但考慮比較奇怪的 case：

  • 某怪國面額為 [1, 4, 5]​
    • 如果你要找給別人 8 塊你會怎麼做？

目標 8 塊

5 + (目標 3 塊)

4 + (目標 4 塊)

5 + 1 + 1 + 1

(四個硬幣)

4 + 4

(兩個硬幣)

給定某個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

Coin Change (leetcode 322)

總結來說，這題只能暴搜。

也就是你幾乎要試遍所有可能。

那不是很慢嗎？

給定某個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

Coin Change (leetcode 322)

某怪國面額為 [1, 4, 5]​，要找 8 塊

目標 8 塊

min

5 + (目標 3 塊)

4 + (目標 4 塊)

1 + (目標 7 塊)

給定某個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

DP8DP_8
DP_8
1+DP31 + DP_3
1 + DP_3
1+DP41 + DP_4
1 + DP_4
1+DP71 + DP_7
1 + DP_7
DP0=0DP_0 = 0
DP_0 = 0
  1. 函式定義：
    • 試試看題目裸定義？
       
  2. 如何拆解：
    • 看看遞迴樹怎麼做的？
       
  3. Base Case :  
DPx=湊出x的最少找法DP_x = 湊出 x 的最少找法
DP_x = 湊出 x 的最少找法
DPx=min⁡c∈C 1+DPx−cDP_x = \underset{c \in C}{\min}\, 1 + DP_{x-c}
DP_x = \underset{c \in C}{\min}\, 1 + DP_{x-c}

Coin Change (leetcode 322)

某怪國面額為 [1, 4, 5]​，要找 8 塊

目標 8 塊

min

5 + (目標 3 塊)

4 + (目標 4 塊)

1 + (目標 7 塊)

給定某個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

DP8DP_8
DP_8
1+DP31 + DP_3
1 + DP_3
1+DP41 + DP_4
1 + DP_4
1+DP71 + DP_7
1 + DP_7
DP0=0DPx=min⁡c∈C 1+DPx−cDP_0 = 0\\ DP_x = \underset{c \in C}{\min}\, 1 + DP_{x-c}
DP_0 = 0\\ DP_x = \underset{c \in C}{\min}\, 1 + DP_{x-c}

這樣的確可以解出題目，
不過有沒有其他種看法呢？

其實這題就是多重背包問題。

所以我們嘗試用背包問題的定義法吧！

Coin Change (leetcode 322)

所以我們嘗試用背包問題的定義！

像背包問題一樣，把面額當成是背包問題的物品！

背包問題怎麼分 Case 的呢？

DPn,x=前n個面額中，找x塊錢的最佳找法DP_{n, x} = 前n個面額中，找x塊錢的最佳找法
DP_{n, x} = 前n個面額中，找x塊錢的最佳找法

有 n 顆相異的物品，

限重 W

取了最
後的

沒取最
後的

❌

...

💎

👑

📿

💎

💎

有 n 個面額，

要求 amount

取了最
後的

沒取最
後的面額

❌

...

5

4

1

5

5

Coin Change (leetcode 322)

DPn,x=min⁡{DPn−1,x不取第n個硬幣1+DPn,x−Cnif x≥Cn取第n個硬幣DP_{n, x} = \min\begin{cases} DP_{n-1, x} && 不取第 n 個硬幣 \\ 1 + DP_{n, x - C_n} & \text{if } x \ge C_n & 取第 n 個硬幣 \end{cases}
DP_{n, x} = \min\begin{cases} DP_{n-1, x} && 不取第 n 個硬幣 \\ 1 + DP_{n, x - C_n} & \text{if } x \ge C_n & 取第 n 個硬幣 \end{cases}
for i : 1->n
  for x : 0->amount
    if (x >= C[i])
      DP[i][x] = min(DP[i-1][x], 1+DP[i][x-C[i]])
    else
      DP[i][x] = DP[i-1][x]

自己試試用滾動優化成空間複雜度 O(amount)！

DPn,x=前n個面額中，找x塊錢的最佳找法DP_{n, x} = 前n個面額中，找x塊錢的最佳找法
DP_{n, x} = 前n個面額中，找x塊錢的最佳找法

所以我們嘗試用背包問題的定義！

Coin Change (leetcode 322)

int dp[10001] = {};

int coinChange(vector<int>& coins, int amount) {
  if (amount == 0)
    return 0;
  if (dp[amount])
    return dp[amount];
  int ans = -1;
  for (int coin : coins) {
    if (coin <= amount) {
      int res = coinChange(coins, amount - coin);
      if (res == -1)
        continue;
      if (ans == -1 || res + 1 < ans)
        ans = res + 1;
    }
  }
  return dp[amount] = ans;
}

C++ : Top-down

int coinChange(vector<int>& coins, int amount) {
    vector<int> DP(amount+1, 10001);
    DP[0] = 0;
    for (int coin : coins)
        for (int i=coin; i<=amount; i++)
            DP[i] = min(DP[i], DP[i-coin]+1);
    return DP[amount] > 10000 ? -1 : DP[amount];
}

C++ : Bottom-up

def coinChange(self, coins, amount):
    DP = [0] + [inf] * (amount)
    for coin in coins:
        for i in range(coin, amount+1):
            DP[i] = min(DP[i-coin]+1, DP[i])
    return DP[-1] if DP[-1] != inf else -1

Python: Top-down

def __init__(self):
  self.DP = {}
def coinChange(self, coins, amount):
  if amount == 0:
    return 0
  if amount not in self.DP:
    ans = -1
    for coin in coins:
      if amount >= coin:
        res = self.coinChange(coins, amount-coin)
      if res == -1:
        continue
      if ans == -1 or res + 1 < ans:
        ans = res + 1
    self.DP[amount] = ans
  return self.DP[amount]

Python: Bottom-up

Coin Change (leetcode 322)

發現了嗎？

明明是同一題，卻有截然不同的 DP 寫法！

有怎麼樣的狀態，就會有相應的轉移

好的狀態就會有好寫的轉移。

動態規劃小小結

動態規劃的時間複雜度

如何分析一個動態規劃的時間複雜度？

  1. 分析有多少「狀態數」，就是你DP表格會怎麼開。
    • 東東爬樓梯：O(n)
    • C(n, m)： O(nm)
    • 0/1 背包問題：O(nW) 或者 O(nV) 
    • 找硬幣問題：O(A)，A 代表 amount / O(AC)，C代表面額數
  • DP表格怎麼開是什麼意思？
    • 爬樓梯的問題有可能會問到 (1~n)，所以會開 DP[n]，這也就是 O(n)。
    • C(n,m) 有可能會問到 (1~n, 1~m)，所以會開 DP[n][m]，這也就是 O(nm)

動態規劃的時間複雜度

如何分析一個動態規劃的時間複雜度？

  1. 分析有多少「狀態數」，就是你DP表格會怎麼開。
    • 東東爬樓梯：O(n)
    • C(n, m)： O(nm)
    • 0/1 背包問題：O(nW) 或者 O(nV) 
    • 找硬幣問題：O(A)，A 代表 amount / O(AC)，C代表面額數
  2. 分析一個遞迴內，時間複雜度是多少。這就叫做「轉移複雜度」
     (你可以把所有遞迴都視作 O(1)，因為你有記憶化。)
    • 前三個問題轉移複雜度都是 O(1)
    • 找硬幣問題：O(C) / O(1)
  3. 「狀態數」*「轉移複雜度」 = DP 的時間複雜度
    • ​​東東爬樓梯： O(n) * O(1) = O(n)
    • C(n, m)：O(nm) * O(1) = O(nm)
    • 0/1 背包問題：O(nW) 或 O(nV)
    • 找硬幣問題：O(A) * O(C) = O(AC) / O(AC) * O(1) = O(AC)

!!!!!!!!!!!!!!!!!!!!!!!!

動態規劃的種類

  • 狀態數量
    • 如果狀態數量是 O(n)，叫做 1D 狀態
    • 如果狀態數量是 O(n^2), O(nm) 等兩個變數相乘，叫做 2D 狀態
  • ​轉移時間
    • 如果轉移複雜度需要 O(1)，叫做 0D 轉移
    • 如果轉移複雜度是 O(n)，叫做 1D 轉移
  • 我們會用 「狀態」/「轉移」 描述你的 DP 種類。
    • 東東爬樓梯：狀態 1D，轉移 0D，所以是 1D0D
    • C(n, m)：狀態 2D，轉移 0D，所以是 2D0D
    • 背包問題：狀態 2D，轉移 0D，所以是 2D0D
    • 找硬幣問題：
      • 方法1: 狀態 1D，轉移 1D，所以是 1D1D
      • 方法2: 狀態 2D，轉移 0D，所以是 2D0D

動態規劃使用時機

  1. 問題具有最佳子結構。

    講人話就是這個大問題可以透過小問題解決。

     
  2. 問題具有重複子問題。

    講人話就是解決大問題的時候，
    小問題會被問不只一次。

optimal substructure

 overlapping subproblems

有這兩種性質的問題，就能動態規劃。

動態規劃使用時機

動態規劃條件: 最佳子結構 以及 重複子問題

給定一個正整數 n ，
請判斷 n 是否為質數

n 是不是質數無法由其他數是不是質數來判定。

沒有最佳子結構。

 

他不是個 DP 題。

*不過質數篩法好像勉強算個DP XD

動態規劃使用時機

動態規劃條件: 最佳子結構 以及 重複子問題

排序數列

排序大數列可以拆成排序兩個一半的數列，並且合併成一個排序的數列。
有最佳子結構。


但每個區間排序只會處理一次，

沒有重複子問題。
 

他不是個 DP 題，他是分治(D&C)題。

動態規劃的思考方法

什麼時候使用DP？

  • 可以暴搜題目的時候，並且狀態可能會重複。
  • 通常都是最佳化答案 (背包問題)，或者計算個數。

DP 的流派 ?

  • Top-down: 遞迴 + 記憶化 (Memoization)
  • Bottom-up: 用迴圈疊出答案

DP 的流程？

  1. 狀態設計 (定義遞迴)，好的狀態會讓你 DP 好寫很多。
  2. 狀態轉移，思考你要怎麼將問題由大變小。
    • 考慮你要怎麼把所有可能分類？
  3. 記得寫 Base case。
  4. 想想看怎麼優化，有時候轉移複雜度 (甚至是狀態複雜度) 都可以被優化下去。 (後面我們會提及優化部分)​

狀態轉移的碎碎念

要怎麼考量好的轉移呢？

只要有辦法把所有可能分類，並且可能數會更小，
那麼這個拆法就是一個可行的轉移

舉例來說，爬樓梯：

🐦

4 階有 5 種走法

1+1+1+1

1+1+2

1+2+1

2+1+1

2+2

條件：

1+1+1+1

1+2+1

2+1+1

1+1+2

2+2

最後一步
是 1

最後一步
是 2

有沒有其他條件也可以拆呢？當然有

狀態轉移的碎碎念

要怎麼考量好的轉移呢？

只要有辦法把所有可能分類，並且可能數會更小，
那麼這個拆法就是一個可行的轉移

舉例來說，爬樓梯：

🐦

4 階有 5 種走法

1+1+1+1

1+1+2

1+2+1

2+1+1

2+2

條件：

1+1+1+1

1+2+1

1+1+2

2 +1+1

2+2

第一步
是 1

第一步
是 2

有沒有其他條件也可以拆呢？當然有

狀態轉移的碎碎念

要怎麼考量好的轉移呢？

只要有辦法把所有可能分類，並且可能數會更小，
那麼這個拆法就是一個可行的轉移

想出一個分類法通常不會太難
(當然也有難到很難分的，這個時候大多數要增加狀態)

但並不是所有分類法的實作難度都一樣​

所以看到問題的時候我們通常在想：

怎麼設計狀態 / 怎麼分類轉移會比較好實作？

題目名稱 來源 備註
Climbing Stairs Leetcode 70 等於爬樓梯
Fibonacci Number Leetcode 509 等於爬樓梯
Min Cost Climbing Stairs Leetcode 746 爬樓梯變形題
House Robber Leetcode 198 上題，但不能選相鄰
House Robber II Leetcode 213 上題，但環狀
Min Cost for Tickets Leetcode 983 爬樓梯+二分搜尋
Triangle Leetcode 120 巴斯卡三角變形題

爬樓梯 / C(n,m) 變形

題目名稱 來源 備註
Target Sum Leetcode 494 類似背包的遞迴
Coin Change II Leetcode 518 Coin Change 的可能數
禮物分配
Equal Subset 		Zj d890
Leetcode 416		 99年北市賽
背包變形題
Split Array with Same Average Leetcode 805

非DP，遞迴+對半拆
置物櫃分配  APCS 2018 / 10 - 4 zj 範圍怪怪的， 直接做
0/1 背包就可以了
Partition to K Equal Sum Leetcode 698 可暴搜可背包

背包 / 找硬幣變形

開始正式介紹各種DP！

可能是各種 DP 的種類

我們說動態規劃是...

可是可以暴搜的題目 ... 這不是很多嗎？

你答對了，所以 ...

動態規劃的題目五花八門，非常多種

可能是各種 DP 的種類

動態規劃的題目五花八門，非常多種

接下來我們會嘗試列舉各種題型，
並且選出其中的經典題。

因為動態規劃很重要，題型也很多，

接下來就感受 DP 的神奇魔力吧！

  1. 選擇類 DP
    • 二維地圖
    • 子序列
    • 區間分割
    • 區間選擇
  2. 記數類 DP
    • 數位 DP
  3. 區間 DP
  4. 博弈型 DP
  5. 機率型 DP
  6. 類遞迴 (喬瑟夫問題) TIOJ
  7. 樹 DP 
    • 全方位木 DP
  8. 圖 DP
    • DP 在 DAG 上
    • Bellman Ford / Floyd-Warshall (最短路)

可能是各種 DP 的種類

  • 轉移優化
    • 線性轉移快速冪次
    • 單調對列 / 滑動窗口優化
    • 斜率優化 (凸包優化)
    • 分治優化
    • 1d/1d 凹凸性
    • Knuth 優化 (2d/1d 凸性)
    • Aliens 優化 (WQS 二分搜優化)​

可能是各種 DP 的技巧們

我們會先把前面類型的DP帶過一遍後，
偷偷的介紹一些優化讓你好有感覺，

最後再正式介紹這些優化跟這些優化的條件！

  • 空間優化
    • 已經介紹的滾動法
    • 常見壓縮技巧
    • 位元DP
      • 輪廓 DP / 插頭 DP
      • SOS 優化

凹性 / 凸性

凹性 / 凸性就是函數是否滿足凹函數 / 凸函數性質。

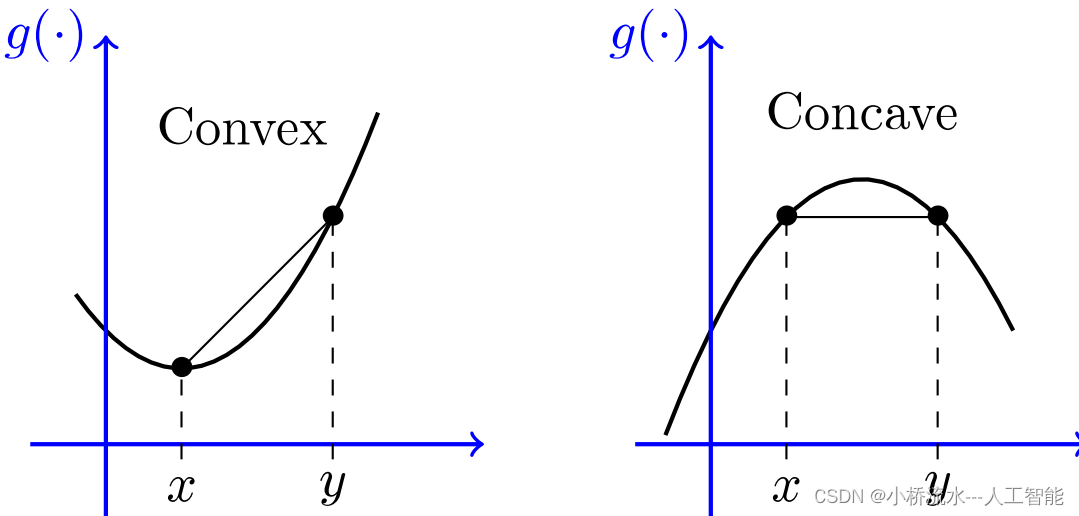
凸性：

f(αx+(1−α)y)≤αf(x)+(1−α)f(y),∀0≤α≤1f(\alpha x+ (1-\alpha)y) \le \alpha f(x) + (1-\alpha) f(y), \forall 0 \le \alpha \le 1
f(\alpha x+ (1-\alpha)y) \le \alpha f(x) + (1-\alpha) f(y), \forall 0 \le \alpha \le 1

講人話就是任兩點的連線都在函數上方。

凹性：

f(αx+(1−α)y)≥αf(x)+(1−α)f(y),∀0≤α≤1f(\alpha x+ (1-\alpha)y) \ge \alpha f(x) + (1-\alpha) f(y), \forall 0 \le \alpha \le 1
f(\alpha x+ (1-\alpha)y) \ge \alpha f(x) + (1-\alpha) f(y), \forall 0 \le \alpha \le 1

講人話就是任兩點的連線都在函數下方。

1−α:α1-\alpha : \alpha
1-\alpha : \alpha
f(αx+(1−α)y)f(\alpha x + (1-\alpha)y)
f(\alpha x + (1-\alpha)y)
αf(x)+(1−α)f(y)\alpha f(x) + (1-\alpha)f(y)
\alpha f(x) + (1-\alpha)f(y)
1−α:α1-\alpha:\alpha
1-\alpha:\alpha
f(αx+(1−α)y)f(\alpha x + (1-\alpha)y)
f(\alpha x + (1-\alpha)y)
αf(x)+(1−α)f(y)\alpha f(x) + (1-\alpha)f(y)
\alpha f(x) + (1-\alpha)f(y)

凹性 / 凸性

凹性 / 凸性就是函數是否滿足凹函數 / 凸函數性質。

α:1−α\alpha : 1-\alpha
\alpha : 1-\alpha
α:1−α\alpha : 1-\alpha
\alpha : 1-\alpha

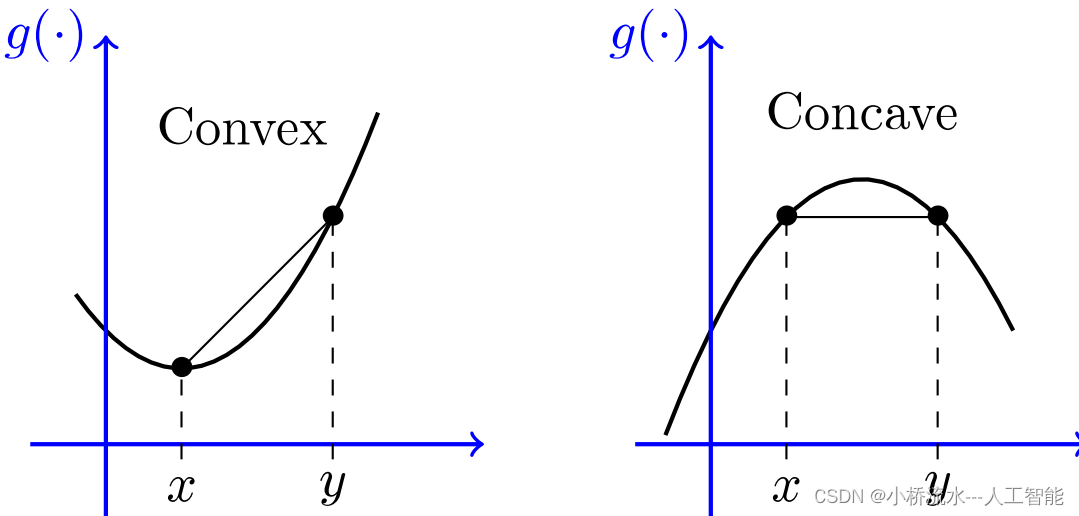
在 DP 優化中，要找                         

min⁡a≤i≤b或max⁡a≤i≤b(DPi)\min_{a \le i \le b} 或 \max_{a \le i \le b} (DP_{i})
\min_{a \le i \le b} 或 \max_{a \le i \le b} (DP_{i})

時，這個 DP(i) 如果具有凸性或凹性，
那麼就可以用比較聰明的方式找到最佳點。

二維地圖類 DP

Unique Paths II (leetcode 63)

二維地圖類 DP

其實高一的排列組合就有上過！

不信嗎？我們來看看這題

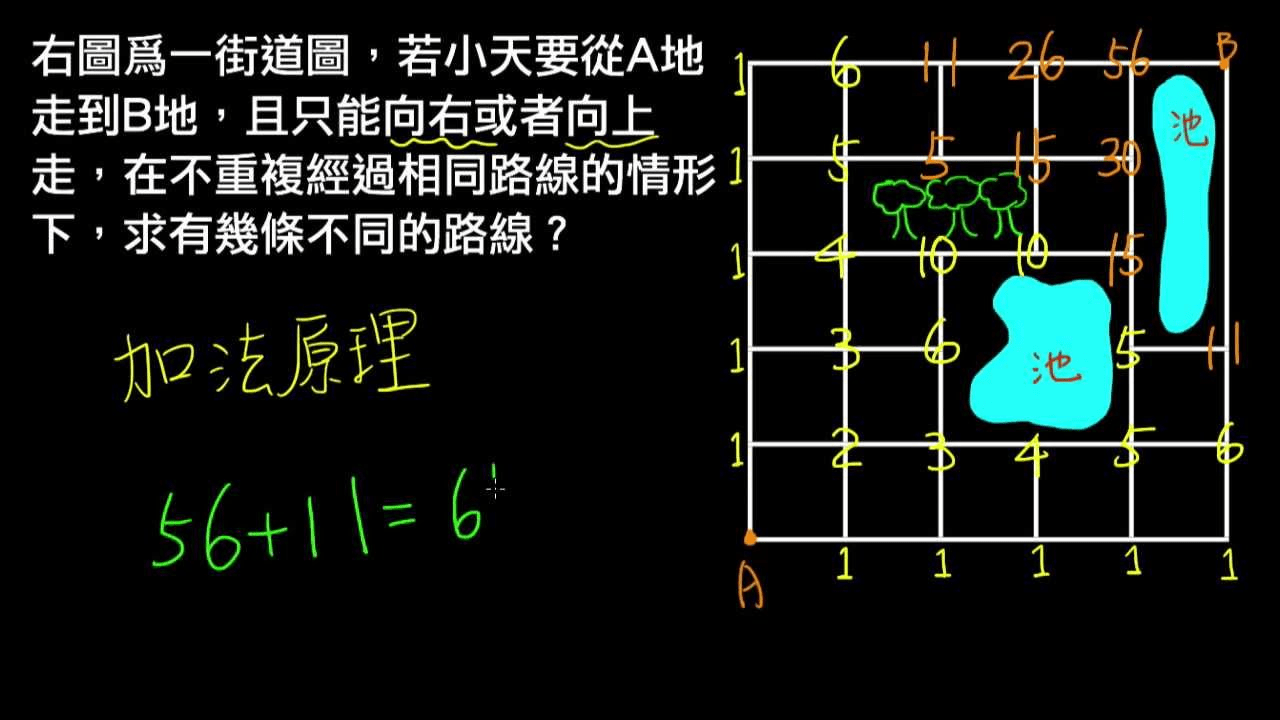
教學影片: Youtube / 更前面的加法原理教學

Unique Paths II (leetcode 63)

給定一個有障礙物的二維地圖，

以左上角當起點，以右下角為終點，

並且每次只能往右或往下走，請問有幾種走法？

答案是: 2

1

1

1

1

1

1

2

做法好像真的一樣？

到底什麼是「加法原理」？

  1. 函式定義：
     
  2. 如何拆解：

f(n, m) = 從 0, 0 走到 n, m 的走法數

0, 0

0, 1

0, 2

1, 0

1, 1

1, 2

2, 0

2, 1

2, 2

Unique Paths II (leetcode 63)

裸給：f(grid) = 答案

單純給 grid 很難繼續往下拆解。

能不能把更多資訊帶入參數，

讓我們方便做拆解呢？

接下來如何拆解呢？

給定一個有障礙物的二維地圖，

以左上角當起點，以右下角為終點，

並且每次只能往右或往下走，請問有幾種走法？

  1. 函式定義：
  2. 如何拆解：

在走樓梯中，我們將「走到 n 階」

的所有可能，可以拆成兩類

在這題中，在「從 (0, 0) → (n, m) 」
的所有可能，可不可以也拆成兩類呢？

f(n, m) = 從 0, 0 走到 n, m 的走法數

  1. 最後一步往下 : f(n-1, m)
    • (0, 0) → ... → (n-1, m) → (n, m)
  2. 最後一步往右 : f(n, m-1)
    • (0, 0) → ... → (n, m-1) → (n, m)

給定一個有障礙物的二維地圖，

以左上角當起點，以右下角為終點，

並且每次只能往右或往下走，請問有幾種走法？

Unique Paths II (leetcode 63)

(最後一步是1階還是2階)

0, 0

0, 1

0, 2

1, 0

1, 1

1, 2

2, 0

2, 1

2, 2

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

f(n, m) = 從 0, 0 走到 n, m 的走法數

f(n-1, m) + f(n, m-1)

Unique Paths II (leetcode 63)

0, 0

0, 1

0, 2

1, 0

1, 1

1, 2

2, 0

2, 1

2, 2

  1. f(0, 0) = 1 (如果 0, 0 沒有障礙物)
  2. f(n, m) = 0，如果是障礙物。

等等，這題不是有障礙物嗎？

怎麼寫在 Base Case 呢？

  • 其實你要寫在Base Case 或者用 if 寫在轉移都可以。

給定一個有障礙物的二維地圖，

以左上角當起點，以右下角為終點，

並且每次只能往右或往下走，請問有幾種走法？

Unique Paths II (leetcode 63)

int dp[100][100] = {};
bool visit[100][100] = {};
int f(vector<vector<int>> &grid, int n, int m) {
    if (n < 0 || m < 0) return 0;
    if (grid[n][m]) return 0;
    if (n == 0 && m == 0) return 1;
    if (visit[n][m]) return dp[n][m];
    visit[n][m] = true;
    dp[n][m] = f(grid, n-1, m) + f(grid, n, m-1);
    return dp[n][m];
}
int uniquePathsWithObstacles(vector<vector<int>>& grid) {
    memset(dp, 0, sizeof(dp));
    memset(visit, 0, sizeof(visit));
    return f(grid, grid.size()-1, grid[0].size()-1);
}
dp = {}
def f(n, m):
    if (n, m) in dp:
        return dp[n, m]
    if n < 0 or m < 0:
        return 0
    if n == 0 and m == 0:
        return 1
    dp[n, m] = f(n-1, m) + f(n, m-1)
    return dp[n, m]

for i, row in enumerate(obstacleGrid):
    for j, cell in enumerate(row):
        if cell:
            dp[i, j] = 0
return f(i, j)

C++

Python

可是這跟高中教的方法不一樣啊 ... ?

其實，高中教的方法就是 Bottom-up。

Top-down Solution

Unique Paths II (leetcode 63)

Bottom-up Solution

  1. 數學老師教你左邊一排 & 下面一排全都是 1 → Base Case
  2. 遇到一個空格就把左邊跟下面的數字加起來 → DP定義式

Unique Paths II (leetcode 63)

Bottom-up Solution

int n = grid.size(), m = grid[0].size();
vector<vector<int>> dp(n, vector<int> (m));
dp[0][0] = 1;
for (int i=0; i<n; i++) {
    for (int j=0; j<m; j++) {
        if (grid[i][j])
            dp[i][j] = 0;
        else {
            if (i) dp[i][j] += dp[i-1][j];
            if (j) dp[i][j] += dp[i][j-1];
        }
    }
}
return dp.back().back();
n = len(obstacleGrid)
m = len(obstacleGrid[0])
dp = [[0] * m for _ in range(n)]
dp[0][0] = 0 if obstacleGrid[0][0] else 1
for i, row in enumerate(obstacleGrid):
    for j, cell in enumerate(row):
        if cell: 
            continue
        if i: 
            dp[i][j] += dp[i-1][j]
        if j:
            dp[i][j] += dp[i][j-1]
return dp[-1][-1]

C++

Python

dp = [1] + [0] * (len(obstacleGrid[0]) - 1)
for row in obstacleGrid:
    for j, cell in enumerate(row):
        if cell:   
          dp[j] = 0
        elif j:    
          dp[j] += dp[j-1]
return dp[-1]
vector<int> dp(grid[0].size());
dp[0] = 1;
for (auto &row : grid) 
    for (int j=0; j<grid[0].size(); j++) 
        if (row[j])    
            dp[j] = 0;
        else if (j)     
            dp[j] += dp[j-1];
return dp.back();

Bottom-up + 滾動

二維地圖類 DP

  1. 比賽很常出現二維地圖類的題目
    • 不管是 BFS，DP等等主題都很常出在二維地圖上。
  2. 通常二維地圖類都是走路類題目，例如：
    • 如果是左上到右下的路徑最小值？ (leetcode 64)
    • 如果不規定起點，求路徑總和最大值？
      • (資訊學科能力競賽) 2018 北市賽 (TIOJ 2182)
      • 也不規定終點，2014 北市賽 (TIOJ 1268)
    • 從最上一排到最下一排，並且可以往左往右往下，那麼路徑最大值？ (APCS 2020/10 - 3，zj f314)
    • 如果格子皆為正數，從左上走到右下，可以朝四方向走，那麼最小值？ (*這題不是DP)

接下來讓我們看看第一題 - leetcode 64 吧！

尋找最小路

Minimum Path Sum (leetcode 64)

Minimum Path Sum (leetcode 64)

給你一個二維地圖，從左上開始，

只能往右或往下地走到右下，

請問經過數字總和最小多少？

答案是: 7

好像跟剛剛類似？

Minimum Path Sum (leetcode 64)

給你一個二維地圖，從左上開始，

只能往右或往下地走到右下，

請問經過數字總和最小多少？

  1. 函式定義：
  2. 如何拆解：

把「從 (0, 0) → (n, m) 」的所有可能，

可不可以也拆成兩類呢？

f(n, m) = 從 0, 0 走到 n, m 的最小路徑

  1. 最後一步往下 : f(n-1, m)
    • (0, 0) → ... → (n-1, m) → (n, m)
       
  2. 最後一步往右 : f(n, m-1)
    • (0, 0) → ... → (n, m-1) → (n, m)
       

0, 0

0, 1

0, 2

1, 0

1, 1

1, 2

2, 0

2, 1

2, 2

+ grid[n][m]

f(n-1, m)

f(n, m-1)

+ grid[n][m]

min⁡{\min \begin{cases} \\ \\ \\ \\ \end{cases}
\min \begin{cases} \\ \\ \\ \\ \end{cases}

Minimum Path Sum (leetcode 64)

C++

Python

dp = [0] + [math.inf] * len(grid[0])
for row in grid:
    for j, cell in enumerate(row):
        dp[j] = min(dp[j], dp[j-1]) + cell
return dp[-2]

Bottom-up + 滾動

vector<int> DP(grid[0].size());
for (int i=0; i<grid.size(); i++) {
  for (int j=0; j<grid[0].size(); j++) {
    if (j == 0)
      DP[j] += grid[i][j];
    else if (i == 0)
      DP[j] = DP[j-1] + grid[i][j];
    else
      DP[j] = min(DP[j-1], DP[j]) + grid[i][j];
  }
}
return DP.back();

像上題一樣，
稍微處理一下就可以寫出很乾淨的程式。

雙人路徑問題

傳紙條 (zj d109, NOIP 2008-3)

  • NOIP 是中國的比賽

傳紙條 (zj d109, NOIP 2008-3)

給定一個二維地圖，

1. 你從左上角出發，往右或往下走直到右下角。

2. 接著從右下角出發，往左或往上走直到起點。

你不能經過重複的格子，問路徑加總最大多少？

0 3 9
2 8 5
5 7 0

舉例來說：

Ans:2+8+7+5+9+3=34Ans: 2 + 8 + 7 + 5 + 9 + 3 = 34
Ans: 2 + 8 + 7 + 5 + 9 + 3 = 34

傳紙條 (zj d109, NOIP 2008-3)

給定一個二維地圖，

1. 你從左上角出發，往右或往下走直到右下角。

2. 接著從右下角出發，往左或往上走直到起點。

你不能經過重複的格子，問路徑加總最大多少？

0 3 9
2 8 5
5 7 0

好像有點難想狀態？

f(n, m) = 左上走到 (n, m) 的最大值

這樣你不知道

你是要過去還是要回來。

f(n, m, c) = 左上走到 (n, m) 的最大值，
c 代表是不是已經經過右下角。

這樣你會轉移了嗎？

傳紙條 (zj d109, NOIP 2008-3)

給定一個二維地圖，

1. 你從左上角出發，往右或往下走直到右下角。

2. 接著從右下角出發，往左或往上走直到起點。

你不能經過重複的格子，問路徑加總最大多少？

0 3 9
2 8 5
5 7 0

好像有點難想狀態？

過去沒有問題 (c=0 的狀況)

你不知道你曾經選了那些路，因此你也沒有足夠資訊轉移

f(n, m, c) = 左上走到 (n, m) 的最大值，
c 代表是不是已經經過右下角。

但回來呢 (c=1 的狀況)？

把走過哪些路記到狀態內嗎？ (會TLE)

傳紙條 (zj d109, NOIP 2008-3)

給定一個二維地圖，

1. 你從左上角出發，往右或往下走直到右下角。

2. 接著從右下角出發，往左或往上走直到起點。

你不能經過重複的格子，問路徑加總最大多少？

0 3 9
2 8 5
5 7 0

好像有點難想狀態？

換個角度思考，其實我們可以變成

兩條路同時從左上往右下走。

因為兩條路同時走，
你就可以比較輕鬆判斷會不會互撞。

定義狀態：把兩個座標都寫進去。

DPx1,y1,x2,y2=第一條路走到(x1,y1),第二條路到(x2,y2)的最大值DP_{x_1, y_1, x_2, y_2} = 第一條路 走到 (x_1, y_1), 第二條路到 (x_2, y_2) 的最大值
DP_{x_1, y_1, x_2, y_2} = 第一條路 走到 (x_1, y_1), 第二條路到 (x_2, y_2) 的最大值

傳紙條 (zj d109, NOIP 2008-3)

0 3 9
2 8 5
5 7 0
DPx1,y1,x2,y2=第一條路走到(x1,y1),第二條路到(x2,y2)的最大值DP_{x_1, y_1, x_2, y_2} = 第一條路 走到 (x_1, y_1), 第二條路到 (x_2, y_2) 的最大值
DP_{x_1, y_1, x_2, y_2} = 第一條路 走到 (x_1, y_1), 第二條路到 (x_2, y_2) 的最大值
  • 在上一題中，如果只有一個人該怎麼寫？
    • 考量最後一步往右還是往下。

       
  • 但是這一題有兩個人？
    • 一樣考量最後一步往右還是往下。
    • 但兩個人的可能都要考慮！
DPx,y=max⁡(DPx−1,y,Dx,y−1)+...DP_{x, y} = \max (DP_{x-1, y}, D_{x, y-1}) + ...
DP_{x, y} = \max (DP_{x-1, y}, D_{x, y-1}) + ...
DPx1,y1,x2,y2=max⁡{DPx1−1,y1,x2−1,y2DPx1−1,y1,x2,y2−1DPx1,y1−1,x2−1,y2DPx1,y1−1,x2,y2−1+...DP_{x_1, y_1, x_2, y_2} = \max \begin{cases} DP_{x_1-1, y_1, x_2-1, y_2} \\ DP_{x_1-1, y_1, x_2, y_2-1}\\ DP_{x_1, y_1-1, x_2-1, y_2}\\ DP_{x_1, y_1-1, x_2, y_2-1}\\ \end{cases} + ...
DP_{x_1, y_1, x_2, y_2} = \max \begin{cases} DP_{x_1-1, y_1, x_2-1, y_2} \\ DP_{x_1-1, y_1, x_2, y_2-1}\\ DP_{x_1, y_1-1, x_2-1, y_2}\\ DP_{x_1, y_1-1, x_2, y_2-1}\\ \end{cases} + ...

(7, 5)

(8, 9)

(8, 8)

(5, 9)

(5, 8)

(不能踩在同一格)

傳紙條 (zj d109, NOIP 2008-3)

C++

Python

import math
n, m = map(int, input().split())
grid = [list(map(int, input().split())) for _ in range(n)]
dp = {}
def rec(xa, ya, xb, yb):
    if xa == xb == ya == yb == 0:
        return 0
    if xa < 0 or xb < 0 or ya < 0 or yb < 0:
        return -math.inf
    if (xa, ya) == (xb, yb):
        return -math.inf
    if (xa, ya, xb, yb) not in dp:
        dp[xa, ya, xb, yb] = max(
            rec(xa-1, ya, xb-1, yb),
            rec(xa-1, ya, xb, yb-1),
            rec(xa, ya-1, xb-1, yb),
            rec(xa, ya-1, xb, yb-1)
        ) + grid[xa][ya] + grid[xb][yb]
    return dp[xa, ya, xb, yb]

print(rec(n-1, m-2, n-2, m-1))
#include <iostream>
#include <algorithm>
#define INF 100000000
using namespace std;
int n, m, grid[50][50], dp[50][50][50][50];
int rec(int xa, int ya, int xb, int yb) {
    if (xa == 0 && ya == 0 && xb == 0 && yb == 0)
        return 0;
    if (xa < 0 || ya < 0 || xb < 0 || yb < 0)
        return -INF;
    if (xa == xb && ya == yb)
        return -INF;
    if (dp[xa][ya][xb][yb])
        return dp[xa][ya][xb][yb];
    return dp[xa][ya][xb][yb] = 
        grid[xa][ya] + grid[xb][yb] + max({
            rec(xa-1, ya, xb-1, yb),
            rec(xa-1, ya, xb, yb-1),
            rec(xa, ya-1, xb-1, yb),
            rec(xa, ya-1, xb, yb-1)
        });
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i=0; i<n; i++) {
        for (int j=0; j<m; j++) {
            scanf("%d",&grid[i][j]);
        }
    }
    printf("%d\n", rec(n-1, m-2, n-2, m-1));
    return 0;
}

傳紙條 (zj d109, NOIP 2008-3)

  1. 這題 Top-down 的時間複雜度是？
  2. 這一題怎麼用 Bottom-up 寫？
  3. 仔細觀察，你會發現有很多狀態是不存在的，請問：
    1. 怎麼將 4D 的狀態壓縮成 3D？
    2. 這樣的 Bottom-up 怎麼滾動？
      (滾動空間複雜度                           ) 
    3. 既然你發現了假 4D 狀態，有沒有辦法在不壓縮處理的情況改善 Top-down 的複雜度？
O(min⁡(N,M)2)O(\min(N, M)^2)
O(\min(N, M)^2)
  • 你第一次看到開超多維陣列的題目！(4D0D)
  • 你第一次看到用狀態壓縮可以降低複雜度的題目！

傳紙條 (zj d109, NOIP 2008-3)

Python 做狀態壓縮的 Top-down 解

import math
n, m = map(int, input().split())
grid = [list(map(int, input().split())) for _ in range(n)]
dp = {}
def rec(xa, ya, dis_ab):
    xb, yb = xa - dis_ab, ya + dis_ab
    if xa == xb == ya == yb == 0:
        return 0
    if xa < 0 or xb < 0 or ya < 0 or yb < 0:
        return -math.inf
    if (xa, ya) == (xb, yb):
        return -math.inf
    if (xa, ya, xb, yb) not in dp:
        dp[xa, ya, xb, yb] = max(
            rec(xa-1, ya, dis_ab),
            rec(xa-1, ya, dis_ab-1),
            rec(xa, ya-1, dis_ab),
            rec(xa, ya-1, dis_ab+1)
        ) + grid[xa][ya] + grid[xb][yb]
    return dp[xa, ya, xb, yb]

print(rec(n-1, m-2, 1))
  • dis_ab 最大是 min(N, M)，所以是狀態數是 NM*min(N+M)

找子序列的 DP

什麼是子區間以及子序列？

  • 子區間/子陣列 (subarray) :
    有序且連續的部分。
     
  • 子序列 (subsequence) :
    有序但不一定連續的部分。

以 azbec 來說：

  • zbe
  • a
  • ec
  • abc
  • ze
  • 子區間都是子序列

找子序列的 DP

我們先了解一下專有名詞：

題目大概：

  • 通常會給你至少一個 Array。
  • 在符合某個限制下，選出某幾個數字具有最佳解。
  • 選？其實就跟背包問題選東西很像。
    • 因為你解背包問題本質上也是挑幾個數字出來，
      但這數字沒有順序問題。
    • 例如 貪心投影片-湖畔大樓 裡面提及的 DP 也是類似。差別在於一開始就必須決定順序。

找子序列的 DP

最長共同子序列

Longest Common Subsequence (LCS)

10405 - LCS (zj c001)

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

範例 1:

a1b2c3d4e
zz1yy2xx3ww4vv

最長共同子序列

範例 2:

abcdgh
aedbhr

這兩個字串的唯一
LCS 為 1234，
因此答案為4。

這兩個字串有兩個 LCS，

分別是 "adh"，"abh"。但答案都是3。

10405 - LCS (zj c001)

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

最長共同子序列

  1. 函式定義：

範例 1:

a1b2c3d4e
zz1yy2xx3ww4vv

範例 2:

abcdgh
aedbhr

試試看題目裸定義？

DPS,T=LCS的長度DP_{S, T} = LCS 的長度
DP_{S, T} = LCS 的長度

不太行 ... 沒法拆解。
跟二維地圖只傳整個grid一樣，

等，當時怎麼定義才可以拆解的？

DPn,m=從(0,0)走到(n,m)的走法數DP_{n, m} = 從 (0, 0) 走到 (n, m) 的走法數
DP_{n, m} = 從 (0, 0) 走到 (n, m) 的走法數

當時我們是用座標當成 DP 的狀態。

那這題怎樣定義才可以拆解呢？

10405 - LCS (zj c001)

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

最長共同子序列

  1. 函式定義：

範例 1:

a1b2c3d4e
zz1yy2xx3ww4vv

範例 2:

abcdgh
aedbhr

那這題怎樣定義才可以拆解呢？

用一個變數 i 表示 S 的前 i + 1 個字元

S = "a1b2c3d4e"

  1. i = 0，表示 "a"
  2. i = 1，表示 "a1" ...

但是我們有兩個字串？

DPi,j={LCS(S[0,i],T[0,j])長度LCS(S前i+1個字元,T前j+1個字元)長度DP_{i, j} = \begin{cases} LCS(S_{[0, i]}, T_{[0, j]}) 長度\\ LCS(S_{前i+1個字元}, T_{前j+1個字元}) 長度 \end{cases}
DP_{i, j} = \begin{cases} LCS(S_{[0, i]}, T_{[0, j]}) 長度\\ LCS(S_{前i+1個字元}, T_{前j+1個字元}) 長度 \end{cases}

10405 - LCS (zj c001)

那轉移式子呢？

也就是怎麼用小問題解決大問題呢？

有點難？回想一下之前的題目：

  1. 爬樓梯考量最後一步走 1 還是 2 階
  2. C(n, m) 考量要不要取最後一顆球 (第 n 顆球)
  3. 背包問題考量要不要取最後的一個物品
  4. 找硬幣考量最後一個硬幣是拿哪種硬幣
  5. 走格子問題考量最後一步是往下還是往右

所以按照慣例我們考量兩個字串的最後一個字。

DPi,j=LCS(S[0,i],T[0,j])長度DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度
DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度

最長共同子序列

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

10405 - LCS (zj c001)

轉移式子：

S[i] 跟 T[j] 匹配一定最好！
代表 LCS 尾巴一定是S[i]！

S =  .........   X

T =  ....   X

S[i]

T[j]

T =  ....   Y

剩下的 LCS 會在哪呢？

在 S[0...i-1] 和 T[0...j-1] 之間

最長共同子序列

DPi,j=LCS(S[0,i−1],T[0,j−1])+1=DPi−1,j−1+1DP_{i, j} = LCS(S_{[0, i-1]}, T_{[0, j-1]}) + 1 \\ = DP_{i-1, j-1} + 1
DP_{i, j} = LCS(S_{[0, i-1]}, T_{[0, j-1]}) + 1 \\ = DP_{i-1, j-1} + 1

S[i] 不能跟 T[j] 匹配。

S[i] 跟 前面的 T 匹配
 T[j] 沒人配，等同沒用。

LCS(S[0,i],T[0,j−1])=DPi,j−1LCS(S_{[0, i]}, T_{[0, j-1]}) = DP_{i, j-1}
LCS(S_{[0, i]}, T_{[0, j-1]}) = DP_{i, j-1}

同理，相反也是。

LCS(S[0,i−1],T[0,j])=DPi−1,jLCS(S_{[0, i-1]}, T_{[0, j]}) = DP_{i-1, j}
LCS(S_{[0, i-1]}, T_{[0, j]}) = DP_{i-1, j}
Si=TjS_i = T_j
S_i = T_j
Si≠TjS_i \ne T_j
S_i \ne T_j

考量最後一個字

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

DPi,j=LCS(S[0,i],T[0,j])長度DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度
DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度

10405 - LCS (zj c001)

最長共同子序列

LCS(S[0,i−1],T[0,j−1])+1=DPi−1,j−1+1LCS(S_{[0, i-1]}, T_{[0, j-1]}) + 1 = DP_{i-1, j-1} + 1
LCS(S_{[0, i-1]}, T_{[0, j-1]}) + 1 = DP_{i-1, j-1} + 1
LCS(S[0,i],T[0,j−1])=DPi,j−1LCS(S_{[0, i]}, T_{[0, j-1]}) = DP_{i, j-1}
LCS(S_{[0, i]}, T_{[0, j-1]}) = DP_{i, j-1}
LCS(S[0,i−1],T[0,j])=DPi−1,jLCS(S_{[0, i-1]}, T_{[0, j]}) = DP_{i-1, j}
LCS(S_{[0, i-1]}, T_{[0, j]}) = DP_{i-1, j}
max⁡{\max \begin{cases} \\ \\ \end{cases}
\max \begin{cases} \\ \\ \end{cases}

if

if

最後一步：Base Case 呢？

一直遞迴下去，直到哪裡會沒有意義或有答案？

DP−1,?=DP?,−1=沒字匹配=0DP_{-1, ?} = DP_{?, -1} = 沒字匹配 = 0
DP_{-1, ?} = DP_{?, -1} = 沒字匹配 = 0
Si=TjS_i = T_j
S_i = T_j
Si≠TjS_i \ne T_j
S_i \ne T_j

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

DPi,j=LCS(S[0,i],T[0,j])長度DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度
DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度

10405 - LCS (zj c001)

DPi,j={0 ,if i=−1 or j=−1DPi−1,j−1+1 ,if Si=Tjmax⁡(DPi−1,j,DPi,j−1), otherwiseDP_{i, j} = \begin{cases} 0\text{ ,if } i=-1 \text{ or } j = -1 \\ DP_{i-1, j-1} + 1 \text{ ,if } S_{i} = T_{j} \\ \max(DP_{i-1, j}, DP_{i, j-1}) \text{, otherwise} \end{cases}
DP_{i, j} = \begin{cases} 0\text{ ,if } i=-1 \text{ or } j = -1 \\ DP_{i-1, j-1} + 1 \text{ ,if } S_{i} = T_{j} \\ \max(DP_{i-1, j}, DP_{i, j-1}) \text{, otherwise} \end{cases}

箭頭表示答案是從哪裡得到的

最長共同子序列

如果用 Bottom-up 寫表格
就會是這樣。

註: 圖中字串編號是從 1 開始數，
所以它的base case 是 i = 0 或 j = 0

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

DPi,j=LCS(S[0,i],T[0,j])長度DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度
DP_{i, j} = LCS(S_{[0, i]}, T_{[0, j]}) 長度

10405 - LCS (zj c001)

string S1, S2;
int DP[1001][1001];
int rec(int i,int j){
    if(i == -1 || j == -1)
        return 0;
    if(DP[i][j] != -1)
        return DP[i][j];
    if(S1[i] == S2[j])
        return DP[i][j] = rec(i-1, j-1) + 1;
    else
        return DP[i][j] = max(rec(i-1, j), rec(i, j-1));
}

int main(){
    while(cin>>S1>>S2){
        memset(DP, -1, sizeof(DP));
        cout << rec(S1.size()-1, S2.size()-1) << endl;
    }
}
DPi,j={0 ,if i=−1 or j=−1DPi−1,j−1+1 ,if Si=Tjmax⁡(DPi−1,j,DPi,j−1), otherwiseDP_{i, j} = \begin{cases} 0\text{ ,if } i=-1 \text{ or } j = -1 \\ DP_{i-1, j-1} + 1 \text{ ,if } S_{i} = T_{j} \\ \max(DP_{i-1, j}, DP_{i, j-1}) \text{, otherwise} \end{cases}
DP_{i, j} = \begin{cases} 0\text{ ,if } i=-1 \text{ or } j = -1 \\ DP_{i-1, j-1} + 1 \text{ ,if } S_{i} = T_{j} \\ \max(DP_{i-1, j}, DP_{i, j-1}) \text{, otherwise} \end{cases}

最長共同子序列

給定兩個字串 S 和 T，請問 LCS(S, T) 的長度？

編輯距離

Edit Distance

1207 - AGTC (zj f507)

給定兩個字串 S 和 T，問 S 和 T 的編輯距離為何？

edit distance

你可以花費 1 個 cost 做以下三種操作

  1. 刪除任何一個字元
  2. 修改任何一個字元
  3. 增加任何一個字元

編輯距離：最少要花多少 cost 才可以讓 S = T?

AGTCTGACGC
AGTAAGTAGGC

3次修改，1次刪除：編輯距離為 4 

1207 - AGTC (zj f507)

給定兩個字串 S 和 T，問 S 和 T 的編輯距離為何？

edit distance

同 LCS ，DP 定義就下成：

DPi,j=編輯距離(S[0,i],T[0,j])=編輯距離(S前i+1個字元,T前j+1個字元)DP_{i, j} = \text{編輯距離}(S_{[0, i]}, T_{[0, j]}) = \text{編輯距離}(S_{前i+1個字元}, T_{前j+1個字元})
DP_{i, j} = \text{編輯距離}(S_{[0, i]}, T_{[0, j]}) = \text{編輯距離}(S_{前i+1個字元}, T_{前j+1個字元})

我們一樣來思考如何從最後一個字轉移吧！

你可以花費 1 個 cost 做以下三種操作

  1. 刪除任何一個字元
  2. 修改任何一個字元

1207 - AGTC (zj f507)

給定兩個字串 S 和 T，問 S 和 T 的編輯距離為何？

edit distance

  1. 刪除任何一個字元
  2. 修改任何一個字元

S[i] 跟 T[j] 匹配一定最好！

剩下的編輯距離？

在 S[0...i-1] 和 T[0...j-1] 之間

DPi−1,j−1=編輯距離(S[0,i−1],T[0,j−1])DP_{i-1, j-1} \\ = \text{編輯距離}(S_{[0, i-1]}, T_{[0, j-1]})
DP_{i-1, j-1} \\ = \text{編輯距離}(S_{[0, i-1]}, T_{[0, j-1]})

S[i] 不能跟 T[j] 匹配。

考量兩種操作：

修改：把 S[i] 修改成 T[j]

DPi−1,j−1+1DP_{i-1, j-1} + 1
DP_{i-1, j-1} + 1
Si=TjS_i = T_j
S_i = T_j
Si≠TjS_i \ne T_j
S_i \ne T_j
DPi,j=編輯距離(S[0,i],T[0,j])DP_{i, j} = \text{編輯距離}(S_{[0, i]}, T_{[0, j]})
DP_{i, j} = \text{編輯距離}(S_{[0, i]}, T_{[0, j]})

S =  .........   X

T =  ....   X

S[i]

T[j]

T =  ....   Y

刪除：刪掉 S[i] 或者 刪掉 T[j]

min⁡(DPi,j−1,DPi−1,j)+1\min (DP_{i, j-1}, DP_{i-1, j}) + 1
\min (DP_{i, j-1}, DP_{i-1, j}) + 1

1207 - AGTC (zj f507)

給定兩個字串 S 和 T，問 S 和 T 的編輯距離為何？

edit distance

DPi−1,j−1=編輯距離(S[0,i−1],T[0,j−1])DP_{i-1, j-1} = \text{編輯距離}(S_{[0, i-1]}, T_{[0, j-1]})
DP_{i-1, j-1} = \text{編輯距離}(S_{[0, i-1]}, T_{[0, j-1]})

修改：

DPi−1,j−1+1DP_{i-1, j-1} + 1
DP_{i-1, j-1} + 1
Si=TjS_i = T_j
S_i = T_j
Si≠TjS_i \ne T_j
S_i \ne T_j
DPi,j=編輯距離(S[0,i],T[0,j])DP_{i, j} = \text{編輯距離}(S_{[0, i]}, T_{[0, j]})
DP_{i, j} = \text{編輯距離}(S_{[0, i]}, T_{[0, j]})

刪除：

min⁡(DPi,j−1,DPi−1,j)+1\min (DP_{i, j-1}, DP_{i-1, j}) + 1
\min (DP_{i, j-1}, DP_{i-1, j}) + 1
min⁡{\min \begin{cases} \\ \end{cases}
\min \begin{cases} \\ \end{cases}

那麼 Base Case 呢？

S為空，那麼編輯距離就是 |T|。

T為空，那麼編輯距離就是 |S|。

練習題！

  1. 給定三個字串，問三個字串的 LCS 長度是多少？ 
    Another LCS (zj a252)
  2. 給定兩個字串，還原 LCS 具體是什麼。
    00531 - Compromise (zj e682)
  3. 給定兩個陣列，問兩個陣列的子序列內積最大為何？
    Max Dot Product of Two Subsequences (leetcode 1458)
    • 註：你不能選空序列，所以你需要一些特判。

k-相鄰子序列

Constrained Subsequence Sum (leetcode 1425)

初探 Sliding Window / 單調對列優化

Constrained Subsequence Sum (leetcode 1425)

A = [10, -2, -10, -5, 20], k = 2

舉例來說：

[10, -2, -10, -5, 20]: 10

[10, -2, -10, -5, 20]: 20

[10, -2, -10, -5, 20]: 20

[10, -2, -10, -5, 20]: 23

最佳解：23。

  • k = 2 表示你最多只能跳一個。
  • k = 1 會退化成選最大子區間。

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

Constrained Subsequence Sum (leetcode 1425)

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

我們先按照LCS的定義試試看？

好像做不出轉移式？

我們缺乏一個重要的資訊：

答案選擇的子序列到底斷在哪？

不知道的話就無法接續。但如果這樣...

DPn=A[0,n]中k相鄰子序列的最大總和DP_n = A_{[0, n]} 中k相鄰子序列的最大總和
DP_n = A_{[0, n]} 中k相鄰子序列的最大總和
DPn=A[0,n]中選了An的k相鄰子序列的最大總和DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和
DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和

你至少就有足夠的資訊可以轉移了！

  1. 函式定義：

Constrained Subsequence Sum (leetcode 1425)

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

DPn=A[0,n]中選了An的k相鄰子序列的最大總和DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和
DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和

不過為什麼這樣定義可以得出全局最佳解呢？

DP0←max⁡(A0,0)DP_0 \leftarrow \max( A_{0, 0})
DP_0 \leftarrow \max( A_{0, 0})
DP1←max⁡(A0,1,A1,1)DP_1 \leftarrow \max( A_{0, 1}, A_{1, 1})
DP_1 \leftarrow \max( A_{0, 1}, A_{1, 1})
DPn←max⁡(A0,n,A1,n...,An,n)DP_n \leftarrow \max( A_{0, n}, A_{1, n} ..., A_{n, n})
DP_n \leftarrow \max( A_{0, n}, A_{1, n} ..., A_{n, n})

...

DPj∗←max⁡(A0,j∗,A1,j∗,...,        ,...Aj∗,j∗)DP_{j^*} \leftarrow \max( A_{0, j^*}, A_{1, j^*}, ... , ~~~~~~~~ ,... A_{j^*, j^*})
DP_{j^*} \leftarrow \max( A_{0, j^*}, A_{1, j^*}, ... , ~~~~~~~~ ,... A_{j^*, j^*})

假設最佳解發生在

Ai∗,j∗A_{i^{*}, j^*}
A_{i^{*}, j^*}
Ai∗,j∗A_{i^*, j^*}
A_{i^*, j^*}
那麼答案會在DPj∗那麼答案會在 DP_{j^*}
那麼答案會在 DP_{j^*}
所以全局答案=max⁡(DP)所以全局答案 = \max(DP)
所以全局答案 = \max(DP)

Constrained Subsequence Sum (leetcode 1425)

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

  1. 函式定義：
  2. 如何拆解：
DPn=A[0,n]中選了An的k相鄰子序列的最大總和DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和
DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和

像之前題目一樣，A[n] 的上一步 (上一個數字)在哪？

10, -2, -10, -5

10

A[0, n-1]

A[n]

k ≤ 1

k ≤ 2

k ≤ 3

k ≤ 4

以 A[n] 為結尾最佳解

DPnDP_n
DP_n
DPiDP_i
DP_i
+An+ A_n
+ A_n
max⁡n−k≤i<n\underset{n-k \le i < n}{\max}
\underset{n-k \le i < n}{\max}

= 以A[i] 為結尾的最佳解 + An

Constrained Subsequence Sum (leetcode 1425)

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

  1. 函式定義：
  2. 如何拆解：
     
  3. Base Case：
DPn=A[0,n]中選了An的k相鄰子序列的最大總和DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和
DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和
DPnDP_n
DP_n
==
=
DP = []
for num in nums:
  DP.append(max([0] + DP[-k:]) + num)
return max(DP)
vector<int> DP({0});
for (int i=0; i<nums.size(); i++) {
  int v = *max_element(DP.end()-min(i+1, k), DP.end());
  DP.push_back(max(0, v) + nums[i]);
}
return *max_element(DP.begin()+1, DP.end());

C++

Python

DPn=AnDP_n = A_n
DP_n = A_n

如果前面太差，你可以從 An 開始選：

DPiDP_i
DP_i
+An+ A_n
+ A_n
max⁡n−k≤i<n\underset{n-k \le i < n}{\max}
\underset{n-k \le i < n}{\max}

Constrained Subsequence Sum (leetcode 1425)

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

  1. 函式定義：
  2. 如何拆解：
     
  3. Base Case：
DPn=A[0,n]中選了An的k相鄰子序列的最大總和DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和
DP_n = A_{[0, n]} 中選了A_n的k相鄰子序列的最大總和
DPnDP_n
DP_n
DPiDP_i
DP_i
+An+ A_n
+ A_n
max⁡n−k≤i<n\underset{n-k \le i < n}{\max}
\underset{n-k \le i < n}{\max}
==
=
DPn=AnDP_n = A_n
DP_n = A_n

分析看看複雜度吧！

O(N)O(N)
O(N)

狀態數量             × 轉移複雜度            =

O(k)O(k)
O(k)
O(Nk)O(Nk)
O(Nk)

狀態應該是不能再壓了，那麼轉移可以更快嗎？

max⁡n−k≤i<nDPi→\max_{n-k \le i < n} DP_{i} \rightarrow
\max_{n-k \le i < n} DP_{i} \rightarrow
  1. i 從 n-k 跑到 n-1。
  2. 對於 An，要找到前面 k 個中最大 DP 值。
  • 有沒有方法可以處理這件事情呢？
  • 其實可以套線段樹但...對

Constrained Subsequence Sum (leetcode 1425)

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

max⁡n−k≤i<nDPi→\max_{n-k \le i < n} DP_{i} \rightarrow
\max_{n-k \le i < n} DP_{i} \rightarrow

對於 An，要找到前面 k 個中最大 DP 值。

觀察一下？

  1. 要算的東西很像，每次都會多一個值，少一個值。
  2. 多加入一個值的時候，有沒有可以縮減池子的大小？
    • 如果          比             還要大，在算之後的                          會怎樣？
    •             再也不會是答案。因為         活得比             還久，還更大。
    • 在轉移範圍內，只要右邊比左邊大，左邊的值再也不會是答案。
DPi+2DP_{i+2}
DP_{i+2}
DPi−kDP_{i-k}
DP_{i-k}
DPi−k+1DP_{i-k+1}
DP_{i-k+1}
DPi−k+2DP_{i-k+2}
DP_{i-k+2}
DPi−1DP_{i-1}
DP_{i-1}
DPiDP_{i}
DP_{i}
DPi+1DP_{i+1}
DP_{i+1}
DPi+2的轉移範圍DP_{i+2} 的轉移範圍
DP_{i+2} 的轉移範圍
DPi+1的轉移範圍DP_{i+1} 的轉移範圍
DP_{i+1} 的轉移範圍
DPi的轉移範圍DP_{i} 的轉移範圍
DP_{i} 的轉移範圍
DPiDP_{i}
DP_{i}
DPi−1DP_{i-1}
DP_{i-1}
DPi+1DP_{i+1}
DP_{i+1}
DPi+2DP_{i+2}
DP_{i+2}
DPi−1DP_{i-1}
DP_{i-1}
DPiDP_{i}
DP_{i}
DPi−1DP_{i-1}
DP_{i-1}

Constrained Subsequence Sum (leetcode 1425)

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

max⁡n−k≤i<nDPi→\max_{n-k \le i < n} DP_{i} \rightarrow
\max_{n-k \le i < n} DP_{i} \rightarrow

對於 An，要找到前面 k 個中最大 DP 值。

  • 在轉移範圍內，只要右邊比左邊大，左邊的值再也不會是答案。
DPi+2DP_{i+2}
DP_{i+2}
DPi−kDP_{i-k}
DP_{i-k}
DPi−k+1DP_{i-k+1}
DP_{i-k+1}
DPi−k+2DP_{i-k+2}
DP_{i-k+2}
DPi−1DP_{i-1}
DP_{i-1}
DPiDP_{i}
DP_{i}
DPi+1DP_{i+1}
DP_{i+1}
DPi+2的轉移範圍DP_{i+2} 的轉移範圍
DP_{i+2} 的轉移範圍
DPi+1的轉移範圍DP_{i+1} 的轉移範圍
DP_{i+1} 的轉移範圍
DPi的轉移範圍DP_{i} 的轉移範圍
DP_{i} 的轉移範圍
  • 可以處理「轉移範圍」，把所有左邊沒比右邊大的都刪掉。
  • 這也代表「轉移範圍」的所有數字一定是嚴格遞減。

只要想辦法維護單調性，應該就可以很快地轉移！

* 單調性 (monotone)： 一個序列是遞增或遞減。

Constrained Subsequence Sum (leetcode 1425)

  • 這也代表「轉移範圍」的所有數字一定是嚴格遞減。
  1. ​對於         ，他要的答案會在哪裡？
    •  
  2. 之後會把           放進下一次的轉移範圍。怎麼維護單調性？
    • ​​把所有沒比         大的都砍掉。
    • 因為有單調性，從屁股一路刪值，刪到你要的位置。
  3.              在下一次轉移 (做             時) 就會過期，怎麼刪？
    • 檢查第一個值的 a 是不是在 i+1 的範圍內 (a = i-k 就刪掉)
    • 哪個線性資料結構可以刪屁股，加屁股，刪頭呢？

Container

DPa>DPb>DPc>DPd>...DP_a > DP_b > DP_c > DP_d > ...
DP_a > DP_b > DP_c > DP_d > ...
DPi的轉移範圍:上面值的範圍都在DPi−k∼DPi−1DP_{i} 的轉移範圍 : 上面值的範圍都在 DP_{i-k} \sim DP_{i-1}
DP_{i} 的轉移範圍 : 上面值的範圍都在 DP_{i-k} \sim DP_{i-1}
DPi想要的答案DP_{i} 想要的答案
DP_{i} 想要的答案
DPiDP_{i}
DP_{i}
DPiDP_{i}
DP_{i}
DPi−kDP_{i-k}
DP_{i-k}
DPi+1DP_{i+1}
DP_{i+1}
DPa=這個範圍最左邊的數字。DP_{a} = 這個範圍最左邊的數字。
DP_{a} = 這個範圍最左邊的數字。
DPn=DPa+AiDP_{n} = DP_a + A_i
DP_{n} = DP_a + A_i
DPiDP_{i}
DP_{i}
DPiDP_{i}
DP_{i}

?

Deque

Constrained Subsequence Sum (leetcode 1425)

  • 這也代表「轉移範圍」的所有數字一定是嚴格遞減。
  1. 如果 a 指 deque 的頭​，那麼                             。
  2. 加入         前，檢查 deque 的屁股直到屁股 >          。
  3. 如果 a 指 deque 的頭，檢查 a = i-k。如果是就刪掉 a
DPiDP_{i}
DP_{i}
DPi=DPa+AiDP_{i} = DP_a + A_i
DP_{i} = DP_a + A_i
DPiDP_{i}
DP_{i}

註：因為你要檢查 a，所以你放入 deque 時至少要放兩個：DP值 和 索引值

A = [10, -2, -10, -5, 20], k = 2

Deque

A0=10A_0 = 10
A_0 = 10
DP0=0+10=10DP_0 = 0 + 10 = 10
DP_0 = 0 + 10 = 10
A1=−2A_1 = -2
A_1 = -2
DP1=10−2=8DP_1 = 10-2 = 8
DP_1 = 10-2 = 8
A2=−10A_2 = -10
A_2 = -10
DP2=10−10=0DP_2 = 10 - 10 = 0
DP_2 = 10 - 10 = 0
A3=−5A_3 = -5
A_3 = -5
DP3=8−5=3DP_3 = 8 - 5 = 3
DP_3 = 8 - 5 = 3
A4=20A_4 = 20
A_4 = 20
DP4=3+20=23DP_4 = 3 + 20 = 23
DP_4 = 3 + 20 = 23
DP0=10DP_0 \\ = 10
DP_0 \\ = 10
DP1=8DP_1 \\ = 8
DP_1 \\ = 8
DP2=0DP_2 \\ = 0
DP_2 \\ = 0
DP3=3DP_3 \\ = 3
DP_3 \\ = 3
DP4=23DP_4 \\ = 23
DP_4 \\ = 23

過期

過期

刪掉

刪掉

Deque的頭

Constrained Subsequence Sum (leetcode 1425) 

int constrainedSubsetSum(vector<int>& nums, int k) {
  deque<pair<int, int>> Q;
  int ans = nums[0];
  for (int i=0; i<nums.size(); i++) {
    // Step 1: DP_i = max(0, DP_a)+ A_n
    int cur_v = max(0, Q.empty() ? 0 : Q.front().first);
    cur_v += nums[i];
    // Step 2: Remove tail for monotone
    while (!Q.empty() && Q.back().first <= cur_v)
      Q.pop_back();
    Q.push_back({cur_v, i});
    // Step 3: Check range for next transition
    if (Q.front().second == i-k)
      Q.pop_front();
    ans = max(ans, cur_v);
  }
  return ans;
}

C++

def constrainedSubsetSum(self, nums, k):
  ans = nums[0]
  Q = deque()
  for i in range(len(nums)):
    # Step 1: DP_i = max(0, DP_a)+ A_n
    cur_v = max(0, Q[0][0] if Q else 0)
    cur_v += nums[i]
    # Step 2: Remove tail for monotone
    while Q and Q[-1][0] <= cur_v:
      Q.pop()
    # Step 3: Check range for next transition
    Q.append((cur_v, i))
    if Q[0][1] == i - k:
      Q.popleft()
    ans = max(ans, cur_v)
  return ans

Python

給定一個數列，請選出一個子序列，使其總和最大。但選法有條件：你選的數字彼此必須距離 k 以下。

分析看看複雜度吧！

O(N)O(N)
O(N)

狀態數量             × 轉移複雜度          =

O(k)O(k)
O(k)
O(N)O(N)
O(N)
均攤O(1)，因為整輪最多刪n個。均攤 O(1)，\\ 因為整輪最多刪n個。
均攤 O(1)，\\ 因為整輪最多刪n個。

Constrained Subsequence Sum (leetcode 1425)

這種利用 Deque 維護單調性的技巧，叫做

Monotonic Queue

單調對列

而上述的題目是單調對列的其中一個特例，
所要求的 DP 範圍會一直往右移，這類題目叫做：

Sliding Window

滑動視窗

恭喜你學會了最簡單的DP優化，單調對列優化！

什麼時候可以用
單調對列優化呢？

等認真上優化的時候，
會再統整一遍，所以別急。

Constrained Subsequence Sum (leetcode 1425)

等我真的寫到那

最長遞增子序列 - I

Longest Increasing Subsequence (LIS)

Part I - 從 1D1D 開始二分搜優化

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

嚴格遞增: 左邊的數 < 右邊的數

數學來說 ai<aj,∀i<j\text{數學來說 } a_i < a_j, \forall i < j
\text{數學來說 } a_i < a_j, \forall i < j

舉例來說:
如果數列為 [10,9,2,5,3,7,101,18]

則其中一個 LIS 為 2 3 7 18，因此答案為 4。

Longest Increasing Subsequence (LIS)

非嚴格遞增是 左邊的數 ≤ 右邊的數

我們先按照LCS的定義試試看？

好像做不出轉移式？

我們缺乏一個重要的資訊：

之前的 LIS 最後一個數字是多少？

不知道的話就無法接續。但如果這樣...

函式定義：

DPn=A[0,n]的LIS長度DP_n = A_{[0, n]} 的 LIS 長度
DP_n = A_{[0, n]} 的 LIS 長度
DPn=A[0,n]選了An的LIS長度DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度

你至少就有足夠的資訊可以轉移了！

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

DPn=A[0,n]選了An的LIS長度DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

像之前題目一樣，A[n] 的上一步 (上一個數字)在哪？

上一步可以是前面的數字 i，只要這個數字 Ai < An

那麼以 A[n] 為結尾的 LIS 長度 ... = 以A[i] 為結尾的 LIS 長度 + 1

DPnDP_n
DP_n
DPiDP_i
DP_i
+1+1
+1

2, 6, 1, 7, 2

3

A[0, n-1]

A[n]

上一步可以是...

max⁡i\underset{i}{\max}
\underset{i}{\max}

函式定義：

如何拆解：

DPn=max⁡0≤i<n{DPi∣Ai<An}+1DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1
DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1
int dp[2505] = {};
int f(vector<int> &nums, int n) {
    if(dp[n]) 
        return dp[n];
    int now = 0;
    for(int i=0; i<n; i++)
        if(nums[i] < nums[n])
            now = max(now, f(nums, i));
    return dp[n] = now+1;
}
int lengthOfLIS(vector<int>& nums) {
    int ans = 1;
    for (int i=0; i<nums.size(); i++)
        ans = max(ans, f(nums, i));
    return ans;
}

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

函式定義：

如何拆解：

Base Case：

DPn=A[0,n]選了An的LIS長度DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DPn=1,如果目前An最小DP_{n} = 1, 如果目前 A_n 最小
DP_{n} = 1, 如果目前 A_n 最小

C++

dp = {}
def rec(n):
    ans = 0
    if n in dp:
        return dp[n]
    for i in range(n):
        if nums[i] < nums[n]:
            ans = max(ans, rec(i))
    dp[n] = ans + 1
    return dp[n]
return max(rec(i) for i in range(len(nums)))

Python

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

分析看看複雜度吧！

O(N)O(N)
O(N)

狀態數量             × 轉移複雜度            =

O(N)O(N)
O(N)
O(N2)O(N^2)
O(N^2)

狀態應該是不能再壓了，那麼轉移可以更快嗎？

max⁡0≤i<n{DPi∣Ai<An}→\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow
\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow

i 從 0 跑到 n-1。

對於 An，要找到比 An 還要小的數字們中，存的最大數字。

有什麼資料結構可以處理呢？

其實可以套線段樹但...對

DPn=max⁡0≤i<n{DPi∣Ai<An}+1DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1
DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1

函式定義：

如何拆解：

Base Case：

DPn=A[0,n]選了An的LIS長度DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DPn=1,如果目前An最小DP_{n} = 1, 如果目前 A_n 最小
DP_{n} = 1, 如果目前 A_n 最小

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

max⁡0≤i<n{DPi∣Ai<An}→\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow
\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow

對於 An，要找到比 An 還要小的數字們中，存的最大數字。

Container

A0=2,DP0=1A1=6,DP1=2A2=1,DP2=1A3=7,DP3=3A4=2,DP4=2A_0 = 2, DP_0 = 1 \\ A_1 = 6, DP_1 = 2 \\ A_2 = 1, DP_2 = 1 \\ A_3 = 7, DP_3 = 3 \\ A_4 = 2, DP_4 = 2
A_0 = 2, DP_0 = 1 \\ A_1 = 6, DP_1 = 2 \\ A_2 = 1, DP_2 = 1 \\ A_3 = 7, DP_3 = 3 \\ A_4 = 2, DP_4 = 2

範例：A = [2, 6, 1, 7, 2, 3] 

A5=3,DP5=                           A_5 = 3, DP_5 = \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
A_5 = 3, DP_5 = \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,

尋找 & 加入

符合條件

2+1=32+1 = 3
2+1 = 3

最大值

等等，哪裡怪怪的？

根本不用存所有紀錄在Container，
因為有些根本不可能是答案。
因為它們有絕對更優的選項。

例如：A2加入時就可以把A0幹掉例如：A_2 加入時就可以把 A_0 幹掉
例如：A_2 加入時就可以把 A_0 幹掉

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

max⁡0≤i<n{DPi∣Ai<An}→\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow
\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow

對於 An，要找到比 An 還要小的數字們中，存的最大數字。

Container

重頭來一遍：

A0=2A_0 = 2
A_0 = 2
A1=6A_1 = 6
A_1 = 6
A2=1A_2 = 1
A_2 = 1
A3=7A_3 = 7
A_3 = 7
A4=2A_4 = 2
A_4 = 2
A5=3A_5 = 3
A_5 = 3
A0=2,DP0=1A_0 = 2, DP_0 = 1
A_0 = 2, DP_0 = 1
A1=6,DP1=2A_1 = 6, DP_1 = 2
A_1 = 6, DP_1 = 2

因為 1 比 2 小但 DP 卻一樣。

A2=1,DP2=1A_2 = 1, DP_2 = 1
A_2 = 1, DP_2 = 1
A3=7,DP3=3A_3 = 7, DP_3 = 3
A_3 = 7, DP_3 = 3
A4=2,DP4=2A_4 = 2, DP_4 = 2
A_4 = 2, DP_4 = 2
A5=3,DP5=3A_5 = 3, DP_5 = 3
A_5 = 3, DP_5 = 3

因為 2 比 6 小但 DP 卻一樣。

範例：A = [2, 6, 1, 7, 2, 3] 

因為 3 比 7 小但 DP 卻一樣。

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

max⁡0≤i<n{DPi∣Ai<An}→\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow
\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow

對於 An，要找到比 An 還要小的數字們中，存的最大數字。

想一下：

Container 內的數字：數值越大，DP值越大。

(具有單調性 / 單調嚴格遞增)

Container

Aa<Ab<Ac<Ad<...A_a < A_b < A_c < A_d < ...
A_a < A_b < A_c < A_d < ...
如果Ac<An≤Ad→DPn=DPc+1如果 A_c < A_n \le A_d \rightarrow DP_n = DP_c + 1
如果 A_c < A_n \le A_d \rightarrow DP_n = DP_c + 1
並且An一定可以取代Ad的位置並且 A_n 一定可以取代 A_d 的位置
並且 A_n 一定可以取代 A_d 的位置
用map的lb搜An的Ac在哪，並取代Ad用 map 的 lb 搜 A_n 的 A_c 在哪，並取代A_d
用 map 的 lb 搜 A_n 的 A_c 在哪，並取代A_d

Container

A0=2,DP0=1A_0 = 2, DP_0 = 1
A_0 = 2, DP_0 = 1
A1=6,DP1=2A_1 = 6, DP_1 = 2
A_1 = 6, DP_1 = 2
A2=1,DP2=1A_2 = 1, DP_2 = 1
A_2 = 1, DP_2 = 1
A3=7,DP3=3A_3 = 7, DP_3 = 3
A_3 = 7, DP_3 = 3
A4=2,DP4=2A_4 = 2, DP_4 = 2
A_4 = 2, DP_4 = 2
A5=3,DP5=3A_5 = 3, DP_5 = 3
A_5 = 3, DP_5 = 3

範例：A = [2, 6, 1, 7, 2, 3] 

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

max⁡0≤i<n{DPi∣Ai<An}→\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow
\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow

對於 An，要找到比 An 還要小的數字們中，存的最大數字。

再重新想一下：

Container

Aa<Ab<Ac<...A_a < A_b < A_c < ...
A_a < A_b < A_c < ...
DP=DP=
DP=
11
1
22
2
33
3
......
...
A0=2A_0 = 2
A_0 = 2
A1=6A_1 = 6
A_1 = 6
A2=1A_2 = 1
A_2 = 1
A3=7A_3 = 7
A_3 = 7
A4=2A_4 = 2
A_4 = 2
A5=3A_5 = 3
A_5 = 3
A0=2A_0 = 2
A_0 = 2
A1=6A_1 = 6
A_1 = 6
A2=1A_2 = 1
A_2 = 1
A3=7A_3 = 7
A_3 = 7
A4=2A_4 = 2
A_4 = 2
A5=3A_5 = 3
A_5 = 3
找到修改位置Aa找到修改位置 A_a
找到修改位置 A_a
找到修改位置Ab找到修改位置 A_b
找到修改位置 A_b
找到修改位置Aa找到修改位置 A_a
找到修改位置 A_a
找到修改位置Ac找到修改位置A_c
找到修改位置A_c
找到修改位置Ab找到修改位置 A_b
找到修改位置 A_b
找到修改位置Ac找到修改位置 A_c
找到修改位置 A_c

lower_bound 查找

範例：A = [2, 6, 1, 7, 2, 3] 

int lengthOfLIS(vector<int>& nums) {
    map<int, int> M;
    M[INT_MIN] = 0;
    int ans = 0;
    for (auto num : nums) {
        auto it = M.lower_bound(num);
        int v = 1 + prev(it)->second;
        ans = max(ans, v);
        if (it != M.end())
            M.erase(it);
        M[num] = v;
    }
    return ans;
}

C++

from sortedcontainers import SortedDict

def lengthOfLIS(self, nums: List[int]) -> int:
    d = SortedDict({-inf: 0})
    for num in nums:
        idx = d.bisect_left(num)
        if idx != len(d):
            del d.iloc[idx]
        d[num] = d[d.iloc[idx-1]] + 1
    return max(d.values())

Python

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

註: Sorted系列不是內建函式庫，
所以比賽/檢定 "應該是" 不支援。

怎麼辦？你可能要換寫法或自己建平衡樹 ;(

DPn=max⁡0≤i<n{DPi∣Ai<An}+1DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1
DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1

函式定義：

如何拆解：

Base Case：

DPn=A[0,n]選了An的LIS長度DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DPn=1,如果目前An最小DP_{n} = 1, 如果目前 A_n 最小
DP_{n} = 1, 如果目前 A_n 最小

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

分析看看複雜度吧！

O(N)O(N)
O(N)

狀態數量             × 轉移複雜度                    =     

O(log⁡N)O(\log N)
O(\log N)
O(Nlog⁡N)O(N \log N)
O(N \log N)

好耶！ 把一個 N 壓成 log！

這裡你就看到 Bottom-up 的優點：

可以進行 Top-down 做不到的轉移優化

DPn=max⁡0≤i<n{DPi∣Ai<An}+1DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1
DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1

函式定義：

如何拆解：

Base Case：

DPn=A[0,n]選了An的LIS長度DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DPn=1,如果目前An最小DP_{n} = 1, 如果目前 A_n 最小
DP_{n} = 1, 如果目前 A_n 最小

最長遞增子序列 - II

Longest Increasing Subsequence (LIS)

Part II - 從 2D0D 開始二分搜優化

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

max⁡0≤i<n{DPi∣Ai<An}→\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow
\max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} \rightarrow

對於 An，要找到比 An 還要小的數字們中，存的最大數字。

Container

Aa<Ab<Ac<...A_a < A_b < A_c < ...
A_a < A_b < A_c < ...
DP=DP=
DP=
11
1
22
2
33
3
......
...
A0=2A_0 = 2
A_0 = 2
A1=6A_1 = 6
A_1 = 6
A2=1A_2 = 1
A_2 = 1
A3=7A_3 = 7
A_3 = 7
A4=2A_4 = 2
A_4 = 2
A5=3A_5 = 3
A_5 = 3

範例：A = [2, 6, 1, 7, 2, 3] 

有什麼必要一定要 map / SortedDict 存嗎？

這個 value 不就把它當成
是 vector / list 的 index
不就好了嗎？

那麼原本在 map / SortedDict 的 lower_bound，
現在就在 vector / list 上
做 lower_bound 就好了！

這樣就不用開複雜資料結構了！

最長遞增子序列 (leetcode 300)

int lengthOfLIS(vector<int>& nums) {
  map<int, int> M;
  M[INT_MIN] = 0;
  int ans = 0;
  for (auto num : nums) {
    auto it = M.lower_bound(num);
    int v = 1 + prev(it)->second;
    ans = max(ans, v);
    if (it != M.end())
      M.erase(it);
    M[num] = v;
  }
  return ans;
}

C++ / map + lb

def lengthOfLIS(self, nums):
  d = SortedDict({-math.inf: 0})
  for num in nums:
    idx = d.bisect_left(num)
    if idx != len(d):
      del d.iloc[idx]
    d[num] = d[d.iloc[idx-1]] + 1
  return max(d.values())

Python / SortedDict + lb

int lengthOfLIS(vector<int>& nums) {
  vector<int> DP;
  DP.push_back(INT_MIN);
  int ans = 0;
  for (auto num : nums) {
    auto it = lower_bound(DP.begin(), DP.end(), num);
    int v = prev(it) - DP.begin() + 1;
    ans = max(ans, v);
    if (it == DP.end())
      DP.push_back(num);
    else
      DP[v] = num;
  }
  return ans;
}

C++ / vector + lb

def lengthOfLIS(self, nums):
  DP = [-math.inf]
  for num in nums:
    idx = bisect_left(DP, num)
    if idx == len(DP):
      DP.append(num)
    else:
      DP[idx] = num
  return len(DP) - 1

Python / list + lb

其實 it - DP.begin() 就好。

DPn=max⁡0≤i<n{DPi∣Ai<An}+1DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1
DP_{n} = \max_{0 \le i < n} \{DP_{i} | A_{i} < A_{n}\} + 1

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

DPn=A[0,n]選了An的LIS長度DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DP_n = A_{[0, n]} 選了 A_n 的 LIS 長度
DPn=1,如果目前An最大DP_{n} = 1, 如果目前 A_n 最大
DP_{n} = 1, 如果目前 A_n 最大

這推導鏈有點太長了...

不是說有好的狀態就有好的轉移嗎？

有沒有其他狀態呢？

我們試試看：

DPn,i=A[0,n]中，長度為i的LIS的最後一個數字的最小數值DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS 的最後一個數字的最小數值
DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS 的最後一個數字的最小數值

這種狀態定義很怪，

但其實很常出現。

只能夠熟記這類題型了。

函式定義：

如何拆解：
 

Base Case：

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

函式定義：

 

如何拆解：

DPn,i=A[0,n]中，長度為i的LIS的最後一個數字的最小數值DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值
DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值
DPn,i=min⁡{DPn−1,iAn if DPn−1,i−1<AnDP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}
DP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}

舉例來說，如果 A = [2, 6, 1, 7, 2, 3] 

DP3,1=1,DP3,2=6,DP3,3=7DP4,1=1,DP4,2=2,DP4,3=7DP5,1=1,DP5,2=2,DP5,3=3DP_{3, 1} = 1, DP_{3, 2} = 6, DP_{3, 3} = 7 \\ DP_{4, 1} = 1, DP_{4, 2} = 2, DP_{4, 3} = 7 \\ DP_{5, 1} = 1, DP_{5, 2} = 2, DP_{5, 3} = 3
DP_{3, 1} = 1, DP_{3, 2} = 6, DP_{3, 3} = 7 \\ DP_{4, 1} = 1, DP_{4, 2} = 2, DP_{4, 3} = 7 \\ DP_{5, 1} = 1, DP_{5, 2} = 2, DP_{5, 3} = 3

轉移呢？考量取 An 或不取 An

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

函式定義：

 

如何拆解：

DPn,i=min⁡{DPn−1,iAn if DPn−1,i−1<AnDP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}
DP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}
int lengthOfLIS(vector<int>& nums) {
  vector<int> DP(nums.size()+1, INT_MAX);
  DP[0] = INT_MIN;
  int ans = 0;
  for (auto num : nums) {
    for (int i = nums.size(); i >= 1; i--) {
      if (DP[i - 1] < num) {
        DP[i] = min(DP[i], num);
        ans = max(ans, i);
      }
    }
  }
  return ans;
}
def lengthOfLIS(self, nums):
  DP = [-math.inf] + [math.inf] * len(nums)
  ans = 0
  for num in nums:
    for i in range(len(nums), 0, -1):
      if DP[i-1] < num:
        DP[i] = min(DP[i], num)
        ans = max(ans, i)
  return ans

C++

Python

這裡我先用滾動壓成一維了。

DPn,i=A[0,n]中，長度為i的LIS的最後一個數字的最小數值DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值
DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

函式定義：

 

如何拆解：

DPn,i=min⁡{DPn−1,iAn if DPn−1,i−1<AnDP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}
DP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}

分析看看複雜度吧！

O(N2)O(N^2)
O(N^2)

狀態數量               × 轉移複雜度             =     

O(1)O(1)
O(1)
O(N2)O(N^2)
O(N^2)

你在逗我？不是一樣是 N^2？

我們來觀察一下...

DPn,i=A[0,n]中，長度為i的LIS的最後一個數字的最小數值DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值
DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值
輸入:
10
1 7 1 5 3 10 4 2 6 8
===========================
DP表格:
    1
    1    7
    1    7
    1    5
    1    3
    1    3   10
    1    3    4
    1    2    4
    1    2    4    6
    1    2    4    6    8

DP 表格一定會是嚴格遞增序列。

你一定最多只會改變其中一個數字。 (因為如果你改兩個就一定不會是嚴格遞增。)

那一個數字在哪裡？用 lb 去找。

最長遞增子序列 (leetcode 300)

給定一個陣列，問最長的嚴格遞增子序列長度為何？

Longest Increasing Subsequence (LIS)

函式定義：

 

如何拆解：

DPn,i=min⁡{DPn−1,iAn if DPn−1,i−1<AnDP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}
DP_{n, i} = \min \begin{cases} DP_{n-1, i} \\ A_{n} \text{ if } DP_{n-1, i-1} < A_{n} \end{cases}

我們來觀察一下...

DPn,i=A[0,n]中，長度為i的LIS的最後一個數字的最小數值DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值
DP_{n, i} = A_{[0, n]} 中，長度為 i 的 LIS \\的最後一個數字的最小數值

最長遞增子序列 (leetcode 300)

int lengthOfLIS(vector<int>& nums) {
  vector<int> DP(nums.size()+1, INT_MAX);
  DP[0] = INT_MIN;
  int ans = 0;
  for (auto num : nums) {
    for (int i = nums.size(); i >= 1; i--) {
      if (DP[i - 1] < num) {
        DP[i] = min(DP[i], num);
        ans = max(ans, i);
      }
    }
  }
  return ans;
}

C++ / 2D0D + 滾動

def lengthOfLIS(self, nums):
  DP = [-math.inf] + [math.inf] * len(nums)
  ans = 0
  for num in nums:
    for i in range(len(nums), 0, -1):
      if DP[i-1] < num:
        DP[i] = min(DP[i], num)
        ans = max(ans, i)
  return ans

Python / 2D0D + 滾動

int lengthOfLIS(vector<int>& nums) {
  vector<int> DP(nums.size()+1, INT_MAX);
  DP[0] = INT_MIN;
  int ans = 0;
  for (auto num : nums) {
    auto it = lower_bound(DP.begin(), DP.end(), num);
    int i = it - DP.begin();
    DP[i] = num;
    ans = max(ans, i);
  }
  return ans;
}

C++ / 2D0D + 滾動 + lb

def lengthOfLIS(self, nums):
  DP = [-math.inf] + [math.inf] * len(nums)
  ans = 0
  for num in nums:
    idx = bisect_left(DP, num)
    DP[idx] = num
    ans = max(ans, idx)
  return ans

Python / 2D0D + 滾動 + lb

很有趣的是，你會得到跟原本的推法接近一樣Code

  1. 求出其中一個 LIS 該怎麼寫？
  2. 求出LIS的個數。(leetcode 683)
  3. LCS 其實可以使用 LIS 來實作，想想看怎麼寫。
    • Hint: 如果所有字元不重複，複雜度是 O(NlogN)
    • 如果字元會重複，複雜度最差會退化到 O(N^2logN)
  4. 給定一堆二維點，請找出一個順序 (可自行選點 + 排列) 使得這些二維點不管是 x 還是  y 都非嚴格遞增。問這樣的順序最長多少。飛黃騰達 (APCS 2021 / 01 - 4, zj j608)

練習題！

區間選擇類 DP

區間選擇類 DP

這類型的題目通常：

  1. 都會給你一個數列。
  2. 你需要選擇不相交的數個子區間 / 子數列 
  3. 接著計算最佳解。

(interval / subarray)

因此這類題型的轉移通常都是 O(n) 找分割點

或者想辦法把分割點內化成狀態後 O(1) 轉移。

區間選擇類 DP

先一個小提醒：
所以你會發現序列有關的 DP，
常見的狀態定義就那幾種

  • 前 n 個數字中，考慮選了 A_n 的最佳解。
  • 前 n 個數字中的最佳解。
    • 基本上就是第一條，但多考慮不選 A_n
      (所以通常還會有一項是 DP_(n-1))
  • 前 n 個數字中，選了 k 個最佳狀態

那怎麼判斷用什麼會比較好寫？
直觀感受...

最大子區間和

最大子區間和 (leetcode 53)

Kadane's Algorithm

給定一個數列 A，請輸出子區間和最大為多少。

 

 

最大子區間和 (leetcode 53)

這不是 Greedy 講過嗎？

max⁡l,r∑i=lrAi\max_{l, r} \sum_{i=l}^{r} A_i
\max_{l, r} \sum_{i=l}^{r} A_i
A={1,−3,4,−1,2,1,−5,4}A = \{1,-3,4,-1,2,1,-5,4 \} % 0 1 2 3 4 5 6 7 % 1 -3 4 -1 2 1 -5 4 % % \begin{cases} A[0, 0] = 1 & = 1 \\ A[0, 2] = 1-3+4 & = 2 \\ A[0, 5] = 1-3+4-1+2+1 & = 4 \\ A[0, 7] = 1-3+4-1+2+1-5+4 &= 3 \\ A[2, 2] = 4 & = 4 \\ A[2, 5] = 4-1+2+1 &= 6 \\ A[2, 7] = 4-1+2+1-5+4 &= 5 \\ A[4, 5] = 2 + 1 &= 3 \\ A[4, 7] = 2 + 1 - 5 + 4 &= 2 \\ A[7, 7] = 4 &= 4 \\ \end{cases}
A = \{1,-3,4,-1,2,1,-5,4 \} % 0 1 2 3 4 5 6 7 % 1 -3 4 -1 2 1 -5 4 % % \begin{cases} A[0, 0] = 1 & = 1 \\ A[0, 2] = 1-3+4 & = 2 \\ A[0, 5] = 1-3+4-1+2+1 & = 4 \\ A[0, 7] = 1-3+4-1+2+1-5+4 &= 3 \\ A[2, 2] = 4 & = 4 \\ A[2, 5] = 4-1+2+1 &= 6 \\ A[2, 7] = 4-1+2+1-5+4 &= 5 \\ A[4, 5] = 2 + 1 &= 3 \\ A[4, 7] = 2 + 1 - 5 + 4 &= 2 \\ A[7, 7] = 4 &= 4 \\ \end{cases}

舉例來說：

我們來從 DP 的角度來思考！

給定一個數列 A，請輸出子區間和最大為多少。

 

 

最大子區間和 (leetcode 53)

max⁡l,r∑i=lrAi\max_{l, r} \sum_{i=l}^{r} A_i
\max_{l, r} \sum_{i=l}^{r} A_i
DPn=A[0,n]選了An的最大子區間和DP_n = A_{[0, n]} 選了 A_n 的最大子區間和
DP_n = A_{[0, n]} 選了 A_n 的最大子區間和
  1. 函式定義：
  2. 如何拆解：
A0A_0
A_0
A1A_1
A_1
A2A_2
A_2
An−2A_{n-2}
A_{n-2}
An−1A_{n-1}
A_{n-1}
AnA_n
A_n
......
...
An−3A_{n-3}
A_{n-3}

你應該能夠知道怎麼定義了！

✅

一定
要選

...

你有好多的選擇！最佳解怎麼算？

好像都跟 A_{n-1} 有關 ...？

給定一個數列 A，請輸出子區間和最大為多少。

 

 

最大子區間和 (leetcode 53)

max⁡l,r∑i=lrAi\max_{l, r} \sum_{i=l}^{r} A_i
\max_{l, r} \sum_{i=l}^{r} A_i
DPn=A[0,n]選了An的最大子區間和DP_n = A_{[0, n]} 選了 A_n 的最大子區間和
DP_n = A_{[0, n]} 選了 A_n 的最大子區間和
  1. 函式定義：
  2. 如何拆解：
DPn=           max⁡{AnAn+An−1An+An−1+An−2...An+An−1+An−2+...+A0DP_n = ~~~~~~~~~~~\max \begin{cases} A_n \\ A_n + A_{n-1} \\ A_n + A_{n-1} + A_{n-2}\\ ... \\ A_n + A_{n-1} + A_{n-2} + ... + A_0 \end{cases}
DP_n = ~~~~~~~~~~~\max \begin{cases} A_n \\ A_n + A_{n-1} \\ A_n + A_{n-1} + A_{n-2}\\ ... \\ A_n + A_{n-1} + A_{n-2} + ... + A_0 \end{cases}
An+A_n +
A_n +
00
0
DPn−1DP_{n-1}
DP_{n-1}
DPn=max⁡(DPn−1,0)+AnDP_n = \max (DP_{n-1}, 0) + A_n
DP_n = \max (DP_{n-1}, 0) + A_n

給定一個數列 A，請輸出子區間和最大為多少。

 

 

最大子區間和 (leetcode 53)

max⁡l,r∑i=lrAi\max_{l, r} \sum_{i=l}^{r} A_i
\max_{l, r} \sum_{i=l}^{r} A_i
DPn=A[0,n]選了An的最大子區間和DP_n = A_{[0, n]} 選了 A_n 的最大子區間和
DP_n = A_{[0, n]} 選了 A_n 的最大子區間和
  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPn=max⁡(DPn−1,0)+AnDP_n = \max (DP_{n-1}, 0) + A_n
DP_n = \max (DP_{n-1}, 0) + A_n
DP0=A0 OR DP−1=0DP_0 = A_0 \text { OR } DP_{-1} = 0
DP_0 = A_0 \text { OR } DP_{-1} = 0
int maxSubArray(vector<int>& nums) {
    int cur_DP = 0, ans = nums[0];
    for (auto num : nums) {
        cur_DP = max(cur_DP, 0) + num;
        ans = max(ans, cur_DP);
    }
    return ans;
}
def maxSubArray(self, nums):
    cur_DP, ans = 0, nums[0]
    for num in nums:
        cur_DP = max(cur_DP, 0) + num
        ans = max(ans, cur_DP)
    return ans

C++

Python

是不是覺得太簡單了？我們來加點難度 :)

這個演算法就叫做 Kadane's Algorithm

美食博覽會

美食博覽會(APCS 2021/9 - P4, zj g278)

美食博覽會 (APCS 2021/9 - P4, zj g278)

舉例來說：

A = [1, 2, 1, 3, 1], k = 1

答案為 3

A = [1, 7, 1, 3, 1, 4, 4, 2, 7, 4], k = 3

答案為 8

給定一個序列以及整數 k。
請找出如何選出 k 個不重疊區間，且各個區間內無重複數字，使選到的數字最多。

只要完成 k = 1 就可以五級分了！

先想想看 k = 1 怎麼做吧！

美食博覽會 (APCS 2021/9 - P4, zj g278)

給定一個序列以及整數 k = 1。
請找出如何選出 k 個不重疊區間，且各個區間內無重複數字，使選到的數字最多。

  1. 函式定義：
     
  2. 如何拆解：
DPn′=前n天，選了第n天時的最多選法DP'_n = 前 n 天，選了第 n 天時的最多選法
DP'_n = 前 n 天，選了第 n 天時的最多選法

k=1 也可以雙指針
(爬行法) 解掉

好像有點麻煩 ...

如果選了第 n 天，那麼選的區間最遠只能到哪？

✅

一定選A_n

A0A_0
A_0
A1A_1
A_1
An−2A_{n-2}
A_{n-2}
An−1A_{n-1}
A_{n-1}
AnA_n
A_n
......
...
An−3A_{n-3}
A_{n-3}
......
...
Ax=AnA_{x} \\ = A_n
A_{x} \\ = A_n

上次 A_n 這個數字出現的位置

DPn′=min⁡{n−(上次An出現的位置)DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ \\ \end{cases}
DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ \\ \end{cases}

美食博覽會 (APCS 2021/9 - P4, zj g278)

給定一個序列以及整數 k = 1。
請找出如何選出 k 個不重疊區間，且各個區間內無重複數字，使選到的數字最多。

  1. 函式定義：
     
  2. 如何拆解：
DPn′=前n天，選了第n天時的最多選法DP'_n = 前 n 天，選了第 n 天時的最多選法
DP'_n = 前 n 天，選了第 n 天時的最多選法

k=1 也可以雙指針
(爬行法) 解掉

DPn′=min⁡{n−(上次An出現的位置)DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ \\ \end{cases}
DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ \\ \end{cases}

這樣考慮不夠完全？
萬一出現 (4, 2, 2, 4) 的 Case ？

DPn−1′+1DP'_{n-1} + 1
DP'_{n-1} + 1

我們還要考慮 n-1，n-2 等等... 怎麼辦？

不怎麼辦，因為考慮這些的數字已經出現了。

DPn−1′=前n−1天，選了第n−1天時的最多選法DP'_{n-1} = 前 n-1 天，選了第 n-1 天時的最多選法
DP'_{n-1} = 前 n-1 天，選了第 n-1 天時的最多選法

美食博覽會 (APCS 2021/9 - P4, zj g278)

給定一個序列以及整數 k = 1。
請找出如何選出 k 個不重疊區間，且各個區間內無重複數字，使選到的數字最多。

  1. 函式定義：
     
  2. 如何拆解：
DPn′=前n天，選了第n天時的最多選法DP'_n = 前 n 天，選了第 n 天時的最多選法
DP'_n = 前 n 天，選了第 n 天時的最多選法

k=1 也可以雙指針
(爬行法) 解掉

DPn′=min⁡{n−(上次An出現的位置)DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ \\ \end{cases}
DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ \\ \end{cases}
DPn−1′+1DP'_{n-1} + 1
DP'_{n-1} + 1
int n, k, x;
scanf("%d%d", &n, &k);
int DP0 = 0, ans = 0;
for (int i=1; i<=n; i++) {
    scanf("%d", &x);
    DP0 = min(DP0+1, i-last[x]);
    last[x] = i;
    ans = max(ans, DP0);
}
printf("%d\n", ans);

from collections import defaultdict
n, k = map(int, input().split())
A = list(map(int, input().split()))
last = defaultdict(lambda:-1)
ans, DP0 = 0, 0
for i, x in enumerate(A):
    DP0 = min(DP0+1, i-last[x])
    last[x] = i
    ans = max(ans, DP0)
print(ans)

C++

Python

美食博覽會 (APCS 2021/9 - P4, zj g278)

DPn=前n天，選了第n天時的最多選法DP_n = 前 n 天，選了第 n 天時的最多選法
DP_n = 前 n 天，選了第 n 天時的最多選法

嘗試看看裸定義？

你沒有「現在選了幾次區間」的資訊。
這導致轉移不了 (或很難轉移)。

DPn,k=前n天已選k區間的最多選法DP_{n,k} = 前n天已選k區間的最多選法
DP_{n,k} = 前n天已選k區間的最多選法
  1. 函式定義：

     
  2. 如何拆解：

給定一個序列以及整數 k。
請找出如何選出 k個不重疊區間，且各個區間內無重複數字，使選到的數字最多。

  • 這裡是沒有選第n天的

考量要不要選第 n 天，如果不考慮呢？

DPn,k=max⁡{DPn−1,kDP_{n, k} = \max \begin{cases} DP_{n-1, k} \\ \\ \end{cases}
DP_{n, k} = \max \begin{cases} DP_{n-1, k} \\ \\ \end{cases}

如果考慮呢？

美食博覽會 (APCS 2021/9 - P4, zj g278)

DPn,k=前n天已選k區間的最多選法DP_{n,k} = 前n天已選k區間的最多選法
DP_{n,k} = 前n天已選k區間的最多選法
  1. 函式定義：

     
  2. 如何拆解：

給定一個序列以及整數 k。
請找出如何選出 k個不重疊區間，且各個區間內無重複數字，使選到的數字最多。

DPn,k=max⁡{DPn−1,kDP_{n, k} = \max \begin{cases} DP_{n-1, k} \\ \\ \end{cases}
DP_{n, k} = \max \begin{cases} DP_{n-1, k} \\ \\ \end{cases}

考慮 A_n

不考慮 A_n

✅

一定選A_n

A0A_0
A_0
A1A_1
A_1
An−2A_{n-2}
A_{n-2}
An−1A_{n-1}
A_{n-1}
AnA_n
A_n
An−3A_{n-3}
A_{n-3}
......
...
A2A_2
A_2

最遠可以選 DP'n 個數字

An−DPn′A_{n - DP'_n}
A_{n - DP'_n}
DPn′=前n天，選了第n天時的最多選法DP'_n = 前 n 天，選了第 n 天時的最多選法
DP'_n = 前 n 天，選了第 n 天時的最多選法
  • 如果花了一個區間選了 A_n，那麼剩下 k-1 個選擇
  • 前 A_{n-DPn'} 天，選了k-1 區間的最多選法是 ...？
DPn−DPn′,k−1+DPn′DP_{n - DP'_n, k-1} + DP'_n
DP_{n - DP'_n, k-1} + DP'_n

最遠可以到哪裡？

美食博覽會 (APCS 2021/9 - P4, zj g278)

DPn,k=前n天已選k區間的最多選法DP_{n,k} = 前n天已選k區間的最多選法
DP_{n,k} = 前n天已選k區間的最多選法
DPn,k=max⁡{DPn−1,kDPn−DPn′,k−1+DPn′DP_{n, k} = \max \begin{cases} DP_{n-1, k} \\ DP_{n - DP'_n, k-1} + DP'_n\\ \end{cases}
DP_{n, k} = \max \begin{cases} DP_{n-1, k} \\ DP_{n - DP'_n, k-1} + DP'_n\\ \end{cases}
DPn′=前n天，選了第n天時的最多選法DP'_n = 前 n 天，選了第 n 天時的最多選法
DP'_n = 前 n 天，選了第 n 天時的最多選法
DPn′=min⁡{n−(上次An出現的位置)DPn−1′+1DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ DP'_{n-1} + 1\\ \end{cases}
DP'_n = \min \begin{cases} n - (上次 A_n 出現的位置)\\ DP'_{n-1} + 1\\ \end{cases}
int n, k, x, ans = 0;
scanf("%d%d", &n, &k);
int DP0 = 0;
for (int i=1; i<=n; i++) {
  scanf("%d", &x);
  DP0 = min(DP0+1, i-last[x]);
  last[x] = i;
  for (int cur_k=1; cur_k<=k; cur_k++) {
    DP[i][cur_k] = max(
      DP[i-1][cur_k], 
      DP[i-DP0][cur_k-1] + DP0);
    ans = max(ans, DP[i][k]);
  }
}
printf("%d\n", ans);
from collections import defaultdict
n, k = map(int, input().split())
A = list(map(int, input().split()))
last = defaultdict(lambda:-1)
ans, DP0 = 0, 0
DP = [[0] * (k+1) for _ in range(n)]
for cur_n, x in enumerate(A):
    DP0 = min(DP0+1, cur_n-last[x])
    last[x] = cur_n
    for cur_k in range(1, k+1):
        DP[cur_n][cur_k] = max(
            DP[cur_n-1][cur_k],
            DP[cur_n-DP0][cur_k-1] + DP0
        )
        ans = max(ans, DP[cur_n][cur_k])
print(ans)

C++

Python

主要多了這些

Python 會 TLE，但就別管了，複雜度是好的

美食博覽會 (APCS 2021/9 - P4, zj g278)

給定一個序列以及整數 k。
請找出如何選出 k個不重疊區間，且各個區間內無重複數字，使選到的數字最多。

分析看看複雜度吧！

O(nk)O(nk)
O(nk)

狀態數量              × 轉移複雜度           =     

O(1)O(1)
O(1)
O(nk)O(nk)
O(nk)
  • 這題其實也有偏向貪心的作法。
    • 做 k = 1 的 Case 可以用雙指針 / 爬行法做完。
      • 當然你要像剛剛的 DP 解也可以。
    • 把第一個區間選的數字移除，再找一次當前最長區間
    • 找完 k 個就結束了。

股票買賣 - IV - I

Best Time to Buy and Sell IV (leetcode 188)

AI-666 賺多少 (2017 學科全國賽 - P6, tioj 2039)

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

舉例來說：

(4 - 1) = 3

Prices = [1,3,2,4]

k = 1

[1,3,2,4]

(3 - 1) + (4 - 2) = 4

k = 2

[1,3,2,4]

你會想怎麼定義呢？

  • 在這裡你可以先想想看 k = 1 怎麼寫

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

DPn=在第n天時的最高利潤DP_n = 在第 n 天時的最高利潤
DP_n = 在第 n 天時的最高利潤

嘗試看看裸定義？

你沒有「現在買了多少次股票」的資訊。
這導致轉移不了 (或很難轉移)。

DPn,k=在第n天時，交易k次的最高利潤DP_{n,k} = 在第 n 天時，交易k次的最高利潤
DP_{n,k} = 在第 n 天時，交易k次的最高利潤
  1. 函式定義：
     
  2. 如何拆解：

如何拆解？ 想想看之前題目怎麼拆解的？

考慮要不要看第 n 天 (也就是考慮要不要在第 n 天賣)

* 如果你定義 DPn, k 在第n天一定要賣，轉移會很麻煩。

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

DPn,k=在第n天時，交易k次的最高利潤DP_{n,k} = 在第 n 天時，交易k次的最高利潤
DP_{n,k} = 在第 n 天時，交易k次的最高利潤
  1. 函式定義：
     
  2. 如何拆解：
DPn,k=max⁡{                                                                   不考慮考慮DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DPn−1,kDP_{n-1, k}
DP_{n-1, k}

考慮好像有點麻煩...

✅

一定在A_n賣

A0A_0
A_0
A1A_1
A_1
A2A_2
A_2
An−2A_{n-2}
A_{n-2}
An−1A_{n-1}
A_{n-1}
AnA_n
A_n
......
...
An−3A_{n-3}
A_{n-3}

❓

不知道什麼時候買？

→枚舉

考慮要不要看第 n 天 (也就是考慮要不要在第 n 天賣)

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

DPn,k=在第n天時，交易k次的最高利潤DP_{n,k} = 在第 n 天時，交易k次的最高利潤
DP_{n,k} = 在第 n 天時，交易k次的最高利潤
  1. 函式定義：
     
  2. 如何拆解：
DPn,k=max⁡{                                                                   不考慮考慮DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DPn−1,kDP_{n-1, k}
DP_{n-1, k}
max⁡i=0n−1(DPi,k−1+An−Ai)\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)
\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)

✅

一定在A_n賣

A0A_0
A_0
A1A_1
A_1
A2A_2
A_2
An−2A_{n-2}
A_{n-2}
An−1A_{n-1}
A_{n-1}
AnA_n
A_n
......
...
An−3A_{n-3}
A_{n-3}

第 i 天買，第 n 天賣的利潤：

An−AiA_n - A_i
A_n - A_i

DP_n, k 表示已經做了 k 次交易，

所以第 i 天的時候最多只能進行 k-1 次交易

在第 i 天時，交易 k-1 次的最高利潤：

DPi,k−1DP_{i, k-1}
DP_{i, k-1}
++
+

❓枚舉：

Best Time to Buy and Sell IV (leetcode 188)

DPn,k=max⁡{                                                                   不考慮考慮DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DPn−1,kDP_{n-1, k}
DP_{n-1, k}
max⁡i=0n−1(DPi,k−1+An−Ai)\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)
\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)
int maxProfit(int k, vector<int>& prices) {
  int n = prices.size();
  vector<vector<int>> DP(n, vector<int> (k+1));
  for (int cur_k=1; cur_k<=k; cur_k++) {
    for (int cur_n=1; cur_n<n; cur_n++) {
      int cur_v = DP[cur_n-1][cur_k];
      for (int i=0; i<cur_n; i++) {
        cur_v = max(cur_v, DP[i][cur_k-1] + prices[cur_n] - prices[i]);
      }
      DP[cur_n][cur_k] = cur_v;
    }
  }
  return DP.back().back();
}
def maxProfit(self, k, prices):
  DP = [[0] * (k+1) for _ in range(len(prices))]
  for cur_k in range(1, k+1):
    for cur_n in range(1, len(prices)):
      cur_v = DP[cur_n-1][cur_k]
      for i in range(cur_n):
        cur_v = max(cur_v, DP[i][cur_k-1] + prices[cur_n] - prices[i])
      DP[cur_n][cur_k] = cur_v
  return DP[-1][-1]

C++

Python

(Python 會 TLE)

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

DPn,k=在第n天時，交易k次的最高利潤DP_{n,k} = 在第 n 天時，交易k次的最高利潤
DP_{n,k} = 在第 n 天時，交易k次的最高利潤
  1. 函式定義：
     
  2. 如何拆解：
DPn,k=max⁡{                                                                   不考慮考慮DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DPn−1,kDP_{n-1, k}
DP_{n-1, k}
max⁡i=0n−1(DPi,k−1+An−Ai)\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)
\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)

分析看看複雜度吧！

O(nk)O(nk)
O(nk)

狀態數量               × 轉移複雜度             =     

O(n)O(n)
O(n)
O(n2k)O(n^2 k)
O(n^2 k)

轉移有辦法在更快嗎？

Best Time to Buy and Sell IV (leetcode 188)

DPn,k=max⁡{                                                                   不考慮考慮DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DPn−1,kDP_{n-1, k}
DP_{n-1, k}
max⁡i=0n−1(DPi,k−1+An−Ai)\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)
\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i)

我們先處理一下轉移式，你會發現 A_n 在這裡是常數。

max⁡i=0n−1(DPi,k−1+An−Ai))\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i))
\max_{i=0}^{n-1}({DP_{i, k-1}} + A_n - A_i))
=An+max⁡i=0n−1(DPi,k−1−Ai))= A_n + \max_{i=0}^{n-1}({DP_{i, k-1}} - A_i))
= A_n + \max_{i=0}^{n-1}({DP_{i, k-1}} - A_i))
DP0,k−1−A0DP_{0,k-1} \\ - A_0
DP_{0,k-1} \\ - A_0
DP1,k−1−A1DP_{1,k-1} \\ - A_1
DP_{1,k-1} \\ - A_1

...

DPn−1,k−1−An−1DP_{n-1,k-1} \\ - A_{n-1}
DP_{n-1,k-1} \\ - A_{n-1}
→DPn,k的答案組成\rightarrow DP_{n, k} \\ 的答案組成
\rightarrow DP_{n, k} \\ 的答案組成
                                                                                      ⏟max⁡\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\max}
\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\max}
                                                                                                             ⏟max⁡\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\max}
\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\max}
→DPn+1,k的答案組成\rightarrow DP_{n+1, k} \\ 的答案組成
\rightarrow DP_{n+1, k} \\ 的答案組成

做完了            ，很棒！那                 呢？

DPn,kDP_{n, k}
DP_{n, k}
DPn+1,kDP_{n+1, k}
DP_{n+1, k}
DP0,k−1−A0DP_{0,k-1} \\ - A_0
DP_{0,k-1} \\ - A_0
DP1,k−1−A1DP_{1,k-1} \\ - A_1
DP_{1,k-1} \\ - A_1

...

DPn−1,k−1−An−1DP_{n-1,k-1} \\ - A_{n-1}
DP_{n-1,k-1} \\ - A_{n-1}
DPn,k−1−AnDP_{n,k-1} \\ - A_{n}
DP_{n,k-1} \\ - A_{n}

只需要再多檢查一個值！

Best Time to Buy and Sell IV (leetcode 188)

DPn,k=max⁡{                                                                   不考慮考慮DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DPn−1,kDP_{n-1, k}
DP_{n-1, k}
An+max⁡i=0n−1(DPi,k−1−Ai)⏞Vn,kA_n + \overbrace{\max_{i=0}^{n-1}({DP_{i, k-1}} - A_i)}^{V_{n, k}}
A_n + \overbrace{\max_{i=0}^{n-1}({DP_{i, k-1}} - A_i)}^{V_{n, k}}
Vn+1,kV_{n+1, k}
V_{n+1, k}

只需要再多檢查一個值！

=max⁡(Vn,k,                                    )= \max (V_{n, k}, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,)
= \max (V_{n, k}, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,)
int maxProfit(int k, vector<int>& prices) {
  int n = prices.size();
  vector<vector<int>> DP(n, vector<int> (k+1));
  for (int cur_k=1; cur_k<=k; cur_k++) {
    int cur_v = DP[0][cur_k-1] - prices[0];
    for (int cur_n=1; cur_n<n; cur_n++) {
      DP[cur_n][cur_k] = max(DP[cur_n-1][cur_k], prices[cur_n] + cur_v);
      cur_v = max(cur_v, DP[cur_n][cur_k-1] - prices[cur_n]);
    }
  }
  return DP.back().back();
}
def maxProfit(self, k: int, prices: List[int]) -> int:
  DP = [[0] * (k+1) for _ in range(len(prices))]
  for cur_k in range(1, k+1):
    cur_v = DP[0][cur_k-1] - prices[0]
    for cur_n, price in enumerate(prices):
      DP[cur_n][cur_k] = max(DP[cur_n-1][cur_k], price + cur_v)
      cur_v = max(cur_v, DP[cur_n][cur_k-1] - price)
  return DP[-1][-1]

C++

Python

DPn,k−1−AnDP_{n,k-1} - A_{n}
DP_{n,k-1} - A_{n}
Vn,kV_{n, k}
V_{n, k}
Vn,kV_{n, k}
V_{n, k}
計算Vn+1,k計算V_{n+1, k}
計算V_{n+1, k}
計算Vn+1,k計算V_{n+1, k}
計算V_{n+1, k}

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

DPn,k=在第n天時，交易k次的最高利潤DP_{n,k} = 在第 n 天時，交易k次的最高利潤
DP_{n,k} = 在第 n 天時，交易k次的最高利潤
  1. 函式定義：
     
  2. 如何拆解：
DPn,k=max⁡{                                                                   不考慮考慮DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DP_{n, k} = \max \begin{cases} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & 不考慮 \\ & 考慮 \end{cases}
DPn−1,kDP_{n-1, k}
DP_{n-1, k}

分析看看複雜度吧！

O(nk)O(nk)
O(nk)

狀態數量               × 轉移複雜度             =     

O(1)O(1)
O(1)
O(nk)O(nk)
O(nk)

好複雜啊... 如果狀態好好定，有沒有簡單的寫法？

Vn+1,kV_{n+1, k}
V_{n+1, k}

只需要再多檢查一個值！

=max⁡(Vn,k,DPn,k−1−An)= \max (V_{n, k}, DP_{n,k-1} - A_{n})
= \max (V_{n, k}, DP_{n,k-1} - A_{n})
An+max⁡i=0n−1(DPi,k−1−Ai)⏞Vn,kA_n + \overbrace{\max_{i=0}^{n-1}({DP_{i, k-1}} - A_i)}^{V_{n, k}}
A_n + \overbrace{\max_{i=0}^{n-1}({DP_{i, k-1}} - A_i)}^{V_{n, k}}

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

{DPn,k,0=在第n天結束時，沒持股，交易k次的最高利潤DPn,k,1=在第n天結束時，有持股，交易k次的最高利潤\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
  1. 函式定義：


     
  2. 如何拆解：

考量第 n 天要不要 (買，當c=1) / (賣，當c=0)

🕒

昨天 (n-1) 的資產

今天 (n) 的資產

DPn,k,0DP_{n, k, 0}
DP_{n, k, 0}
DPn,k,1DP_{n, k, 1}
DP_{n, k, 1}

今天結束後沒股票

今天結束後有股票

❓

Best Time to Buy and Sell IV (leetcode 188)

{DPn,k,0=在第n天結束時，沒持股，交易k次的最高利潤DPn,k,1=在第n天結束時，有持股，交易k次的最高利潤\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
  1. 函式定義：


     
  2. 如何拆解：

考量第 n 天要不要 (買，當c=1) / (賣，當c=0)

🕒

昨天 (n-1) 的資產

今天 (n) 的資產

DPn,k,0DP_{n, k, 0}
DP_{n, k, 0}
DPn,k,1DP_{n, k, 1}
DP_{n, k, 1}

今天結束後沒股票

今天結束後有股票

Pass 今天

DPn−1,k,0DP_{n-1, k, 0}
DP_{n-1, k, 0}

昨天結束後沒股票

今天賣 + An

DPn−1,k,1DP_{n-1, k, 1}
DP_{n-1, k, 1}

昨天結束後有股票

Pass 今天

DPn−1,k−1,0DP_{n-1, k-1, 0}
DP_{n-1, k-1, 0}

昨天結束後沒股票

今天買 - An

(但昨天只交易了 k-1 次的狀況)

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

{DPn,k,0=在第n天結束時，沒持股，交易k次的最高利潤DPn,k,1=在第n天結束時，有持股，交易k次的最高利潤\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
  1. 函式定義：


     
  2. 如何拆解：
{DPn,k,0=max⁡{DPn−1,k,0跳過這天，繼續沒持股DPn−1,k,1+An     以An價格賣股DPn,k,1=max⁡{DPn−1,k,1跳過這天，繼續持股DPn−1,k−1,0−An以An價格買股\begin{cases} DP_{n, k, 0} = \max \begin{cases} DP_{n-1, k, 0} & 跳過這天，繼續沒持股\\ DP_{n-1, k, 1} + A_n \,\,\,\,\, & 以 A_n 價格賣股 \end{cases} \\ DP_{n, k, 1} = \max \begin{cases} DP_{n-1, k, 1} & 跳過這天，繼續持股 \\ DP_{n-1, k-1, 0} - A_{n} & 以 A_n 價格買股 \end{cases} \end{cases}
\begin{cases} DP_{n, k, 0} = \max \begin{cases} DP_{n-1, k, 0} & 跳過這天，繼續沒持股\\ DP_{n-1, k, 1} + A_n \,\,\,\,\, & 以 A_n 價格賣股 \end{cases} \\ DP_{n, k, 1} = \max \begin{cases} DP_{n-1, k, 1} & 跳過這天，繼續持股 \\ DP_{n-1, k-1, 0} - A_{n} & 以 A_n 價格買股 \end{cases} \end{cases}

考量第 n 天要不要 (買，當c=1) / (賣，當c=0)

int dp[1000][101][2] = {}, visit[1000][101][2] = {};
int rec(vector<int>& prices, int n, int k, bool c) {
    if (n == -1 && k == 0 && c == 0) 
    	return 0;
    if (n == -1 || k == -1) 
    	return INT_MIN + 1000;
    if (visit[n][k][c]) 
    	return dp[n][k][c];
    visit[n][k][c] = true;
    if (c == 1)
        return dp[n][k][c] = max(
                rec(prices, n-1, k-1, 0)-prices[n], 
                rec(prices, n-1, k, 1));
    else
        return dp[n][k][c] = max(
                rec(prices, n-1, k, 1)+prices[n], 
                rec(prices, n-1, k, 0));
}
int maxProfit(int k, vector<int>& prices) {
    int ans = 0;
    for (int i=0; i<=k; i++)
        ans = max(ans, rec(prices, prices.size()-1, i, 0));
    return ans;
}

C++

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

DPn,k,0=max⁡{DPn−1,k,0DPn−1,k,1+AnDPn,k,1=max⁡{DPn−1,k,1DPn−1,k−1,0−AnDP_{n, k, 0} = \\ \max \begin{cases} DP_{n-1, k, 0} \\ DP_{n-1, k, 1} + A_n \end{cases}\\ DP_{n, k, 1} = \\ \max \begin{cases} DP_{n-1, k, 1} \\ DP_{n-1, k-1, 0} - A_n \end{cases}\\
DP_{n, k, 0} = \\ \max \begin{cases} DP_{n-1, k, 0} \\ DP_{n-1, k, 1} + A_n \end{cases}\\ DP_{n, k, 1} = \\ \max \begin{cases} DP_{n-1, k, 1} \\ DP_{n-1, k-1, 0} - A_n \end{cases}\\

Python

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

DPn,k,0=max⁡{DPn−1,k,0DPn−1,k,1+AnDPn,k,1=max⁡{DPn−1,k,1DPn−1,k−1,0−AnDP_{n, k, 0} = \\ \max \begin{cases} DP_{n-1, k, 0} \\ DP_{n-1, k, 1} + A_n \end{cases}\\ DP_{n, k, 1} = \\ \max \begin{cases} DP_{n-1, k, 1} \\ DP_{n-1, k-1, 0} - A_n \end{cases}\\
DP_{n, k, 0} = \\ \max \begin{cases} DP_{n-1, k, 0} \\ DP_{n-1, k, 1} + A_n \end{cases}\\ DP_{n, k, 1} = \\ \max \begin{cases} DP_{n-1, k, 1} \\ DP_{n-1, k-1, 0} - A_n \end{cases}\\ 
def maxProfit(self, k: int, prices: List[int]) -> int:
    dp = {}
    def rec(prices, n, k, c):
        if n == -1 and k == 0 and c == 0:
            return 0
        if n == -1 or k == -1:
            return float('-inf')
        if (n, k, c) not in dp:
            if c == 1:
                dp[n, k, c] = max(
                    rec(prices, n-1, k-1, 0) - prices[n],
                    rec(prices, n-1, k, 1)
                )
            else:
                dp[n, k, c] = max(
                    rec(prices, n-1, k, 1) + prices[n],
                    rec(prices, n-1, k, 0)
                )
        return dp[n, k, c]
    ans = 0
    for i in range(0, k+1):
        ans = max(ans, rec(prices, len(prices)-1, i, 0))
    return ans

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

{DPn,k,0=在第n天結束時，沒持股，交易k次的最高利潤DPn,k,1=在第n天結束時，有持股，交易k次的最高利潤\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
\begin{cases} DP_{n,k,0} = 在第 n 天結束時，沒持股，交易k次的最高利潤 \\ DP_{n,k,1} = 在第 n 天結束時，有持股，交易k次的最高利潤 \end{cases}
  1. 函式定義：

     

    2.  

分析看看複雜度吧！

O(nk⋅2)O(nk \cdot 2)
O(nk \cdot 2)

狀態數量                  × 轉移複雜度           =     

O(1)O(1)
O(1)
O(nk)O(nk)
O(nk)

結束了...

還沒！DP 還可以更快！

股票買賣 - IV - II

初探 Aliens 優化 / WQS 二分搜

(Weight Quick Select)

Aliens 優化 / WQS 二分搜

據說很久之前大陸發明這個技巧。

Aliens (TIOJ 1961)

但是紅起來的是因為 IOI 2016 的一題

然後近年台灣競程圈不知道為什麼突然流行了起來(?)

搞得很多不是 Aliens 的題大家都想用 Aliens 炸炸看

但在介紹之前

先來點簡單題吧！

Best Time to Buy and Sell II (leetcode 122)

給定數列 P（第 i 天的股票價格）和整數 k = ∞，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

除了本題，這裡額外要求你算出此時的交易最少幾次

{DPn,0=在第n天結束時，沒持股DPn,1=在第n天結束時，有持股\begin{cases} DP_{n,0} = 在第 n 天結束時，沒持股 \\ DP_{n,1} = 在第 n 天結束時，有持股 \end{cases}
\begin{cases} DP_{n,0} = 在第 n 天結束時，沒持股 \\ DP_{n,1} = 在第 n 天結束時，有持股 \end{cases}
  1. 函式定義：
     

  2. 如何拆解：
=max⁡{DPn−1,0跳過這天，繼續沒持股DPn−1,1+An     以An價格賣股= \max \begin{cases} DP_{n-1, 0} & 跳過這天，繼續沒持股\\ DP_{n-1, 1} + A_n \,\,\,\,\, & 以 A_n 價格賣股 \end{cases}
= \max \begin{cases} DP_{n-1, 0} & 跳過這天，繼續沒持股\\ DP_{n-1, 1} + A_n \,\,\,\,\, & 以 A_n 價格賣股 \end{cases}

不過我們要怎麼得出最大利潤下，最少交易幾次呢？

{\begin{cases} \\ \\ \\ \\ \end{cases}
\begin{cases} \\ \\ \\ \\ \end{cases}
=max⁡{DPn−1,1跳過這天，繼續持股DPn−1,0−An     以An價格買股= \max \begin{cases} DP_{n-1, 1} & 跳過這天，繼續持股 \\ DP_{n-1, 0} - A_{n} \,\,\,\,\, & 以 A_n 價格買股 \end{cases}
= \max \begin{cases} DP_{n-1, 1} & 跳過這天，繼續持股 \\ DP_{n-1, 0} - A_{n} \,\,\,\,\, & 以 A_n 價格買股 \end{cases}
DPn,0DP_{n, 0}
DP_{n, 0}
DPn,1DP_{n, 1}
DP_{n, 1}

Best Time to Buy and Sell II (leetcode 122)

{DPn,0=max⁡(DPn−1,0,DPn−1,1+An)DPn,1=max⁡(DPn−1,1,DPn−1,0−An)\begin{cases} DP_{n, 0} = \max (DP_{n-1, 0} , & DP_{n-1, 1} + A_n) \\ DP_{n, 1} = \max (DP_{n-1, 1} , & DP_{n-1, 0} - A_{n}) \end{cases}
\begin{cases} DP_{n, 0} = \max (DP_{n-1, 0} , & DP_{n-1, 1} + A_n) \\ DP_{n, 1} = \max (DP_{n-1, 1} , & DP_{n-1, 0} - A_{n}) \end{cases}

原本存的「利潤」，改成 (利潤，-交易次數)

這樣第一條件就是利潤最大，如果一樣就會選次數最小！

int maxProfit(vector<int>& prices) {
  pair<int, int> DP0(0, 0), DP1(INT_MIN, -1), ans(0, 0);
  for (int price : prices) {
    DP0 = max(DP0, {DP1.first + price, DP1.second});
    DP1 = max(DP1, {DP0.first - price, DP0.second - 1});
    ans = max(ans, DP0);
  }
  return ans.first;
}
int maxProfit(vector<int>& prices) {
  int DP0 = 0, DP1 = INT_MIN, ans = 0;
  for (int price : prices) {
    DP0 = max(DP0, DP1 + price);
    DP1 = max(DP1, DP0 - price);
    ans = max(ans, DP0);
  }
  return ans;
}

C++ 原題

C++ 原題 + 最少次數

然後你在買股票的時候，順便多記錄一次交易就好

(也就是存成 pair)

多交易一次

不過我們要怎麼得出最大利潤下，最少交易幾次呢？

註：這裡的 DP(n,1) 其實是從 DP(n, 0) 轉移，而不是 DP (n-1, 0)。但答案不影響。

Best Time to Buy and Sell II (leetcode 122)

{DPn,0=max⁡(DPn−1,0,DPn−1,1+An)DPn,1=max⁡(DPn−1,1,DPn−1,0−An)\begin{cases} DP_{n, 0} = \max (DP_{n-1, 0} , & DP_{n-1, 1} + A_n) \\ DP_{n, 1} = \max (DP_{n-1, 1} , & DP_{n-1, 0} - A_{n}) \end{cases}
\begin{cases} DP_{n, 0} = \max (DP_{n-1, 0} , & DP_{n-1, 1} + A_n) \\ DP_{n, 1} = \max (DP_{n-1, 1} , & DP_{n-1, 0} - A_{n}) \end{cases}

不過我們要怎麼最少交易紀錄幾次呢？

原本存的「利潤」，改成 (利潤，-交易次數)

這樣第一條件就是利潤最大，如果一樣就會選次數最小！

def maxProfit(self, prices):
  DP0, DP1 = (0, 0), (-inf, -1)
  ans = 0
  for price in prices:
    DP0, DP1 = (
      max(DP0, (DP1[0] + price, DP1[1])),
      max(DP1, (DP0[0] - price, DP0[1] - 1))
    )
    ans = max(ans, DP0)
  return ans[0]
def maxProfit(self, prices):
  DP0, DP1 = 0, -inf
  ans = 0
  for price in prices:
    DP0, DP1 = (
      max(DP0, DP1 + price),
      max(DP1, DP0 - price)
    )
    ans = max(ans, DP0)
  return ans

Python 原題

Python 原題 + 最少次數

(也就是存成 tuple)

多交易一次

然後你在買股票的時候，順便多記錄一次交易就好

Best Time to Buy and Sell with fee (leetcode 714)

給定數列 P（第 i 天的股票價格），
你可以進行無限次交易，但每次交易都會有手續費 fee。
請求出最大利潤為何？
此外，你只能同時持有一張股票，

除了本題，這裡額外要求你算出最大利潤下時的最少交易次數。

{DPn,0=在第n天結束時，沒持股DPn,1=在第n天結束時，有持股\begin{cases} DP_{n,0} = 在第 n 天結束時，沒持股 \\ DP_{n,1} = 在第 n 天結束時，有持股 \end{cases}
\begin{cases} DP_{n,0} = 在第 n 天結束時，沒持股 \\ DP_{n,1} = 在第 n 天結束時，有持股 \end{cases}
  1. 函式定義：
     

  2. 如何拆解：
=max⁡{DPn−1,0跳過這天，繼續沒持股DPn−1,1+An          以An價格賣股= \max \begin{cases} DP_{n-1, 0} & 跳過這天，繼續沒持股\\ DP_{n-1, 1} + A_n \,\,\,\,\,\,\,\,\,\, & 以 A_n 價格賣股 \end{cases}
= \max \begin{cases} DP_{n-1, 0} & 跳過這天，繼續沒持股\\ DP_{n-1, 1} + A_n \,\,\,\,\,\,\,\,\,\, & 以 A_n 價格賣股 \end{cases}
{\begin{cases} \\ \\ \\ \\ \end{cases}
\begin{cases} \\ \\ \\ \\ \end{cases}
=max⁡{DPn−1,1跳過這天，繼續持股DPn−1,0−An          以An價格買股= \max \begin{cases} DP_{n-1, 1} & 跳過這天，繼續持股 \\ DP_{n-1, 0} - A_{n} \,\,\,\,\,\,\,\,\,\, & 以 A_n 價格買股 \end{cases}
= \max \begin{cases} DP_{n-1, 1} & 跳過這天，繼續持股 \\ DP_{n-1, 0} - A_{n} \,\,\,\,\,\,\,\,\,\, & 以 A_n 價格買股 \end{cases}
DPn,0DP_{n, 0}
DP_{n, 0}
DPn,1DP_{n, 1}
DP_{n, 1}
−fee- fee
- fee

給定數列 P（第 i 天的股票價格），
你可以進行無限次交易，但每次交易都會有手續費 fee。
請求出最大利潤為何？
此外，你只能同時持有一張股票，

除了本題，這裡額外要求你算出最大利潤下時的最少交易次數。

def maxProfit(self, prices, fee):
  DP0, DP1 = (0, 0), (-inf, -1)
  ans = 0
  for price in prices:
    DP0, DP1 = (
      max(DP0, (DP1[0] + price, DP1[1])),
      max(DP1, (DP0[0] - price - fee, DP0[1] - 1))
    )
    ans = max(ans, DP0)
  return ans[0]

Python 原題 + 最少次數

int maxProfit(vector<int>& prices, int fee) {
  pair<int, int> DP0(0, 0), DP1(INT_MIN, -1);
  pair<int, int> ans(0, 0);
  for (int price : prices) {
    DP0 = max(DP0, 
      {DP1.first + price, DP1.second});
    DP1 = max(DP1, 
      {DP0.first - price - fee, DP0.second - 1});
    ans = max(ans, DP0);
  }
  return ans.first;
}

C++ 原題 + 最少次數

接下來讓我們開始介紹 Aliens 優化吧！

Best Time to Buy and Sell with fee (leetcode 714)

Best Time to Buy and Sell with fee (leetcode 714)

給定數列 P（第 i 天的股票價格），
你可以進行無限次交易，但每次交易都會有手續費 fee。
請求出最大利潤為何？
此外，你只能同時持有一張股票，

除了本題，這裡額外要求你算出最大利潤下時的最少交易次數。

觀察一下題目：

  • 如果手續費為 0，你就會盡可能的交易到最佳解。 (=上一題的答案)
  • 如果需要一點手續費，你就會比較不那麼想交易，除非很賺。
  • 如果手續費為 ∞，你就不會做交易。 (交易次數 = 0)

隨著手續費升高，「最大利潤下的最少交易次數」會隨之遞減。

? 這有什麼用

隨著手續費升高，「最大利潤下的最少交易次數」會隨之遞減。

交易次數

交易手續費

手續費為 ∞，交易次數為0

Best Time to Buy and Sell IV (leetcode 188)

怎麼知道交易 k 次的最大利潤？

k

手續費為 x，交易次數剛好為 k

如果非常的剛好的，有個手續費剛剛好讓最佳次數 = k ...

利潤 = 「交易 k 次，沒手續費的最佳利潤」 - kx

所以只要我們發現有個手續費 x 可以讓交易次數剛好是 k，

那麼就可以反推交易次數是 k 的最佳利潤。

為什麼答案不會變？明明跑的程式差了手續費？

交易次數

交易手續費

手續費為 ∞，交易次數為0

Best Time to Buy and Sell IV (leetcode 188)

k

手續費為 x，交易次數剛好為 k

利潤 = 「交易 k 次，沒手續費的最佳利潤」 - kx

如果沒有手續費，假設 「沒手續費交易 k 次的最佳解的選法」 比 「有手續費，剛好最少交易次數是 k 次的選法」 還要好 (利潤更高)

  • 那麼你會發現這個選法可以直接套用在有手續費的 Case 上。
  • 所以前提不可能，反證法得證。

不過我們要怎麼剛好搜到手續費 x，剛好使次數 = k 呢？

因為交易次數有單調性，所以使用二分搜尋法。

隨著手續費升高，「最大利潤下的最少交易次數」會隨之遞減。

Best Time to Buy and Sell IV (leetcode 188)

因為交易次數有單調性，所以使用二分搜尋法。

不過這裡有個問題，交易次數是離散的。找不到剛好的 k 怎麼辦？

交易次數

交易手續費

手續費為 ∞，交易次數為0

k

k = 100

(L, Lk = 102)

(R, Rk = 99)

二分搜手續費: L, R

L 的交易次數為 Lk

R 的交易次數為 Rk

(Rk次交易，手續費R最大利潤)=(k次交易，手續費R最大利潤)(R_k 次交易，手續費 R 最大利潤) = (k 次交易，手續費 R 最大利潤)
(R_k 次交易，手續費 R 最大利潤) = (k 次交易，手續費 R 最大利潤)
(Rk次交易，手續費R最大利潤)+kR=(k次交易，最大利潤)(R_k 次交易，手續費 R 最大利潤) + kR = (k 次交易，最大利潤)
(R_k 次交易，手續費 R 最大利潤) + kR = (k 次交易，最大利潤)

(如果不等於，那就表示二分搜根本沒結束)

隨著手續費升高，「最大利潤下的最少交易次數」會隨之遞減。

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

讓我們來整理一下原題：

  1. 寫一個函數，可以給定手續費
    回傳最高價值跟這個時候的最少次數。
  2. 二分搜尋手續費，使得最後的範圍是
    ​L > k， R ≤ k。
  3. 因為 R 不一定等於 k，所以需要修正答案：
O(n)O(n)
O(n)
O(log⁡max⁡A)=O(log⁡C)O(\log \max A) \\ = O(\log C)
O(\log \max A) \\ = O(\log C)
(Rk次交易，手續費R最大利潤)+kR=(k次交易，最大利潤)(R_k 次交易，手續費 R 最大利潤) + kR = (k 次交易，最大利潤)
(R_k 次交易，手續費 R 最大利潤) + kR = (k 次交易，最大利潤)

整體複雜度：                        

O(nlog⁡C)O(n \log C)
O(n \log C)

一般情況下比原本的 O(nk) 還要好！

Best Time to Buy and Sell IV (leetcode 188) 

pair<int, int> trial(vector<int>& prices, int fee) {
  pair<int, int> DP0(0, 0), DP1(INT_MIN, -1);
  pair<int, int> ans(0, 0);
  for (int price : prices) {
    DP0 = max(DP0, 
    {DP1.first + price, DP1.second});
    DP1 = max(DP1, 
    {DP0.first - price - fee, DP0.second - 1});
    ans = max(ans, DP0);
  }
  return ans;
}
int maxProfit(int k, vector<int>& prices) {
  double L = 0, R =1000;
  while (R - L > 1e-4) {
    double M = (L + R) / 2;
    if (-trial(prices, M).second > k)
      L = M;
    else
      R = M;
  }
  return round(trial(prices, R).first + k*R); 
}
def maxProfit(self, k, prices):
  def trial(cost):
    DP0, DP1 = (0, 0), (-inf, -1)
    ans = DP0
    for price in prices:
      DP0, DP1 = (
        max(DP0, 
          (DP1[0] + price, DP1[1])),
        max(DP1,
          (DP0[0] - price - cost, DP0[1] - 1))
      )
    ans = max(ans, DP0)
    return ans
  L, R = 0, max(prices)
  while R-L > 1e-2:
    M = (L+R) / 2
    if -trial(M)[1] > k:
      L = M
    else:
      R = M
  
  val, _ = trial(R)
  return round(val + k * R)

Python (Aliens 優化)

C++ (Aliens 優化)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

區間分割類 DP

區間分割類 DP

這類型的題目通常：

  1. 都會給你一個數列。
  2. 你需要將這個數列分割成數個子區間 / 子數列 (interval / subarray)
  3. 接著計算最佳值。
  4. 跟之後的區間 DP 基本上是類似的。
    但差別在於這裡的題目是 1D狀態。

因此這類題型的轉移通常都是 O(n) 找分割點

平衡字串切割

Minimum Substring Partition (leetcode 3144)

Minimum Substring Partition (leetcode 3144)

給定一字串，問最少能將 S 分成幾段使其每段字串都是「平衡」的。

這裡定義「平衡」表示該字串內每個字的出現次數皆一樣。

狀態怎麼定呢？

舉例來說：

S = "fabccddg"

切割成 "fab", "ccdd", "g"

  • "fab" 所有字元出現一次
  • "ccdd" 所有字元出現兩次
  • "g" 所有字元出現一次
  • 答案：最少需要分成三段

Minimum Substring Partition (leetcode 3144)

給定一字串，問最少能將 S 分成幾段使其每段字串都是「平衡」的。

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法

好像有點麻煩 ...

如果最後一個片段選了第 n 個字元，那麼這個片段可以到哪？

S0S_0
S_0
S1S_1
S_1
S2S_2
S_2
......
...
SnS_n
S_n
Sn−1S_{n-1}
S_{n-1}
S3S_3
S_3
S4S_4
S_4

最後片段，如果平衡

=1= 1
= 1

最後片段，如果平衡

DP0DP_{0}
DP_{0}
=DP0+1= DP_{0} + 1
= DP_{0} + 1

最後片段，如果平衡

DP1DP_{1}
DP_{1}
=DP1+1= DP_{1} + 1
= DP_{1} + 1

...

...

DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是平衡的}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是平衡的}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是平衡的}\}

但 ... 這要怎麼知道？

Check occurence in string  (leetcode 1941)

給定一字串，回傳這個字串是不是「平衡」的。

沒事，這不是DP :p

你可能會這樣寫：搜尋每個字母然後檢查次數

int criteria = 0;
for (char check='a'; check<='z'; check++) {
  int cnt = 0;
  for (auto c : s)
    if (c == check)
      cnt ++;
  if (cnt)
    if (criteria == 0)
      criteria = cnt;
    else if (criteria != cnt)
      return false;
}
return true;
L = []
for check in string.ascii_lowercase:
  cnt = 0
  for c in s:
    if check == c:
      cnt += 1
  if cnt:
    L.append(cnt)
return all(l==L[0] for l in L)

C++

Python

O(∣∑∣×N)O( |\sum| \times N)
O( |\sum| \times N)

字母有幾種

時間複雜度：                     

那如果我們加大點難度呢？

Check occurence in string  (leetcode 1941) 改

給定一字串，回傳這個字串的所有後綴是不是「平衡」的。
所有後綴：                                                                              

S[0,n],S[1,n],S[2,n],...,S[n−2,n],S[n−1,n],S[n,n]S_{[0, n]}, S_{[1, n]}, S_{[2, n]}, ... , S_{[n-2, n]}, S_{[n-1, n]}, S_{[n, n]}
S_{[0, n]}, S_{[1, n]}, S_{[2, n]}, ... , S_{[n-2, n]}, S_{[n-1, n]}, S_{[n, n]}

原本的做法也不是不行，對每個字元做區間和也是可以... 但很麻煩

S[0,5]="abccba"→TS_{[0, 5]} = "abccba" \rightarrow T
S_{[0, 5]} = "abccba" \rightarrow T
S[2,5]="ccba"→FS_{[2, 5]} = "ccba"\rightarrow F
S_{[2, 5]} = "ccba"\rightarrow F
S[1,5]="bccba"→FS_{[1, 5]} = "bccba"\rightarrow F
S_{[1, 5]} = "bccba"\rightarrow F
S[3,5]="cba"→TS_{[3, 5]} = "cba"\rightarrow T
S_{[3, 5]} = "cba"\rightarrow T
S[4,5]="ba"→TS_{[4, 5]} = "ba"\rightarrow T
S_{[4, 5]} = "ba"\rightarrow T
S[5,5]="a"→TS_{[5, 5]} = "a"\rightarrow T
S_{[5, 5]} = "a"\rightarrow T

舉例來說：

Counting Table

由後往前慢慢把字元加進 Table，

也許就可以做出來了？

也就是開一個陣列 A，
A[c] = c 出現幾次

那該怎麼做呢？
如果暴力做就會             ...

O(n2)O(n^2)
O(n^2)

Check occurence in string  (leetcode 1941) 改

給定一字串，回傳這個字串的所有後綴是不是「平衡」的。
所有後綴：                                                                              

S[0,n],S[1,n],S[2,n],...,S[n−2,n],S[n−1,n],S[n,n]S_{[0, n]}, S_{[1, n]}, S_{[2, n]}, ... , S_{[n-2, n]}, S_{[n-1, n]}, S_{[n, n]}
S_{[0, n]}, S_{[1, n]}, S_{[2, n]}, ... , S_{[n-2, n]}, S_{[n-1, n]}, S_{[n, n]}

原本的做法也不是不行，對每個字元做區間和也是可以... 但很麻煩

舉例來說：

S[0,5]="abccba"→TS_{[0, 5]} = "abccba" \rightarrow T
S_{[0, 5]} = "abccba" \rightarrow T
S[2,5]="ccba"→FS_{[2, 5]} = "ccba"\rightarrow F
S_{[2, 5]} = "ccba"\rightarrow F
S[1,5]="bccba"→FS_{[1, 5]} = "bccba"\rightarrow F
S_{[1, 5]} = "bccba"\rightarrow F
S[3,5]="cba"→TS_{[3, 5]} = "cba"\rightarrow T
S_{[3, 5]} = "cba"\rightarrow T
S[4,5]="ba"→TS_{[4, 5]} = "ba"\rightarrow T
S_{[4, 5]} = "ba"\rightarrow T
S[5,5]="a"→TS_{[5, 5]} = "a"\rightarrow T
S_{[5, 5]} = "a"\rightarrow T

2  2  2

1  2  2

1  1  2

1  1  1

1  1  0

1  0  0

a  b  c

不過怎麼知道每次添加都是不是平衡的呢？

  • Hint: 多紀錄兩個數字。

字串長度 =
最大次數 * 出現的種類

3 種
3 種
3 種
3 種
2 種
1 種

出現的種類可以
從 0 變成 1 的瞬間維護。

1  1  1

1  1  0

1  0  0

Minimum Substring Partition (leetcode 3144)

給定一字串，問最少能將 S 分成幾段使其每段字串都是「平衡」的。

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法
DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是平衡的}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是平衡的}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是平衡的}\}

回歸原題，那這樣你會寫了嗎？

只要第二層迴圈 j 從 n 做到 0，順便跑剛剛的算法就可以知道 S[j, n] 是不是平衡的！

分析看看複雜度吧！

O(n)O(n)
O(n)

狀態數量             × 轉移複雜度            =

O(n)O(n)
O(n)
O(n2)O(n^2)
O(n^2)

Minimum Substring Partition (leetcode 3144)

給定一字串，問最少能將 S 分成幾段使其每段字串都是「平衡」的。

int minimumSubstringsInPartition(string s) {
  vector<int> dp(s.length(), 1001);
  dp[0] = 1;
  for (int i=1; i<s.length(); i++) {
    int table[26] = {0};
    int max_v = 0, uniq = 0;
    for (int j=i; j>=0; j--) {
      max_v = max(max_v, ++table[s[j] - 'a']);
      uniq += (table[s[j] - 'a'] == 1);
      if (max_v*uniq == i-j+1)
        dp[i] = min(dp[i], j==0 ? 1 : dp[j-1]+1);
    }
  }
  return dp.back();
}

C++

def minimumSubstringsInPartition(self, s):
  dp = [inf] * len(s) + [0]
  for i in range(len(s)):
    table = defaultdict(int)
    uniq, max_v = 0, 0
    for j in range(i, -1, -1):
      table[s[j]] += 1
      if table[s[j]] == 1:
        uniq += 1
      max_v = max(max_v, table[s[j]])
      if uniq * max_v == i-j+1:
        dp[i] = min(dp[i], dp[j-1]+1)
  return dp[-2]

Python

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法
DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是平衡的}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是平衡的}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是平衡的}\}

最少回文切割

Palindrome Partitioning II (leetcode 132)

Palindrome Partitioning II (leetcode 132)

舉例來說：

給你一個字串，請問最少可以切幾刀，使得所有子字串皆回文？

S = "bacdcaba"

 "bacdcab" / "a"

最少必須切一刀，
才可以使所有片段都是回文。

狀態怎麼定呢？

Palindrome Partitioning II (leetcode 132)

給你一個字串，請問最少可以切幾刀，使得所有子字串皆回文？

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法
DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是回文}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}

但 ... 這要怎麼知道？

這不就跟上題一樣嗎？

如果每一個不同的 j 就重新判斷回文怎麼樣？

分析看看複雜度吧！

O(n)O(n)
O(n)

狀態數量             × 轉移複雜度            =

O(n2)O(n^2)
O(n^2)
O(n3)O(n^3)
O(n^3)

大噴爛，有沒有方法可以降低判斷回文的複雜度呢？

Palindrome Partitioning II (leetcode 132)

請預處理後， O(1) 判斷一個字串的
任何一個子字串是不是回文

如何問一個子區間？

我們會用兩個變數來指定一個區間。

DPi,j′=S[i,j]是不是回文DP'_{i, j} = S_{[i, j]} 是不是回文
DP'_{i, j} = S_{[i, j]} 是不是回文
DPi,j′=DPi+1,j−1′∧(Si=Sj)DP'_{i, j} = DP'_{i+1, j-1} \land (S_i = S_j)
DP'_{i, j} = DP'_{i+1, j-1} \land (S_i = S_j)
  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPi,j′=True if i≥jDP'_{i, j} = True \text{ if } i \ge j
DP'_{i, j} = True \text{ if } i \ge j 
memo = {}
def is_palin(l, r):
  if l >= r:
    return True
  if (l, r) not in memo:
    memo[l, r] = s[l] == s[r] and is_palin(l+1, r-1)
  return memo[l, r]

Python

bool is_palin(vector<vector<int>> &memo, 
              string &s, int l, int r) {
  if (l >= r)
    return true;
  if (memo[l][r] == -1)
    memo[l][r] = is_palin(memo, s, l+1, r-1) && s[l]==s[r];
  return memo[l][r];
}

C++

Palindrome Partitioning II (leetcode 132)

給你一個字串，請問最少可以切幾刀，使得所有子字串皆回文？

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法
DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是回文}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}

剩下不就跟上題一樣嗎？

def minCut(self, s: str) -> int:
  def is_palin(l, r):
    if l >= r:
      return True
    if (l, r) not in memo:
      memo[l, r] = s[l] == s[r] and is_palin(l+1, r-1)
    return memo[l, r]

  memo = {}
  dp = [inf] * len(s) + [-1]
  for i in range(0, len(s)):
    for j in range(i+1):
      if is_palin(j, i):
        dp[i] = min(dp[i], dp[j-1]+1)
  return dp[-2]

Python

int minCut(string s) {
  int n = s.size();
  vector<vector<int>> memo(n, vector<int>(n, -1));
  vector<int> dp(n, 2001);
  dp[0] = 0;
  for (int i=1; i<n; i++) {
    for (int j=0; j<=i; j++) {
      if (is_palin(memo, s, j, i))
        dp[i] = min(dp[i], j==0 ? 0 : dp[j-1]+1);
    }
  }
  return dp.back();
}

C++

Palindrome Partitioning II (leetcode 132)

給你一個字串，請問最少可以切幾刀，使得所有子字串皆回文？

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法
DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是回文}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}

那為什麼要選這題呢？
其實這題有比較漂亮的轉移

某個回文 S[i, j]

把整個轉移反過來想，我們就會變成這樣：

如果我們找到

DPi−1DP_{i-1}
DP_{i-1}
DPjDP_{j}
DP_{j}

更新一個答案

Palindrome Partitioning II (leetcode 132)

給你一個字串，請問最少可以切幾刀，使得所有子字串皆回文？

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法
DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是回文}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}

某個回文 S[i, j]

如果我們找到

DPi−1+1DP_{i-1} + 1
DP_{i-1} + 1
DPjDP_{j}
DP_{j}

更新

怎麼簡單地 (不用遞迴 / DP) 找到回文呢？

S = abcdcba

枚舉中心往外擴散就好了。

(不過回文長度是偶數，中心會在中間，要特別處理。)

S = abccba

Palindrome Partitioning II (leetcode 132)

給你一個字串，請問最少可以切幾刀，使得所有子字串皆回文？

  1. 函式定義：
  2. 如何拆解：
DPn=S[0,n]的最小切法DP_{n} = S_{[0, n]} 的最小切法
DP_{n} = S_{[0, n]} 的最小切法
DPn=min⁡0≤j<n{DPj−1+1∣S[j,n]是回文}DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}
DP_{n} = \min_{0 \le j < n}\{DP_{j-1} + 1 | S_{[j,n]} \text{是回文}\}
def minCut(self, s: str) -> int:
  dp = [inf] * len(s) + [-1]
  for i in range(0, len(s)):
    L, R = i, i
    while L >= 0 and R < len(s) and s[L] == s[R]:
      dp[R] = min(dp[R], dp[L-1] + 1)
      L, R = L-1, R+1
    L, R = i-1, i
    while L >= 0 and R < len(s) and s[L] == s[R]:
      dp[R] = min(dp[R], dp[L-1] + 1)
      L, R = L-1, R+1
  return dp[-2]

Python

不固定轉移

int n = s.size();
vector<int> dp(n, 2001);
for (int i=0; i<n; i++) {
  for (int L=i, R=i; L>=0 && R<n && s[L] == s[R]; --L, ++R)
    dp[R] = min(dp[R], L ? dp[L-1]+1: 0);
  for (int L=i-1, R=i; L>=0 && R<n && s[L] == s[R]; --L, ++R)
    dp[R] = min(dp[R], L ? dp[L-1]+1: 0);
}
return dp.back();

C++
不固定轉移

* 不固定轉移是我自己取的，
目前沒有這種講法。

Palindrome Partitioning II (leetcode 132)

這題目前最佳是 O(nlgn)!

附上論文連結

關於不固定順序轉移

另外我在台大資工演算法當助教時
出了兩題我自認為出的簡單又很棒的題目(或這裡?)
你可以想想看，解答在這裡 (P6: 分治 / P7: DP)

另外回文有個著名的演算法：
Manacher's Algorithm

最小化區間總和

Split Array Largest Sum (leetcode 410)

Split Array Largest Sum (leetcode 410)

答案：這四個可能中，最小的是 18。

舉例來說：

註：如果是 APCS，那麼應該會有小測資是 k = 2 。
這樣的 Case 可能就會給你 30 分。

將數列切成 kkk 個區間，
最小化這 kkk 個區間總和的最大值。

  •  [7] / [2, 5, 10, 8] → max(7, 25) = 25
  •  [7, 2] / [5, 10, 8] → max(9, 23) = 23
  •  [7, 2, 5] / [10, 8] → max(14, 18) = 18
  •  [7, 2, 5, 10] / [8] → max(24, 8) = 24

A = [7, 2, 5, 10, 8], k = 2

將數列切成 kkk 個區間，
最小化這 kkk 個區間總和的最大值。

  1. 函式定義：
  2. 如何拆解：

試試看裸定義！

DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和

我們之前的題目，在拆解的時候都是考量最後一步的所有可能。

  • 這題的最後一步是？
  •              的最後一個區間有可能在哪裡？
    • ​用迴圈暴搜，取最小的那個可能。
An}max⁡\begin{rcases} \\ A_n \end{rcases} \max
\begin{rcases} \\ A_n \end{rcases} \max
DPn−1,k−1DP_{n-1, k-1}
DP_{n-1, k-1}
An−1+An}max⁡\begin{rcases} \\ A_{n-1} + A_{n} \end{rcases} \max
\begin{rcases} \\ A_{n-1} + A_{n} \end{rcases} \max
DPn−2,k−1DP_{n-2, k-1}
DP_{n-2, k-1}
DPn,kDP_{n, k}
DP_{n, k}
An−2+An−1+An}max⁡\begin{rcases} \\ A_{n-2} + A_{n-1} + A_{n} \end{rcases} \max
\begin{rcases} \\ A_{n-2} + A_{n-1} + A_{n} \end{rcases} \max
DPn−3,k−1DP_{n-3, k-1}
DP_{n-3, k-1}
A0A_0
A_0
A1A_1
A_1
A2A_2
A_2
An−2A_{n-2}
A_{n-2}
An−1A_{n-1}
A_{n-1}
AnA_n
A_n
......
...

Split Array Largest Sum (leetcode 410)

將數列切成 kkk 個區間，
最小化這 kkk 個區間總和的最大值。

  1. 函式定義：
  2. 如何拆解：
DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]

你可能要寫一個區間和
處理這個會好寫一點。

我們之前的題目，在拆解的時候都是考量最後一步的所有可能。

  • 這題的最後一步是？
  •              的最後一個區間有可能在哪裡？
    • ​用迴圈暴搜，取最小的那個可能。
DPn,kDP_{n, k}
DP_{n, k}

Split Array Largest Sum (leetcode 410) 

int splitArray(vector<int>& nums, int k) {
  // Prefix Sum
  vector<int> PS({0});
  for (auto num : nums)
    PS.push_back(PS.back() + num);
  auto Isum = [=](int l, int r) {return PS[r+1] - PS[l];};

  vector<vector<int>> DP(nums.size(), vector<int> (k+1, INT_MAX));
  // Base Case
  for (int cur_n=0; cur_n < nums.size(); cur_n++)
    DP[cur_n][1] = Isum(0, cur_n);
    

  for (int cur_k=2; cur_k <= k; cur_k++) {
    for (int cur_n=cur_k-1; cur_n < nums.size(); cur_n++) {
      for (int i=cur_k-2; i < cur_n; i++) {
        DP[cur_n][cur_k] = min(
          DP[cur_n][cur_k], 
          max(DP[i][cur_k-1], Isum(i+1, cur_n)));
      }
    }
  }
  return DP.back().back();
}

C++

  1. 函式定義：
     
  2. 如何拆解：

    3.  
DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]

Split Array Largest Sum (leetcode 410)

Base case:
k=1表示全選

想想看左右界是什麼：

i : [k-2, n-1]

* 這份程式 cur_n 跟 cur_k 可以對調，

但因為一些原因所以我們先跑 cur_k

def splitArray(self, nums: List[int], k: int) -> int:
  # Prefix Sum
  Psum = list(accumulate(nums)) + [0]
  def Isum(l, r):
    return Psum[r] - Psum[l-1]

  DP = [[math.inf] * (k+1) for _ in range(len(nums))]
  # Base Case
  for i in range(len(nums)):
    DP[i][1] = Isum(0, i)

  for cur_k in range(2, k+1):
    for cur_n in range(cur_k-1, len(nums)):
      cur_v = math.inf
      for i in range(cur_k-2, cur_n):
        cur_v = min(cur_v, max(DP[i][cur_k-1], Isum(i+1, cur_n)))
      DP[cur_n][cur_k] = cur_v

  return DP[len(nums)-1][k]

Python

Base case:
k=1表示全選

想想看左右界是什麼：

i : [k-2, n-1]

Split Array Largest Sum (leetcode 410)

  1. 函式定義：
     
  2. 如何拆解：

    3.  
DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]

* 這份程式 cur_n 跟 cur_k 可以對調，

但因為一些原因所以我們先跑 cur_k

  1. 函式定義：
     
  2. 如何拆解：

    3.  
DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]

將數列切成 kkk 個區間，
最小化這 kkk 個區間總和的最大值。

分析看看複雜度吧！

O(nk)O(nk)
O(nk)

狀態數量             × 轉移複雜度            =

O(n)O(n)
O(n)
O(n2k)O(n^2k)
O(n^2k)

狀態應該是不能再壓了，那麼轉移可以更快嗎？

An}max⁡\begin{rcases} \\ A_n \end{rcases} \max
\begin{rcases} \\ A_n \end{rcases} \max
DPn−1,k−1DP_{n-1, k-1}
DP_{n-1, k-1}
An−1+An}max⁡\begin{rcases} \\ A_{n-1} + A_{n} \end{rcases} \max
\begin{rcases} \\ A_{n-1} + A_{n} \end{rcases} \max
DPn−2,k−1DP_{n-2, k-1}
DP_{n-2, k-1}
An−2+An−1+An}max⁡\begin{rcases} \\ A_{n-2} + A_{n-1} + A_{n} \end{rcases} \max
\begin{rcases} \\ A_{n-2} + A_{n-1} + A_{n} \end{rcases} \max
DPn−3,k−1DP_{n-3, k-1}
DP_{n-3, k-1}
A0A_0
A_0
A1A_1
A_1
A2A_2
A_2
An−2A_{n-2}
A_{n-2}
An−1A_{n-1}
A_{n-1}
AnA_n
A_n
......
...

Split Array Largest Sum (leetcode 410)

  1. 函式定義：
     
  2. 如何拆解：

    3.  
DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]

狀態應該是不能再壓了，那麼轉移可以更快嗎？

An−2+...+AnA_{n-2} + ... + A_{n}
A_{n-2} + ... + A_{n}
DPn−3,k−1DP_{n-3, k-1}
DP_{n-3, k-1}
An−1+AnA_{n-1} + A_{n}
A_{n-1} + A_{n}
DPn−2,k−1DP_{n-2, k-1}
DP_{n-2, k-1}
DPn−1,k−1DP_{n-1, k-1}
DP_{n-1, k-1}
AnA_n
A_n
DP0,k−1DP_{0, k-1}
DP_{0, k-1}
A1+...+AnA_{1} + ... + A_{n}
A_{1} + ... + A_{n}

...

}max⁡\begin{rcases} \\ \\ \end{rcases} \max
\begin{rcases} \\ \\ \end{rcases} \max
                                                                                                                                        ⏟min⁡\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\min}
\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\min}

這些數值有什麼關係呢？

  • Hint：所有數字都是非負整數
≥\ge
\ge
≥\ge
\ge
≥\ge
\ge
≤\le
\le
≤\le
\le
≤\le
\le

不是，這個有什麼用？

Split Array Largest Sum (leetcode 410)

DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
An−2+...+AnA_{n-2} + ... + A_{n}
A_{n-2} + ... + A_{n}
DPn−3,k−1DP_{n-3, k-1}
DP_{n-3, k-1}
An−1+AnA_{n-1} + A_{n}
A_{n-1} + A_{n}
DPn−2,k−1DP_{n-2, k-1}
DP_{n-2, k-1}
DPn−1,k−1DP_{n-1, k-1}
DP_{n-1, k-1}
AnA_n
A_n
DP0,k−1DP_{0, k-1}
DP_{0, k-1}
A1+...+AnA_{1} + ... + A_{n}
A_{1} + ... + A_{n}

...

}max⁡\begin{rcases} \\ \\ \end{rcases} \max
\begin{rcases} \\ \\ \end{rcases} \max
                                                                                                                                        ⏟min⁡\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\min}
\underbrace{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}_{\min}
≥\ge
\ge
≥\ge
\ge
≥\ge
\ge
≤\le
\le
≤\le
\le
≤\le
\le

數值

i

DP 項

區間和項

你想要知道一個 i：

  • max(區間和項, DP項)
    要最小。
  • 會發生在哪裡？
    • 兩項交叉時候。
  • 怎麼找？
    • 二分搜尋法

Split Array Largest Sum (leetcode 410) 

def splitArray(self, nums, k):
  # Prefix Sum
  Psum = list(accumulate(nums)) + [0]
  def Isum(l, r):
    return Psum[r] - Psum[l-1]

  DP = [[math.inf] * (k+1) for _ in range(len(nums))]
  # Base Case
  for i in range(len(nums)):
    DP[i][1] = Isum(0, i)

  for cur_k in range(2, k+1):
    for cur_n in range(cur_k-1, len(nums)):
      L, R = cur_k-2, cur_n
      while R-L > 1:
        M = (L+R) // 2
        if DP[M][cur_k-1] < Isum(M+1, cur_n):
          L = M
        else:
          R = M
      DP[cur_n][cur_k] = min(
        max(DP[L][cur_k-1], Isum(L+1, cur_n)),
        max(DP[R][cur_k-1], Isum(R+1, cur_n))
      )

  return DP[len(nums)-1][k]

Python

注意：二分搜到交叉項時，最大值有可能在 DP 項也可能在區間和項，
所以你必須要取左界 (L) 和右界 (R) 的最小值。

int splitArray(vector<int>& nums, int k) {
  // Prefix Sum
  vector<int> PS({0});
  for (auto num : nums)
    PS.push_back(PS.back() + num);
  auto Isum = [=](int l, int r) {return PS[r+1] - PS[l];};

  vector<vector<int>> DP(nums.size(), vector<int> (k+1, INT_MAX));
  // Base Case
  for (int cur_n=0; cur_n < nums.size(); cur_n++)
    DP[cur_n][1] = Isum(0, cur_n);
    

  for (int cur_k=2; cur_k <= k; cur_k++) {
    for (int cur_n=cur_k-1; cur_n < nums.size(); cur_n++) {
      int L = cur_k-2, R = cur_n;
      while (R-L > 1) {
        int M = (L+R)/2;
        if (DP[M][cur_k-1] < Isum(M+1, cur_n))
            L = M;
        else
            R = M;
      }
      DP[cur_n][cur_k] = min(
        max(DP[L][cur_k-1], Isum(L+1, cur_n)),
        max(DP[R][cur_k-1], Isum(R+1, cur_n))
      );
    }
  }
  return DP.back().back();
}

C++

二分搜
的地方

Split Array Largest Sum (leetcode 410)

  1. 函式定義：
     
  2. 如何拆解：
DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]

將數列切成 kkk 個區間，
最小化這 kkk 個區間總和的最大值。

分析看看複雜度吧！

O(nk)O(nk)
O(nk)

狀態數量             × 轉移複雜度                 =

O(log⁡n)O(\log n)
O(\log n)
O(nklog⁡n)O(nk\log n)
O(nk\log n)

這個複雜度滿意了嗎？

還沒！還有其他轉移

注意：二分搜到交叉項時，最大值有可能在 DP 項也可能在區間和項，
所以你必須要取左界 (L) 和右界 (R) 的最小值。

Split Array Largest Sum (leetcode 410)

DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
An−2+...+AnA_{n-2} + ... + A_{n}
A_{n-2} + ... + A_{n}
DPn−3,k−1DP_{n-3, k-1}
DP_{n-3, k-1}
An−1+AnA_{n-1} + A_{n}
A_{n-1} + A_{n}
DPn−2,k−1DP_{n-2, k-1}
DP_{n-2, k-1}
DPn−1,k−1DP_{n-1, k-1}
DP_{n-1, k-1}
AnA_n
A_n
DP0,k−1DP_{0, k-1}
DP_{0, k-1}
A1+...+AnA_{1} + ... + A_{n}
A_{1} + ... + A_{n}

...

≥\ge
\ge
≥\ge
\ge
≥\ge
\ge
≤\le
\le
≤\le
\le
≤\le
\le

數值

i

DP 項

區間和項

你算完了          ，很棒！

  • 但               呢？
  • 你會發現區間和項只會多差一個          。
  • 如果看二維圖你會發現...
    • 這又代表什麼？
    • 下次的交叉必在右邊。
    • 所以直接往右掃找到交叉點就好。
DPn,kDP_{n, k}
DP_{n, k}
DPn+1,kDP_{n+1, k}
DP_{n+1, k}

下一次的區間和項

An+1A_{n+1}
A_{n+1}
+An+1+A_{n+1}
+A_{n+1}
+An+1+A_{n+1}
+A_{n+1}
+An+1+A_{n+1}
+A_{n+1}
+An+1+A_{n+1}
+A_{n+1}
An+1A_{n+1}
A_{n+1}
DPn,k−1DP_{n, k-1}
DP_{n, k-1}
≥\ge
\ge
≤\le
\le
An+1A_{n+1}
A_{n+1}

Split Array Largest Sum (leetcode 410) 

def splitArray(self, nums , k):
  # Prefix Sum
  Psum = list(accumulate(nums)) + [0]
  # Interval Sum
  def Isum(l, r):
    return Psum[r] - Psum[l-1]

  DP = [[math.inf] * (k+1) for _ in range(len(nums))]
  # Base Case
  for i in range(len(nums)):      
    DP[i][1] = Isum(0, i)

  for cur_k in range(2, k+1):
    L = cur_k-2
    for cur_n in range(cur_k-1, len(nums)):
      while L < cur_n and DP[L+1][cur_k-1] < Isum(L+2, cur_n):
        L += 1
      R = L + 1
      DP[cur_n][cur_k] = min(
        max(DP[L][cur_k-1], Isum(L+1, cur_n)),
        max(DP[R][cur_k-1], Isum(R+1, cur_n))
      )
  return DP[len(nums)-1][k]

Python

注意：掃描到交叉項時，最大值有可能在 DP 項也可能在區間和項，
所以你必須要取左界 (L) 和右界 (R) 的最小值。

int splitArray(vector<int>& nums, int k) {
  // Prefix Sum
  vector<int> PS({0});
  for (auto num : nums)
    PS.push_back(PS.back() + num);
  auto Isum = [=](int l, int r) {return PS[r+1] - PS[l];};

  vector<vector<int>> DP(nums.size(), vector<int> (k+1, INT_MAX));
  // Base Case
  for (int cur_n=0; cur_n < nums.size(); cur_n++)
    DP[cur_n][1] = Isum(0, cur_n);
    

  for (int cur_k=2; cur_k <= k; cur_k++) {
    int L = cur_k-2;
    for (int cur_n=cur_k-1; cur_n < nums.size(); cur_n++) {
      while (L < cur_n && DP[L+1][cur_k-1] < Isum(L+2, cur_n))
        L++;
      int R = L+1;
      DP[cur_n][cur_k] = min(
        max(DP[L][cur_k-1], Isum(L+1, cur_n)),
        max(DP[R][cur_k-1], Isum(R+1, cur_n))
      );
    }
  }
  return DP.back().back();
}

C++

Split Array Largest Sum (leetcode 410)

如果下一項還沒交叉，就往前

  1. 函式定義：
     
  2. 如何拆解：
DPn,k=在A[0,n]中，切成k個區間的最小化總和DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DP_{n, k} = 在A_{[0,n]} 中，切成 k 個區間的最小化總和
DPn,k=min⁡0≤i<n[max⁡(DPi,k−1,∑j=i+1nAj)]DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]
DP_{n, k} = \underset{0\le i < n}{\min} [ \max (DP_{i, k-1}, \sum_{j=i+1}^{n} A_{j})]

將數列切成 kkk 個區間，
最小化這 kkk 個區間總和的最大值。

分析看看複雜度吧！

O(nk)O(nk)
O(nk)

狀態數量             × 轉移複雜度             =

O(n)O(n)
O(n)
O(nk)O(nk)
O(nk)

注意：掃描到交叉項時，最大值有可能在 DP 項也可能在區間和項，
所以你必須要取左界 (L) 和右界 (R) 的最小值。

每輪最多移動 n 次，
均攤 O(1)

Split Array Largest Sum (leetcode 410)

將數列切成 kkk 個區間，
最小化這 kkk 個區間總和的最大值。

  • 原始的DP：
    • 2D1D，狀態 O(nk) 轉移 O(n)，整體 O(nnk)
  • 二分搜優化：
    • 狀態 O(nk) 轉移 O(log n)，整體 O(nk log n)
  • ​轉移點單調優化 (or 這裡叫做 2D/1D 凸性優化)：​
    • 整體 O(nk)
  • 你可以再做滾動把空間複雜度壓下去。
  • 貪心法 (其實才是這題的標程解)：
    • ​O(n log C)，C 為所有數字的總和。
    • 你知道怎麼寫嗎？ (比 DP 還要簡單很多)

Split Array Largest Sum (leetcode 410)

(選擇類) 動態規劃小結

動態規劃小結

恭喜你，被我恭喜到了。

如果你看的到這句話，那你真的很有毅力與勇氣在 DP 上。

在進入下個類型前先回憶一下吧！

複習一下所有上課題目

主題 題目名稱 大概作法
二維地圖類 二維圖路徑數  ☆ DP[n][m] = DP[n-1][m] + DP[n][m-1]。
二維圖最小路 ☆ 同上，但變成 min 。
雙人路徑問題

增加狀態，把兩個人的座標紀錄變4D後又狀態壓縮成3D
子序列選擇 最長共同子序列 (LCS)
☆ 

判斷結尾一不一樣。一樣就 DP[n][m] = DP[n-1][m-1]+1，
不一樣就  DP[n][m] = max(DP[n-1][m], DP[n][m-1])
編輯距離 ☆ 跟 LCS 一樣。
k-相鄰子序列 ☆ 單調對列優化 / Sliding Window
最長遞增子序列 (LIS) ☆ 可以做的跟 LCS 一樣，然後用二分搜優化成 O(nlogn)
區間選擇 最大子區間和 ☆ 簡單題目。也可以用掃描線 + 區間和概念做
美食博覽會 (APCS)  內層轉移 - k = 1：不重複區間可以用雙指針或 DP。
外層轉移 - 選k次：可以再做一次DP或貪心 (DP 套 DP)
股票買賣 有簡單的狀態配上比較難看的轉移，或者比較難想的狀態
配上簡單的轉移(有沒有持股)。隨後是 Aliens 優化。
區間分割 平衡字串分割 寫出轉移很簡單，但優化轉移要利用 Counting Table。
最少回文分割 寫出轉移很簡單，但要漂亮的寫轉移要反過來想，
從順序的找到回文再想怎麼轉移過去。(不固定順序的轉移)
最小化區間總和 轉移式很複雜，可以進一步用二分搜優化成轉移 O(logn)
又可以進一步發現轉移單調優化成轉移 O(1)

動態規劃小結

所以動態規劃怎麼解呢？

  1. 函式定義 / 動態規劃定義
    • 基本上可以朝著兩種大方向定義：
    1. DP(A) = 「B」這個 B 就是題目要的答案 (可能附帶一些條件)。
      • 東東爬樓梯：
        • DP(n) = 題目要的 = 爬到 n 階的可能數。
      • 最大子區間：
        • DP(n) = 「右界為 An 」的最大子區間。
    2. DP(A) = 「B」這個 A 就是題目要的答案，B 為最優條件。
      • LIS：
        • DP(L) = 長度為 L 的遞增子序列的最小結尾是誰。

動態規劃小結

所以動態規劃怎麼解呢？

  1. 函式定義 / 動態規劃定義
    • 基本上可以朝著兩種大方向定義：
    1. DP(A) = 「B」這個 B 就是題目要的答案 (可能附帶一些條件)。
    2. DP(A) = 「B」這個 A 就是題目要的答案，B 為最優條件。
  2. 如何拆解？
    • 思考這個定義下的最後一步是什麼？怎樣拆才能考慮所有可能？
      • 東東爬樓梯：
        • 最後一次爬樓梯是走一階還是走兩階？
      • 背包問題 / 找硬幣問題：
        • 最後要不要選這個物品 / 用這個硬幣找錢
      • 區間選擇 / 區間分割：
        • 最後一次選的區間是從哪裡到 An？

動態規劃小結

所以動態規劃怎麼解呢？

  1. 函式定義 / 動態規劃定義
    • 基本上可以朝著兩種大方向定義：
    1. DP(A) = 「B」這個 B 就是題目要的答案 (可能附帶一些條件)。
    2. DP(A) = 「B」這個 A 就是題目要的答案，B 為最優條件。
  2. 如何拆解？
    • 思考這個定義下的最後一步是什麼？怎樣拆才能考慮所有可能？
    • 如果找不到，那就表示狀態定義不完全。
      • 嘗試在「函式定義」中給入更多資訊。
      • 雙人走路問題：
        • 嘗試直接給兩個人的當前狀態
      • 美食博覽會 / 選 k 個區間的題目：
        • 把「選了幾個區間」放入狀態裡面。

動態規劃小結

所以動態規劃怎麼解呢？

  1. 函式定義 / 動態規劃定義
    • 基本上可以朝著兩種大方向定義：
    1. DP(A) = 「B」這個 B 就是題目要的答案 (可能附帶一些條件)。
    2. DP(A) = 「B」這個 A 就是題目要的答案，B 為最優條件。
  2. 如何拆解？
    • 思考這個定義下的最後一步是什麼？怎樣拆才能考慮所有可能？
    • 如果找不到，那就表示狀態定義不完全。
  3. 轉移優化
    • 思考轉移有什麼方法可以更快？(當然轉移 1D 以上才需要)
      • 思考轉移的所有狀態，有沒有人一定不會是解？(例如LIS)
        • 想辦法維護所有可能的單調性
      • 將             /                的狀態列出來，看差了多少？
DPnDP_n
DP_n
DPn+1DP_{n+1}
DP_{n+1}

動態規劃小結

所以動態規劃怎麼解呢？

  1. 函式定義 / 動態規劃定義
    • 基本上可以朝著兩種大方向定義：
    1. DP(A) = 「B」這個 B 就是題目要的答案 (可能附帶一些條件)。
    2. DP(A) = 「B」這個 A 就是題目要的答案，B 為最優條件。
  2. 如何拆解？
    • 思考這個定義下的最後一步是什麼？怎樣拆才能考慮所有可能？
    • 如果找不到，那就表示狀態定義不完全。
  3. 轉移優化
    • 思考轉移有什麼方法可以更快？(當然轉移 1D 以上才需要)
      • 思考轉移的所有狀態，有沒有人一定不會是解？(例如LIS)
      • 將             /                的狀態列出來，看差了多少？
  4. 除了位元DP以外比較少見，但可以考慮空間壓縮。
DPnDP_n
DP_n
DPn+1DP_{n+1}
DP_{n+1}

動態規劃小結

知道了轉移式，該怎麼寫呢？

  • 考慮用 Top-down 還是 Bottom-up。
    • Bottom-up 的難點在於考慮還要多考慮堆的順序。
    • 如果不需要考慮轉移優化，可以寫 Top-down。
    • 如果你堆的順序寫得很卡，也可以寫 Top-down。
    • 如果狀態具有稀疏性 (Sparsity)，也就是很多地方都跑不到，並且跑不到的地方不好省空間，那麼建議寫 Top-down。
    • 其餘狀況建議寫 Bottom-up。
  • ​轉移不知道怎麼優化，記住你可以使用的工具，也許你就會寫了。
    (有些可以預處理後 O(1) 查詢)
    • 資料結構：單調對列 (deque)、二分搜尋 + map / set 
    • 技巧：區間和、二分搜尋、Counting Table、雙指針、再一次DP
  • 不只這樣，還有更多技巧等著你發現！

二維地圖類

題目名稱 來源 備註
Unique Paths Leetcode 62 沒有障礙物，更簡單
Unique Paths III Leetcode 980 不是DP，純遞迴
Paths Sum Is Divisible by K Leetcode 2435 路總和為 K 倍的路有幾種
Minimum Path Cost in a Grid Leetcode 2304 2D1D，很躁
Dungeon Game Leetcode 174 反做純 DP 解，或
正做+對答案二分搜
Cherry Pickup Leetcode 714 走過去然後走回來最大值
幸運表格 (Lucky) 北市賽 2018, TIOJ 2182 不限定起點找最大路徑
得分高手 (Master) 北市賽 2014, TIOJ 1268 不限定起點找最大路徑
勇者修煉 APCS 2020 / 10 - 3, zj f314 可以走左，走右，走下

子序列類

題目名稱 來源 備註
Another LCS 成高校內賽, zj a252 找三個字串的 LCS
Compromise zj e682 還原 LCS
有限間距最長共同子序列 /
股票趨勢 (每個字元不同限制) 		zj b478, zj a374
學科決賽 100 - 5

限制 LCS 間距不能太大，
維護二維窗口最大值。
Regular Expression Matching Leetcode 10 .* wildcard 匹配
Max Dot of Two Subseqs Leetcode 1458 最大子序列內積
Number of LIS Leetcode 683 計算 LIS 的個數
Maximal Square Leetcode 221 找最大全都是 1 的正方形
飛黃騰達 APCS 2021 / 01 - 4, zj f608 二維的 LIS
Maximize Win From Two Segments leetcode 2555 不是 DP，但 Sliding Window

區間選擇類

題目名稱 來源 備註
Best SightSeeing Pair leetcode 1014 最大化 A[i]-A[j]+i-j
內積 APCS 2022 / 06 - 4, zj i402 很多個最大子區間和
Maximum Subarray Sum
with One Deletion		 leetcode 1186

選一個最大和區間，
但可以無視其中 1 個值
投資遊戲 APCS 2023 / 10 - 4, zj 373

同上，但可無視 k 個
Maximum of Spliced Array leetcode 2321 給兩個陣列，選同樣位置的
兩個子區間互換，要求其一總和最大
Max sum of 3 subarrays leetcode 689 可以寫 O(nk), k=3 的DP
或者掃描第二個區間，詳見貪心
股票買賣 III leetcode 123 股票買賣 IV 但是 k=2。
除了裸套上課的算法外還可以對半拆。
美食博覽會 (困難版) zj h926 美食博覽會，但 k 很大
分組開會 APCS 2025 / 01 - 4, zj q184 Sliding Window 處理 + 選 k 個子區間

leetcode 1696, 1425, 2944, 375, 3117

區間分割類

題目名稱 來源 備註
Partition String into min substgrings leetcode 2767 切出來的字串是5的倍數
且沒有前綴0
Partition Array for Maximum Sum leetcode 1043  
Minimum Cost to Split an Array leetcode 2547 轉移要 Counting Table
Allocate Mail Boxes leetcode 1478 APCS 分組開會困難版

https://leetcode.com/problems/divide-an-array-into-subarrays-with-minimum-cost-ii/description/

https://leetcode.com/problems/minimum-cost-to-cut-a-stick/description/

https://leetcode.com/problems/minimum-sum-of-values-by-dividing-array/description/

其他的選擇類DP

題目名稱 來源 備註
Max Value of piles leetcode 2218 要區間和的類背包問題
Max profit in job scheduling leetcode 1235 有權重的排程問題
Max num of events II leetcode 1751 類似上題

記數類DP

記數類DP

  • 記數類題目就是問你最後有幾種可能。
    • 例如爬樓梯 / C(n, m) 就是記數類。
    • 部分題目涉及大量數學，做好準備。
  • 基本上分成兩類題目：
    • 題目沒什麼限制 (輸入非常單純)
      • 特別考驗你的排列組合的功力，
        還有定狀態的想像力
    • 題目有限制 (輸入比較複雜)
      • 這類題目通常比較簡單，但實作會牽涉其他算法。
  • 請複習一下同餘定理 (詳見遞迴投影片的同餘定理)。

骨牌問題

Domino and Tromino Tiling (leetcode 790)

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：



(Domino)    (Tromino)

請問有幾種方法可以填滿 2 x N 的空間？

N = 3 的 Case：五種

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

  1. 函式定義：
DPn=2×N的可能數DP_{n} =2\times N 的可能數
DP_{n} =2\times N 的可能數

...

這種 Case 會很難算，嘗試多給一些狀態？

DPn,0=DP_{n, 0} =
DP_{n, 0} =

...

                     ⏞n\overbrace{~~~~~~~~~~~~~~~~~~~~~}^{n}
\overbrace{~~~~~~~~~~~~~~~~~~~~~}^{n}

的可能數

DPn,1=DP_{n, 1} =
DP_{n, 1} =

...

                     ⏞n\overbrace{~~~~~~~~~~~~~~~~~~~~~}^{n}
\overbrace{~~~~~~~~~~~~~~~~~~~~~}^{n}

的可能數

  • 因為對稱，
    上面缺洞的可能數
    = 下面缺洞的可能數

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

  1. 函式定義：
     
  2. 如何拆解：
{DPn,0=2×N的可能數DPn,1=2×N，但缺一個的可能數\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}
\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}

考慮最後可以怎麼放！

Case 0:

...

                          ⏞n−1\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}

...

                          ⏞n−1\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}

...

                          ⏞n−1\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}

...

                          ⏞n−2\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-2}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-2}
DPn,0=2×DPn−1,1+DPn−1,0+DPn−2,0DP_{n, 0} \\ = 2\times DP_{n-1, 1} \\ + DP_{n-1, 0} \\ + DP_{n-2, 0} \\
DP_{n, 0} \\ = 2\times DP_{n-1, 1} \\ + DP_{n-1, 0} \\ + DP_{n-2, 0} \\

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

  1. 函式定義：
     
  2. 如何拆解：
{DPn,0=2×N的可能數DPn,1=2×N，但缺一個的可能數\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}
\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}

Case 1:

...

                     ⏞n−2\overbrace{~~~~~~~~~~~~~~~~~~~~~}^{n-2}
\overbrace{~~~~~~~~~~~~~~~~~~~~~}^{n-2}

...

                          ⏞n−1\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~}^{n-1}
DPn,1=DPn−1,1+DPn−2,0DP_{n, 1} \\ = DP_{n-1, 1} \\ + DP_{n-2, 0}
DP_{n, 1} \\ = DP_{n-1, 1} \\ + DP_{n-2, 0}

考慮最後可以怎麼放！

Case 0:

DPn,0=2×DPn−1,1+DPn−1,0+DPn−2,0DP_{n, 0} \\ = 2\times DP_{n-1, 1} \\ + DP_{n-1, 0} \\ + DP_{n-2, 0} \\
DP_{n, 0} \\ = 2\times DP_{n-1, 1} \\ + DP_{n-1, 0} \\ + DP_{n-2, 0} \\

Domino and Tromino Tiling (leetcode 790)

  1. 函式定義：

     
  2. 如何拆解：
{DPn,0=2×N的可能數DPn,1=2×N，但缺一個的可能數\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}
\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}
{DPn,0=DPn−1,0+2×DPn−1,1+DPn−2,0DPn,1=DPn−1,1+DPn−2,0\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
還沒寫

C++

Domino and Tromino Tiling (leetcode 790)

  1. 函式定義：

     
  2. 如何拆解：
{DPn,0=2×N的可能數DPn,1=2×N，但缺一個的可能數\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}
\begin{cases} DP_{n, 0} =2\times N 的可能數 \\ DP_{n, 1} =2\times N，但缺一個的可能數 \end{cases}
{DPn,0=DPn−1,0+2×DPn−1,1+DPn−2,0DPn,1=DPn−1,1+DPn−2,0\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
dp = {}
def f(n, t):
  M = 1_000_000_007
  if n == 1:
    return 1 if t==0 else 0
  if n == 2:
    return 2 if t==0 else 1
  if (n, t) not in dp:
    if t == 0:
      dp[n, t] = (f(n-1, 0) + f(n-2, 0) + 2 * f(n-1, 1)) % M
    else:
      dp[n, t] = (f(n-1, 1) + f(n-2, 0)) % M
  return dp[n, t]
return f(n, 0)

Python

骨牌問題 - II

Domino and Tromino Tiling (leetcode 790)

矩陣快速冪

先備知識：矩陣乘法

A的rowi⋅B的colj=Ci,jA 的 row_i \cdot B 的 col_j = C_{i, j}
A 的 row_i \cdot B 的 col_j = C_{i, j}
A×B=CCi,j=∑kAi,kBk,jA\times B = C \\ C_{i, j} = \sum_{k} A_{i, k} B_{k, j}
A\times B = C \\ C_{i, j} = \sum_{k} A_{i, k} B_{k, j}

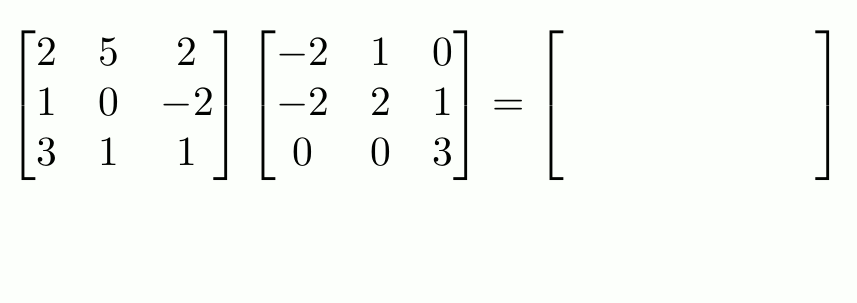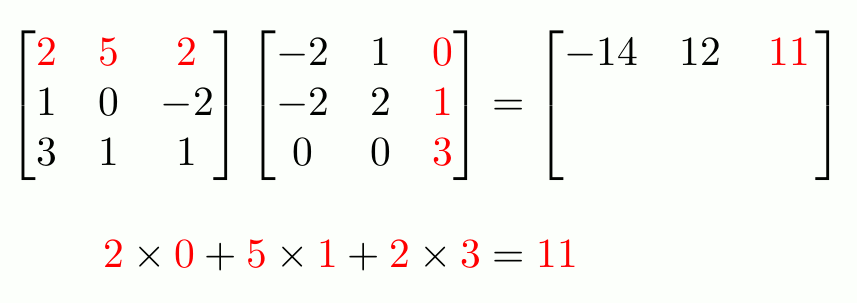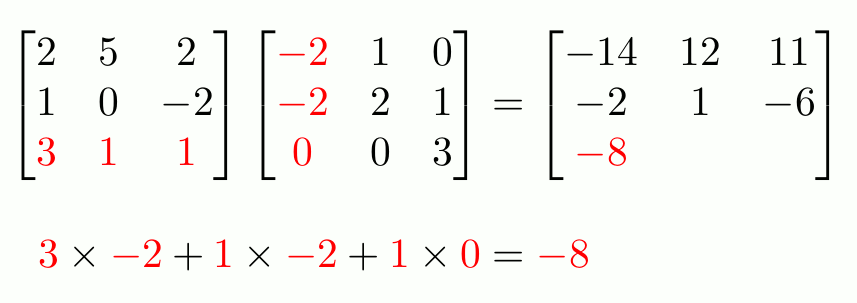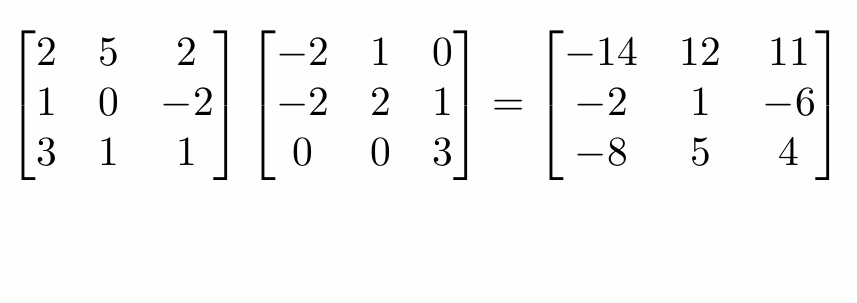
所以 A 的 (col) 列數要等於 B 的 (row) 行數，否則不能乘法。

先備知識：矩陣乘法

Ci,j=∑kAi,kBk,jC_{i, j} = \sum_{k} A_{i, k} B_{k, j}
C_{i, j} = \sum_{k} A_{i, k} B_{k, j}
def mat_mul(A, B):
    n, m, p = len(A), len(A[0]), len(B[0])
    C = [[0] * p for _ in range(n)]
    for i in range(n):
        for j in range(p):
            for k in range(m):
                C[i][j] = (C[i][j] + A[i][k] * B[k][j])
    return C
還在寫

Python

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

{DPn,0=DPn−1,0+2×DPn−1,1+DPn−2,0DPn,1=DPn−1,1+DPn−2,0\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
[121011100][DPn−1,0DPn−1,1DPn−2,0]=[DPn,0DPn,1DPn−1,0]\begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} DP_{n-1, 0} \\ DP_{n-1, 1} \\ DP_{n-2, 0} \end{bmatrix} = \begin{bmatrix} DP_{n, 0} \\ DP_{n, 1} \\ DP_{n-1, 0} \end{bmatrix}
\begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} DP_{n-1, 0} \\ DP_{n-1, 1} \\ DP_{n-2, 0} \end{bmatrix} = \begin{bmatrix} DP_{n, 0} \\ DP_{n, 1} \\ DP_{n-1, 0} \end{bmatrix}
                    ⏟A\underbrace{~~~~~~~~~~~~~~~~~~~~}_{A}
\underbrace{~~~~~~~~~~~~~~~~~~~~}_{A}
                ⏟vn−1\underbrace{~~~~~~~~~~~~~~~~}_{v_{n-1}}
\underbrace{~~~~~~~~~~~~~~~~}_{v_{n-1}}
                ⏟vn\underbrace{~~~~~~~~~~~~~~~~}_{v_{n}}
\underbrace{~~~~~~~~~~~~~~~~}_{v_{n}}

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

{DPn,0=DPn−1,0+2×DPn−1,1+DPn−2,0DPn,1=DPn−1,1+DPn−2,0\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
\begin{cases} DP_{n, 0} = DP_{n-1, 0} + 2\times DP_{n-1, 1} + DP_{n-2, 0} \\ DP_{n, 1} = DP_{n-1, 1} + DP_{n-2, 0} \end{cases}
A=[121011100]A = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix}
A = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix}
Avn−1=vnA v_{n-1} = v_{n}
A v_{n-1} = v_{n}
A(Avn−1)=A(vn)=vn+1A(A v_{n-1}) = A(v_{n}) = v_{n+1}
A(A v_{n-1}) = A(v_{n}) = v_{n+1}
∵矩陣有結合率(AB)C=A(BC)∴A(Avn−1)=(AA)vn−1=A2vn−1=vn+1\because 矩陣有結合率 (AB)C = A(BC) \\ \therefore A(A v_{n-1}) = (AA) v_{n-1} = A^2 v_{n-1} = v_{n+1}
\because 矩陣有結合率 (AB)C = A(BC) \\ \therefore A(A v_{n-1}) = (AA) v_{n-1} = A^2 v_{n-1} = v_{n+1}
→An−2v2=vn\rightarrow A^{n-2} v_2 = v_n
\rightarrow A^{n-2} v_2 = v_n

阿這有什麼用？

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

[121011100]n−2⏟An−2[211]⏟v2=[DPn,0DPn,1DPn−1,0]⏟vn\underbrace{ \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix}^{n-2}}_{A^{n-2}} \underbrace{\begin{bmatrix} 2 \\ 1 \\ 1 \end{bmatrix}}_{v_{2}} = \underbrace{ \begin{bmatrix} DP_{n, 0} \\ DP_{n, 1} \\ DP_{n-1, 0} \end{bmatrix} }_{v_n}
\underbrace{ \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix}^{n-2}}_{A^{n-2}} \underbrace{\begin{bmatrix} 2 \\ 1 \\ 1 \end{bmatrix}}_{v_{2}} = \underbrace{ \begin{bmatrix} DP_{n, 0} \\ DP_{n, 1} \\ DP_{n-1, 0} \end{bmatrix} }_{v_n}
An−2v2=vnA^{n-2} v_2 = v_n
A^{n-2} v_2 = v_n

這樣複雜度是多少呢？

矩陣乘法:O(33)×O(n)次=O(n)矩陣乘法: O(3^3) \times O(n) 次 = O(n)
矩陣乘法: O(3^3) \times O(n) 次 = O(n)

那不是一樣嗎？我們先介紹一個技巧

Pow(x, n) (leetcode 50)

現在給你一個浮點數 x 以及整數 n，
請求出                                                        

xn,其中n範圍(2−31≤n≤231−1)x^n, 其中 n 範圍 (2^{-31} \le n \le 2^{31 - 1})
x^n, 其中 n 範圍 (2^{-31} \le n \le 2^{31 - 1})

不過高中學指數的時候好像有這麼一回事：

xnm=(xn)mx^{nm} = (x^n)^m
x^{nm} = (x^n)^m

所以如果 n 是偶數 (=2k) 的話，可以變成這樣：

xn=x2k=(x2)kx^{n} = x^{2k} = (x^2)^k
x^{n} = x^{2k} = (x^2)^k

指數的數字會剩一半！

直接用 for 迴圈：

O(∣n∣)噴爛O(|n|) 噴爛
O(|n|) 噴爛

那麼 n 是奇數 (=2k+1) 呢？ n-1不就是偶數了嗎

xn=x2k+1=x×(x2)kx^{n} = x^{2k+1} = x \times (x^2)^k
x^{n} = x^{2k+1} = x \times (x^2)^k

快速冪次 Pow(x, n) (leetcode 50)

現在給你一個浮點數 x 以及整數 n，
請求出                                                        

xn,其中n範圍(2−31≤n≤231−1)x^n, 其中 n 範圍 (2^{-31} \le n \le 2^{31 - 1})
x^n, 其中 n 範圍 (2^{-31} \le n \le 2^{31 - 1})
xn=pow(x,n)={(x2)n2=pow(x2,n2) if n是偶數x×xn−1=x×pow(x,n−1) if n是奇數x^{n} = pow(x, n) = \begin{cases} (x^2)^{\frac n2} = pow(x^2, \frac n2)& \text{ if }n 是偶數 \\ x \times x^{n-1} = x \times pow(x, n-1) &\text{ if }n 是奇數 \\ \\ \\ \end{cases}
x^{n} = pow(x, n) = \begin{cases} (x^2)^{\frac n2} = pow(x^2, \frac n2)& \text{ if }n 是偶數 \\ x \times x^{n-1} = x \times pow(x, n-1) &\text{ if }n 是奇數 \\ \\ \\ \end{cases}

Base Case 呢？

n < 0 呢?

11
1
=(x−1)−n=pow(1x,−n)= (x^{-1})^{-n} = pow(\frac 1x, -n)
= (x^{-1})^{-n} = pow(\frac 1x, -n)
 if n=0\text{ if } n = 0
\text{ if } n = 0
 if n<0\text{ if } n < 0
\text{ if } n < 0

這個函數的複雜度是多少呢？

最多兩步就會砍一半：

O(log⁡∣n∣)O(\log |n|)
O(\log |n|)

這個方法叫做快速冪 (Fast Pow)

Pow(x, n) (leetcode 50)

現在給你一個浮點數 x 以及整數 n，
請求出                                                        

xn,其中n範圍(2−31≤n≤231−1)x^n, 其中 n 範圍 (2^{-31} \le n \le 2^{31 - 1})
x^n, 其中 n 範圍 (2^{-31} \le n \le 2^{31 - 1})
double myPow(double x, int n) {
  if (n == 0)
    return 1;
  if (n < 0)
    return myPow(1/x, -(n+1))/x;
  if (n % 2 == 0)
    return myPow(x*x, n/2);
  else
    return x * myPow(x, n-1);
}
def myPow(self, x: float, n: int):
  if n == 0:
    return 1
  if n < 0:
    return self.myPow(1/x, -n)
  if n % 2 == 0:
    return self.myPow(x * x, n // 2)
  else:
    return x * self.myPow(x, n - 1)

Python

C++

註：當 n = INT_MIN 的時候，-n 會噴掉，所以需要把 n + 1 避免 overflow

xn=pow(x,n)={(x2)n2=pow(x2,n2) if n是偶數x×xn−1=x×pow(x,n−1) if n是奇數1 if n=0=(x−1)−n=pow(1x,−n) if n<0x^{n} = pow(x, n) = \begin{cases} (x^2)^{\frac n2} = pow(x^2, \frac n2)& \text{ if }n 是偶數 \\ x \times x^{n-1} = x \times pow(x, n-1) &\text{ if }n 是奇數 \\ 1 & \text{ if } n = 0 \\ = (x^{-1})^{-n} = pow(\frac 1x, -n) & \text{ if } n < 0 \\ \end{cases}
x^{n} = pow(x, n) = \begin{cases} (x^2)^{\frac n2} = pow(x^2, \frac n2)& \text{ if }n 是偶數 \\ x \times x^{n-1} = x \times pow(x, n-1) &\text{ if }n 是奇數 \\ 1 & \text{ if } n = 0 \\ = (x^{-1})^{-n} = pow(\frac 1x, -n) & \text{ if } n < 0 \\ \end{cases}

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

[121011100]n−2⏟An−2[211]⏟v2=[DPn,0DPn,1DPn−1,0]⏟vn\underbrace{ \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix}^{n-2}}_{A^{n-2}} \underbrace{\begin{bmatrix} 2 \\ 1 \\ 1 \end{bmatrix}}_{v_{2}} = \underbrace{ \begin{bmatrix} DP_{n, 0} \\ DP_{n, 1} \\ DP_{n-1, 0} \end{bmatrix} }_{v_n}
\underbrace{ \begin{bmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \end{bmatrix}^{n-2}}_{A^{n-2}} \underbrace{\begin{bmatrix} 2 \\ 1 \\ 1 \end{bmatrix}}_{v_{2}} = \underbrace{ \begin{bmatrix} DP_{n, 0} \\ DP_{n, 1} \\ DP_{n-1, 0} \end{bmatrix} }_{v_n}

回來看這題，好像也可以用一樣的方法做？

An=pow(x,n)={(A2)n2=pow(mul(A,A),n2) if n是偶數A×An−1=mul(A,pow(A,n−1)) if n是奇數A if n=1A^{n} = pow(x, n) = \begin{cases} (A^2)^{\frac n2} = pow(mul(A, A), \frac n2)& \text{ if }n 是偶數 \\ A \times A^{n-1} = mul(A, pow(A, n-1)) &\text{ if }n 是奇數 \\ A & \text{ if } n = 1 \\ \end{cases}
A^{n} = pow(x, n) = \begin{cases} (A^2)^{\frac n2} = pow(mul(A, A), \frac n2)& \text{ if }n 是偶數 \\ A \times A^{n-1} = mul(A, pow(A, n-1)) &\text{ if }n 是奇數 \\ A & \text{ if } n = 1 \\ \end{cases}

這樣複雜度是多少呢？

矩陣乘法:O(33)×O(log⁡n)次=O(log⁡n)矩陣乘法: O(3^3) \times O(\log n) 次 = O(\log n)
矩陣乘法: O(3^3) \times O(\log n) 次 = O(\log n)

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

還沒寫

C++

因為題目要將答案 % M，
所以所有的運算記得要 % M。
但為什麼可以在中間就 % M，
請參考同餘定理。

Domino and Tromino Tiling (leetcode 790)

現在你有兩種骨牌：Domino & Tromino

請問有幾種方法可以填滿 2 x N 的空間？

def numTilings(self, n, t=0) -> int:
  M = 1_000_000_007
  def mat_mul(A, B):
    n, m, p = len(A), len(A[0]), len(B[0])
    C = [[0] * p for _ in range(n)]
    for i in range(n):
      for j in range(p):
        for k in range(m):
          C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % M
    return C
  def fast_pow(A, n):
    if n == 1:
      return A
    if n % 2 == 0:
      return fast_pow(mat_mul(A, A), n//2)
    else:
      return mat_mul(A, fast_pow(A, n-1))
  A = [[1, 2, 1], [0, 1, 1], [1, 0, 0]]
  if n == 1:
    return 1
  if n == 2:
    return 2
  return mat_mul(fast_pow(A, n-2), [[2], [1], [1]])[0][0]

Python

因為題目要將答案 % M，
所以所有的運算記得要 % M。
但為什麼可以在中間就 % M，
請參考同餘定理。

練習題！

  • 這種可以寫成矩陣的形式，通稱線性轉換。
    (因為矩陣乘法加法都是線性函數)
    這個矩陣 (如上題的 A)，我們叫它 轉移矩陣。 
    (以前高中有教，但現在我不知道有沒有拔掉，參見這裡。

 

  1. 東東爬樓梯的轉移矩陣怎麼寫？
    • 這樣你就知道東東爬樓梯可以 O(log n) 算出解答了！
  2. 請問將 Domino 放入 2xN 的空間有幾種放法？
  3. 請問將 Domino 放入 3xN 的空間有幾種放法？
  4. 請問將 Domino 放入 MxN 的空間有辦法這樣寫嗎？
    • ​​講義後面的「位元DP」環節會正式介紹這題的解法

卡特蘭數

配對連線 (學科決賽 107 - 1, zj e876)

Catalan Number

配對連線 (學科決賽 107 - 1, zj e876)

現在有一個圓，圓上有 2n 個點。
將這些點分成兩個一組，並連線。
請問有幾種可能使得所有連線不相交？

不合法。

當 n = 2，答案為 2

舉例來說：

當 n = 3，答案為 5

配對連線 (學科決賽 107 - 1, zj e876)

現在有一個圓，圓上有 2n 個點。
將這些點分成兩個一組，並連線。
請問有幾種可能使得所有連線不相交？

  • 切的時候，會將圓切成左右兩部分。
    • 切的時候左右兩邊的點要是偶數。否則無解。
  • 以 n = 3 來看：
    • 橘色：順時針有 4 個點，逆時針有 0 個點
      • 左邊有        個可能，右邊有        個可能
    • 紅色：順時針有 2 個點，逆時針有 2 個點
      • 左邊有        個可能，右邊有        個可能
    • 綠色：順時針有 0 個點，逆時針有 4 個點
      • 左邊有        個可能，右邊有        個可能
  1. 函式定義：
  2. 如何拆解：
DPn=答案DP_{n} = 答案
DP_{n} = 答案

考慮隨便一個點可以怎麼連線？

DP2DP_2
DP_2
DP0DP_0
DP_0
DP1DP_1
DP_1
DP1DP_1
DP_1
DP2DP_2
DP_2
DP0DP_0
DP_0

配對連線 (學科決賽 107 - 1, zj e876)

現在有一個圓，圓上有 2n 個點。
將這些點分成兩個一組，並連線。
請問有幾種可能使得所有連線不相交？

  1. 函式定義：
  2. 如何拆解：
DPn=答案DP_{n} = 答案
DP_{n} = 答案

考慮隨便一個點可以怎麼連線？

...

...

2A 個點

2B 個點

  • 想想看變數版本：
    • 如果砍一刀，順 2A 個點，逆 2B 個點
      • 左邊可能數：
      • 右邊可能數：
      • 那麼總共呢？
    • 枚舉所有可能：
DPADP_A
DP_A
DPBDP_B
DP_B
DPA×DPBDP_A \times DP_B
DP_A \times DP_B
DPn=DP0×DPn−1+DP1×DPn−2+...+DPn−1×DP0DP_{n} = DP_{0} \times DP_{n-1} + DP_{1} \times DP_{n-2} + \\ ... + DP_{n-1} \times DP_{0}
DP_{n} = DP_{0} \times DP_{n-1} + DP_{1} \times DP_{n-2} + \\ ... + DP_{n-1} \times DP_{0}

配對連線 (學科決賽 107 - 1, zj e876)

現在有一個圓，圓上有 2n 個點。
將這些點分成兩個一組，並連線。
請問有幾種可能使得所有連線不相交？

  1. 函式定義：
     
  2. 如何拆解：
DPn=答案DP_{n} = 答案
DP_{n} = 答案
DPn=∑i=0n−1DPi×DPn−i−1DP_{n} = \sum_{i = 0}^{n-1} DP_{i} \times DP_{n-i-1}
DP_{n} = \sum_{i = 0}^{n-1} DP_{i} \times DP_{n-i-1} 
dp = {0: 1}
def f(n):
  if n not in dp:
    cur = 0
    for i in range(n):
      cur += f(i) * f(n-i-1)
    dp[n] = cur
  return dp[n]

import sys
for row in sys.stdin:
    n = int(row)
    if n != 0:
      print(f(n))

Python

C++ 這題很靠北
要實作大數

很麻煩捏 自己寫

配對連線 (學科決賽 107 - 1, zj e876)

現在有一個圓，圓上有 2n 個點。
將這些點分成兩個一組，並連線。
請問有幾種可能使得所有連線不相交？

這個 DP 的定義式，有個著名的稱呼：

卡特蘭數

(Catalan Number)

他有非常多的變形題目，
但最後的答案都指向卡特蘭數，
讓我們一起來看個幾題吧！

跟卡特蘭數相關的題目

從 (0, 0) 走到 (n, n) 的最短路徑的數量，並且
不能跨越過對角線 (也就是整個過程            ) 有幾種

N = 4 的 Case: 14種

x≥yx \ge y
x \ge y

枚舉最後一次碰到
對角線的可能

假設最後一次碰到 (2, 2)：

(0,0)→(2,2)⏞DP2→(3,2)→(5,4)⏞DP2→(5,5)\overbrace{(0, 0) \rightarrow (2, 2)}^{DP_2} \rightarrow \overbrace{(3, 2) \rightarrow (5, 4)}^{DP_2} \rightarrow (5, 5)
\overbrace{(0, 0) \rightarrow (2, 2)}^{DP_2} \rightarrow \overbrace{(3, 2) \rightarrow (5, 4)}^{DP_2} \rightarrow (5, 5)

跟卡特蘭數相關的題目

從 (0, 0) 走到 (n, n) 的最短路徑的數量，並且
不能跨越過對角線 (也就是整個過程            ) 有幾種

x≥yx \ge y
x \ge y

n 組括號的合法匹配可能數有幾種

((()))
()(())
()()()
(())()
(()())
 

n = 3 的 Case

判斷一個字串匹配是否合法：

遇到 ( +1，遇到 ) -1。

那麼只要最後是 0 且中間過程全程 ≥ 0
這個組合就合法。

看起來跟上一題一樣？

因為變成往右 + 1，往上 - 1。

( ( ) ( ) )
1 2 1 2 1 0

跟卡特蘭數相關的題目

有 n 個節點的二元樹有幾種？

n = 3 的 Case

這題就比較好理解，因為自己 root 少了一個節點，接著枚舉左右兩棵樹的節點樹就可以。

a 個節點的樹

n - a - 1 個節點的樹

更多等價問題可以參見 Wiki

卡特蘭數的公式

Catalann=Cn2n−Cn−12n=Cn2nn+1=Catalann−1×4n−2n+1Catalan_{n} \\ = C^{2n}_{n} - C^{2n}_{n-1} \\ = \frac {C^{2n}_{n}}{n+1} \\ = Catalan_{n-1} \times \frac{4n-2}{n+1}
Catalan_{n} \\ = C^{2n}_{n} - C^{2n}_{n-1} \\ = \frac {C^{2n}_{n}}{n+1} \\ = Catalan_{n-1} \times \frac{4n-2}{n+1}

更多詳細的證明以及其他公式請看這裡

卡特蘭數有一些公式在：

各種排組問題

國小排列組合 (zj h997)

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下幾種 Case 的可能數：

  1. 球不同，箱子不同
  2. 球相同，箱子不同
  3. 球不同，箱子相同
  4. 球相同，箱子相同

這裡並不是排列組合課

我們一個一個討論吧！

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球不同，箱子不同

A📦

⚽a

B📦

C📦

⚽b

          ⏟m個箱子\underbrace{~~~~~~~~~~}_{m個箱子}
\underbrace{~~~~~~~~~~}_{m個箱子}
          ⏟n顆球\underbrace{~~~~~~~~~~}_{n顆球}
\underbrace{~~~~~~~~~~}_{n顆球}
  • 每顆球都有 m 個可能
m×m...⏟n=mn\underbrace{m \times m ...}_{n} = m^n
\underbrace{m \times m ...}_{n} = m^n

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球相同，箱子不同
定義：DPn,m=可能數定義：DP_{n, m} = 可能數
定義：DP_{n, m} = 可能數

如何拆解？考量最後一個箱子

如果最後一個箱子有 i 顆球：

DPn−i,m−1DP_{n-i, m-1}
DP_{n-i, m-1}
                        ⏟n−i顆球\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~}_{n-i顆球}
\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~}_{n-i顆球}
DPn,m=DPn,m−1+DPn−1,m−1+...+DP0,m−1+=∑i=0nDPi,m−1DP_{n,m} = DP_{n, m-1} \\+ DP_{n-1, m-1} + ... + DP_{0, m-1} + \\ = \sum_{i=0}^{n} DP_{i, m-1}
DP_{n,m} = DP_{n, m-1} \\+ DP_{n-1, m-1} + ... + DP_{0, m-1} + \\ = \sum_{i=0}^{n} DP_{i, m-1}

A📦

B📦

C📦

m📦

...

⚽⚽⚽
⚽⚽

          ⏟i顆球\underbrace{~~~~~~~~~~}_{i顆球}
\underbrace{~~~~~~~~~~}_{i顆球}

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球相同，箱子不同
定義：DPn,m=可能數=∑i=0nDPi,m−1定義：DP_{n, m} = 可能數 = \sum_{i=0}^{n} DP_{i, m-1}
定義：DP_{n, m} = 可能數 = \sum_{i=0}^{n} DP_{i, m-1}

你稍微觀察會發現：                                 的前綴和

所以對著 Base Case (n=0可能數為1) 做 n 次前綴和就好了。

from itertools import accumulate
M = int(1e9+7)
dp = [1] * max_m
for _ in range(n):
  dp = [x % M for x in accumulate(dp)]
print(*dp)

Python

C++

DPn,m=∑i=0n−1DPi,m−1+DPn,m−1=DPn−1,m+DPn,m−1DP_{n, m} = \sum_{i=0}^{n-1} DP_{i, m-1} + DP_{n, m-1} = DP_{n-1, m} + DP_{n, m-1}
DP_{n, m} = \sum_{i=0}^{n-1} DP_{i, m-1} + DP_{n, m-1} = DP_{n-1, m} + DP_{n, m-1}
DP?,m=DP?,m−1DP_{?, m} = DP_{?, m-1}
DP_{?, m} = DP_{?, m-1}

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球相同，箱子不同

事實上，這在高中被刪除
的課綱叫做重複組合

我們可以用排列組合的形式來看這題：

假設現在有五顆球，三個箱子，可以看成是
五顆球 + 兩個隔板的排列組合

⚽|⚽⚽⚽|⚽

舉例來說：

箱子分別有: 1/3/1

⚽⚽⚽⚽⚽||

箱子分別有: 5/0/0

n個箱子+m−1個隔板排列組合=(n+m−1)!n!×(m−1)!=Cm−1n+m−1=Hm−1nn個箱子 + m-1 個隔板排列組合 \\= \frac{(n+m-1)!}{n! \times (m-1)!} = C^{n+m-1}_{m-1} = H^{n}_{m-1}
n個箱子 + m-1 個隔板排列組合 \\= \frac{(n+m-1)!}{n! \times (m-1)!} = C^{n+m-1}_{m-1} = H^{n}_{m-1}

接下來就可以套C的公式。

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球不同，箱子相同
DPn,m=有m個不為空的盒子的可能數DP_{n, m} = 有 m 個不為空的盒子的可能數
DP_{n, m} = 有 m 個不為空的盒子的可能數
  1. 函式定義：
  2. 如何拆解：

n = 2
m = 2

ABC
AB C
AC B
A BC
AB
A B

n = 3
m = 2 

DP3,1DP_{3, 1}
DP_{3, 1}
DP2,1DP_{2, 1}
DP_{2, 1}
DP2,2DP_{2, 2}
DP_{2, 2}
DP3,2DP_{3, 2}
DP_{3, 2}

我們先從 n = 2,3, m = 2
的 Case，找尋靈感。
觀察下狀態是怎麼轉移的。

每多一顆球，會根據原本
有幾個非空的箱子而轉移。

不考慮 C 自己一個箱子，

C 放在 |AB| 中只有一種可能

C 放在 |A|B| 中有兩種可能

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球不同，箱子相同
DPn,m=有m個不為空的盒子的可能數DP_{n, m} = 有 m 個不為空的盒子的可能數
DP_{n, m} = 有 m 個不為空的盒子的可能數
  1. 函式定義：
  2. 如何拆解：
ABC
AB C
AC B
A BC
AB
A B
DP3,1DP_{3, 1}
DP_{3, 1}
DP2,1DP_{2, 1}
DP_{2, 1}
DP2,2DP_{2, 2}
DP_{2, 2}
DP3,2DP_{3, 2}
DP_{3, 2}

考量新的一顆球要放哪？

  • 獨立放一個新的

     
  • 放在任一個之前的盒子

     
}=DPn,m\begin{rcases} \\ \\ \\ \\ \\ \\ \end{rcases} = DP_{n, m}
\begin{rcases} \\ \\ \\ \\ \\ \\ \end{rcases} = DP_{n, m}
DPn−1,m−1DP_{n-1, m-1}
DP_{n-1, m-1}
m×DPn−1,mm \times DP_{n-1, m}
m \times DP_{n-1, m}
DPn,m=DPn−1,m−1+m×DPn−1,mDP_{n, m} = DP_{n-1, m-1} + m \times DP_{n-1, m}
DP_{n, m} = DP_{n-1, m-1} + m \times DP_{n-1, m}

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球不同，箱子相同
DPn,m=有m個不為空的盒子的可能數DP_{n, m} = 有 m 個不為空的盒子的可能數
DP_{n, m} = 有 m 個不為空的盒子的可能數
  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPn,m=DPn−1,m−1+m×DPn−1,mDP_{n, m} = DP_{n-1, m-1} + m \times DP_{n-1, m}
DP_{n, m} = DP_{n-1, m-1} + m \times DP_{n-1, m} 
M = int(1e9+7)
dp = [[0] * (max_m+1) for _ in range(n+1)]
for i in range(1, n+1):
  for j in range(1, i+1):
    if j == 1 or i == j:
      dp[i][j] = 1
    else:
      dp[i][j] = (dp[i-1][j-1] + (j) * dp[i-1][j]) % M
print(*map(lambda x: x%M, accumulate(dp[n][1:max_m+1])))

Python

C++

DPn,n=1⏟全都分開放,DPn,1=1⏟全都放一起\underbrace{DP_{n, n} = 1}_{全都分開放}, \underbrace{DP_{n, 1} = 1}_{全都放一起}
\underbrace{DP_{n, n} = 1}_{全都分開放}, \underbrace{DP_{n, 1} = 1}_{全都放一起}

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球相同，箱子相同
  1. 函式定義：

既然球沒有分，那應該用數字
表示箱子有幾顆球？

x1+x2+...+xm=n,∀xi∈Z0+x_1 + x_2 + ... +x_m = n, \forall x_i \in \mathbb Z^+_0
x_1 + x_2 + ... +x_m = n, \forall x_i \in \mathbb Z^+_0

順帶一提，第二個 Case
(球相同，箱子不同) 也可以寫成
這樣的形式，這也是
重複組合的基本寫法。

接著思考一樣看怎麼轉

4

n = 3 的
所有 Case

n = 4 的
所有 Case

3 + 1

2 + 2

3

2 + 1

2 + 1 + 1

1 + 1 + 1

1 + 1 + 1 + 1

DPn,m=有m個不為空的盒子的可能數DP_{n, m} = 有 m 個不為空的盒子的可能數
DP_{n, m} = 有 m 個不為空的盒子的可能數

註：這又叫做整數拆分

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球相同，箱子相同
DPn,m=有m個不為空的盒子的可能數DP_{n, m} = 有 m 個不為空的盒子的可能數
DP_{n, m} = 有 m 個不為空的盒子的可能數
DP8,3所有可能DP_{8, 3} 所有可能
DP_{8, 3} 所有可能

6 + 1 + 1

5 + 2 + 1

4 + 3 + 1

4 + 2 + 2

3 + 3 + 2

  1. 函式定義：
  2. 如何拆解：

怎麼拆呢？考慮 Case 有沒有 1

  • 數字拆分有 1

     
  • 數字拆分沒有 1
DPn−1,m−1DP_{n-1, m-1}
DP_{n-1, m-1}

說實話有點難...

國小排列組合 (zj h997)

DPn,m=有m個不為空的盒子的可能數DP_{n, m} = 有 m 個不為空的盒子的可能數
DP_{n, m} = 有 m 個不為空的盒子的可能數
DP8,3沒有1的可能DP_{8, 3} 沒有 1 的可能
DP_{8, 3} 沒有 1 的可能

4 + 2 + 2

3 + 3 + 2

  1. 函式定義：

怎麼拆呢？考慮 Case 沒有 1

考慮從                  轉移？

DPn−1,mDP_{n-1, m}
DP_{n-1, m}
DP7,3DP_{7, 3}
DP_{7, 3}

5 + 1 + 1

4 + 2 + 1

3 + 3 + 1

3 + 2 + 2

會有以下問題：

  1. 不知道加完有沒有 1
  2. 可能會重複：
    • 3 + (2 + 1) + 2
    • 3 + 2 + (2 + 1)

這是因為+1有不對稱的問題。

有沒有方法可以公平的對待所有數字呢？

  • 好像全部都加上 1 就好了？

從                  轉移

DPn−m,mDP_{n-m, m}
DP_{n-m, m}
DP5,3DP_{5, 3}
DP_{5, 3}

3 + 1 + 1

2 + 2 + 1

→ 4 + 2 + 2

→ 3 + 3 + 2

DP8,3沒有1的可能DP_{8, 3} 沒有 1 的可能
DP_{8, 3} 沒有 1 的可能

這樣可以同時解決兩個問題！

也就是可能會重複

國小排列組合 (zj h997)

給定球數 n 跟箱子數 m，盒子可為空，
求以下 Case 的可能數：

  1. 球相同，箱子相同
DPn,m=有m個不為空的盒子的可能數DP_{n, m} = 有 m 個不為空的盒子的可能數
DP_{n, m} = 有 m 個不為空的盒子的可能數

考慮 Case 有沒有 1。有 1 (                       ) + 沒有 1 (                    )

DPn−1,m−1DP_{n-1, m-1}
DP_{n-1, m-1}
DPn−m,mDP_{n-m, m}
DP_{n-m, m}
DPn,m=DPn−1,m−1+DPn−m,mDP_{n, m} = DP_{n-1, m-1} + DP_{n-m, m}
DP_{n, m} = DP_{n-1, m-1} + DP_{n-m, m}
  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPn,n=1⏟全都分開放,DPn,1=1⏟全都放一起\underbrace{DP_{n, n} = 1}_{全都分開放}, \underbrace{DP_{n, 1} = 1}_{全都放一起}
\underbrace{DP_{n, n} = 1}_{全都分開放}, \underbrace{DP_{n, 1} = 1}_{全都放一起}
M = int(1e9+7)
dp = [[0] * (max_m+1) for _ in range(n+1)]
for i in range(1, n+1):
  for j in range(1, i+1):
    if j == 1 or i == j:
      dp[i][j] = 1
    else:
      dp[i][j] = (dp[i-1][j-1] + (j) * dp[i-j][j]) % M
print(*map(lambda x: x%M, accumulate(dp[n][1:max_m+1])))

Python

C++

國小排列組合 (zj h997)

如果你很有興趣，那麼關於
如果箱子不可以為空的 Case，
可以參考這個網站。

Case 4 好難想...

但我覺得這題是整個投影片裡面
最通靈的地方了 (？)

計算正方形個數

Count Square Submatrices with All Ones  (leetcode 1277)

Count Square Submatrices (leetcode 1277)

給一個矩陣，問有多少個全部都是 1 個正方形？

1 0 1
0 1 1
1 1 1
0 1 1 1
1 1 1 1
0 1 1 1

舉例來說：

  • 1x1: 7個
  • 2x2: 1個
  • 3x3: 0個
  • 共 8 個
  • 1x1: 10個
  • 2x2: 4個
  • 3x3: 1個
  • 共 15 個

讓我們回歸比較正常的題目吧！
(雖說那些數學題比賽也會出)

Count Square Submatrices (leetcode 1277)

給一個矩陣，問有多少個全部都是 1 個正方形？

DPn,m=1+min⁡(DPn,m−1,DPn−1,m,DPn−1,m−1)DP_{n, m} = 1 + \min (DP_{n, m-1}, DP_{n-1, m}, DP_{n-1, m-1} )
DP_{n, m} = 1 + \min (DP_{n, m-1}, DP_{n-1, m}, DP_{n-1, m-1} )
  1. 函式定義：
     
  2. 如何拆解：
DPn,m=以(n,m)為右下角有幾個正方形DP_{n, m} = 以 (n, m) 為右下角有幾個正方形
DP_{n, m} = 以 (n, m) 為右下角有幾個正方形

函式定義這題比較特別，
想想看怎麼定義會比較有機會轉移吧！

DPn,m=以(n,m)為右下角正方形最大多少DP_{n, m} = 以 (n, m) 為右下角正方形最大多少
DP_{n, m} = 以 (n, m) 為右下角正方形最大多少
0 1 1 1
1 1 1 1
0 1 1 1

以這格為右下角，最大矩形為 3x3

怎麼從其他 DP 推出 3 呢？

如果這格答案要是 3，
那麼這兩個 2x2 一定要全是 1。

並且左上角，右下角一定要是 1。

或者，判斷左上角其實也可以用這個 2x2 來判斷。

Count Square Submatrices (leetcode 1277)

給一個矩陣，問有多少個全部都是 1 個正方形？

DP_{n,m} 怎麼推到答案?

Count Square Submatrices (leetcode 1277)

給一個矩陣，問有多少個全部都是 1 個正方形？

DPn,m=1+min⁡(DPn,m−1,DPn−1,m,DPn−1,m−1)DP_{n, m} = 1 + \min (DP_{n, m-1}, DP_{n-1, m}, DP_{n-1, m-1} )
DP_{n, m} = 1 + \min (DP_{n, m-1}, DP_{n-1, m}, DP_{n-1, m-1} )
  1. 函式定義：
     
  2. 如何拆解：
DPn,m=以(n,m)為右下角有幾個正方形DP_{n, m} = 以 (n, m) 為右下角有幾個正方形
DP_{n, m} = 以 (n, m) 為右下角有幾個正方形
DPn,m=以(n,m)為右下角正方形最大多少DP_{n, m} = 以 (n, m) 為右下角正方形最大多少
DP_{n, m} = 以 (n, m) 為右下角正方形最大多少
def countSquares(self, matrix):
  n, m = len(matrix), len(matrix[1])
  DP = [[0] * m for _ in range(n)]
  ans = 0
  for i, row in enumerate(matrix):
    for j, cell in enumerate(row):
      if cell:
        DP[i][j] = 1 + min(
          DP[i-1][j],
          DP[i][j-1],
          DP[i-1][j-1],
        )
      ans += DP[i][j]
  return ans

Python

C++

Count Square Submatrices (leetcode 1277)

給一個矩陣，問有多少個全部都是 1 個正方形？

如果是矩形呢？

類 DAG 路徑數量

搭到終點 (APCS 2024/10 - 4, zj o714)

一般的DP，但+數值離散化 / 區間和

搭到終點 (APCS 2024/10 - 4, zj o714)

現在有一條一維數線，並在上面有 n 個公車路線。
每個公車路線會有兩個變數 start, end，這表示
你可以從 [start, end-1] 搭車搭到 end 下車。

請問從 0 搭車搭到 m 有幾種搭法？(方法數需要 % p)

舉例來說：

4 7 11
0 4 0 3
4 6 6 7
n m p
s0 s1 ... sn
e0 e1 ... en

0

4

6

7

一號車

二號車

三號車

四號車

  • 所有可能：
    • 0 -(一號)-> 4 -(二號)-> 6 -(四號)-> 7
    • 0 -(一號)-> 4 -(三號)-> 6 -(四號)-> 7
    • 0 -(一號)-> 4 -(四號)-> 7
    • 0 -(三號)-> 6 -(四號)-> 7
  • 答案：總共四種，% 11 = 4

搭到終點 (APCS 2024/10 - 4, zj o714)

現在有一條一維數線，並在上面有 n 個公車路線。
每個公車路線會有兩個變數 start, end，這表示
你可以從 [start, end-1] 搭車搭到 end 下車。

請問從 0 搭車搭到 m 有幾種搭法？(方法數需要 % p)

好像有點熟悉？

如果一樣用 Bottom up
的角度來思考的話：

0

4

6

7

三號車

四號車

二號車

一號車

1

1

1

- 3

4

答案是: 2

1

1

1

1

1

1

2

Unique Paths II (leetcode 63)

搭到終點 (APCS 2024/10 - 4, zj o714)

現在有一條一維數線，並在上面有 n 個公車路線。
每個公車路線會有兩個變數 start, end，這表示
你可以從 [start, end-1] 搭車搭到 end 下車。

請問從 0 搭車搭到 m 有幾種搭法？(方法數需要 % p)

如果一樣用 Bottom up
的角度來思考的話：

0

4

6

7

三號車

四號車

二號車

一號車

1

1

1

- 3

4

考慮 Bottom up 的順序，
我們應該是先填完
前面的位置，再填後面的位置。

實作上來說，
對每班公車的結尾排序，
由前往後做。

以左邊的例子：處理順序為
一號 / 二號 / 三號 / 四號

搭到終點 (APCS 2024/10 - 4, zj o714)

# Input
n, m, p = map(int, input().split())
S = list(map(int, input().split()))
E = list(map(int, input().split()))
bus = sorted(list(zip(E, S)))
# Start DP
DP = [1 % p] + [0] * m
for e, s in bus:
    if e <= m:
        DP[e] = (DP[e] + sum(DP[s:e])) % p
print(DP[-1])

Python

int n, m, p;
cin >> n >> m >> p;
vector<pair<int, int>> bus(n);
vector<long long> DP(m + 1);
DP[0] = 1 % p;
for (int i=0; i<n; i++)
    scanf("%d", &bus[i].second);
for (int i=0; i<n; i++)
    scanf("%d", &bus[i].first);
sort(bus.begin(), bus.end());
for (auto &[end, start] : bus) {
    for (int i=start; i<end; i++)
        DP[end] = (DP[end] + DP[i]) % p;
}
printf("%lld\n", DP[m] % p);

C++

分析看看複雜度吧！

排序O(nlog⁡n)排序 O(n \log n)
排序 O(n \log n)

超胖... 有沒有辦法可以加速呢？

+O(m)+O(n)×O(m)=O(nlog⁡n+nm)+ O(m) + O(n) \times O(m) = O(n \log n + nm)
+ O(m) + O(n) \times O(m) = O(n \log n + nm)

紅色區域看起來好像是區間和？

動態計算前綴和，就可以把一個 O(m) 壓掉！

(因為DP陣列是動態產生的)

搭到終點 (APCS 2024/10 - 4, zj o714)

n, m, p = map(int, input().split())
S = list(map(int, input().split()))
E = list(map(int, input().split()))
bus = sorted(list(zip(E, S)))
DP = [1] + [0] * m
PS = [1] + [0] * m
PS_top = 1
IS = lambda l, r: PS[r] - (PS[l - 1] if l > 0 else 0)
for e, s in bus:
  while PS_top < e:
    PS[S_top] = (PS[PS_top - 1] + DP[PS_top]) % p
    PS_top += 1
    if e <= m:
      DP[e] = (DP[e] + IS(s, e - 1)) % p
print(DP[-1])

Python

int n, m, p;
cin >> n >> m >> p;
vector<pair<int, int>> bus(n);
vector<long long> DP(m + 1);
vector<long long> PS{1 % p};
DP[0] = 1 % p;
for (int i=0; i<n; i++) cin >> bus[i].second;
for (int i=0; i<n; i++) cin >> bus[i].first;
sort(bus.begin(), bus.end());
for (auto &[end, start] : bus) {
  while (PS.size() < end)
    PS.push_back((PS.back() + DP[PS.size()]) % p);
  DP[end] = (DP[end] + PS[end - 1] - (start ? PS[start - 1] : 0) + p) % p;
}
printf("%lld\n", DP[m] % p);

C++

分析看看複雜度吧！

+O(n)=O(nlog⁡n+m)+ O(n) = O(n \log n+m)
+ O(n) = O(n \log n+m)
排序O(nlog⁡n)排序 O(n \log n)
排序 O(n \log n)
+動態前綴和O(m)+ 動態前綴和 O(m)
+ 動態前綴和 O(m)

有沒有辦法向雙人走路一樣，做到空間壓縮呢？

觀察一下，DP「有值」的地方只有             個，
但要開            個空間很浪費。

n+2n+2
n+2
m+1m+1
m+1

註: 這個值有可能是一個 -p+1 ~ 0  的負數，所以可以多加一個 p 讓它變成正數。

數值離散化 (Discretization)

有沒有辦法向雙人走路一樣，做到空間壓縮呢？

0

4

6

7

三號車

四號車

二號車

一號車

0

三號車

四號車

二號車

一號車

原本的座標們

0 4 0 3
4 6 6 7

0   1   2   3

被壓縮的座標們

1

2

3

神奇方法?

觀察一下，DP「有值」的地方只有             個，
但要開            個空間很浪費。

n+2n+2
n+2
m+1m+1
m+1

數值離散化 (Discretization)

有沒有辦法向雙人走路一樣，做到空間壓縮呢？

0   1   2   3   4

原本的座標們

被壓縮的座標們

用 set / map 把
重複座標刪掉

0 4 0 3
4 6 6 7

原本座標的可能

0  4  3  6  7

0  3  4  6  7

排序的座標可能

用 map / dict 把
原本座標對應到
他們的 index

觀察一下，DP「有值」的地方只有             個，
但要開            個空間很浪費。

n+2n+2
n+2
m+1m+1
m+1

+ 數值離散化 (Discretization)

n, m, p = map(int, input().split())
S = list(map(int, input().split()))
E = list(map(int, input().split()))
bus = sorted(list(zip(E, S)))
mapping = set([0, m] + E + S)
mapping = {x:i for i, x in enumerate(sorted(mapping))}
bus = [(mapping[e], mapping[s]) for e, s in bus]
m = mapping[m]
DP = [1] + [0] * m
PS = [1] + [0] * m
PS_top = 1
IS = lambda l, r: PS[r] - (PS[l - 1] if l > 0 else 0)
for e, s in bus:
  while PS_top < e:
    PS[PS_top] = (PS[PS_top - 1] + DP[PS_top]) % p
    PS_top += 1
  if e <= m:
    DP[e] = (DP[e] + IS(s, e - 1)) % p
print(DP[-1])

Python

int n, m, p;
cin >> n >> m >> p;
vector<pair<int, int>> bus(n);
map<int, int> mapping({{0, 0}, {m, 0}});
for (int i=0; i<n; i++) {
  scanf("%d", &bus[i].second);
  mapping[bus[i].second] = 0;
}
for (int i=0; i<n; i++) {
  scanf("%d", &bus[i].first);
  mapping[bus[i].first] = 0;
}
int idx = 0;
for (auto &[k, v] : mapping)
  v = idx++;
for (auto &[end, start] : bus)
  end = mapping[end], start = mapping[start];
m = mapping[m];
// 下略，跟原本 DP 一樣

C++

分析看看複雜度吧！

+DP(狀態O(n)×轉移O(1))=O(nlog⁡n)+ DP (狀態 O(n) \times 轉移 O(1)) = O(n \log n)
+ DP (狀態 O(n) \times 轉移 O(1)) = O(n \log n)
排序O(nlog⁡n)排序 O(n \log n)
排序 O(n \log n)
+動態前綴和O(n)+ 動態前綴和 O(n)
+ 動態前綴和 O(n)
+離散化O(nlog⁡n)+ 離散化 O(n \log n)
+ 離散化 O(n \log n)

搭到終點 (APCS 2024/10 - 4, zj o714)

數值離散化 (Discretization)

  • (應該) 常數比較小的實作方法 (C++)：
    • 蒐集所有點 O(n)。
    • 排序所有點 (sort) O(n)。
    • 掃描過去把連著重複地點忽略 (unique) O(n)。
    • resize vector 的大小 O(n)
    • 建立 unordered_map / dict 將數值對應到 index O(n)。
    • 接下來每次對應都是 O(1)。
    • Note:
      • unordered_map  / Python 的 dict 一般操作是 O(1)
      • map 一般操作 O(log N)
  • 這種技巧不是專屬 DP 的技巧，只要你看到數值範圍太大的都可以離散化。

數位 DP

Count of Integers (leetcode 2719)

Digit DP

Count of Integers (leetcode 2719)

舉例來說：
num1 = "5", num2 = "12",
min_sum = 2, max_sum = 4

5→5(X)6→6(X)7→7(X)8→8(X)9→9(X)10→1(X)11→2(O)12→3(O)}總共2個\begin{rcases} 5 \rightarrow 5 (X) \\ 6 \rightarrow 6 (X) \\ 7 \rightarrow 7 (X) \\ 8 \rightarrow 8 (X) \\ 9 \rightarrow 9 (X) \\ 10 \rightarrow 1 (X) \\ 11 \rightarrow 2 (O) \\ 12 \rightarrow 3 (O) \\ \end{rcases} 總共 2 個
\begin{rcases} 5 \rightarrow 5 (X) \\ 6 \rightarrow 6 (X) \\ 7 \rightarrow 7 (X) \\ 8 \rightarrow 8 (X) \\ 9 \rightarrow 9 (X) \\ 10 \rightarrow 1 (X) \\ 11 \rightarrow 2 (O) \\ 12 \rightarrow 3 (O) \\ \end{rcases} 總共 2 個

定義 S(x) = x 的所有 digit 加總。問在 num1 到 num2 的數字中，
有多少數字的 S 在 min_sum 到 max_sum 之間？(答案要 % 1e9+7)

Count of Integers (leetcode 2719)

  • 看到有左右界的題目，高機率先拆解會比較簡單！
=∣{x∣x≤B,C≤S(x)≤D}∣−∣{x∣x<A,C≤S(x)≤D}∣= |\{x | x \le B, C \le S(x) \le D\}| - |\{x | x < A, C \le S(x) \le D\}|
= |\{x | x \le B, C \le S(x) \le D\}| - |\{x | x < A, C \le S(x) \le D\}|
∣{x∣A≤x≤B,C≤S(x)≤D}∣|\{x | A \le x \le B, C \le S(x) \le D\}|
|\{x | A \le x \le B, C \le S(x) \le D\}|

所以現在我們只需考慮：

定義 S(x) = x 的所有 digit 加總。問 0 ~ num 的數字中，
有多少數字的 S ≤ max_sum 之間？(答案要 % 1e9+7)

=∣{x∣x≤B,S(x)≤D}∣−∣{x∣x≤B,S(x)<C}∣−(∣{x∣x<A,S(x)≤D}∣−∣{x∣x<A,S(x)<C}∣)= |\{x | x \le B, S(x) \le D\}| - |\{x | x \le B, S(x) < C\}| \\ - (|\{x | x < A, S(x) \le D\}| - |\{x | x < A, S(x) < C\}|)
= |\{x | x \le B, S(x) \le D\}| - |\{x | x \le B, S(x) < C\}| \\ - (|\{x | x < A, S(x) \le D\}| - |\{x | x < A, S(x) < C\}|)

定義 S(x) = x 的所有 digit 加總。問在 num1 到 num2 的數字中，
有多少數字的 S 在 min_sum 到 max_sum 之間？(答案要 % 1e9+7)

Count of Integers (leetcode 2719)

定義 S(x) = x 的所有 digit 加總。問 0 ~ num 的數字中，
有多少數字的 S ≤ max_sum 之間？(答案要 % 1e9+7)

(132457,c)=∑{(?[0−0]?????,c)=(?????,c)(1?[0−2]????,c)=(  ????,c−1−[0−2])(13?[0−1]???,c)=(    ???,c−4−[0−1])(132?[0−3]??,c)=(      ??,c−6−[0−3])(1324?[0−4]?,c)=(        ?,c−10−[0−4])(13245?[0−6],c)(132457, c) = \sum \begin{cases} (?_{[0-0]}?????, c) = (?????, c) \\ (1?_{[0-2]}????, c) = (~~????, c-1 - [0-2]) \\ (13?_{[0-1]}???, c) = (~~~~???, c-4 - [0-1])\\ (132?_{[0-3]}??, c) = (~~~~~~??, c-6 - [0-3]) \\ (1324?_{[0-4]}?, c) = (~~~~~~~~?, c-10 - [0-4]) \\ (13245?_{[0-6]}, c) \\ \end{cases}
(132457, c) = \sum \begin{cases} (?_{[0-0]}?????, c) = (?????, c) \\ (1?_{[0-2]}????, c) = (~~????, c-1 - [0-2]) \\ (13?_{[0-1]}???, c) = (~~~~???, c-4 - [0-1])\\ (132?_{[0-3]}??, c) = (~~~~~~??, c-6 - [0-3]) \\ (1324?_{[0-4]}?, c) = (~~~~~~~~?, c-10 - [0-4]) \\ (13245?_{[0-6]}, c) \\ \end{cases}

首先我們觀察一下題目：

可以得到一個比較簡單的 DP 定義：

DPn,c=∣{x=??...?⏞n∣S(x)≤c}∣=所有n位數中，加總≤c的個數DP_{n, c} = |\{ x = \overbrace{??...?}^{n} | S(x) \le c \}| = 所有 n 位數中，加總 \le c 的個數
DP_{n, c} = |\{ x = \overbrace{??...?}^{n} | S(x) \le c \}| = 所有 n 位數中，加總 \le c 的個數

理論上是 [0-7]，但這樣寫，
之後再處理會比較好寫。

Count of Integers (leetcode 2719)

定義 S(x) = x 的所有 digit 加總。問 0 ~ num 的數字中，
有多少數字的 S ≤ max_sum 之間？(答案要 % 1e9+7)

DPn,c=所有n位數中，加總≤c的個數DP_{n, c} = 所有 n 位數中，加總 \le c 的個數
DP_{n, c} = 所有 n 位數中，加總 \le c 的個數
M = int(1e9+7)
DP = {}
def rec(num_len, high_sum):
  if high_sum < 0: return 0
  if num_len == 0: return 1
  if (num_len, high_sum) not in DP:
    ans = 0
    for i in range(10):
      ans += rec(num_len-1, high_sum-i)
    DP[num_len, high_sum] = ans % M
  return DP[num_len, high_sum]

Python

const long long M = 1000000007;
map<pair<int, int>, long long> DP;
long long rec(int num_len, int max_sum) {
  if (max_sum < 0) return 0;
  if (num_len == 0) return 1;
  if (DP.find({num_len, max_sum}) == DP.end()) {
    long long ans = 0;
    for (int i=0; i<10; i++)
      ans = (ans + rec(num_len-1, max_sum-i)) % M;
    DP[{num_len, max_sum}] = ans;
  }
  return DP[{num_len, max_sum}];
}

C++

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：

枚舉第一個數是什麼

DPn,c=∑0≤i≤9DPn−1,c−iDP_{n, c} = \sum_{0 \le i \le 9} DP_{n-1, c-i}
DP_{n, c} = \sum_{0 \le i \le 9} DP_{n-1, c-i}
DP?,負數=0,DP0,?=1DP_{?, 負數} = 0, DP_{0, ?} = 1
DP_{?, 負數} = 0, DP_{0, ?} = 1

Count of Integers (leetcode 2719)

DPn,c=所有n位數中，加總≤c的個數DP_{n, c} = 所有 n 位數中，加總 \le c 的個數
DP_{n, c} = 所有 n 位數中，加總 \le c 的個數
def find(num, max_sum):
  ans = 0
  for idx, start in enumerate(map(int, num)):
    for cur_start in range(start):
      ans = (ans + rec(len(num)-idx-1, max_sum-cur_start)) % M
    max_sum -= start
  return ans

Python

long long find(string num, int max_sum) {
  long long ans = 0;
  for (int idx=0; idx < num.size(); idx++) {
    for (int cur_start=0; cur_start < num[idx]-'0'; cur_start++)
      ans = (ans + rec(num.size()-idx-1, max_sum-cur_start)) % M;
    max_sum -= num[idx]-'0';
  }
  return ans;
}

C++

  1. 函式定義：
(132457,c)=∑{(?[0−0]?????,c)=(?????,c)(1?[0−2]????,c)=(  ????,c−1−[0−2])(13?[0−1]???,c)=(    ???,c−4−[0−1])...(132457, c) = \sum \begin{cases} (?_{[0-0]}?????, c) = (?????, c) \\ (1?_{[0-2]}????, c) = (~~????, c-1 - [0-2]) \\ (13?_{[0-1]}???, c) = (~~~~???, c-4 - [0-1])\\ ... \end{cases}
(132457, c) = \sum \begin{cases} (?_{[0-0]}?????, c) = (?????, c) \\ (1?_{[0-2]}????, c) = (~~????, c-1 - [0-2]) \\ (13?_{[0-1]}???, c) = (~~~~???, c-4 - [0-1])\\ ... \end{cases}

根據上面的邏輯
寫出這樣的函數：

find(num, max_sum) =
「在 0 到 num-1 的數字中，有幾個數字加總 ≤ max_sum」

Count of Integers (leetcode 2719)

class Solution {
public:
  const long long M = 1000000007;
  map<pair<int, int>, long long> DP;
  long long rec(int num_len, int max_sum) {
    if (max_sum < 0)
      return 0;
    if (num_len == 0)
      return 1;
    if (DP.find({num_len, max_sum}) == DP.end()) {
      long long ans = 0;
      for (int i = 0; i < 10; i++)
        ans = (ans + rec(num_len - 1, max_sum - i)) % M;
      DP[{num_len, max_sum}] = ans;
    }
    return DP[{num_len, max_sum}];
  }
  long long find(string num, int max_sum) {
    long long ans = 0;
    for (int idx = 0; idx < num.size(); idx++) {
      for (int cur_start = 0; cur_start < num[idx] - '0'; cur_start++)
        ans =
          (ans + rec(num.size() - idx - 1, max_sum - cur_start)) % M;
      max_sum -= num[idx] - '0';
    }
    return ans;
  }
  int count(string num1, string num2, int min_sum, int max_sum) {
    long long A = find(num2, max_sum) - find(num2, min_sum - 1);
    long long B = find(num1, max_sum) - find(num1, min_sum - 1);
    int sum = 0;
    for (char c : num2)
      sum += c - '0';
    bool num2_valid = min_sum <= sum && sum <= max_sum;
    return ((A - B + (num2_valid)) % M + M) % M;
  }
};

C++

最後把題目要的答案更出來就可以了。

find(num2+1, max_sum) -

find(num2+1, min_sum-1) -
find(num1, max_sum) + 

find(num1, min_sum-1)

num2+1 在 C++ 轉 long long 會噴範圍 (overflow)，所以只能要 find(num2)
然後特判 num2 本身。

定義 S(x) = x 的所有 digit 加總。問在 num1 到 num2 的數字中，
有多少數字的 S 在 min_sum 到 max_sum 之間？(答案要 % 1e9+7)

Count of Integers (leetcode 2719)

class Solution:
  def count(self, num1: str, num2: str, min_sum: int, max_sum: int):
    M = int(1e9 + 7)
    DP = {}

    def rec(num_len, high_sum):
      if high_sum < 0:
        return 0
      if num_len == 0:
        return 1
      if (num_len, high_sum) not in DP:
        ans = 0
        for i in range(10):
          ans += rec(num_len - 1, high_sum - i)
        DP[num_len, high_sum] = ans % M
      return DP[num_len, high_sum]

    def find(num, _max_sum):
      ans = 0
      max_sum = _max_sum
      for idx, start in enumerate(map(int, num)):
        for cur_start in range(start):
          ans = (ans + rec(len(num) - idx - 1, max_sum - cur_start)) % M
        max_sum -= start
      return ans

    num2 = str(int(num2) + 1)
    A = find(num2, max_sum) - find(num2, min_sum - 1)
    B = find(num1, max_sum) - find(num1, min_sum - 1)
    return (A - B) % M

Python

最後把題目要的答案更出來就可以了。

find(num2+1, max_sum) -

find(num2+1, min_sum-1) -
find(num1, max_sum) + 

find(num1, min_sum-1)

定義 S(x) = x 的所有 digit 加總。問在 num1 到 num2 的數字中，
有多少數字的 S 在 min_sum 到 max_sum 之間？(答案要 % 1e9+7)

記數類DP小結

記數類 DP 上課習題

主題 題目名稱 大概作法
記數類DP 骨牌問題  ☆ 列舉最後一排可能，枚舉最後所有疊法。
矩陣快速覓：寫成轉移矩陣的形式後 + 快速冪技巧算出來
配對連線  ☆ 枚舉第一跟線怎麼畫，最後得出卡特蘭數的公式。
國小排列組合  ☆

球相同，箱不同：分箱法 - 重複組合 / 推完轉移變成多次前綴和 
球不同，箱相同：考慮新的球要不要獨立放。
球相同，箱相同：(拆分數) 把所有可能分成有沒有 1 這兩個 Case。
計算正方形個數 ☆ 定義DP = 最大正方形，觀察轉移的關係。
搭到終點 給定拓樸順序的 DAG 上路徑，用離散化壓縮空間，用區間和快速轉移。
數位 DP Count of Ints ☆ 將數字拆成各個前綴後，歸納出 DP 狀態。

這個章節比較多排列組合的感覺，
大概可以算是 DP 題目裡面比較偏門的題目。

記數類 DP 小結

找個尋找最大矩形

質方圖舉行不知道是不是和放

把條件寫到狀態內

記數類 DP 練習題

題目名稱 來源 備註
円円數磁磚 資芽算法班作業 Domino 放 3xN 的可能數
Painting Grid leetcode 1932 不相鄰塗3色，問塗 (1~5)xN 的可能數
白色世界 (困難版) zj g566 簡單的轉移但要矩陣快速冪
Critical Mass zj a388 骰n次硬幣有連續三+的次數
三元樹 TOI 2009 1!

求三元樹的可能數 (需要優化到 O(N^2))
Combination Sum IV leetcode 377 裸數字拆分
Count Pyramids leetcode 2088 數等腰三角形有幾個
Find All Stable Arrays leetcode 3130 要求長度為k的子陣列都要包含 0/1 的可能數

離散化練習題 (不一定是 DP)

題目名稱 來源 備註
blank

https://leetcode.com/problems/falling-squares/
純離散化可以過 但可以線段樹+懶人標

區間DP

Range DP

區間 DP

  • 基本上就是指：
    • 狀態是指一個區間的題目。
    • 恩...就這樣。

類矩陣鏈乘積

合併成本 (APCS 2024/1 - 4, zj m934)

給定一個序列，每次可選兩相鄰數 u,v 合併成一個數字 u+v，
並寫需要花費 |u-v|。問合併到只剩一個數字的最小花費？

合併成本 (APCS 2024/1 - 4, zj m934)

舉例來說：[-5, 3, 0, -4, 3, -2] 的最佳解操作：

答案：8 + 7 + 1 + 1 + 1 = 18

合併成本 (APCS 2024/1 - 4, zj m934)

給定一個序列，每次可選兩相鄰數 u,v 合併成一個數字 u+v，
並寫需要花費 |u-v|。問合併到只剩一個數字的最小花費？

  1. 函式定義：

我們先來試試看最原始的定義吧！

DPn=合併完前n個數字的最小成本DP_n = 合併完前 n 個數字的最小成本
DP_n = 合併完前 n 個數字的最小成本

想想看這個數字往前可以怎麼合併吧！

-5 3 0 -4 3 -2

好像怪怪的？

你不知道怎麼跟上個數字合併會最好。

因為上個數字可能會先跟別人合併再跟 An 併

合併成本 (APCS 2024/1 - 4, zj m934)

給定一個序列，每次可選兩相鄰數 u,v 合併成一個數字 u+v，
並寫需要花費 |u-v|。問合併到只剩一個數字的最小花費？

  1. 函式定義：
-5 3 0 -4 3 -2

你不知道怎麼跟上個數字合併會最好。

因為上個數字可能會先跟別人合併再跟 An 併

換句話說，我們必須枚舉上個數字是怎麼合併的。

DPl,r=合併[Al,Ar]的最小成本DP_{l, r} = 合併 [A_l, A_r] 的最小成本
DP_{l, r} = 合併 [A_l, A_r] 的最小成本

怎樣的定義才有足夠的資訊知道
前一個數字會併到哪裡去呢？

合併成本 (APCS 2024/1 - 4, zj m934)

給定一個序列，每次可選兩相鄰數 u,v 合併成一個數字 u+v，
並寫需要花費 |u-v|。問合併到只剩一個數字的最小花費？

  1. 函式定義：
-5 3 0 -4 3 -2
DPl,r=合併[Al,Ar]的最小成本DP_{l, r} = 合併 [A_l, A_r] 的最小成本
DP_{l, r} = 合併 [A_l, A_r] 的最小成本

解答的最後一次合併

也可以這樣想：
考量解答的最後一個合併

DP0,5=DP0,1+DP2,5+合併成本DP_{0, 5} = DP_{0, 1} + DP_{2, 5} \\ + 合併成本
DP_{0, 5} = DP_{0, 1} + DP_{2, 5} \\ + 合併成本

我們其實可以用
一個區間表達合併的前一步。

合併成本 (APCS 2024/1 - 4, zj m934)

給定一個序列，每次可選兩相鄰數 u,v 合併成一個數字 u+v，
並寫需要花費 |u-v|。問合併到只剩一個數字的最小花費？

  1. 函式定義：
  2. 如何拆解：
-5 3 0 -4 3 -2
DPl,r=合併[Al,Ar]的最小成本DP_{l, r} = 合併 [A_l, A_r] 的最小成本
DP_{l, r} = 合併 [A_l, A_r] 的最小成本

考量最後一步的什麼？

考量最後一次的合併

Sl,r=∑i=lrAiS_{l, r} = \sum_{i = l}^{r} A_i
S_{l, r} = \sum_{i = l}^{r} A_i

一個區間合併完的數字
= 這個區間的總和

拆解 = 枚舉每一種合併方法，或者說最後一次的切割點。

DPl,r=min⁡l≤m<r(∣Sl,m−Sm+1,r∣⏞最後一次合併的成本+DPl,m⏞合併左邊最佳成本+DPm+1,r⏞合併右邊最佳成本)DP_{l, r} = \min_{l \le m < r} ( \overbrace{|S_{l, m} - S_{m+1, r}| }^{最後一次合併的成本}+ \overbrace{DP_{l, m}}^{合併左邊最佳成本} + \overbrace{DP_{m+1, r}}^{合併右邊最佳成本})
DP_{l, r} = \min_{l \le m < r} ( \overbrace{|S_{l, m} - S_{m+1, r}| }^{最後一次合併的成本}+ \overbrace{DP_{l, m}}^{合併左邊最佳成本} + \overbrace{DP_{m+1, r}}^{合併右邊最佳成本})

合併成本 (APCS 2024/1 - 4, zj m934)

給定一個序列，每次可選兩相鄰數 u,v 合併成一個數字 u+v，
並寫需要花費 |u-v|。問合併到只剩一個數字的最小花費？

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPl,r=合併[Al,Ar]的最小成本DP_{l, r} = 合併 [A_l, A_r] 的最小成本
DP_{l, r} = 合併 [A_l, A_r] 的最小成本
DPl,r=min⁡l≤m<r(∣Sl,m−Sm+1,r∣⏞最後一次合併的成本+DPl,m⏞合併左邊最佳成本+DPm+1,r⏞合併右邊最佳成本)DP_{l, r} = \min_{l \le m < r} ( \overbrace{|S_{l, m} - S_{m+1, r}| }^{最後一次合併的成本}+ \overbrace{DP_{l, m}}^{合併左邊最佳成本} + \overbrace{DP_{m+1, r}}^{合併右邊最佳成本})
DP_{l, r} = \min_{l \le m < r} ( \overbrace{|S_{l, m} - S_{m+1, r}| }^{最後一次合併的成本}+ \overbrace{DP_{l, m}}^{合併左邊最佳成本} + \overbrace{DP_{m+1, r}}^{合併右邊最佳成本})
DPl,l=0DP_{l, l} = 0
DP_{l, l} = 0

分析看看複雜度吧！

O(n2)O(n^2)
O(n^2)

狀態數量             × 轉移複雜度            =

O(n)O(n)
O(n)
O(n3)O(n^3)
O(n^3)
看起來雖然很胖，但1≤n≤100，可以過！看起來雖然很胖，但 1 \le n \le 100，可以過！
看起來雖然很胖，但 1 \le n \le 100，可以過！
int IS(int l, int r) {
  return PS[r] - (l == 0 ? 0 : PS[l-1]);
}

int rec(int l, int r) {
  if (l == r) return 0;
  if (dp[l][r]) return dp[l][r];
  dp[l][r] = INT_MAX;
  for (int m=l; m<r; m++){
    dp[l][r] = min(
      dp[l][r],
      rec(l, m) + rec(m+1, r) +  \
        abs(IS(l, m) - IS(m+1, r)) 
    );
  }
  return dp[l][r];
}

int main() {
  scanf("%d", &n);
  for (int i=0; i<n; i++) {
    scanf("%d", &ary[i]);
    PS[i] = ary[i] + (i == 0 ? 0 : PS[i-1]);
  }
  printf("%d\n", rec(0, n-1));
  return 0;
}

合併成本 (APCS 2024/1 - 4, zj m934)

DPl,r=min⁡l≤m<r(∣Sl,m−Sm+1,r∣⏞最後一次合併的成本+DPl,m⏞合併左邊最佳成本+DPm+1,r⏞合併右邊最佳成本)DP_{l, r} = \min_{l \le m < r} ( \overbrace{|S_{l, m} - S_{m+1, r}| }^{最後一次合併的成本}+ \overbrace{DP_{l, m}}^{合併左邊最佳成本} + \overbrace{DP_{m+1, r}}^{合併右邊最佳成本})
DP_{l, r} = \min_{l \le m < r} ( \overbrace{|S_{l, m} - S_{m+1, r}| }^{最後一次合併的成本}+ \overbrace{DP_{l, m}}^{合併左邊最佳成本} + \overbrace{DP_{m+1, r}}^{合併右邊最佳成本})
from math import inf
from itertools import accumulate
n = int(input())
A = list(map(int, input().split()))
PS = list(accumulate(A))
IS = lambda l, r: PS[r] - (PS[l-1] if l > 0 else 0)
dp = {}
def rec(l, r):
  if l == r: return 0
  if (l, r) not in dp:
    ans = inf
    for k in range(l, r):
      cost = rec(l, k) + rec(k+1, r)
      cost += abs(IS(l, k) - IS(k+1, r))
      ans = min(ans, cost)
    dp[l, r] = ans
  return dp[l, r]
print(rec(0, n-1))

C++

Python

矩陣鏈乘積 Matrix Chain Multiplication

這題出自於這樣子的實用題：

現在你有很多個矩陣要相乘，
請問怎麼乘最有效率？

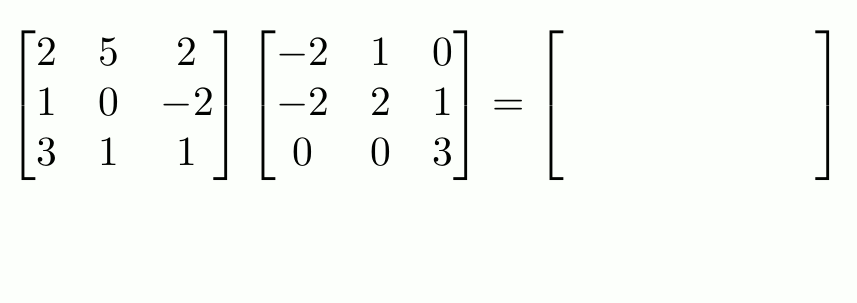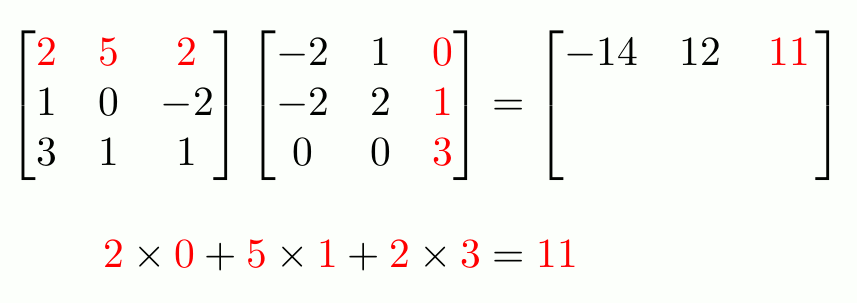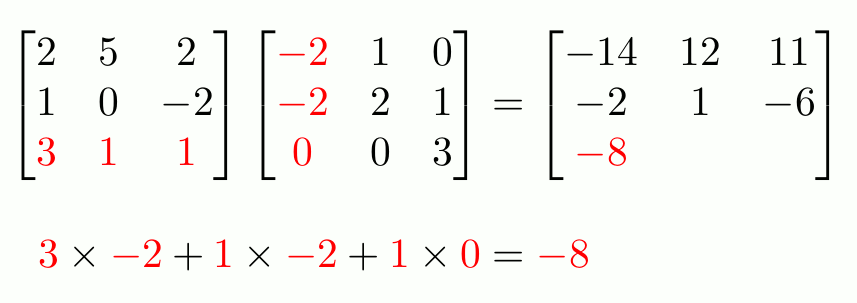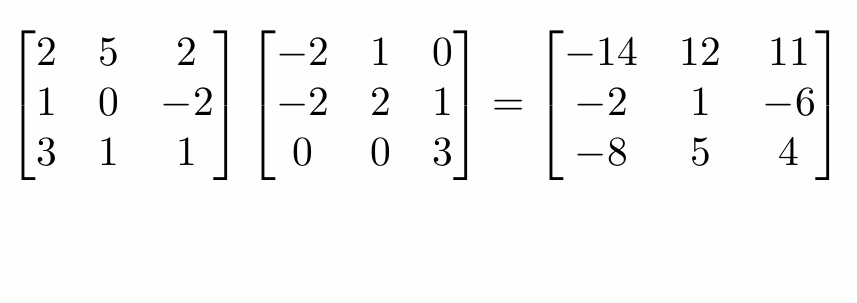
An×m×Bm×p=Cn×pA×B做了 nmp 個乘法A_{n \times m} \times B_{m \times p} = C_{n \times p} \\ A \times B \text{做了 nmp 個乘法}
A_{n \times m} \times B_{m \times p} = C_{n \times p} \\ A \times B \text{做了 nmp 個乘法}

矩陣乘法長這樣子：

舉例來說，現在有三個矩陣要乘

A1×10×B10×1×C1×10A_{1 \times 10} \times B_{10 \times 1} \times C_{1 \times 10} \\
A_{1 \times 10} \times B_{10 \times 1} \times C_{1 \times 10} \\
(A1×10×B10×1)×C1×10=X1×1×C1×10(Cost:10)=Y1×10(Cost:10+10)(A_{1 \times 10} \times B_{10 \times 1}) \times C_{1 \times 10} \\ = X_{1 \times 1} \times C_{1 \times 10} (Cost: 10) \\ = Y_{1 \times 10} (Cost: 10 + 10) \\
(A_{1 \times 10} \times B_{10 \times 1}) \times C_{1 \times 10} \\ = X_{1 \times 1} \times C_{1 \times 10} (Cost: 10) \\ = Y_{1 \times 10} (Cost: 10 + 10) \\
A1×10×(B10×1×C1×10)=A1×10×X10×10(Cost:100)=Y1×10(Cost:100+100)A_{1 \times 10} \times (B_{10 \times 1} \times C_{1 \times 10}) \\ = A_{1 \times 10} \times X_{10 \times 10} (Cost: 100) \\ = Y_{1 \times 10} (Cost: 100 + 100) \\
A_{1 \times 10} \times (B_{10 \times 1} \times C_{1 \times 10}) \\ = A_{1 \times 10} \times X_{10 \times 10} (Cost: 100) \\ = Y_{1 \times 10} (Cost: 100 + 100) \\

先做
AB：

先做
BC：

矩陣鏈乘積 Matrix Chain Multiplication

舉例來說，現在有三個矩陣要乘

A1×10×B10×1×C1×10A_{1 \times 10} \times B_{10 \times 1} \times C_{1 \times 10} \\
A_{1 \times 10} \times B_{10 \times 1} \times C_{1 \times 10} \\
  1. 函式定義：
  2. 如何拆解：
DPl,r=第l個矩陣到第r個矩陣乘完的CostDP_{l, r} = 第 l 個矩陣到第 r 個矩陣乘完的 \text{Cost}
DP_{l, r} = 第 l 個矩陣到第 r 個矩陣乘完的 \text{Cost}
DPl,r=min⁡l≤m<r(Diml,0×Dimm,1×Dimr,1⏞最後一次乘法的成本+DPl,m⏟乘完左邊最佳成本+DPm+1,r⏟乘完右邊最佳成本)DP_{l, r} = \min_{l \le m < r} ( \overbrace{ Dim_{l, 0} \times Dim_{m, 1} \times Dim_{r, 1} }^{最後一次乘法的成本} +\\ \underbrace{DP_{l, m}}_{乘完左邊最佳成本} + \underbrace{DP_{m+1, r}}_{乘完右邊最佳成本})
DP_{l, r} = \min_{l \le m < r} ( \overbrace{ Dim_{l, 0} \times Dim_{m, 1} \times Dim_{r, 1} }^{最後一次乘法的成本} +\\ \underbrace{DP_{l, m}}_{乘完左邊最佳成本} + \underbrace{DP_{m+1, r}}_{乘完右邊最佳成本})

雖然設定有點複雜，但 DP 式仔細看是一樣的！

挑戰看看GCJ? - 1

Bribe the Prisoners (GCJ 2009, Round 1C-C)

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

Bribe the Prisoners (GCJ 2009, Round 1C-C)

😈

1

😈

2

😭

3

😈

4

😈

5

😭

6

😈

7

...

😈

13

😭

14

😈

15

...

😈

20

舉例來說，P = 20, Q = {3, 6, 14}

🔓 Cost $19

🔓 Cost $4

🔓 Cost $12

順序：14，6，3，這樣成本總共 19 + 12 + 4 = 35

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

😈

1

😈

2

😭

3

😈

4

😈

5

😭

6

😈

7

...

😈

13

😭

14

😈

15

...

😈

20

  1. 函式定義：
  2. 如何拆解：

我們先來試試看向上一題一樣的定義吧！

像往常一樣，考量最後一次釋放會在哪裡？

🔓

假設最後解放第六個人會怎樣？

Bribe the Prisoners (GCJ 2009, Round 1C-C)

DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

😈

1

😈

2

😭

3

😈

4

😈

5

😭

6

😈

7

...

😈

13

😭

14

😈

15

...

😈

20

像往常一樣，考量最後一次釋放會在哪裡？

🔓

假設最後解放第六個人會怎樣？

Bribe the Prisoners (GCJ 2009, Round 1C-C)

如果最後一次釋放第六個人，
那麼左右邊的囚犯也要互相考慮，沒有比較好做...

DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
  1. 函式定義：
  2. 如何拆解：

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

😈

1

😈

2

😭

3

😈

4

😈

5

😭

6

😈

7

...

😈

13

😭

14

😈

15

...

😈

20

按照正常遞迴的寫法就會變成：
考量第一次釋放會在哪裡？

🔓

假設先解放第六個人會怎樣？

Bribe the Prisoners (GCJ 2009, Round 1C-C)

怎麼辦呢？想想看如果你在寫遞迴 (dfs-style) 暴搜會怎麼樣？

DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
  1. 函式定義：
  2. 如何拆解：

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

😈

1

😈

2

😭

3

😈

4

😈

5

😭

6

😈

7

...

😈

13

😭

14

😈

15

...

😈

20

  1. 函式定義：
  2. 如何拆解：
DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本

考量第一次釋放會在哪裡？

🔓

假設先解放第六個人會怎樣？

1~5 的牢房和 7~20的牢房從此隔開！

可以直接往下遞迴算 (1~5) 的成本 + (7~20) 的成本

這樣你好像就知道遞迴怎麼取了！枚舉第一次釋放的位置就可以！

Bribe the Prisoners (GCJ 2009, Round 1C-C)

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

...

  1. 函式定義：
  2. 如何拆解：
DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本

🔓

😈

😭

😈

😈

😭

...

😭

😈

AmA_m
A_m
AlA_{l}
A_{l}
ArA_{r}
A_{r}
DPl,r=min⁡l≤m≤r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本}
DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本}
                               )⏞第一次合併的成本\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~)}^{第一次合併的成本}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~)}^{第一次合併的成本}
+Ar+1−Al−1−2+ A_{r+1} - A_{l-1} - 2
+ A_{r+1} - A_{l-1} - 2

中間總共有                            個人，
這個成本再 -1 因為釋放的人不用給錢。

+Ar+1−Al−1−1+ A_{r+1} - A_{l-1} - 1
+ A_{r+1} - A_{l-1} - 1

這樣你好像就知道遞迴怎麼取了！枚舉第一次釋放的位置就可以！

Bribe the Prisoners (GCJ 2009, Round 1C-C)

...

💨

😈

Al−1A_{l-1}
A_{l-1}

...

😈

💨

Ar+1A_{r+1}
A_{r+1}

已經烙幹了

已經烙幹了

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DPl,l=Al+1−Al−1−2DP_{l,l} = A_{l+1} - A_{l-1} - 2
DP_{l,l} = A_{l+1} - A_{l-1} - 2

分析看看複雜度吧！

O(n2)O(n^2)
O(n^2)

狀態數量             × 轉移複雜度            =

O(n)O(n)
O(n)
O(n3)O(n^3)
O(n^3)

雖然標程到這裡已經 OK 了，但其實還可以更快！

DPl,r=min⁡l≤m≤r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

Bribe the Prisoners (GCJ 2009, Round 1C-C)

在優化前，你想得出怎麼寫成 Bottom-up 嗎？

DPl,r=min⁡l≤m≤r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

實作上，我們假想有 0 號囚犯 跟 (P+1) 號囚犯已經被釋放，這樣就不用判斷邊界了。

vector<vector<int>> dp;
int rec(const vector<int> &A, int l, int r){
  if (l > r)  return 0;
  if (l == r) return A[r + 1] - A[l - 1] - 2;
  if (dp[l][r] != -1) return dp[l][r];
  int ans = INT_MAX;
  for (int m = l; m <= r; ++m)
    ans = min(ans, 
      rec(A, l, m - 1) + rec(A, m + 1, r));
  dp[l][r] = ans + A[r + 1] - A[l - 1] - 2;
  return dp[l][r];
}
// 省略一些些
vector<int> A(Q+2, 0);
A[Q+1] = P+1;
for (int i = 1; i <= Q; ++i)
  cin >> A[i];
dp.assign(Q + 2, vector<int>(Q + 2, -1));
printf("Case #%d: %d\n", t, rec(A, 1, Q));
from math import inf
T = int(input())
def rec(A, l, r):
  if l > r:
    return 0
  if l == r:
    return A[r+1] - A[l-1] - 2
  if (l, r) not in dp:
    ans = inf
    for m in range(l, r+1):
      ans = min(ans, rec(A, l, m-1) + rec(A, m+1, r))
    dp[l, r] = ans + A[r+1] - A[l-1] - 2
  return dp[l, r]

for t in range(1, T+1):
  P, Q = map(int, input().split())
  dp = {}
  A = [0] + list(map(int, input().split())) + [P+1]
  print(f"Case #{t}: {rec(A, 1, Q)}")

C++ (Top-down)

Python (Top-down)

Bribe the Prisoners (GCJ 2009, Round 1C-C)

DPl,r=min⁡l≤m≤r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} ) 
int main() {
  int T, P, Q;
  scanf("%d", &T);
  for (int t = 1; t <= T; ++t){
    cin >> P >> Q;
    vector<int> A(Q+2, 0);
    A[Q+1] = P+1;
    for (int i = 1; i <= Q; ++i)
      cin >> A[i];
    vector<vector<int>> dp(Q + 2, 
    	vector<int>(Q + 2, 0));
    for (int w=0; w < Q; w++) {
      for (int l=1, r=l+w; r<=Q; l++, r++) {
        if (w == 0) {
          dp[l][r] = A[r+1] - A[l-1] - 2;
          continue;
        }
        int ans = INT_MAX;
        for (int m = l; m <= r; ++m)
          ans = min(ans, dp[l][m-1] + dp[m+1][r]);
        dp[l][r] = ans + A[r+1] - A[l-1] - 2;
      }
    }    
	printf("Case #%d: %d\n", t, dp[1][Q]);
  }
}
for t in range(1, T+1):
  P, Q = map(int, input().split())
  dp = [[0] * (Q+2) for _ in range(Q+2)]
  A = [0] + list(map(int, input().split())) + [P+1]
  for w in range(Q):
    for l in range(1, Q-w+1):
      r = l + w
      if w == 0:
        dp[l][r] = A[r+1] - A[l-1] - 2
        continue
      ans = inf
      for m in range(l, r+1):
        ans = min(ans, dp[l][m-1] + dp[m+1][r])
      dp[l][r] = ans + A[r+1] - A[l-1] - 2
  print(f"Case #{t}: {dp[1][Q]}")

C++ (Bottom-up)

Python (Bottom-up)

Bribe the Prisoners (GCJ 2009, Round 1C-C)

先從長度 = 0 開始 (Base Case)
接著在做長度 = 1的Case
直到做完 (1, Q)

DPl,r=min⁡l≤m≤r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

Bribe the Prisoners (GCJ 2009, Round 1C-C)

先從長度 = 0 開始 (Base Case)
接著在做長度 = 1的 Case，直到做完 (1, Q)

走訪順序大概是長這樣

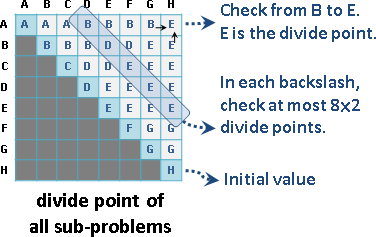
挑戰看看GCJ? - 2

Bribe the Prisoners (GCJ 2009, Round 1C-C)

初探 Knuth 優化 (Knuth's Optimization)

Bribe the Prisoners (GCJ 2009, Round 1C-C)

DPl,r=min⁡l≤m≤r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
  1. 有個人是這樣問的：
    • 左邊成本隨著 m 增加，該值遞增。
    • 右邊成本隨著 m 增加，該值遞減。
    • 所以我們可以用像「最小化區間總和」那題一樣的技巧，二分搜尋 m。搜尋左邊成本跟右邊成本的交叉處。
    • 但這其實是錯的，你覺得問題在哪？
    • 交叉處不代表該值最小，舉例來說： L = [1, 4, 6, 10], R = [5, 4, 1, 0]，
      交叉處總和為 4 + 4 = 8，但最小成本是 1 + 5 = 6
  2. 不過仔細觀察一下你會發現一件很重要的事情：
    • 轉移點會單調移動
      • ​不過不滿足凸性喔，所以無法用三分搜找最低點。
    • 也就是算完 (l, r) 的時候 (l+1, r+1) 的轉移點一定在右邊。

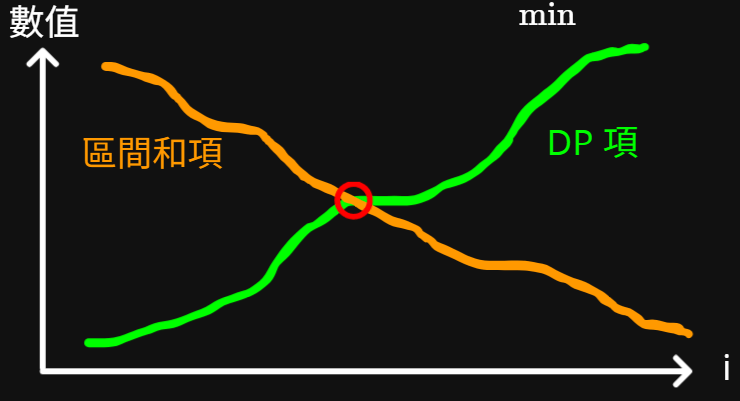
Bribe the Prisoners (GCJ 2009, Round 1C-C)

不過仔細觀察一下你會發現：轉移點會單調移動

假設optl,r=DPl,r的最佳切割點假設 opt_{l, r} = DP_{l, r} 的最佳切割點
假設 opt_{l, r} = DP_{l, r} 的最佳切割點

...

😈

😭

ArA_{r}
A_{r}

...

🔓

😈

😭

😈

😈

😭

...

😭

😈

Aoptl,r−1A_{opt_{l, r-1}}
A_{opt_{l, r-1}}
AlA_{l}
A_{l}
Ar−1A_{r-1}
A_{r-1}
DPl,r−1的最佳切割點DP_{l, r-1} 的最佳切割點
DP_{l, r-1} 的最佳切割點
如果多了一個囚犯Ar呢？DPl,r的最佳切割點:optl,r會在哪？如果多了一個囚犯 A_r 呢？ \\ DP_{l, r} 的最佳切割點: opt_{l, r} 會在哪？
如果多了一個囚犯 A_r 呢？ \\ DP_{l, r} 的最佳切割點: opt_{l, r} 會在哪？
optl,r−1≤optl,ropt_{l ,r-1} \le opt_{l ,r}
opt_{l ,r-1} \le opt_{l ,r}

此時的最佳切割點不會往左邊跑，因為你會希望你切的時候是可以「平衡」的切的。

(也就是第一次要釋放誰)

Bribe the Prisoners (GCJ 2009, Round 1C-C)

不過仔細觀察一下你會發現：轉移點會單調移動

假設optl,r=DPl,r的最佳切割點假設 opt_{l, r} = DP_{l, r} 的最佳切割點
假設 opt_{l, r} = DP_{l, r} 的最佳切割點

...

😈

😭

ArA_{r}
A_{r}
DPl,r的最佳切割點DP_{l, r} 的最佳切割點
DP_{l, r} 的最佳切割點
如果少了一個囚犯Al呢？DPl+1,r的最佳切割點:optl+1,r會在哪？如果少了一個囚犯 A_l 呢？ \\ DP_{l+1, r} 的最佳切割點: opt_{l+1, r} 會在哪？
如果少了一個囚犯 A_l 呢？ \\ DP_{l+1, r} 的最佳切割點: opt_{l+1, r} 會在哪？
optl,r−1≤optl,ropt_{l ,r-1} \le opt_{l ,r}
opt_{l ,r-1} \le opt_{l ,r}

😈

😭

😈

🔓

...

Aoptl,rA_{opt_{l, r}}
A_{opt_{l, r}}

😭

😈

Al+1A_{l+1}
A_{l+1}

...

≤optl+1,r\le opt_{l+1 ,r}
\le opt_{l+1 ,r}

此時的最佳切割點不會往左邊跑，因為你會希望你切的時候是可以「平衡」的切的。

😭

😈

AlA_{l}
A_{l}

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

  1. 函式定義：
  2. 如何拆解：
DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DPl,r=min⁡l≤m≤r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{l \le m \le r} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

Bribe the Prisoners (GCJ 2009, Round 1C-C)

optl,r−1≤optl,r≤optl+1,ropt_{l ,r-1} \le opt_{l ,r}\le opt_{l+1 ,r}
opt_{l ,r-1} \le opt_{l ,r}\le opt_{l+1 ,r}
算DPl,r的時候，DPl,r−1跟DPl+1,r都算過了！算DP_{l, r} 的時候，DP_{l, r-1} 跟 DP_{l+1, r} 都算過了！
算DP_{l, r} 的時候，DP_{l, r-1} 跟 DP_{l+1, r} 都算過了！
可以限縮DPl,r的尋找範圍！可以限縮 DP_{l, r} 的尋找範圍！
可以限縮 DP_{l, r} 的尋找範圍！
optl,r−1≤m≤optl+1,ropt_{l, r-1} \le m \le opt_{l+1, r}
opt_{l, r-1} \le m \le opt_{l+1, r}
DPl,r=min⁡optl,r−1≤m≤optl+1,r(DPl,m−1⏞釋放左邊最佳成本+DPm+1,r⏞釋放右邊最佳成本+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}}^{釋放左邊最佳成本} + \overbrace{DP_{m+1, r}}^{釋放右邊最佳成本} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} ) 
// 省略前面
vector<vector<int>> dp(Q + 2, vector<int>(Q + 2));
vector<vector<int>> opt(Q + 2, vector<int>(Q + 2));
for (int w=0; w < Q; w++) {
  for (int l=1, r=l+w; r<=Q; l++, r++) {
    if (w == 0) {
      dp[l][r] = A[r+1] - A[l-1] - 2;
      opt[l][r] = l;
      continue;
    } else {
      dp[l][r] = INT_MAX;
      int lb = opt[l][r-1];
      int ub = opt[l+1][r];
      for (int m = lb; m <= ub; m++) {
        int val = dp[l][m-1] + dp[m+1][r];
        if (val < dp[l][r]) {
          dp[l][r] = val;
          opt[l][r] = m;
        }
      }
      dp[l][r] += A[r+1] - A[l-1] - 2;
    }
  }
}    
printf("Case #%d: %d\n", t, dp[1][Q]);
from math import inf
T = int(input())

for t in range(1, T+1):
  P, Q = map(int, input().split())
  dp = [[0] * (Q+2) for _ in range(Q+2)]
  opt = [[0] * (Q+2) for _ in range(Q+2)]
  A = [0] + list(map(int, input().split())) + [P+1]
  for w in range(Q):
    for l in range(1, Q-w+1):
      r = l + w
      if w == 0:
        dp[l][r] = A[r+1] - A[l-1] - 2
        opt[l][r] = l
      else:
        dp[l][r] = inf
        for m in range(opt[l][r-1], opt[l+1][r]+1):
          if dp[l][m-1] + dp[m+1][r] < dp[l][r]:
            dp[l][r] = dp[l][m-1] + dp[m+1][r]
            opt[l][r] = m
        dp[l][r] += A[r+1] - A[l-1] - 2
  print(f"Case #{t}: {dp[1][Q]}")

C++ (Bottom-up + Knuth opt)

Python (Bottom-up + Knuth opt)

Bribe the Prisoners (GCJ 2009, Round 1C-C)

修改跑的範圍

修改跑的範圍

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DPl,l=Al+1−Al−1−2DP_{l,l} = A_{l+1} - A_{l-1} - 2
DP_{l,l} = A_{l+1} - A_{l-1} - 2

分析看看複雜度吧！

O(n2)O(n^2)
O(n^2)

狀態數量             × 轉移複雜度            =

O(n)O(n)
O(n)
O(n3)O(n^3)
O(n^3)

看起來好像沒有比較快啊？

DPl,r=min⁡optl,r−1≤m≤optl+1,r(DPl,m−1+DPm+1,r⏞左右兩邊成本加總+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

Bribe the Prisoners (GCJ 2009, Round 1C-C)

轉移雖然最多 O(n) ，但我們稍微分析一下...

DPl,r=min⁡optl,r−1≤m≤optl+1,r(DPl,m−1+DPm+1,r⏞左右兩邊成本加總+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

Bribe the Prisoners (GCJ 2009, Round 1C-C)

轉移雖然最多 O(n) ，但我們稍微分析一下...

第一層迴圈決定 w，第二層迴圈決定 l，而 r = l + w

第二層迴圈中的搜尋總共會跑幾次？

次數=opt2,1+w−opt1,w+1⏞DP1,1+w的計算項+opt3,2+w−opt2,1+w+1⏞DP2,2+w的計算項+...+optn−w,n−1−optn−w−1,n−2+1⏟DPn−w−1,n−1的計算項+optn−w+1,n−optn−w,n−1+1⏟DPn−w,n的計算項次數 = \overbrace{opt_{2, 1+w} -opt_{1, w} + 1}^{DP_{1, 1+w} 的計算項} + \overbrace{opt_{3, 2+w} -opt_{2, 1+w} + 1}^{DP_{2, 2+w} 的計算項} + ... \\ + \underbrace{opt_{n-w, n-1} -opt_{n-w-1, n-2} + 1}_{DP_{n-w-1, n-1} 的計算項} + \underbrace{opt_{n-w+1, n} -opt_{n-w, n-1} + 1}_{DP_{n-w, n} 的計算項}
次數 = \overbrace{opt_{2, 1+w} -opt_{1, w} + 1}^{DP_{1, 1+w} 的計算項} + \overbrace{opt_{3, 2+w} -opt_{2, 1+w} + 1}^{DP_{2, 2+w} 的計算項} + ... \\ + \underbrace{opt_{n-w, n-1} -opt_{n-w-1, n-2} + 1}_{DP_{n-w-1, n-1} 的計算項} + \underbrace{opt_{n-w+1, n} -opt_{n-w, n-1} + 1}_{DP_{n-w, n} 的計算項}
次數=−opt1,w+optn−w+1,n+n−w≤2n=O(n)次數 = -opt_{1, w} + opt_{n-w+1, n} + n - w \le 2n = O(n)
次數 = -opt_{1, w} + opt_{n-w+1, n} + n - w \le 2n = O(n)

總共 O(n)，尋找 n 次，所以尋找均攤 O(1)

在一個長度為 P 的線性牢籠中，釋放第 x 個人時，你必須支付錢給他左右連續的鄰居，每人 1 塊錢，直到遇到邊界或空位為止。
請問釋放指定的 Q 個人時，最少需要花費多少？

  1. 函式定義：
  2. 如何拆解：
  3. Base Case：
DPl,r=釋放l∼r個指定囚犯的最小成本DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本
DP_{l,r} = 釋放l \sim r 個指定囚犯 的最小成本

分析看看複雜度吧！

O(n2)O(n^2)
O(n^2)

狀態數量             × 轉移複雜度                    =

均攤O(1)均攤 O(1)
均攤 O(1)
O(n2)O(n^2)
O(n^2)
DPl,r=min⁡optl,r−1≤m≤optl+1,r(DPl,m−1+DPm+1,r⏞左右兩邊成本加總+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{opt_{l, r-1} \le m \le opt_{l+1, r}} ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

Bribe the Prisoners (GCJ 2009, Round 1C-C)

是不是覺得這種做法很玄乎呢？

這種優化就叫做 Knuth's Optimization

DPl,l=Al+1−Al−1−2DP_{l,l} = A_{l+1} - A_{l-1} - 2
DP_{l,l} = A_{l+1} - A_{l-1} - 2

四邊形不等式 + Knuth 優化

在寫題目的時候，如果你發現 DP 轉移是這種形式：

DPi,j=min⁡i≤k<jDPi,k+DPk+1,j+w(i,j)DP_{i, j} = \min_{i \le k < j}DP_{i, k} + DP_{k+1, j} + w(i, j)
DP_{i, j} = \min_{i \le k < j}DP_{i, k} + DP_{k+1, j} + w(i, j)

這裡的 w 函數符合四邊形不等式 (Monge 性質)

w(a,c)+w(b,d)≤w(a,d)+w(b,c),∀a≤b≤c≤dw(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d
w(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d

那麼轉移就滿足單調性，也就是

opti,j−1≤opti,j≤opti+1,jopt_{i ,j-1} \le opt_{i ,j}\le opt_{i+1 ,j}
opt_{i ,j-1} \le opt_{i ,j}\le opt_{i+1 ,j}

也就可以套 Knuth's Optimization (Knuth 優化)

四邊形不等式 + Knuth 優化

1.轉移式長的類似DPi,j=min⁡i≤k<jDPi,k+DPk+1,j+w(i,j)1. 轉移式長的類似 DP_{i, j} = \min_{i \le k < j}DP_{i, k} + DP_{k+1, j} + w(i, j)
1. 轉移式長的類似 DP_{i, j} = \min_{i \le k < j}DP_{i, k} + DP_{k+1, j} + w(i, j)
2.滿足w(a,c)+w(b,d)≤w(a,d)+w(b,c),∀a≤b≤c≤d2.滿足 w(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d
2.滿足 w(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d
(Ac+1−Aa−1−2)+(Ad+1−Ab−1−2)≤(Ad+1−Aa−1−2)+(Ac+1−Ab−1−2)(A_{c+1}- A_{a-1} - 2) + (A_{d+1}- A_{b-1} - 2) \le (A_{d+1}- A_{a-1} - 2) + (A_{c+1}- A_{b-1} - 2)
(A_{c+1}- A_{a-1} - 2) + (A_{d+1}- A_{b-1} - 2) \le (A_{d+1}- A_{a-1} - 2) + (A_{c+1}- A_{b-1} - 2)
DPl,r=min⁡l≤m≤r(DPl,m−1+DPm+1,r⏞左右兩邊成本加總+Ar+1−Al−1−2⏞第一次合併的成本)DP_{l, r} = \min_{l \le m \le r } ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )
DP_{l, r} = \min_{l \le m \le r } ( \overbrace{DP_{l, m-1}+ DP_{m+1, r}}^{左右兩邊成本加總} + \overbrace{A_{r+1} - A_{l-1} - 2}^{第一次合併的成本} )

思考看看這題有沒有滿足 Knuth 優化條件吧！

差不多滿足！除了一些邊界問題，另外w(i,j)=Aj+1−Ai−1−2差不多滿足！除了一些邊界問題，另外 w(i, j) = A_{j+1} - A_{i-1} - 2
差不多滿足！除了一些邊界問題，另外 w(i, j) = A_{j+1} - A_{i-1} - 2
0≤0→不等式成立！不如說左右兩邊完全相等！0 \le 0 \rightarrow 不等式成立！不如說左右兩邊完全相等！
0 \le 0 \rightarrow 不等式成立！不如說左右兩邊完全相等！

四邊形不等式 + Knuth 優化

1.轉移式類似DPi,j=min⁡i≤k<jDPi,k+DPk+1,j+w(i,j)1. 轉移式類似 DP_{i, j} = \min_{i \le k < j}DP_{i, k} + DP_{k+1, j} + w(i, j)
1. 轉移式類似 DP_{i, j} = \min_{i \le k < j}DP_{i, k} + DP_{k+1, j} + w(i, j)
2.滿足w(a,c)+w(b,d)≤w(a,d)+w(b,c),∀a≤b≤c≤d2.滿足 w(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d
2.滿足 w(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d

只要上面這兩項都成立，那麼轉移符合單調性。

optl,r−1≤optl,r≤optl+1,ropt_{l ,r-1} \le opt_{l ,r}\le opt_{l+1 ,r}
opt_{l ,r-1} \le opt_{l ,r}\le opt_{l+1 ,r}

也就可以套上我們原本寫的算法，好耶！

至於為什麼 ... 等到認真講優化再證明給你看吧！

四邊形不等式 / Monge 性質的來源

w(a,c)+w(b,d)≤w(a,d)+w(b,c),∀a≤b≤c≤dw(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d
w(a, c) + w(b, d) \le w(a, d) + w(b, c), \forall a \le b \le c \le d

為什麼叫做四邊形不等式呢？

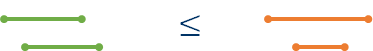
速記：「交叉≤包含」

如果對一個四邊形做交叉編號，

那麼滿足以下不等式：

AC‾+BD‾≤AD‾+BC‾\overline{AC} + \overline{BD} \le \overline{AD} + \overline{BC}
\overline{AC} + \overline{BD} \le \overline{AD} + \overline{BC}

跟上面寫的四邊形不等式很像！

A

B

C

D

稍微複雜的區間 DP - 1

Remove Boxes (leetcode 546, UVA 10559)

現在有一排方塊，並且給你每個方塊的顏色。

你可以刪除任一個同顏色連續方塊，並獲得長度²的分數，
並且刪除完後左右會合併。請問刪完後最高分數是多少？

Remove Boxes (leetcode 546)

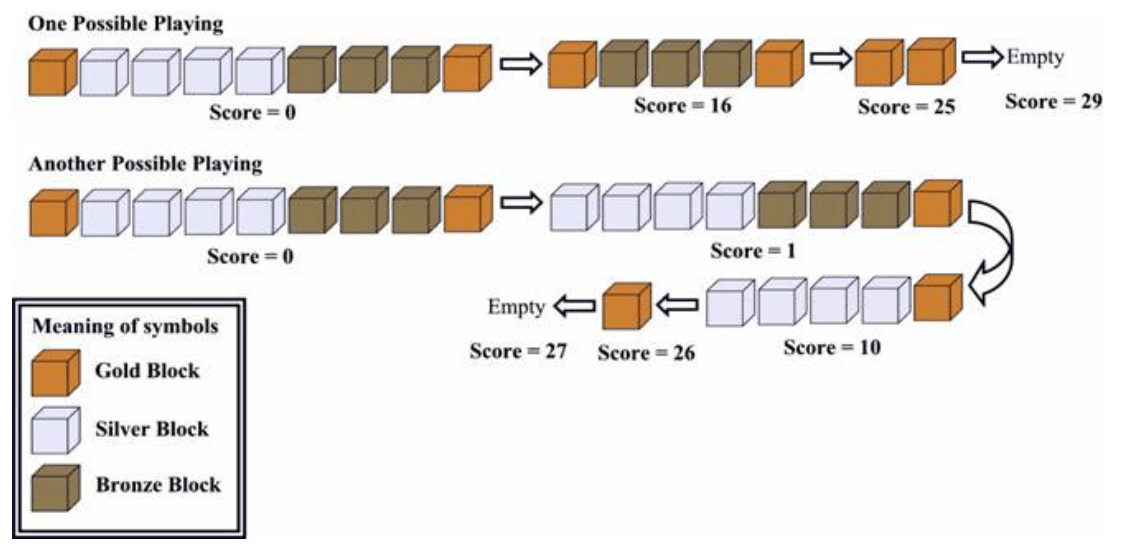
舉例來說，[1, 2, 2, 2, 2, 3, 3, 3, 1] 最高答案是 29

  • 這圖是UVA的。

註：你可以先計算連續方塊的個數，但複雜度一般來說不變。

Remove Boxes (leetcode 546)

  1. 函式定義：
  2. 如何拆解：

想想看之前的例題？

DPl,r=刪除[l,r]區間的最高分數DP_{l, r} = 刪除 [l, r] 區間的最高分數
DP_{l, r} = 刪除 [l, r] 區間的最高分數

想想看最後一次刪除可以怎麼分 Case？

現在有一排方塊，並且給你每個方塊的顏色。

你可以刪除任一個同顏色連續方塊，並獲得長度²的分數，
並且刪除完後左右會合併。請問刪完後最高分數是多少？

刪左邊

...

...

枚舉刪的切割點

刪右邊

DPl,r=max⁡l≤m<rDPl,m+DPm+1,rDP_{l, r} = \max_{l \le m < r} DP_{l, m} + DP_{m+1, r}
DP_{l, r} = \max_{l \le m < r} DP_{l, m} + DP_{m+1, r}

這是錯的！為什麼？

Remove Boxes (leetcode 546)

  1. 函式定義：
  2. 如何拆解：
DPl,r=刪除[l,r]區間的最高分數DP_{l, r} = 刪除 [l, r] 區間的最高分數
DP_{l, r} = 刪除 [l, r] 區間的最高分數

現在有一排方塊，並且給你每個方塊的顏色。

你可以刪除任一個同顏色連續方塊，並獲得長度²的分數，
並且刪除完後左右會合併。請問刪完後最高分數是多少？

DPl,r=max⁡l≤m<rDPl,m+DPm+1,rDP_{l, r} = \max_{l \le m < r} DP_{l, m} + DP_{m+1, r}
DP_{l, r} = \max_{l \le m < r} DP_{l, m} + DP_{m+1, r}

這是錯的！為什麼？

沒有考量到合併後的刪除。

上面的 Case 的最佳解不能把它拆成兩個區塊處理。

這也代表這個切法沒有考慮到所有 Case。

Remove Boxes (leetcode 546)

  1. 函式定義：
  2. 如何拆解：

那換另外的想法！

DPl,r=刪除[l,r]區間的最高分數DP_{l, r} = 刪除 [l, r] 區間的最高分數
DP_{l, r} = 刪除 [l, r] 區間的最高分數

想想看最後一個方塊有哪些刪法？

現在有一排方塊，並且給你每個方塊的顏色。

你可以刪除任一個同顏色連續方塊，並獲得長度²的分數，
並且刪除完後左右會合併。請問刪完後最高分數是多少？

自己刪

刪一個區間的雜色，合併再刪

刪兩個區間的雜色，合併再刪

DPl,r=找前i個與Ar同顏色的方塊，∑中間DP區間+i2DP_{l, r} = 找前i個與A_r同顏色的方塊，\sum 中間 DP 區間 + i^2
DP_{l, r} = 找前i個與A_r同顏色的方塊，\sum 中間 DP 區間 + i^2

這也錯！為什麼？

...

...

Remove Boxes (leetcode 546)

  1. 函式定義：
  2. 如何拆解：
DPl,r=刪除[l,r]區間的最高分數DP_{l, r} = 刪除 [l, r] 區間的最高分數
DP_{l, r} = 刪除 [l, r] 區間的最高分數

現在有一排方塊，並且給你每個方塊的顏色。

你可以刪除任一個同顏色連續方塊，並獲得長度²的分數，
並且刪除完後左右會合併。請問刪完後最高分數是多少？

DPl,r=找前i個與Ar同顏色的方塊，∑中間DP區間+i2DP_{l, r} = 找前i個與A_r同顏色的方塊，\sum 中間 DP 區間 + i^2
DP_{l, r} = 找前i個與A_r同顏色的方塊，\sum 中間 DP 區間 + i^2

這也錯！為什麼？

這樣的切法相當於要求橘色被刪除時，一定是連續的。

這代表想合併右邊+左邊的橘色，你也會要求中間橘色也要一起合併。

但上面的 Case 的最佳解是先把中間刪掉: 1² + 4² + 2² = 21。

而不是先把藍色削掉，把橘色合併：2² + 2² + 3² = 17。 

這也代表這個切法沒有考慮到所有 Case。

Remove Boxes (leetcode 546)

  1. 函式定義：
  2. 如何拆解：
DPl,r=刪除[l,r]區間的最高分數DP_{l, r} = 刪除 [l, r] 區間的最高分數
DP_{l, r} = 刪除 [l, r] 區間的最高分數

我們可以借鏡「卡特蘭數 - 對角線」那題的拆法：

這樣拆解好像就可以了！

那題是枚舉最後一次碰到對角線的點，這題呢？

到底怎麼拆才可以考量所有Case呢？

...

...

...

考量下一個要合併的橘色在哪？

最右邊的刪除

...

最右邊的刪除

...

最右邊的刪除

...

Remove Boxes (leetcode 546)

  1. 函式定義：
     
  2. 如何拆解：
DPl,r=刪除[l,r]區間的最高分數DP_{l, r} = 刪除 [l, r] 區間的最高分數
DP_{l, r} = 刪除 [l, r] 區間的最高分數

考量下一個要合併的橘色在哪？

DPl,r=max⁡l≤m≤rAm=ArDPl,m+DPm+1,r−1DP_{l, r} = \max_{\substack{l \le m \le r \\ A_m = A_r} }DP_{l, m} + DP_{m+1, r-1}
DP_{l, r} = \max_{\substack{l \le m \le r \\ A_m = A_r} }DP_{l, m} + DP_{m+1, r-1}
AmA_m
A_m
ArA_r
A_r

不是？好像哪裡怪怪的？

Am跟Ar之後會合併成兩個橘色A_m 跟 A_r 之後會合併成兩個橘色
A_m 跟 A_r 之後會合併成兩個橘色
Am也有可能跟後面很多橘色合併，無法區分！A_m 也有可能跟後面很多橘色合併，無法區分！
A_m 也有可能跟後面很多橘色合併，無法區分！
DPl,r,nR=刪除[l,r]區間的最高分數並且尾巴多接了nR個與Ar同顏色方塊DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r 同顏色方塊 \end{array}
DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r 同顏色方塊 \end{array}
AlA_l
A_l
DPl,mDP_{l, m}
DP_{l, m}

❓

DPm+1,r−1DP_{m+1, r-1}
DP_{m+1, r-1}

最右邊的刪除

需要再多一個狀態：

尾巴的橘色有幾個併在一起？

Remove Boxes (leetcode 546)

DPl,r,nR=刪除[l,r]區間的最高分數並且尾巴多接了nR個與Ar同顏色方塊DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r 同顏色方塊 \end{array}
DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r 同顏色方塊 \end{array}
AmA_m
A_m
ArA_r
A_r
AlA_l
A_l
DPl,mDP_{l, m}
DP_{l, m}

❓

DPm+1,r−1DP_{m+1, r-1}
DP_{m+1, r-1}

最右邊的刪除

,0{}_{,0}
{}_{,0}

...

                               ⏞nR個跟Ar同顏色的方塊\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}^{nR個跟A_r同顏色的方塊}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}^{nR個跟A_r同顏色的方塊}

把右邊的刪除後

,nR+1{}_{,nR+1}
{}_{,nR+1}
DPl,mDP_{l, m}
DP_{l, m}
,nR+1{}_{,nR+1}
{}_{,nR+1}
DPl,r,nR=max⁡l≤m<rAm=ArDPl,m,nR+1+DPm+1,r−1,0DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } DP_{l, m, nR+1} + DP_{m+1, r-1, 0}
DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } DP_{l, m, nR+1} + DP_{m+1, r-1, 0}
  1. 函式定義：
     
  2. 如何拆解：
AmA_m
A_m
ArA_r
A_r
AlA_l
A_l

❓

...

                               ⏞nR個跟Ar同顏色的方塊\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}^{nR個跟A_r同顏色的方塊}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}^{nR個跟A_r同顏色的方塊}

Remove Boxes (leetcode 546)

vector<int> boxes;
int dp[101][101][101] = {0};
int rec(int l, int r, int nR) {
  if (l > r) return 0;
  if (dp[l][r][nR]) 
    return dp[l][r][nR];
  int ans = rec(l, r-1, 0) + (nR+1)*(nR+1);
  for (int m=l; m<r; m++) {
    if (boxes[m] == boxes[r])
      ans = max(ans, rec(l, m, nR+1) + 
                    rec(m+1, r-1, 0));
  }
  return dp[l][r][nR] = ans;
}
int removeBoxes(vector<int>& boxes) {
  this->boxes = boxes;
  return rec(0, boxes.size()-1, 0);
}
def removeBoxes(self, boxes):
  dp = {}
  def rec(l, r, nR):
    if l > r: return 0
    if (l, r, nR) in dp:
      return dp[l, r, nR]
    ans = rec(l, r-1, 0) + (nR + 1) ** 2
    for m in range(l, r):
      if boxes[m] == boxes[r]:
        ans = max(ans, rec(l, m, nR+1) + \
                  rec(m+1, r-1, 0))
    dp[l, r, nR] = ans
    return ans
  return rec(0, len(boxes)-1, 0)

C++ (Top-down)

Python (Top-down)

  1. 函式定義：
     
  2. 如何拆解：

     
  3. Base Case：
DPl,r,nR=刪除[l,r]區間的最高分數並且尾巴多接了nR個與Ar方塊DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DPl,r,nR=max⁡l≤m<rAm=ArDPl,m,nR+1⏟屁股多接nR+1個+DPm+1,r−1,0⏟最後一次刪除[m+1,r−1]DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DPl,r,nR=DPl,r−1,0+(nR+1)2DP_{l, r, nR} = DP_{l, r-1, 0} + (nR + 1)^2
DP_{l, r, nR} = DP_{l, r-1, 0} + (nR + 1)^2

沒有合併了：

Remove Boxes (leetcode 546)

  1. 函式定義：
     
  2. 如何拆解：

     
  3. Base Case：
DPl,r,nR=刪除[l,r]區間的最高分數並且尾巴多接了nR個與Ar方塊DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DPl,r,nR=max⁡l≤m<rAm=ArDPl,m,nR+1⏟屁股多接nR+1個+DPm+1,r−1,0⏟最後一次刪除[m+1,r−1]DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DPl,r,nR=DPl,r−1,0+(nR+1)2DP_{l, r, nR} = DP_{l, r-1, 0} + (nR + 1)^2
DP_{l, r, nR} = DP_{l, r-1, 0} + (nR + 1)^2

沒有合併了：

分析看看複雜度吧！

O(n3)O(n^3)
O(n^3)

狀態數量             × 轉移複雜度            =

O(n)O(n)
O(n)
O(n4)O(n^4)
O(n^4)

結束了嗎？也許還可以更快！

Yeh, Here we go again

稍微複雜的區間 DP - 2

Remove Boxes (leetcode 546, UVA 10559)

初探分治優化 (Divide and Conquer / D&C DP)

Remove Boxes (leetcode 546)

我們來稍微想一下有沒有單調性：

  1. 函式定義：
     
  2. 如何拆解：
DPl,r,nR=刪除[l,r]區間的最高分數並且尾巴多接了nR個與Ar方塊DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DPl,r,nR=max⁡l≤m<rAm=ArDPl,m,nR+1⏟屁股多接nR+1個+DPm+1,r−1,0⏟最後一次刪除[m+1,r−1]DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
AmA_m
A_m
ArA_r
A_r
AlA_l
A_l
DPl,mDP_{l, m}
DP_{l, m}

❓

DPm+1,r−1DP_{m+1, r-1}
DP_{m+1, r-1}

最右邊的刪除

,0{}_{,0}
{}_{,0}

...

                               ⏞nR個跟Ar同顏色的方塊\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}^{nR個跟A_r同顏色的方塊}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}^{nR個跟A_r同顏色的方塊}
,nR+1{}_{,nR+1}
{}_{,nR+1}

如果 nR 變多了，那麼你會有更大的可能去合併更多

所以你會希望最右邊的刪除會往右移 (保留更多合併的可能)

意即optl,r,nR≤optl,r,nR+1，nR轉移單調意即 opt_{l, r, nR} \le opt_{l, r, nR+1}，nR 轉移單調
意即 opt_{l, r, nR} \le opt_{l, r, nR+1}，nR 轉移單調

Remove Boxes (leetcode 546)

  1. 函式定義：
     
  2. 如何拆解：
DPl,r,nR=刪除[l,r]區間的最高分數並且尾巴多接了nR個與Ar方塊DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DPl,r,nR=max⁡l≤m<rAm=ArDPl,m,nR+1⏟屁股多接nR+1個+DPm+1,r−1,0⏟最後一次刪除[m+1,r−1]DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
optl,r,nR≤optl,r,nR+1/nR轉移單調opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調
opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調

這可以做什麼呢？

optl,r,0opt_{l, r, 0}
opt_{l, r, 0}
ll
l
rr
r
optl,r,0∼nRmax⁡的搜尋範圍opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
optl,r,1∼nRmax⁡的搜尋範圍opt_{l, r, 1 \sim nR_{\max}} 的搜尋範圍
opt_{l, r, 1 \sim nR_{\max}} 的搜尋範圍

可以一直縮短範圍，減少搜尋的次數！

optl,r,1opt_{l, r, 1}
opt_{l, r, 1}
optl,r,2∼nRmax⁡的搜尋範圍opt_{l, r, 2\sim nR_{\max}} 的搜尋範圍
opt_{l, r, 2\sim nR_{\max}} 的搜尋範圍

分治優化 (Divide and Conquer DP)

optl,r,nR≤optl,r,nR+1/nR轉移單調opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調
opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調
optl,r,0opt_{l, r, 0}
opt_{l, r, 0}
ll
l
rr
r
optl,r,0∼nRmax⁡的搜尋範圍opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
optl,r,1∼nRmax⁡的搜尋範圍opt_{l, r, 1 \sim nR_{\max}} 的搜尋範圍
opt_{l, r, 1 \sim nR_{\max}} 的搜尋範圍

可以一直縮短範圍，減少搜尋的次數！

...

不過如果前期找到的 opt 都在前面，
那麼還是會變整體                                    ...

O(nRmax×(r−l))O(nR_{max} \times (r-l))
O(nR_{max} \times (r-l))

我們可以採用類似二分搜的方法，一開始從中間找，也許比較好！

ll
l
rr
r
optl,r,0∼nRmax⁡的搜尋範圍opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
optl,r,nRmax⁡2∼nRmax⁡的搜尋範圍opt_{l, r, \frac{nR_{\max}}{2} \sim nR_{\max}} 的搜尋範圍
opt_{l, r, \frac{nR_{\max}}{2} \sim nR_{\max}} 的搜尋範圍
optl,r,nRmax⁡2opt_{l, r, \frac{nR_{\max}}{2}}
opt_{l, r, \frac{nR_{\max}}{2}}
optl,r,0∼nRmax⁡2的搜尋範圍opt_{l, r, 0 \sim \frac{nR_{\max}}{2} } 的搜尋範圍
opt_{l, r, 0 \sim \frac{nR_{\max}}{2} } 的搜尋範圍

分治優化 (Divide and Conquer DP)

optl,r,nR≤optl,r,nR+1/nR轉移單調opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調
opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調

我們可以採用類似二分搜的方法，一開始從中間找，也許比較好！

ll
l
rr
r
optl,r,0∼nRmax⁡的搜尋範圍opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
optl,r,nRmax⁡2∼nRmax⁡的搜尋範圍opt_{l, r, \frac{nR_{\max}}{2} \sim nR_{\max}} 的搜尋範圍
opt_{l, r, \frac{nR_{\max}}{2} \sim nR_{\max}} 的搜尋範圍
optl,r,nRmax⁡2opt_{l, r, \frac{nR_{\max}}{2}}
opt_{l, r, \frac{nR_{\max}}{2}}
optl,r,0∼nRmax⁡2的搜尋範圍opt_{l, r, 0 \sim \frac{nR_{\max}}{2} } 的搜尋範圍
opt_{l, r, 0 \sim \frac{nR_{\max}}{2} } 的搜尋範圍
optl,r,nRmax⁡4opt_{l, r, \frac{nR_{\max}}{4}}
opt_{l, r, \frac{nR_{\max}}{4}}
optl,r,3nRmax⁡4opt_{l, r, \frac{3nR_{\max}}{4}}
opt_{l, r, \frac{3nR_{\max}}{4}}
optl,r,0∼nRmax⁡4opt_{l, r, 0 \sim \frac{nR_{\max}}{4} }
opt_{l, r, 0 \sim \frac{nR_{\max}}{4} }
optl,r,nRmax⁡4∼nRmax⁡2opt_{l, r, \frac{nR_{\max}}{4} \sim \frac{nR_{\max}}{2} }
opt_{l, r, \frac{nR_{\max}}{4} \sim \frac{nR_{\max}}{2} }
optl,r,nRmax⁡4∼3nRmax⁡4opt_{l, r, \frac{nR_{\max}}{4} \sim \frac{3nR_{\max}}{4} }
opt_{l, r, \frac{nR_{\max}}{4} \sim \frac{3nR_{\max}}{4} }
optl,r,3nRmax⁡4∼opt_{l, r, \frac{3nR_{\max}}{4} \sim }
opt_{l, r, \frac{3nR_{\max}}{4} \sim }

這樣一直分下去，就叫做分治優化。

def DC(nR_L, nR_R, opt_lb, opt_rb):
  if nR_L > nR_R: return
  nR_M = (nR_L + nR_R) // 2
  ans_m, opt_m = solve(nR_M, opt_lb, opt_rb)
  DC(nR_L, nR_M-1, opt_lb, opt_m)
  DC(nR_M+1, nR_R, opt_m, opt_rb)
void DC(int nR_L, int nR_R, int lb, int rb) {
  if (nR_L > nR_R) return;
  int nR_M = (nR_L + nR_R) / 2;
  auto [ans_m, opt_m] = solve(nR_M, lb, rb);
  DC(nR_L, nR_M - 1, lb, opt_m);
  DC(nR_M + 1, nR_R, opt_m, rb);
};

C++ (分治優化)

Python (分治優化)

分治優化 (Divide and Conquer DP)

optl,r,nR≤optl,r,nR+1/nR轉移單調opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調
opt_{l, r, nR} \le opt_{l, r, nR+1} / nR 轉移單調

我們可以採用類似二分搜的方法，一開始從中間找，也許比較好！

ll
l
rr
r
optl,r,0∼nRmax⁡的搜尋範圍opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
opt_{l, r, 0 \sim nR_{\max}} 的搜尋範圍
optl,r,nRmax⁡2∼nRmax⁡的搜尋範圍opt_{l, r, \frac{nR_{\max}}{2} \sim nR_{\max}} 的搜尋範圍
opt_{l, r, \frac{nR_{\max}}{2} \sim nR_{\max}} 的搜尋範圍
optl,r,0∼nRmax⁡2的搜尋範圍opt_{l, r, 0 \sim \frac{nR_{\max}}{2} } 的搜尋範圍
opt_{l, r, 0 \sim \frac{nR_{\max}}{2} } 的搜尋範圍
def DC(nR_L, nR_R, opt_lb, opt_rb):
  if nR_L > nR_R: return
  nR_M = (nR_L + nR_R) // 2
  ans_m, opt_m = solve(nR_M, opt_lb, opt_rb)
  DC(nR_L, nR_M-1, opt_lb, opt_m)
  DC(nR_M+1, nR_R, opt_m, opt_rb)
void DC(int nR_L, int nR_R, int lb, int rb) {
  if (nR_L > nR_R) return;
  int nR_M = (nR_L + nR_R) / 2;
  auto [ans_m, opt_m] = solve(nR_M, lb, rb);
  DC(nR_L, nR_M - 1, lb, opt_m);
  DC(nR_M + 1, nR_R, opt_m, rb);
};

C++ (分治優化)

Python (分治優化)

  1. 尋找 [nR_L, nR_R] 的範圍，然後
    他的搜尋界線是 [lb, rb]
  2. 直接搜尋中間的 nR_M，得到他的最佳轉移點 opr_m
  3. 分治尋找兩邊：
    • [nR_L, nR_M] 的搜尋界線是 [lb, opt_m]
    • [nR_M, nR_R] 的搜尋界線是 [opt_m, rb]
  4. ​這樣時間複雜度就不一樣嗎？

分治優化的時間複雜度

def DC(nR_L, nR_R, opt_lb, opt_rb):
  if nR_L > nR_R: return
  nR_M = (nR_L + nR_R) // 2
  ans_m, opt_m = solve(nR_M, opt_lb, opt_rb)
  DC(nR_L, nR_M-1, opt_lb, opt_m)
  DC(nR_M+1, nR_R, opt_m, opt_rb)
void DC(int nR_L, int nR_R, int lb, int rb) {
  if (nR_L > nR_R) return;
  int nR_M = (nR_L + nR_R) / 2;
  auto [ans_m, opt_m] = solve(nR_M, lb, rb);
  DC(nR_L, nR_M - 1, lb, opt_m);
  DC(nR_M + 1, nR_R, opt_m, rb);
};

C++ (分治優化)

Python (分治優化)

用分析的不好寫，我們改用樹法，假設一開始搜尋           

[0,2h][0, 2^h]
[0, 2^h]
2h−1→[lb,rb]2^{h-1} \rightarrow [lb, rb]
2^{h-1} \rightarrow [lb, rb]
[lb,opt2h−1]←2h−2[lb, opt_{2^{h-1}}] \leftarrow 2^{h-2}
[lb, opt_{2^{h-1}}] \leftarrow 2^{h-2}
2h−1+2h−2→[opt2h−1,rb]2^{h-1} + 2^{h-2} \rightarrow [opt_{2^{h-1}}, rb]
2^{h-1} + 2^{h-2} \rightarrow [opt_{2^{h-1}}, rb]

你會發現每一層的搜尋範圍加總 =              

rb−lb+該層點的個數−1rb - lb + 該層點的個數 - 1
rb - lb + 該層點的個數 - 1

總共最多                                             所以總共為 

O(h)=O(log⁡(r−l))層O(h) = O(\log (r-l)) 層
O(h) = O(\log (r-l)) 層
(log⁡(r−l)+1)×(rb−lb)=這題rb−lb是O(n)O(nlog⁡n)(\log (r-l) + 1) \times (rb - lb) \overset{這題 rb - lb 是 O(n)}{=} O(n\log n)
(\log (r-l) + 1) \times (rb - lb) \overset{這題 rb - lb 是 O(n)}{=} O(n\log n)

Remove Boxes (leetcode 546)

  1. 函式定義：
     
  2. 如何拆解：

     
  3. Base Case：
DPl,r,nR=刪除[l,r]區間的最高分數並且尾巴多接了nR個與Ar方塊DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DP_{l, r, nR} = \begin{array}{l} 刪除 [l, r] 區間的最高分數 \\ 並且尾巴多接了 nR 個與 A_r方塊 \end{array}
DPl,r,nR=max⁡l≤m<rAm=ArDPl,m,nR+1⏟屁股多接nR+1個+DPm+1,r−1,0⏟最後一次刪除[m+1,r−1]DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DP_{l, r, nR} = \max_{\substack{l \le m < r \\ A_m = A_r} } \underbrace{DP_{l, m, nR+1}}_{屁股多接 nR + 1 個} + \underbrace{DP_{m+1, r-1, 0}}_{最後一次刪除 [m+1, r-1]}
DPl,r,nR=DPl,r−1,0+(nR+1)2DP_{l, r, nR} = DP_{l, r-1, 0} + (nR + 1)^2
DP_{l, r, nR} = DP_{l, r-1, 0} + (nR + 1)^2

沒有合併了：

分析看看複雜度吧！

對於每個 (l, r)，用分治算完所有 (l, r, nR)

O(n2)×O(nlog⁡n)=O(n3log⁡n)O(n^2) \times O(n \log n) = O(n^3 \log n)
O(n^2) \times O(n \log n) = O(n^3 \log n)

好耶！

雖然 leetcode / UVA 都可以 AC，但這其實是錯的！

nR 沒有單調性！ (但如果有單調性，分治會是好的。)

Remove Boxes (leetcode 546)

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
  int removeBoxes(vector<int>& boxes) {
    // color_table[color] = The indices that the boxes with color
    // color_table_idx[i] = The i-th color in the boxes
    unordered_map<int, vector<int>> color_table;

    vector<int> color_table_idx(boxes.size());
    for (int i = 0; i < boxes.size(); i++) {
      int c = boxes[i];
      color_table_idx[i] = color_table[c].size();
      color_table[c].push_back(i);
    }

    int n = boxes.size();
    vector<vector<vector<int>>> dp(n, vector<vector<int>>(n));

    function<int(int,int,int)> rec = [&](int l, int r, int nR) -> int {
      // Base Case
      if (l > r)        return 0;
      // Memoization
      if (dp[l][r].size())  return dp[l][r][nR];

      // We only need to consider the transition point
      // with the boxes[r] color
      int color = boxes[r];

      // ----------------------------------------------------
      // solve(cur_nR, opt_lb, opt_rb):
      //   Search DP[l, r, nR] with the bounds [opt_lb, opt_rb]
      //   and return [optimal value, optimal transition point]
      // ----------------------------------------------------
      function< pair<int,int>(int,int,int) > solve =
        [&](int cur_nR, int opt_lb, int opt_rb) -> pair<int,int> {
          int ans = rec(l, r - 1, 0) + (cur_nR + 1) * (cur_nR + 1);
          // We let the opt be opt_lb when the base case is the ans.
          int ans_opt = opt_lb; 
          for (int m_idx = opt_lb; m_idx <= opt_rb; m_idx++) {
            int m = color_table[color][m_idx];
            if (m == r)
              break;
            int tmp = rec(l, m, cur_nR + 1) + rec(m + 1, r - 1, 0);
            if (tmp > ans) {
              ans = tmp;
              ans_opt = m_idx;
            }
          }
          // Record answer ans return it's best trans point
          dp[l][r][cur_nR] = ans;
          return {ans, ans_opt};
        };
      // D&C solve all the nR in [nR_L, nR_R] with bounds
      // [opt_lb, opt_rb]
      function<void(int,int,int,int)> DC =
        [&](int nR_L, int nR_R, int lb, int rb) {
          if (nR_L > nR_R) {
            return;
          }
          int nR_M = (nR_L + nR_R) / 2;

          auto [ans_m, opt_m] = solve(nR_M, lb, rb);

          DC(nR_L, nR_M - 1, lb, opt_m);
          DC(nR_M + 1, nR_R, opt_m, rb);
        };

      int opt_rb = color_table_idx[r];
      int max_nR = color_table[color].size() - opt_rb - 1;
      dp[l][r].resize(max_nR+1);
      int opt_lb = opt_rb;
      for (int i = l; i <= r; i++) {
        if (boxes[i] == color) {
          opt_lb = color_table_idx[i];
          break;
        }
      }

      DC(0, max_nR, opt_lb, opt_rb);
      return dp[l][r][nR];
    };

    return rec(0, (int)boxes.size() - 1, 0);
  }
};
class Solution:
  def removeBoxes(self, boxes):
    # color_table[color] = The indices that the boxes with color
    # color_table_idx[i] = The i-th color in the boxes
    color_table = defaultdict(list)
    color_table_idx = []
    for idx, box in enumerate(boxes):
      color_table_idx.append(len(color_table[box]))
      color_table[box].append(idx)

    dp = {}
    def rec(l, r, nR):
      if l > r:
        return 0
      if (l, r, nR) in dp:
        return dp[l, r, nR]

      # We only need to consider the transition point
      # with the boxes[r] color
      color = boxes[r]

      # Search DP[l, r, nR] with the bounds [opt_lb, opt_rb]
      # and return [optimal value, optimal transition point]
      def solve(nR, opt_lb, opt_rb):
        ans = rec(l, r - 1, 0) + (nR + 1) ** 2
        ans_opt = opt_lb
        for m_idx in range(opt_lb, opt_rb+1):
          m = color_table[color][m_idx]
          if m == r:
            break
          tmp = rec(l, m, nR + 1) + rec(m + 1, r - 1, 0)
          if tmp > ans:
            ans = tmp
            ans_opt = m_idx
        dp[l, r, nR] = ans
        return ans, ans_opt

      # D&C solve all the nR in [nR_L, nR_R] with bounds
      # [opt_lb, opt_rb]
      def DC(nR_L, nR_R, opt_lb, opt_rb):
        if nR_L > nR_R:
          return
        nR_M = (nR_L + nR_R) // 2
        ans_m, opt_m = solve(nR_M, opt_lb, opt_rb)
        DC(nR_L, nR_M-1, opt_lb, opt_m)
        DC(nR_M+1, nR_R, opt_m, opt_rb)

      opt_rb = color_table_idx[r]
      max_nR = len(color_table[color]) - opt_rb - 1

      # Find the first block with color boxes[r]
      # after l.
      opt_lb = opt_rb
      for i in range(l, r+1):
        if boxes[i] == boxes[r]:
          opt_lb = color_table_idx[i]
          break

      DC(0, max_nR, opt_lb, opt_rb)
      return dp[l, r, nR]

    return rec(0, len(boxes) - 1, 0)

C++ (分治優化 / 假解)

Python (分治優化 / 假解)

提供一下最後的 AC Code，可以參考一下

Remove Boxes 事蹟

講古時間 - 分享個有趣的事件

Remove Boxes (leetcode 546) - 講古時間

我 (筆者) 當時看到這題，是在 IOI Camp 2015 的講義上

然後它在後面寫上這句話：

Remove Boxes (leetcode 546) - 講古時間

我 (筆者) 笨笨，想不出解答，所以有事就問脆

然後我自己「感覺」到了 n^3logn 的 nR 單調性

但我也只是「感覺」，沒有證明，所以疊了甲

Remove Boxes (leetcode 546) - 講古時間

然後我自己「感覺」到了 n^3logn 的 nR 單調性

然後被學弟打臉說這是假解 Orz

註: 這裡指的127 (不包括大神) 是我

Remove Boxes (leetcode 546) - 講古時間

接著我發到 NTUCPC (台大解題社) 尋求協助...

然後 baluteshih 得知的 IOI Camp 這句話的原處：

這個 PDF 是台大競賽程式課程的第一個作業的解答的補充

Remove Boxes (leetcode 546) - 講古時間

這個 PDF 是台大競賽程式課程的第一個作業的解答的補充

裡面寫到 nR 單調性

然後用魔法把 O(n^3logn) 優化成 O(n^3)

這裡有個問題：1. 單調是假解。2. 這個麻煩實作是什麼我也不知道

不過下面有寫證明！難道只是程式寫錯嗎？

Remove Boxes (leetcode 546) - 講古時間

證明 nR 單調性

不過下面有寫證明！難道只是程式寫錯嗎？

歐不... 證明留給大家想

Remove Boxes (leetcode 546) - 講古時間

 dreamoon 提供了這個「證明」的出處：

 oToToT 提供了這本書的節錄

附個證明很難嗎 Orz

Remove Boxes (leetcode 546) - 講古時間

最後進展：

所以結論就是路上台灣的大神們都不會。

如果你找到 O(n^3) 歡迎偷偷跟我說喔！

區間DP 小結

恭喜你!
接下來幾乎 APCS
都不太會考了！

其實前面的優化相關扣掉LIS也不會考...

區間 DP 練習題

題目名稱 來源 備註
Burst Balloons Leetcode 312 矩陣鍊成積類似題
Cut a Stick Leetcode 1547 抓囚犯類似題
刪除邊界 APCS 2019 / 10 - 4 n 很小，4D/1D 都會過
彩色紙條 104 學科決賽 - D  簡單的 Remove Boxes

博奕型 DP

博奕型 DP

先讓我們回想起「單人遊戲暴搜」的解法

4

1

2

5

-

3

4

1

2

5

3

-

4

1

2

-

5

3

4

-

2

5

1

3

4

1

-

5

3

2

4

1

2

5

-

3

4

2

-

5

1

3

-

4

2

5

1

3

4

1

2

5

-

3

4

1

2

5

-

3

-

1

2

4

5

3

(順序: 右上左下)

看怎樣搜尋到解答。

博奕型 DP

「雙人遊戲」的必勝解就會是長這樣

⭕

先手回合

後手回合

⭕

⭕

                                                       ⏞\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}{}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}{}

⭕

...

先手回合

                                 ⏞\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}{}
\overbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}{}

⭕

❌

⭕

⭕

❌

⭕

⭕

❌

⭕

...

...

每回合，每個人都會選對自己有利的的局面。

博奕型 DP

「雙人遊戲」的必勝解就會是長這樣

每回合，每個人都會選對自己有利的的局面。

感覺有點模糊？
讓我們直接進題目吧！

如果只以一個角度來看的話：

  1. 先手第一步：在所有下一步的可能中，會選擇對自己有利的盤面。
  2. 接著考量下一步，換位思考對面會選擇對自己最不有利的盤面。
  3. 一直考慮，直到 Base Case 為止。

所以博弈型 DP 基本上都是採 dfs + memo 的寫法。

數數字對決

Nim Game (leetcode 292)

Nim Game (leetcode 292)

現在有兩個人要對決，前方有 n 個石頭，每個人輪流拿石頭，
一次可以拿 1~3 顆石頭，拿到最後一顆石頭的人獲勝。

請問先手有必勝解嗎？

4

舉例來說： n = 4

1

2

3

拿 3 顆

拿 2 顆

拿 1 顆

先手回合

後手回合

後手贏

後手贏

後手贏

所以 n = 4 後手贏， n = 1~3 先手贏

博奕型 DP 小結

Stone Game (leetcode 877) 拿左拿右，雙人對弈最佳，其實O(1)

 

 

Stone Game V 一樣簡單區間

https://leetcode.com/problems/guess-number-higher-or-lower-ii/description/

https://leetcode.com/problems/predict-the-winner/description/

三角尼姆https://oj.ntucpc.org/problems/525

樹 DP

題目名稱 來源 備註
House Robber III Leetcode 337 樹 DP
病毒演化 APCS 2020 / 07 - 4 樹 DP

https://leetcode.com/problems/minimize-the-total-price-of-the-trips/description/?envType=problem-list-v2&envId=dynamic-programming
先做LCA在做DP，複雜度 O(NlogN)

全方位木DP

圖DP

把 bellman ford 跟 floyd-warshall 放這裡

Minimum Cost Homecoming of a Robot in a Grid - LeetCode

放圖論
 

DAG 最長路?

把圖論的邏輯電路那堤野放進來

搭到終點 (APCS 2024/10 - 4, zj o714)

現在有一條一維數線，並在上面有 n 個公車路線。
每個公車路線會有兩個變數 start, end，這表示
你可以從 [start, end-1] 搭車搭到 end 下車。

請問從 0 搭車搭到 m 有幾種搭法？(方法數需要 % p)

如果一樣用 Bottom up
的角度來思考的話：

0

4

6

7

三號車

四號車

二號車

一號車

1

1

1

- 3

4

0

4

6

7

1

1

3

4

這題其實就是在
問 DAG 的路徑可能！

DAG: 有向無環圖

位元DP

位元運算

要提到位元DP前，我們要先熟悉位元運算

bit operation

你知道 && 和 & 的差別嗎？

5 & 6 = ?

     510=1012&610=1102−−−−−−−−     410=1002\,\,\,\,\,5_{10} = 101 _{2} \\ \& 6_{10} = 110_{2} \\ --------\\ \,\,\,\,\,4_{10} = 100_{2} \\
\,\,\,\,\,5_{10} = 101 _{2} \\ \& 6_{10} = 110_{2} \\ --------\\ \,\,\,\,\,4_{10} = 100_{2} \\

同理可以應用在 ^, | 上。

另外， ! 的位元運算是 ~

位元運算

bit operation

給定一個數字n，請枚舉所有選法 (2^n)

來個簡單題吧！

這一看不就是遞迴題嗎？


0
1
01
2
02
12
012
3
03
13
013
23
023
123
0123
4
04
14
014
24
024
124
0124
34
034
134
0134
234
0234
1234
01234
#include <stdio.h>
int main() {
    int n = 5;
    for (int i=0; i<(1<<n); i++) {
        for (int j=0; j<n; j++) {
            if (i & (1 << j))
                printf("%d", j);
        }
        printf("\n");
    }
}

* 1<<n = 2^n

位元運算

bit operation

給定一個數字n，請枚舉所有選法 (2^n)

來個簡單題吧！

這一看不就是遞迴題嗎？


0
1
01
2
02
12
012
3
03
13
013
23
023
123
0123
4
04
14
014
24
024
124
0124
34
034
134
0134
234
0234
1234
01234
00000
10000
10000
11000
10000
10100
11000
11100
10000
10010
10100
10110
11000
11010
11100
11110
10000
10001
10010
10011
10100
10101
10110
10111
11000
11001
11010
11011
11100
11101
11110
11111

位元DP

接著我們來做做看位元DP的題目吧，

單調對列優化

有限間距 LCS (zj b478)

給定兩個字串，並且限制子序列的每個元素間距必須 <= k，那麼請問LCS的長度為何？

Hint: 你可能需要會做固定範圍的2維區間最大值

斜率優化

Convex Hull Optimization / 凸包優化

四邊形優化

Quadrilateral Inequality Optimization

CDQ DC

四邊形 - Knuth

https://oi-wiki.org/dp/opt/quadrangle/

Aliens 優化

Legacy Slides

被拋棄的題目 Critical Mass (zj a388)

如何設計狀態?

在先前的題目，我們的DP狀態
都是怎麼定義的呢？

東東爬樓梯

DP[n] = 爬到第 n 階的可能數

C(n, m)

DP[n, m] = C(n, m)，也就是n相異球取m球的方法數

0/1 背包問題 (祖靈)

DP[n, W] = 前 n 個背包中，限重 W 的情況可攜帶最高價值

這些狀態都定義的很 ... 直觀

但有時，你需要很精巧的設計狀態！

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

嘗試想一下DP定義吧！

嘗試看看無腦定義狀態？

DP[n] = 連續三次正面的可能數

那麼 DP[n] 會包含著這些 case

你該怎麼寫？

n 個硬幣

x 個硬幣

➕

➕

➕

n-x-3 個硬幣

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

DP[n] = 連續三次正面的可能數

n 個硬幣

x 個硬幣

➕

➕

➕

n-x-3 個硬幣

∑2x×2n−x−3?\sum 2^x \times 2^{n-x-3}?
\sum 2^x \times 2^{n-x-3}?

x = 0

x = 1
會被重複算！

不行了...在討論下去沒完沒了，可能還要排容原理

➕

➕

➕

➕

4個硬幣

這個定義行不通，我們需要想其他狀態定義！

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

好像不能無腦定義狀態 :(

DP[n] = 沒有連續三次正面的可能數

這樣 DP[n] 可以分成哪些 Case 呢？

n 個硬幣

排組教過你：如果正攻不行，就反攻

➖

n-1次，沒有連續三次正面

➕

➖

n-2次，沒有連續三次正面

➕

➕

➖

n-3次，沒有連續三次正面

➕

➕

➖

Critical Mass (zj a388)

好像不能無腦定義狀態 :(

DP[n] = 沒有連續三次正面的可能數

n 個硬幣

排組教過你：如果正攻不行，就反攻

➖

n-1次，沒有連續三次正面

➕

➖

n-2次，沒有連續三次正面

➕

➕

➖

n-3次，沒有連續三次正面

➕

➕

➖

DPn=DPn−1+DPn−2+DPn−3DP_{n} = DP_{n-1} + DP_{n-2} + DP_{n-3}
DP_{n} = DP_{n-1} + DP_{n-2} + DP_{n-3}

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

DPn−1DP_{n-1}
DP_{n-1}
DPn−2DP_{n-2}
DP_{n-2}
DPn−3DP_{n-3}
DP_{n-3}

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

DP[n] = 沒有連續三次正面的可能數

n 個硬幣

➖

n-1次，沒有連續三次正面

➕

➖

n-2次，沒有連續三次正面

➕

➕

➖

n-3次，沒有連續三次正面

➕

➕

➖

DP[n-1]

DP[n-2]

DP[n-3]

DPn=DPn−1+DPn−2+DPn−3DP_{n} = DP_{n-1} + DP_{n-2} + DP_{n-3}
DP_{n} = DP_{n-1} + DP_{n-2} + DP_{n-3}

答案 = 全部的可能 - 沒有連續三次正面

2n2^n
2^n
−DPn-DP_n
-DP_n

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

DP[n] = 沒有連續三次正面的可能數

答案 = 全部的可能 - 沒有連續三次正面

2n2^n
2^n
−DPn-DP_n
-DP_n
Ans=Ans=
Ans=
#include <stdio.h>
unsigned long long DP[1000] = {1, 2, 4, 7};
unsigned long long rec(int n) {
    if (DP[n])
        return DP[n];
    return DP[n] = rec(n-1) + rec(n-2) + rec(n-3);
}
int main() {
    int n;
    while(~scanf("%d", &n) && n != 0) {
        printf("%llu\n", (1 << (n)) - rec(n));
    }
    return 0;
}

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

好難... 有沒有其他作法...

定義 DP[n][k] =
沒有連續3次，且最後連續 k 個 ➕

n 個硬幣

➖

n-1次，沒有連續三次正面

➕

➖

n-2次，沒有連續三次正面

➕

➕

➖

n-3次，沒有連續三次正面

➕

➕

➖

如果分成 3 個 case 做呢？

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

定義 DP[n][k] = 沒有連續3次，且最後連續 k 個➕

不管是哪個Case，
加上一個➖都會在這裡。

➖

n-1次，沒有連續三次正面

➕

➖

n-2次，沒有連續三次正面

➕

➕

➖

n-3次，沒有連續三次正面

➕

➕

➖

DPn,0=DPn−1,0+DPn−1,1+DPn−1,2DP_{n, 0} = DP_{n-1, 0} + DP_{n-1, 1} + DP_{n-1, 2}
DP_{n, 0} = DP_{n-1, 0} + DP_{n-1, 1} + DP_{n-1, 2}

最後是 ➖，再加上一個 ➕才會在這裡。

最後是➖➕，再加上一個 ➕ 才會在這裡。

DPn,1=DPn−1,0DP_{n, 1} = DP_{n-1, 0}
DP_{n, 1} = DP_{n-1, 0}
DPn,2=DPn−1,1DP_{n, 2} = DP_{n-1, 1}
DP_{n, 2} = DP_{n-1, 1}

DP的狀態定義
決定了你的轉移！

看你覺得怎麼寫最順，
有非常多種方法都可以算出答案。

Critical Mass (zj a388)

擲了n次硬幣，過程中出現連續3次正面的可能數為何？

其實正攻也可以！

DP[n][k][0] = n個硬幣，還沒有出現連續三次➕，最後有連續 k 個 ➕

DP[n][k][1] = n個硬幣，已經出現連續三次➕，最後有連續 k 個 ➕

你覺得這樣子的設計要怎麼轉移呢？

Made with Slides.com