RRRecursion - I

Arvin Liu @ Sprout 2021

RRRRRRRRRRRRRRRRRRRRR

什麼是遞迴?

感受一下?

碎形

處處連續但處處不可微分的特別圖形(?)
for迴圈只能做一條，做不出其他條碎形

碎形

n = 無限大的碎形

黃金體驗鎮魂曲

看看數學的遞迴吧!

斐波那契數列

Fibonacci Sequence

\begin{cases} F_1 = 1 \\ F_2 = 1 \\ F_n = F_{n-1} + F_{n-2} \\ \end{cases}

f(n)= \begin{cases} 1, \text{if \,n=1\,or \,2}\\ f(n-1)+f(n-2), \text{otherwise} \end{cases}

寫成這樣也OK (在數學上)。

otherwise:
否則的意思

常見的表達式長這樣:

這怎麼看呢?

F_4 = F_3 + F_2

F_3 = F_2 + F_1

= 1 + 1 = 2

= 2 + 1 = 3

斐波那契數列

Fibonacci Sequence

f(n)= \begin{cases} 1, \text{if \,n=1\,or \,2}\\ f(n-1)+f(n-2), \text{otherwise} \end{cases}

數學上式子是長這樣的。

int f(int n){
  if(n == 1 || n == 2)
    return 1;
  else 
    return f(n-1) + f(n-2);
}

程式就...照著式子寫 (?)

- 程式化

一般的手寫題目!

遞迴的觀念題

reference: APCS 106-3 觀念題-21

Question: 問F(5, 2)的值?

int F (int x, int y) {
  if (x<1)
    return 1;
  else
    return F(x-y,y)+F(x-2*y,y);
}

- Q

遞迴的觀念題

reference: APCS 106-3 觀念題-21

int F (int x, int y) {
  if (x<1)
    return 1;
  else
    return F(x-y,y)+F(x-2*y,y);
}

F(5, 2) = F(3, 2) + F(1, 2)

F(3, 2) = F(1, 2) + F(-1, 2)

F(1, 2) = F(-1, 2) + F(-3, 2)

= 1 + 1 = 2

= 2 + 1 = 3

= 3 + 2 = 5

- A

遞迴怎麼被做出來的?

(Optional) 記憶體空間分布

想要知道更多記憶體相關的知識，可以參見算法班手寫作業 - 3

這就是你自己寫的程式碼，可能還有include進來的

全域變數 & 修飾字有static的變數會放在這裡

malloc / new 系列的
空間所在 (還沒教到)

在函式裡宣告的變數都會在stack空間。 (包括main)

沒有教，可能也不會教。

int table[10];
double haha = 5.0;
int main(){
    int x;
    int y=5;
}

haha

table

x

(Optional) 記憶體空間分布

y

想要知道更多記憶體相關的知識，可以參見算法班手寫作業 - 3

Stack空間的變化

區域變數如何使用"尚未使用區域"呢?

Stack空間

....

int g(int n){
  return n+1;
}
int f(int n){
  return g(n+1);
}
int main(){
  int x = 3;
  cout << f(x);
  cout << g(5);
}

main(), x=3

f(n), n = 3

g(n), n = 4

1. 某個人呼叫main

2. 呼叫f(3)

3. 呼叫g(4)

4. 算出答案5，回傳

g(n), n = 4

5. 收到5，回傳5

f(n), n = 3

6. 收到f(3)=5，cout

7. 呼叫g(5)

g(n), n = 5

9. 收到g(5)=6，cout

8. 算出答案6，回傳

g(n), n = 5

每呼叫一個函式，
就向下開一個空間。

return就收回這個空間

所以每層變數都是獨立的。

想要知道更多記憶體相關的知識，可以參見算法班手寫作業 - 3

算法班這週的手寫作業 (?)

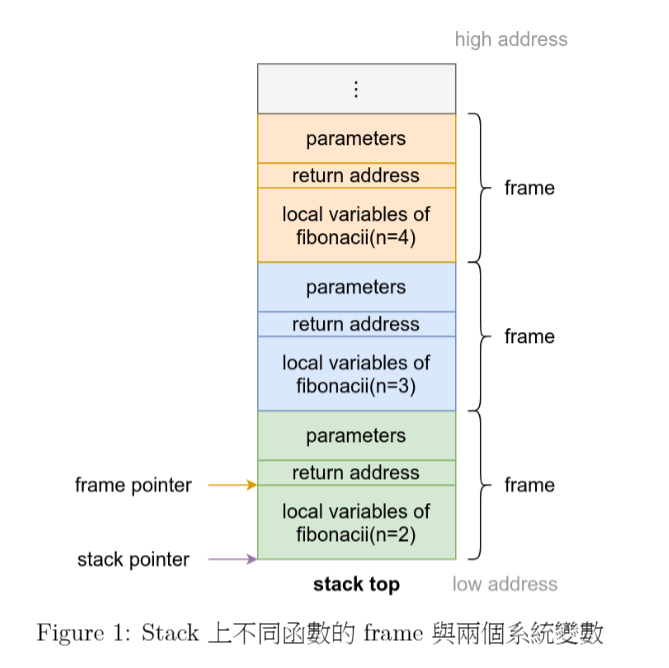
Stack空間

fib(n), n=4

一個function的空間 (俗稱stack frame)
裡面具體來說到底有什麼東西呢 ?

想要知道更多遞迴 + 記憶體相關的知識，可以參見算法班手寫作業 - 8

模擬fib(4)!

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

1. 呼叫 f(4)

= f(3) + f(2)

1

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

2. 呼叫 f(3)

f(n), n = 3

= f(2) + f(1)

2

1. 呼叫 f(4)

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

f(n), n = 3

= f(2) + f(1)

3

2. 呼叫 f(3)

3. 呼叫 f(2)

= 1

f(n), n = 2

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

f(n), n = 3

4

= 1

= f(2) + f(1)

3. 呼叫 f(2)

4. 回傳 f(2) = 1

f(n), n = 2

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

f(n), n = 3

= 1 + f(1)

5

5. 收回空間

5. 更新 f(2) 為 1

= 1

= f(2) + f(1)

4. 回傳 f(2) = 1

f(n), n = 2

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

f(n), n = 3

= 1 + f(1)

6

6. 呼叫 f(1)

f(n), n = 1

= 1

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

f(n), n = 3

= 1 + f(1)

7

7. 回傳 f(1) = 1

f(n), n = 1

= 1

6. 呼叫 f(1)

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

f(n), n = 3

= 1 + 1

8

8. 收回空間

8. 更新 f(1) 為 1

= 1 + f(1)

f(n), n = 1

= 1

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= f(3) + f(2)

f(n), n = 3

= 2

9

9. 回傳 f(3) = 2

= 1 + 1

8. 收回空間

8. 更新 f(1) 為 1

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= 2 + f(2)

10

10. 回收空間

10. 收到並更新 f(3) = 2

9. 回傳 f(3) = 2

= f(3) + f(2)

f(n), n = 3

= 2

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= 2 + f(2)

11

11. 呼叫 f(2) = 1

f(n), n = 2

= 1

10. 回收空間

10. 收到並更新 f(3) = 2

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= 2 + f(2)

12

12. 回傳 f(2) = 1

f(n), n = 2

= 1

11. 呼叫 f(2) = 1

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= 2 + 1

13

13. 回收空間

13. 收到 f(2) 為 1

= 2 + f(2)

12. 回傳 f(2) = 1

f(n), n = 2

= 1

fib(4)在stack空間的變化

Stack空間 / 運算

int f(int n){
  if(n <= 2) return 1;
  else return f(n-1) + f(n-2);
}

f(n), n = 4

= 3

14

14. 更新答案 = 3

= 2 + 1

13. 回收空間

13. 收到 f(2) 為 1

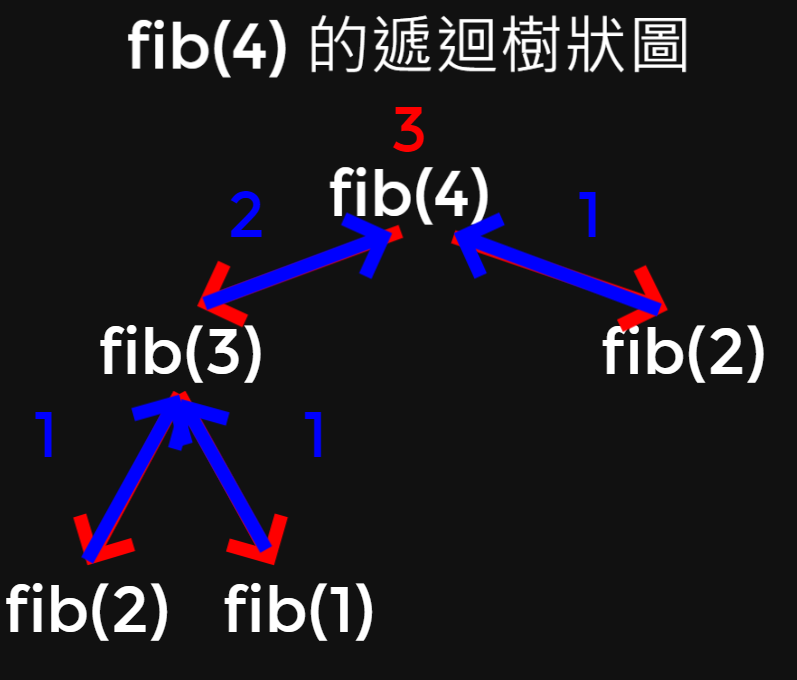
fib(4) - 遞迴樹狀圖

fib(4) 的遞迴樹狀圖

fib(4)

fib(3)

fib(2)

fib(1)

1

2

1

3

怎麼寫出一個遞迴呢?

How to do a recursion?

給個轉換例子!

f(n)= \begin{cases} 1, \text{if \,n=1\,or \,2}\\ f(n-1)+f(n-2), \text{otherwise} \end{cases}

斐波那契數列的數學與程式的轉換

int f(int n){
  if(n == 1 || n == 2) return 1;
  else return f(n-1) + f(n-2);
}

底下的數學式你會轉換成程式嗎? (f(5, 2) = 5)

f(x, y)= \begin{cases} 1, \text{if \,} x \lt 1\\ f(x-y, y)+f(x-2y,y), \text{otherwise} \end{cases}

這其實就是剛剛的APCS題(?)

int F (int x, int y) {
  if (x<1)
    return 1;
  else
    return F(x-y,y)+F(x-2*y,y);
}

底下的數學式你會轉換成程式嗎? (f(5, 2) = 5)

沒寫終止條件的話...

小知識: 對google搜尋遞迴

按按看(?)

Exercise!

350 - Pascal Triangle

巴斯卡三角形

1

2

1

3

1

4

6

1

4

1

....

(1, 1)

(2, 1)

(2, 2)

(3, 1)

(3, 2)

(3, 3)

(4, 1)

(4, 2)

(4, 3)

(4, 4)

(5, 1)

(5, 2)

(5, 3)

(5, 4)

(5, 5)

巴斯卡三角形 - Analysis

1

2

1

3

1

4

6

1

4

1

(1, 1)

(2, 1)

(2, 2)

(3, 1)

(3, 2)

(3, 3)

(4, 1)

(4, 2)

(4, 3)

(4, 4)

(5, 1)

(5, 2)

(5, 3)

(5, 4)

(5, 5)

在中間的時候

f(n, m) = \\f(n-1, m-1) + \\ f(n-1, m)

在邊邊的時候

f(n, m) = 1

所以...

f(n, m) = \begin{cases} 1 \text{\,\,\,if \,} m = 1 \text{\,\,\,or \,} n = m \\ f(n-1, m-1) + f(n-1, m) \text{ otherwise } \end{cases}

巴斯卡三角形 - Code

#include <iostream>
using namespace std;
int f(int n, int m){
    if(m==1 || n==m) return 1;
    else return f(n-1, m-1) + f(n-1, m);
}
int main(){
    int T;
    cin >> T;
    while (T--) {
        int n, m;
        cin >> n >> m;
        cout << f(n, m) << endl;
    }
    
}

f(n, m) = \begin{cases} 1 \text{\,\,\,if \,} m = 1 \text{\,\,\,or \,} n = m \\ f(n-1, m-1) + f(n-1, m) \text{ otherwise } \end{cases}

cout f(33, 16)看看!

是不是好像有點慢呢?

那是為甚麼呢?

記憶化

Memoization

這怎麼可以這麼冗?

fib(3)一樣
卻會重算！

fib(4)

fib(3)

fib(2)

fib(1)

fib(5)

fib(3)

fib(2)

fib(1)

Redundancy

這怎麼可以這麼冗?

Redundancy

如何解決?

把所有過程都記錄下來。
如果算過的就直接輸出。
怎麼判斷有沒有算過?

int f(int n, int m){
    if(m==1 || n==m) 
        return 1;
    return f(n-1, m-1) + f(n-1, m);
}

原始的巴斯卡三角形

記憶化 Memorization - I

把所有過程都記錄下來。
如果算過的就直接輸出。
怎麼判斷有沒有算過?
- 如果答案不會有0，用記錄是不是0判斷。

int f(int n, int m){
    if(m==1 || n==m) 
        return 1;
    return f(n-1, m-1) + f(n-1, m);
}

原始的巴斯卡三角形

Memorization I - 判斷答案是不是 0。


int f(int n, int m){


    if(m==1 || n==m) 
        return 1;
    int x = f(n-1, m-1) + f(n-1, m); 
    return x;
}

int mem[100][100];
int f(int n, int m){
    if(mem[n][m] != 0)
        return mem[n][m];
    if(m==1 || n==m) 
        return 1;
    mem[n][m] = f(n-1, m-1) + f(n-1, m);
    return mem[n][m];
}

記憶化 Memorization - I

把所有過程都記錄下來。
如果算過的就直接輸出。
怎麼判斷有沒有算過?
- 如果答案不會有0，用記錄是不是0判斷。
- 如果答案會有0，多開一個陣列紀錄有沒有算過。

I

int f(int n, int m){
    if(m==1 || n==m) 
        return 1;
    return f(n-1, m-1) + f(n-1, m);
}

原始的巴斯卡三角形

int mem[100][100];
bool visit[100][100];
int f(int n, int m){
    if(visit[n][m])
        return mem[n][m];
    if(m==1 || n==m) 
        return 1;
    mem[n][m] = f(n-1, m-1) + f(n-1, m);
    visit[n][m] = true;
    return mem[n][m];
}

Memorization II - 維護一個visit陣列判斷。

這其實就是簡單DP!

DP : Dynamic Programming 動態規劃

DP的一個實作法就是遞迴 + 記憶化

輾轉相除法

Euclidean Algorithm

如何算出 5 和 12 的最大公因數?

reference: wiki

酷酷的解說圖片 - 小動畫

酷酷的解說圖片 - 小發現

兩個數字一直互減，
就會減到剩下最大公因數。

reference: wiki

GCD(a, b) = GCD(a, b-a)

如果，那麼下面這個式子成立

b \ge a

兩個數字一直互減，
就會減到剩下最大公因數。

如果是的公因數，

a = ck \\ b = dk

k

a, b

互減不會影響到公因數

k

互減到其中一個為0為止。

酷酷的解說圖片 - 小證明

GCD(a, b) = GCD(a, b-a)

如果，那麼下面這個式子成立

b \ge a

GCD(a, b) = GCD(a, b\%a)

上面成立，那麼下面也會成立

因為 % 就是減到不能再減 (?)

酷酷的解說圖片 - 小縮減

如果，那麼下面這個式子成立

b \ge a

GCD(a, b) = GCD(a, b\%a)

酷酷的解說圖片 - 小整理

如果，那麼下面這個式子成立

a \ge b

GCD(a, b) = GCD(a \% b, b)

如果其中一個 = 0，那麼下面這個式子成立

GCD(a, b) = a + b

那麼，你會寫GCD的遞迴版本了嗎?

如果，那麼下面這個式子成立

b \ge a

GCD(a, b) = GCD(a, b\%a)

輾轉相除法 - 程式實作

如果，那麼下面這個式子成立

a \ge b

GCD(a, b) = GCD(a \% b, b)

如果其中一個 = 0，那麼下面這個式子成立

GCD(a, b) = a + b

int GCD(int a, int b){
  if(a == 0 || b == 0)
    return a + b;
  if (b >= a)
    return GCD(a, b % a);
  else
    return GCD(a % b, b);
}

輾轉相除法 - 程式簡化

int GCD(int a, int b){
  if(a * b == 0)
    return a + b;
  return GCD(b, a % b);
}

int GCD(int a, int b){
  if(a == 0 || b == 0)
    return a + b;
  if (b >= a)
    return GCD(a, b % a);
  else
    return GCD(a % b, b);
}

你能看懂為甚麼可以簡化成下面這樣嗎?

Exercise - II

算法班作業 - 円円數磁磚

(可能有一點難，可以回家慢慢看)

(Challenge?)

Problem Description

假設有 3 x N 的格子，那麼用 1 x 2 的方塊
填滿所有格子的方法有幾種?
(答案要%1000007)

N = 2

3 種

N = 4

3 \times 3 種 \\ + 2 種

3x3的來源:
格子切一半，一邊有3種

多的兩種

思考最後一排可能性

Type 1

Type 2

Type 4

Type 5

Type 3

做不出來:(

假設前面都放滿了

上一排 -> 下一排可能數轉換

Type 1

Type 2

Type 3

從上一排的 Type 2 轉過來 (兩種對稱可能) +
上兩排的Type 1

從上一排的
Type 1 + Type3轉過來

從上一排的 Type2 轉過來

(從上兩排來的，上一排是空的)

Q: 為甚麼不用考慮上兩排的其他case?

(從上一排
來的)

上一排 -> 下一排可能數轉換

Type 1

Type 2

Type 3

f(n, 1) = \\2f(n-1, 2) + f(n-2, 1)

f(n, 2) = \\f(n-1, 1) + f(n-1, 3)

f(n, 3) = f(n-1, 2)

從上一排的 Type 2 轉過來 (兩種對稱可能) + 上兩排的Type 1

從上一排的
Type 1 + Type3轉過來

從上一排的 Type2 轉過來

終止條件?

f(0, 1) = 1

其他第一個參數<=0的都是0，
因為這樣的條件不存在。

因為第0排放滿 = 甚麼都不放也是一個放法。

Type 1

Type 2

Type 3

f(n, 1) = \\2f(n-1, 2) + \\f(n-2, 1)

f(n, 2) = \\f(n-1, 2) + \\f(n-1, 3)

f(n, 3) =\\ f(n-1, 1)

Type 1

Type 2

Type 3

f(n, 1) = \\2f(n-1, 2) + \\f(n-2, 1)

f(n, 2) = \\f(n-1, 1) + \\f(n-1, 3)

f(n, 3) =\\ f(n-1, 1)

Solution (w/o memorization)

#include <iostream>
#define M 1000007
using namespace std;
int f(int n, int type){
    if (n == 0 && type == 1)
        return 1;
    else if(n <= 0)
        return 0;

    int ans = 0;
    if (type == 1)
        ans = 2 * f(n-1, 2) + f(n-2, 1);
    else if (type == 2)
        ans = f(n-1, 1) + f(n-1, 3);
    else
        ans = f(n-1, 2);
    return ans % M;
}

int main(){
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        cout << f(n, 1) << endl;
    }
    return 0;
}

沒有記憶化，吃了TLE...

你能把它改成有記憶化的版本嗎?

Time Limit Exceeded

不是.. code看起來爆掉了啊?

相信我，寫完記憶化丟上去就可以AC了。

這麼不負責任的嗎?

Stack Overflow

遞迴爆掉了 :-s

什麼是Stack Overflow?

不是指某個回答問題的網站。

什麼是Stack Overflow?

在函式裡宣告的變數都會在stack空間。 (包括main)

當你呼叫非常非常非常多的函式...

stack
警戒線

超出stack警戒線就會導致程式執行錯誤。

(所以是Runtime Error)

怎麼解決Stack Overflow?

stack
警戒線

不要用遞迴寫 (這在幹話?)
- 如果可以，用for迴圈寫。
  (例如fib可直接用for。)
如果不行
- 使用全域變數或heap空間，用別的方法模擬遞迴 (詳見2! - stack)
- ~~黑魔法 - 內嵌組合語言強制遞迴用heap空間~~

vector之類的 (2!會教)

黑魔法 - 強制調用heap空間

extern int main2(void) __asm__ ("main2"); 
 
int main2() { 
    run();
    exit(0); 
} 
 
int main() { 
    // 跟heap借256MB
    int size = 256 << 20;
    char *p = (char *)malloc(size) + size; 
    __asm__ __volatile__( 
        "movq  %0, %%rsp\n" 
        "pushq $exit\n"  
        "jmp main2\n" 
        :: "r"(p)); 
}

要
把你原本程式的main改名成run。
把上面這份code貼在你的程式的最下面。

#include <cstdlib>

黑魔法 - 強制調用heap空間

用黑魔法就OK了。
(本來會Stack Overflow是因為windows的警戒線放太前面了，oj上的不會)

Review

小小複習

Review

數學的遞迴式 <-> 程式的遞迴式的轉換?
- 直接照寫就可以了。

f(n)= \begin{cases} 1, \text{if \,n=1\,or \,2}\\ f(n-1)+f(n-2), \text{otherwise} \end{cases}

int f(int n){
  if(n == 1 || n == 2)
    return 1;
  else 
    return f(n-1) + f(n-2);
}

例子: 斐波那契數列

Review

遞迴重複的東西太多次導致TLE? 使用記憶化。
- 開陣列去記錄答案。
- 答案有可能為0就再開一個visit陣列，
  用來紀錄這個遞迴有沒有被解過。

int f(int n, int m){
    if(m==1 || n==m) 
        return 1;
    return f(n-1, m-1) + f(n-1, m);
}

int mem[100][100];
bool visit[100][100];
int f(int n, int m){
    if(visit[n][m])
        return mem[n][m];
    if(m==1 || n==m) 
        return 1;
    mem[n][m] = f(n-1, m-1) + f(n-1, m);
    visit[n][m] = true;
    return mem[n][m];
}

例子: 巴斯卡三角形

Review

遞迴的練習題
- 巴斯卡三角形 (圖形 -> 數學式 -> 遞迴)
- 輾轉相除法求最大公因數 GCD (數學式 -> 遞迴)
- 磁磚擺法總數 (應用問題 -> 數學式 -> 遞迴)
  - 事實上，磁磚這題可以用更快的方法解出來。
遞迴還有甚麼可以解決?
- 事實上，所有問題，只要你不怕TLE。
- 怎麼做到的?
  - 期待下一次上課 Recursion - II。 :)

Review

「遞迴只應天上有，凡人應當用迴圈」
- 看起來好像有些遞迴可以用迴圈寫啊?
- 那就用迴圈寫。
那為甚麼要用遞迴寫code?
- 有些題目用迴圈還真的寫不出來...
- 為了寫快一點! (遞迴的code通常很短)
- 注意stack overflow.

Q & A ?

遞迴是難在怎麼把問題轉換成遞迴

所以可以好好練習一下題目(?)

Homework - 349

349 - 瞬間移動 - 利用非歐幾里得幾何的世界

題序可以不要看(?)

RRRecursion - II

Arvin Liu @ Sprout 2021

RRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR

Here we go again

Recap - Recursion I

請左轉看遞迴 I 的複習 (?)

Outline

上課題目

作業題目

小小警告

接下來的內容一開始聽
會覺得很難很難，但非常非常重要

所以不會的話記得匿名發問喔!

在這之前，
讓我們補講一個東西...

什麼是遞迴樹?

首先，什麼是樹呢?

Tree

起先，你以為樹是往上長的。

樹根

樹葉

但其實，樹是往下長的。

樹根(root)

樹葉(leaf)

你發現，遞迴的過程就像是棵樹，

而這棵樹又叫做遞迴樹

樹根(root)

樹葉(leaf)

但其實，樹是往下長的。

首先，什麼是樹呢?

Tree

問題拆解 - 河內塔

154 - Tower of Hanoi

什麼是河內塔?

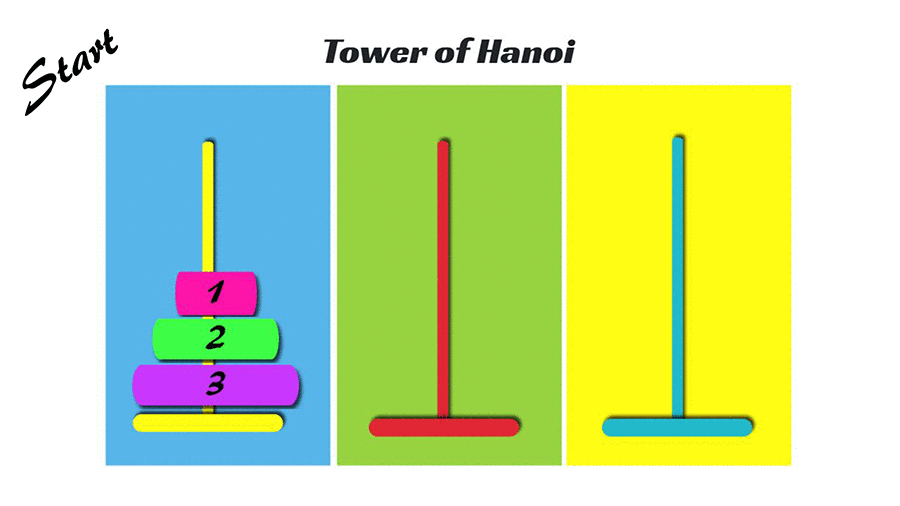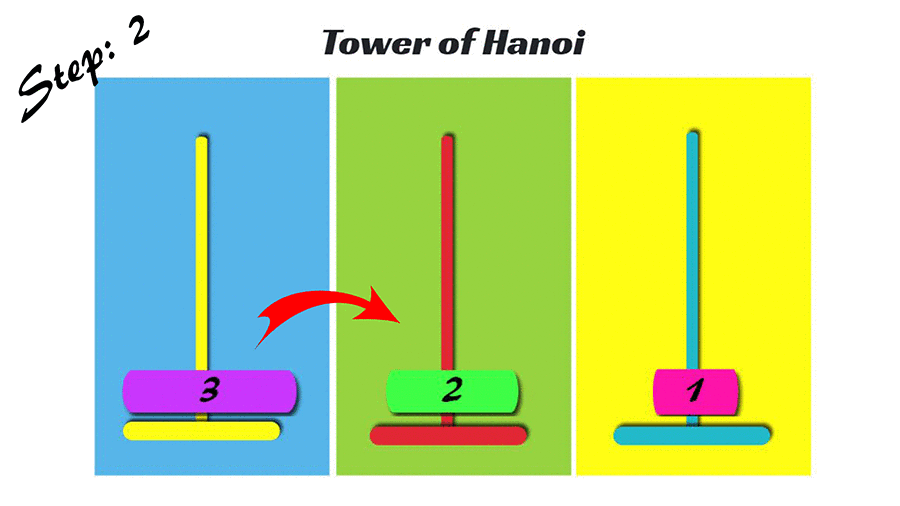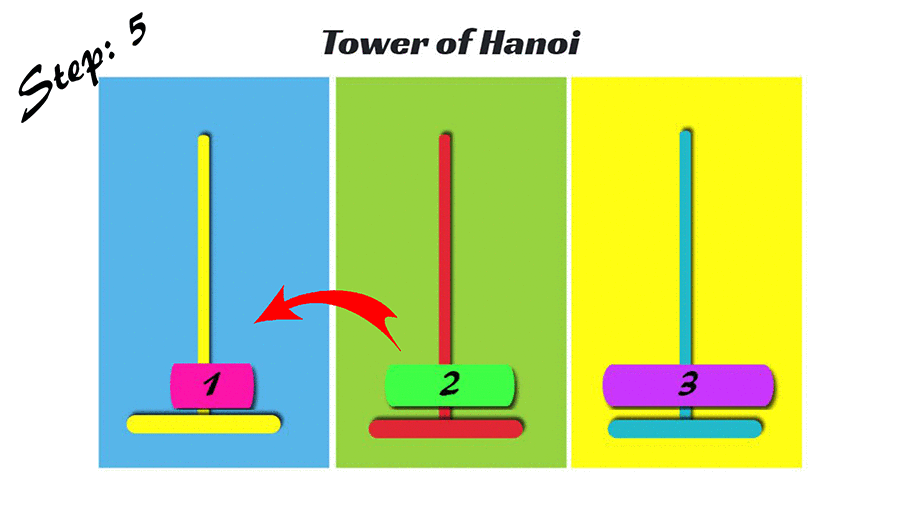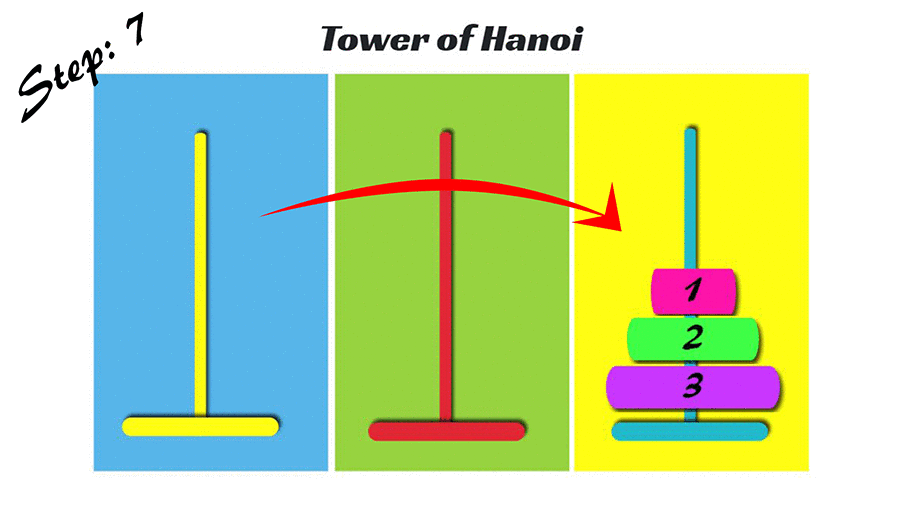
Tower of Hanoi

初始: 有大小1~n的圓盤，都在第一個塔。
每次可以移動一個圓盤，移動後只能讓比較小的在上面。
問題: 如何最少次把大小1~n的圓盤都搬到最後一層？

n=4的河內塔

想得出來要怎麼做嗎? 玩玩看!

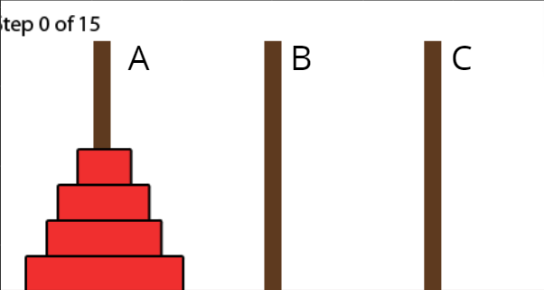
n=4的河內塔

連猩猩都會，你不會嗎(?)

n=4的河內塔

1號圓盤從A->B
2號圓盤從A->C
1號圓盤從B->C
3號圓盤從A->B
1號圓盤從C->A

2號圓盤從C->B
1號圓盤從A->B
4號圓盤從A->C
1號圓盤從B->C
2號圓盤從B->A

1號圓盤從C->A
3號圓盤從B->C
1號圓盤從A->B
2號圓盤從A->C
1號圓盤從B->C

n=4的河內塔，答案總共15步

A

B

C

歸納一下河內塔...

n

n-2

1

...

一開始，你要拿第n圓盤，
必須把第n-1圓盤放旁邊才可以。

(當然，n-1個圓盤放旁邊也要把第n-2個圓盤放旁邊)

n

怎麼把第n圓盤從A放到C呢？
- 把1~n-1的塔從A放到B。
同理，怎麼把第n-1圓盤從B放到C呢？
- 把1~n-2的塔從B放到A。

A

B

C

最後，顯然n=1就不用做事。

n-1

n-2

1

...

n-1

歸納一下河內塔...

如果你想把1~n的塔從A放到C？
- 先把1~n-1的塔從A搬到B。
- 把第n圓盤從A放到C。
- 再把1~n-1的塔從B搬回C。

n

n-2

1

...

n-1

A

B

C

n

n-2

1

...

n-1

n-2

1

...

n-1

n

怎麼把第n圓盤從A放到C呢？
- 把1~n-1的塔從A放到B。
同理，怎麼把第n-1圓盤從B放到C呢？
- 把1~n-2的塔從B放到A。

A

B

C

n-2

1

...

n-1

歸納一下河內塔...

void rec(int n, char from, char to, char other) {
  // n = 0為中止條件，因為沒這個盤子。
  if (n == 0) return ;
  rec(n-1, from, other, to);
  // 總之就是print從哪裡移盤子到哪裡
  printf("Move plate %d from %c to %c\n", n, from, to);
  rec(n-1, other, to, from);
}

rec(5, 'A', 'C', 'B');

假設總共有5圓盤，
要從'A'放到'C'，另一個閒置的是'B'

如果你想把1~n的塔從A放到C？
- 先把1~n-1的塔從A搬到B。
- 把第n圓盤從A放到C。
- 再把1~n-1的塔從B搬回C。

n

n-2

1

...

n-1

A

B

C

n

n-2

1

...

n-1

n-2

1

...

n-1

154 - 河內塔

#include <iostream>
using namespace std;

void rec(int n, char from, char to, char other) {
  // n = 0為中止條件，因為沒這個盤子。
  if (n == 0) return ;
  rec(n-1, from, other, to);
  // 總之就是print從哪裡移盤子到哪裡
  printf("Move ring %d from %c to %c\n", n, from, to, other);
  rec(n-1, other, to, from);
}

int main() {
  int n;
  cin >> n;
  rec(n, 'A', 'C', 'B');
  return 0;
}

Move ring 1 from A to B
Move ring 2 from A to C
Move ring 1 from B to C
Move ring 3 from A to B
Move ring 1 from C to A
Move ring 2 from C to B
Move ring 1 from A to B
Move ring 4 from A to C
Move ring 1 from B to C
Move ring 2 from B to A
Move ring 1 from C to A
Move ring 3 from B to C
Move ring 1 from A to B
Move ring 2 from A to C
Move ring 1 from B to C

輸入4，結果大概長這樣子

遞迴比你想像的更強大..

遞迴的本質

遞迴就是個定義遊戲。

在河內塔中，

rec(int n, char from, char to);

1. 你先定義你的遞迴可以解決河內塔。

2. 利用這個定義，把大問題拆成小問題。

如果你想把1~n的塔從A放到C？ rec(n, 'A', 'C')
- 先把1~n-1的塔從A搬到B。rec(n-1, 'A', 'B')
- 把第n圓盤從A放到C。
- 再把1~n-1的塔從B搬回C。 rec(n-1, 'B', 'C')

背包問題 - I

Knapsack Problem

什麼是背包問題?

Knapsack Problem

現在有n個東西，
每個東西都有其重量w & 價值v。
你有限制重量W的背包，
那麼你最高可以帶走多少價值？

什麼是背包問題?

Knapsack Problem

現在有n個東西，
每個東西都有其重量w & 價值v。
你有限制重量W的背包，
那麼你最高可以帶走多少價值？

拿走什麼?	總重	價值
G+C+S	15kg	$8
Y+C+S+B	10kg	$15
...	...	...

C

B

Y

G

S

東西代號	重量	價值
B	1kg	$1
S	1kg	$2
C	2kg	$2
Y	4kg	$10
G	12kg	$4

怎麼解背包問題?

Knapsack Problem

現在有n個東西，
每個東西都有其重量w & 價值v。
你有限制重量W的背包，
那麼你最高可以帶走多少價值？

暴力搜尋每種可能。

O(2^n)

複雜度 = O(所有可能) =

怎麼暴力搜尋背包問題?

Knapsack Problem

編號	0	1	2	3	4
重量	1kg	1kg	2kg	4kg	12kg
價值	$1	$2	$2	$10	$4

(目前重量，目前價值)

(0, 0)

放不放第0個?

Y

N

(1, 1)

(0, 0)

Y

(2, 3)

放不放第1個?

(1, 1)

N

Y

(1, 2)

(0, 0)

N

放不放第2個?

(4, 5)

(2, 3)

(3, 3)

(1, 1)

(3, 4)

(1, 2)

(2, 2)

(0, 0)

Y

N

Y

N

Y

N

Y

N

Y

...

暴力搜尋背包問題 - Code

Knapsack Problem

參數:

(目前重量，目前價值 )

(現在拿到第幾個物品，目前重量，目前價值)

終止條件:

現在拿到第幾個物品 = n (表示看完)
目前重量大於總重 (違反規則)

(目前重量，目前價值)

(0, 0)

放不放第0個?

Y

N

(1, 1)

(0, 0)

Y

(2, 3)

放不放第1個?

(1, 1)

N

Y

(1, 2)

(0, 0)

N

放不放第2個?

(4, 5)

(2, 3)

(3, 3)

(1, 1)

(3, 4)

(1, 2)

(2, 2)

(0, 0)

Y

N

Y

N

Y

N

Y

N

Y

...

暴力搜尋背包問題 - Code

Knapsack Problem

參數:

(目前重量，目前價值 )

(現在拿到第幾個物品，目前重量，目前價值)

終止條件:

現在拿到第幾個物品 = n (表示看完)
目前重量大於總重 (違反規則)

void rec(int now, int now_w, int now_v) {
    if (now_w > W) return ;
    if (now == n) {
        now_ans = max(now_ans, now_v);
        return ;
    }
    // 放第i個物品
    // V[i], W[i]表示第i個物品的價值和重量
    rec(now+1, now_w + w[now], now_v + v[now]);
    // 不放第i個物品
    rec(now+1, now_v, now_w);
}

(目前重量，目前價值)

(0, 0)

放不放第0個?

Y

N

(1, 1)

(0, 0)

暴力搜尋背包問題 - Code

Knapsack Problem

複雜度太慢了!

有沒有更快的方法呢?

記憶化...?

O(2^n)

void rec(int now, int now_w, int now_v) {
    if (now_w > W) return ;
    if (now == n) {
        now_ans = max(now_ans, now_v);
        return ;
    }
    // 放第i個物品
    // V[i], W[i]表示第i個物品的價值和重量
    rec(now+1, now_w + w[now], now_v + v[now]);
    // 不放第i個物品
    rec(now+1, now_v, now_w);
}

背包問題 - II

Knapsack Problem

Rethink Knapsack

假設你將rec(i, w)定義成
可以拿第0~i號的物品，

回傳背包w可以裝得下的最大價值。

所以到時候呼叫rec(n-1, W)就可以得到答案。

rec(2, 5): 如果可以拿0~2號的物品，背包限重為5，回傳最大價值。

舉例來說:

rec(7, 10): 如果可以拿0~7號的物品，背包限重為10，回傳最大價值。

rec(i, W): 如果可以拿0~i號的物品，背包限重為W，回傳最大價值。

那麼要完成rec(i, W)，要怎麼拆解問題呢?

Hint: 怎麼利用rec(i-1, ?) ?

Rethink Knapsack

假設你將rec(i, w)定義成
可以拿第0~i號的物品，

回傳背包w可以裝得下的最大價值。

rec(i, w)

可拿0~i號，
限重w

rec(i-1, w)

可拿0~i-1號，
限重w

不拿第i號

拿第i號

rec(i-1, w-wi) + vi

可拿0~i-1號，
限重w-wi

不拿:
就是忽略
第i個物品

拿:
背包扣wi，
答案價值+vi

rec(-1, ?) = 0

終止條件 ?

Rethink Knapsack

編號	0	1	2
重量	1kg	1kg	2kg
價值	$2	$1	$2

假設負重3，遞迴樹就會變成這樣

rec(1, 1) + 2

rec(1, 3)

rec(0, 0) + 1

rec(0, 1)

rec(0, 3)

rec(0, 2) + 1

rec(-1, 0)

rec(-1, 1)

rec(-1, 3)

rec(-1, 2)

放不了0號

rec(-1, 0) + 2

rec(-1, 2) + 2

rec(-1, 1) + 2

1

2

3

2

3

4

rec(2, 3)

Rewrite Knapsack

rec(i, w)

可拿0~i號，
限重w

rec(i-1, w)

可拿0~i-1號，
限重w

不拿第i號

拿第i號

rec(i-1, w-wi) + vi

可拿0~i-1號，
限重w-wi

不拿:
就是忽略
第i個物品

拿:
背包扣wi，
答案價值+vi

int rec(int i, int W) {
    // 沒東西可以拿了，回傳價值0。
    if (i == -1)
        return 0;
    if ( W-w[i] >= 0 ) {
        // 可以選擇i或不選擇i。
        return max(rec(i-1, W), rec(i-1, W - w[i]) + v[i]);
    } else {
        // 不能放i了，只能選擇不放。
        return rec(i-1, W);
    }
}

耶?

怎麼好像可以記憶化了?

Rewrite Knapsack

int rec(int i, int W) {
    // 沒東西可以拿了，回傳價值0。
    if (i == -1)
        return 0;
    if ( W-w[i] >= 0 ) {
        // 可以選擇i或不選擇i。
        return max(rec(i-1, W), rec(i-1, W - w[i]) + v[i]);
    } else {
        // 不能放i了，只能選擇不放。
        return rec(i-1, W);
    }
}

耶?

怎麼好像可以記憶化了?

Rewrite Knapsack

int rec(int i, int W) {
    // 沒東西可以拿了，回傳價值0。
    if (i == -1)
        return 0;
    // 記憶化，以前做過直接回傳答案。
    if (dp[i][W] > 0) 
        return dp[i][W];
    if ( W-w[i] >= 0 ) {
        // 可以選擇i或不選擇i。
        dp[i][W] = max(rec(i-1, W), rec(i-1, W - w[i]) + v[i]);
    } else {
        // 不能放i了，只能選擇不放。
        dp[i][W] = rec(i-1, W);
    }
    return dp[i][W];
}

複雜度? 每個狀態只會做一次，

O(nW)

471 - 總之就是背包問題。

#include <iostream>
#include <algorithm>
#define MAXN 1000
#define MAXM 1000

using namespace std;
int w[MAXN], v[MAXN];
int dp[MAXN][MAXM+1] = {0};

int rec(int i, int W) {
    // 沒東西可以拿了，回傳價值0。
    if (i == -1)
        return 0;
    // 記憶化，以前做過直接回傳答案。
    if (dp[i][W] > 0) 
        return dp[i][W];
    if ( W-w[i] >= 0 ) {
        // 可以選擇i或不選擇i。
        dp[i][W] = max(rec(i-1, W), rec(i-1, W - w[i]) + v[i]);
    } else {
        // 不能放i了，只能選擇不放。
        dp[i][W] = rec(i-1, W);
    }
    return dp[i][W];
}
int main() {
    int n, W;
    cin >> n >> W;
    for(int i=0; i<n; i++) {
        cin >> w[i] >> v[i];
    }
    cout << rec(n-1, W) << endl;
    return 0;
}

小小總結

用遞迴拆解問題

很多問題都很複雜，
但是所有的問題都可以枚舉的，像我們剛剛暴力搜尋每一種背包裝法。~~(只是會TLE)~~
用遞迴最簡單的想法就是把所有狀態全部丟進參數(或全域變數)，然後爆搜。
像背包暴力搜尋rec(now, v, w)爆搜。
不是所有遞迴都可以記憶化，你可能要換個遞迴方式才可以用記憶化。

什麼是動態規劃?

Dynamic Programming

動態規劃就是
"有技巧性的暴力搜尋"

什麼是動態規劃?

動態規劃就是
"有技巧性的暴力搜尋"

Dynamic Programming

像剛剛O(nW)的背包遞迴，
因為可以重複使用rec(i, w)的結果，
所以讓程式變得更快!

小小工商
如果想更詳細的知道什麼是動態規劃 (DP)，
可以明年去報名
資芽算法班 / IOI Camp / APCS Camp喔!

名稱	大概意思
0/1背包問題	就是只能放或不放這個物品。(同剛剛的題目)
完全背包問題	每個物品都可以拿很多個。
有限背包問題	每個物品都有其數量限制。

關於0/1背包問題

背包問題的解法	時間複雜度

直接暴力搜尋

遞迴限定背包大小，求最大價值

遞迴求達到某個價值的最小負重是多少

拆兩邊暴力搜尋，排序狀態後
Meet in the middle.

O(2^n)

O(nW)

O(n\sum v)

O(n 2^{\frac n2})

其實背包問題有很多種解法，
如果背包限制重量很小就用第二個方法，

如果總價值很小就用第三個方法，

n大概在40左右，就對半暴力搜尋。

稍微休息一下吧!

稍微看一下前面在幹嘛喔?

破解密碼 - 暴力搜尋法

brute-force password cracking

直接來看遞迴樹思考吧!

假設我們從A猜到Z，猜長度為3的密碼

Pass Crack - Recursion Tree

假設我們從A猜到Z，猜長度為3的密碼

Q:怎麼紀錄現在字串長怎樣?

Start!

第一個字

猜A

猜B

猜C

猜Z

...

第二個字

猜A

猜B

猜Z

...

猜A

猜B

猜Z

...

第三個字

猜A

猜B

猜Z

...

猜C

假設我們從A猜到Z，猜長度為3的密碼

A: 都可以用陣列紀錄。

Pass Crack - Recursion Tree

Q:怎麼紀錄現在字串長怎樣?

Start!

第一個字

猜A

猜B

猜C

猜Z

...

第二個字

猜A

猜B

猜Z

...

猜A

猜B

猜Z

...

第三個字

猜A

猜B

猜Z

...

猜C

假設我們從A猜到Z，猜長度為3的密碼。

Start!

第一個字

猜A

猜B

猜C

猜Z

...

第二個字

猜A

猜B

猜Z

...

猜A

猜B

猜Z

...

第三個字

S[0]='A';

S[1]='B';

S[2]='C';

猜A

猜B

猜Z

...

猜C

用S陣列
紀錄當前字串。

Pass Crack - Recursion Tree

Pass Crack - Code

#include <iostream>
using namespace std;

void rec(int top, char S[10]) {
    // 長度3就輸出答案後停止遞迴
    if (top == 3) {
        cout << S << endl;
    } else {
        for (char c='A'; c<='Z'; c++) {
            // 現在猜c
            S[top] = c;
            rec(top+1, S);
        }
    }
}

int main() {
    char S[10] = {};
    rec(0, S);
    return 0;
}

AAA
AAB
AAC
AAD
AAE
AAF
AAG
AAH
AAI
AAJ
AAK
AAL
AAM
AAN
AAO
AAP
AAQ
AAR
AAS
AAT
AAU
AAV
AAW
AAX
AAY
...

試試看解出zip吧!

如果你是電腦有unzip，可以使用

來對這個zip猜密碼。

system("unzip -P 你猜的密碼 secret.zip");

要 !

#include <cstdlib>

Exercise

怎麼暴力搜尋所有排列呢?

153 - 文字轉轉轉

稍微改一下就可以AC這題了!

但是，怎樣才可以不要重複猜呢?

用visit陣列去紀錄猜過甚麼

假設我們從A猜到Z，猜長度為3的密碼。

Start!

第一個字

猜A

猜B

猜C

猜Z

...

第二個字

猜A

猜B

猜Z

...

猜A

猜B

猜Z

...

第三個字

visit['A'] = true; S[0]='A';

visit['B'] = true; S[1]='B';

visit['C'] = true; S[2]='C';

猜A

猜B

猜Z

...

猜C

用visit陣列紀錄
還可以猜甚麼。

用S陣列
紀錄當前字串。

文字轉轉轉 - Recursion Tree

文字轉轉轉 - Code (Fake)

#include <iostream>
#include <cstring>
using namespace std;
char input[10];
int len = 0;
void rec(int top, bool visit[10], char S[10]) {
    if (top == len) {
        cout << S << endl;
    } else {
        for (int i=0; i<len; i++) {
            // 如果沒猜過第i個字
            if (!visit[i]) {
                // 猜第i個字
                S[top] = input[i];
                // 紀錄猜過第i個字。
                visit[i] = true;
                rec(top+1, visit, S);
                
                
            }
        }
    }
}

int main() {
    cin >> input;
    len = strlen(input);
    bool visit[10] = {};
    char S[10] = {};
    rec(0, visit, S);
    return 0;
}

答案好像怪怪的 ... ?

visit只會變true len次。

ABC

文字轉轉轉 - Code (Real)

遞迴結束後，要把猜的紀錄還原，讓visit[i]=false。

ABC
ACB
BAC
BCA
CAB
CBA

#include <iostream>
#include <cstring>
using namespace std;
char input[10];
int len = 0;
void rec(int top, bool visit[10], char S[10]) {
    if (top == len) {
        cout << S << endl;
    } else {
        for (int i=0; i<len; i++) {
            // 如果沒猜過第i個字
            if (!visit[i]) {
                // 猜第i個字
                S[top] = input[i];
                // 紀錄猜過第i個字。
                visit[i] = true;
                rec(top+1, visit, S);
                // 回溯狀態。
                visit[i] = false;
            }
        }
    }
}

int main() {
    cin >> input;
    len = strlen(input);
    bool visit[10] = {};
    char S[10] = {};
    rec(0, visit, S);
    return 0;
}

Actually...

如果你以後看到這題，可以直接使用next_perumutation。 (Peipei等等會講)

Flood Fill Problem

我們先來看題目: 42 - 庭院裡的水池

灰色是地板，藍色是水。

請問這個地圖有幾攤水池?

A: 2攤水池

A: 4攤水池

我們先來看題目: 42 - 庭院裡的水池

灰色是地板，藍色是水。

請問這個地圖有幾攤水池?

A: 2攤水池

你會怎麼做? 直接數說不定兩攤水池底下相通也?

如果你可以汙染水源(?)，那你可以怎麼做?

我們先來看題目: 42 - 庭院裡的水池

灰色是地板，藍色是水。

請問這個地圖有幾攤水池?

滴幾滴紅墨水讓它擴散，就知道這個水池跟誰相通了!

1

2

1

滴了兩滴紅墨水，
全部水都變紅色，
所以只有兩攤水池!

我們先來看題目: 42 - 庭院裡的水池

灰色是地板，藍色是水。

請問這個地圖有幾攤水池?

滴幾滴紅墨水讓它擴散，就知道這個水池跟誰相通了!

1

??

那怎麼做到墨水擴散呢?
把第一步我們想做的事情
定義成遞迴。

定義rec(x, y)代表
(x, y)格變成紅墨水並擴散

我們先來看題目: 42 - 庭院裡的水池

1

??

定義rec(x, y)代表
(x, y)格變成紅墨水並擴散

void rec(int x, int y) {
    // 只有一般的水才需要遞迴。
    // 如果是墨水格表示已經跑過了，
    // 如果是障礙物就也不能點墨水。
    if (table[x][y] == '.') {
        // 滴下墨水，填成x。
        table[x][y] = 'x';
        // 讓墨水往四方位擴散。
        rec(x+1, y);
        rec(x-1, y);
        rec(x, y+1);
        rec(x, y-1);
    }
}

擴散還真的就這樣而已。

42 - 庭院裡的水池 - code

#include <iostream>
#include <cstring>
using namespace std;
char table[1002][1002];

void rec(int x, int y) {
    // 只有一般的水才需要遞迴。
    // 如果是墨水格表示已經跑過了，
    // 如果是障礙物就也不能點墨水。
    if (table[x][y] == '.') {
        // 滴下墨水，填成x。
        table[x][y] = 'x';
        // 讓墨水往四方位擴散。
        rec(x+1, y), rec(x-1, y);
        rec(x, y+1), rec(x, y-1);
    }
}

int main() {
    int T;
    cin >> T;
    while(T--) {
        memset(table, '#', sizeof(table));
        int n, m, count = 0;
        cin >> n >> m;
        for (int i=1; i<=n; i++) {
            cin >> (table[i]+1);
        }
        for (int i=1; i<=n; i++) {
            for (int j=1; j<=m; j++) {
                // 如果這格還是一般的水，點下墨水
                // 水灘的數量 + 1
                if (table[i][j] == '.') {
                    rec(i, j);
                    count ++;
                }
            }
        }
        cout << count << endl;
    }
    return 0;
}

為了不用處理邊界，
我們讓地圖周圍都是'#'或'\0'。

單人解謎遊戲

352 - Sudoku

單人解謎遊戲

Puzzle

以數獨為例...

最笨的方法 → 爆搜所有可能!
~~(反正電腦可以跑很快)~~

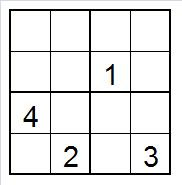
2

3

1

4

3

4

1

2

1

3

4

2

如果把遊戲決策融合遞迴樹，

這就是一棵Game Tree。

遊戲決策樹

Game Tree

遊戲開始!

第1步走A

第1步走B

第2步走B

第2步走C

直到你找到解答或
滿意為止。

...

你發現，遞迴的過程就像是棵樹，

而這棵樹又叫做遞迴樹

所以大致上，3x3數獨遞迴(猜)的順序大概會是這樣...

Start!

第一個空格

猜1

猜2

猜3

猜9

...

第二個空格

猜1

猜2

遊戲決策樹

Game Tree

猜9

...

猜1

猜2

猜9

...

第三個空格

...

猜1

猜2

猜9

...

猜1

猜2

猜9

...

猜1

猜2

猜9

...

猜1

猜2

猜9

...

最後空格

...

猜完一種可能後，判斷這個數獨合不合法。

我們都知道爆搜很沒有效率
~~(雖然有時候還是可以AC)~~，

~~結果你還是爆搜啊~~

那有沒有效率比較好的爆搜呢?

好慢啊...

回溯法

Backtracking

~~SL大法~~

遊戲決策樹

Game Tree

怎麼比較有效率爆搜呢?
其實很簡單，每次遞迴前都判斷合不合法，不合法就直接跳掉。

....

行不通!

....

OK!

猜1

猜2

1

3

2

4

3

1

?

2

1

3

4

2

3

2

1

4

2

1

2

1

3

遊戲決策樹

Game Tree

所以大致上，3x3數獨遞迴(猜)的順序大概會是這樣...

Start!

第一個空格

猜1

猜2

猜3

猜8

...

第二個空格

第三個空格

猜1

猜2

失敗了:(

猜1

沒其他可能了:(

...

失敗了:(

...

填完了:)

...

失敗了:(

...

失敗了:(

這類的方法
就叫做回溯法
(Backtracking)

遊戲決策樹

Game Tree

怎麼用遞迴實作呢?

Start!

第一個格子

猜1

猜8

第二個格子

第三個格子

猜1

猜2

失敗了:(

猜1

沒其他可能了:(

...

失敗了:(

...

填完了:)

遞迴

必要的參數
- 整個數獨表本身
- 數字猜到哪了?
結束條件?
- 失敗了:(
  (沒可能可以填了)
- 成功了 :)
  (全部都填完了!)

遊戲決策樹

Game Tree

遞迴

rec(S, 0)

第一個格子

第二個格子

第三個格子

猜1

猜2

猜1

沒其他可能了:(

...

rec(S, 1)

rec(S, 2)

rec(S, 3)

return false;

return true;

rec(S, ...)

失敗了:(

填完了:)

猜1

猜8

怎麼用遞迴實作呢?

必要的參數
- 整個數獨表本身
- 數字猜到哪了?
結束條件?
- 失敗了:(
  (沒可能可以填了)
- 成功了 :)
  (全部都填完了!)

遊戲決策樹

Game Tree

遞迴

rec(S, 0)

第一個格子

第二個格子

第三個格子

猜1

猜2

猜1

沒其他可能了:(

...

rec(S, 1)

rec(S, 2)

rec(S, 3)

return false;

return true;

rec(S, ...)

失敗了:(

填完了:)

猜1

猜8

怎麼用遞迴實作呢?

// table: 數獨本身, pos: 現在看到哪格
bool rec (int table[9][9], int pos) {
    if (pos == 81) {
        這表示已經填完了，return true;
    }
    // 把pos轉成第x行第y格的表示方法
    int x = pos / 9, y = pos % 9;
    if ((x,y)這格還沒填) {
       for (對這格從1猜到9) {
         if (如果可以填不會違背規則) {
           把數字填進去;
           if (遞迴下去，如果有解) {
              return true;
           }
         }
       }
       如果到這邊了，表示這個狀態無解。
       還原盤面，然後return false表示無解。
    } else {
       // 把問題丟給下一個位置;
       return rec(table, pos+1);
    }
}

大致的寫法

352 - SuDoKu

#include <iostream>
using namespace std;

bool valid (int table[9][9], int pos, int guess) {
    int x = pos / 9, y = pos % 9;
    for (int i=0; i<9; i++) {
        // column check
        if (table[i][y] == guess)
            return false;
        // row check
        if (table[x][i] == guess)
            return false;
    }
    // block check
    for (int block_x = x/3*3; block_x < x/3*3+3; block_x++) {
        for (int block_y = y/3*3; block_y < y/3*3+3; block_y++) {
            if(table[block_x][block_y] == guess) {
                return false;
            }
        }
    }
    return true;
}

bool rec (int table[9][9], int pos) {
    if (pos == 81) {
        // 如果已經填到第81個位置，表示
        //  填完了，回傳true。
        return true;
    }
    int x = pos / 9, y = pos % 9;
    // 如果數字是0才要猜，不是0就跳過
    if (table[x][y] == 0) {
        // 猜的這一格，從1猜到9
        for (int guess=1; guess<=9; guess++) {
            // 如果在pos可以填guess，is_ok就是true。
            //  反之則是false。
            bool is_ok = valid(table, pos, guess);
            if (is_ok) {
                // 如果可以填，我們先假設table[x][y]
                //  是我們猜的數字(guess)
                table[x][y] = guess;
                //  然後繼續遞迴猜下去。
                if (rec(table, pos+1)) {
                    // 如果遞迴是true，表示這個有解，
                    // 直接終止遞迴。
                    // 否則的話就繼續猜。
                    return true;
                }
            }
        }
        // 如果沒有一種可能有解，表示一開始的狀態
        //  就無解。 這個時候我們先**重設版面**，
        //  再回傳false表示無解。
        table[x][y] = 0;
        return false;
    } else {
        return rec(table, pos+1);
    }
}
int main() {
    int table[9][9];
    for(int i=0; i<9; i++) {
        for(int j=0; j<9; j++) {
            cin >> table[i][j];
        }
    }
    bool is_ok = rec(table, 0);
    if (is_ok) {
        for(int i=0; i<9; i++) {
            for(int j=0; j<9; j++)
                cout << table[i][j] << " ";
            cout << "\n";
        }
    } else {
        cout << "IMPOSSIBLE\n";
    }
    return 0;
}

判斷這格可不可以填 (valid function) 其實也不好寫，
可以稍微看一下怎麼判斷區塊不能有重複的條件。

對局遊戲

你怎麼跟別人對弈呢?

那就是我預測你的預測^...!

Game Tree

輪到我了!

我走A

我走B

我走C

敵人走D

敵人走E

敵人走F

敵人走H

敵人走G

如果我走A，
敵人會怎麼走?

我走I

我走J

敵人思考如果我走A後他走D，
我會怎麼走?

如果我走A，
敵人會怎麼走?

敵人走J

敵人走K

...

... 做到結束為止

搶數字

從數字1開始數，每次數可以往下數1~2個數字，輪流數。那麼誰可以數到第6個數字呢?

假設我數 1, 2

對方接著數 3

我接著數 4

對方接著數 5, 6，
這樣對方就贏了。

搶數字

從數字1開始數，每次數可以往下數1~2個數字，輪流數。那麼誰可以數到第6個數字呢?

如果我數到...

如果對方數到...

1

2

3

如果我數到...

如果對方數到...

4

3

4

5

6

4

5

6

如果我數到...

5

6

綠色表示我贏的狀況，

紅色表示對方贏的狀況

從數字1開始數，每次數可以往下數1~2個數字，輪流數。那麼誰可以數到第6個數字呢?

如果我數到...

如果對方數到...

1

2

3

如果我數到...

如果對方數到...

4

3

4

5

6

4

5

6

如果我數到...

5

6

綠色表示我贏的狀況，

紅色表示對方贏的狀況

如果對方數到4/5，
換我數我一定會數到6。

所以對方數到4我就會贏。

搶數字

從數字1開始數，每次數可以往下數1~2個數字，輪流數。那麼誰可以數到第6個數字呢?

如果我數到...

如果對方數到...

1

2

3

如果我數到...

如果對方數到...

4

3

4

5

6

4

5

6

如果我數到...

5

6

綠色表示我贏的狀況，

紅色表示對方贏的狀況

如果對方數到6表示我輸，
所以我如果數到4/5，
就會輸。

搶數字

從數字1開始數，每次數可以往下數1~2個數字，輪流數。那麼誰可以數到第6個數字呢?

如果我數到...

如果對方數到...

1

2

3

如果我數到...

如果對方數到...

4

3

4

5

6

4

5

6

如果我數到...

5

6

綠色表示我贏的狀況，

紅色表示對方贏的狀況

搶數字

從數字1開始數，每次數可以往下數1~2個數字，輪流數。那麼誰可以數到第6個數字呢?

如果我數到...

如果對方數到...

1

2

3

如果我數到...

如果對方數到...

4

3

4

5

6

4

5

6

如果我數到...

5

6

綠色表示我贏的狀況，

紅色表示對方贏的狀況

所以其實我必輸 :(
但要是對方下一步
沒數到3我就會贏!

搶數字

#include <iostream>
using namespace std;
#define N 13


pair<int, int> f(int cur) {
    // 0: 先手勝, 1: 後手勝
    if (cur+1 == N || cur+2 == N)
        return {0, N-cur};
    auto result_1 = f(cur+1);
    auto result_2 = f(cur+2);
    // 找先手勝 -> 找下一步後手勝
    if (result_1.first == 1)
        return {0, 1};
    if (result_2.first == 1)
        return {0, 2};
    // 無法先手勝 -> 後手勝 
    return {1, 1};
}

int main() {
    int n;
    while(scanf("%d", &n)!=EOF) {
        auto result = f(n);
        if (result.first == 0) {
            printf("Win, count %d", n+1);
            if (result.second == 2)
                printf(" %d", n+2);
            printf("\n");
        } else {
            printf("Lose, count %d\n", n+1);
        }
    }
    return 0;
}

那對局不是都要遞迴到結束?

跑得完才有鬼啦...

估價函數

Evaluation Function

怎麼樣才可以不要遞迴到結束呢?

想辦法遞到一半就回傳結果。

乾，你通靈是吧?

我們雖然不知道某些盤面可不可以必勝，
但我們有時候可以大概知道那些盤面比較容易獲勝。

估價函數

Evaluation Function

f(\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,) = 比較高的分數

f(\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,) = 比較低的分數

f(\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,) = 不好不壞的分數

估價函數就是一個評估局勢的函數。

Minimax / Min-Max / MM

輪到我了!

盤面A

盤面B

盤面C

盤面D

盤面E

盤面F

盤面H

盤面G

如果我走A，
敵人會怎麼走?

盤面I

盤面J

敵人思考如果我走A後他走D，
我會怎麼走?

盤面K

盤面L

盤面M

f(I) = 3

f(J) = 10

f(K) = 9

f(L) = 6

f(M) = 4

假設現在只遞迴三層，
f(盤面)越高表示對我越好，
那麼會怎麼遞迴呢?

對方下手

我下手

Minimax / Min-Max / MM

輪到我了!

盤面A

盤面B

盤面C

盤面D

盤面E

盤面F

盤面H

盤面G

如果我走A，
敵人會怎麼走?

盤面I

盤面J

敵人思考如果我走A後他走D，
我會怎麼走?

盤面K

盤面L

盤面M

f(I) = 3

f(J) = 10

f(K) = 9

f(L) = 6

f(M) = 4

假設現在只遞迴三層，
f(盤面)越高表示對我越好，
那麼會怎麼遞迴呢?

對方下手

我下手

要是輪到我 (綠色)，
就會選最高的那條，
輪到對方 (紅色)，
就會選最低的那條。

Minimax / Min-Max / MM

輪到我了!

盤面A

盤面B

盤面C

盤面D

盤面E

盤面F

盤面H

盤面G

如果我走A，
敵人會怎麼走?

盤面I

盤面J

敵人思考如果我走A後他走D，
我會怎麼走?

盤面K

盤面L

盤面M

f(I) = 3

f(J) = 10

f(K) = 9

f(L) = 6

f(M) = 4

對方下手

我下手

10

9

6

4

假設現在只遞迴三層，
f(盤面)越高表示對我越好，
那麼會怎麼遞迴呢?

要是輪到我 (綠色)，
就會選最高的那條，
輪到對方 (紅色)，
就會選最低的那條。

Minimax / Min-Max / MM

輪到我了!

盤面A

盤面B

盤面C

盤面D

盤面E

盤面F

盤面H

盤面G

如果我走A，
敵人會怎麼走?

盤面I

盤面J

敵人思考如果我走A後他走D，
我會怎麼走?

盤面K

盤面L

盤面M

f(I) = 3

f(J) = 10

f(K) = 9

f(L) = 6

f(M) = 4

對方下手

我下手

10

9

6

4

假設現在只遞迴三層，
f(盤面)越高表示對我越好，
那麼會怎麼遞迴呢?

9

4

要是輪到我 (綠色)，
就會選最高的那條，
輪到對方 (紅色)，
就會選最低的那條。

Minimax / Min-Max / MM

輪到我了!

盤面A

盤面B

盤面C

盤面D

盤面E

盤面F

盤面H

盤面G

如果我走A，
敵人會怎麼走?

盤面I

盤面J

敵人思考如果我走A後他走D，
我會怎麼走?

盤面K

盤面L

盤面M

f(I) = 3

f(J) = 10

f(K) = 9

f(L) = 6

f(M) = 4

對方下手

我下手

10

9

6

4

假設現在只遞迴三層，
f(盤面)越高表示對我越好，
那麼會怎麼遞迴呢?

要是輪到我 (綠色)，
就會選最高的那條，
輪到對方 (紅色)，
就會選最低的那條。

9

4

9

Minimax / Min-Max / MM

極小化極大演算法 (MM) 算是對局遊戲
非常重要的基礎，
很多遊戲AI都是基於MM算法延伸的。

AlphaGo?

用MCTS模擬MiniMax +
用NN做估價函數 + 決策函數

蒙地卡羅樹搜尋

神經網路

遞迴作業題

6666 - 孔明の罠 - Kaizo Trap (Peg Solitaire)

Peg Solitaire

點擊此處，玩玩看?

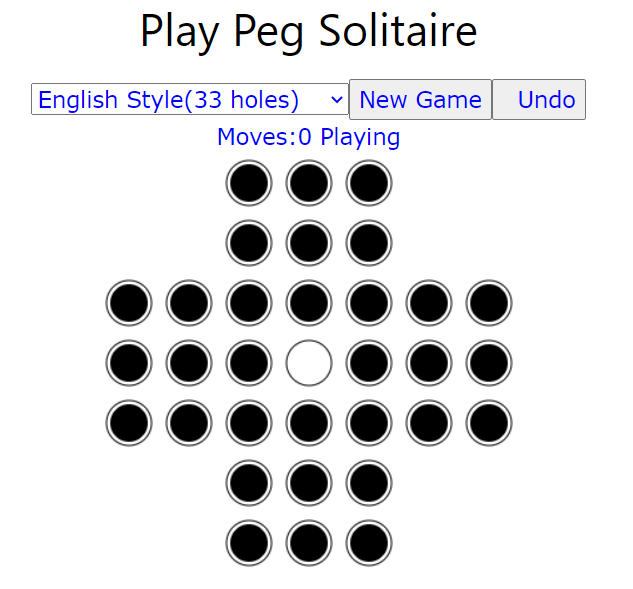
作業就是判斷現在的狀態可不可以做到剩下最後一個棋子