Search, Tree & Graph
Arvin Liu
圖論是個...
前言
考驗所學多寡的一個主題
還有實作的能力...
Tree? Graph?
Tree
Graph
就是樹狀圖的感覺
就是一堆點連來連去


資工系的樹是倒著長的 !?
目錄的目錄
| 內容 | 快速連結 | APCS範圍 |
|---|---|---|
| 前言 | Link | |
| Disjoint Set | Link | ❓ |
| 搜尋法 | Link | ⭕ |
| - 廣度優先搜尋法 Breadth First Search (BFS) | Link | ⭕ |
| - 深度優先搜尋法 Depth First Search (DFS) | Link | ⭕ |
| - BFS 變種 - Uniform Cost Search | Link | ❌ |
| - DFS 變種 - 回溯法 (Backtracking) | Link | ⭕ |
|
樹論 (Tree) |
Link | ⭕ |
| - 二元搜尋樹 Binary Search Tree (BST) | Link | ❓ |
|
圖論 (Graph) |
Link | ⭕ |
| - 單源最短路徑 Dijkstra's Algorithm | Link | ❌ |
| - 環檢測 (Cycle Detection) + 拓樸排序 Topological Sort | Link | ⭕ |
目錄 - Disjoint Set
目錄 - Searching Algorithm
目錄 - Tree
目錄 - Graph
會提到很多算法!
前言
有些可能會稍稍偏離 APCS 的範圍,
但還是希望大家可以看一下 :)
Disjoint Set
or Union Find Tree, 併查集
or 簡稱 DSU (Disjoint Set Union)
讓我們直接上題目吧!
新手訓練系列- 我的朋友很少 (zj a445)
現在有N個人,M個關係,Q筆詢問。
每個關係會給兩個人,表示這兩人是朋友。
我們定義朋友的朋友也是朋友。
每筆詢問會問兩個人,請輸出他們是不是朋友。
5 3 2
1 2
2 5
3 4
1 5
1 3 舉例來說:
1
2
5
3
4
輸出:)
輸出:(
關係圖
Disjoint Set
給定關係圖,接著詢問任兩人有沒有關係。
你會怎麼做?
關係
1 2
2 5
3 4
| 誰 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 初始 | 1 | 2 | 3 | 4 | 5 |
| 1-2 | 1 | 1 | 3 | 4 | 5 |
| 2-5 | 1 | 1 | 3 | 4 | 2 |
| 3-4 | 1 | 1 | 3 | 3 | 2 |
查詢時看B可不可以while到A就好了!
嗎?
下一個關係是 2-4 怎麼辦?
2 4
Disjoint Set
給定關係圖,接著詢問任兩人有沒有關係。
最簡單的解法:讓每個朋友群有個老大
關係
1 2
2 5
3 4
| 誰 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 老大 | 1 | 2 | 3 | 4 | 5 |
| 1-2 | 1 | 1 | 3 | 4 | 5 |
| 2-5 | 1 | 1 | 3 | 4 | 1 |
| 3-4 | 1 | 1 | 3 | 3 | 1 |
| 2-4 | 1 | 1 | 1 | 3 | 1 |
A跟B變成朋友 = (A老大) 跟 (B老大) 變成朋友!
2 4
這樣就不會不知道要跟誰,因為老大的老大只會是自己。
Disjoint Set
給定關係圖,接著詢問任兩人有沒有關係。
最簡單的解法:讓每個朋友群有個老大
關係
1 2
2 5
3 4
2 4
A跟B變成朋友 = (A老大) 跟 (B老大) 變成朋友!
這樣就不會不知道要跟誰,因為老大的老大只會是自己。
1
2
5
3
4
Disjoint Set
給定關係圖,接著詢問任兩人有沒有關係。
最簡單的解法:讓每個朋友群有個老大
A跟B變成朋友 = (A老大) 跟 (B老大) 變成朋友!
int boss[N];
void init() {
for (int i=0; i<N; i++)
boss[i] = i;
}
int find_boss(int x) {
if (x == boss[x])
return x;
return find_boss(boss[x]);
}
int merge(int x, int y) {
boss[find_boss(y)] = find_boss(x);
}boss = list(range(n))
def find_boss(x):
if x == boss[x]:
return x
return find_boss(boss[x])
def merge(x, y):
boss[find_boss(y)] = find_boss(x)C++
Python
Disjoint Set
給定關係圖,接著詢問任兩人有沒有關係。
int boss[N];
void init() {
for (int i=0; i<N; i++)
boss[i] = i;
}
int find_boss(int x) {
if (x == boss[x])
return x;
return find_boss(boss[x]);
}
int merge(int x, int y) {
boss[find_boss(y)] = find_boss(x);
}boss = list(range(n))
def find_boss(x):
if x == boss[x]:
return x
return find_boss(boss[x])
def merge(x, y):
boss[find_boss(y)] = find_boss(x)最差複雜度?
關係
4 5
3 4
2 3
1 2
1
2
5
3
4
Disjoint Set 優化 - 1
路徑壓縮 Path Compression
Disjoint Set - Path Compression
給定關係圖,接著詢問任兩人有沒有關係。
int boss[N];
void init() {
for (int i=0; i<N; i++)
boss[i] = i;
}
int find_boss(int x) {
if (x == boss[x])
return x;
return find_boss(boss[x]);
}
int merge(int x, int y) {
boss[find_boss(y)] = find_boss(x);
}boss = list(range(n))
def find_boss(x):
if x == boss[x]:
return x
return find_boss(boss[x])
def merge(x, y):
boss[find_boss(y)] = find_boss(x)1
2
5
3
4
每問一次都更新到最大的boss?
C++
Python
給定關係圖,接著詢問任兩人有沒有關係。
int boss[N];
void init() {
for (int i=0; i<N; i++)
boss[i] = i;
}
int find_boss(int x) {
if (x == boss[x])
return x;
return boss[x] = find_boss(boss[x]);
}
int merge(int x, int y) {
boss[find_boss(y)] = find_boss(x);
}boss = list(range(n))
def find_boss(x):
if x == boss[x]:
return x
boss[x] = find_boss(boss[x])
return boss[x]
def merge(x, y):
boss[find_boss(y)] = find_boss(x)啊?這樣就可以比較快喔?
不只快,他的最差複雜度是:
(均攤複雜度)
Disjoint Set - Path Compression
什麼Case會有
最差複雜度呢?
這題好難QQ,我也不會
Disjoint Set 優化 - 2
啟發式合併 Union by Rank
Disjoint Set - Link Priority
1
2
在我們合併的時候,
其實應該是有個「輩分」在的。
.
.
.
.
.
?
那我們應該要誰當老大呢?
體感上來說:感覺小併大好一點。
那麼怎樣叫小,怎樣叫大呢?
- Union by size: 看小弟有幾個
- Union by rank: 看小弟最深在哪
兩個實作完的複雜度都是
Rank = 2
Rank = 1
給定關係圖,接著詢問任兩人有沒有關係。
Disjoint Set - Union by Rank
我們以 Union by Rank 做說明:
Case - 1:
兩邊 Rank 不同
Case - 2:
兩邊 Rank 相同
小指到大,
Rank不變。
隨便指,
但 Rank + 1。
X 4
1
2
Rank = 2
Rank = 3
1
2
Rank = 3
Rank = 3
(與最遠的屬下距離)
給定關係圖,接著詢問任兩人有沒有關係。
int boss[N], rank[N]={};
void init() {
for (int i=0; i<N; i++)
boss[i] = i;
}
int find_boss(int x) {
if (x == boss[x])
return x;
return find_boss(boss[x]);
}
void merge(int x, int y) {
int boss_x = find_boss(x);
int boss_y = find_boss(y);
if (boss_x == boss_y)
return ;
if (rank[boss_x] > rank[boss_y]) {
boss[boss_y] = boss_x;
} else {
boss[boss_x] = boss_y;
if (rank[boss_x] == rank[boss_y])
rank[boss_y] ++;
}
}boss = list(range(N))
rank = [0] * N
def find_boss(x):
if x == boss[x]:
return x
return find_boss(boss[x])
def merge(x, y):
boss_x = find_boss(x)
boss_y = find_boss(y)
if boss_x == boss_y:
return
if rank[boss_x] > rank[boss_y]:
boss[boss_y] = boss_x
else:
boss[boss_x] = boss_y
if rank[boss_x] == rank[boss_y]:
rank[boss_y] += 1Disjoint Set - Union by Rank
可以自己想想看
Union by Size 要怎麼寫!
C++
Python
Disjoint Set - Two optimizations

Path Compression
Union by Rank/Size
Union by Rank/Size with Path Compression
給定關係圖,接著詢問任兩人有沒有關係。
Disjoint Set - Two optimizations
int boss[N], rank[N]={};
void init() {
for (int i=0; i<N; i++)
boss[i] = i;
}
int find_boss(int x) {
if (x == boss[x])
return x;
return boss[x] = find_boss(boss[x]);
}
void merge(int x, int y) {
int boss_x = find_boss(x);
int boss_y = find_boss(y);
if (boss_x == boss_y)
return ;
if (rank[boss_x] > rank[boss_y]) {
boss[boss_y] = boss_x;
} else {
boss[boss_x] = boss_y;
if (rank[boss_x] == rank[boss_y])
rank[boss_y] ++;
}
}boss = list(range(N))
rank = [0] * N
def find_boss(x):
if x != boss[x]:
boss[x] = find_boss(boss[x])
return boss[x]
def merge(x, y):
boss_x = find_boss(x)
boss_y = find_boss(y)
if boss_x == boss_y:
return
if rank[boss_x] > rank[boss_y]:
boss[boss_y] = boss_x
else:
boss[boss_x] = boss_y
if rank[boss_x] == rank[boss_y]:
rank[boss_y] += 1C++
Python
Inverse Ackermann Function
WTF is ?
首先我們要介紹阿克曼函數 A(m, n):
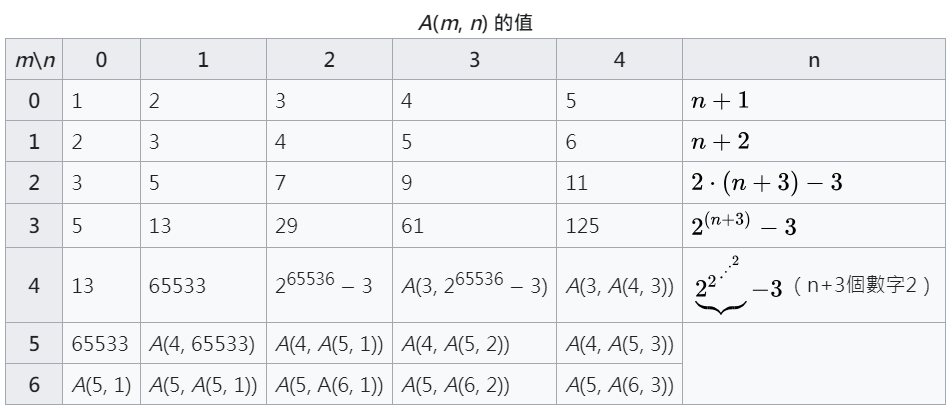
數字膨脹
非常誇張的函數!
跟手遊戰力一樣
Inverse Ackermann Function
WTF is ?
阿克曼函數:成長超級快速
阿克曼反函數:成長超級緩慢
一般來說,我們可以假設這個數字 < 5
新手訓練系列- 我的朋友很少 (zj a445)
#include <stdio.h>
#define N 10001
int boss[N], rank[N] = {};
// DSU 模板 code
int main()
{
int n, m, q, x, y;
scanf("%d%d%d", &n, &m, &q);
init();
while (m--) {
scanf("%d%d", &x, &y);
merge(x, y);
}
while (q--) {
scanf("%d%d", &x, &y);
printf(":%c\n", "()"[find_boss(x) == find_boss(y)]);
}
return 0;
}N, m, q = map(int, input().split())
boss = list(range(N+1))
rank = [0] * (N+1)
# DSU 模板 code
for _ in range(m):
x, y = map(int, input().split())
merge(x, y)
for _ in range(q):
x, y = map(int, input().split())
if find_boss(x) == find_boss(y):
print(":)")
else:
print(":(")在正常情況下...
其實只需要寫 Path Compression,
就已經足夠快了!
DSU 好像很侷限...?
Accounts Merge (Leetcode 721)
Accounts Merge (Leetcode 721)
現在有N筆資料,每筆資料有一個人名,多個信箱。
人名可能會重複,但信箱的持有人只會有一個。
現在請你將資料重新整理,把該合併的資料合併。
舉例來說:
| 人名 | 持有信箱 |
|---|---|
| John | johnsmith@mail.com, john_newyork@mail.com, john00@mail.com |
| John | johnnybravo@mail.com |
| 人名 | 持有信箱 |
|---|---|
| John | johnsmith@mail.com, john_newyork@mail.com |
| John | johnsmith@mail.com, john00@mail.com |
| John | johnnybravo@mail.com |
輸出應該是:
Accounts Merge (Leetcode 721)
現在有N筆資料,每筆資料有一個人名,多個信箱。
人名可能會重複,但信箱的持有人只會有一個。
現在請你將資料重新整理,把該合併的資料合併。
你覺得該用什麼當作 DSU 的單位呢?
- 信箱
- 人名
- 第幾筆資料 (index)
Accounts Merge (Leetcode 721)
現在有N筆資料,每筆資料有一個人名,多個信箱。
人名可能會重複,但信箱的持有人只會有一個。
現在請你將資料重新整理,把該合併的資料合併。
你覺得該用什麼當作 DSU 的單位呢?
- 信箱
A
B
B
C
A
D
John
E
John
John
John
A B 應該指到同個 boss
A D 應該指到同個 boss
這樣你會寫了嗎?
Accounts Merge (Leetcode 721)
你寫這題需要知道的注意事項:
- 比對兩個字串的複雜度 O(|S1|+|S2|)
- 這題字串長度僅30,所以直接字串判斷還好。
- 如果字串長度很長,應該要先用
unordered_map / dict 將字串導到一個編號,在利用這個編號比對。拿到編號的複雜度: O(S)
- 題目輸出的 list 需要排序。使用 set / map 本身就已經是排序過後的東西了。
- Python 就只能寫 sorted() / .sort() 了
- 使用 & 避免複製到整個 vector。
class Solution {
public:
unordered_map<string, string> boss;
unordered_map<string, int> rank;
unordered_map<string, int> account_to_idx;
// DSU 模板
string find_boss(string x) {
if (boss[x] == x)
return x;
return boss[x] = find_boss(boss[x]);
}
void merge(string x, string y) {
string bossX = find_boss(x);
string bossY = find_boss(y);
if (bossX != bossY) {
if (rank[bossX] > rank[bossY]) {
boss[bossY] = bossX;
} else{
boss[bossX] = bossY;
if (rank[bossX] == rank[bossY])
rank[bossY]++;
}
}
}
// .....
Accounts Merge (Leetcode 721)
C++ Solution - Page 1
Accounts Merge (Leetcode 721)
vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {
// 初始化,以及開始合併
for (int i = 0; i < accounts.size(); i++) {
auto &account_list = accounts[i];
for (int j = 1; j < account_list.size(); j++) {
string &account = account_list[j];
if (boss.find(account) == boss.end()) {
boss[account] = account;
rank[account] = 0;
}
account_to_idx[account] = i;
merge(account, account_list[1]);
}
}
// 蒐集答案
unordered_map<string, set<string>> pre_answer;
for (int i = 0; i < accounts.size(); i++) {
auto &account_list = accounts[i];
for (int j = 1; j < account_list.size(); j++) {
string &account = account_list[j];
pre_answer[find_boss(account)].insert(account);
}
}
// 輸出答案
vector<vector<string>> answer;
for (auto &[root, account_set] : pre_answer) {
vector<string> merged_account;
merged_account.push_back(accounts[account_to_idx[root]][0]);
// Set 會自己排序。
merged_account.insert(merged_account.end(), account_set.begin(), account_set.end());
answer.push_back(merged_account);
}
return answer;
}
};
C++ Solution - Page 2
# email 對應到第幾個資料
account_to_idx = {}
boss = {}
rank = defaultdict(lambda: 0)
# 這裡插入 DSU 模板 code
# 開始合併。
for i, account_list in enumerate(accounts):
for account in account_list[1:]:
account_to_idx[account] = i
if account not in boss:
boss[account] = account
merge(account_list[1], account)
pre_answer = defaultdict(lambda: set())
# 開始統整答案
for i, account_list in enumerate(accounts):
for account in account_list[1:]:
boss_name_idx = account_to_idx[find_boss(account)]
pre_answer[boss_name_idx].add(account)
return [ [accounts[i][0]] + sorted(list(l)) for i, l in pre_answer.items()]Accounts Merge (Leetcode 721)
Python Solution
DSU 小結
Disjoint Set...
-
如果需要「合併」,那麼可能跟 Disjoint Set 有關。
-
看是不是一種等價操作 (就是某種條件下 A = B)
-
有時候,這種等價問題也不是這麼直觀,例如剪刀石頭布問題。
-
有時候,merge的順序也是很重要的,請看貪心投影片的這題
-
-
很多時候,使用到 Disjoint Set 的題目都不是這麼的直觀
-
你很好奇的話,期待一下之後的 LCA 吧!
-
| 題目名稱 | 來源 | 備註 |
|---|---|---|
| 感染風險 | CB / C 班圖論 II - 5 | |
| 真假子圖 | Zerojudge g598 |
APCS 2021 / 4 |
| 11987 - Almost Union-Find | Zerojudge f292 | Hint: 別真的刪點。 |
| ... Make Network Connected | Leetcode 1319 |
練習題!
基礎搜尋法
Searching Algorithms
什麼是搜尋法?
大概就是你找到「解答」需要一些「過程」
而你找到「解答」的方法,就叫做搜尋法
一些「直觀」搜尋法的例子
大概就是你找到「解答」需要一些「過程」
而你找到「解答」的方法,就叫做搜尋法
給你兩個座標,
請問 A 走到 B 最快怎麼走?
過程:中間可能經過的城市
給你老鼠跟起司的位置,
請問老鼠到起司怎麼走最快?
過程:中間可能經過的格子
一些比較不「直觀」搜尋法的例子
大概就是你找到「解答」需要一些「過程」
而你找到「解答」的方法,就叫做搜尋法

給你目前的棋局,
下步怎麼走最可以贏?
過程:中間可能的所有棋盤可能

給你目前的數獨,
怎樣可以填完所有格子?
過程:中間經過所有可能的數獨
搜尋法的優劣
不同搜尋法差很多嗎?
我只能說,差超級多。
但在這裡我們只介紹兩種:
廣度優先搜尋 (BFS)
深度優先搜尋 (DFS)

不同搜尋法的視覺化
- 如果每一步的 cost 是一樣的,BFS ~= Dijkstra。
開始真正介紹吧!
廣度優先搜尋 - I
Breadth-first Search (二維平面版本)
迷宮問題 (zj a982)
給定一個二維迷宮,求從左上 (2, 2) 走到右下 (n-1, n-1) 的最短路徑長度
舉例來說:
#########
#.......#
#.#####.#
#.......#
##.#.####
#..#.#..#
#.##.##.#
#.......#
##################
#1......#
#2#####.#
#3456...#
##.#7####
#..#8#..#
#.##9##.#
#...ABCD#
#########最短路徑為:
迷宮問題 (zj a982)
給定一個二維迷宮,求從左上 (2, 2) 走到右下 (n-1, n-1) 的最短路徑長度
起點
2, 2
2, 3
2, 4
3, 2
3, 4
4, 2
4, 3
4, 4
2, 5
...
我們要怎麼知道哪一條路比較快呢?
#########
#.......#
#.#.###.#
#...###.#
#######.#
#######.#
#######.#
#######.#
#########BFS 核心概念 - 擴散

跟你玩 minecraft
的水 87% 像

從中間開始擴散,
一開始擴散到距離中心為 1 的格子,
再擴散到距離中心為 2 的格子,
最大擴散到距離 7 的格子。
迷宮問題 (zj a982)
給定一個二維迷宮,求從左上 (2, 2) 走到右下 (n-1, n-1) 的最短路徑長度
起點
2, 2
2, 3
2, 4
3, 2
3, 4
4, 2
4, 3
4, 4
2, 5
...
t=1
t=1
t=2
t=2
t=3
t=4
t=3
t=5 ?
t=3
走過不要再走了!
理論通過,開始實踐

迷宮問題 (zj a982)
給定一個二維迷宮,求從左上 (2, 2) 走到右下 (n-1, n-1) 的最短路徑長度
理論通過,開始實踐
起點
t=1
的所有點
t=2
的所有點
t=3
的所有點
...
大致上的流程就是這樣
怎麼做呢?你大概可以這麼做:

迷宮問題 (zj a982)
起點
t=1 的所有點
t=2 的所有點
t=3 的所有點
BFS (?) 大致上的流程是這樣
2, 2
2, 3
3, 2
一個可以裝很多東西的容器。
2, 4
4, 2
3, 4
2, 5
4, 3
迷宮問題 (zj a982)
需要注意的實作細節
- 這種二維地圖題,通常可以用單位向量來加速實作。
-
避免跑過重複的點。常見有兩種方法:
- 開 visit 陣列紀錄有沒有跑過這個點。
- 經過某個點就塞住回去的路 (讓當下的點變牆壁)
- 一直找,會有兩種情況:
- 找到你要的解,想辦法跳出去結算答案。
- 找不到你要的解,這個時候整個空間都會沒有點。
int dx[]={1, 0, -1, 0}, dy[]={0, 1, 0, -1};DIRS = [(1, 0), (0, 1), (-1, 0), (0, -1)]C++
Python
迷宮問題 (zj a982)
所以整個流程會是:
- 設一個 cur_cost (初始 0) 表示現在處理哪一個 list
- 把起點放在 cost = 0 的 list 上
- 接著重複以下:
-
跑所有 cost = cur_cost 的 list 中的所有點
- 如果這個 list 為空,表示沒東西擴散,無解。
- 如果這個點已經被擴散過了,就跳過。
- 如果這個點是終點,結束。
- 對於上述的每個點,找出下一個擴散點,新增到 cost = cur_cost + 1 的 list 上
- cur_cost += 1 來跑下一個時間的擴散點。
-
跑所有 cost = cur_cost 的 list 中的所有點
迷宮問題 (zj a982)
#include <iostream>
#include <vector>
using namespace std;
char table[101][101];
int ix[] = {1, 0, -1, 0};
int iy[] = {0, 1, 0, -1};
vector<pair<int, int>> Q[10000];
int main(){
int n, ans=-1;
scanf("%d", &n);
for(int i=0; i<n; i++)
scanf("%s", table[i]);
Q[0].push_back({1, 1});
for(int cur_cost=0; !Q[cur_cost].empty(); cur_cost++){
for (auto &[x, y] : Q[cur_cost]) {
if(x == n-2 && y == n-2) {
printf("%d\n", cur_cost+1);
return 0;
}
for(int k=0; k<4; k++){
int nx = x + ix[k], ny = y + iy[k];
if(table[nx][ny] == '.'){
Q[cur_cost+1].push_back({nx, ny});
table[nx][ny] = '#';
}
}
}
}
printf("No solution!");
return 0;
}C++ Solution
from collections import defaultdict
DIRS = [[0, 1], [0, -1], [1, 0], [-1, 0]]
n = int(input())
maze = [input() for _ in range(n)]
Q = defaultdict(list)
Q[0].append((1, 1))
cur_cost = 0
visit = set()
answer = None
while Q[cur_cost] and answer is None:
for x, y in Q[cur_cost]:
# If it's answer, break
if x == n-2 and y == n-2:
answer = cur_cost
break
# If visit, skip
if (x, y) in visit:
continue
visit.add((x, y))
# Search next states
for dx, dy in DIRS:
nx, ny = x + dx, y + dy
if maze[nx][ny] == '.':
Q[cur_cost+1].append((nx, ny))
cur_cost += 1
if answer is None:
print("No solution!")
else:
print(answer + 1)Python Solution
廣度優先搜尋 - II
Breadth-first Search (二維平面版本)
迷宮問題 (zj a982)
起點
t=1 的所有點
t=2 的所有點
t=3 的所有點
BFS 的流程
2, 2
2, 3
3, 2
一個可以裝很多東西的容器。
2, 4
4, 2
3, 4
2, 5
4, 3
好像每一次都只會用到兩排...?
有辦法可以只開兩排嗎?
迷宮問題 (zj a982)
t=1 的所有點
t=2 的所有點
t=3 的所有點
2, 3
3, 2
2, 4
4, 2
3, 4
2, 5
4, 3
有辦法可以只開兩排嗎?
你可能會回答:動態規劃中的滾動法
(pst=0, cur=1)
(pst=1, cur=0)
(pst=0, cur=1)
那...有辦法可以只開一排嗎?
迷宮問題 (zj a982)
t=1 的所有點
t=2 的所有點
t=3 的所有點
那...有辦法可以只開一排嗎?
起點
生成
生成
生成
在 t 生成 t + 1 的時候,不存在 t / t + 1 以外的狀態(點)存在。
在 t 生成 t + 1 的時候,不會再新增 t 的狀態(點)存在。
Q: 有什麼 (線性的) 資料結構,可以一邊生成狀態,
一邊消耗狀態,並保證先生成的先消耗呢?
怕你聽不懂,講個人話:
Q: 有什麼資料結構,是先進先出呢?
Queue
所以這個時候,好像可以把 t+1的點放在 t 的狀態點後面..?
迷宮問題 (zj a982)
BFS 大致上的流程是這樣
2, 2
2, 3
3, 2
Queue
2, 4
4, 2
3, 4
2, 5
4, 3
起點
t=1 的所有點
t=2 的所有點
t=3 的所有點
❌
❌
❌
❌
❌
迷宮問題 (zj a982)
需要注意的實作細節
- 因為你不知道這個點的 cost (離起點的距離) 是多少,所以基本上你有幾種方法去紀錄:
- 開一個紀錄 cost 的二維陣列 / map / dict。
- 如果條件允許,你可以直接覆寫地圖上。
-
把 cost 塞到狀態點裡面,讓狀態跟 cost 一起在Queue。
- 例如原本狀態是 (x, y),你把 cost 塞進去就變成了 (x, y, cost)。
- 其實走到 (x, y) 的最低 cost 你也可以看作是一種狀態。
迷宮問題 (zj a982)
所以整個流程會是:
- 在 queue 裡面放 {起點狀態, 起點的cost}
- 接著重複以下:
- 從 queue 裡面拿出一個準備要擴散的狀態
- 如果 queue 為空,表示沒東西擴散,無解。
- 如果這個點已經被擴散過了,就跳過。
- 如果這個點是終點,結束。
- 對於這個狀態,找出下一個擴散點,新增到 queue 的尾巴。
- 從 queue 裡面拿出一個準備要擴散的狀態
迷宮問題 (zj a982)
#include <iostream>
#include <queue>
using namespace std;
char table[101][101];
int cost[101][101];
int ix[] = {1, 0, -1, 0};
int iy[] = {0, 1, 0, -1};
int main(){
int n, ans=-1;
scanf("%d", &n);
for(int i=0; i<n; i++)
scanf("%s", table[i]);
queue<pair<int, int> > Q({{1, 1}});
while(!Q.empty()){
auto now = Q.front();
Q.pop();
if(now.first == n-2 && now.second == n-2){
printf("%d\n", cost[n-2][n-2]+1);
return 0;
}
for(int k=0; k<4; k++){
int nx = now.first + ix[k];
int ny = now.second + iy[k];
if(table[nx][ny] == '.'){
cost[nx][ny] = cost[now.first][now.second] + 1;
Q.push({nx, ny});
table[nx][ny] = '#';
}
}
}
printf("No solution!");
return 0;
}C++ Solution (BFS with queue)
#include <iostream>
#include <queue>
using namespace std;
char table[101][101];
int ix[] = {1, 0, -1, 0};
int iy[] = {0, 1, 0, -1};
int main(){
int n, ans=-1;
scanf("%d", &n);
for(int i=0; i<n; i++)
scanf("%s", table[i]);
queue<vector<int> > Q({{1, 1, 1}});
while(!Q.empty()){
auto tmp = Q.front();
int x = tmp[0], y = tmp[1], cost = tmp[2];
Q.pop();
if(x == n-2 && y == n-2){
printf("%d\n", cost);
return 0;
}
for(int k=0; k<4; k++){
int nx = x + ix[k], ny = y + iy[k];
if(table[nx][ny] == '.'){
Q.push({nx, ny, cost+1});
table[nx][ny] = '#';
}
}
}
printf("No solution!");
return 0;
}解1: 把 cost 塞到狀態內
解2: 開 cost 陣列紀錄
迷宮問題 (zj a982)
from collections import deque
DIRS = [[0, 1], [0, -1], [1, 0], [-1, 0]]
n = int(input())
maze = [input() for _ in range(n)]
# Starts at (1, 1) with cost 1
Q = deque([(1, 1, 1)])
visit = set()
answer = None
while Q:
x, y, cost = Q.popleft()
# If gets answer, break
if x == n-2 and y == n-2:
answer = cost
break
# If visit, skip
if (x, y) in visit:
continue
visit.add((x, y))
# Search next states
for dx, dy in DIRS:
nx, ny = x + dx, y + dy
if maze[nx][ny] == '.':
Q.append((nx, ny, cost+1))
if answer is None:
print("No solution!")
else:
print(answer)Python Solution (BFS + queue)
BFS (二維圖版本) 小結
你在這章節學到了兩種實作BFS的方法,
來找到二維圖單源最短路徑。
- 使用二維陣列
- 使用 Queue 實作
你去外面上課所講的 BFS,
以及大家公認的 BFS 都是第二種方法。
(它也比較好寫)
但第一個方法對你之後學真正的最短路徑演算法有幫助,敬請期待吧 :)。
這兩個的時間複雜度都是...
O(地圖格子數量)
深度優先搜尋
Depth-first Search (二維平面版本)
Flood Fill (Leetcode 733)
給定一個二維圖片,請你實作油漆桶功能。
舉例來說:
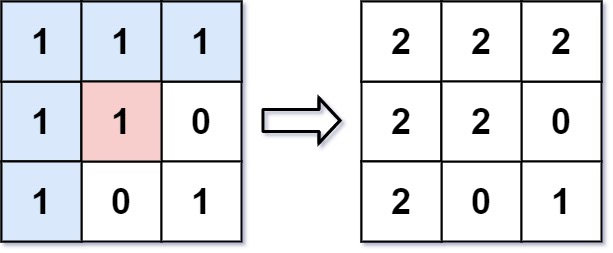
對這格使用顏色 2 到油漆桶
小樣!這不就是BFS裸題嗎?
Flood Fill (Leetcode 733)
給定一個二維圖片,請你實作油漆桶功能。
小樣!這不就是BFS裸題嗎?
你先別急!
論功能性,BFS 跟 DFS 幾乎一樣,
但 BFS 跟 DFS 各有優劣。
DFS 其實就是用遞迴的概念擴散
所以先想想看這題
怎麼用遞迴吧!
Flood Fill (Leetcode 733)
給定一個二維圖片,請你實作油漆桶功能。
所以先想想看這題怎麼用遞迴吧!
0, 0
0, 1
0, 2
1, 0
1, 1
2, 0
2, 2
1, 2
2, 1
在遞迴的課程中,我們講過:
遞迴就是一個定義遊戲。
的定義是在這個位置倒油漆桶。
這個遞迴式可以做什麼呢?
做題目所說的事情。
sol(位置)
(可能還有顏色跟地圖,看個人實作)
Flood Fill (Leetcode 733)
給定一個二維圖片,請你實作油漆桶功能。
所以先想想看這題怎麼用遞迴吧!
0, 0
0, 1
0, 2
1, 0
1, 1
2, 0
2, 2
1, 2
2, 1
在遞迴的課程中,我們講過:
遞迴就是一個定義遊戲。
sol(位置) = 在這個位置到油漆桶
sol(x, y) - 在 x, y 倒油漆桶
- 改變 x, y 的顏色
- 呼叫 sol(x-1, y) - 往這格上面倒油漆桶
- 呼叫 sol(x, y-1) - 往這格左邊倒油漆桶
- 呼叫 sol(x+1, y) - 往這格下面倒油漆桶
- 呼叫 sol(x, y+1) - 往這格右邊倒油漆桶
看起來好像跟
BFS一樣?別急
Flood Fill (Leetcode 733)
sol(x, y) - 在 x, y 倒油漆桶
- 改變 x, y 的顏色
- 呼叫 sol(x-1, y) - 往這格上面倒油漆桶
- 呼叫 sol(x, y-1) - 往這格左邊倒油漆桶
- 呼叫 sol(x+1, y) - 往這格下面倒油漆桶
- 呼叫 sol(x, y+1) - 往這格右邊倒油漆桶
0, 0
0, 1
0, 2
1, 0
1, 1
2, 0
2, 2
1, 2
2, 1
- 在 (1, 1) 倒入
- 往上倒 (0, 1)
- 往左倒 (0, 0)
- 往下倒 (1, 0)
- 往下倒 (2, 0)
- 往下倒 (1, 0)
- 往右倒 (0, 2)
- 往左倒 (0, 0)
- 往上倒 (0, 1)
想想看遞迴順序吧!
0, 0
0, 1
0, 2
1, 0
1, 1
2, 0
是不是跟 BFS 很不一樣呢?
Flood Fill (Leetcode 733)
class Solution {
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
int original_color = image[sr][sc];
if (color == original_color)
return image;
image[sr][sc] = color;
for (int k=0; k<4; k++) {
int nx = sr + dx[k], ny = sc + dy[k];
if (nx < 0 || nx >= image.size() || ny < 0 || ny >= image[nx].size())
continue;
if (image[nx][ny] == original_color)
floodFill(image, nx, ny, color);
}
return image;
}
};一些實作細節
- 如果 color == original_color 你還遞迴,也就是少寫了第6-7行會怎麼樣?
- 同個顏色的色塊會來回跑,導致無窮遞迴。
- 要在什麼時候改顏色?
- 應該在遞迴前改顏色,不然也會無窮遞迴。
- 因為你在遞迴前改了顏色,所以必須用變數記錄起來原本的顏色長什麼樣子。
C++ Solution
Flood Fill (Leetcode 733)
class Solution:
def floodFill(self, image: List[List[int]], sr: int, sc: int, color: int) -> List[List[int]]:
original_color = image[sr][sc]
if color == original_color:
return image
image[sr][sc] = color
for dx, dy in [[1, 0], [0, 1], [-1, 0], [0, -1]]:
nx, ny = sr + dx, sc + dy
if not (0 <= nx < len(image) and 0 <= ny < len(image[nx])):
continue
if image[nx][ny] == original_color:
self.floodFill(image, nx, ny, color)
return image一些實作細節
- 如果 color == original_color 你還遞迴,也就是少寫了第5-6行會怎麼樣?
- 同個顏色的色塊會來回跑,導致無窮遞迴。
- 要在什麼時候改顏色?
- 應該在遞迴前改顏色,不然也會無窮遞迴。
- 因為你在遞迴前改了顏色,所以必須用變數記錄起來原本的顏色長什麼樣子。
Python Solution

急完了,你來自己做做看這題 BFS 怎麼寫吧!
搜尋法小小結
大致了解了 BFS/DFS
重新看一下示意圖吧!
重新看一次不同搜尋法的視覺化
- 如果每一步的 cost 是一樣的,BFS ~= Dijkstra。
有感受到 fu 了嗎?
BFS 就像是水源擴散一樣,
會先把深度淺的都搜尋完才會進下一層。
DFS 就像是強力水柱一樣,
會往一個方向全搜尋完才會搜尋另一個方向。
搜尋法的優劣
廣度優先搜尋
深度優先搜尋
Breath-first Search (BFS)
Depth-first Search (DFS)
- 通常用迴圈實作
- Code 通常比較長
- 通常用在尋找最優解上
- 空間複雜度通常較高
- 通常用遞迴實作
- Code 通常比較短
- 通常用在只想找一個解上
- 空間複雜度通常較低
- 注意會 Stack Overflow。
- 想想看為什麼空間複雜度有差?
Stack Overflow 的問題
關於 C++ 的 Stack Overflow,請看 遞迴-StackOverflow
關於 Python 的 Stack Overflow 會有這樣的錯誤訊息

這個時候你可以打這幾行指令放鬆限制
import sys
sys.setrecursionlimit(1000000)這是因為 python 直接加了硬限制,
遞迴呼叫鍊只能 1000 次 (stack frame只能疊1000次)
Stack 模擬遞迴
其實...
你已經會了你知道嗎?
寫出一個 BFS,
把 queue 改成 stack 就好。
想想看為什麼?
Number of Islands (leetcode 200)
給定一個二維圖,判斷有幾個島。
舉例來說:
11000
11000
00100
00011三個島
11110
11010
11000
00000一個島
請嘗試寫出三個解法:
- BFS (使用 Queue)
- DFS (使用遞迴)
- Disjoint Set
- 提示 : 把每個格子當作是一個個體。
枚舉與搜尋法
Enumerate by BFS / DFS
只上二維圖版本 :(
接著讓我們來看 BFS / DFS
的進階用途吧!
接著讓我們來看 BFS / DFS 的進階用途吧!
我們會介紹兩種進階用法
- 單人遊戲 - 找唯一解 (利用 DFS)
- 單人遊戲 - 找最優解 (利用 BFS)
什麼是唯一解?
就是只在乎能不能夠解出來,
不在乎過程怎麼走的。
對於走迷宮來說:
- 找唯一解 : 是否可以從起點到終點?
- 找最優解 : 請問從起點到終點的最短路徑
單人解謎 - 唯一解
Enumerate by DFS - Backtracking
Sudoku Solver (Leetcode 37)
給你一個未完成的數獨,完成他。
舉例來說:


在此之前,先完成一個東西...
Sudoku Solver (Leetcode 37)
給你一個未完成的數獨,給定位置,
回傳這個位置的所有可能。
vector<char> getPossibilities(vector<vector<char>>& board, int x, int y) {
bool visit[256] = {};
for (int i=0; i<9; i++) {
visit[board[i][y]] = true;
visit[board[x][i]] = true;
visit[board[x/3*3 + i/3][y/3*3 + i%3]] = true;
}
vector<char> V;
for (char c='1'; c<='9'; c++)
if (!visit[c])
V.push_back(c);
return V;
}def getPossibilities(self, board: List[List[str]], x: int, y: int) -> bool:
possibles = set('123456789')
for i in range(9):
possibles.discard(board[i][y])
possibles.discard(board[x][i])
possibles.discard(board[x//3*3 + i//3][y//3*3 + i%3])
return possiblesSudoku Solver (Leetcode 37)
給你一個未完成的數獨,完成他。
我們嘗試 DFS 它吧!
怎麼定義遞迴式呢?
sol (board) = 完成數獨
好像有點寫不出來過程 (拆成更小的步驟)...
硬要寫的話就會變成這樣
求數獨解 -> 找第一個洞 -> 嘗試答案 -> 再求數獨解
這樣寫也不是不行,但有個更好的寫法。
Sudoku Solver (Leetcode 37)
給你一個未完成的數獨,完成他。
我們嘗試 DFS 它吧!
怎麼定義遞迴式呢?
sol (board, pos) = 從第pos個格子完成數獨
這樣好像就比較好遞迴了!
因為我們要先解決完第 pos 格填什麼,再去解決第 pos + 1 格填什麼。
Base Case: 當你填滿的時候
Sudoku Solver (Leetcode 37)
所以大致上,遞迴(猜)的順序大概會是這樣...
Start!
猜第一格
猜1
猜2
猜3
猜8
...
猜第二格
猜第三格
猜1
猜2
猜1
...
...
填完了:)
...
...
這種錯了就回去
重試其他答案
的DFS,
就叫做回溯法
(Backtracking)
沒其他可能了:(
沒其他可能了:(
沒其他可能了:(
沒其他可能了:(
Sudoku Solver (Leetcode 37)
給你一個未完成的數獨,完成他。
再想得細一點吧!
sol (board, pos) = 從第pos個格子完成數獨
sol(board, pos)
-
如果 board[pos] 不是空格,那就跳過。
- 也就是直接呼叫 sol (board, pos+1)
-
如果 board[pos] 是空格
- 猜一個可能答案進去 board[pos]
- 呼叫 sol (board, pos+1)
- 如果 pos 已經到尾了,表示填完所有答案。
先解決完第 pos 格填什麼,再解決第 pos + 1 格填什麼。
Sudoku Solver (Leetcode 37)
給你一個未完成的數獨,完成他。
bool solveSudoku(vector<vector<char>>& board, int start=0) {
if (start == 81)
return true;
int x = start / 9, y = start % 9;
if (board[x][y] != '.')
return solveSudoku(board, start+1);
for (char guess : getPossibilities(board, x, y)) {
board[x][y] = guess;
if (solveSudoku(board, start+1))
return true;
board[x][y] = '.';
}
return false;
}def solveSudoku(self, board: List[List[str]], start=0) -> None:
if start == 81:
return True
x, y = start // 9, start % 9
if board[x][y] != '.':
return self.solveSudoku(board, start+1)
else:
for guess in self.getPossibilities(board, x, y):
board[x][y] = guess
if self.solveSudoku(board, start+1):
return True
board[x][y] = '.'
return False C++
Solution
Python
Solution
記得清理狀態
記得清理狀態
Sudoku Solver (Leetcode 37)
Start!
猜第一格
猜1
猜2
猜第二格
猜第三格
猜1
猜2
猜1
...
沒其他可能了:(
沒其他可能了:(
記得清理狀態
這個時候第二格不是 '.'
而是上一輪的2
DFS 與 Backtracking
Start!
猜第一格
猜1
猜2
猜第二格
猜第三格
猜1
猜2
猜1
...
沒其他可能了:(
沒其他可能了:(
重新想想看倒油漆跟猜數獨的關係吧!
1, 1
0, 1
0, 0
1, 0
2, 0
0, 2
從 (1, 1) 開始倒
DFS 與 Backtracking
重新想想看倒油漆跟猜數獨的關係吧!
Start!
猜第一格
猜1
猜2
猜第二格
猜1
猜2
1, 1
0, 1
0, 0
0, 2
從 (1, 1) 開始倒
在數獨的 Backtracking 中,
是以每一個 (遊戲) 狀態為單位。
在倒油漆的 DFS 中
是以每一個格子為單位。
所以其實 Backtracking 就是把抽象的遊戲狀態當成是格子在做 DFS !
單人解謎 - 最優解
Enumerate by BFS - Uniform Cost Search (UCS)
讓我們玩個小遊戲吧!
Sliding Puzzle (Leetcode 773)
給你一個 2 x 3 的拼盤,
求最優解的步數
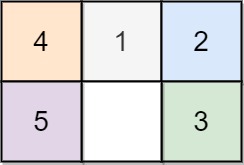
舉例來說:
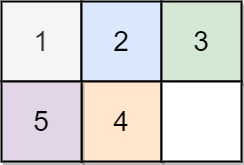
解答: 5
解答: -1 (無解)
在此之前,先完成一些東西...
Sliding Puzzle (Leetcode 773)
給你一個 2 x 3 的拼盤,
- 判斷是否結束。
- 回傳下一步的可能。
vector<vector<int>> endBoard{{1, 2, 3}, {4, 5, 0}};
bool isEnd(vector<vector<int>> &board) {
return board == endBoard;
}
vector<vector<vector<int>>> getPossibilites(vector<vector<int>> &board) {
vector<vector<vector<int>>> possibilities;
// Find zero
int x, y;
for (int i = 0; i < 2; i++)
for (int j = 0; j < 3; j++)
if (board[i][j] == 0)
x = i, y = j;
// Get Possibilities
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
for (int k = 0; k < 4; k++) {
int nx = x + dx[k], ny = y + dy[k];
if (nx < 0 || nx > 1 || ny < 0 || ny > 2)
continue;
vector<vector<int>> nxt_board(board);
swap(nxt_board[nx][ny], nxt_board[x][y]);
possibilities.push_back(nxt_board);
}
return possibilities;
}vector可以接直接==,但陣列不行喔
Sliding Puzzle (Leetcode 773)
給你一個 2 x 3 的拼盤,
- 判斷是否結束。
- 回傳下一步的可能。
def isEnd(self, board):
return board == [[1, 2, 3], [4, 5, 0]]
def getPossibilities(self, board):
# Find Zero
x, y = [(i, j) for i in range(2) for j in range(3) if board[i][j] == 0][0]
possibilities = []
for dx, dy in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
nx, ny = x + dx, y + dy
if not (0 <= nx <= 1 and 0 <= ny <= 2):
continue
nxt_board = deepcopy(board)
nxt_board[x][y], nxt_board[nx][ny] = nxt_board[nx][ny], nxt_board[x][y]
possibilities.append(nxt_board)
return possibilitieslist / tuple 都可以接直接==
要使用 copy.deepcopy 進行深度複製
要是沒有使用 deepcopy,
你會改到原本的list。
Sliding Puzzle (Leetcode 773)
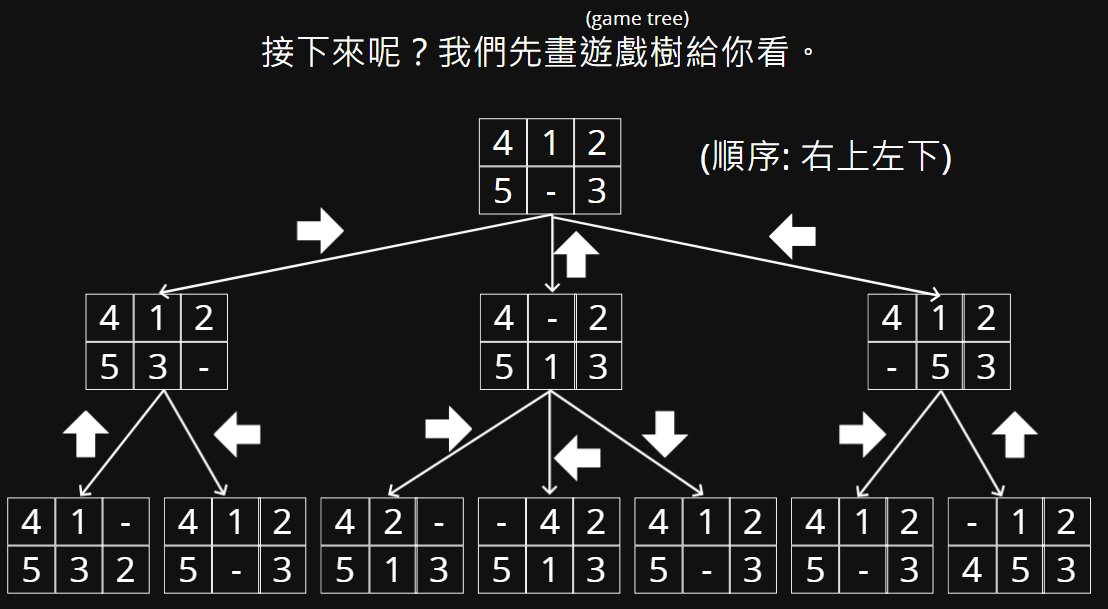
接下來呢?我們先畫遊戲樹給你看。
(game tree)
4
1
2
5
-
3
4
1
2
5
3
-
4
1
2
-
5
3
4
-
2
5
1
3
4
1
-
5
3
2
4
1
2
5
-
3
4
2
-
5
1
3
-
4
2
5
1
3
4
1
2
5
-
3
4
1
2
5
-
3
-
1
2
4
5
3
(順序: 右上左下)
重複
重複
重複
Sliding Puzzle (Leetcode 773)
所以其實 Backtracking 就是把抽象的遊戲狀態當成是格子在做 DFS !
在解數獨中,我們說:
在解 sliding puzzle 也是一樣!
Uniform Cost Search 其實就是把抽象的遊戲狀態當成是格子在做 BFS !
Sliding Puzzle (Leetcode 773)
所以整個流程會是:
- 在 queue 裡面放 {起始遊戲狀態, 起點的cost}
- 接著重複以下:
- 從 queue 裡面拿出一個準備要擴散的狀態
- 如果 queue 為空,表示沒有其他可能了,無解。
- 如果這個遊戲盤面已經被擴散過了,就跳過。
- 如果這個遊戲盤面是終點,結束。
- 對於這個狀態,找出下一步的遊戲盤面,新增到 queue 的尾巴。
- 從 queue 裡面拿出一個準備要擴散的狀態
表示跟之前的BFS不同的地方
Sliding Puzzle (Leetcode 773)
Uniform Cost Search 其實就是把抽象的遊戲狀態當成是格子在做 BFS !
int slidingPuzzle(vector<vector<int>>& board) {
queue<pair<vector<vector<int>>, int>> Q;
Q.push({board, 0});
unordered_set<string> visit;
while (!Q.empty()) {
auto [cur_board, cost] = Q.front();
Q.pop();
if (isEnd(cur_board))
return cost;
auto key = compress(cur_board);
if (visit.find(key) != visit.end())
continue;
visit.insert(key);
for (auto nxt_board : getPossibilites(cur_board))
Q.push({nxt_board, cost + 1});
}
return -1;
}string compress(
vector<vector<int>>& board) {
string result;
for (const auto& row : board)
for (int val : row)
result += to_string(val);
return result;
}將版面壓縮成 str 的函數。
為什麼要這一步之後會提。
Sliding Puzzle (Leetcode 773)
Uniform Cost Search 其實就是把抽象的遊戲狀態當成是格子在做 BFS !
def slidingPuzzle(self, board: List[List[int]]) -> int:
Q = deque([(board, 0)])
visit = set()
while Q:
cur_board, cost = Q.popleft()
if self.isEnd(cur_board):
return cost
key = str(cur_board)
if key in visit:
continue
visit.add(key)
for nxt_board in self.getPossibilities(cur_board):
Q.append((nxt_board, cost+1))
return -1將版面壓縮成 str。
為什麼要這一步之後會提。
補充 : 變成 set 的 key 的條件
我們說...
C++ 的 set / map
Python 的 set / dict
是一個存放 的資料結構
(包括 unordered)
key / key-value
這個key
是唯一的。
這個 key 至少要能夠判斷兩個東西是不是一樣的。
- C++ 的 set / map : 必須定義小於運算子 <
- C++ 的 unordered_set / unordered_map 以及
Python 的 set / dict : 必須定義 hash() 以及相等運算子 == - 如果你很懶,就直接壓成字串或數字最方便。
- python 可以只寫 hash 而不會錯誤,
但結果應該不會是你想要的。
想想看
- 你能夠還原解答嗎?
- Hint 1: 想想看 DP 中的 LCS 怎麼還原的。
- 想想看空間 / 時間複雜度
- 我們換一個題目:
- 如果把空格往上的 cost 變為 2,其他維持 1,
你會怎麼寫? - 你能保證你的解法是最佳解嗎?
- 如果 cost range 很大,有沒有更合適的資料結構呢?
- 事實上,這樣才是最完整的 UCS 算法。
- 如果把空格往上的 cost 變為 2,其他維持 1,
- 擴散的時候紀錄 visit 好還是從 queue 拿出來的時候紀錄 visit 好?分享你的看法吧!
搜尋法小結
搜尋法小結
- 廣度優先搜尋 - 找兩點最短路徑
- 二維地圖搜尋
- 利用水源擴散的想法搜尋
- 方法 1: 開一排容器去紀錄擴散的點
- 方法 2: 開一個queue去紀錄擴散的點
- Uniform Cost Search
- 把「擴散的點」當作是「下一步的遊戲狀態」
- 使用 priority_queue / heapq 來找下一個要擴散的源頭
- 二維地圖搜尋
- 深度優先搜尋
- 二維地圖搜尋:
- 利用遞迴的想法搜尋
- 回溯法 (Backtracking)
- 一樣把「擴散的點」當作「下一步的遊戲狀態」去遞迴
- 二維地圖搜尋:
想想看 ?

我們先前提到這樣的一句話
那麼請你想想看:
- BFS / UCS 怎麼做數獨?
- 跟 DFS 的空間複雜度 / 時間複雜度誰優誰劣?
- DFS 怎麼做 sliding puzzle?
- 你可以去查查看 Iterative Deepening DFS (IDDFS)
#include <iostream>
#include <unordered_set>
#include <set>
using namespace std;
struct A {
int x;
bool operator <(const A &other) const {
return x < other.x;
}
};
struct B {
int x;
bool operator ==(const B &other) const {
return x == other.x;
}
};
namespace std {
template<> struct hash<B> {
size_t operator()(const B& p) const noexcept {
return p.x;
}
};
}
int main() {
set<A> S1;
S1.insert(A());
unordered_set<B> S2;
S2.insert(B());
}class A:
def __init__(self):
self.x = 0
def __eq__(self, value: object) -> bool:
return self.x == value.x
def __hash__(self) -> int:
return self.x
print(len({A(), A()}))補充 : 讓 sturct 可以塞進 set 的實作
具體 set / map / dict 怎麼實作的,
以及什麼是hash,
這個實在是太複雜了,
所以我們暫時不提。
練習題!
| 題目名稱 | 來源 | 備註 | CodingBar |
|---|---|---|---|
| 傳送點 | Zerojudge f166 | APCS 2019/10 - 4 | C 班圖論 2-2 |
| 開啟寶盒 | Zerojudge k734 |
APCS 2023/6 - 4 其實比較像 Kahn |
C 班圖論 2-1 |
| 搬家 | Zerojudge m372 | APCS 2023/10 - 3 | |
| 靈犬尋寶 | Zerojudge b059 | 95年學科競賽 - 4 | C 班圖論 1-5 |
| Numbers of Islands | Leetcode 200 | C 班圖論 1-1 | |
| 最少障礙物 | Leetcode 2290 | 0/1 最短路 | |
| 暴雨降臨 | C 班圖論 3-1 | ||
| 星際旅行 | C 班圖論 3-4 | ||
| Find a safe walk through a grid |
Leetcode 787 | 二維圖最短路, 但不太一樣 |
Tree
我們說 Tree 是長這樣的...
有沒有一些範例呢?
前言
遊戲樹
遞迴樹
這些都是樹!
分析樹
決策樹
這些都是樹!

(Decision Tree)
(Parsing Tree)
但我們接下來只會著重上...
點裡面是一份資料的。
前言
樹的各種術語
Terminology of Tree
樹的構造
A
B
C
D
E
F
G
H
I
A
- 節點 : 一棵樹最小的單位
- 邊 : 節點跟節點連結的樹枝 (?)
- 樹根 : 唯一的源頭
- 樹葉 / 葉節點 : 沒有往下分岔的節點
(Root Node)
(Leaf / Outer / Terminal Node)
D
F
G
(Edge)
(Node)
C
H
I
樹節點的關係
以 C 為準:
- C 的 父節點 : 來源是哪個點
- C 的 子節點 : 往下一層有誰
- C 的 兄弟 : 父節點的子節點扣掉自己
- C 的 祖先 : C走到樹根經過的所有點
- C 的 子孫 : 根源為 C 的所有點
- C 的 鄰居 : 連著 C 的所有點 (父+子)
- C 的 度 : 有幾個子節點
(Parent Node)
A
B
C
D
E
F
G
H
I
A
(Children Node)
E
F
G
(Sibling Node)
B
(Ancestors)
(Descendants)
(Neighbor)
E
F
G
H
I
A
A
E
F
G
(Degree)
1
2
3
樹的性質
A
B
C
D
E
F
G
H
I
- 樹的 高度 : 樹根到最遠樹葉的距離
- 樹的 大小 : 總共有幾個節點
- 樹的 度 : 所有節點中最大的度
(Height)
(Size)
(Degree)
高
度
為
3
* 有些人的高度定義是4,你爽就好。
大小為 9
度為 3
樹的種類
- 樹的 度 如果是 2,稱為 二元樹
- 如果這個二元樹緊密排列,(由左往右再由上往下長) 稱為 完全二元樹
- 如果這棵樹是 完全二元樹,且最後一層長滿,稱為 滿/完美二元樹
(Binary Tree)
(Complete Binary Tree)
(Perfect / Full Binary Tree)
- 這是一棵二元樹
* 3 就 三元樹,同理。
- 這是一棵完全二元樹
- 這是一棵滿的二元樹
A
B
C
D
E
G
H
I
J
K
L
M
N
O
P
術語統整
| 中文 | 英文 | 意思 |
|---|---|---|
| 樹根 | Root Node | 沒有父節點的點 (孤兒) |
| 樹葉 / 葉節點 | Leaf / Outer / Terminal Node | 沒有小孩的節點 |
| 父節點 | Parent Node | 上游的那個點 |
| 子節點 | Children Node | 下游的點們 |
| 兄弟節點 | Sibling Node | 父節點的子節點扣掉自己 |
| 祖先 | Ancestors | 上游的所有點 |
| 子孫 | Descendants | 下游的所有點 |
| 鄰居 | Neighbor | 父節點+子節點 (= 距離為 1 的點) |
| 節點的度 | Degree of Node | 有幾個子節點 |
| 樹的度 | Degree of Tree | 樹中所有節點中最大的度 |
| 樹的大小 | Size | 總共有幾個節點 |
| 樹的高度 | Height | 從樹根到樹葉的最大距離 |
| 二元樹 | Binary Tree | 樹的度為 2 |
| 完全二元樹 | Complete Binary Tree | 排列緊湊的二元樹 |
| 完美 / 滿二元樹 | Full / Perfect Binary Tree | 樹葉都在同深度的完全二元樹 |
(僅列舉比較重要的)
練習題!
- 有一個完美 / 滿的二元樹,高度為 h ,
請問這棵樹大小 (size)? - 有一個完美 / 滿的二元樹,大小為 n,
請問這棵樹的高度是多少? - 有一棵樹,大小為 n:
- 這棵樹有幾條邊 ? (Edge)
- 樹的高度最高多少?長怎麼樣?
- 樹的高度最低多少?長怎麼樣?
- 你覺得這樣是一棵樹嗎?
A
B
C
D
樹的建構法
How to build a tree?
樹的建構法
-
如果是個完全樹,可以使用陣列。 - 如果不能保證完全樹,使用指標 + struct / class。
- 把樹當成是一種圖,使用圖的建構法。
- 我們講圖的時候才會講這種建構法。
-
你只要存的起來,你想怎麼做隨便你。-
Disjoint Set 其實就是很多棵樹 (= 森林)
-
完全樹 -> 陣列
不是完全樹 -> 開 struct / class
樹的建構法 1 - 陣列
如果這棵樹是一顆完全二元樹
A
B
E
D
C
G
F
我們來嘗試對其編號:
如果一個點的編號為 x :
- 左小孩編號為多少?
- 右小孩編號為多少?
- 你有辦法證明出來這是對的嗎?
0
1
2
3
4
5
6
樹的建構法 1 - 陣列
char tree[] = "ABEDFCG";
int x = 1;
printf("Node %d: %c", x, tree[x]);
int x_l = 2*x+1;
printf("L %d: %c", x_l, tree[x_l]);
int x_r = 2*x+2;
printf("R %d: %c", x_r, tree[x_r]);tree = "ABEDFCG"
x = 1
print(f"Node {x}: {tree[x]}")
x_l = 2*x+1
print(f"L {x_l}: {tree[x_l]}")
x_r = 2*x+2
print(f"R {x_r}: {tree[x_r]}")A
B
E
D
C
G
F
0
1
2
3
4
5
6
C++
Python
樹的建構法 2 - struct / class
struct Tree {
char data;
Tree *l, *r;
Tree (char d, Tree *l, Tree *r):
data(d), l(l), r(r) {}
};A
B
E
D
C
G
F
class Tree:
def __init__(self, d, l, r):
self.data = d
self.l = l
self.r = r
C++
Python
樹的建構法 2 - struct / class
#include <stdio.h>
struct Tree {
char data;
Tree *l, *r;
Tree (char d, Tree *l, Tree *r):
data(d), l(l), r(r) {}
};
int main() {
Tree *root = new Tree('A',
new Tree('B',
new Tree('D', nullptr, nullptr),
new Tree('F', nullptr, nullptr)
),
new Tree('E',
new Tree('C', nullptr, nullptr),
new Tree('G', nullptr, nullptr)
)
);
printf("%c\n", root->l->r->data); // F
printf("%c\n", root->r->l->data); // C
}A
B
E
D
C
G
F
C++
樹的建構法 2 - struct / class
class Tree:
def __init__(self, d, l, r):
self.data = d
self.l = l
self.r = r
root = Tree('A',
Tree('B',
Tree('D', None, None),
Tree('F', None, None)),
Tree('E',
Tree('C', None, None),
Tree('G', None, None))
)
print(root.l.r.data) # F
print(root.r.l.data) # CA
B
E
D
C
G
F
Python
練習題!
- 我指標好爛,不想要指標嗚嗚...
- 可以這樣寫嗎?
- 其實你可以開一個陣列先做好所有點,然後 l, r 指的是這個陣列的第幾個點。
你能夠實作出來嗎?
- 可以這樣寫嗎?
struct Tree {
char data;
Tree l, r;
Tree (char d, Tree l, Tree r):
data(d), l(l), r(r) {}
};struct Tree {
char data;
int l, r;
Tree (char d, int l, int r):
data(d), l(l), r(r) {}
};練習題!
- 我指標好爛,不想要指標嗚嗚...
- 如果現在不是二元樹,現在是三元樹,
- 你要怎麼使用陣列來存呢?
- x 的 L / M / R 的編號是多少呢?
- 有些人 Root 的編號習慣用 1,那麼 x 的 L / R 編號?
- 如果現在就是一棵樹,幾元未知:
- 有辦法用陣列做嗎?
- 有辦法用 struct / class 做嗎?
- 怎麼存小孩?
- 如果有一棵二元樹,size = N,但他不是完全二元樹:
- 用陣列做法可以嗎?
- 如果形狀未知,最壞情況陣列要開多大?
練習題!
5
3
6
1
9
6. 請嘗試做出這樣的一棵樹,使用 struct / class
樹的遍歷
BFS / DFS a tree
給你一個 struct / class 建構
出來的二元樹,輸出所有點的資訊
樹的遍歷 - BFS
A
B
E
D
C
G
F
想想看 BFS 怎麼做!

t=1
t=1
t=2
t=2
t=2
t=2
如果在 Root 倒水
所以跟之前只差在
擴散的點是由樹決定的,
並且 BFS 的單位是一顆節點!
(而且不會回流)
給你一個 struct / class 建構
出來的二元樹,輸出所有點的資訊
樹的遍歷 - BFS
A
B
E
D
C
G
F
t=1
t=1
t=2
t=2
t=2
t=2

queue<Tree *> Q({root});
while (!Q.empty()) {
Tree *cur = Q.front();
Q.pop();
printf("-> %c ", cur->data);
if (cur->l) Q.push(cur->l);
if (cur->r) Q.push(cur->r);
}
-> A -> B -> E -> D -> F -> C -> G Q = deque([root])
while Q:
cur = Q.popleft()
print(" ->", cur.data, end='')
if cur.l: Q.append(cur.l)
if cur.r: Q.append(cur.r)C++
Python
輸出
給你一個 struct / class 建構
出來的二元樹,輸出所有點的資訊
樹的遍歷
A
B
E
D
C
G
F
想想看 DFS 怎麼做!
遞迴定義:輸出整棵樹
rec(root):
- 輸出自己
- 輸出左邊的樹 rec(root.l)
- 輸出右邊的樹 rec(root.r)
給你一個 struct / class 建構
出來的二元樹,輸出所有點的資訊
樹的遍歷
A
B
E
D
C
G
F
void dfs(Tree *root) {
if (!root) return;
printf("-> %c ", root->data);
dfs(root->l);
dfs(root->r);
}-> A -> B -> D -> F -> E -> C -> Gdef dfs(root):
if root:
print(" ->", root.data, end='')
dfs(root.l)
dfs(root.r)C++
Python
輸出
1
2
3
4
5
6
7
給你一個 struct / class 建構
出來的二元樹,輸出所有點的資訊
樹的遍歷
A
B
E
D
C
G
F
rec(root):
- 輸出自己
- 輸出左邊的樹 rec(root.l)
- 輸出右邊的樹 rec(root.r)
這個順序很重要嗎?
- 輸出自己 / 輸出左小孩 / 輸出右小孩
- 輸出左小孩 / 輸出自己 / 輸出右小孩
- 輸出左小孩 / 輸出右小孩 / 輸出自己
你能夠講出其他兩種的輸出嗎?
給你一個 struct / class 建構
出來的二元樹,輸出所有點的資訊
樹的遍歷
A
B
E
D
C
G
F
- 輸出自己 / 輸出左小孩 / 輸出右小孩
- 輸出左小孩 / 輸出自己 / 輸出右小孩
- 輸出左小孩 / 輸出右小孩 / 輸出自己
- BFS 的走訪順序
Preorder: ABDFECG
Inorder: DBFACEG
Postorder: DFBCGEA
Level Order: ABEDFCG
| 題目名稱 | 來源 |
|---|---|
| Binary Tree Level Order Traversal | Leetcode 102 |
| Binary Tree Level Order Traversal II | Leetcode 107 |
| Binary Tree Preorder Traversal | Leetcode 144 |
| Binary Tree Inorder Traversal | Leetcode 94 |
| Binary Tree Postorder Traversal | Leetcode 145 |
練習題!
基礎走訪
| 題目名稱 | 來源 |
|---|---|
| Same Tree | Leetcode 100 |
| Binary Tree Zigzag Level Order Traversal | Leetcode 103 |
| Serialize and Deserialize Binary Tree | Leetcode 297 |
進階
練習題!
- 給定 Inorder ,請嘗試給出一個具有這樣 Inorder 的二元樹
- 給定 Preorder ,有這樣 Preorder 順序的二元樹是唯一的嗎?
-
給定 Preorder 以及 Postorder,有這樣的順序的二元樹是唯一的嗎?
- 如果有,要怎麼建構?
- 給定 Preorder 以及 Inorder,有這樣順序的二元樹是唯一的嗎?
- 如果有,要怎麼建構?
- 寫寫看吧!Leetcode 105
尋找各種樹的性質
嘗試用遞迴去寫吧!
Maximum Depth of Binary Tree (Leetcode 104)
給你一個 struct / class 建構
出來的二元樹,求樹的深度 (1個點算深度1)
A
B
E
D
F
想想看 DFS 怎麼做!
遞迴定義:輸出整棵樹的高度
rec(root):
- 1 + 左邊樹的高度 rec(root.l)
- 1 + 右邊樹的高度 rec(root.r)
一般情況下,
樹題我們都會用 DFS 去做
Base case 呢?
rec(NULL / None) = 0
Maximum Depth of Binary Tree (Leetcode 104)
給你一個 struct / class 建構
出來的二元樹,求樹的深度 (1個點算深度1)
A
B
E
D
F
int maxDepth(TreeNode* root) {
if (!root) return 0;
return 1 + max(
maxDepth(root->left),
maxDepth(root->right));
}def maxDepth(self, root):
if root is None:
return 0
return 1 + max(
self.maxDepth(root.left),
self.maxDepth(root.right))C++
Python
Diameter of Binary Tree (Leetcode 543)
給你一個 struct / class 建構出來的二元樹,
輸出樹的直徑長度
A
B
D
F
I
J
K
F
J
樹的直徑定義:
一棵樹距離最遠的兩個點的連線
直徑為5
無腦下遞迴定義:
rec(root) = 樹的直徑
好像有點困難?
像 DP 一樣分個 Case 吧!
Diameter of Binary Tree (Leetcode 543)
給你一個 struct / class 建構出來的二元樹,
輸出樹的直徑長度
A
B
D
F
I
J
K
F
J
樹的直徑定義:
一棵樹距離最遠的兩個點的連線
直徑為5
rec(root) = 樹的直徑
像 DP 一樣分個 Case 吧!
有經過 Root
沒經過 Root
rec(root.l)
rec(root.r)
1
+ height(root.l)
+ height(root.r)
(自己)
所以你還要順便算 height!
(每次重算複雜度會炸)
Diameter of Binary Tree (Leetcode 543)
給你一個 struct / class 建構出來的二元樹,
輸出樹的直徑長度
class Solution {
public:
// Return height, diameter
pair<int, int> height_and_diameter(TreeNode *root) {
if (!root) return {0, 0};
auto [L_h, L_d] = height_and_diameter(root->left);
auto [R_h, R_d] = height_and_diameter(root->right);
return {1 + max(L_h, R_h), max({L_d, R_d, 1+L_h+R_h})};
}
int diameterOfBinaryTree(TreeNode* root) {
return height_and_diameter(root).second - 1;
}
};class Solution:
def diameterOfBinaryTree(self, root):
def rec(root):
if root is None:
return 0, 0
L_h, L_d = rec(root.left)
R_h, R_d = rec(root.right)
return 1 + max(L_h, R_h), max(L_h + R_h + 1, L_d, R_d)
return rec(root)[1]-1C++
Python
L_h: L的height
L_d: L的diameter
| 題目名稱 | 來源 | 備註 |
|---|---|---|
| 子樹大小 | C 班 圖論 I - 4 | 算每個節點的大小 |
| Balanced Binary Tree | Leetcode 110 | |
| Path Sum | Leetcode 112 | |
| Path Sum II | Leetcode 113 | 好像是經典題 |
| Binary Tree Maximum Path Sum | Leetcode 124 | 處理很像算直徑 |
| Find minimum diameter after mergeing | Leetcode 124 | 處理很像算直徑 |
| 血緣關係 | Zerojudge b967 |
APCS 2016/3 - 4 拓樸更直觀一點 |
| 樹狀圖分析 (Tree Analyses) | Zerojudge c463 | APCS 2017/10 - 3 |
| 貨物分配 | Zerojudge h029 | APCS 2020/1 - 4 |
練習題!
二元搜尋樹
Binary Search Tree
來介紹一種資料結構吧!
Search in a Binary Search Tree (Leetcode 700)
給你一個 struct / class 建構出來的二元搜尋樹,
給你一個值,請回傳擁有這個值的節點。
7
4
9
1
6
二元搜尋樹的定義:
對於每個點,滿足下列條件:
如果這個點改8,那麼這就不是BST
x
l
r
怎麼找到題目要求的值?
(Binary Search Tree, BST)
Search in a Binary Search Tree (Leetcode 700)
給你一個 struct / class 建構出來的二元搜尋樹,
給你一個值,請回傳擁有這個值的節點。
7
4
9
1
6
二元搜尋樹的定義:
(Binary Search Tree, BST)
如果現在要搜尋 2 這個數字
可以通過跟現在的
root.val 比較,
知道 2 會在哪裡。
find 2
find 2
find 2
7
<7
>7
Base Case:
找到沒東西 (NULL / None),
就是不存在
Search in a Binary Search Tree (Leetcode 700)
給你一個 struct / class 建構出來的二元搜尋樹,
給你一個值,請回傳擁有這個值的節點。
(Binary Search Tree, BST)
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (!root) return NULL;
if (val == root->val) return root;
if (val < root->val) return searchBST(root->left, val);
return searchBST(root->right, val);
}
};class Solution:
def searchBST(self, root, val):
if root is None: return None
if root.val == val: return root
if val < root.val: return self.searchBST(root.left, val)
return self.searchBST(root.right, val)C++
Python
Validate Binary Search Tree (Leetcode 98)
給你一個 struct / class 建構出來的二元樹,
判斷其是否為二元搜尋樹 (Binary Search Tree)
7
4
9
1
6
先來個無腦定義
rec(root) = 判斷這棵樹是不是BST
好像不好下手,
仔細想想看每個點的限制
(考慮祖先們的限制就好,為什麼?)
對於每個點,都有其上下界。
只要都遵循,就是BST
把上下界加入遞迴參數內!
Validate Binary Search Tree (Leetcode 98)
給你一個 struct / class 建構出來的二元樹,
判斷其是否為二元搜尋樹 (Binary Search Tree)
7
4
9
1
6
rec(root, L, R) = 判斷是不是BST,
並限定之後的數字只能 > L 且 < R
祖先的數字
會限制他的子孫們
怎麼個限制?
- 左小孩的限制是右界
- 右小孩的限制是左界
遞迴的時候順便
檢查自己的數值就好了!
Validate Binary Search Tree (Leetcode 98)
給你一個 struct / class 建構出來的二元樹,
判斷其是否為二元搜尋樹 (Binary Search Tree)
class Solution {
public:
bool isValidBST(
TreeNode* root,
long long L_bound=LLONG_MIN,
long long R_bound=LLONG_MAX) {
if (!root)
return true;
if (root->val <= L_bound || R_bound <= root->val)
return false;
return
isValidBST(root -> left, L_bound, root->val) && \
isValidBST(root -> right, root->val, R_bound);
}
};class Solution:
def isValidBST(self, root, L=-2**32, R=2**32) -> bool:
if root is None:
return True
if root.val <= L or root.val >= R:
return False
return self.isValidBST(root.left, L, root.val) and \
self.isValidBST(root.right, root.val, R)C++
Python
練習題!
- 給你一個二元搜尋樹,詢問 x 存不存在的時間複雜度為何?
- 如果有一種魔法,可以確保一棵二元搜尋樹是平衡的,那麼時間複雜度為何?
平衡的定義:
任一棵節點 x 的
Hint:
- 考量數量最少但平衡的樹 f(height) = size。
- f(0) = 1, f(1) = 2, f(2) = 4
- 嘗試寫出遞迴式,你會發現它比某個東西還要大
- 想想看這個遞迴式的複雜度大概是多少
(可以用查的!)
練習題!
- 給你一個二元搜尋樹,詢問 x 存不存在的時間複雜度為何?
- 如果有一種魔法,可以確保一棵二元搜尋樹是平衡的,那麼時間複雜度為何?
- 在判斷二元搜尋數時,我們是由上往下給限制。如果由下往上給限制你會寫嗎?
- 判別一棵樹是否為二元搜尋樹其實有一個很巧妙的方法。Hint:
- 跟走訪順序有關
- 二元搜尋樹不允許有值重複。
- 其實 C++ 的 set / map 就是使用平衡的二元搜尋樹! (大多是使用紅黑樹 RB-tree)
樹的小結
樹的小結
- 各種樹的專有名詞
- 樹的建構法
- 陣列建構法 / 物件建構法 / 還有一些圖論會教
- 怎麼遍例 BFS / DFS 一棵樹?
- 就跟你之前 BFS / DFS 一樣
- 不同的遍例有不一樣的名詞
- preorder, inorder, postorder and level order
- 怎麼得到樹的各種性質?
- 樹的大小,高度,直徑等等
- 介紹一個有特別性質的二元樹:二元搜尋樹 (BST)
- 怎麼找到 BST 中特定的值?
- 怎麼判斷一棵樹是不是 BST?
- 你覺得 BST 屌在哪裡?
- 還有很多很特別的樹,等你發現!
樹才不只是這樣!
只是我們先教點 Graph 再說吧!
還有APCS的樹也不會考很難
Graph
Graph 創始之初...
前言

其實 18 世紀就在玩免洗手遊
柯尼斯堡七橋問題 (1735)
Seven Bridges of Königsberg
現在有四個區域,七座橋。
請問可以在每個橋
都只走一遍的情況下,
走完所有七個橋嗎?
Graph 創始之初...
前言

柯尼斯堡七橋問題 (1735)
Seven Bridges of Königsberg
簡化一下圖
- 點的位置只影響你的視覺,不影響答案
A
B
C
D
A
B
C
D
這些也是圖!
樹 就是一種特殊的圖
森林 就是一種特殊的圖
很多棵樹
這些也是圖!
地圖 也是一種圖
關係圖 也是一種圖
(很混亂的)
這些也是圖!
電路設計 也是一種圖
知識圖 也是一種圖
(Knowledge Graph)

這張圖是一種CPU的電路架構
就是畫出各種東西的關係鍊
但我們接下來只會著重上...
點裡面是一份資料的。
前言
A
B
C
D
圖的各種術語
Terminology of Graph
圖的構造
A
B
C
D
- (節)點 : 一個圖最小的單位
-
邊 : 節點與節點之間的連線
- <A, B> 表示從 A 可以指到 B
- 有向圖 : 圖的邊有方向性
- 無向圖 : 圖的邊沒有方向性
(Directed Graph / Digraph)
(Edge)
(Vertex)
A
B
C
D
A
A
Undirected Graph
有向圖
無向圖
通常無向圖會當作有向圖做。
<B, C> 無向圖 = <B, C>, <C, B> 有向圖
我們會用 G = (V, E) 來定義一個圖。
Graph = (Vertex, Edge)
點與邊的性質
點的性質,以 B 為準:
- B 的 相鄰 : B下一步可以去哪
- B 的 入度 : 有多少個箭頭指向 B
- B 的 出度 : B 有多少的箭頭指出去
(Adjacent)
(in-degree)
(out-degree)
A
B
C
D
邊的性質:
- 自環 : 指向自己的邊
- 重邊 : 兩個一模一樣的箭頭
- 沒有自環和重邊的圖,叫做簡單圖
(self-edge / loop)
(multiple / parallel edges)
(simple graph)
C
入度=3
出度=1
路的性質
- walk : 從某個點出發到某個點的路線
- 路徑 : 沒有重複經過點的 walk
- Trial : 沒有重複經過邊的 walk
- 迴路 / 迴圈 : 起點跟終點一樣的 Trial
- 環 : 起點跟終點一樣的路徑
(circuit)
A
B
C
D
(Path / Simple Path)
(cycle)
ABCDBCDADAD
ADCB
ADCBDE
ABCDA
ABEDCBDA
E
圖的性質
A
B
C
D
A
B
C
D
A
B
C
D
(弱)連通圖
(weakly) connected graph
每個點都是
被連起來的。
強連通圖
strongly connected graph
任兩個節點都
有一條路可以到。
不是個連通圖
圖中連通的塊稱做元件 (component)
圖的性質
A
B
C
D
A
B
C
D
有向無環圖
Directed Acyclic Graph, DAG
沒有任何環的
有向圖
無向無環圖
Undirected Acyclic Graph
沒有任何環的
無向圖
沒有任何環的無向圖,並且連通
A
B
C
D
森林
Forest
樹
Tree
好多名詞!
吸收一下吧!
練習題!
- 一個無向的圖,|V| = n,|E|最大多少?
- 一個無向的簡單圖,|V| = n,|E|最大多少?
- 這樣的圖稱為 團 / 完全圖 Clique,寫作
- 如果一個圖的所有邊可以不相交,我們稱為
平面圖 (Planar Graph)。- 請問 分別是平面圖嗎?
Vertex 的個數
Edge 的個數
這也是一個平面圖
A
B
C
D
A
B
C
D
因為它可以
變成這樣
練習題!
- 在有向圖 G 中,|V| = n,請問 |E| 至少要多 少才可以使
- G 為 弱連通圖
- G 為 強連通圖
- 所有 V 的入度加總 ,以及所有 V 的出度加總 這兩個數字誰大誰小?
- 子圖 (subgraph) 的意思是從原本的圖選
些邊跟點構成的一個小圖,就叫做子圖。
這張圖有幾種子圖?
- 給定一個星狀圖,問中心是誰?
Find Center of Star Graph (Leetcode 1791)
A
B
C
術語統整
(僅列舉比較重要的)
| 中文 | 英文 | 意思 |
|---|---|---|
| (節)點 | Vertex | 就...點? |
| 邊 | Edge | 連結兩個點的箭頭 |
| 圖 | Graph | 由點跟邊定義的一個關係圖 |
| 相鄰 | Adjacent | 一個點往外箭頭指誰 |
| 入度 | in-degree | 有多少個箭頭指向這個點 |
| 出度 | out-degree | 有多少個箭頭從這個點指出去 |
| 自環 | Self-edge / loop | 有這樣的邊 <u, u> |
| 重邊 | multiple / parallel edges | 有兩個一模一樣的箭頭 |
| (簡單) 路徑 | (Simple) Path | 沒有經過重複 V 的 walk |
| 環 | Cycle | 起終點一樣的 path |
| 簡單圖 | Simple Graph | 沒有自環,重邊的圖 |
| (弱)連通圖 | (Weakly) Connected Graph | 每個點都跟其他人連著的圖 |
| 強連通圖 | Strongly Connected Graph | 每兩個點都有 Path 可以到達 |
| 元件 | Component | 連通的子圖 (subgraph) |
圖的建構法
How to build a graph?
圖的建構法
- 主流使用相鄰串列 (Adjacency List)
- 還有一種叫做相鄰矩陣 (Adjacency Matrix)
- 跟樹一樣,只有你想的到,沒有你建不到。
- 只要是個圖,就可以這樣建。
- 例如 樹 是個 圖,所以建樹也可以用類似方法建。
0
1
2
3
圖的建構法
0
1
2
3
紀錄一下每個點
的 adjacent 有誰吧!
1
3
2
1
1
2
這種叫做 相鄰串列 (Adjacency List)
0
1
2
3
圖的建構法
0
1
2
3
1
3
2
1
1
2
相鄰串列 (Adjacency List)
vector<vector<int>> G {
{1, 3},
{2},
{1},
{1, 2}
};G = {
0: [1, 3],
1: [2],
2: [1],
3: [1, 2]
}C++
Python
用 map/dict 存還是用
set/map 存其實都可以。
0
1
2
3
圖的建構法
相鄰串列 (Adjacency List)
vector<vector<int>> G(n);
cin >> n;
for (int x=0; x<n; x++) {
cin >> m;
while (m--) {
cin >> y;
G[x].push_back(y);
}
}C++ 相鄰串列
4 6
0 1
0 3
1 2
2 1
3 1
3 24
2 1 3
1 2
1 1
2 1 2題目常見的兩種給法:
相鄰串列
只給邊
vector<vector<int>> G(n);
cin >> n >> m;
while (m--) {
cin >> x >> y;
G[x].push_back(y);
}4個點
6條邊
4個點
C++ 只給邊
* 如果是無向圖
要push <x,y> 跟 <y,x>
0
1
2
3
圖的建構法
相鄰串列 (Adjacency List)
n = int(input())
G = {i:[] for i in range(n)}
for i in range(n):
G[i] = list(map(int, input().split()))[1:]
Python 相鄰串列
4 6
0 1
0 3
1 2
2 1
3 1
3 24
2 1 3
1 2
1 1
2 1 2題目常見的兩種給法:
相鄰串列
只給邊
n, m = map(int, input().split())
G = {i:[] for i in range(n)}
for _ in range(m):
x, y = map(int, input().split())
G[x].append(y)4個點
6條邊
4個點
Python 只給邊
* 如果是無向圖
要push <x,y> 跟 <y,x>
0
1
2
3
圖的建構法
相鄰矩陣 (Adjacency Matrix)
vector<vector<int>> G {
{0, 1, 0, 1},
{0, 0, 1, 0},
{0, 1, 0, 0},
{0, 1, 1, 0}
};G = [
[0, 1, 0, 1],
[0, 0, 1, 0],
[0, 1, 0, 0],
[0, 1, 1, 0],
]C++
Python
對於解題向
比較少在用
0
1
2
3
0
1
2
3
圖的遍歷
BFS / DFS a Graph
給你一個圖 G 的 Adjacency List,
輸出從 0 開始可以碰到的所有點
圖的遍歷 - BFS
想想看 BFS 怎麼做!

t=2
如果在 0 倒水
所以跟之前只差在
擴散的點是由鄰居決定的,
並且 BFS 的單位是一顆節點!
0
1
2
3
t=1
t=1
t=2
走過不要
再走了!
給你一個圖 G 的 Adjacency List,
輸出從 0 開始可以碰到的所有點
圖的遍歷 - BFS

t=2
0
1
2
3
t=1
t=1
t=2
走過不要
再走了!
vector<bool> visit(4, false);
queue<int> Q({0});
while (!Q.empty()) {
int cur = Q.front();
Q.pop();
if (visit[cur])
continue;
visit[cur] = true;
printf("-> %d ", cur);
for (auto neighbor: G[cur])
Q.push(neighbor);
}-> A -> B -> E -> D -> F -> C -> G Q = deque([0])
visit = set()
while Q:
cur = Q.popleft()
if cur in visit:
continue
visit.add(cur)
print(" ->", cur, end='')
for neighbor in G[cur]:
Q.append(neighbor)C++
Python
-> 0 -> 3 -> 1 -> 2輸出
圖的遍歷 - DFS
想想看 DFS 怎麼做!
遞迴定義:
輸出從0開始碰的到的點
rec(cur=0):
- 輸出自己
- 自己的鄰居碰的到,那麼我也碰的到。
- rec(cur.neighbor)
給你一個圖 G 的 Adjacency List,
輸出從 0 開始可以碰到的所有點
0
1
2
3
圖的遍歷 - DFS
給你一個圖 G 的 Adjacency List,
輸出從 0 開始可以碰到的所有點
0
1
2
3
vector<bool> visit(4, false);
void dfs(int cur) {
if (visit[cur])
return ;
visit[cur] = true;
printf(" -> %d", cur);
for (int neighbor : G[cur])
dfs(neighbor);
}def dfs(cur, visit):
if cur in visit:
return
visit.add(cur)
print(" ->", cur, end='')
for neighbor in G[cur]:
dfs(neighbor, visit)C++
Python
-> 0 -> 1 -> 2 -> 3輸出
Find if Path Exists in Graph (Leetcode 1971)
給你一個圖 G 的 E,
問 source 可不可以到 destination
嘗試自己做做看吧!
二分圖判別
Is Graph Bipartite? (Leetcode 785)
給你一個 簡單圖 G,
請判斷 G 是不是個二分圖 (Bipartite)
什麼是二分圖?
顧名思義就是可以把圖二分的意思
A
B
C
D
E
F
完全二分圖
A
B
C
非二分圖的
最小例子
可以把點分成兩群,
每群之間沒有邊,
就叫做二分圖
A
B
C
D
(無向)
Is Graph Bipartite? (Leetcode 785)
給你一個 簡單圖 G,
請判斷 G 是不是個二分圖 (Bipartite)
A
B
C
D
集合 1
集合 2
如果是二分圖,則
可以將點分成 集合 1 和 集合 2
- 集合 1 的鄰居一定是 集合 2
- 集合 2 的鄰居一定是 集合 1
先對第一個點標成集合 1,
接著 1 2 1 2 的往外擴散。
如果任何一個點的標記衝突,
則這就不是二分圖
Is Graph Bipartite? (Leetcode 785)
給你一個 簡單圖 G,
請判斷 G 是不是個二分圖 (Bipartite)
A
B
C
D
如果任何一個點的標記衝突,
則這就不是二分圖
1
2
2
1
先對第一個點標成集合 1,
接著 1 2 1 2 的往外擴散。
使用 DFS 擴散
要怎麼定義 dfs()?
- 應該要從某個點
- 起點給 編號 1
- 鄰居的編號要是 3 - 自己的編號
(給編號2也是可以啦)
dfs (起點, 這個點的編號)
= 判斷這個點的元件是不是二分圖
Is Graph Bipartite? (Leetcode 785)
給你一個 簡單圖 G,
請判斷 G 是不是個二分圖 (Bipartite)
class Solution {
public:
bool dfs(vector<vector<int>>& graph,
vector<int>& group, int start, int group_num) {
if (group[start])
return group[start] == group_num;
group[start] = group_num;
for(auto nxt: graph[start])
if (!dfs(graph, group, nxt, 3-group_num))
return false;
return true;
}
bool isBipartite(vector<vector<int>>& graph) {
vector<int> group(graph.size(), 0);
for (int i=0; i<graph.size(); i++)
if (!group[i] && !dfs(graph, group, i, 1))
return false;
return true;
}
};group = 0 表示沒走過
group = 1 表示編號1
group = 2 表示編號 2
如果沒走過 (group[i] == 0),那麼就對 i 開始跑檢測,並幫 i 給編號1
如果 group != 0,
檢查編號有沒有衝突,
並且回傳,結束 (不回流)
1 的鄰居是 2
2 的鄰居是 1
如果任何一個檢測是 false
就回傳 false
C++
Is Graph Bipartite? (Leetcode 785)
給你一個 簡單圖 G,
請判斷 G 是不是個二分圖 (Bipartite)
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
def dfs(start, group_num):
if group[start]:
return group[start] == group_num
group[start] = group_num
for nxt in graph[start]:
if not dfs(nxt, 3 - group_num):
return False
return True
group = [0] * len(graph)
for i in range(len(graph)):
if group[i] == 0:
if not dfs(i, 1):
return False
return True
Python
group = 0 表示沒走過
group = 1 表示編號1
group = 2 表示編號 2
如果沒走過 (group[i] == 0),那麼就對 i 開始跑檢測,並幫 i 給編號1
如果 group != 0,
檢查編號有沒有衝突,
並且回傳,結束 (不回流)
1 的鄰居是 2
2 的鄰居是 1
如果任何一個檢測是 false
就回傳 false
練習題!
- 如果你把點分成 A 群 跟 B 群,並且將 A 群跟 B 群互相連線,這就叫做完全二分圖。
-
如果|A| = n,|B| = m,我們可以用
表示。請問 的
-
如果|A| = n,|B| = m,我們可以用
- 如果可以將點分成 K 個群體,每個群體彼此都沒有邊,就稱之為 K 分圖 (K-partite)。其中,K 代入 2 就是二分圖。
- 能夠用原本的方法判別三分圖嗎?
- 其實這題完全可以用 Disjoint Set 來完成,你會寫嗎?
- 想想看現實世界上有什麼例子是二分圖?
練習題!
| 題目名稱 | 來源 | 備註 |
|---|---|---|
| Clone Graph | Leetcode 133 | 用 struct / class 建圖 |
單源最短路 - 1
Dijkstra's Algorithm (偽)
How to pronounce Dijkstra?
- 發明這個算法的是個荷蘭人 Edsger Wybe Dijkstra
Network Delay Time (Leetcode 743)
給你一個 帶邊權簡單圖 G,邊權 = 擴散所需時間
從第 k 點擴散,需要多久才可以擴散所有點?
1
3
2
4
5
5
2
2
1
1
1
3

t=2
t=4
t=3
t=5
答案 = 5
我們要怎麼存帶邊權圖 ?
(也有帶點權圖)
Adjacency List
G[u].push_back(v)G[u].push_back({v, w})G[u].append(v)G[u].append((v, w))Network Delay Time (Leetcode 743)
給你一個 帶邊權簡單圖 G,邊權 = 擴散所需時間
從第 k 點擴散,需要多久才可以擴散所有點?
1
3
2
4
5
5
2
2
1
1
1
3

t=2
t=4
t=3
t=5
答案 = 5
使用 BFS 會有什麼問題?
1
3
2
5
2
2
你會不知道哪條路比較好
Network Delay Time (Leetcode 743)
給你一個 帶邊權簡單圖 G,邊權 = 擴散所需時間
從第 k 點擴散,需要多久才可以擴散所有點?
1
3
2
4
5
5
2
2
1
1
1
3

t=2
t=4
t=3
t=5
答案 = 5
使用 BFS 會有什麼問題?
你會不知道哪條路比較好
學習水的思路!
1
3
2
5
2
2

等 t = 5
擴散
等 t = 2
擴散
t=0
/ 1
/ 2
/ 3
/ 4


x 4
Network Delay Time (Leetcode 743)
給你一個 帶邊權簡單圖 G,邊權 = 擴散所需時間
從第 k 點擴散,需要多久才可以擴散所有點?
1
3
2
4
5
5
2
2
1
1
1
3

t=2
t=4
t=3
t=5
答案 = 5
學習水的思路!
1
3
2
5
2
2

等 t = 5
擴散
等 t = 2
擴散
t=0
/ 1
/ 2
/ 3
/ 4


x 4
- queue 沒法做...
- 使用我們教BFS的第一個方法!
Network Delay Time (Leetcode 743)
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<int> delay(n+1, -1);
// Build Graph
vector<vector<pair<int, int>>> G(n+1);
for (auto edge : times) {
int u = edge[0], v = edge[1], w = edge[2];
G[u].push_back({v, w});
}
// BFS
vector<vector<int>> Q(10001);
Q[0].push_back({k});
for (int t=0; t<Q.size(); t++) {
for (int i=0; i<Q[t].size(); i++) {
int cur = Q[t][i];
if (delay[cur] != -1)
continue;
delay[cur] = t;
for (auto [nxt, w] : G[cur]) {
Q[t+w].push_back(nxt);
}
}
}
// Get answer
// There is a node not being touched
if (*min_element(delay.begin()+1, delay.end()) == -1)
return -1;
// return max delay
return *max_element(delay.begin()+1, delay.end());
}
};不寫
是因為 w 有可能為 0
for (int cur : Q[t])Network Delay Time (Leetcode 743)
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
# Build Graph
G = defaultdict(list)
for u, v, w in times:
G[u].append((v, w))
# BFS
delay = [-1] * (n+1)
Q = defaultdict(list)
Q[0].append((k))
for t in range(10001):
while Q[t]:
cur = Q[t].pop()
if delay[cur] != -1:
continue
delay[cur] = t
for nxt, w in G[cur]:
Q[t+w].append(nxt)
if min(delay[1:]) == -1:
return -1
return max(delay)不寫
是因為 w 有可能為 0
for cur in Q[t]:Network Delay Time (Leetcode 743)
嘗試分析時間複雜度吧!
不重複會跑幾個點?
每個點都會擴散最多多少個點?
最多會有多少的 queue / vector ?
等等, 呢?
Network Delay Time (Leetcode 743)
嘗試分析時間複雜度吧!
不重複會跑幾個點?
最多擴散多少次?
最多會有多少的 queue / vector ?
- 在這裡我們當作 |E| > |V|
單源最短路 - 2
Dijkstra's Algorithm

我們在上 BFS 單人解謎 - 最優解 (UCS) 時...
這個資料結構,就是
priority_queue / heapq
你只要每次拿最小時間點,
且還沒看過的點就可以了!
Network Delay Time (Leetcode 743)
Network Delay Time (Leetcode 743)
C++ 實作細節:
- priority_queue 預設是拿最大的元素。
要怎麼樣才可以拿到最小的 delay 的 {node, delay} 呢?- 讓 delay 在前面,並且取負號 {-delay, node} 就可以了。
- 使用 <funtional> 的 greater
// Dijkstra's Algorithm
priority_queue<
pair<int, int>, vector<pair<int, int>>,
greater<> > pq;
pq.push({0, k});
while (!pq.empty()) {
auto [cur_delay, cur] = pq.top();
pq.pop();
if (delay[cur] != -1)
continue;
delay[cur] = cur_delay;
for (auto [nxt, w] : G[cur])
pq.push({cur_delay + w, nxt});
}2. 使用 greater
// Dijkstra's Algorithm
priority_queue<pair<int, int>> pq;
pq.push({0, k});
while (!pq.empty()) {
auto [cur_delay, cur] = pq.top();
pq.pop();
if (delay[cur] != -1)
continue;
delay[cur] = -cur_delay;
for (auto [nxt, w] : G[cur])
pq.push({cur_delay - w, nxt});
}1. 乘以 -1
Network Delay Time (Leetcode 743)
C++ 實作細節:
-
- 寫一個 comparator class/struct 定義 pair 的比對
- 自己寫 comparator function + <funtional> 的 decltype
// Dijkstra's Algorithm
// Lambda函數。跟 sort 的 cmp 是反的
auto cmp = [](
pair<int, int>& a,
pair<int, int>& b) {
return a.first > b.first;
};
priority_queue< pair<int, int>,
vector<pair<int, int>>,
decltype(cmp) > pq;
pq.push({0, k});
while (!pq.empty()) {
auto [cur_delay, cur] = pq.top();
pq.pop();
if (delay[cur] != -1)
continue;
delay[cur] = cur_delay;
for (auto [nxt, w] : G[cur])
pq.push({cur_delay + w, nxt});
}4. 使用 declytpe
struct Compare {
// 方向跟 sort 的 cmp 是反的。
bool operator()(
pair<int, int>& a,
pair<int, int>& b) {
return a.first > b.first;
}
};
...
// Dijkstra's Algorithm
priority_queue< pair<int, int>,
vector<pair<int, int>>, Compare > pq;
pq.push({0, k});
while (!pq.empty()) {
auto [cur_delay, cur] = pq.top();
pq.pop();
if (delay[cur] != -1)
continue;
delay[cur] = cur_delay;
for (auto [nxt, w] : G[cur])
pq.push({cur_delay + w, nxt});
}3. 寫 comparator class / struct
Network Delay Time (Leetcode 743)
Python 實作細節:
- 使用 heapq 這個套件。
heapify(Q) # 讓 Q 變成 heap
heappush(Q, x) # 將 x 插入進 Q
heappop(Q) # 將 Q pop 最小值
Q[0] # 拿最小值什麼是 heap?
heap是一種完全二元樹
但想知道更多請參見 heap 章節
Q = [(0, k)] # 一個點不用 heapify
while Q:
cur_delay, cur = heappop(Q)
if delay[cur] != -1:
continue
delay[cur] = cur_delay
for nxt, w in G[cur]:
heappush(Q, (cur_delay+w, nxt))Network Delay Time (Leetcode 743)
嘗試分析時間複雜度吧!
不重複會跑幾個點?
每個點都會擴散最多多少個點?
等等,heapq / pq 的 push 複雜度呢?
還有更快的實作,目前是
- 在這裡我們當作 |E| > |V|
練習題!
| 題目名稱 | 來源 | 備註 |
|---|---|---|
| 最短路徑 | C 班 圖論 I - 2 | |
| 黑白城市 | C 班 圖論 III - 2 | 邊權只有 0 / 1 |
| 長途跋涉 | C 班 圖論 III - 3 | 變形題,需要做三次 |
| Path with Maximum Probability | Leetcode 1514 | 換個運算符號而已 |
| Minimum cost to make at least one valid path | Leetcode 1368 | 我覺得很有趣 |
| Cheapest Flights within k stops | Leetcode 787 | 只能走k次的最短路 可能算是對圖做DP |
拓樸排序 - 1
BFS-based Topological Algorithm / Kahn's Algorithm
給你一個 有向簡單圖 G,每個節點表示一堂課,
<u, v> 表示 v 的擋修是 u (要完成 u 才可以修 v)。
請判斷你能不能夠修完所有課?
0
1
2
0
1
2
- 修 0 要先修1, 2
- 修 1 要先修2
- 2 沒有擋修
- 修 0 要先修 1
- 修 1 要先修 2
- 修 2 要先修 0
可以,2 -> 1 -> 0
不行,死結 (deadlock)
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,每個節點表示一堂課,
<u, v> 表示 v 的擋修是 u (要完成 u 才可以修 v)。
請判斷你能不能夠修完所有課?
什麼樣的情況下才會有死結?
有環的時候。
這題就是要請你判斷一個圖是不是
有向無環圖 (DAG)
也就是請你做環的檢測
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,每個節點表示一堂課,
<u, v> 表示 v 的擋修是 u (要完成 u 才可以修 v)。
請判斷你能不能夠修完所有課?
0
1
2
- 修 0 要先修1, 2
- 修 1 要先修2
- 2 沒有擋修
可以,2 -> 1 -> 0
很簡單的貪心策略:
把已經可以修的課
全部修完不就好了嗎?
沒有擋修的課
有什麼性質?
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,每個節點表示一堂課,
<u, v> 表示 v 的擋修是 u (要完成 u 才可以修 v)。
請判斷你能不能夠修完所有課?
0
1
2
很簡單的貪心策略:
把已經可以修的課
全部修完不就好了嗎?
沒有擋修的課
有什麼性質?
in_deg = 2
in_deg = 1
in_deg = 0
2
修課順序:
-> 1
-> 0
/ 0
/ 1
/ 0
這個算法習慣用BFS做!
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,每個節點表示一堂課,
<u, v> 表示 v 的擋修是 u (要完成 u 才可以修 v)。
請判斷你能不能夠修完所有課?
很簡單的貪心策略:
把已經可以修的課
全部修完不就好了嗎?
沒有擋修的課
有什麼性質?
這個算法習慣用BFS做!
Kahn's Algorithm 流程
- 找出入度 = 0 的點,放入 queue
- 對於 queue 內每個點:
- 現在可以修這個課
- 刪掉點,更新鄰居的入度
- 如果有入度變 0,放入 queue
- 如果整個 queue 空了:
- 還有課沒修,表示有環,死結
- 所有課修完了,Hooray!
Course Schedule (Leetcode 207)
Kahn's Algorithm 流程
- 找出入度 = 0 的點,放入 queue
- 對於 queue 內每個點:
- 現在可以修這個課
- 刪掉點,更新鄰居的入度
- 如果有入度變 0,放入 queue
- 如果整個 queue 空了:
- 還有課沒修,表示有環,死結
- 所有課修完了,Hooray!
class Solution {
public:
bool canFinish(int numCourses,
vector<vector<int>>& prerequisites) {
// Build Graph
vector<vector<int>> G(numCourses);
vector<int> deg_in(numCourses);
for (auto &tmp : prerequisites) {
int u=tmp[0], v=tmp[1];
G[v].push_back(u);
deg_in[u]++;
}
// Find course with in-degree = 0
queue<int> Q;
for (int i=0; i<numCourses; i++) {
if (deg_in[i] == 0)
Q.push(i);
}
// Iteratively delete node
while (!Q.empty()) {
int cur = Q.front();
Q.pop();
for (int nxt : G[cur]) {
// Update in_deg and find next course.
deg_in[nxt]--;
if (deg_in[nxt] == 0) {
Q.push(nxt);
}
}
}
// All in_deg = 0 means you finished all.
return *max_element(deg_in.begin(),
deg_in.end()) == 0;
}
};C++
1
1
2
3
Course Schedule (Leetcode 207)
Kahn's Algorithm 流程
- 找出入度 = 0 的點,放入 queue
- 對於 queue 內每個點:
- 現在可以修這個課
- 刪掉點,更新鄰居的入度
- 如果有入度變 0,放入 queue
- 如果整個 queue 空了:
- 還有課沒修,表示有環,死結
- 所有課修完了,Hooray!
class Solution:
def canFinish(self, numCourses, prerequisites):
G = defaultdict(list)
# Build Graph
deg_in = [0] * numCourses
for u, v in prerequisites:
deg_in[u] += 1
G[v].append(u)
# Find course with in-degree = 0
Q = deque(i for i, deg
in enumerate(deg_in) if deg == 0)
# Iteratively delete node
while Q:
cur = Q.popleft()
for nxt in G[cur]:
# Update in_deg and find next course.
deg_in[nxt] -= 1
if deg_in[nxt] == 0:
Q.append(nxt)
# All courses in_deg = 0
# means you finished all.
return max(deg_in) == 0
Python
1
1
2
3
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,每個節點表示一堂課,
<u, v> 表示 v 的擋修是 u (要完成 u 才可以修 v)。
請找出一種可以修完課的順序,
如果不可能的話回傳空陣列。
0
1
2
0
1
2
- 修 0 要先修1, 2
- 修 1 要先修2
- 2 沒有擋修
- 修 0 要先修 1
- 修 1 要先修 2
- 修 2 要先修 0
回傳 [2, 1, 0]
無解,回傳 []
Course Schedule II (Leetcode 208)
這種順序,稱作
拓樸順序
Topological Order
給你一個 有向簡單圖 G,找出拓樸順序
Course Schedule II (Leetcode 208)
Topological Order
0
1
2
in_deg = 2
in_deg = 1
in_deg = 0
2
修課順序:
-> 1
-> 0
/ 0
/ 1
/ 0
還記得剛剛的概念嗎?
把你 BFS 的順序印出來
就是拓樸順序了。
拓樸排序 - 2
White-Gray-Black Cycle Detection
DFS-based Topological Sort
不能用 DFS 嗎?
可能有點難理解,但我們來試試看吧
給你一個 有向簡單圖 G,請檢測有沒有環
0
1
2
3
4
5
我們來用尤拉導覽來分析吧!
(Euler tour technique, ETT)
Euler Tour 就是將 DFS 的順序
寫出來分析的一個技巧。
Euler Tour
0
1
2
3
3
4
4
5
5
2
1
0
1
2
3
4
5
6
7
8
9
10
11
12
來看看怎麼實作吧!
(Euler Tour ≠ Euler Circuit,別搞混 )
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,請檢測有沒有環
0
1
2
3
4
5
Euler Tour
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
3
4
5
5
4
2
1
0
來看看怎麼實作吧!
其實也就是 DFS 的頭跟尾加一些程式
vector<int> tour;
void dfs(int cur) {
if (visit[cur])
return;
visit[cur]=true;
tour.push_back(cur);
for (int nxt : G[cur])
dfs(nxt);
tour.push_back(cur);
}tour = []
def dfs(cur):
if cur in visit[cur]:
return
visit.add(cur)
tour.append(cur)
for nxt in G[cur]:
dfs(nxt)
tour.append(cur)
C++
Python
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,請檢測有沒有環
0
1
2
3
4
5
Euler Tour
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
3
4
5
5
4
2
1
0
怎麼檢測迴路呢?
如果碰到一個點:
- 還沒走過:那就沒事,繼續判斷。
- 正在走:有環。
-
當碰到 時,
正在走的順序: 0 1 2 4 5 1
-
當碰到 時,
- 走完了:表示之前走的時候,下面無環。
1
5
Course Schedule (Leetcode 207)
底下所有點都被走完了
給你一個 有向簡單圖 G,請檢測有沒有環
0
1
2
3
4
5
Euler Tour
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
3
4
5
5
4
2
1
0
如果碰到一個點,在 Euler Tour...
- 還沒走過:
- 正在走:
- 走完了:
沒藍色
有藍色
沒橘色
Course Schedule (Leetcode 207)
有藍色
有橘色
沒橘色
用陣列 / Dict 去紀錄每個點是哪種狀態!
怎麼檢測迴路呢?
class Solution {
public:
int euler_top = 0;
bool dfs(vector<vector<int>>& G, vector<vector<int>>& euler_idx, int cur) {
if (euler_idx[cur].size())
return euler_idx[cur].size() == 2;
euler_idx[cur].push_back(euler_top++);
for (int nxt : G[cur]) {
if (!dfs(G, euler_idx, nxt))
return false;
}
euler_idx[cur].push_back(euler_top++);
return true;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> G(numCourses);
vector<vector<int>> euler_idx(numCourses);
int euler_top = 0;
// Build Graph
for (auto &tmp : prerequisites) {
int u=tmp[0], v=tmp[1];
G[v].push_back(u);
}
for (int i=0; i<numCourses; i++) {
if (!dfs(G, euler_idx, i))
return false;
}
return true;
}
};Course Schedule (Leetcode 207)
C++ Solution
class Solution:
def canFinish(self, numCourses, prerequisites):
G = defaultdict(list)
# Build Graph
for u, v in prerequisites:
G[v].append(u)
euler_top = 1
euler_idx = defaultdict(list)
def dfs(cur):
nonlocal euler_top
if euler_idx[cur]:
return len(euler_idx[cur]) == 2
euler_idx[cur].append(euler_top)
euler_top += 1
for nxt in G[cur]:
if not dfs(nxt):
return False
euler_idx[cur].append(euler_top)
euler_top += 1
return True
return all(dfs(i) for i in range(numCourses))Course Schedule (Leetcode 207)
Python Solution
Course Schedule (Leetcode 207)
給你一個 有向簡單圖 G,請檢測有沒有環
如果碰到一個點,在 Euler Tour...
- 還沒走過:
- 正在走:
- 走完了:
沒藍色
有藍色
沒橘色
有藍色
有橘色
沒橘色
這樣的算法其實叫做:
White-Gray-Black Cycle Detection
(還沒走過)
(正在走)
(走過了)
不過你改成 White-Gray-Black
就沒辦法做下一題了 D:
給你一個 有向簡單圖 G,找出拓樸順序
Course Schedule II (Leetcode 208)
Topological Order
還記得剛剛的概念嗎?
把橘色的順序反著看就是拓樸順序。
4
9
10
0
1
2
3
1
6
3
4
2
5
7
8
Euler Tour
0
1
2
3
3
4
4
2
1
0
如果 A -> B,那麼一定是 B 先 結束 dfs ,
才會是 A 結束 dfs。
B 的 橘色數字 一定比 A 的橘色數字前面。
finish[B]
幹嘛教兩種?
- BFS-based 比較直觀
- 後面還有演算法 (SCC) 跟
DFS-based 的有關係 - 多教多會,教了不虧 (?)
練習一下吧!
給你一個有向無環的電路圖,並給定輸入信號。
問輸出信號,並且最大延遲為何?
邏輯電路 (zj m933)
4 5 4 13
1 0 1 0
1 2 3 4 1
1 5
2 5
2 6
3 6
3 7
4 7
4 8
5 10
6 9
6 11
7 9
8 13
9 124輸入,5閘, 4輸出, 13線
編號: 1~4 , 5~9 , 10~13
輸入信號
閘的型態
型態1: &
型態2: |
型態3: ^
型態4: !
型態1: &
線的輸入
線的輸出
答案: 延遲 2,輸出 0 1 1 1
t=0
t=0
t=0
t=0
t=0
t=1
t=1
t=1
t=1
t=2
t=1
t=1
t=1
t=2
給你一個有向無環的電路圖,並給定輸入信號。
問輸出信號,並且最大延遲為何?
邏輯電路 (zj m933)
最重要的就是決定順序!
我們每次處理的閘道都必須先算好輸入
-> 照著拓樸順序
給你一個有向無環的電路圖,並給定輸入信號。
問輸出信號,並且最大延遲為何?
邏輯電路 (zj m933)
在這之前,我們先建圖
struct Gate{
// type: 如果是邏輯閘,他是哪類。in_deg: 入度。
// out: 輸出的結果。delay: 延遲。 inp: 邏輯閘的輸入,至多兩個。
// out_idx: 輸出到哪些邏輯閘或者輸出端口上。
int type, in_deg, out, delay;
vector<int> inp, out_idx;
};
Gate gate[100000];
int main() {
int p,q,r,m,max_delay=0;
queue<int> Q;
scanf("%d%d%d%d", &p, &q, &r, &m);
for (int i=1; i<=p; i++) {
scanf("%d", &gate[i].out);
// 輸入端口一定入度為零,所以放進 queue。
Q.push(i);
}
for (int i=p+1; i<=p+q; i++) {
scanf("%d", &gate[i].type);
}
for (int i=0; i<m; i++) {
int u, v;
scanf("%d%d", &u, &v);
// 紀錄入度以及該點的下游是誰。
gate[u].out_idx.push_back(v);
gate[v].in_deg ++;
}因為變數很多,
所以就開 struct / class吧!
每個Gate需要:
- 閘的型態
- Delay
- 鄰居有誰 (用Adj List)
- 輸入的結果
- 輸出的結果
- 現在的入度 (用 BFS 做)
給你一個有向無環的電路圖,並給定輸入信號。
問輸出信號,並且最大延遲為何?
邏輯電路 (zj m933)
在這之前,我們先建圖
class Gate:
def __init__(self):
self.in_deg = 0 # 入度
self.type = None # 邏輯閘的種類
self.out = None # 該gate的輸出結果
self.delay = 0 # 該gate的延遲
self.inp = [] # 輸入
self.nxt = [] # 下游
p, q, r, m = map(int, input().split())
# 要加 1 是因為編號從 1 開始,所以第零號是空的。
gate = [Gate() for _ in range(p+q+r+1)]
# 處理輸入的訊號
for i, in_signal in enumerate(list(map(int, input().split()))):
gate[i+1].out = in_signal
# 處理邏輯閘的種類
for i, gate_type in enumerate(list(map(int, input().split()))):
gate[p+i+1].type = gate_type
# 處理入度並記錄下游
for _ in range(m):
u, v = map(int, input().split())
gate[v].in_deg += 1
gate[u].nxt.append(gate[v])
# 輸入 [1 ~ p]
Q = [gate[i] for i in range(1, p+1)]因為變數很多,
所以就開 struct / class吧!
每個Gate需要:
- 閘的型態
- Delay
- 鄰居有誰 (用Adj List)
- 輸入的結果
- 輸出的結果
- 現在的入度 (用 BFS 做)
給你一個有向無環的電路圖,並給定輸入信號。
問輸出信號,並且最大延遲為何?
邏輯電路 (zj m933)
And
Gate
對於每個 Gate:
- 通過輸入的訊號算出結果
- 將這個結果存到下個鄰居的輸入
- 計算 Delay
- 做拓樸該做的事。
剩下就是實作細節了,可以參考我寫的解析
圖的小結
圖的小結
BFS
一路下來,我們都上了什麼?
DFS
二維地圖
BFS
DFS
樹
抽象地圖
(遊戲搜尋)
Uniform Cost Search
Backtracking
圖
Dijkstra's Algorithm
Kahn's Algorithm
White-Gray-Black Cycle Detection
DFS
BFS
Traverse
Binary Search Tree
Disjoint Set
Verify Bipartite
圖的小結
後面還有什麼有趣的?
各式各樣的樹:
- 超實用字串搜尋的樹:Trie
- 競賽圈常見的
- 線段樹 Segment Tree
- 樹堆 Treap
- C++ map / set 的實作原理 RB-tree:(一種平衡二元搜尋樹)
- C++ 的 priority_queue / Python 的 heapq 的原理:heap
- 最小生成樹 (Minimum Spanning Tree)
各式各樣的技巧
- 最低共同祖先 (Lowest Common Ancestor, LCA)
- 樹鍊剖分,樹重心拆解,樹DP ... 太多啦
圖的小結
後面還有什麼有趣的?
各式各樣的圖技巧:
- 網路流 / 最大流 / 最小割
- Cover Set Problem
- 尤拉路徑
- 二分圖的完美匹配 (匈牙利演算法)
- 強連通元件 SCC
- 關節點 (Articulation Point) / 橋 (Bridge)
- 還有很多很多...
歡迎參考這個
圖的小結
圖 / 樹有很多要學!
不過 APCS 通常的圖論都只會
考 DFS / BFS 的衍生 + 拓樸路徑而已,
不用太擔心!
還有記得有些圖看起來不是圖論,
但其實也是圖論題喔!
練習題!
| 題目名稱 | 來源 | 備註 |
|---|---|---|
| 最短路徑 | C 班 圖論 I - 2 | |
| 題目名稱 | 來源 | 備註 |
|---|---|---|
| 病毒演化 | Zerojudge f582 | APCS 2020/7 - 4 很像樹DP但其實偏DP |
| Redundant Connection | Leetcode 684 | 無向圖環檢測 也可以 disjoint set |
| Longest Cycle in a Graph | Leetcode 2360 |
進階資料結構 (樹)
Heap - 1
Heap 性質介紹 / 建構 / pop
7
4
2
1
3
Heap的定義:
對於每個點,滿足下列條件:
x
l
r
Search in a Binary Search Tree (Leetcode 700)
請實作一個完全二元樹,包含三種操作:
1. 查看最大值,2. 刪除最大值,3. 插入數值
(Complete Binary Tree)
- Heap 不一定要是完全二元樹,
但完全二元樹比較好實作。
Heap - 2
Heap 在線刪除 / 懶人刪除
線段樹 - 1
Segment Tree 性質 / 建構 / 查詢 / 單點修改
Range Sum Query (Leetcode 307)
請實作一個 Class,從一個數列初始化,支援兩種操作:
- update(index, val): 把第 index 的數字 (A[index]) 改成 val
- sumRange(left, right): 詢問從 A[left] 加到 A[right] 是多少
只要看到這種跟「區間」有關的操作,
那麼就有機會會使用到線段樹。
我們先來看一下線段樹的 fu 吧!
線段樹就是一個節點為「一個區間」的樹。
murmur: 所以其實他應該要叫區間樹,
因為線段樹其實名字重疊了。
線段樹 (Segment Tree)
線段樹就是一個節點為「一個區間」的樹。
假設一開始有 8 個數字 (index 為 [0, 7])
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
線段樹大概就會變成這樣子。
線段樹 (Segment Tree)
線段樹就是一個節點為「一個區間」的樹。
假設一開始有 8 個數字 (index 為 [0, 7])
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
這有什麼用呢?
你會發現你想要計算一個區間,
都可以拆出若干個子區間。
舉例來說,你想要查詢 [0, 5]:
- 你訪問 [0, 3] + [4, 5] 的區間就可以了。
- 具體來說,最多只會拆成總計 的區間
- 那麼在原題 (詢問區間加總),我們在樹上的每個點紀錄該區間的總和就可以了!
線段樹 (Segment Tree) - Build
線段樹就是一個節點為「一個區間」的樹。
假設一開始有 8 個數字 (index 為 [0, 7])
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
如果你想要紀錄 [0, 7] 的總和:
- 那麼他其實就是左右區間 (也就是 [0, 3] 跟 [4, 7]) 的總和
- 通常會用一個函數 (pull) 更新
實作上來說我們會用遞迴去建構。
- 函數定義:
build(L, R) = 建構出 [L, R] 的樹 - 拆解:每次會把區間拆一半。
- Base Case:
- 當然就是剩一個點的時候。
[0, 7]
[0, 3]
[4, 7]
線段樹 (Segment Tree) - Build
[0, 7].val = 左右區間的和 = [0, 3].val + [4, 7].val
實作上來說我們會用遞迴去建構。
- 函數定義: build(L, R) = 建構出 [L, R] 的樹
- 如何拆解:每次會把區間拆一半。
- Base Case:當然就是剩一個點的時候。
Python
class SegTree:
def __init__(self, nums, L, R):
if L == R:
self.left = self.right = None
self.val = nums[L]
else:
M = (L+R)//2
self.left = SegTree(nums, L, M)
self.right = SegTree(nums, M+1, R)
# update the value of this segment
self.pull()
def pull(self):
# only interal nodes can pull
self.val = self.left.val + self.right.valC++
class SegTree {
public:
SegTree *lft, *rgt;
int val;
SegTree(vector<int>& nums, int L, int R) {
if (L == R) {
lft = rgt = nullptr;
val = nums[L];
} else {
int M = (L+R) / 2;
lft = new SegTree(nums, L, M);
rgt = new SegTree(nums, M+1, R);
pull();
}
}
void pull() {
// Only internal nodes can pull
val = lft->val + rgt->val;
}線段樹 (Segment Tree) - Query
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
前面我們說:你想要查詢 [0, 5]
- 訪問 [0, 3] + [4, 5] 即可。
這個該怎麼想像?
- 一開始 query 的區間不動。
- 如果現在區間太大,往下細拆
- 如果現在區間完全包含,回傳答案。
- 如果現在區間完全不包含,回傳不影響答案的值。
(例如 sum -> 0, min -> inf)
Query: [0, 5]
所以 query 會帶四個參數:
- 現在區間 (L, R)
- 詢問區間 (qL, qR)
[0, 7]
[0, 7]
[0, 3]
[4, 7]
[0, 3]
[4, 7]
[4, 5]
[6, 7]
[6, 7]
[4, 5]
線段樹 (Segment Tree) - Query
- 一開始 query 的區間不動。
- 如果現在區間太大,往下細拆
- 如果現在區間完全包含,回傳答案。
- 如果現在區間完全不包含,回傳不影響答案的值。
(例如 sum -> 0, min -> inf)
所以 query 會帶四個參數:現在區間 (L, R) 以及詢問區間 (qL, qR)
Python
# 接續前面的 code
def query(self, L, R, qL, qR):
if qR < L or R < qL:
return 0
if qL <= L and R <= qR:
return self.val
M = (L + R) // 2
return self.left.query(L, M, qL, qR) + \
self.right.query(M+1, R, qL, qR)int query(int L, int R, int qL, int qR) {
if (qR < L || R < qL)
return 0;
if (qL <= L && R <= qR)
return val;
int M = (L+R) / 2;
return lft->query(L, M, qL, qR) +
rgt->query(M+1, R, qL, qR);
}C++
線段樹 (Segment Tree) - Modify
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
在這題的最後只剩下 modify 了:
- 如果現在想要改動 A[5],
那麼會影響哪些區間呢? - 你會發現每層只有一個區間
的值要修改。
A5
[0, 7]
[4, 7]
[4, 5]
怎麼找到每一層改的區間呢?
- 用類似二元搜尋樹的查詢方法就好了。
- 這些區間會重新計算 val。
請實作一個 Class,從一個數列初始化,支援兩種操作:
- update(index, val): 把第 index 的數字 (A[index]) 改成 val
- sumRange(left, right): 詢問從 A[left] 加到 A[right] 是多少
線段樹 (Segment Tree) - Modify
如果現在想要改動 A[5],那麼會影響哪些區間呢?
- 你會發現每層只有一個區間的值要修改。
怎麼找到每一層改的區間呢?
- 用類似二元搜尋樹的查詢方法就好了。
- 這些區間會重新計算 val。
Python
# 接續前面的 code
def pull(self):
# Only interal nodes can pull.
self.val = self.left.val + self.right.val
def modify(self, L, R, idx, val):
if L == R:
self.val = val
else:
M = (L + R) // 2
if idx <= M:
self.left.modify(L, M, idx, val)
else:
self.right.modify(M+1, R, idx, val)
self.pull() void pull() {
// Only internal nodes can pull
val = lft->val + rgt->val;
}
void modify(int L, int R, int idx, int x) {
if (L == R)
val = x;
else {
int M = (L+R) / 2;
if (idx <= M)
lft->modify(L, M, idx, x);
else
rgt->modify(M+1, R, idx, x);
pull();
}
}C++
Range Sum Query (Leetcode 307)
class SegTree {
public:
SegTree *lft, *rgt;
int val;
SegTree(vector<int>& nums, int L, int R) {
if (L == R) {
lft = rgt = nullptr;
val = nums[L];
} else {
int M = (L+R) / 2;
lft = new SegTree(nums, L, M);
rgt = new SegTree(nums, M+1, R);
pull();
}
}
void pull() {
// Only internal nodes can pull
val = lft->val + rgt->val;
}
int query(int L, int R, int qL, int qR) {
if (qR < L || R < qL)
return 0;
if (qL <= L && R <= qR)
return val;
int M = (L+R) / 2;
return lft->query(L, M, qL, qR) +
rgt->query(M+1, R, qL, qR);
}
void modify(int L, int R, int idx, int x) {
if (L == R)
val = x;
else {
int M = (L+R) / 2;
if (idx <= M)
lft->modify(L, M, idx, x);
else
rgt->modify(M+1, R, idx, x);
pull();
}
}
};請實作一個 Class,從一個數列初始化,支援兩種操作:
- update(index, val)
- sumRange(left, right)
重新看一下所有程式碼吧!
(C++)
class NumArray {
public:
SegTree *tree = nullptr;
int n;
NumArray(vector<int>& nums) {
n = nums.size();
tree = new SegTree(nums, 0, n-1);
}
void update(int index, int val) {
tree->modify(0, n-1, index, val);
}
int sumRange(int left, int right) {
return tree->query(0, n-1, left, right);
}
};Range Sum Query (Leetcode 307)
class SegTree:
def __init__(self, nums, L, R):
if L == R:
self.left = self.right = None
self.val = nums[L]
else:
M = (L+R)//2
self.left = SegTree(nums, L, M)
self.right = SegTree(nums, M+1, R)
self.pull()
def pull(self):
# Only interal nodes can pull.
self.val = self.left.val + self.right.val
def query(self, L, R, qL, qR):
if qR < L or R < qL:
return 0
if qL <= L and R <= qR:
return self.val
M = (L + R) // 2
return self.left.query(L, M, qL, qR) + \
self.right.query(M+1, R, qL, qR)
def modify(self, L, R, idx, val):
if L == R:
self.val = val
else:
M = (L + R) // 2
if idx <= M:
self.left.modify(L, M, idx, val)
else:
self.right.modify(M+1, R, idx, val)
self.pull()
請實作一個 Class,從一個數列初始化,支援兩種操作:
- update(index, val)
- sumRange(left, right)
重新看一下所有程式碼吧!
(Python)
class NumArray:
def __init__(self, nums: List[int]):
self.N = len(nums)
self.segTree = SegTree(nums, 0, self.N-1)
def update(self, index, val):
self.segTree.modify(
0, self.N-1, index, val)
def sumRange(self, left, right):
return self.segTree.query(
0, self.N-1, left, right)
線段樹 - 2
Segment Tree - 區間修改 (懶人標記)
Falling Squares (Leetcode 699)
現在有 n 個 (位置,邊長) 表示模擬 n 個正方形掉落在該位置上。
如果掉落的時候會卡到以前的正方形,則會直接停在上面。
請輸出每個時間點,正方形們可以到達的最高高度。
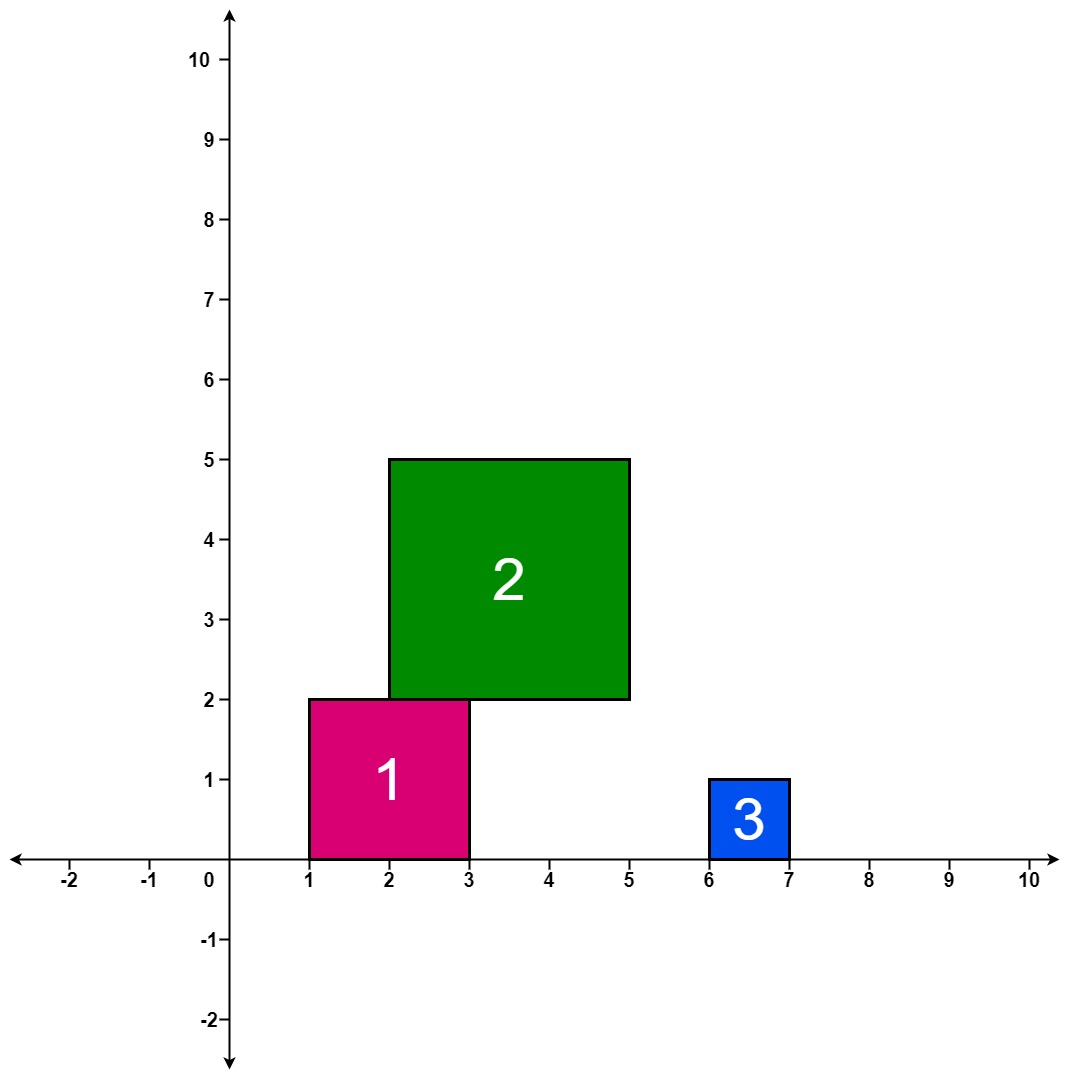
舉例來說:
依序放落三個方塊:
| 編號 | 位置 | 邊長 |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 2 | 3 |
| 3 | 6 | 1 |
最終答案:[2, 5, 5]
Falling Squares (Leetcode 699)
現在有 n 個 (位置,邊長) 表示模擬 n 個正方形掉落在該位置上。
如果掉落的時候會卡到以前的正方形,則會直接停在上面。
請輸出每個時間點,正方形們可以到達的最高高度。
首先我們先預處理一下:
這題的位置可能會到 1e8,但個數只有 1e3,
所以我們可以先數值離散化。
Python
S = set()
for pos, width in positions:
S.add(pos)
S.add(pos+width-1)
mapping = {}
for i, x in enumerate(sorted(S)):
mapping[x] = imap<int, int> mapping;
for (auto &v : positions) {
int pos = v[0], width = v[1];
mapping[pos] = 0;
mapping[pos + width - 1] = 0;
}
int idx = 0;
for (auto &[k, v] : mapping)
v = idx++;
C++
註: 線段樹要離散化,但 Treap 可以不用
Falling Squares (Leetcode 699)
現在有 n 個 (位置,邊長) 表示模擬 n 個正方形掉落在該位置上。
如果掉落的時候會卡到以前的正方形,則會直接停在上面。
請輸出每個時間點,正方形們可以到達的最高高度。
這題如果直接模擬,
需要什麼操作?
- 如果每個位置代表高度:
- 查詢所有數字的最大值
- 在一個區間疊方塊
- 可以拆成兩個步驟
- 詢問區間最大值
- 修改區間的值

怎麼做?
線段樹 (Segment Tree) - 區間修改
線段樹如何做到區間修改?
rangeModify(qL, qR, val) = 修改 [qL, qR] 的數字變成 val
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
- Naive:
- 每修改一次需要
- 總共
- 爆了... 怎麼更好?
- 學習 heap 的 lazy 技巧!
- Lazy Tag (懶人標記) 的精神:
- 在該點上標記:
「這裡要修改成 val 喔!」
- 來想想看要怎麼利用
「懶人的精神」吧!
- 在該點上標記:
線段樹 (Segment Tree) - 區間修改
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
- Lazy Tag (懶人標記) 的精神:
- 在該點上標記:
「這裡要修改成 val 喔!」
- 在該點上標記:
RangeModify A[1, 7] = 3
[2, 3]
A1
tag = 3
tag = 3
val = 3
線段樹如何做到區間修改?
- 像區間詢問一樣,把目標區間上一個標記。
- 修改時,哪些區間會影響到?
- 這些點必須重新 「pull」
跟 modify 單點修改一樣。 - pull 時小孩有 tag 怎麼辦?
我們需要「push」它們,把
它們持有的 "tag" 下放。
- 這些點必須重新 「pull」
- 哪裡還需要 push?只要摸到順便 push 下去就可以了。
[0, 7]
[0, 3]
[0, 1]
[4, 7]
pull!
pull!
push!
A2
A3
val = 3
push!
pull!
[4, 5]
[6, 7]
tag = 3
[2, 3]
[4, 7]
線段樹 (Segment Tree) - 區間修改 / 懶人標記
- 像區間詢問一樣,把目標區間上一個標記
- 影響到的區間必須重新 「pull」,並 「push」小孩 ( 把持有的 "tag" 下放 )
- 所有操作經過的節點都需要順便 push
class SegTree {
public:
SegTree *lft, *rgt;
int val, lazy=0;
SegTree(vector<int> &nums, int L, int R) {
if (L == R) {
lft = rgt = nullptr;
val = nums[L];
} else {
int M = (L+R) / 2;
lft = new SegTree(nums, L, M);
rgt = new SegTree(nums, M+1, R);
pull();
}
}
void pull() {
// Only internal nodes can pull
lft->push(), rgt->push();
val = max(lft->val, rgt->val);
}
void push() {
if (lazy) {
val = lazy;
if (lft)
lft->lazy = rgt->lazy = lazy;
lazy = 0;
}
}
C++
int query(int L, int R, int qL, int qR) {
if (qR < L || R < qL)
return 0;
push();
if (qL <= L && R <= qR)
return val;
int M = (L+R) / 2;
return max(lft->query(L, M, qL, qR),
rgt->query(M+1, R, qL, qR));
}
void rangeModify(int L, int R, int qL,
int qR, int x) {
if (qR < L || R < qL)
return;
if (qL <= L && R <= qR) {
lazy = x;
return;
}
push();
int M = (L+R) / 2;
lft->rangeModify(L, M, qL, qR, x);
rgt->rangeModify(M+1, R, qL, qR, x);
pull();
}
};1. 多一個標記的變數
1. 像區間查詢一樣的做法,
差別在於一個要 return 一個是修改
2. 影響到的要重新 pull
2. pull 的時候順便 push
2. push: 把 tag 下放,
更新 val
3. 經過一個點順便 push
3. 經過一個點順便 push
這題要 max
線段樹 (Segment Tree) - 區間修改 / 懶人標記
- 像區間詢問一樣,把目標區間上一個標記
- 影響到的區間必須重新 「pull」,並 「push」小孩 ( 把持有的 "tag" 下放 )
- 所有操作經過的節點都需要順便 push
class SegTree:
def __init__(self, nums, L, R):
self.lazy = 0
if L == R:
self.left = self.right = None
self.val = nums[L]
else:
M = (L+R)//2
self.left = SegTree(nums, L, M)
self.right = SegTree(nums, M+1, R)
self.pull()
def pull(self):
# Only interal nodes can pull.
self.left.push()
self.right.push()
self.val = max(self.left.val, self.right.val)
def push(self):
if self.lazy:
self.val = self.lazy
if self.left:
self.left.lazy = self.lazy
self.right.lazy = self.lazy
self.lazy = 0Python
def query(self, L, R, qL, qR):
if qR < L or R < qL:
return 0
self.push()
if qL <= L and R <= qR:
return self.val
M = (L + R) // 2
return max(self.left.query(L, M, qL, qR),
self.right.query(M+1, R, qL, qR))
def rangeModify(self, L, R, qL, qR, x):
if qR < L or R < qL:
return
if qL <= L and R <= qR:
self.lazy = x
return
self.push()
M = (L + R) // 2
self.left.rangeModify(L, M, qL, qR, x)
self.right.rangeModify(M+1, R, qL, qR, x)
self.pull()
1. 多一個標記的變數
1. 像區間查詢一樣的做法,
差別在於一個要 return 一個是修改
2. 影響到的要重新 pull
2. pull 的時候順便 push
2. push: 把 tag 下放,
更新 val
3. 經過一個點順便 push
3. 經過一個點順便 push
這題要 max
Falling Squares (Leetcode 699)
現在有 n 個 (位置,邊長) 表示模擬 n 個正方形掉落在該位置上。
如果掉落的時候會卡到以前的正方形,則會直接停在上面。
請輸出每個時間點,正方形們可以到達的最高高度。
Python
def fallingSquares(self, positions):
# Discretization
S = set()
for pos, width in positions:
S.add(pos)
S.add(pos+width-1)
mapping = {x : i for i, x in enumerate(sorted(S))}
n = len(mapping)
tree = SegTree([0] * n, 0, n-1)
ans = []
for pos, width in positions:
L, R = mapping[pos], mapping[pos+width-1]
v = tree.query(0, n-1, L, R)
tree.rangeModify(0, n-1, L, R, v + width)
ans.append(tree.query(0, n-1, 0, n-1))
return ansvector<int> fallingSquares(
vector<vector<int>>& positions) {
// Descritization
map<int, int> mapping;
for (auto &vec : positions) {
int pos = vec[0], width = vec[1];
mapping[pos] = 0;
mapping[pos + width - 1] = 0;
}
int idx = 0;
for (auto &[k, v] : mapping)
v = idx++;
int n = mapping.size();
vector<int> init_vec(n), ans;
SegTree *tree = new SegTree(init_vec, 0, n-1);
for (auto &vec : positions) {
int pos = vec[0], width = vec[1];
int L = mapping[pos], R = mapping[pos+width-1];
int v = tree->query(0, n-1, L, R);
tree->rangeModify(0, n-1, L, R, v + width);
ans.push_back(tree->query(0, n-1, 0, n-1));
}
return ans;
}C++
Falling Squares (Leetcode 699)
現在有 n 個 (位置,邊長) 表示模擬 n 個正方形掉落在該位置上。
如果掉落的時候會卡到以前的正方形,則會直接停在上面。
請輸出每個時間點,正方形們可以到達的最高高度。
想想看時間複雜度吧!
- build:
- push:
- pull:
- query:
- modify:
- rangeModify:
整體複雜度:
BIT
Fenwick Tree / Binary Indexed Tree
Binary Indexed Tree / Fenwick Tree
恭喜你學會了線段樹!
我們來介紹一下線段樹的變種 - BIT。
BIT 支援線段樹的所有操作,
但是所有的區間操作都必須是對 [1, n] 操作,也就是題目必須:
- 題目只會修改 / 詢問 [1, n]
- 題目修改 / 詢問 [l, r] ,但可以拆成兩次 [1, n] 操作
[l, r]
[1, r]
[1, l-1]
舉例來說,如果要做到區間詢問總和[l, r]
你可以用 [1, r] - [1, l-1] 就可以算出答案。
Binary Indexed Tree / Fenwick Tree
BIT 與線段樹的結構差異:
BIT 只用一個長度為 n 的陣列存數值,並且從 1 開始算
[0, 7]
[0, 3]
[4, 7]
[0, 1]
[2, 3]
[4, 5]
[6, 7]
A0
A1
A2
A3
A4
A5
A6
A7
[1, 8]
[1, 4]
[5, 8]
[1, 2]
[3, 4]
[5, 6]
[7, 8]
A1
。
A3
A5
A7
(1-indexed)
線段樹 Segment Tree
Binary Indexed Tree / BIT
。
。
。
BIT 就只存這一個陣列。圓點表示一個區間的值
Binary Indexed Tree / Fenwick Tree
BIT 與線段樹的結構差異:
BIT 只用一個長度為 n 的陣列存數值,並且從 1 開始算
[1, 8]
[1, 4]
[5, 8]
[1, 2]
[3, 4]
[5, 6]
[7, 8]
A1
。
A3
A5
A7
(1-indexed)
Binary Indexed Tree / BIT
。
。
。
BIT 就只存這一個陣列。圓點表示一個區間的值
為什麼會這樣設計呢?
- 如果操作只在乎 [1, n],
那麼你不會操作到 [2, 2] 。- 所以根本不需要 A[2] 這個數字。因為涉及到 A[2] 的詢問只會是 [1, 2]。
所以只需存 [1, 2] 的結果就好。 - 舉例來說,如果你區間總和,想要修改 A[2] 這個點,你直接改 [1, 2] 這個區間就好,因為你詢問不會詢問到單純的 A[2],也就是 [2, 2]
- 所以根本不需要 A[2] 這個數字。因為涉及到 A[2] 的詢問只會是 [1, 2]。
Binary Indexed Tree / Fenwick Tree
BIT 與線段樹的結構差異:
BIT 只用一個長度為 n 的陣列存數值,並且從 1 開始算
[1, 8]
[1, 4]
[5, 8]
[1, 2]
[3, 4]
[5, 6]
[7, 8]
A1
。
A3
A5
A7
(1-indexed)
Binary Indexed Tree / BIT
。
。
。
BIT 就只存這一個陣列。圓點表示一個區間的值
為什麼會這樣設計呢?
- 如果操作只在乎 [1, n],
那麼你不會操作到 [2, 2] 。
所以不用特地存 A[2]。 - 想想看 [1, ?] 需要詢問那些區間?
- ? = 1: [1, 1] -> (1)
- ? = 2: [1, 2] -> (2)
- ? = 3: [1, 2], [3, 3] -> (3, 2)
- ? = 4: [1, 4] -> (4)
- ? = 5: [1, 4], [5, 5] -> (5, 4)
- ? = 6: [1, 4], [5, 6] -> (6, 4)
- ? = 7: [1, 4], [5, 6], [7, 7]-> (7, 6, 4)
- 你想的出規律嗎?
Binary Indexed Tree / Fenwick Tree
BIT 與線段樹的結構差異:
BIT 只用一個長度為 n 的陣列存數值,並且從 1 開始算
[1, 8]
[1, 4]
[5, 8]
[1, 2]
[3, 4]
[5, 6]
[7, 8]
A1
。
A3
A5
A7
(1-indexed)
Binary Indexed Tree / BIT
。
。
。
BIT 就只存這一個陣列。圓點表示一個區間的值
- q(1): (1)
- q(2): (2)
- q(3): (3, 2)
- q(4): (4)
- q(5): (5, 4)
- q(6): (6, 4)
- q(7): (7, 6, 4)
- q(8): (8)
用二進位制觀察一下性質:
- 第一層(最底層)都是奇數
- 第二層 % 2 = 0
- 第三層 % 4 = 0 ...
- 每一層最多只會有一個代表
- q(n) = {n, q(n-x)},例如
- q(7) -> 7, q(7-1 = 6)
- q(6) -> 6, q(6-2 = 4)
- 這裡的 x 要怎麼算出來呢?
Binary Indexed Tree - Query
Query
Needs
十進位
二進位
十進位
二進位
你想得出規律嗎?
線段樹小結
逆隊
樹堆 Treap
Treap = Tree + Heap
進階樹/圖論
最小生成樹
Minimum Spanning Tree
在線 LCA - 1
Lowest common ancestor (Online - 倍增算法 / binary lifting)
(最低共同祖先)
在線 LCA - Naive 作法
A
B
C
D
E
F
G
H
I
LCA (最低共同祖先) 的定義:
每筆詢問給定兩個點,
請問它們共同的祖先中最低的是?
- LCA(H, G) = C
- LCA(D, I) = A
最簡單的做法就是:
- 幫每個點標深度 (跟 parent )
- 先讓比較深的點走到跟淺的點一樣的深度
- 兩邊同時往上走,碰到一起即為LCA
- 做一次的複雜度為多少呢?
H(A) = 0
H(B) = 1
H(C) = 1
H(D) = 2
H(E) = 2
H(F) = 2
H(G) = 2
H(H) = 3
H(I) = 3
D
I
E
B
C
A
在線 LCA - Naive 作法
- 幫每個點標深度 ( 跟 parent )
- 先讓比較深的點走到跟淺的點一樣的深度
- 兩邊同時往上走,碰到一起即為LCA
H = {}
# get height & parent by recursion
def dfs(root, depth, parent):
if not root: return
H[root] = depth, parent
dfs(root.left, depth+1, root)
dfs(root.right, depth+1, root)
dfs(root, 0, None)
def query(p, q):
# Assure the deepest node is p
if H[p][0] < H[q][0]:
return query(q, p)
cur_p, cur_q = p, q
# Move p, q to same level
while H[cur_p][0] != H[cur_q][0]:
cur_p = H[cur_p][1]
# Move p, q at the same time
while cur_p != cur_q:
cur_p = H[cur_p][1]
cur_q = H[cur_q][1]
return cur_p
return query(p, q)Python
unordered_map<TreeNode*, int> height;
unordered_map<TreeNode*, TreeNode*> parents;
// get height & parent by recursion
void dfs(TreeNode *root, int depth, TreeNode* parent) {
if (!root) return;
height[root] = depth;
parents[root] = parent;
dfs(root->left , depth+1, root);
dfs(root->right, depth+1, root);
}
TreeNode* query(TreeNode *p, TreeNode *q) {
// Assure the deepest node is p
if (height[p] < height[q])
return query(q, p);
// Move p, q to same level
while (height[p] != height[q])
p = parents[p];
// Move p, q at the same time
while (p != q)
p = parents[p], q = parents[q];
return p;
}
TreeNode* lowestCommonAncestor(
TreeNode* root, TreeNode* p, TreeNode* q) {
dfs(root, 0, nullptr);
return query(p, q);
}C++
在線 LCA - 倍增算法
binary lifting
A
B
C
D
E
F
G
H
I
Naive 在一次詢問的情況下是OK的。
不幸的是,大部分情況需要很多次。
要怎麼樣才可以降低詢問的複雜度?
- 一個簡單的想法:每次往上移的時候,跳多一點。
-
「多」具體來說是多少呢?
- 簡單上來說就是做二分搜尋的反向版,倍增搜尋。
- 每個點紀錄上 個 parent 是誰
在線 LCA - 倍增算法
binary lifting
- 建 的 parent 是誰 (建到 就好了)
- 你會發現 X 的上個 的 parents 就會等於...
- 「X 的上個 的 parent = Y」的上個 的 parent
- Base Case:k=0 就是該點的 parent。
Y
X
Z
在線 LCA - 倍增算法
binary lifting
heights, parents = {}, {}
MAX_H = 17
def dfs(root, depth, parent):
if not root: return
heights[root] = depth
parents[root, 0] = parent
for k in range(1, MAX_H):
Y = parents[root, k-1]
parents[root, k] = parents[Y, k-1]
dfs(root.left, depth+1, root)
dfs(root.right, depth+1, root)
dfs(root, 0, root)const static int MAX_H = 17;
unordered_map<TreeNode*, int> height;
unordered_map<TreeNode*, TreeNode*> parents[MAX_H];
void dfs(TreeNode *root, int depth, TreeNode* parent) {
if (!root) return;
height[root] = depth;
parents[0][root] = parent;
for (int k=1; k<MAX_H; k++) {
auto Y = parents[k-1][root];
parents[k][root] = parents[k-1][Y];
}
dfs(root->left , depth+1, root);
dfs(root->right, depth+1, root);
}
// When build first
dfs(root, 0, root);Python
C++
- 建 的 parent 是誰 (建到 就好了)
- 你會發現 X 的上個 的 parents 就會等於...
- 「X 的上個 的 parent = Y」的上個 的 parent
- Base Case:k=0 就是該點的 parent。
在線 LCA - 倍增算法
binary lifting
- 建 的 parent 是誰 (建到 就好了)
- 先讓比較深的點走到跟淺的點一樣的深度
假設 height[p] > height[q]:
假設 p 跟 q 的深度差為 x,那麼 x 可以寫成二進位制。
TreeNode* query(TreeNode *p, TreeNode *q) {
if (height[p] < height[q])
return query(q, p);
// Let h[p] = h[q]
for (int k=0; k<MAX_H; k++)
if ((height[p] - height[q]) & (1 << k))
p = parents[k][p];
// ...def LCA(p, q):
if heights[p] < heights[q]:
return LCA(q, p)
# Let h[p] = h[q]
for k in range(MAX_H):
if (heights[p] - heights[q]) & (1 << k):
p = parents[p, k]
# ...Python
C++
只需移動 log N 次!
在線 LCA - 倍增算法
binary lifting
- 建 的 parent 是誰 (建到 就好了)
- 先讓比較深的點走到跟淺的點一樣的深度
- 二分搜 p 和 q 要跨多少步
體感上會是這樣:
P
Q
X
- 步伐從最大步開始測,也就是
- 假設現在正在考慮從 P / Q 走 步
- 如果相等,表示太過。
- 步伐下次小一點,變 步
- 如果相等,表示太過。
在線 LCA - 倍增算法
binary lifting
體感上會是這樣:
P
Q
- 步伐從最大步開始測,也就是
- 假設現在正在考慮從 P / Q 走 步
- 如果相等,表示太過。
- 步伐下次小一點,變 步
- 如果不相等,表示可以直接跳。
- 下次跳 一定會太過,所以步伐下次也會變成 步
- 如果相等,表示太過。
- 跳完後,P / Q 的下一步 ( = 它們的 parent ) 就會等於 LCA(P, Q)
X
Y
Z
- 建 的 parent 是誰 (建到 就好了)
- 先讓比較深的點走到跟淺的點一樣的深度
- 二分搜 p 和 q 要跨多少步
在線 LCA - 倍增算法
binary lifting
- 建 的 parent 是誰 (建到 就好了)
- 先讓比較深的點走到跟淺的點一樣的深度
- 二分搜 p 和 q 要跨多少步
- 步伐從最大步開始測,也就是
- 假設現在正在考慮從 P / Q 走 步,每次縮減一半
- 如果不相等,表示可以直接跳。
- 跳完後,P / Q 的 parent 就會等於 LCA(P, Q)
// ...
// Special Case: No move
if (p == q)
return p;
for (int h=MAX_H-1; h>=0; h--)
if (parents[h][p] != parents[h][q])
p = parents[h][p], q = parents[h][q];
return parents[0][p];
} # ...
# Special Case: No Move
if p == q:
return p
for h in range(MAX_H-1, -1, -1):
if parents[p, h] != parents[q, h]:
p = parents[p, h]
q = parents[q, h]
return parents[p, 0]Python
C++
在線 LCA - 倍增算法
binary lifting
class Solution {
public:
const static int MAX_H = 17;
unordered_map<TreeNode*, int> height;
unordered_map<TreeNode*, TreeNode*> parents[MAX_H];
void dfs(TreeNode *root, int depth, TreeNode* parent) {
if (!root) return;
height[root] = depth;
parents[0][root] = parent;
for (int log_h=1; log_h<MAX_H; log_h++) {
auto hop = parents[log_h-1][root];
parents[log_h][root] = parents[log_h-1][hop];
}
dfs(root->left , depth+1, root);
dfs(root->right, depth+1, root);
}
TreeNode* query(TreeNode *p, TreeNode *q) {
if (height[p] < height[q])
return query(q, p);
for (int i=0; i<MAX_H; i++)
if ((height[p] - height[q]) & (1 << i))
p = parents[i][p];
if (p == q)
return p;
for (int i=MAX_H-1; i>=0; i--)
if (parents[i][p] != parents[i][q])
p = parents[i][p], q = parents[i][q];
return parents[0][p];
}
TreeNode* lowestCommonAncestor(
TreeNode* root, TreeNode* p, TreeNode* q) {
dfs(root, 0, root);
return query(p, q);
}
};C++
重點整理:
- 建 2^h 的 parent 表
- 2^h = 2^{h-1} 兩次
- 查詢 p, q
- 先讓 p 比較深
- 讓 p, q 深度一樣。
- 用深度差算出每次移動多少步
- 用二分搜尋找 p, q 可以跳到哪裡還沒一樣
- 整體複雜度:
在線 LCA - 倍增算法
binary lifting
class Solution:
def lowestCommonAncestor(self, root, p, q):
heights, parents = {}, {}
MAX_H = 17
def dfs(root, depth, parent):
if not root: return
heights[root] = depth
parents[root, 0] = parent
for log_h in range(1, MAX_H):
hop = parents[root, log_h-1]
parents[root, log_h] = parents[hop, log_h-1]
dfs(root.left, depth+1, root)
dfs(root.right, depth+1, root)
dfs(root, 0, root)
def LCA(p, q):
if heights[p] < heights[q]:
return LCA(q, p)
# Let h[p] = h[q]
for i in range(MAX_H):
if (heights[p] - heights[q]) & (1 << i):
p = parents[p, i]
if p == q:
return p
for log_h in range(MAX_H-1, -1, -1):
if parents[p, log_h] != parents[q, log_h]:
p = parents[p, log_h]
q = parents[q, log_h]
return parents[p, 0]
return LCA(p, q)Python
重點整理:
- 建 2^h 的 parent 表
- 2^h = 2^{h-1} 兩次
- 查詢 p, q
- 先讓 p 比較深
- 讓 p, q 深度一樣。
- 用深度差算出每次移動多少步
- 用二分搜尋找 p, q 可以跳到哪裡還沒一樣
- 整體複雜度:
在線 LCA - 2
Lowest common ancestor (Online - ETT + RMQ)
(最低共同祖先)
在線 LCA - 尤拉導覽
Euler Tour Technique (ETT)
A
B
C
D
E
F
G
H
I
先觀察一棵樹的尤拉導覽 (ETT),
每次回跟進都會記錄進導覽內:
Euler Tour:
ABDDBACEHHEIIECFFCGGCA
假設我們要問 LCA(B, I),
那麼 ETT 從 B 到 I 是哪一段呢?
ABDDBACEHHEIIECFFCGGCA
那麼你就會發現有很有趣的事情:
- LCA (B, I) = ETT 經過最低的點
- 可以想想看你要怎麼證明 / 說幅這一點?
在線 LCA - 尤拉導覽
Euler Tour Technique (ETT)
- 建構 ETT,並且記錄深度以及該點,以及進出的位置
- 尋找 LCA 時,尋找先進的位置 <-> 最後出的位置
- 把這段 ETT 中最低深度的找出來,回傳。
ETT = []
I, O = {}, {}
def dfs(root, depth):
if not root: return
I[root] = len(ETT)
ETT.append((depth, root))
dfs(root.left, depth+1)
ETT.append((depth, root))
dfs(root.right, depth+1)
O[root] = len(ETT)
ETT.append((depth, root))
dfs(root, 0)
def query(p, q):
ETT_I = min(I[p], I[q])
ETT_O = max(O[p], O[q])
ans_depth, ans = inf, None
for i in range(ETT_I, ETT_O+1):
cur_depth, cur_node = ETT[i]
if cur_depth < ans_depth:
ans_depth = cur_depth
ans = cur_node
return ans
return query(p, q)Python
vector<pair<TreeNode*, int>> ETT;
unordered_map<TreeNode*, int> I, O;
void dfs(TreeNode *root, int depth) {
if (!root) return;
I[root] = ETT.size(); ETT.push_back({root, depth});
dfs(root->left, depth+1); ETT.push_back({root, depth});
dfs(root->right, depth+1);
O[root] = ETT.size(); ETT.push_back({root, depth});
}
TreeNode* query(TreeNode *p, TreeNode *q) {
int ETT_I = min(I[p], I[q]), ETT_O = max(O[p], O[q]);
int ans_depth = 1e9;
TreeNode* ans;
for (int i=ETT_I; i<=ETT_O; i++) {
auto [cur_node, cur_depth] = ETT[i];
if (cur_depth < ans_depth) {
ans_depth = cur_depth;
ans = cur_node;
}
}
return ans;
}
TreeNode* lowestCommonAncestor(
TreeNode* root, TreeNode* p, TreeNode* q) {
dfs(root, 0);
return query(p, q);
}C++
在線 LCA - 尤拉導覽
Euler Tour Technique (ETT)
- 建構 ETT,並且記錄深度以及該點,以及進出的位置
- 尋找 LCA 時,尋找先進的位置 <-> 最後出的位置
- 把這段 ETT 中最低深度的找出來,回傳。
這段好像怪怪的...?
你會發現 LCA 通過 ETT 後會變成 RMQ 問題!
接著我們可以套任何一個 RMQ 模板,就可以降到 log 等級了!
- 例如你可能剛學過的線段樹。
- 或比較快的 Sparse Table (離線RMQ,Query O(1))
整體複雜度:
😭
離線 LCA
Lowest common ancestor (Tarjan's Offline LCA)
(最低共同祖先)
強連通元件
Strongly Connected Component, SCC
負環檢測
Bellman-Ford Algorithm
多元最短路徑
Floyd-Warshall Algorithm