RRRecursion
Arvin Liu
RRRRRRRRRRRRRRRRRRRRR
什麼是遞迴?
什麼是遞迴?

感受一下?
什麼是遞迴?
現場來寫寫看吧!
N!
求出 N!
給你一個數字 N,請輸出 N!
那還不簡單?
不就是基礎 for 迴圈嗎?
來想想看有沒有其他寫法!
int factorial(int N) {
int ans = 1;
for (int i=1; i<=N; i++)
ans *= i;
return ans;
}C++
def factorial(N):
ans = 1
for i in range(1, N):
ans *= i
return ans
Python
求出 N!
給你一個數字 N,請輸出 N!
假設現在有一個函數:
如果不用 "!" 該怎麼寫?
求出 N!
給你一個數字 N,請輸出 N!
直接把它轉成程式?
跑跑看!
int factorial(int N) {
return N * factorial(N-1);
}def factorial(N):
return N * factorial(N-1)C++
Python
求出 N!
輸出結果 :
4
3
2
1
0
-1
-2
....跑不完!
這裡就該停了!
#include <stdio.h>
int factorial(int N) {
printf("%d\n", N);
return N * factorial(N-1);
}
int main() {
printf("%d", factorial(4));
}def factorial(N):
print(N)
return N * factorial(N-1)
print(factorial(4))C++
Python
求出 N!
給你一個數字 N,請輸出 N!
這樣就可以了!
int factorial(int N) {
if (N == 0) return 1;
return N * factorial(N-1);
}def factorial(N):
if N == 0: return 1
return N * factorial(N-1)C++
Python
怎麼寫遞迴?
怎麼寫遞迴?
-
定義遞迴函式要做什麼? 等於什麼?
- f(n) = n! 的數值
- 觀察如何將大函式用小函式完成?
- f(n) 跟 f(n-1) 有點關係
- 記得寫終止條件 (Base Case)
- f(0) = 1
- 思考的時候,不要從一開始往上推,例如 n=0 怎麼樣,n=1怎麼樣...
- 通常情況下,要逆向思考,習慣倒推。
- 例如 n 要怎麼用n-1表示,或者n-2表示..
記得寫終止條件!

N!遞迴的逐步過程
以 作為舉例
呼叫
呼叫
呼叫
回傳
回傳
回傳
回傳
實際例子可以參考另一個投影片
練習題!
- 如果題目改成 1 + 2 + ... + n,你會寫嗎?
- 有沒有覺得遞迴很沒用?不就迴圈可以寫的事情?試著想想看遞迴有什麼優點吧!
- Clumsy Factorial
小知識: 對google搜尋遞迴
按按看(?)
爬樓梯問題
東東爬樓梯 (zj d212)
東東爬階梯每次可以走一或兩階。
假設階梯有 n 階,那有幾種走法?
🐦
🐦
3 階有 3 種走法
4 階有 5 種走法
1+1+1+1
1+1+2
1+2+1
2+1+1
2+2
1+1+1
1+2
2+1
有點難?
東東爬樓梯 (zj d212)
- 函式定義:
- 如何拆解:
- Base Case:
f(n) = 走 n 階的可能數
f(n-1) f(n-2)
🐦
...
可以將到第n階的走法分成兩類
-
最後一步走1階的
- 最後一步走1階有幾種可能?
- f(n-1)
-
最後一步走2階的
- f(n-2)
+
東東爬階梯每次可以走一或兩階。
假設階梯有 n 階,那有幾種走法?
東東爬樓梯 (zj d212)
- 函式定義:
- 如何拆解:
- Base Case:
f(n) = 走 n 階的可能數
f(n-1) f(n-2)
+
輸入可能是 1 以後的正整數。
f(1) 可以用遞迴算出嗎?
f(2) 可以用遞迴算出嗎?
f(3) 可以用遞迴算出嗎?
⭕
❌
❌
f(1) = 1, f(2) = 2
東東爬階梯每次可以走一或兩階。
假設階梯有 n 階,那有幾種走法?
東東爬樓梯 (zj d212)
- 函式定義:
- 如何拆解:
- Base Case:
f(n) = 走 n 階的可能數
f(n-1) f(n-2)
+
f(1) = 1, f(2) = 2
東東爬階梯每次可以走一或兩階。
假設階梯有 n 階,那有幾種走法?
int fib(int N) {
if (N == 1) return 1;
if (N == 2) return 2;
return fib(N-1) + fib(N-2);
}def fib(N):
if N == 1: return 1
if N == 2: return 2
return fib(N-1) + fib(N-2)C++
Python
爬樓梯問題與費波那契數列
這就是鼎鼎大名的費波那契數列
fibonacci

- f(0) = 1
費波那契數列的遞迴過程
以 作為舉例
2
1
3
2
練習題!
- 如果題目改成東東每次可以走 1, 2, 3 階,遞迴會怎麼寫?
- 你會用迴圈寫這題嗎?
- 你覺得
- 遞迴版本的時間複雜度多少?
- 迴圈版本的時間複雜度多少?
C(n, m)
00369 - Combinations (zj d134)
請問從 N 顆不同的球裡,
有幾種取出 M 顆球的方法?
有 4 顆相異的球
如果取三顆,共 4 種取法
如果取兩顆,共 6 種取法
00369 - Combinations (zj d134)
請問從 N 顆不同的球裡,
有幾種取出 M 顆球的方法?
有 4 顆相異的球
如果取三顆,共 4 種取法
- 函式定義:
- 如何拆解:
- Base Case:
這個也好難....
C(n, m) = N 取 M 的可能數
00369 - Combinations (zj d134)
請問從 N 顆不同的球裡,
有幾種取出 M 顆球的方法?
有 4 顆相異的球
如果取三顆,共 4 種取法
- 函式定義:
- 如何拆解:
- Base Case:
取了最
後的球
沒取最
後的球
取了 後
需要再從三顆中取兩顆
放棄 後
需要再從三顆中取三顆
C(n, m) = N 取 M 的可能數
❌
00369 - Combinations (zj d134)
請問從 N 顆不同的球裡,
有幾種取出 M 顆球的方法?
有 n 顆相異的球
想要取 m 顆
- 函式定義:
- 如何拆解:
- Base Case:
取了最
後的球
沒取最
後的球
❌
...
還剩m顆要選
還剩m-1顆要選
C(n-1, m)
C(n-1, m-1)
+
C(n, m) = N 取 M 的可能數
放棄 後
需要再從n-1顆中取m顆
取了 後
需要再從n-1顆中取m-1顆
00369 - Combinations (zj d134)
請問從 N 顆不同的球裡,
有幾種取出 M 顆球的方法?
- 函式定義:
- 如何拆解:
- Base Case:
f(N,M) = N 取 M 的可能數
C(n-1, m)
C(n-1, m-1)
+
C(3, 2)
C(2, 1)
C(2, 2)
C(1, 0)
C(1, 1)
- m = 0 的時候,表示不取,答案為1
- m = n 的時候,表示全取,答案為1
n 跟 m 減到哪裡該停?
想想看 C(3, 2) 的例子吧!
m = 0 或者 n = m 時為1
00369 - Combinations (zj d134)
請問從 N 顆不同的球裡,
有幾種取出 M 顆球的方法?
- 函式定義:
- 如何拆解:
- Base Case:
f(N,M) = N 取 M 的可能數
C(n-1, m)
C(n-1, m-1)
+
m = 0 或者 n = m 時為1
一個看似複雜的題目,遞迴程式卻非常少!
這就是遞迴的魅力之處 (?)
int C(int n, int m){
if (m == 0 || m == n) return 1;
return C(n-1, m-1) + C(n-1, m);
}def C(n, m):
if m == 0 or m == n: return 1
return C(n-1, m) + C(n-1, m-1)C++
Python
練習題!
- C(n, m) 其實是有公式。
-
- 使用這個公式如果直接在 C++ 用 for 實作,其實會有些問題在,你知道為什麼嗎?
-
0/1 背包問題
祖靈好孝順 ˋˇˊ (zj a587)
給你 N 個物品和物品的重量和價值,以及祖靈的背包的重量限制。
請問祖靈最多可以帶價值東西回家?

| 拿走什麼? | 總重 | 價值 |
|---|---|---|
| G+C+S | 15kg | $8 |
| Y+C+S+B | 8kg | $15 |
| ... | ... | ... |
C
B
Y
G
S
祖靈好孝順 ˋˇˊ (zj a587)
給你 N 個物品和物品的重量和價值,以及祖靈的背包的重量限制。
請問祖靈最多可以帶價值東西回家?
- 函式定義:
f(n, W) = 前 n 個物品中,
限重 W 的情況下的最大價值
有點複雜... 試試看裸套題目定義
f(2, 5): 如果可以拿0~2號的物品,
背包限重為5,回傳所有可能中的的最大價值。
f(7, 10): 如果可以拿0~7號的物品,
背包限重為10,回傳所有可能中的最大價值。
祖靈好孝順 ˋˇˊ (zj a587)
給你 N 個物品和物品的重量和價值,以及祖靈的背包的重量限制。
請問祖靈最多可以帶價值東西回家?
- 函式定義:
- 如何拆解:
又卡住了 :( ...
其實背包問題跟 C(n,m) 很像!
都是 n 個物品裡面挑幾個東西出來
- C(n, m) 的限制是只能挑 m 個
- 背包問題的限制是挑出來的物品限重不能超過 W
f(n, W) = 前 n 個物品中,
限重 W 的情況下的最大價值
祖靈好孝順 ˋˇˊ (zj a587)
給你 N 個物品和物品的重量和價值,以及祖靈的背包的重量限制。
請問祖靈最多可以帶價值東西回家?
- 函式定義:
- 如何拆解:
又卡住了 :( ...
f(n, W) = 前 n 個物品中,
限重 W 的情況下的最大價值
有 n 顆相異的物品,
限重 W
取了最
後的
沒取最
後的
❌
...
💎
👑
📿
💎
💎
0/1 背包問題
有 n 顆相異的球
想要取 m 顆
取了最
後的球
沒取最
後的球
❌
...
C(n, m) 問題
祖靈好孝順 ˋˇˊ (zj a587)
給你 N 個物品和物品的重量和價值,以及祖靈的背包的重量限制。
請問祖靈最多可以帶價值東西回家?
- 函式定義:
- 如何拆解:
有 n 顆相異的物品,
限重 W
取了最
後的
沒取最
後的
❌
...
💎
👑
📿
💎
💎
放棄第 n 個物品,
當它不存在。
可以裝的重量剩
但多了價值
f(n, W) = 前 n 個物品中,
限重 W 的情況下的最大價值
背包還剩
背包還剩
祖靈好孝順 ˋˇˊ (zj a587)
給你 N 個物品和物品的重量和價值,以及祖靈的背包的重量限制。
請問祖靈最多可以帶價值東西回家?
- 函式定義:
- 如何拆解:
- Base Case :
f(n, W) = 前 n 個物品中,
限重 W 的情況下的最大價值
n 會一直往下減... 考慮第零號物品!
祖靈好孝順 ˋˇˊ (zj a587)
- 函式定義:
- 如何拆解:
- Base Case :
f(n, W) = 前 n 個物品中,限重 W 的情況下的最大價值
int f(int n, int w) {
if (n == 0)
return w >= W[n] ? V[n] : 0;
if (w >= W[n])
return max(
f(n-1, w),
f(n-1, w - W[n]) + V[n]
);
return f(n-1, w);
}def f(n, w):
if n == 0:
return V[n] if w >= W[n] else 0
if w >= W[n]:
return max(
f(n-1, w),
f(n-1, w-W[n]) + V[n]
);
return f(n-1, w);
C++
Python
練習題!
- 如果將有個函數 f(n, V) 的定義為n個物品裡面選到價值為V的最低重量
( 例如f(n,10)=3 表示選到價值為10的物品時,重量最低為3 )
那麼你會寫出遞迴式嗎?
- 你要怎麼使用第一題的函數定義來找出限重為 W 的背包最高價值為何?
- 如果每個物品都可以拿無限次,請問你有辦法改寫遞迴式嗎?
記憶化
記憶化 Memoization
為什麼 fib(40) 很慢?
試試看算出 fib(40) !
理論上不該啊?
記憶化 Memoization
我們以爬樓梯的題目來看
fib(3)一樣
卻會重算!
fib(4)
fib(3)
fib(2)
fib(2)
fib(1)
fib(5)
fib(3)
fib(2)
fib(1)
記憶化 Memoization
如何避免重算?
想像有個函數...
輸入 A
輸入 B
輸入 A
第一次碰到!
算出f(A)
第一次碰到!
算出f(B)
算過 A 了!
拿出之前算過的答案
你必須在第一次碰到的時候記錄起來!
記憶化 Memoization
- 如果沒算過,就算出答案,記錄起來。
- 如果有算過,就直接從記憶裡撈出來。
用一個方法可以記錄 「問題」 -> 「答案」
例如 陣列、unordered_map、dict 等等
long long dp[1000];
long long fib(int n){
if (n == 0 || n == 1)
return 1;
if (!dp[n])
dp[n] = fib(n-1) + fib(n-2);
return dp[n];
}dp = {}
def fib(n):
if n == 0 or n == 1 :
return 1
if n not in dp:
dp[n] = fib(n-1) + fib(n-2)
return dp[n]C++
Python
因為 fib 都會 > 0,所以我們可以用
dp[n] 是不是 0 來決定有沒有算過。
記憶化 Memoization
來分析看看複雜度吧!
重複計算 (原本的code)
不重複計算 (記憶化)
f(n) = f(n-1) + f(n-2)
"大概"每多一個n,
就會多算一倍
算完 f(n-1) 時,
f(n-2) 已經算過了,不用重算
差超多
記憶化 Memoization
long long dp[1000];
long long f(int n){
if (n == 0 || n == 1)
return 1;
if (!dp[n])
dp[n] = f(n-1) + f(n-2);
return dp[n];
}來用人腦跑一次看看吧!如果呼叫 f(4)...
| n | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| f(n) | 1 | 1 | ? | ? | ? |
| - | f(1) | f(2) | f(3) | ||
| - | f(0) | f(1) | f(2) |
1
1
2
2
1
3
3
2
5
f(2) 不用再重新遞迴一次 f(1) 跟 f(0) 了!
練習題
- 請問背包問題 (祖靈好孝順 ˋˇˊ) 經過記憶化後的時間複雜度是多少?
- 我們確信問題的答案都大於零,所以才可以使用 !dp[n] 來表示沒有算過。
那麼如果答案可能是 0 怎麼辦?
- 如果參數的範圍很大,大到無法開陣列,但問題的種類數量很小 (DP為稀疏陣列),那怎麼使用記憶化?
(例如 dp[n] 的 n 有可能超大,但 dp[n] 不為0的值其實沒有那麼多,那要怎麼節省空間?)
遞迴小結
遞迴小結
-
定義遞迴函式要做什麼? 等於什麼?
- f(n) = n! 的數值
- 觀察如何將大函式用小函式完成?
- f(n) 跟 f(n-1) 有點關係
- 記得寫終止條件 (Base Case)
- f(0) = 1
- 如果遞迴有可能會重複計算,
使用記憶化 (Memoization)
遞迴小結
-
「遞迴只應天上有,凡人應當用迴圈」
- 看起來好像有些遞迴可以用迴圈寫啊?
- 那就用迴圈寫。
- 那為甚麼要用遞迴寫code?
- 有些題目用迴圈還真的寫不出來...
- 為了寫快一點! (遞迴的code通常很短)
- 注意 stack overflow.
Stack Overflow
什麼是Stack Overflow?

不是指某個回答問題的網站。
什麼是Stack Overflow?
在函式裡宣告的變數都會在stack空間。 (包括main)

當你呼叫非常非常非常多的函式...
stack
警戒線
超出stack警戒線就會導致程式執行錯誤。
(所以是Runtime Error)
解決Stack Overflow - C++

stack
警戒線
- 不要用遞迴寫 (這在幹話?)
- 如果可以,用for迴圈寫。
(例如fib可直接用for。)
- 如果可以,用for迴圈寫。
- 如果不行
- 使用全域變數或heap空間,用別的方法模擬遞迴 (詳見圖論投影片-bfs/dfs)
C++ 黑魔法 - 內嵌組合語言強制遞迴用heap空間
C++ 黑魔法 - 強制調用heap空間
extern int main2(void) __asm__ ("main2");
int main2() {
run();
exit(0);
}
int main() {
// 跟heap借256MB
int size = 256 << 20;
char *p = (char *)malloc(size) + size;
__asm__ __volatile__(
"movq %0, %%rsp\n"
"pushq $exit\n"
"jmp main2\n"
:: "r"(p));
}- 要
- 把你原本程式的main改名成run。
- 把上面這份code貼在你的程式的最下面。
#include <cstdlib>解決Stack Overflow - Python
- sys.setrecursionlimit
- Tail Recursion
- DP - Call small case first
輾轉相除法
Euclidean Algorithm
同餘定理
再繼續上之前,
先讓我們介紹同餘定理
同餘定理
在猥瑣罐頭下樓梯(zj a272) 中,
除了要寫東東爬樓梯以外,
多了一個奇怪的條件...

你可能會輸出
但在運算的過程中數字太大噴掉...
在每次運算完後直接%就可以避免溢位!
練習題
- (a * b) % M 有辦法用像 (a + b) % M 一樣的技巧嗎?
- (a ^ b) % M 呢?
- (a - b) % M 呢?
- 如果 a = 7, b = 5, M = 6
- (7 - 5) % 6 = 2
- ((7 % 6 = 1) - (5 % 6 = 5)) % 6 = (1 - 5) % 6
= -4 % 6 ???? (在C++中會是 -4,但python是2) - 你該怎麼解決這個問題?
- 如果 a = 7, b = 5, M = 6
輾轉相除法
輾轉相除法
輾轉相除法
想想看程式要怎麼寫吧!
練習題
- 可以簡化成這樣,想想看為什麼?
- Hint 1: % b 的一種看法-b-b-b...減到不能再減
- Hint 2: 參數的位置不一樣,這確定了 a 跟 b 的一個關係
- 你會求出 LCM (最小公倍數) 嗎?
int GCD(int a, int b){
if(b == 0)
return a + b;
return GCD(b, a % b);
}2^n 暴力搜尋
int f(vector<int> &cur, int n){
if (cur.size() == n) {
for (auto x : cur)
printf("%d", x);
puts("");
}
else {
for (int nxt : {0, 1}) {
cur.push_back(nxt);
f(cur, n);
cur.pop_back();
}
}
}
// Call
vector<int> V;
f(V, 3);def f(L, n):
if len(L) == n:
print(L)
else:
for nxt in [0, 1]:
L.append(nxt)
f(L, n)
L.pop()
# Call
f([], 3)C++
Python
2^n 暴力搜尋
n! 暴力搜尋
int f(vector<int> &cur, int n, vector<int> &visit){
if (cur.size() == n) {
for (auto x : cur)
printf("%d", x);
puts("");
}
else {
for (int nxt=0; nxt<n; nxt++) {
if (!visit[nxt]) {
cur.push_back(nxt);
visit[nxt] = 1;
f(cur, n, visit);
cur.pop_back();
visit[nxt] = 0;
}
}
}
}
// Call
int n = 3;
vector<int> V, visit(3, 0);
f(V, 3, visit);
def f(L, n, visit):
if len(L) == n:
print(L)
else:
for nxt in range(n):
if nxt not in visit:
L.append(nxt)
visit.add(nxt)
f(L, n, visit)
L.pop()
visit.remove(nxt)
# Call
f([], 3, set())C++
Python
n! 暴力搜尋
int n = 3;
vector<int> V(n);
for (int i=0; i<n; i++)
V[i] = i;
do {
for (auto v : V) {
printf("%d", v);
}puts("");
} while(next_permutation(V.begin(), V.end()));
n = 3
L = list(range(n))
from itertools import permutations
for p in permutations(L):
print(p)C++
Python
n! 暴力搜尋
int n = 3;
vector<int> V(n);
for (int i=0; i<n; i++)
V[i] = i;
do {
for (auto v : V) {
printf("%d", v);
}puts("");
} while(next_permutation(V.begin(), V.end()));
n = 3
L = list(range(n))
from itertools import permutations
for p in permutations(L):
print(p)C++
Python
next_permutation 的原理
分治法
Divide & Conquer (D&C)
分治法 Divide & Conquer
分治法 Divide & Conquer
Divide
Conquer
Combine
分割:
將大問題切割成小問題
擊破:
將各個小問題解決掉
整合:
將各個小問題的答案整合起來
其實你也不用想太多,把它當遞迴想就可以了。
分治法 Divide & Conquer
快速冪
Fast Pow
int f(vector<int> &cur, int n, vector<int> &visit){
if (cur.size() == n) {
for (auto x : cur)
printf("%d", x);
puts("");
}
else {
for (int nxt=0; nxt<n; nxt++) {
if (!visit[nxt]) {
cur.push_back(nxt);
visit[nxt] = 1;
f(cur, n, visit);
cur.pop_back();
visit[nxt] = 0;
}
}
}
}
// Call
int n = 3;
vector<int> V, visit(3, 0);
f(V, 3, visit);
def f(L, n, visit):
if len(L) == n:
print(L)
else:
for nxt in range(n):
if nxt not in visit:
L.append(nxt)
visit.add(nxt)
f(L, n, visit)
L.pop()
visit.remove(nxt)
# Call
f([], 3, set())C++
Python
快速冪
河內塔
Tower of Hanoi
什麼是河內塔?
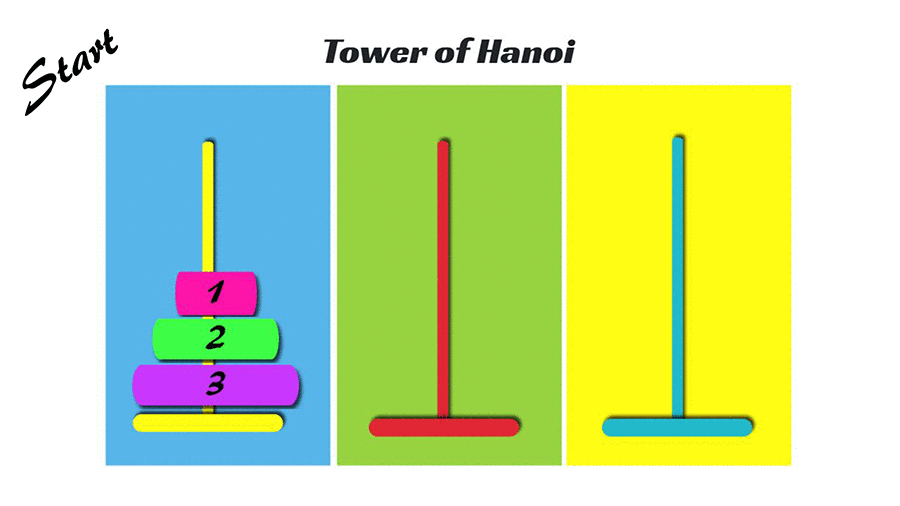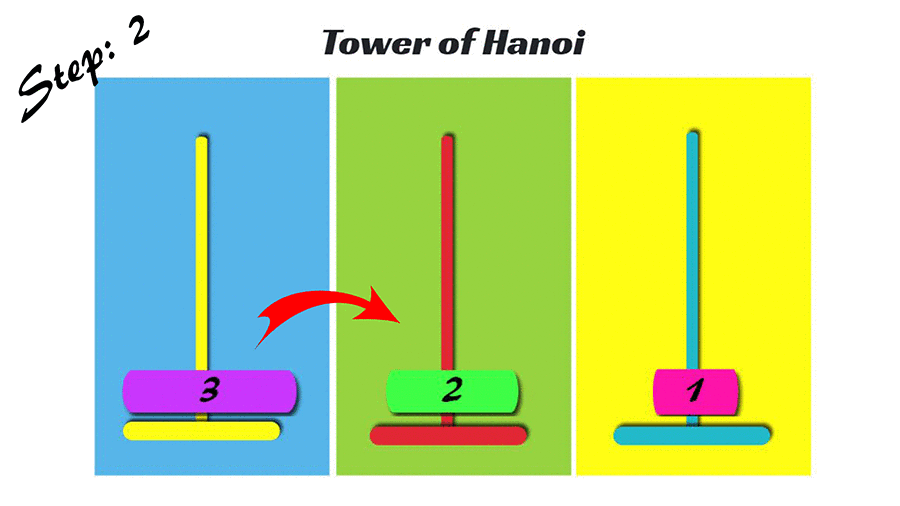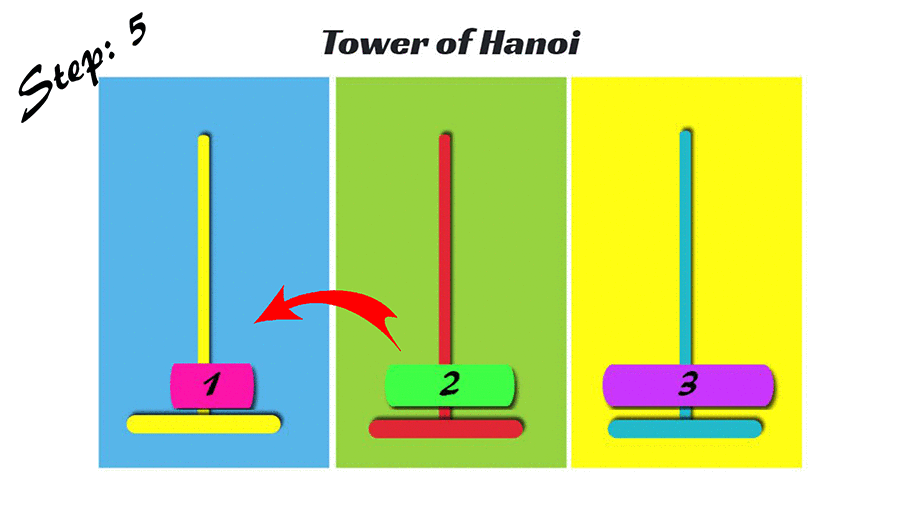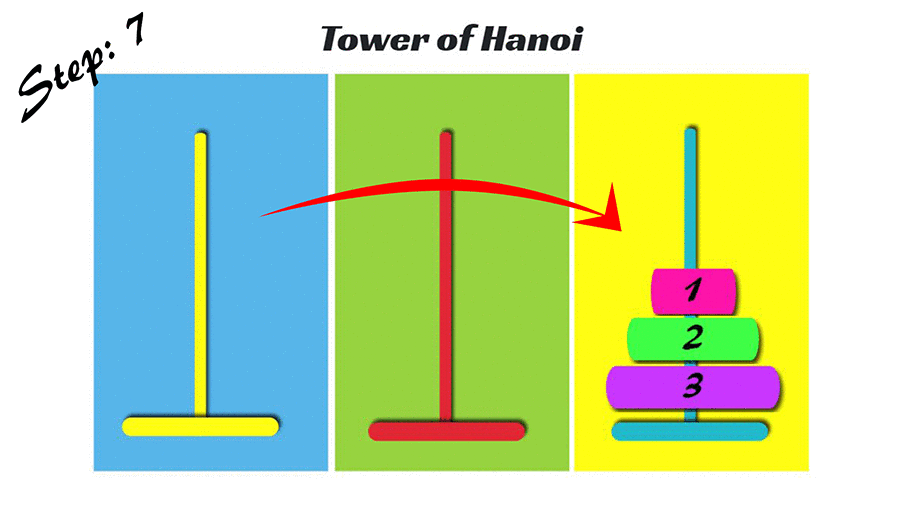
Tower of Hanoi
- 初始: 有大小1~n的圓盤,都在第一個塔。
- 每次可以移動一個圓盤,移動後只能讓比較小的在上面。
- 問題: 如何最少次把大小1~n的圓盤都搬到最後一層?
n=4的河內塔
想得出來要怎麼做嗎? 玩玩看!
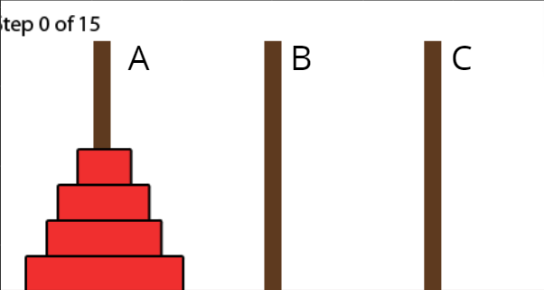
n=4的河內塔

連猩猩都會,你不會嗎(?)
n=4 的河內塔
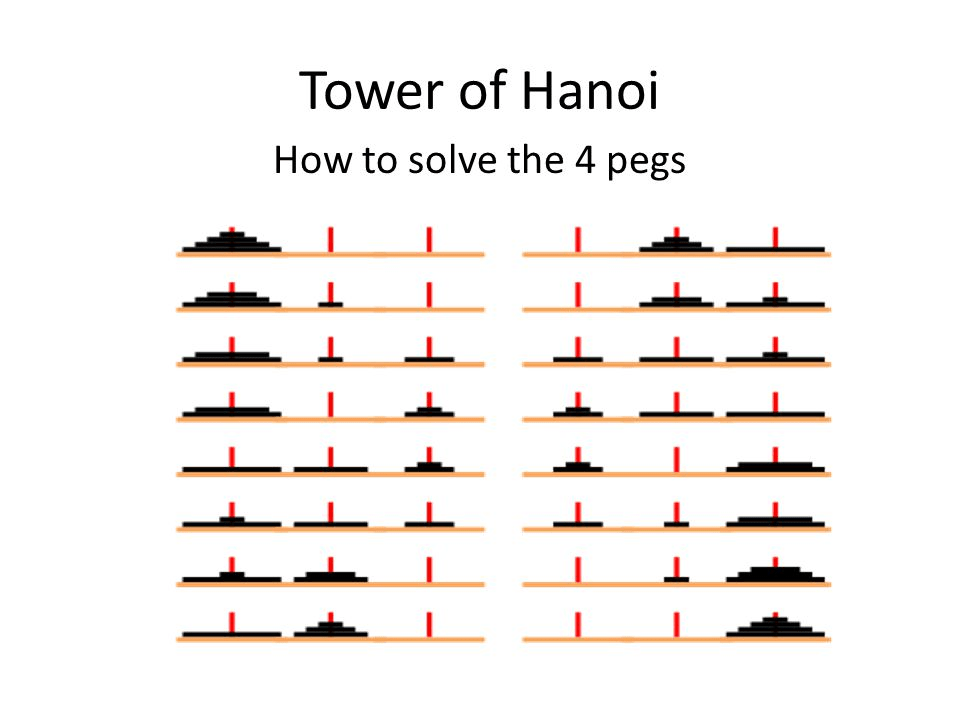
n = 4 的解法
河內塔 (zj a227)
n
n-2
1
...
n-1
- 函式定義:
f(n) = 把 1~n 的圓盤從A移到C
A
B
C
好像不夠詳細... 拆不出來
f(n, s, t) = 把 1~n 的圓盤從 s 移到 t
例如 f(5, A, C) 表示把 1~n 的圓盤從 A 移到 C
來想想看這樣可不可以拆吧!
n
n-2
1
...
n-1
- 函式定義:
- 如何拆解:
A
B
C
f(n, s, t) = 把 1~n 的圓盤從 s 移到 t
n
n
A
B
C
n-2
1
...
n-1
只有在你把 1~n-1的盤子搬到中間,你才可以把第n個圓盤搬到你想要的位置
河內塔 (zj a227)
- 函式定義:
- 如何拆解:
f(n, s, t) = 把 1~n 的圓盤從 s 移到 t
只有在你把 1~n-1的盤子搬到中間,你才可以把第n個圓盤搬到你想要的位置
- 如果你想把1~n的塔從A放到C?
- 先把1~n-1的塔從A搬到B。
- 把第n圓盤從A放到C。
- 再把1~n-1的塔從B搬回C。
n
n-2
1
...
n-1
A
B
C
n
n-2
1
...
n-1
n-2
1
...
n-1
f(n, A, C)
f(n-1, A, B)
f(n-1, B, C)
<print>
f(n, s, t, o)
f(n-1, s, o, t)
<print>
f(n-1, o, t, s)
河內塔 (zj a227)
- 函式定義:
- 如何拆解:
- Base Case:n = 1 的時候輸出 / n = 0 的時候不做事
f(n, s, t, o) = 把 1~n 的圓盤從 s 移到 t
河內塔 (zj a227)
(source, target, other)
f(n, s, t, o)
f(n-1, s, o, t)
操作: 將 n 從 s 移到 t
f(n-1, o, t, s)
void rec(int n, char from, char to, char other) {
if (n == 0) return ;
rec(n-1, from, other, to);
printf("Move ring %d from %c to %c\n", n, from, to);
rec(n-1, other, to, from);
}def rec(n, source, target, other):
if n == 0: return
rec(n-1, source, other, target)
print(f"Move ring {n} from {source} to {target}\n")
rec(n-1, other, target, source)
C++
Python
遞迴的複雜度分析
!數學警告!
遞迴的複雜度分析
假設你學會了時間複雜度...
不覺得遞迴的時間複雜度好像看不出來嗎?
來上點難度吧!
def f(n):
if n == 0:
return
f(n-1)這段程式碼的時間分析大概就長這樣
遞迴的複雜度分析
假設你學會了時間複雜度...
來上點難度吧!
遞迴的複雜度分析
來更難的吧!
遞迴的複雜度分析
遞迴的複雜度分析
遞迴的複雜度分析
這種函式的程式碼大概長這樣
f(l, r):
if l+1 == r:
return
m = (l + r) / 2
f(l, m)
f(m, r)遞迴的複雜度分析
遞迴的複雜度分析
遞迴的複雜度分析
遞迴的複雜度分析 - 常見統整
合併排序
Merge Sort
給定兩個已排序數列 <A_n>, <B_m>,
請把它合併成一個排序好的序列。
合併排序 Merge Sort - Merge
在講排序之前,我們先來思考這個問題:
A+B
1
2
3
4
5
6
7
8
1
3
4
6
A
2
5
7
8
B
給定兩個已排序數列 <A_n>, <B_m>,
請把它合併成一個排序好的序列。
合併排序 Merge Sort - Merge
在講排序之前,我們先來思考這個問題:
1
3
4
6
A
2
5
7
8
B
小樣!直接 call sort 不就好了嗎?
有更好複雜度的做法!想想看吧!
給定兩個已排序數列 <A_n>, <B_m>,
請把它合併成一個排序好的序列。
合併排序 Merge Sort - Merge
在講排序之前,我們先來思考這個問題:
1
3
4
6
A
2
5
7
8
B
A+B
1
2
3
4
5
6
7
8
看 A,B 最前面的兩個數字,誰最小誰就表示整個最小。
給定兩個已排序數列 <A_n>, <B_m>,
請把它合併成一個排序好的序列。
合併排序 Merge Sort - Merge
在講排序之前,我們先來思考這個問題:
vector<int> merge(vector<int> &A, int Al, int Ar,
vector<int> &B, int Bl, int Br){
vector<int> C;
while (Al < Ar || Bl < Br) {
if (Bl == Br || Al < Ar && A[Al] < B[Bl])
C.push_back(A[Al++]);
else
C.push_back(B[Bl++]);
}
return C;
}from collections import deque
def merge(A, B):
A, B = deque(A), deque(B)
C = []
while A or B:
if not B or A and A[0] < B[0]:
C.append(A.popleft())
else:
C.append(B.popleft())
return CC++
Python
看 A,B 最前面的兩個數字,誰最小誰就表示整個最小。
用兩個指針維護
用兩個deque維護
合併排序 Merge Sort
- 函式定義:
f(A) = 將陣列 A 排序。
這樣好像...沒法拆?
如果硬要這樣遞迴,
那麼你需要「真的」拆這個陣列。
讓我們來想想看這要怎麼排序吧!
Merge Sort 的核心概念
利用遞迴 + 每次將問題拆一半來排序。
合併排序 Merge Sort
- 函式定義:
f(A) = 將陣列 A 排序。
Merge Sort 的核心概念
利用遞迴 + 每次將問題拆一半來排序。
為了有效率處理,
我們通常會用兩個數字 [l, r)
表示處理 [l, r) 區間。
[l, r) = 左閉右開,
包含左界不包含右界
f(A, l, r) = 將陣列的 A[l:r] 排序。
讓我們來想想看這要怎麼排序吧!
f(A, 3, 7) = 將陣列的 A[3:7] 排序。
A[l] ~ A[r-1]
A[3] ~ A[6]
合併排序 Merge Sort
- 函式定義:
- 如何拆解:
f(A, l, r) = 將陣列的 A[l:r] 排序。
拆一半排序?就是先各自排序左半邊跟右半邊
Merge Sort 的核心概念
利用遞迴 + 每次將問題拆一半來排序。
A
希望 m-l 會等於 r-m,這樣才可以切一半
中點公式(?) :
合併排序 Merge Sort
- 函式定義:
- 如何拆解:
f(A, l, r) = 將陣列的 A[l:r] 排序。
拆一半排序?就是先各自排序左半邊跟右半邊
Merge Sort 的核心概念
利用遞迴 + 每次將問題拆一半來排序。
A
排序 A[2, 3, 4, 5] -> [l=2, r=6), m=4 -> [2, 4) + [4, 6)
排序 A[2, 3, 4] -> [l=2, r=5), m=3 -> [2, 3) + [3, 5)
舉例來說:
合併排序 Merge Sort
- 函式定義:
- 如何拆解:
- Base Case:
f(A, l, r) = 將陣列的 A[l:r] 排序。
f(A, l, r) 要做的事情
- 排序左半邊: f(A, l, m)
- 排序右半邊: f(A, m, r)
- 想辦法排序 A[l:r]。
- 兩邊都是排序好的要排序? 好像講過!
Merge Sort 的核心概念
利用遞迴 + 每次將問題拆一半來排序。
拆一半排序?就是先各自排序左半邊跟右半邊
(你呼叫 f(A, l, r) 就會無窮遞迴)
只剩一個元素的時候:
l+1 = r
合併排序 Merge Sort - 實作
f(A, l, r): Merge sort A[l:r]
- 排序左半邊: f(A, l, m)
- 排序右半邊: f(A, m, r)
- Merge 左半邊跟右半邊
vector<int> merge(vector<int> &A, int Al, int Ar,
vector<int> &B, int Bl, int Br){
vector<int> C;
while (Al < Ar || Bl < Br) {
if (Al == Ar || Bl < Br && B[Bl] < A[Al])
C.push_back(B[Bl++]);
else
C.push_back(A[Al++]);
}
return C;
}from collections import deque
def merge(A, B):
A, B = deque(A), deque(B)
C = []
while A or B:
if not B or A and A[0] < B[0]:
C.append(A.popleft())
else:
C.append(B.popleft())
return CC++
Python
def merge_sort(A, l, r):
if l+1 == r: return
m = (l+r) // 2
merge_sort(A, l, m)
merge_sort(A, m, r)
A[l:r] = merge(A[l:m], A[m:r])void merge_sort(vector<int> &A, int l, int r) {
if (l+1 == r) return;
int m = (l+r) / 2;
merge_sort(A, l, m);
merge_sort(A, m, r);
auto tmp = merge(A, l, m, A, m, r);
copy(tmp.begin(), tmp.end(), &A[l]);
}(C++其實有內建的Merge)
合併排序 Merge Sort - 遞迴樹狀圖
f(A, l, r): Merge sort A[l:r]
- 排序左半邊: f(A, l, m)
- 排序右半邊: f(A, m, r)
- Merge 左半邊跟右半邊
[0, 9)
目標:排序9個元素
m = 4
[0, 4)
m = 2
[4, 9)
m = 6
[0, 2)
[0, 1)
[1, 2)
[2, 4)
[2, 3)
[3, 4)
[6, 9)
[4, 5)
[5, 6)
[4, 6)
[6, 7)
[7, 9)
m = 8
[7, 8)
[8, 9)
m = 2
m = 3
m = 5
m = 7
⭕
⭕
⭕
⭕
⭕
⭕
⭕
⭕
合併排序 Merge Sort - 視覺化
看一下 Merge Sort 的視覺化吧!
合併排序 Merge Sort - 複雜度
f(A, l, r): Merge sort A[l:r]
- 排序左半邊: f(A, l, m)
- 排序右半邊: f(A, m, r)
- Merge 左半邊跟右半邊
如果你很懶得 Merge,直接 Call Sort
不過你都Call Sort 了,直接 Sort 整個陣列不就好了(?)
練習題
- 拆成兩個排序的 Merge Sort 是 n log n。
如果拆成k個呢?- 現在有k個排序好的序列,要怎麼merge?
- 整體複雜度會變得怎麼樣?
- Quick Sort 的時間複雜度?
f(A, l, r): Quick Sort A[l:r]
- 隨機在 A[l:r] 中找一個數字 Pivot。
- 把 Pivot 小的放左邊,
把 Pivot 放中間, (假設 Pivot 在 m 的位置上)
然後把 Pivot 大的放右邊。 - f(A, l, m)
- f(A, m, r)
逆序數對
Inversion Pair
給定一個數列 <A_n>,
請問有多少對 (i, j) 滿足以下條件:
- 函式定義:
- 如何拆解:
- Base Case:
....?
這題老實說直接想是很難想出來的。
我們先來亂拆看看吧!
逆序數對 Inversion
| 1 | 5 | 2 | 7 | 0 | 9 | 3 | 8 | 4 | 6 |
|---|
A
f(n) = f(n-1) + A_n 跟前面數字的逆序數對
跟裸做一樣😭
逆序數對 Inversion
| 1 | 5 | 2 | 7 | 0 | 9 | 3 | 8 | 4 | 6 |
|---|
A
如果每次切一半有辦法更好嗎...?
如果我們考慮左邊跟右邊,
那麼逆序數對會有三種可能:
- 都在左側的逆序數對
- 都在右側的逆序數對
- 在兩側的逆序數對
怎麼定義函式?
逆序數對 Inversion
| 1 | 5 | 2 | 7 | 0 | 9 | 3 | 8 | 4 | 6 |
|---|
A
暴力搜尋兩側逆對:
想這麼多還是跟裸做一樣😭
逆序數對 Inversion
想這麼多還是跟裸做一樣😭
等等!如果兩側都是排序好的呢?
| 0 | 1 | 2 | 5 | 7 |
|---|
| 3 | 4 | 6 | 8 | 9 |
|---|
L
R
你想得出來怎麼更有效率的做嗎?
逆序數對 Inversion
想這麼多還是跟裸做一樣😭
等等!如果兩側都是排序好的呢?
| 0 | 1 | 2 | 5 | 7 |
|---|
| 3 | 4 | 6 | 8 | 9 |
|---|
L
R
從 L 的每個元素看:
我們目標是要找到 R 有幾個元素比 L 還要小
二分搜!
好像很有機會喔?
逆序數對 Inversion
想這麼多還是跟裸做一樣😭
等等!如果兩側都是排序好的呢?
def f(l, r):
- 算出沒有交叉的逆對 f(l, m) + f(m, r)
- 排序 [l, m) 以及排序 [m, r)
- 二分搜交叉的逆對
逆序數對 Inversion
想這麼多還是跟裸做一樣😭
等等!如果兩側都是排序好的呢?
| 0 | 1 | 2 | 5 | 7 |
|---|
| 3 | 4 | 6 | 8 | 9 |
|---|
L
R
再等等!
好像有更好的算法!
你會發現指到的地方
永遠是遞增的!
→雙指針
逆序數對 Inversion
等等!如果兩側都是排序好的呢?
| 0 | 1 | 2 | 5 | 7 |
|---|
| 3 | 4 | 6 | 8 | 9 |
|---|
L
R
→雙指針
l
r
r
r
r
l
l
l
l
+0
+0
+0
+2
+3
逆序數對 Inversion
=5
def f(l, r):
- 算出沒有交叉的逆對 f(l, m) + f(m, r)
-
- 排序 [l, m) 以及排序 [m, r)
- 二分搜交叉的逆對
如果你做 Merge Sort 就不用排序
逆序數對 Inversion
逆序數對 - 變形
幼稚園 (TOI 2020/08 - 8 新手賽)
幼稚園 (TOI 2020/08 - 8 新手賽)
給定一個數列 A,
你可以交換A中任兩相鄰數。
請問最少交換幾次才可使數列滿足
「遞增」或「遞減」或「先遞增再遞減」?
好像有點困難?
我們先換成簡單版的題目:
(弱化版原題)
給定一個數列 A,
你可以交換A中任兩相鄰數。
請問最少交換幾次才可使數列「遞增」?
(非嚴格)
(弱化版原題) 給定一個數列 A,
你可以交換A中任兩相鄰數。
請問最少交換幾次才可使數列「遞增」?
2
3
1
考量三個數字
交換一個相鄰的逆對
2
3
1
逆序數對會 - 1
幼稚園 (TOI 2020/08 - 8 新手賽)
(弱化版原題) 給定一個數列 A,
你可以交換A中任兩相鄰數。
請問最少交換幾次才可使數列「遞增」?
交換一個相鄰的逆對
逆序數對會 - 1
遞增數列逆序數對是 0
最少交換次數 =
A的逆序數對
這也就是說:如果你對 A 做泡沫排序,
交換的次數 = A 的逆序數對
如果使數列「遞減」呢?
幼稚園 (TOI 2020/08 - 8 新手賽)
給定一個數列 A,你可以交換A中任兩相鄰數。
問最少交換幾次才可使數列滿足
「遞增」或「遞減」或「先遞增再遞減」?
考慮 A 裡面的一個數字 x,
那麼 x 的最終歸屬只有兩種可能。
A
x
x
x
將 x 往右所需交換次數:x 往右看的順序數對
將 x 往左所需交換次數:x 往左看的逆序數對
幼稚園 (TOI 2020/08 - 8 新手賽)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void rec(vector<int> &inv, vector<pair<int, int>> &A, int l, int r) {
if (l+1 == r) return;
int m = (l + r) / 2;
rec(inv, A, l, m);
rec(inv, A, m, r);
int pr = m;
for (int pl = l; pl < m; pl++) {
while(pr != r && A[pl].first >= A[pr].first) pr++;
inv[A[pl].second] += r-pr;
}
vector<pair<int, int>> tmp(r-l);
merge(&A[l], &A[m], &A[m], &A[r], tmp.begin());
copy(tmp.begin(), tmp.end(), &A[l]);
}int main() {
int n, x;
scanf("%d", &n);
vector<pair<int, int>> A;
for (int i=0; i<n; i++) {
scanf("%d", &x);
A.push_back({x, i});
}
auto B = A;
reverse(B.begin(), B.end());
vector<int> inv_f(n), inv_b(n);
rec(inv_f, A, 0, n);
rec(inv_b, B, 0, n);
int ans = 0;
for (int i=0; i<n; i++)
ans += min(inv_f[i], inv_b[i]);
printf("%d\n", ans);
return 0;
}Karatsuba 大數乘法
APCS 不會考,純介紹性質 :)
大數乘法
實作 A * B,
但數字很大。

小學直式乘法!
陣列 A
陣列 B
陣列 C
好慢...
大數乘法
實作 A * B,
但數字很大。
嘗試切一半!
A_L
A_R
B_R
B_L
A_R * B_R
A_L * B_R
A_R * B_L
A_L * B_L
大數乘法
實作 A * B,
但數字很大。
嘗試切一半!
在做 A*B 的大數乘法的時候,
會需要做四次的一半的乘法
跟裸做一樣😭
大數乘法
實作 A * B,
但數字很大。
A_L
A_R
B_R
B_L
A_R * B_R
A_L * B_R
A_R * B_L
A_L * B_L
四次乘法,一次加法→兩次加法,三次乘法,兩次減法
大數乘法
實作 A * B,
但數字很大。
四次乘法,一次加法→兩次加法,三次乘法,兩次減法
- f(A, B):
- 左邊的: f(A_L, B_L)
- 右邊的: f(A_R, B_R)
- 中間的: f(A_L + A_R, B_L + B_R) - 左邊的 - 右邊的
A_R * B_R
A_L * B_R
A_R * B_L
A_L * B_L
大數乘法 - 變形
APCS 不會考,純介紹性質 :)
我找不到好題目 :(
預計會是多項式乘法 + DP
分治小結
Title Text
- 矩陣乘法
- O(n) 中位數
逆對: 線段樹
https://tioj.ck.tp.edu.tw/problems/1232: 題目要求複雜度很低 (r, n le 10),但你可以做得很漂亮