Identification of Humpback Whales using Deep Metric Learning

Artsiom Sanakoyeu

PhD candidate, Computer Vision Group
Kaggle Master (45-th out of 113.000+)

Content

  1. Introduction
  2. Metric Learning Overview
  3. Sampling For Metric Learning

  4. Divide and Conquer the Embedding Space for Metric Learning (CVPR 2019)

  5. Kaggle Humpback Whale Identification Challenge

How to compare images?

How similar/dissimilar are these images?

How to compare images?

How to compare images?

Project images in d-dimensional Euclidean space where distances directly correspond to a measure of similarity

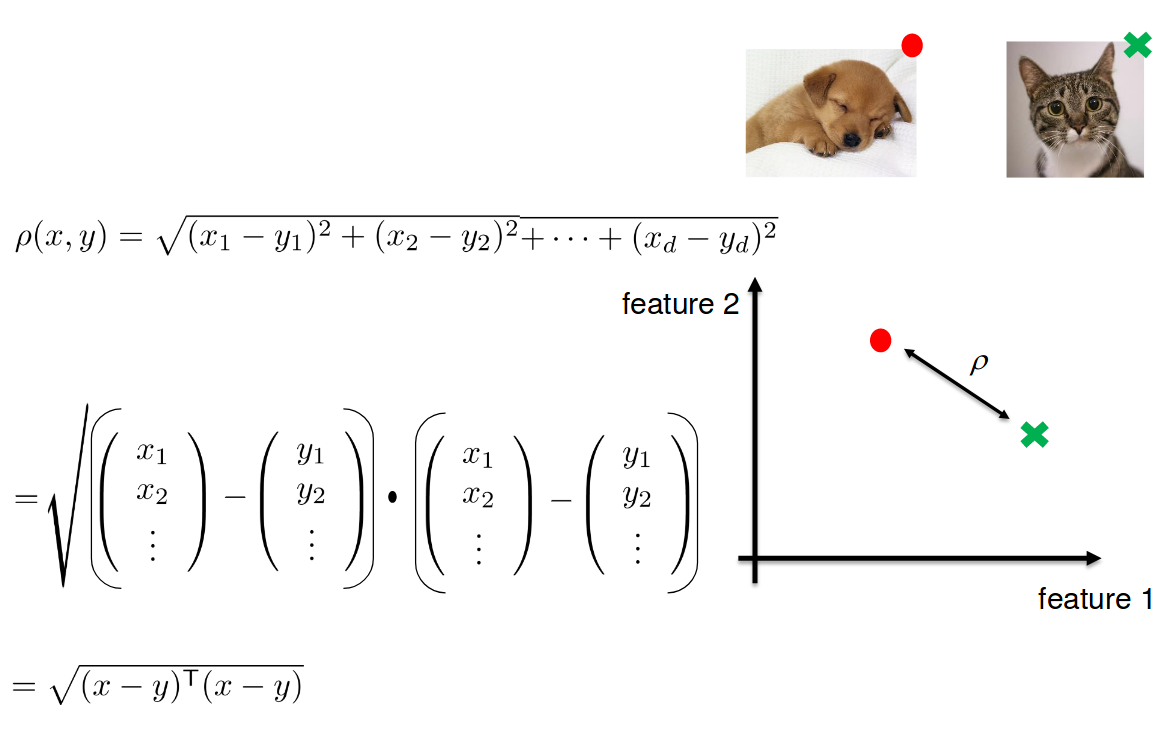
How to compare images?
Metric Learning

Basic idea: learn a metric that assigns small (resp. large) distance to pairs of examples that are semantically similar (resp. dissimilar).

Metric Learning

d-dimensional Embedding Space

How to compare images?
Metric Learning

Basic idea: learn a metric that assigns small (resp. large) distance to pairs of examples that are semantically similar (resp. dissimilar).

Metric Learning

d-dimensional Embedding Space

Small distance

How to compare images?
Metric Learning

Basic idea: learn a metric that assigns small (resp. large) distance to pairs of examples that are semantically similar (resp. dissimilar).

Metric Learning

d-dimensional Embedding Space

Large distance

Metric Learning Applications

Handwriting recognition

Person identification

Image Search

Metric Learning Applications

Deep Metric Learning (DML)

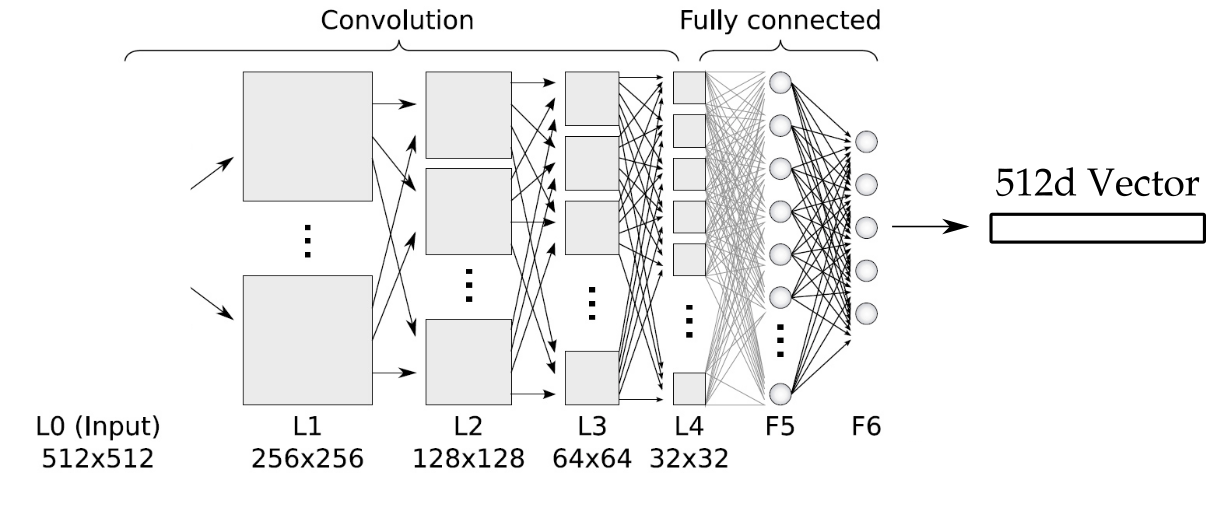
Project Image in d-dimensional space where Euclidean distance would make sense

Deep Metric Learning (DML)

  • Each layer to compose the representations of the previous layer to learn a higher level abstraction
  • Map from the image space into feature (embedding) space ℝd
    Pixels -> Edges -> Contours -> Object parts -> Embedding Space ℝd
  • Local Features -> Global Features

Training: Triplet Loss

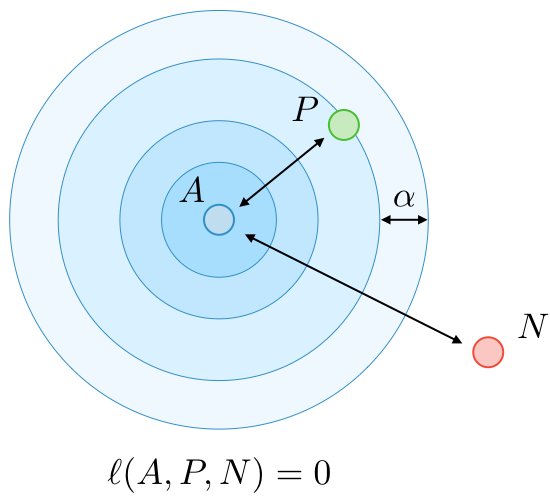
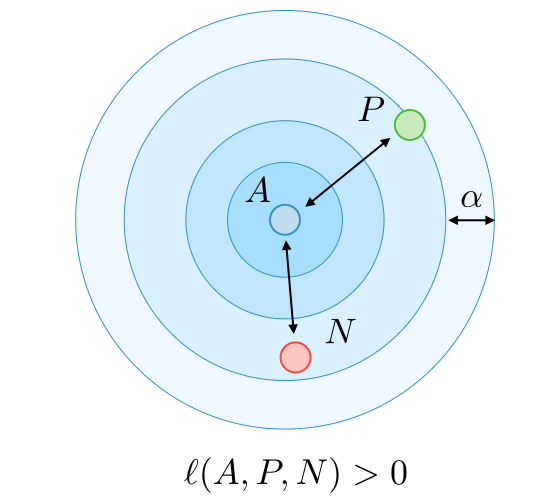
\boxed{\ell(A,P,N)=\max\left(d(A,P)-d(A,N)+\alpha,0\right)}

Courtesy: cs-230 course, Stanford University

A = Anchor

P = Positive

N = Negative

Training: Siamese Network

\boxed{\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)}

Ex: Learn a Distance Metric for Animals Dataset

Why sampling?

Leopard

Lion

Easy!

Why sampling?

Leopard

Jaguar

Difficult!

Why sampling?

Sampling Layer

N^3

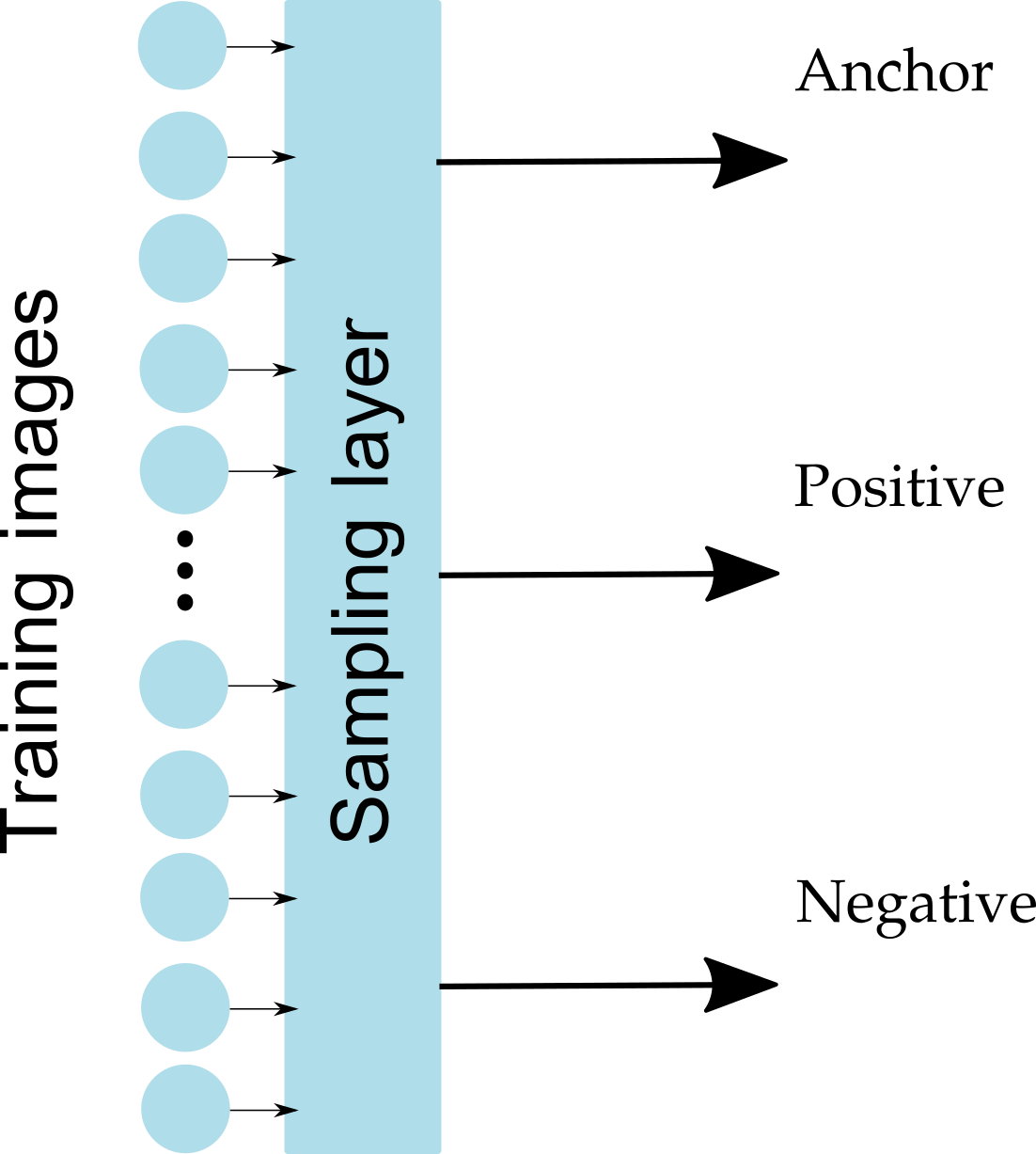
possible triplets in the dataset

Sample randomly?!
NO. Only small portion of all triplets is meaningful and has non-zero loss

Sampling Layer

N^3

possible triplets in the dataset

Sample randomly?!
NO. Only small portion of all triplets is meaningful and has non-zero loss

Sample only meaningful triplets!
 

It’s important to select “hard” triplets (which would contribute to improving the model) to use in training. How do we do that?

Hard Negative Sampling

Sample "hard" (informative) triplets, where loss > 0

Sampling must select different triplets as training progresses

\boxed{\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)}

Hard Negative Sampling

\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)
  • An idea: Given an anchor image A, select the “hardest” positive image (of the same class) as P (i.e. the one that’s furthest away in the dataset) and select the “hardest” negative image (of a different class) as N (i.e. the one that’s closest in the dataset).
     
  • Problem: Infeasible to compute these argmax and argmin across the whole dataset. Also this might lead to poor training (considering that mislabeled images and outliers would dominate the hard positives and negatives).
     
  • Solution: Generate triplets online.
    Select P     and N (argmax and argmin) from a mini-batch (not from the entire dataset) for each anchor A.

[*] FaceNet: A Unified Embedding for Face Recognition and Clustering, Schroff et al., 2015

Hard Negative Sampling

Hard triplet

\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)
\frac{\partial \ell(\cdot) }{\partial f(N)} = \frac{h_{AN}}{||h_{AN}||} w(\cdot)

1. Gradient with respect to negative example f(N) takes form of

 - some function

w(\cdot)

determines the gradient direction. 

Hard Negative Sampling

Hard triplet

\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)
\frac{\partial \ell(\cdot) }{\partial f(N)} = \frac{h_{AN} + {\color{red} z} }{||h_{AN} + {\color{red} z}||} w(\cdot)

1. Gradient with respect to negative example f(N) takes form of

determines the gradient direction. Dominated by noise if                 is too small

 - some function

w(\cdot)
||h_{AN}||

noise

||\mathrm{Cov} \nabla_{f(N)} \ell ||_{*}

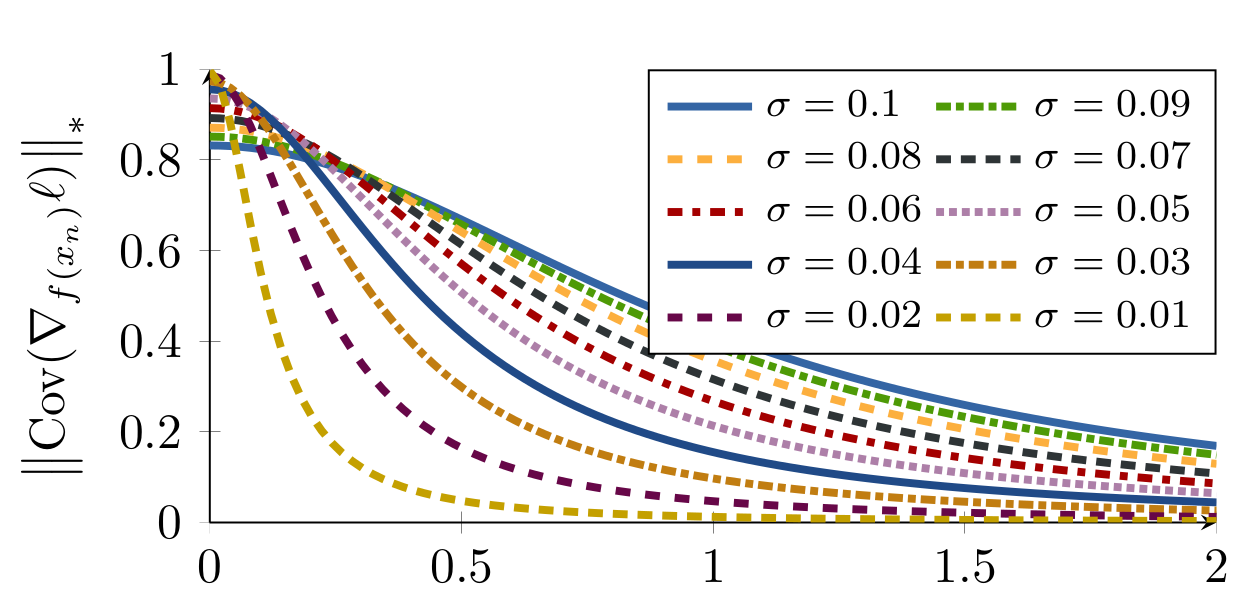
Variance of gradient at different noise levels

d(i, j)

Sampling Matters in Deep Embedding Learning, Wu et al., ICCV 2017

Hard Negative Sampling

Hard triplet

\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)

2. Selecting the hardest negatives can in practice lead to bad local minima early on in training, specifically it can result in a collapsed model (i.e. f(x) = 0) [1].

[1] FaceNet: A Unified Embedding for Face Recognition and Clustering, Schroff et al., 2015

Semi-hard Negative Sampling

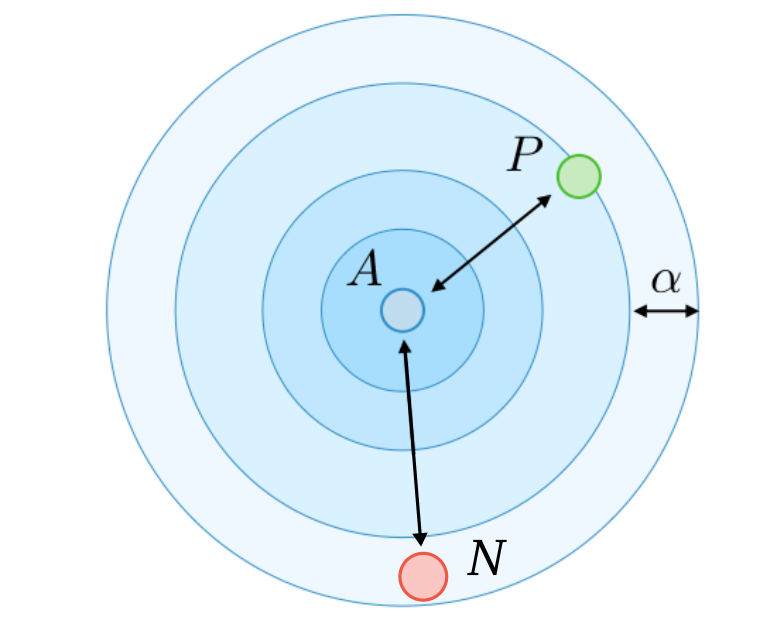
\boxed{\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)}
0 < \ell(A,P,N) \le \alpha

Semi-Hard triplet

Hard triplet

Semi-hard Negative Sampling

\boxed{\ell(A,P,N)=\max\left(d(f(A),f(P))-d(f(A),f(N))+\alpha,0\right)}
0 < \ell(A,P,N) \le \alpha

Semi-Hard triplet

Semi-hard Negative Sampling is not The Best

d(f(A), f(N))

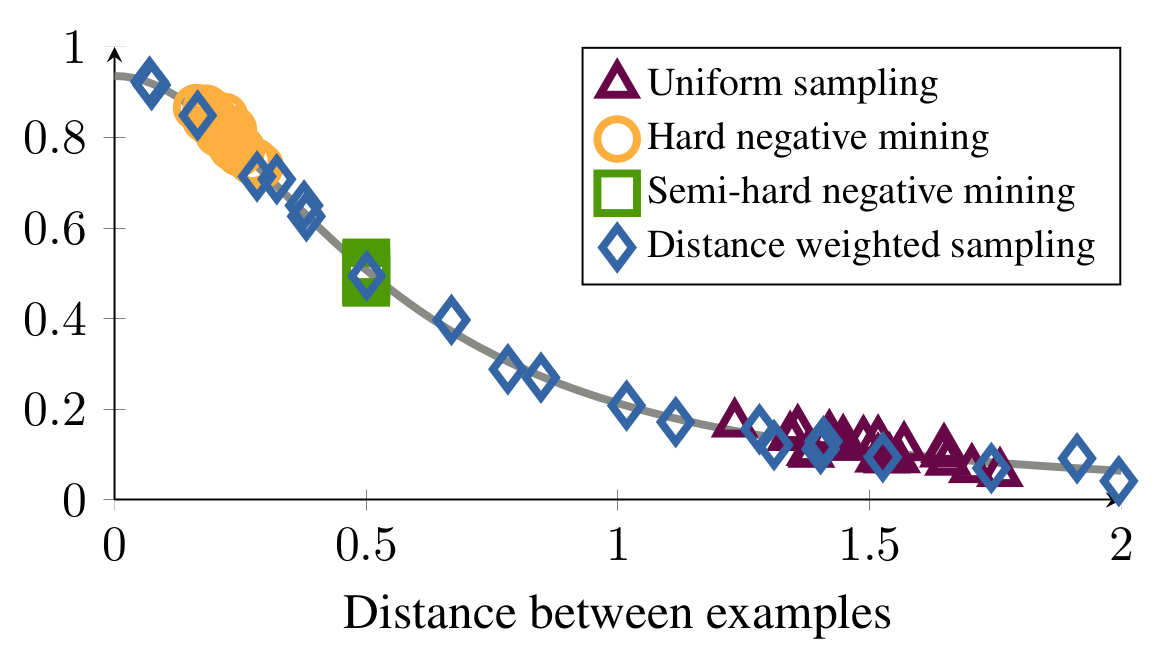
Fig. 2: Distribution of distances between anchor and negative for different  strategies

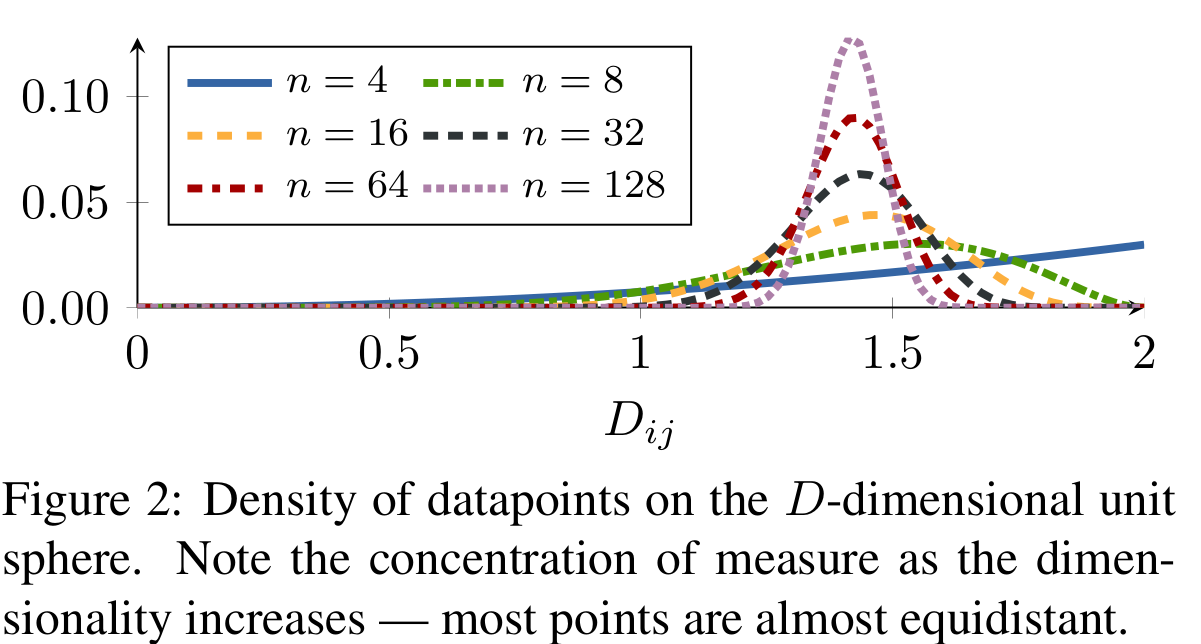
Fig. 1: Density of datapoints on the n-dimensional unit
sphere. Note the concentration of measure as the dimensionality increases — most points are almost equidistant.

d(i, j)

Variance of gradient

||\mathrm{Cov} \nabla_{f(N)} \ell ||_{*}
q(d)

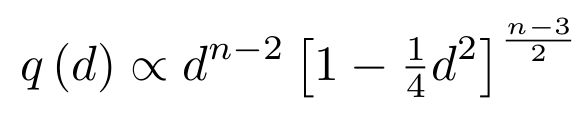
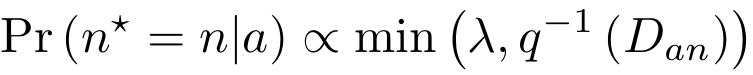
Distance weighted sampling

Sampling Matters in Deep Embedding Learning, Wu et al., ICCV 2017

Margin Loss

\beta \, \text{is learnable, per class}

Sampling Matters in Deep Embedding Learning, Wu et al., ICCV 2017

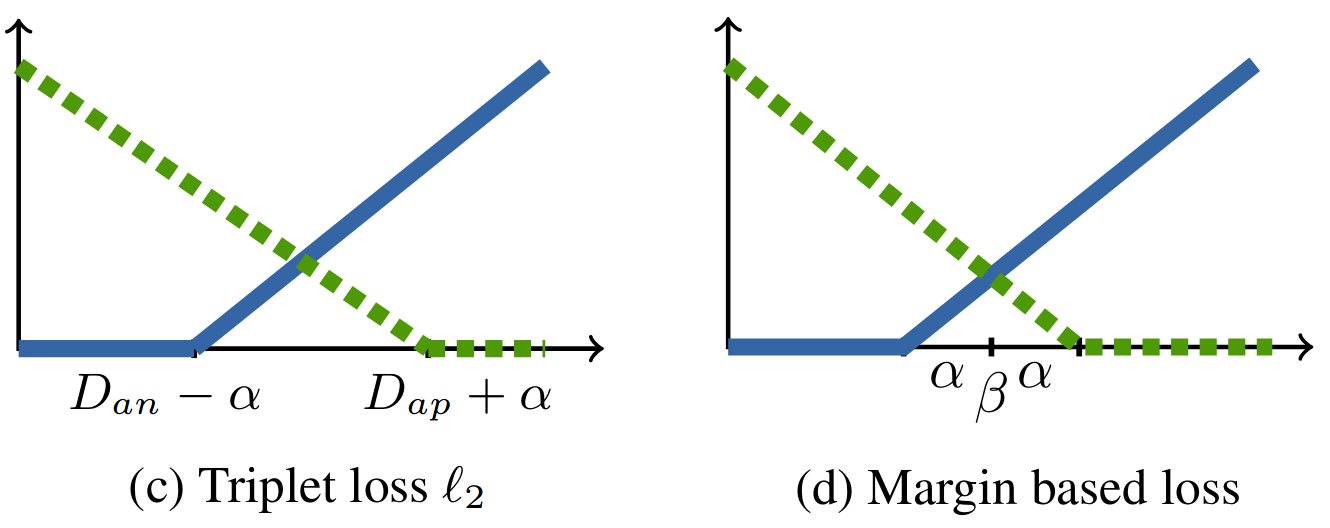
Triplet Loss

Loss for positive pairs

Loss for negative pairs

Triplet Loss

Margin Loss

Conclusion

To learn image similarities:

  1. Use Siamese Networks
  2. Triplet Loss / Margin Loss
  3. Triplets sampling (offline / online):
    - Hard negative mining
    - Semi-hard negative mining

Divide and Conquer the Embedding Space for Metric Learning

Artsiom Sanakoyeu*, Vadim Tschernezki*, Uta Büchler, Björn Ommer

CVPR 2019

Universal approximation theorem:
A feed-forward network with a single hidden layer containing a finite number of neurons can approximate continuous functions on compact subsets of R, under mild assumptions on the activation function — Wikipedia

 

In simple terms:  you can always come up with a deep neural network that will approximate any complex relation between input and output.

Motivation: Representational Power of Deep Neural Networks

IN PRACTICE: It is extremely difficult to get an optimal solution since the objective function is highly non-convex. We always get stuck in local optima.

~

Motivation: Data distribution is complex and multimodal

 

~

Motivation: Data distribution is complex and multimodal

 

Existing Approaches: Learn a single distance metric for all training data

→ Overfit and fail to generalize well.

~

Existing Approaches: Learn a single distance metric for all training data

→ Overfit and fail to generalize well.

To alleviate this problem: Learn several different distance metrics on non-overlaping subsets of the data.

Motivation: Data distribution is complex and multimodal

 

Method

 

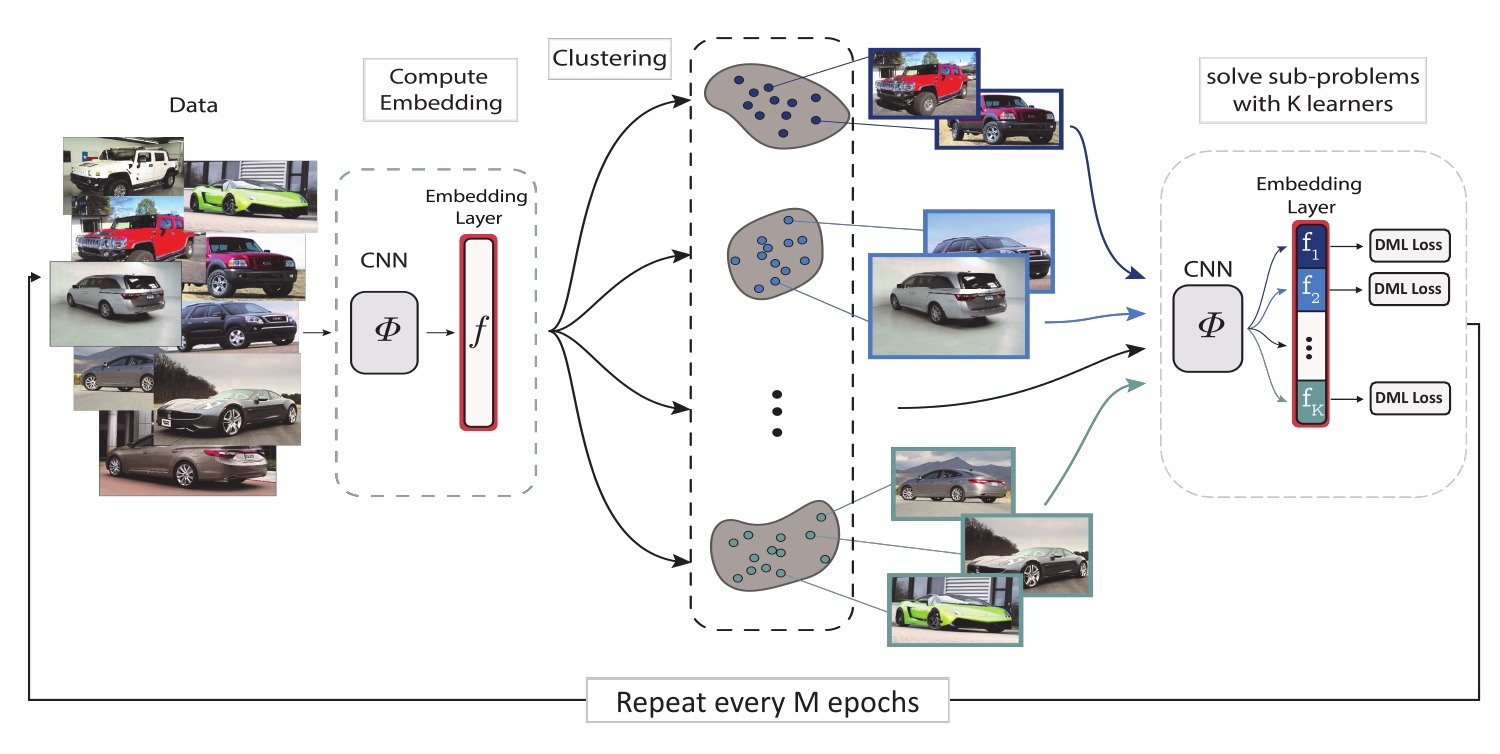
1. Compute embeddings for all train images

K clusters

2. Split the data into K disjoint subsets

Method

 

3. Split the embedding space in K subspaces of d/K dimensions each.

Split the embedding space in K subspaces

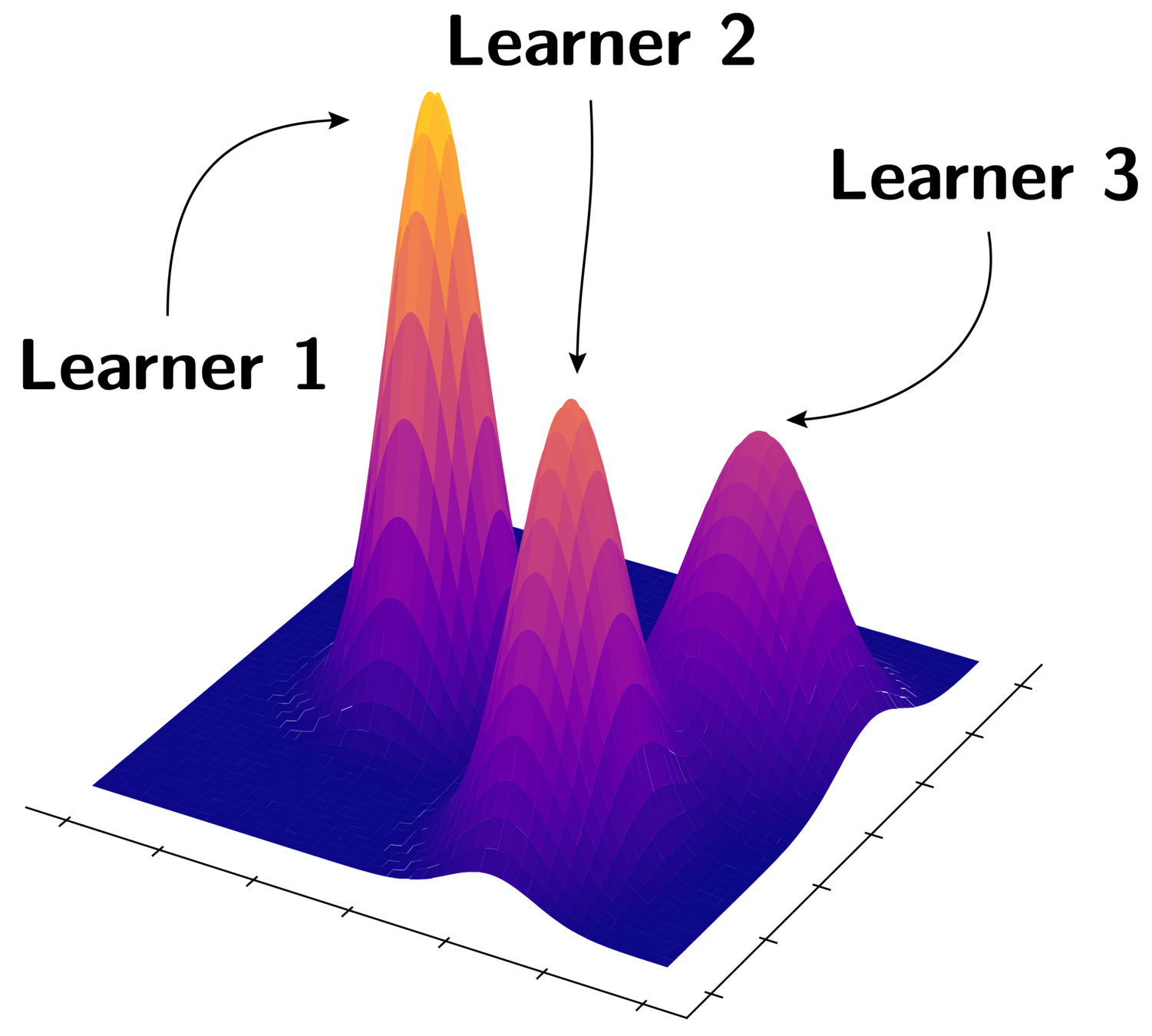
4. Assign a separate learner (loss) to each subspace.

Method

5. Train K different distance metrics using K learners.

K Learners

Method

 

6. Repeat every M epochs

Method: Summary

  1. Compute embeddings for all train images
  2. Split the data into K disjoint subsets

  3. Split the embedding space in K subspaces of d/K dimensions each.

  4. Assign a separate learner (loss) to each subspace.

  5. Train K different distance metrics using K learners.

  6. Repeat steps 1-5 every M epochs

Implicit Hard-negative Mining

Every learner is trained on the data within one cluster

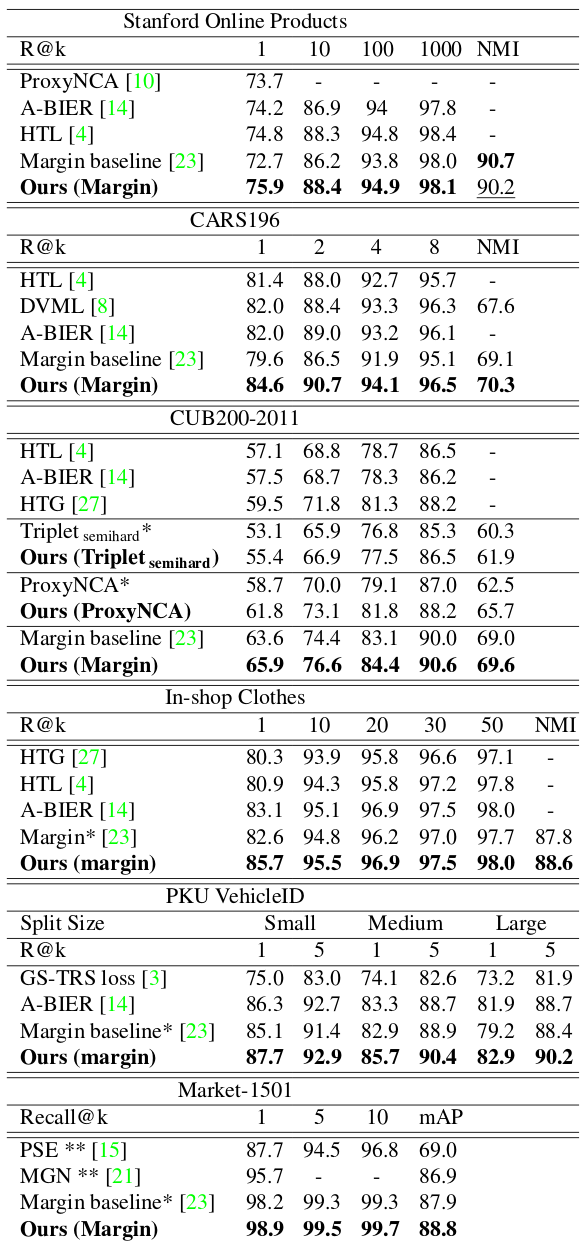
Comparison with SOTA

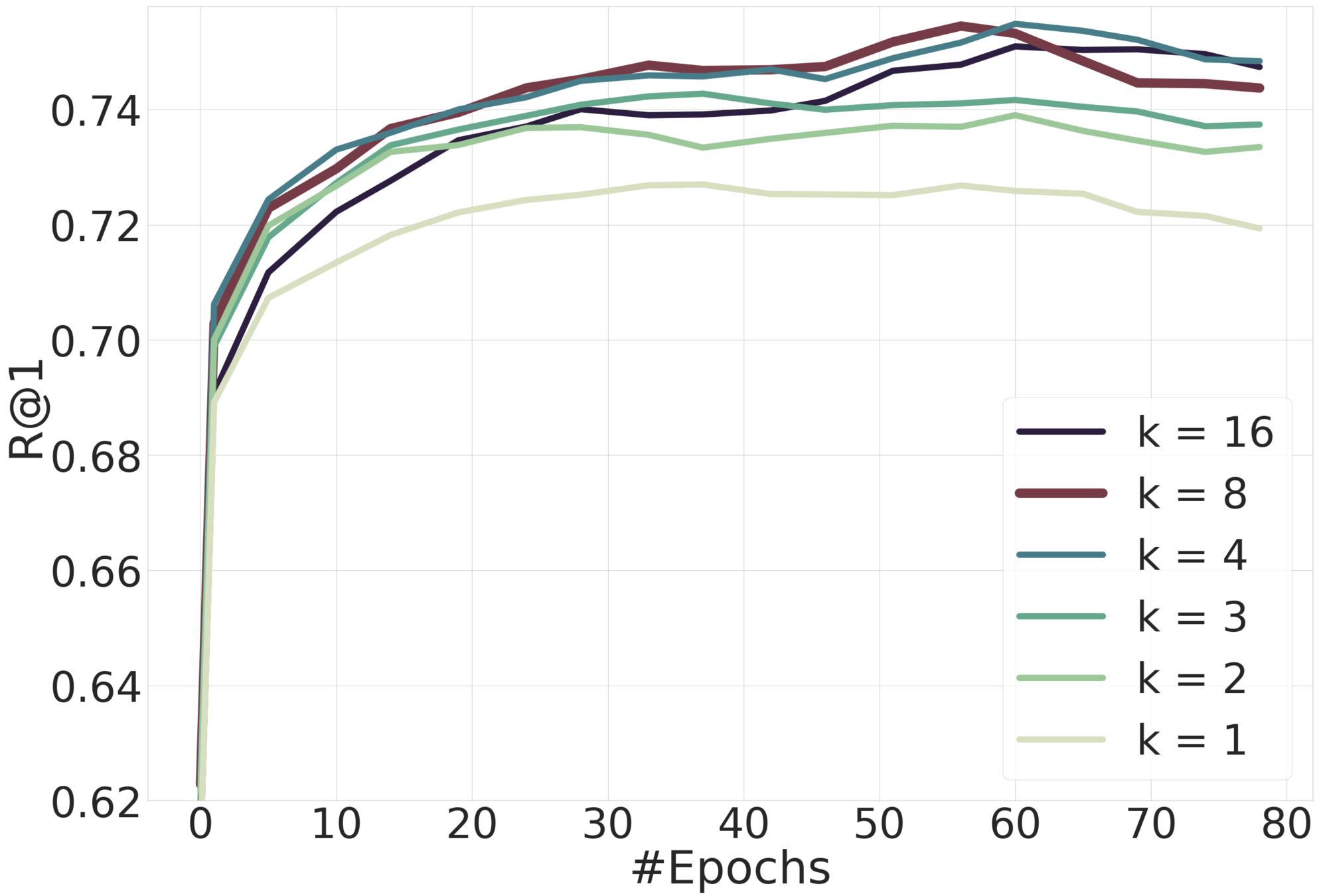
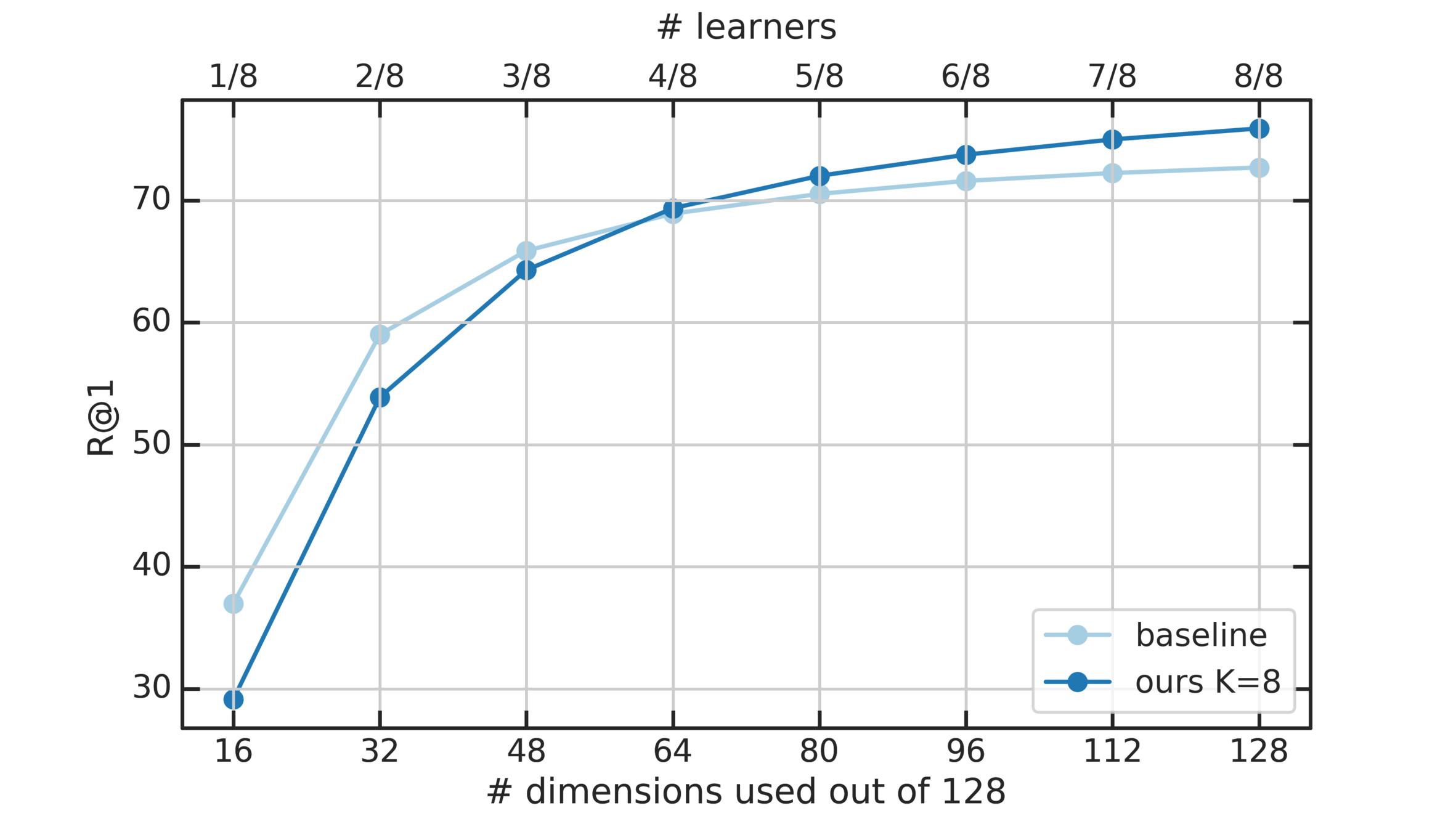
Let's Look at Learners

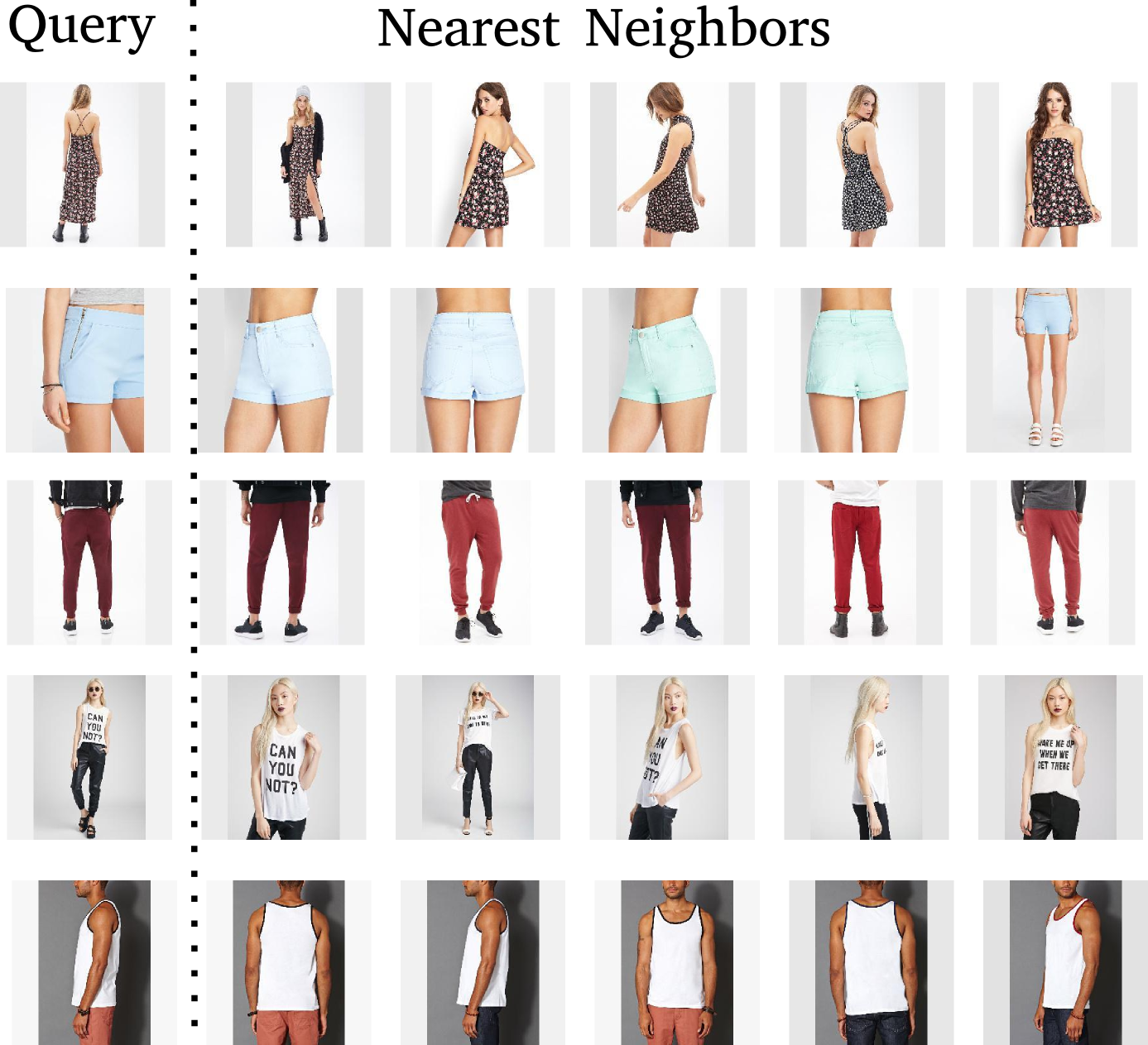
Qualitative results

Qualitative results

Conclusion

https://github.com/CompVis/metric-learning-divide-and-conquer

  1. Jointly split the data into K disjoint subsets and the embedding space in K subspaces of d/K dimensions each.
    Train K different distance metrics using K learners.
  2. Does not require network architecture change
  3. The proposed method can be applied to any metric learning loss function. 
  4. Achieves state-of-the art results on 6 benchmark datasets.
     

Humpback Whale Identification Challenge

Problem Overview

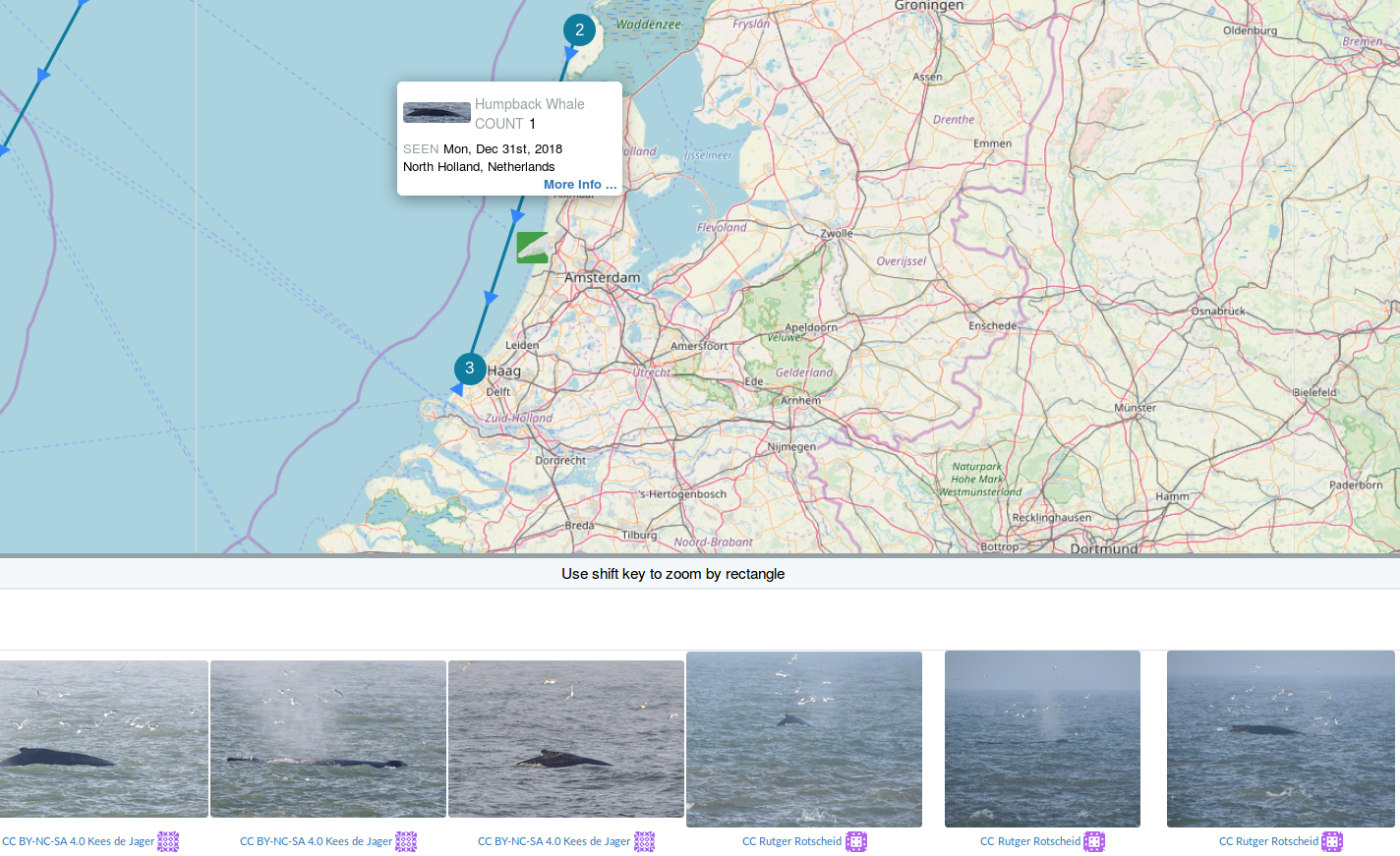
Can you identify a whale by its tail?

  • 2,131 Teams
  • $25,000 Prize Money
  • 3 Month Time

www.kaggle.com/c/humpback-whale-identification/

Which whale is it?

Oscar

Match!

Challenge Organizer

https://happywhale.com

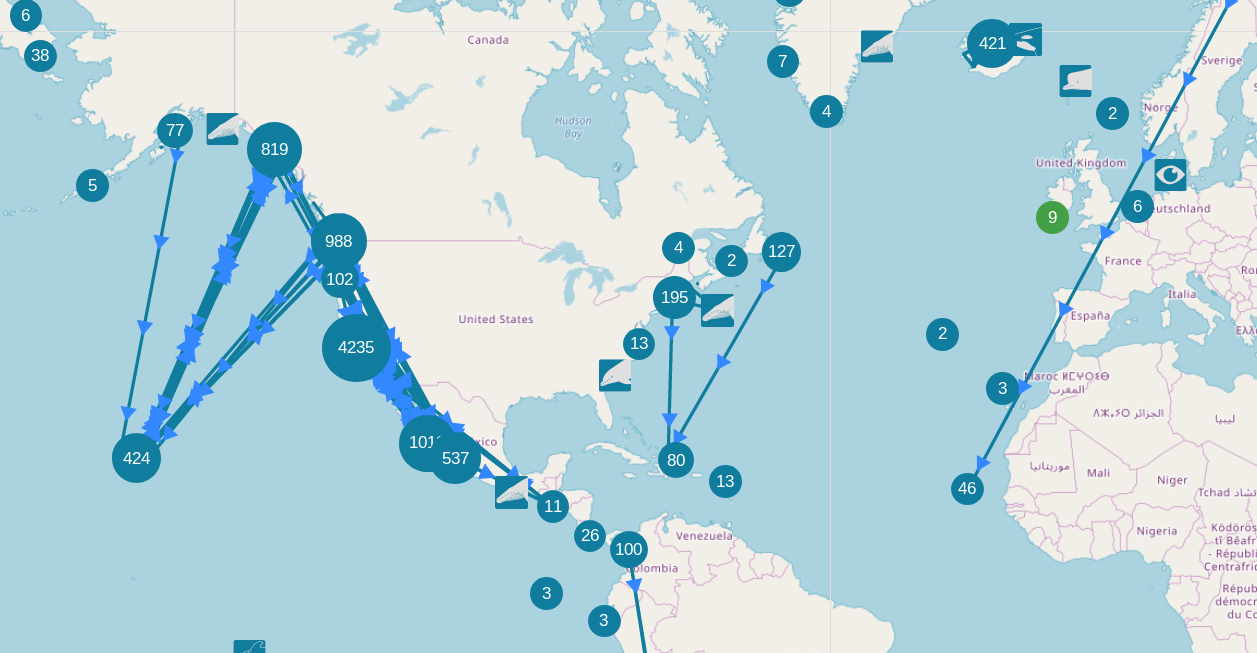
Happywhale engages citizen scientists to identify individual marine mammals, for fun and for science

They tracks your whales around the globe

Team

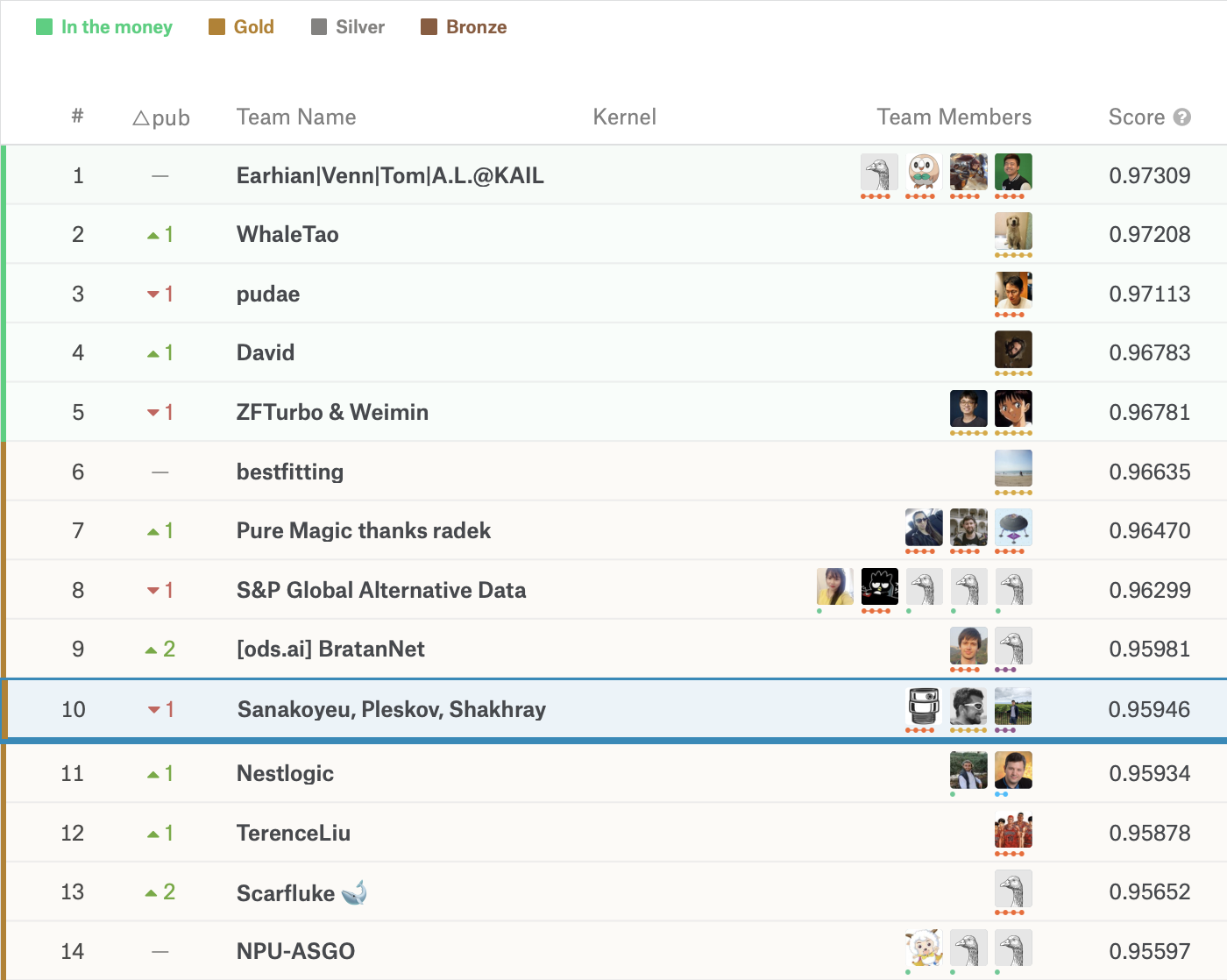
We finished #10 / 2131 Teams

Vladislav Shakhray
MIPT Student,
Russia

Artsiom Sanakoyeu
Me

Pavel Pleskov
Data Scientist at Point API
Russia

Open Data Science - Russian Speaking Data Science Community: ODS.ai

Data Overview

  • 5004 classes
  • 25.361 Train images
  • 7.960  Test images

Problem Overview

Identify among 5004 whale IDs or predict "new whale"

Query image

Find a match in the train set

Other train images

  • 5004 classes +
    "new whale"
    (yet unknown whales)
  • Highly imbalanced data
     
  • 25.361 Train images
  • 7.960   Test images
     
  • Public test / Private test = 20%/80%

Class size distribution

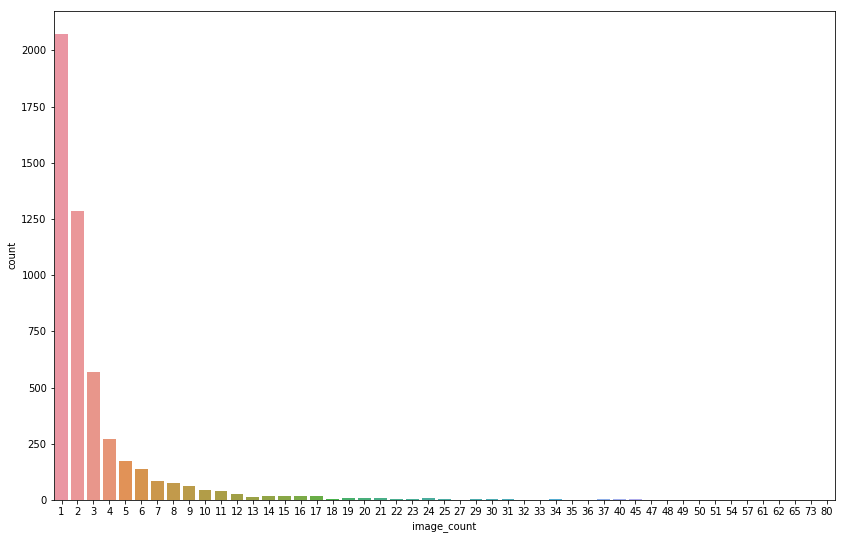
Data Overview

Evaluation Metric

MAP@5 = \frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{min(n,5)} P(k) \times rel(k)

Mean Average Precision @ 5

N is the number of images,
P(k) is the precision at cutoff k,
n is the number predictions per image,
rel(k) is an indicator function equaling 1 if the item at rank k is a relevant (correct) label, zero otherwise.

Validation and Preprocessing

  • Hold-out validation set (20% of Train)
  • Remove "new whale" from train
  • Train detector and detect flukes
  • Crop the flukes
  • Convert to black&white
  • Resize to square

Typical

Step 1: More layers!

Step 2: More Different Models!

????????

Step 3: PROFIT!!!

Our Models

A. Ensemble of:

  1. Two-stream Siamese Networks
  2. Three-stream Siamese Networks
  3. Total: 29 networks.

B.
Softmax classifier on top of features from 29 networks.

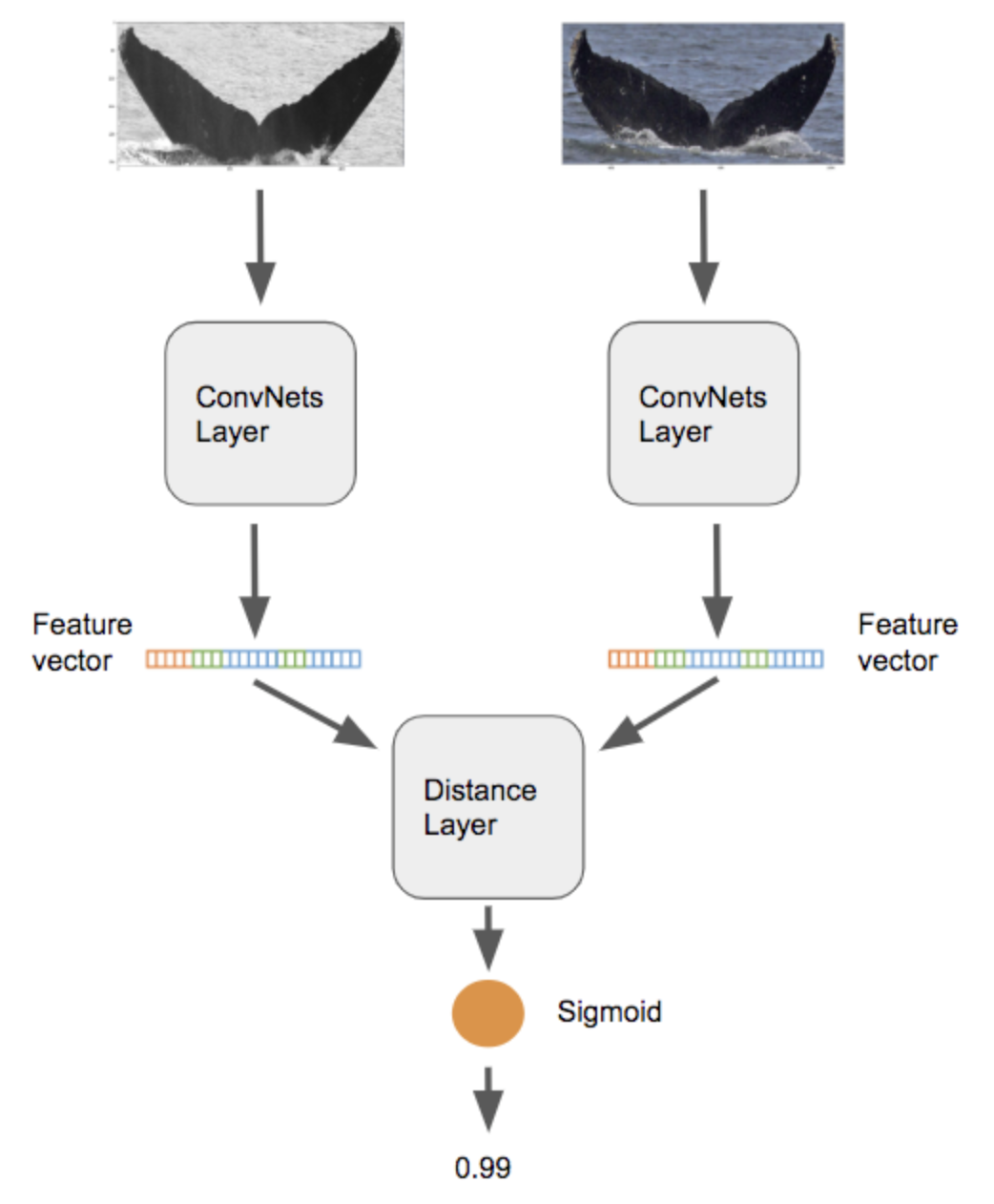
A1. Two-Stream Siamese Network

Backbones:

  • ResNet-18, ResNet-34, ResNet-50
  • SE-ResNeXt-50 (MAP@5=0.929)

 

Tricks:

  • Hard-negative, hard-positive mining
  • Progressive learning (299->384)
  • Adam, reduce 5 times on plateau
  • Batch size: 64
  • Test-time augmentations (TTA)

 

A1. Two-Stream Siamese Network: Augmentations

  • Smart flipping strategy
  • Gaussian noise, blur, brightness, contrast

A2. Three-Stream Siamese Network

Backbones:

  • ResNet (50, 101, 152),
    DenseNet (121, 169)
  • Best single model:
    DenseNet-169 (MAP@5=0.931)

 

Tricks:

  • Margin loss
  • Progressive learning (448->672)
  • Hard-negative mining
  • Adam, batch size 96
  • Random flips +
    Color augmentations
  • Inference: dot product

 

“Divide and Conquer the Embedding Space for Metric Learning”, Sanakoyeu et al., In CVPR 2019

B. Softmax Classifier on Aggregated Features

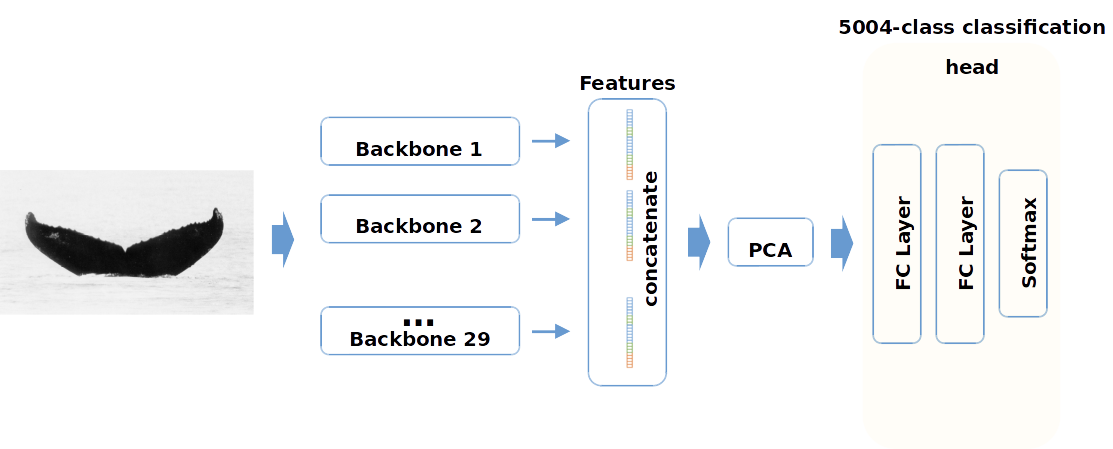
MAP@5=0.924 LB

~12.000 dim

2048 dim

B. Softmax Classifier on Aggregated Features

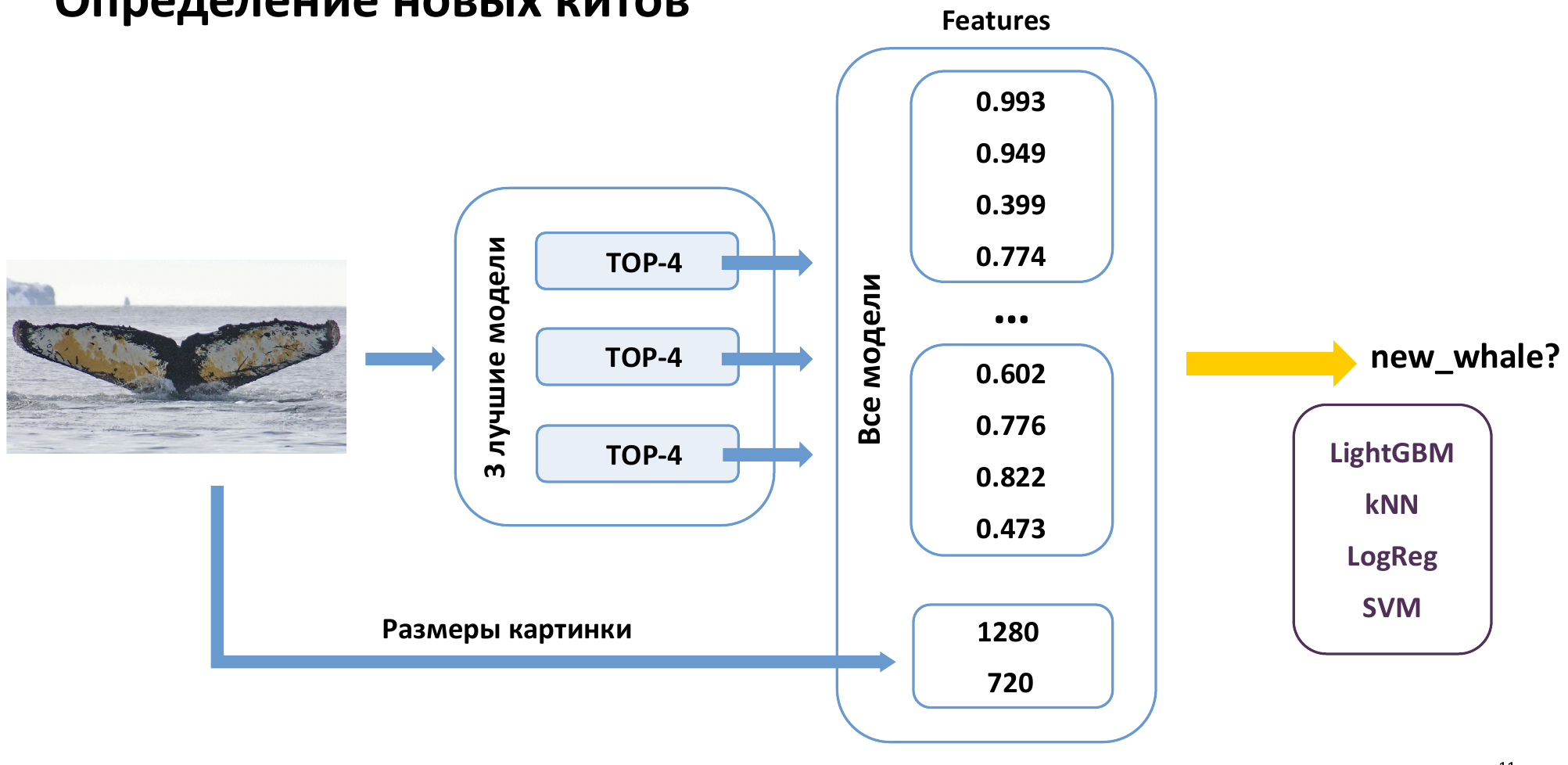
Image size

3 Best models

class probabilities

Extra Tricks

  • The backbones were ImageNet-pretrained
  • Pseudo-labeling (semi-supervised learning) helped:
      1. Impute labels for test images using the best ensemble
      2. Add test images from the previous step in train and retrain models.

Conclusion

  1. Finished #10 out out 2131 Teams -> Gold medal
  2. Final ensemble on private test: MAP@5=0.959
  3. Had a lot fun and polished practical skills
  4. Blog post: https://towardsdatascience.com/a-gold-winning-solution-review-of-kaggle-humpback-whale-identification-challenge-53b0e3ba1e84

Thank you!

@asanakoy

@artsiom_s

https://github.com/CompVis/metric-learning-divide-and-conquer

Slides:      https://slides.com/asanakoy/metric-learning-kaggle-whales

Made with Slides.com