Flow

Lecturer: 22527 Brine

我是誰

22527 鄭竣陽
Brine
BrineTW#7355
  • 建中資訊參伍 學術長
  • 建中電研肆貳 學術
  • 為了排版走火入魔
  • 想學網路流所以當網路流講師
  • 大家的偶像
  • 名詞定義
 
Index
  • 例題
  • 最大流問題
  • MFMC 定理
  • 最大流演算法
  • 例題講解
  • 最小費用流
  • 例題
  • Ford-Fulkerson
  • Dinitz(Dinic)
  • Push-Relabel
  • Edmond-Karp
  • 模板區

有用的學習資源

Glossary

名詞定義

Flow

  • 什麼是「Flow」？
    • 一張很猛的 Warframe MOD
    • 人類一種完全沉浸（專注）和完全投入於活動本身的心智狀態
    • 不要瞎掰好嗎

Flow Network

  • 又稱 Capacity Graph（容量圖）
  • 一張帶權有向圖 \(G(V,E)\)
    • 每個邊有一非負權重 \(c(u, v) \ge 0\) 代表容量
      • \((u, v) \notin E \rightarrow c(u,v) = 0\)
0
1
2
5
3
4
0/5
0/4
0/5
0/2
0/3
0/6
0/2
0/1

s-t Flow

  • 有一入度為 \(0\) 之點 \(s\) 和一出度為 \(0\) 之點 \(t\)
2
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1
0
1
2
5
3
4

s-t Flow

  • 有一入度為 \(0\) 之點 \(s\) 和一出度為 \(0\) 之點 \(t\)
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

s-t Flow

  • 有一入度為 \(0\) 之點 \(s\) 和一出度為 \(0\) 之點 \(t\)
  • 定義 \(f(u, v)\) 為 \((u, v)\) 上的流函數，其滿足：
    • 流量限制：\(\forall (u, v) \in V \times V, f(u, v) \le c(u, v)\)
    • 流量對稱：\(\forall (u, v) \in V \times V, f(u, v) = -f(v, u)\)
    • 流量守恆：\(\forall u\in V - \{s, t\}, \displaystyle \sum_{v \in V} f(u, v) = 0\)
s
t
2/5
2/4
2/2
0/5
4/5
3/3
1/6
1/1
1
2
3
4

s-t Flow

  • 定義一個流函數的值 \(|f|\) 到匯點 \(t\) 的流量和
    • \(|f| = \displaystyle \sum_{u \in V} f(u, t)\)
s
t
2/5
2/4
2/2
0/5
4/5
3/3
1/6
1/1
1
2
3
4

s-t Flow

  • 定義一個流函數的值 \(|f|\) 到匯點 \(t\) 的流量和
    • \(|f| = \displaystyle \sum_{u \in V} f(u, t)\)
    • \(|f| = \displaystyle \sum_{v \in V} f(s, v)\)
s
t
2/5
2/4
2/2
0/5
4/5
3/3
1/6
1/1
1
2
3
4

s-t Cut

  • 什麼是割（cut）？
    • 將一張圖的點集 \(V\) 分為 \(V_a, V_b\)
      • \(V_a \cup V_b = V\)
      • \(V_a \cap V_b = \varnothing\)
    • 得到一個割集（cut-set）
      • \(E_{cut}\) 為跨越 \(V_a, V_b\) 的邊集

s-t Cut

  • 什麼是割（cut）？
    • 將一張圖的點集 \(V\) 分為 \(V_a, V_b\)
      • \(V_a \cup V_b = V\)
      • \(V_a \cap V_b = \varnothing\)
    • 得到一個割集（cut-set）
      • \(E_{cut}\) 為跨越 \(V_a, V_b\) 的邊集
0
1
3
2
4

s-t Cut

  • 什麼是割（cut）？
    • 將一張圖的點集 \(V\) 分為 \(V_a, V_b\)
      • \(V_a \cup V_b = V\)
      • \(V_a \cap V_b = \varnothing\)
    • 得到一個割集（cut-set）
      • \(E_{cut}\) 為跨越 \(V_a, V_b\) 的邊集
0
1
3
2
4

s-t Cut

  • 什麼是割（cut）？
    • 將一張圖的點集 \(V\) 分為 \(V_a, V_b\)
      • \(V_a \cup V_b = V\)
      • \(V_a \cap V_b = \varnothing\)
    • 得到一個割集（cut-set）
      • \(E_{cut}\) 為跨越 \(V_a, V_b\) 的邊集
0
1
3
2
4

s-t Cut

0
1
3
2
4
  • 那什麼是一個 s-t cut 呢？

s-t Cut

  • 那什麼是一個 s-t cut 呢？
0
1
3
2
4

s-t Cut

  • 那什麼是一個 s-t cut 呢？
    • 將容量圖之點集 \(V\) 分割成兩子點集
      • \(s, t\) 分別在其中一個，標記為 \(S, T\)
      • 記作 \(C(S,T)\)
    • \(C(S,T)\) 的值為所有從 \(S\) 到 \(T\) 的邊之權和
      • \(\text{cut}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)

s-t Cut

  • \(\text{cut}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

s-t Cut

  • \(\text{cut}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

s-t Cut

  • \(\text{cut}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

s-t Cut

  • \(\text{cut}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

s-t Cut

  • \(\text{cut}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)
  • \(\text{flow}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} f(u, v) - \displaystyle \sum_{u \in S} \sum_{v \in T} f(v, u)\)
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

s-t Cut

  • \(\text{cut}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)
  • \(\text{flow}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} f(u, v) - \displaystyle \sum_{u \in S} \sum_{v \in T} f(v, u)\)
s
t
1
2
3
4
4/5
2/4
1/2
3/5
3/5
2/3
4/6
1/1
Maximum Flow

最大流問題

最大流問題

  • 給定一張容量圖 \(G(V, E)\)，求該圖上的最大流
  • 隨便流，流到不能流為止
    • 真的嗎？

最大 vs. 極大

  • 最大流 maximum flow
    • 若一個流 \(f\) 為最大，則不存在 \(f'\) 使得 \(|f'| > |f|\)
    • 沒有辦法以任何形式增加 \(|f|\)
  • 極大流 maximal flow
    • 若一個流 \(f\) 為極大，則不存在 \(f'\) 使得 \(|f'| > |f|\) 且：
      • \(\forall (u, v) \in V \times V, f'(u, v) \ge f(u, v)\)
    • 沒有辦法以當前的流為基礎下增加 \(|f|\) 
    • 蛤？

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
0/5
0/4
0/2
0/5
0/5
0/3
0/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
2/5
0/4
2/2
0/5
2/5
2/3
0/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
2/5
0/4
2/2
0/5
2/5
2/3
0/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
5/5
0/4
2/2
3/5
2/5
2/3
3/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
5/5
0/4
2/2
3/5
2/5
2/3
3/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
5/5
1/4
2/2
3/5
3/5
3/3
3/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
5/5
1/4
2/2
3/5
3/5
3/3
3/6
0/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
s
t
1
2
3
4
5/5
2/4
2/2
3/5
4/5
3/3
4/6
1/1

來看例子

  • 這是一張很好用的流量圖
    • 我們假設我們的演算法會優先填入字典序最小的流
    • 這樣是最大流嗎？
      • 顯然否，但這是極大流
    • 哪裡笨笨的？
s
t
1
2
3
4
5/5
2/4
2/2
3/5
4/5
3/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
2/4
2/2
3/5
4/5
3/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
2/4
2/2
3/5
4/5
3/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
2/4
0/2
3/5
2/5
1/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
2/4
0/2
3/5
2/5
1/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
4/4
0/2
3/5
4/5
3/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
4/4
0/2
3/5
4/5
3/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
4/4
0/2
3/5
4/5
3/3
4/6
1/1

來看例子

  • 這段不要流過來！
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

來看例子

  • 這段不要流過來！
    • 這樣就是最大流了
  • 流量有改變的邊有哪些？
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

來看例子

  • 這段不要流過來！
    • 這樣就是最大流了
  • 流量有改變的邊有哪些？
    • 看起來像不像一條路徑？
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

新概念

  • 要怎麼找到一個很爛的 \(f(u, v)\) 並修改？
    • 好像很難去處理
    • 那不如我們把圖重畫！
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

逆流而上

  • 將一條邊的流 \(f(u, v)\) 減少，就像是讓水逆著流
    • 可以逆著流（取消）的量會是 \(f(u, v)\)
    • 可以正著流的量會是 \(c(u,v) - f(u, v)\)
    • 還需要記錄容量嗎？
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

剩餘圖

  • Residual Graph
    • 雖然我覺得很爛但我想不到更好的名字
  • 對於每個容量圖 \(G(V, E)\) 存在一個剩餘圖 \(G'(V', E')\)
    • \(\forall (u, v) \in E,\ (u, v) \in E' \land (v, u) \in E'\)
    • \(w(u,v) = c(u, v) - f(u, v), w(v,u) = f(u, v)\)
    • \(G'_f\) 為 \(G\) 的流函數為 \(f\) 時的剩餘圖
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

剩餘圖

  • Residual Graph
  • 對於每個容量圖 \(G(V, E)\) 存在一個剩餘圖 \(G'(V', E')\)
    • \(\forall (u, v) \in E,\ (u, v) \in E' \cap (v, u) \in E'\)
    • \(w(u,v) = c(u, v) - f(u, v), w(v,u) = f(u, v)\)
    • \(G'_f\) 為 \(G\) 的流函數為 \(f\) 時的剩餘圖
s
t
1
2
3
4
0
0
2
0
1
0
0
0
6
3
1
4
5
0
5
4

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
s
t
1
2
3
4
0
0
2
0
1
0
0
0
6
3
1
4
5
0
5
4

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
s
t
1
2
3
4
5
4
2
5
5
3
6
1
0
0
0
0
0
0
0
0

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
s
t
1
2
3
4
5
4
2
5
5
3
6
1

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
s
t
1
2
3
4
5
4
2
5
5
3
6
1

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
s
t
1
2
3
4
5
3
2
5
4
3
5
0
1
1
1
1

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
s
t
1
2
3
4
5
3
2
5
4
3
5
1
1
1
1

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
s
t
1
2
3
4
5
3
2
5
4
3
5
1
1
1
1

剩餘圖

  • 把邊權為零的邊視為不存在
  • 如此一來，只要在 \(G'_f\) 上找到一條從 \(s\) 到 \(t\) 的路徑 \(\mathcal P\) 就好了
  • 這些路徑被稱為擴增路徑（augmenting paths）
s
t
1
2
3
4
4
3
2
4
4
2
5
1
0
1
1
1
1
1
1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
s
t
1
2
3
4
5/5
4/4
0/2
5/5
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
s
t
1
2
3
4
5/5
4/4
0/2
5/9
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
s
t
1
2
3
4
5/5
4/4
0/2
5/9
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
s
t
1
2
3
4
5/5
4/8
0/2
5/9
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
    • 好像沒有變欸
    • 是什麼地方「堵住了」
s
t
1
2
3
4
5/5
4/8
0/2
5/9
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
    • 好像沒有變欸
    • 是什麼地方「堵住了」
s
t
1
2
3
4
5/5
4/8
0/2
5/9
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
    • 好像沒有變欸
    • 是什麼地方「堵住了」
s
t
1
2
3
4
5/5
4/8
0/2
5/9
4/5
3/3
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
    • 好像沒有變欸
    • 是什麼地方「堵住了」
s
t
1
2
3
4
5/5
4/8
0/2
5/9
4/5
3/5
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
    • 好像沒有變欸
    • 是什麼地方「堵住了」
s
t
1
2
3
4
5/5
4/8
0/2
5/9
4/5
3/5
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
    • 好像沒有變欸
    • 是什麼地方「堵住了」
s
t
1
2
3
4
5/5
5/8
0/2
5/9
5/5
4/5
6/6
1/1

🈹與流的關係

  • 我們再次回到這張圖
    • 把它隨便改改，看最大流會不會改變
    • 好像沒有變欸
    • 是什麼地方「堵住了」
    • 割？！
s
t
1
2
3
4
5/5
5/8
0/2
5/9
5/5
4/5
6/6
1/1

🈹與流的關係

  • 一張圖的最大流 \(\max |f|\) 看起來跟最小割 \(\min \text{cut}(S,T)\) 相關
    • 真的嗎
    • 如果是，對於解決最大流問題有什麼用？
s
t
1
2
3
4
5/5
5/8
0/2
5/9
5/5
4/5
6/6
1/1
Max-Flow Min-Cut

最大流最小割定理

最大流最小割定理

  • 對於一個流量圖 \(G\) 及 \(G\) 的一個流函數 \(f\)，以下三者等價：
    • \(|f|\) 為最大
    • \(G'_f\) 上沒有擴增路徑
    • 存在 \(\text{cut}(S,T) = |f|\)
  • 接下來我們會簡單的證明以下三項等價

容量限制

  • \(\text{flow}(S, T) \le \text{cut}(S,T)\)
    • 顯然
    • \(\text{flow}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T} f(v, u)\)
    • \(\forall (u, v) \in V \times V, f(u, v) \ge 0\)
    • \(\displaystyle \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T} f(v, u) \le \sum_{u \in S} \sum_{v \in T} f(u, v)\)
    • \(\forall (u, v) \in V \times V, f(u, v) \le c(u,v)\)
    • \(\displaystyle \sum_{u \in S} \sum_{v \in T} f(u, v) \le \displaystyle \sum_{u \in S} \sum_{v \in T} c(u, v)\)

流量相等

  • 在 \(G\) 上流為 \(f\) 的任意 s-t cut，\(\text{flow}(S,T) = |f|\)
  • 將 \(v \in S - \{s\}\) 換到 \(T\)，形成 \(S' = S - \{v\}, T' = T \cup \{v\}\)
  • \(\text{flow}(S, T) = \displaystyle \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T} f(v, u)\)
  • \(\text{flow}(S', T') = \text{flow}(S, T) + \displaystyle \sum_{u \in S'} f(u, v) - \sum_{u \in T'} f(v, u)\)
  • \(\displaystyle \sum_{u \in S'} f(u, v) - \sum_{u \in T'} f(v, u) = \sum_{u \in S'} f(u, v) + \sum_{u \in T'} f(u, v)\)
    • \(\because\) 流量對稱
  • \(\displaystyle \sum_{u \in S'} f(u, v) + \sum_{u \in T'} f(u, v) = \sum_{u \in S' \cup T'} f(u, v) = 0\)
    • \(\because \forall v \notin \{s, t\}\) 流量守恆

流量相等，倒過來

  • 在 \(G\) 上流為 \(f\) 的任意 s-t cut，\(\text{flow}(S,T) = |f|\)
  • 將 \(v \in T - \{t\}\) 換到 \(S\)，形成 \(S' = S \cup \{v\}, T' = T - \{v\}\)
  • 證明 \(\text{flow}(S', T') = \text{flow}(S, T)\)
  • \(\text{The proof is left as an exercise for the reader.}\)

綜合以上兩點

  • 對於任意點的 s-t cut \(C(S, T)\)
    • \(\text{flow}(S,T) \le \text{cut}(S,T)\)
    • \(|f| = \text{flow}(S,T)\)
  • \(|f| \le \text{cut}(S,T)\)

真．熱血證明

  • 回顧一下，MFMC 定理宣稱以下三者等價：
    • \(|f|\) 為最大
    • \(G_f'\) 上沒有擴增路徑
    • 存在 \(\text{cut}(S,T) = |f|\)
  • 使三個點屬於同一個強連通分量至少需要幾條邊？
    • 三個！
    • 所以我們將分三步證明以下三者等價

最大流無法擴增

  • \((|f| \text{ is maximum}) \rightarrow (G'_f \text{ has no augmenting path})\)
  • \(p \rightarrow q \implies \lnot q \rightarrow \lnot p\)
  • \((G'_f \text{ has augmenting paths}) \rightarrow (|f| \text{ is not maximum})\)
  • 根據定義，擴增路徑 \(\mathcal P\) 上的最小權大於零
  • 故採取擴增路徑必然使 \(|f|\) 上升
  • 敘述成立

有割等於流

  • 這裡要證明若 \(G_f'\) 上沒有擴增路徑則存在 \(\text{cut}(S,T) = |f|\)
  • 我們來構造一個 \(C(S,T)\) 使得 \(\text{cut}(S,T) = |f|\) 吧 
    • 由於 \(G'_f\) 沒有擴增路徑，必定有點和 \(s\) 不連通（如 \(t\)）
    • 令和 \(s\) 連通的點屬於 \(S\)，否則屬於 \(T\)
    • 由於 \(S \not = \varnothing \cap T \not = \varnothing\)，\(C(S,T)\) 是一個合法的 s-t cut
    • \(\text{flow}(S,T)\) 會是多少?
  • 根據流量相等，\(\text{flow}(S,T) = |f|\)！

有割即是最大流

  • 令 \(\text{cut}(S,T) = |f|\) 
  • 由於 \(|f| \le \text{cut}(S,T)\)，敘述成立
  • 至此證明三者等價
  • 由於有 \(f\) 使得 \(\text{cut}(S,T) = |f|\)，\(\min \text{cut}(S, T) = \max |f|\)
Max Flow Algorithm

最大流演算法

Ford-Fulkerson

問了就是唬爛

Ford-Fulkerson

  • 根據 MFMC 定理，若還有擴增路徑，則 \(|f|\) 非最大
  • 聰明如你，一定會想到怎麼做
  • 一直找擴增路徑，直到沒有為止
    • 蛤
    • 對，就這樣
  • 複雜度長怎樣

複雜度分析

複雜度分析

s
t
1
2
0/1
0/225
0/225
0/225
0/225
  • 最大流是多少
    • MFMC，最大流為 450
    • 怎麼跑？

複雜度分析

s
t
1
2
0/1
0/225
0/225
0/225
0/225
  • 最大流是多少
    • MFMC，最大流為 450
    • 怎麼跑？

複雜度分析

s
t
1
2
1/1
1/225
0/225
1/225
0/225
  • 最大流是多少
    • MFMC，最大流為 450
    • 怎麼跑？

複雜度分析

s
t
1
2
0/1
1/225
0/225
1/225
0/225
  • 最大流是多少
    • MFMC，最大流為 450
    • 怎麼跑？

複雜度分析

  • 最大流是多少
    • MFMC，最大流為 450
    • 怎麼跑？
s
t
1
2
0/1
1/225
0/225
1/225
0/225

複雜度分析

  • 最大流是多少
    • MFMC，最大流為 450
    • 怎麼跑？
s
t
1
2
1/1
1/225
1/225
1/225
1/225

複雜度分析

  • 最大流是多少
    • MFMC，最大流為 450
    • 怎麼跑？
s
t
1
2
0/1
1/225
1/225
1/225
1/225

複雜度分析

  • 在最糟情況下，\(|f|\) 每增加 1 就要找一次擴增路徑
  • 怎麼找擴增路徑？
    • 從起點 DFS
s
t
1
2
0/1
1/225
1/225
1/225
1/225

複雜度分析

  • 複雜度為 \(\mathcal O((|V| + |E|) \times \max |f|)\)
  • \(G\) 連通 \(\rightarrow |V| \in \mathcal O(|E|)\) 
  • \(\mathcal O((|V| + |E|) \times \max |f|) \subset \mathcal O(|E| \max |f|)\)
s
t
1
2
0/1
1/225
1/225
1/225
1/225

複雜度分析

  • 看起來不太糟？
    • 複雜度是偽多項式時間（pseudo polynomial），超爛
  • 那怎麼辦？
    • 哭阿
s
t
1
2
0/1
1/225
1/225
1/225
1/225

複雜度分析

  • 其實那個複雜度也不是真的
    • 如果容量是無理數怎麼辦
    • 我沒有要畫，自己讀
s
t
1
2
0/1
1/225
1/225
1/225
1/225

Ford-Fulkerson Code

  • 記得把相反邊的權重 += \(\min w(u, v) \in \mathcal P\)
typedef long long ll;

struct FordFulkerson {
    int s, t, V;
    vector< vector<int> > graph;
    vector< vector<ll> > cap;
    vector<bool> visited;

    FordFulkerson(int V): V(V), graph(V), visited(V) {
        cap.resize(V, vector<ll>(V));
    }

    void addEdge(int u, int v, int w) {
        graph[u].push_back(v);
        graph[v].push_back(u);
        cap[u][v] += w;
    }

    ll dfs(int u, ll f = INT64_MAX) {
        if (u == t) return f;
        visited[u] = 1;

        for (auto& v: graph[u]) {
            if (cap[u][v] == 0 || visited[v]) continue;

            ll fv = dfs(v, min(f, cap[u][v]));
            if (fv) {
                cap[u][v] -= fv;
                cap[v][u] += fv;
                return fv;
            }
        }

        return 0;
    }

    ll maximumFlow(int s, int t) {
        this->s = s, this->t = t;
        ll f = 0;

        for (ll augFlow; augFlow = dfs(s); f += augFlow) {
            visited.assign(V, 0);
        }

        return f;
    }
};

小插曲

  • 爛測資模擬器
Edmonds-Karp

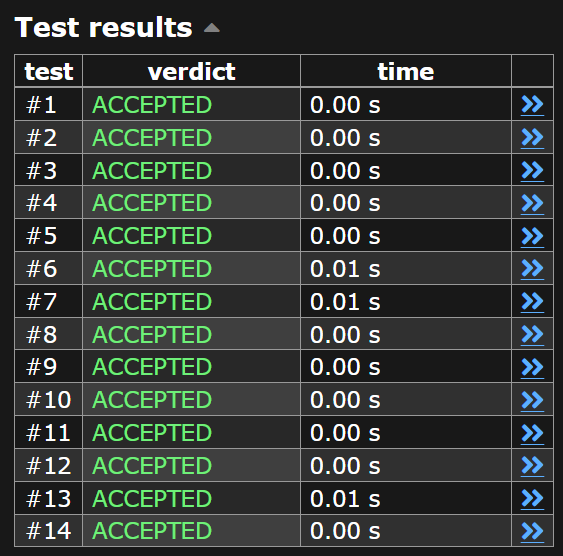
可以不要偽多項式嗎

強多項式時間的作法

  • 偽多項式時間聽起來超級恐怖的爛
    • 可是你剛才不是過了嗎
    • 閉嘴
  • 為了讓執行時間和邊權與答案沒有關係，我們要採取新的策略
  • 找擴增路徑時，找路徑長最短的擴增路徑
    • 經過的點最少的
    • 用這條路徑增廣
    • 做完了
    • 蛤

複雜度分析

  • 每次找擴增路徑做一次 BFS，複雜度 \(\mathcal O(|V| + |E|)\)
  • 每個邊最多被填滿 \(\mathcal O(|V|)\) 次
    • 擴增完要經過剛被填滿的邊或它的反向邊的距離會單調增加
    • 一條簡單路徑長度最多為 \(|V| - 1\)
  • 圖上總共有 \(|E|\) 條邊
  • 複雜度 \(\mathcal O(|E| \times |V| \times |E|) = \mathcal O(|V||E|^2)\)

Edmonds-Karp Code

  • 鄰接矩陣存容量，鄰接串列存鄰邊
typedef long long ll;

struct EdmondsKarp {
    int V;
    vector< vector<ll> > cap;
    vector< vector<int> > graph;
    vector<int> p;

    EdmondsKarp(int V): V(V), graph(V), p(V) {
        cap.resize(V, vector<ll>(V));
    }

    void addEdge(int u, int v, int w) {
        graph[u].push_back(v);
        graph[v].push_back(u);
        cap[u][v] += w;
    }

    bool bfs(int s, int t) {
        p.assign(V, 0);
        queue<int> q;
        q.push(s);

        while (q.size()) {
            auto u = q.front();
            q.pop();

            for (auto& v: graph[u]) {
                if (p[v] || !cap[u][v]) continue;

                p[v] = u;
                if (v == t) return 1;
                q.push(v);
            }
        }

        return 0;
    }

    ll maximumFlow(int s, int t) {
        ll f = 0;

        while (bfs(s, t)) {
            ll augFlow = INT64_MAX;
            for (int u = t; u != s; u = p[u]) {
                augFlow = min(augFlow, cap[p[u]][u]);
            }

            for (int u = t; u != s; u = p[u]) {
                cap[p[u]][u] -= augFlow;
                cap[u][p[u]] += augFlow;
            }

            f += augFlow;
        }

        return f;
    }
};
Dinitz

那個名字被念錯的男人

這個人有多可憐

  • Yefim A. Dinitz.
  • 這個人發明了最大流問題最常被使用的演算法
  • 然後結果推廣他的演算法的人把他的名字念錯了
  • 然後其他人都把演算法的名字記成錯的名字
  • 他甚至沒有自己的維基百科頁面
  • 只有錯的名字的演算法頁面

所以演算法是什麼

  • 剛剛一次找到一條最短路徑
  • 現在我們把當前可以走的所有最短路徑都走完
  • 做完了
  • 蛤

作法與複雜度

  • 先 BFS 一次，將所有點和原點距離標示出來
  • 一直 DFS 找上面的路徑並增廣
  • 複雜度分析
    • 最多更新所有點距離 \(|V|-1\) 次（簡單路徑長度上限）
      • BFS \(\mathcal O(|V| + |E|)\)
      • 把當前每個路徑走完最多 \(\mathcal O(|V||E|)\)
      • 每次更新複雜度 \(\mathcal O(|V| + |E| + |V||E|) = \mathcal O(|V||E|)\) 
    • 總複雜度 \(\mathcal O(|V| \times |V||E|) = \mathcal O(|V|^2|E|)\) 
    • 夠好了！

Dinitz Code

  • 不要浪費時間做沒用的事
typedef long long ll;

struct Dinitz {
    int s, t, V;
    vector< vector<int> > graph;
    vector< vector<ll> > cap;
    vector<int> level, toCheck;

    Dinitz(int V): V(V), graph(V), level(V), toCheck(V) {
        cap.resize(V, vector<ll>(V));
    }

    void addEdge(int u, int v, int w) {
        graph[u].push_back(v);
        graph[v].push_back(u);
        cap[u][v] += w;
    }

    int bfs() {
        level.assign(V, 0);
        level[s] = 1;
        queue<int> q;
        q.push(s);

        while (q.size()) {
            int u = q.front();
            q.pop();

            for (auto& v: graph[u]) {
                if (level[v] || !cap[u][v]) continue;

                level[v] = level[u] + 1;
                q.push(v);
            }
        }

        return level[t];
    }

    ll dfs(int u, ll f = INT64_MAX) {
        if (u == t) return f;

        for (auto& i = toCheck[u]; i < graph[u].size(); i++) {
            auto& v = graph[u][i];
            if (!cap[u][v] || level[v] != level[u] + 1) continue;

            ll fv = dfs(v, min(f, cap[u][v]));
            if (fv) {
                cap[u][v] -= fv;
                cap[v][u] += fv;
                return fv;
            }
        }

        return 0;
    }

    ll maximumFlow(int s, int t) {
        this->s = s, this->t = t;
        ll f = 0, augFlow;

        while (bfs()) {
            fill(toCheck.begin(), toCheck.end(), 0);
            while (augFlow = dfs(s)) f += augFlow;
        }

        return f;
    }
};
Push Relabel

亂改複雜度就亂降，真好

大暴流

  • 你有沒有那種水開太大然後滿出來的經驗
  • 假設今天源點 \(s\) 就是那個水龍頭
    • 滿出來的水想辦法倒掉，剩下的就是最大流
    • 蛤

演算法

  • 打開水龍頭
  • 讓水往下流
  • 上下左右擺動讓水能夠往下流
  • 沒辦法的就倒出來
  • 我需要動畫，沒有 BrineTW 的動畫我看不懂

先用鏈來看

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
0/5
3
0/6
0/4
0/7

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
0/5
3
0/6
0/4
0/7
0
0
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
0/5
3
0/6
0/4
0/7
\infty
0
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
0/5
3
0/6
0/4
0/7
\infty
0
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
0/5
3
0/6
0/4
0/7
\infty
0
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
0/6
0/4
0/7
\infty
5
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
0/6
0/4
0/7
\infty
5
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
0/6
0/4
0/7
\infty
5
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
0/6
0/4
0/7
\infty
5
0
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
5/6
0/4
0/7
\infty
0
5
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
5/6
0/4
0/7
\infty
0
5
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
5/6
0/4
0/7
\infty
0
5
0
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
5/6
4/4
0/7
\infty
0
1
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
5/6
4/4
0/7
\infty
0
1
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
5/6
4/4
0/7
\infty
0
1
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
5/6
4/4
0/7
\infty
0
1
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
s
t
1
2
5/5
3
4/6
4/4
0/7
\infty
1
0
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
5/5
3
4/6
4/4
0/7
\infty
1
0
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
5/5
3
5/6
4/4
0/7
\infty
0
1
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
5/5
3
5/6
4/4
0/7
\infty
0
1
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
4/5
3
4/6
4/4
0/7
\infty
0
0
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
4/5
3
4/6
4/4
0/7
\infty
0
0
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
4/5
3
4/6
4/4
0/7
\infty
0
0
4
0

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
4/5
3
4/6
4/4
4/7
\infty
0
0
0
4

先用鏈來看

  • 這邊如果有人看不出來最大流是多少可以先出去罰站
  • 接下來會重複來回幾次
s
t
1
2
4/5
3
4/6
4/4
4/7
\infty
0
0
0
4

更專業一點

  • 這個演算法在結束之前的流並非遵循所有流量相關定律
    • 預流（preflow）
    • 不遵守流量守恆，有些水會卡在點上，之後想辦法排掉
    • 將邊上的預流標為 \(f_p(u, v)\)
  • 定義 \(\text{excess(u)} = \displaystyle \sum_{v \in V} f_p(u, v)\)
  • 為了不要不斷重複把水倒入深處再回流，定義高度函數 \(h(u)\)：
    • \(h(s) = V\)
    • \(\forall u \not = s,\ h(u) = 0\)

送水 discharge

  • 規定若要將水從 \(u\) 送到 \(v\)，須滿足：
    • \(\text{excess}(u) > 0\)
    • \(\text{cap}(u, v) > 0\)
    • \(h(u) > h(v)\)
  • 看起來送不了水阿
    • 當發現水無法從 \(u\) 流出時，改變 \(u\) 的高度（relabel）
    • 改變方法：\(h'(u) = h(u) + 1\)
    • 會發現這跟直接找 \(\min h(v)\) 並令 \(h'(u) = \min h(v) + 1\) 等價
    • \(h(t)\) 永遠是 0

如何選誰開始送水

  • 大哉問
  • 不同的選法會造成不一樣的複雜度
  • 我完全不會證明你大可相信他是好的
    • 下一屆資讀講師看到了嗎，我叫你明年講證明
  • 任意選一個可以 discharge 的點：\(\mathcal O(|V|^2|E|)\)
    • 亂做就跟 Dinic 一樣快
    • 其實沒有很好寫
  • 把能送水的點放上 active 的標記
  • 怎麼選有 active 標記的點？
    • 先有 active 標記的先處理 \(\mathcal O(|V|^3)\)
    • 有 active 標記且是最高的 \(\mathcal O(|V|^2 \sqrt{|E|})\)

Push Relabel Code

  • 我改超久，哭了
typedef long long ll;

struct PushRelabel {
    int V, i;
    vector<vector<int>> graph, Q;
    vector<vector<ll>> cap;
    vector<int> h;
    vector<ll> excess;
    vector<bool> active;

    PushRelabel(int V): V(V), graph(V), Q(V << 1 ^ 1), h(V), excess(V), active(V) {
        cap.resize(V, vector<ll>(V));
    }

    void addEdge(int u, int v, int w) {
        graph[u].push_back(v);
        graph[v].push_back(u);
        cap[u][v] += w;
    }

    void enqueue(int u) {
        if (!active[u] && excess[u]) {
            active[u] = 1;
            Q[h[u]].push_back(u);
            i = max(i, h[u]);
        }
    }

    void push(int u, int v) {
        ll f = min(excess[u], cap[u][v]);
        if (h[u] > h[v] && f) {
            cap[u][v] -= f;
            cap[v][u] += f;
            excess[v] += f;
            excess[u] -= f;
            enqueue(v);
        }
    }

    void relabel(int u) {
        h[u] = V * 2 + 1;
        for (auto& v: graph[u]) if (cap[u][v]) {
            h[u] = min(h[u], h[v] + 1);
        }
        enqueue(u);
    }

    void discharge(int u) {
        for (auto& v: graph[u]) {
            if (!excess[u]) break;

            push(u, v);
        }

        if (excess[u]) relabel(u);
    }

    ll maximumFlow(int s, int t) {
        excess[s] = INT64_MAX;

        h[s] = V;
        active[s] = active[t] = 1;
        for (auto& v: graph[s]) push(s, v);

        for (i = 0; i >= 0; i--) {
            while (Q[i].size()) {
                int u = Q[i].back();
                Q[i].pop_back();
                active[u] = 0;
                discharge(u);
            }
        }

        return excess[t];
    }
};

啟發式演算法

  • 什麼是啟發式演算法？
    • 很有道理的唬爛
    • 犧牲某些東西換取另外一些東西
  • 當你發現有一個點 \(u\)，\(\text{excess(u)} > 0\) 且沒有其他相同高度的點
    • 水沒有辦法往下流了
    • 比 \(u\) 高的點的水再也不可能流到 \(t\)
    • 直接放棄他們，把他們的高度調到 \(|V|\)
  • 這樣可以加速演算法，但犧牲了什麼？
    • 可能沒辦法得到最大流的解

Gap Heuristic Code

  • 偷扣要先試跑再決定要不要學 source 
struct PushRelabel {
    int V, i;
    vector<vector<int>> graph, Q;
    vector<vector<ll>> cap;
    vector<ll> excess;
    vector<int> h, count;
    vector<bool> active;
 
    PushRelabel(int V): V(V), graph(V), Q(V), h(V), excess(V), count(V + 1), active(V) {
        cap.resize(V, vector<ll>(V));
    }
 
    void addEdge(int u, int v, int w) {
        graph[u].push_back(v);
        graph[v].push_back(u);
        cap[u][v] += w;
    }
 
    void enqueue(int u) {
        if (!active[u] && excess[u] && h[u] < V) {
            active[u] = 1;
            Q[h[u]].push_back(u);
            i = max(i, h[u]);
        }
    }
 
    void push(int u, int v) {
        ll f = min(excess[u], cap[u][v]);
        if (h[u] == h[v] + 1 && f) {
            cap[u][v] -= f;
            cap[v][u] += f;
            excess[v] += f;
            excess[u] -= f;
            enqueue(v);
        }
    }
 
    void gap(int k) {
        for (int u = 0; u < V; u++) if (h[u] >= k) {
            count[h[u]]--;
            h[u] = max(h[u], V);
            count[h[u]]++;
            enqueue(u);
        }
    }
 
    void relabel(int u) {
        count[h[u]]--;
        h[u] = V;
        for (auto& v: graph[u]) if (cap[u][v]) {
            h[u] = min(h[u], h[v] + 1);
        }
        count[h[u]]++;
        enqueue(u);
    }
 
    void discharge(int u) {
        for (auto& v: graph[u]) {
            if (!excess[u]) break;
            
            push(u, v);
        }
 
        if (excess[u]) (count[h[u]] == 1) ? gap(h[u]) : relabel(u);
    }
 
    ll maximumFlow(int s, int t) { 
        excess[s] = INT64_MAX;
 
        count[0] = V;
        enqueue(s);
        active[t] = 1;
 
        for (i = 0; i >= 0; i--) {
            while (Q[i].size()) {
                int u = Q[i].back();
                Q[i].pop_back();
                active[u] = 0;
                discharge(u);
            }
        }

        return excess[t];
    }
};

圖論怪談

　　聽說，每次有人在建國中學資訊讀書會遇到看不懂的圖論概念的時候，就會有一位不知名先生出現，在你最絕望的時候從你背後輕拍你的肩膀，當你在想「到底是誰設計出這個演算法的啦幹」的時候，他就會到你的耳邊輕輕跟你說：

 

圖論怪談

　　聽說，每次有人在建國中學資訊讀書會遇到看不懂的圖論概念的時候，就會有一位不知名先生出現，在你最絕望的時候從你背後輕拍你的肩膀，當你在想「到底是誰設計出這個演算法的啦幹」的時候，他就會到你的耳邊輕輕跟你說：

 

 

「哈哈，是我啦」

圖論怪談

　　聽說，每次有人在建國中學資訊讀書會遇到看不懂的圖論概念的時候，就會有一位不知名先生出現，在你最絕望的時候從你背後輕拍你的肩膀，當你在想「到底是誰設計出這個演算法的啦幹」的時候，他就會到你的耳邊輕輕跟你說：

 

 

「哈哈，是我啦」

\text{This algorithm was designed by Tarjan and Goldberg.}

例題

Solutions

例題講解

練習建模的重要性

  • 大概所有有關 flow 的題目的形狀都不會是原本的樣子
  • 練習怎麼把題目轉換成可以用 flow 演算法解決的樣子吧

二分圖最大匹配

  • CSES 1696 School Dance
  • 二分圖：給定一張圖 \(G\)，能夠找到一個割 \(C(L, R)\)，使得：
    • \(\forall (u, v) \in E\)
      • \(u \in L \rightarrow v \in R\)
      • \(v \in L \rightarrow u \in R\)
    • 中文：所有邊會跨過兩個點集
  • 匹配（matching）：選若干條邊使得點不重複
  • 怎麼做？

二分圖

  • 看出來了嗎？

二分圖

  • 看出來了嗎？
s
t

二分圖講師表示不服

  • 二分圖匹配用二分圖的擴增路徑找的時間複雜度是 \(\mathcal O(|V||E|)\)
  • 用 Dinitz 找的時間複雜度會是 \(\mathcal O(|E|\sqrt{|V|})\)
    • 若一張圖所有除了 \(s, t\) 之外的點 \(u\) 皆符合：
      • 入度或出度其中一個是一
      • 該邊權為 1
    • 則用 Dinitz 找最大流時間複雜度會是 \(\mathcal O(|E|\sqrt{|V|})\)
  • 快到不像話，你還要學其它二分圖演算法嗎
  • 二分圖的課會介紹其他可以解其它東西的演算法，要來欸

出題者不講武德

  • 模板爛了？
    • 沒有
  • 有重邊
    • 題目沒說沒有就可以有
    • 智慧鐵人欸

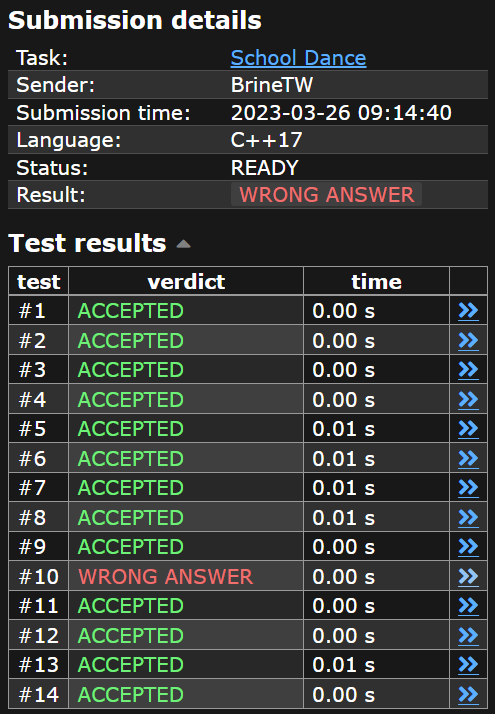
小知識：我是笨

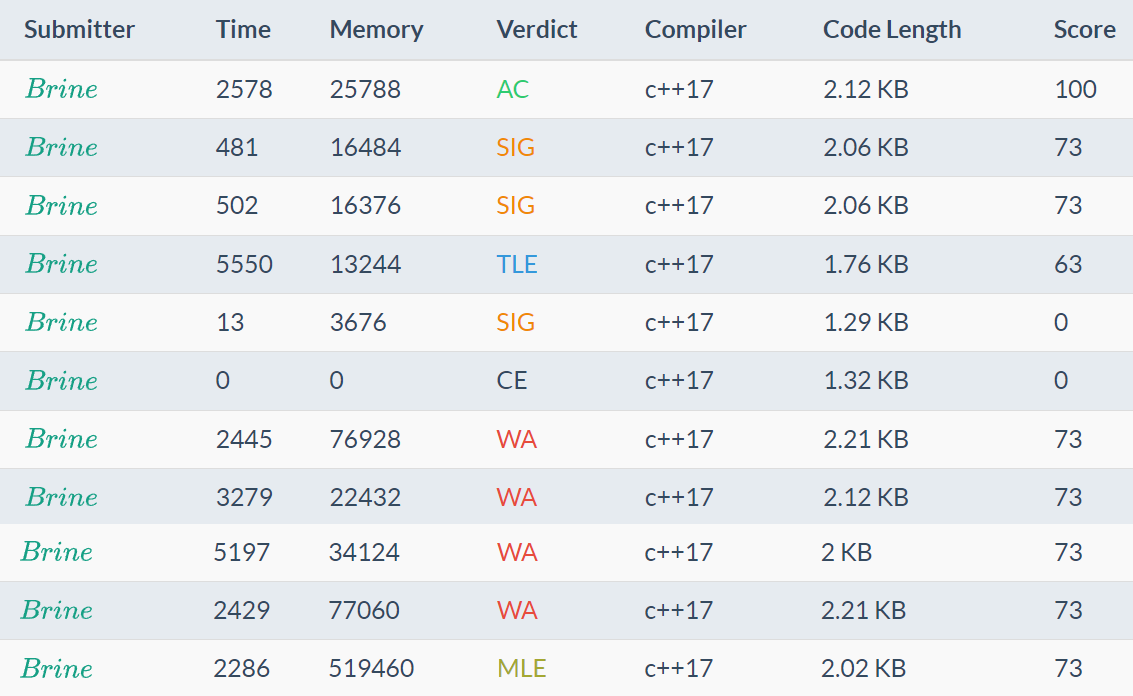
MLE?

  • 前面那個是我寫的比較好讀一點點的模板
    • 我覺得記錄回邊很煩而且不好讀
    • 所以我用了
      • 一個 \(\mathcal O(|V| + |E|)\) 的陣列記錄邊
      • 一個 \(\mathcal O(|V|^2)\) 的陣列記錄容量
    • 第三子題的測試資料警力配置圖為連結圖且不存在環路。
      圖形為連結圖代表此圖的任意兩個節點皆存在一條路徑；
      而環路表示起點和終點為同一節點的路徑。
      \(1 \le p \le 100000, 1 \le q \le 100000, 1 \le k \le 210000\)
      全部解出可獲 27 分。
    • \(|V|^2 \le (p + q)^2 = 40000000000\)

Ver. Adjacency List

  • 常數跟空間一定比較小，但我就不喜歡這樣寫
struct Dinitz {
    struct Edge {
        int v, c, r;
        Edge(int v, int c, int r): v(v), c(c), r(r) {}
    };

    int s, t, V;
    vector< vector<Edge> > graph;
    vector<int> level, toCheck;

    Dinitz(int V): V(V), graph(V), level(V), toCheck(V) {}

    void addEdge(int u, int v, int w) {
        graph[u].push_back({v, w, graph[v].size()});
        graph[v].push_back({u, 0, graph[u].size() - 1});
    }

    int bfs() {
        level.assign(V, 0);
        level[s] = 1;
        queue<int> q;
        q.push(s);

        while (q.size()) {
            int u = q.front();
            q.pop();

            for (auto& [v, c, r]: graph[u]) {
                if (level[v] || !c) continue;

                level[v] = level[u] + 1;
                q.push(v);
            }
        }

        return level[t];
    }

    int dfs(int u, int f = INT32_MAX) {
        if (u == t) return f;

        for (auto& i = toCheck[u]; i < graph[u].size(); i++) {
            auto& [v, c, r] = graph[u][i];
            if (!c || level[v] != level[u] + 1) continue;

            int fv = dfs(v, min(f, c));
            if (fv) {
                c -= fv;
                graph[v][r].c += fv;
                return fv;
            }
        }

        return 0;
    }

    ll maximumFlow(int s, int t) {
        this->s = s, this->t = t;
        ll f = 0, augFlow;

        while (bfs()) {
            fill(toCheck.begin(), toCheck.end(), 0);
            while (augFlow = dfs(s)) f += augFlow;
        }

        return f;
    }
};

「比較小」

  • 真好

多源點與多匯點

  • 假設今天有很多個源點或很多個匯點怎麼辦

多源點與多匯點

  • 假設今天有很多個源點或很多個匯點怎麼辦
s_1
t_1
1
2
6
4
s_2
t_2
t_3
3
5

多源點與多匯點

  • 假設今天有很多個源點或很多個匯點怎麼辦
  • 把源點流到一個共同源點，匯點也是
s_1
t_1
1
2
6
4
s_2
t_2
t_3
3
5
s
t

多源點與多匯點

  • 假設今天有很多個源點或很多個匯點怎麼辦
  • 把源點流到一個共同源點，匯點也是
  • 或是用 push relabel 直接全部設成 \(\text{excess}[s_i]=\infty, h[s_i] = |V|\)
s_1
t_1
1
2
6
4
s_2
t_2
t_3
3
5
s
t
\infty
\infty
\infty
\infty
\infty

點容量？

  • 如果今天不只邊有流量限制，點也有怎麼辦

點容量？

  • 如果今天不只邊有流量限制，點也有怎麼辦
1
2
s
t

點容量？

  • 如果今天不只邊有流量限制，點也有怎麼辦
    • 把點變成邊！
1
2
2
2
2
s
t
2
5
7

點容量？

  • 如果今天不只邊有流量限制，點也有怎麼辦
    • 把點變成邊！
s
t
2
5
7
2
2

點容量？

  • 如果今天不只邊有流量限制，點也有怎麼辦
    • 把點變成邊！
1_i
2_i
s
t
2
5
7
2
2
1_o
2_o

分成兩邊

  • 有時候，你需要把東西分成兩邊
    • 像是在比北市賽的時候
    • 選或不選
    • 紅隊或藍隊
    • 笨或不笨
    • 是不是 BrineTW 的粉絲
  • 以賺錢來說，可能會有
    • 選了 \(i\) 會賺 \(w_i\) 或賠 \(w_i\)
    • 選了 \(i\) 不選 \(j\) 要付出 \(w_{ij}\)

聽起來怎麼這麼像 DP

  • 聽起來一臉是 DP 的東西
  • 左想右想就是寫不出來轉移式
  • 這時候不妨砸砸看 flow！
    • 這跟 flow 有什麼關係
    • 關鍵在於「二分」
    • 什麼東西會把圖分成兩分？
      • 🈹

用通靈建圖

  •  要選還是不選呢？
    • 選了 \(u\) 會得到 \(2\)
    • 選了 \(u\) 得付出 \(5\)

用通靈建圖

  •  要選還是不選呢？
    • 選了 \(u\) 會得到 \(2\)
    • 選了 \(u\) 得付出 \(5\)
u
t
2
0
5

用通靈建圖

  •  要選還是不選呢？
    • 選了 \(u\) 會得到 \(2\)
    • 選了 \(u\) 得付出 \(5\)
  • 如果到最後還有剩下的水在 \(u\) 中代表 \(u\) 值得被選
    • 這看起來不是做加減法就可以得出的結論嗎？
5
u
t
2
0

用通靈建圖

  •  要選還是不選呢？
    • 選了 \(u\) 會得到 \(2\)
    • 選了 \(u\) 得付出 \(5\)
  • 如果到最後還有剩下的水在 \(u\) 中代表 \(u\) 值得被選
    • 這看起來不是做加減法就可以得出的結論嗎？
5
u
t
2
0

用通靈建圖

  •  要選還是不選呢？
    • 選了 \(u\) 會得到 \(2\)
    • 選了 \(u\) 得付出 \(5\)
  • 如果到最後還有剩下的水在 \(u\) 中代表 \(u\) 值得被選
    • 這看起來不是做加減法就可以得出的結論嗎？
5
u
t
2
0
v
2
4

用通靈建圖

  • 那如果在中間加上邊呢？
    • 如果選了 \(v\)，就得付出 \(2\) 在 \(u\) 上
    • 選 \(v\) 不選 \(u\) 要 \(c(v, u)\)
5
u
t
2
0
v
2
4
2

用通靈建圖

  • 多源點不如換成單源點？
5
u
t
2
0
v
2
4
2
s

用通靈建圖

  • 多源點不如換成單源點？
    • 如此一來就可以表示：
      • 選了 \(u\) 會得到 \(w\)：\(c(s, u) = w\)
      • 選了 \(u\) 得付出 \(w\)：\(c(u, t) = w\)
      • 選 \(v\) 不選 \(u\) 得要付出 \(w\)：\(c(v, u) = w\)
5
u
t
2
v
2
4
2
s

想想看

  • 不選 \(u\) 會得到 \(w\)
  • 不選 \(u\) 得付出 \(w\)
  • \(u, v\) 同一邊會得到 \(w\)
  • ...
Min Cost Flow

最小費用流

有成本的流

  • 假設今天題目給定：
    • 指定流量 \(|f|\)
    • 各邊單位流量成本
  • 求在流量為 \(|f|\) 的最小成本
  • 怎麼做

暴力做

  • 一直選成本最短的路會是好的
    • 連續最短路演算法（Successive Shortest Path Algorithm）
  • 找 \(|f|\) 次最段路徑就做完了
    • 無負邊：用 Dijkstra，複雜度 \(\mathcal O(|E|\log|E||f|)\)
    • 無負環：用 Bellman-Ford，複雜度 \(\mathcal O(|V||E||f|)\)
      • 用 SPFA，複雜度還是 \(\mathcal O(|V||E||f|)\)
    • 有負環：要把負環消掉，我沒做過
    • 是不是哪裡怪怪的？
  • 如果用用 Dijkstra，複雜度 \(\mathcal O(|E|\log|E||f|)\)
  • 聽起來快要比 Dinitz 好了欸，那我是不是可以不要用 Dinitz
    • 確實

確實個頭

確實個頭

  • 需要流量為 3
  • 成本為單位流量成本
s
t
1
2
3
4
0/2
0/4
0/2
0/5
0/5
0/3
0/6
0/1
1
1
2
2
225
3
3
8

確實個頭

  • 需要流量為 3
  • 成本為單位流量成本
s
t
1
2
3
4
0/2
0/4
0/2
0/5
0/5
0/3
0/6
0/1
1
1
2
2
225
3
3
8

確實個頭

  • 需要流量為 3
  • 成本為單位流量成本
s
t
1
2
3
4
1/2
0/4
1/2
0/5
1/5
1/3
0/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 6

確實個頭

  • 需要流量為 3
  • 成本為單位流量成本
s
t
1
2
3
4
2/2
0/4
2/2
0/5
2/5
2/3
0/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 12

確實個頭

  • 需要流量為 3
  • 成本為單位流量成本
  • 等等，不對吧
s
t
1
2
3
4
2/2
0/4
2/2
0/5
2/5
2/3
0/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 12

確實個頭

  • 需要流量為 3
  • 成本為單位流量成本
  • 等等，不對吧
    • 這段成本怎麼算？
    • 回想剩餘圖的想法！
s
t
1
2
3
4
2/2
0/4
2/2
0/5
2/5
2/3
0/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 12

確實個頭

  • 將上面的流「取消」
    • 走反邊的距離為負
s
t
1
2
3
4
2/2
0/4
2/2
0/5
2/5
2/3
0/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 12

確實個頭

  • 將上面的流「取消」
    • 走反邊的距離為負
s
t
1
2
3
4
2/2
0/4
2/2
0/5
2/5
2/3
0/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 12

確實個頭

  • 將上面的流「取消」
    • 走反邊的距離為負
s
t
1
2
3
4
2/2
1/4
1/2
1/5
2/5
2/3
1/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 25

確實個頭

  • 將上面的流「取消」
    • 走反邊的距離為負
    • 沒有辦法用 Dijkstra 直接做！
    • 可以把負邊消掉，或直接用其他演算法（像是 SPFA）
s
t
1
2
3
4
2/2
1/4
1/2
1/5
2/5
2/3
1/6
0/1
1
1
2
2
225
3
3
8
\text{cost: } 25

Min Cost Flow Code

  • 複雜度 \(\mathcal O(|V||E||f|)\)
typedef long long ll;

struct SuccessiveSP {
    struct Edge {
        int v, c, w, r;
        Edge(int v, int c, int w, int r): v(v), c(c), w(w), r(r) {}
    };

    int V;
    vector< vector<Edge> > graph;
    vector<ll> d;
    vector<int> p, edgeId;
    vector<bool> visited, inQueue;


    SuccessiveSP(int V): V(V), graph(V) {}

    void addEdge(int u, int v, int c, int w) {
        graph[u].emplace_back(v, c, w, graph[v].size());
        graph[v].emplace_back(u, 0, -w, graph[u].size() - 1);
    }

    void reset() {
        d.assign(V, INT64_MAX);
        p.assign(V, 0);
        edgeId.assign(V, 0);
        visited.assign(V, 0);
        inQueue.assign(V, 0);
    }

    pair<ll, ll> SPFA(int s, int t) {
        reset();
        d[s] = 0;
        queue<int> q;
        q.push(s);

        while (q.size()) {
            int u = q.front();
            q.pop();
            inQueue[u] = 0;

            for (int i = 0; i < graph[u].size(); i++) {
                auto& [v, c, w, r] = graph[u][i];
                if (c && d[u] + w < d[v]) {
                    p[v] = u;
                    edgeId[v] = i;
                    d[v] = d[u] + w;

                    if (inQueue[v]) continue;
                    inQueue[v] = 1;
                    q.push(v);
                }
            }
        }

        if (d[t] == INT64_MAX) return {0, 0};
        int f = INT32_MAX;
        for (int u = t; u != s; u = p[u]) {
            f = min(f, graph[p[u]][edgeId[u]].c);
        }
        for (int u = t; u != s; u = p[u]) {
            graph[p[u]][edgeId[u]].c -= f;
            graph[u][graph[p[u]][edgeId[u]].r].c += f;
        }

        return {f, d[t]};
    }
};

例題

Templates

模板區

Dinitz

  • 鄰接串列
typedef long long ll;

struct Dinitz {
    struct Edge {
        int v, c, r;
        Edge(int v, int c, int r): v(v), c(c), r(r) {}
    };

    int s, t, V;
    vector< vector<Edge> > graph;
    vector<int> level, toCheck;

    Dinitz(int V): V(V), graph(V), level(V), toCheck(V) {}

    void addEdge(int u, int v, int w) {
        graph[u].push_back({v, w, graph[v].size()});
        graph[v].push_back({u, 0, graph[u].size() - 1});
    }

    int bfs() {
        level.assign(V, 0);
        level[s] = 1;
        queue<int> q;
        q.push(s);

        while (q.size()) {
            int u = q.front();
            q.pop();

            for (auto& [v, c, r]: graph[u]) {
                if (level[v] || !c) continue;

                level[v] = level[u] + 1;
                q.push(v);
            }
        }

        return level[t];
    }

    int dfs(int u, int f = INT32_MAX) {
        if (u == t) return f;

        for (auto& i = toCheck[u]; i < graph[u].size(); i++) {
            auto& [v, c, r] = graph[u][i];
            if (!c || level[v] != level[u] + 1) continue;

            int fv = dfs(v, min(f, c));
            if (fv) {
                c -= fv;
                graph[v][r].c += fv;
                return fv;
            }
        }

        return 0;
    }

    ll maximumFlow(int s, int t) {
        this->s = s, this->t = t;
        ll f = 0, augFlow;

        while (bfs()) {
            fill(toCheck.begin(), toCheck.end(), 0);
            while (augFlow = dfs(s)) f += augFlow;
        }

        return f;
    }
};

Push Relabel

  • 鄰接串列
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

struct PushRelabel {
    struct Edge {
        int v, c, r;
        Edge(int v, int c, int r): v(v), c(c), r(r) {}
    };

    int V, i;
    vector< vector<Edge> > graph;
    vector< vector<int> > Q;
    vector<int> h;
    vector<ll> excess;
    vector<bool> active;

    PushRelabel(int V): V(V), graph(V), Q(V << 1 ^ 1), h(V), excess(V), active(V) {}

    void addEdge(int u, int v, int w) {
        graph[u].push_back({v, w, graph[v].size()});
        graph[v].push_back({u, 0, graph[u].size()});
    }

    void enqueue(int u) {
        if (!active[u] && excess[u]) {
            active[u] = 1;
            Q[h[u]].push_back(u);
            i = max(i, h[u]);
        }
    }

    void push(int u, Edge& e) {
        auto& [v, c, r] = e;
        int f = min(int(excess[u]), c);
        if (h[u] > h[v] && f) {
            c -= f;
            graph[v][r].c += f;
            excess[v] += f;
            excess[u] -= f;
            enqueue(v);
        }
    }

    void relabel(int u) {
        h[u] = V * 2 + 1;
        for (auto& [v, c, r]: graph[u]) if (c) {
            h[u] = min(h[u], h[v] + 1);
        }
        enqueue(u);
    }

    void discharge(int u) {
        for (auto& e: graph[u]) {
            if (!excess[u]) break;

            push(u, e);
        }

        if (excess[u]) relabel(u);
    }

    ll maximumFlow(int s, int t) {
        excess[s] = INT64_MAX;

        h[s] = V;
        active[s] = active[t] = 1;
        for (auto& v: graph[s]) push(s, v);

        for (i = 0; i >= 0; i--) {
            while (Q[i].size()) {
                int u = Q[i].back();
                Q[i].pop_back();
                active[u] = 0;
                discharge(u);
            }
        }

        return excess[t];
    }
};

int main() {

}

Minimum Cost Flow

  • 鄰接串列
typedef long long ll;

struct SuccessiveSP {
    struct Edge {
        int v, c, w, r;
        Edge(int v, int c, int w, int r): v(v), c(c), w(w), r(r) {}
    };

    int V;
    vector< vector<Edge> > graph;
    vector<ll> d;
    vector<int> p, edgeId;
    vector<bool> visited, inQueue;


    SuccessiveSP(int V): V(V), graph(V) {}

    void addEdge(int u, int v, int c, int w) {
        graph[u].emplace_back(v, c, w, graph[v].size());
        graph[v].emplace_back(u, 0, -w, graph[u].size() - 1);
    }

    void reset() {
        d.assign(V, INT64_MAX);
        p.assign(V, 0);
        edgeId.assign(V, 0);
        visited.assign(V, 0);
        inQueue.assign(V, 0);
    }

    pair<ll, ll> SPFA(int s, int t) {
        reset();
        d[s] = 0;
        queue<int> q;
        q.push(s);

        while (q.size()) {
            int u = q.front();
            q.pop();
            inQueue[u] = 0;

            for (int i = 0; i < graph[u].size(); i++) {
                auto& [v, c, w, r] = graph[u][i];
                if (c && d[u] + w < d[v]) {
                    p[v] = u;
                    edgeId[v] = i;
                    d[v] = d[u] + w;

                    if (inQueue[v]) continue;
                    inQueue[v] = 1;
                    q.push(v);
                }
            }
        }

        if (d[t] == INT64_MAX) return {0, 0};
        int f = INT32_MAX;
        for (int u = t; u != s; u = p[u]) {
            f = min(f, graph[p[u]][edgeId[u]].c);
        }
        for (int u = t; u != s; u = p[u]) {
            graph[p[u]][edgeId[u]].c -= f;
            graph[u][graph[p[u]][edgeId[u]].r].c += f;
        }

        return {f, d[t]};
    }
};
啪！沒了

謝謝聆聽

Made with Slides.com