foundations of data science for everyone
X: Neural Networks
Farid Qamar
this slide deck: https://slides.com/faridqamar/fdfse_10
1
NN: Neural Networks
origins


1943
McCulloch & Pitts 1943
M-P Neuron
1943
McCulloch & Pitts 1943
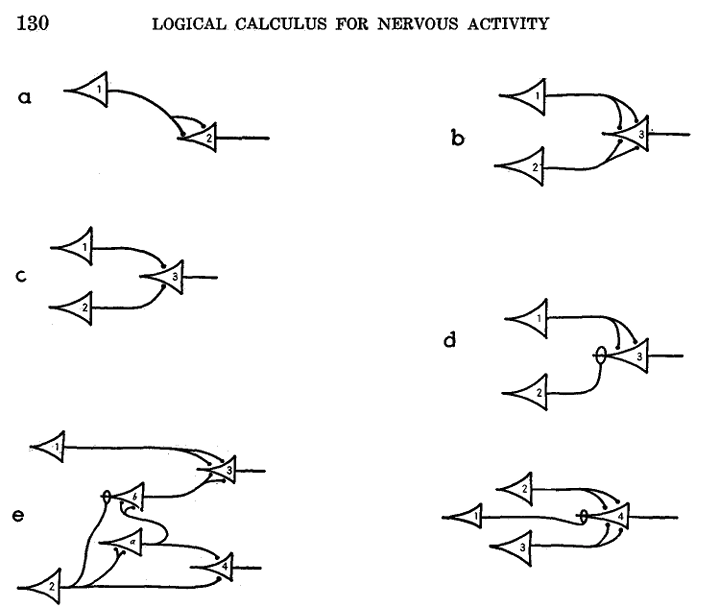
M-P Neuron
1943
McCulloch & Pitts 1943

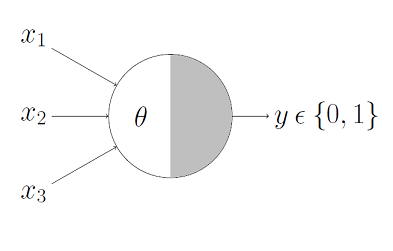
M-P Neuron
1943
McCulloch & Pitts 1943
M-P Neuron
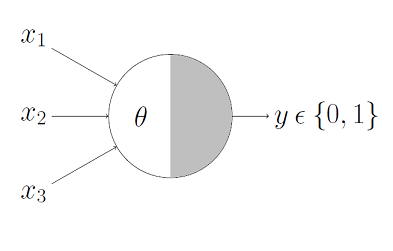

1943
McCulloch & Pitts 1943
M-P Neuron
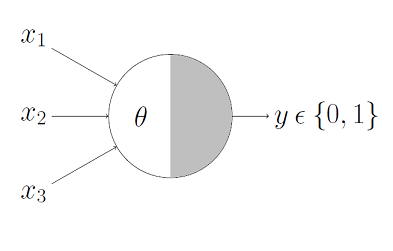

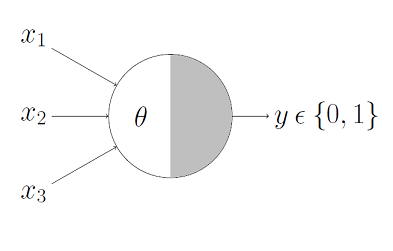

Question:
If is binary (1 or 0) or boolean(True/False)
what value of corresponds to the logical operator AND ?
1943
McCulloch & Pitts 1943
M-P Neuron
If is binary (1 or 0):
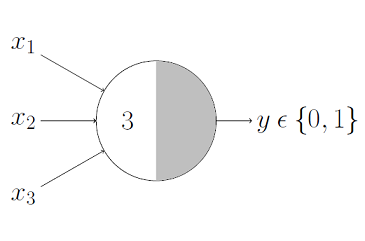
AND
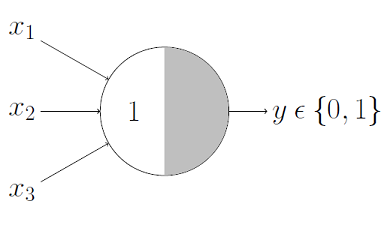
OR
1958
Frank Rosenblatt 1958
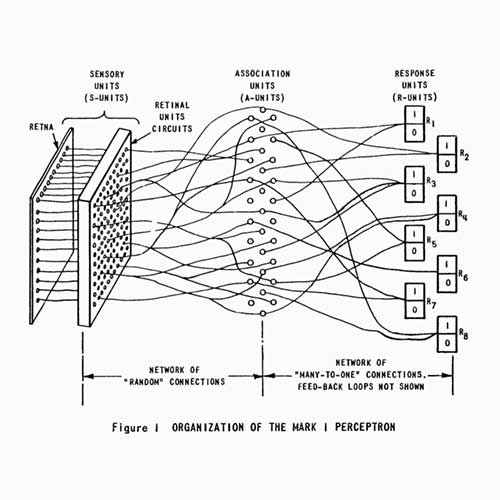
Perceptron


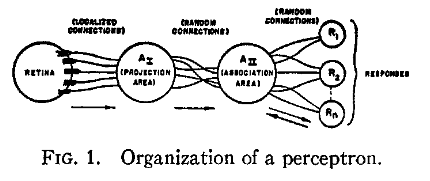
1958
Frank Rosenblatt 1958
Perceptron
.
.
.
output
weights
bias
1958
Frank Rosenblatt 1958
Perceptrons are linear classifiers: make their predictions based on a linear predictor function
combining a set of weights (=parameters) with the feature vector
Frank Rosenblatt 1958
.
.
.
output
linear regression:
weights
bias
Perceptrons are linear classifiers: make their predictions based on a linear predictor function
combining a set of weights (=parameters) with the feature vector
activation function
perceptron

Frank Rosenblatt 1958
.
.
.
output
linear regression:
weights
bias
Perceptrons are linear classifiers: make their predictions based on a linear predictor function
combining a set of weights (=parameters) with the feature vector
activation function
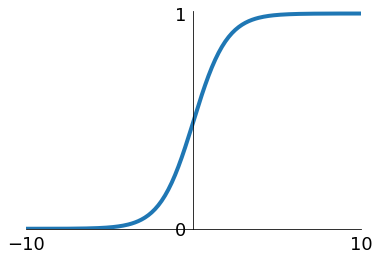
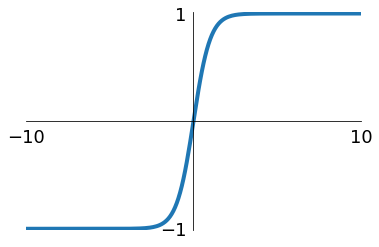
sigmoid
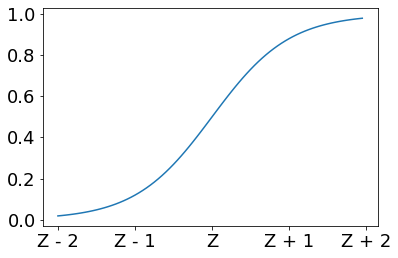
Sigmoid
tanh
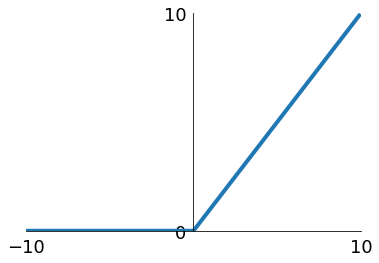
ReLU
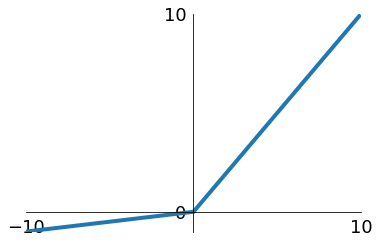
Leaky ReLU
Maxout
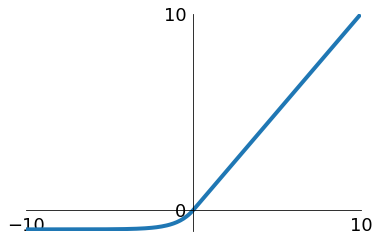
ELU
Frank Rosenblatt 1958
Perceptron

output
linear regression:
weights
bias
activation function
Frank Rosenblatt 1958
Perceptron
.
.
.

Frank Rosenblatt 1958
Perceptron


July 8, 1958
NEW NAVY DEVICE LEARNS BY DOING
Psychologist Shows Embryo of Computer Designed to Read and Grow Wiser
The Navy revealed the embryo of an electronic computer today that it expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence.
The embryo - the Weather Bureau's $2,000,000 "704" computer - learned to differentiate between left and right after 50 attempts in the Navy's demonstration
2
MLP: Multilayer Perceptron
Deep Learning
multilayer perceptron (MLP)
output
layer of perceptrons
multilayer perceptron (MLP)
output
hidden layer
input layer
output layer
1970: multilayer perceptron architecture
Fully connected: all nodes go to all nodes of the next layer
multilayer perceptron (MLP)
output
layer of perceptrons
multilayer perceptron (MLP)
output
layer of perceptrons
multilayer perceptron (MLP)
output
layer of perceptrons
multilayer perceptron (MLP)
output
layer of perceptrons
Fully connected: all nodes go to all nodes of the next layer
multilayer perceptron (MLP)
output
layer of perceptrons
Fully connected: all nodes go to all nodes of the next layer
learned parameters
: weight
sets the sensitivity of a neuron
: bias
up-down weights a neuron
multilayer perceptron (MLP)
output
layer of perceptrons
Fully connected: all nodes go to all nodes of the next layer
: weight
sets the sensitivity of a neuron
: bias
up-down weights a neuron
: activation function
turns neurons on-off
3
DNN: Deep Neural Networks
hyperparameters
output
hidden layer
input layer
output layer
EXERCISE
how many parameters?
output
hidden layer
input layer
output layer
EXERCISE
how many parameters?
21
output
hidden layer 1
input layer
output layer
EXERCISE
how many parameters?
hidden layer 2
output
hidden layer 1
input layer
output layer
EXERCISE
how many parameters?
hidden layer 2
35
output
hidden layer 1
input layer
output layer
how many hyperparameters?
hidden layer 2
- number of layers - 1
- number of neurons/layer -
- activation function/layer -
- layer connectivity -
- optimization metric - 1
- optimization method - 1
- parameters in optimization - M
GREEN: architecture hyperparameters
RED: training hyperparameters
EXERCISE
4
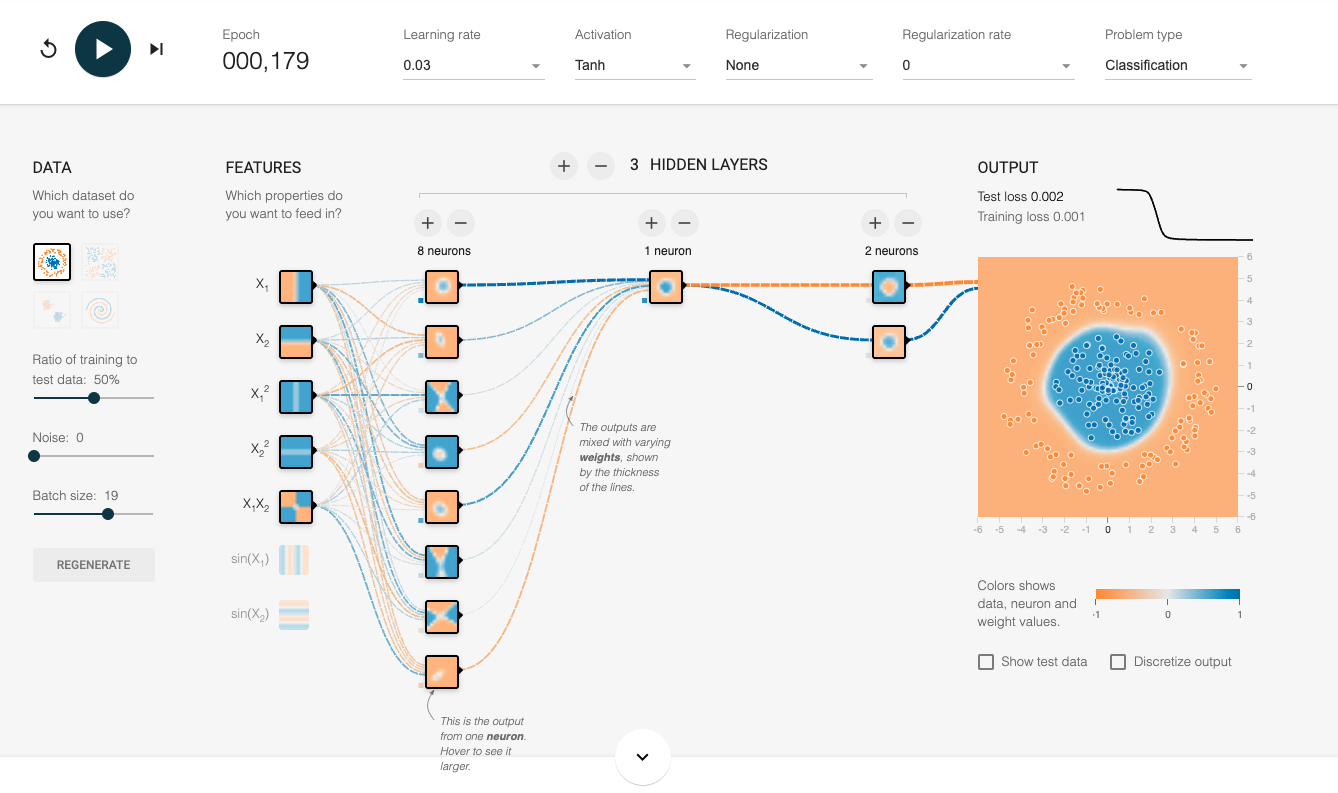
DNN: Deep Neural Networks
training DNN
deep neural networks
1986: Deep Neural Nets
Fully connected: all nodes go to all nodes of the next layer


: activation function
turns neurons on-off
Sigmoid

: weight
sets the sensitivity of a neuron
: bias
up-down weights a neuron
back-propagation
.
.
.
A linear model:
back-propagation
.
.
.
A linear model:
: prediction
: target
Error (e.g.):
back-propagation
.
.
.
A linear model:
Error (e.g.):
Need to find the best parameters by finding the minimum of
: prediction
: target
back-propagation
.
.
.
A linear model:
Need to find the best parameters by finding the minimum of
Stochastic Gradient Descent
Error (e.g.):
: prediction
: target
back-propagation
How does gradient descent look when you have a whole network structure with hundreds of weights and biases to optimize??
output
back-propagation

Rumelhart et al., 1986

Define cost function, e.g.
feed data forward through network and calculate cost metric
for each layer, calculate effect of small changes on next layer
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
back-propagation algorithm:
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
Forward Propagation
back-propagation algorithm:
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
Forward Propagation
back-propagation algorithm:
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
Forward Propagation
back-propagation algorithm:
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
Forward Propagation
back-propagation algorithm:
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
Forward Propagation
back-propagation algorithm:
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
Forward Propagation
back-propagation algorithm:
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
back-propagation algorithm:
Error Estimation

- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
back-propagation algorithm:
Error Estimation

Back Propagation
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
back-propagation algorithm:
Error Estimation

Back Propagation
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
back-propagation algorithm:
Error Estimation

Back Propagation
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
back-propagation algorithm:
Error Estimation

Back Propagation
- randomly assign weights and biases everywhere
- forward propagate through the network to calculate the output (predict the target)
- calculate the cost metric (the error in the prediction)
- backwards propagate through the network, updating weights and biases using stochastic gradient descent
- stop if error is less than a set amount, or after a set number of iterations...otherwise, return to step 2 and repeat
back-propagation algorithm:
Error Estimation

Back Propagation
Repeat!
Punch Line
Simply put: Deep Neural Networks are essentially linear models with a bunch of parameters
Simply put: Deep Neural Networks are essentially linear models with a bunch of parameters
Because they have so many parameters they are difficult to "interpret" (no easy feature extraction)
they are a
Black Box
but that is ok because they are prediction machines
Punch Line
resources
Neural Networks and Deep Learning
an excellent and free book on NN and DL
History of Neural Networks
https://cs.stanford.edu/people/eroberts/courses/soco/projects/neural-networks/History/history2.html