Recursion

Review

  • 把大問題分割成小問題
  • 函式中呼叫自己
  • 定義終止條件
階乘

費氏數列

long long factorial(long long n){
  if(n==1)
    return 1;
  return n*factorial(n-1);
}
long long Fibonacci(long long n){
	if(n==1||n==2)
    	return 1;
    return Fibonacci(n-1)+Fibonacci(n-2);
}

Review

  • 把大問題分割成小問題
  • 函式中呼叫自己
  • 定義終止條件

最大公因數

int gcd(int a, int b){
  if(b==0)
    return a;
  return gcd(b,a%b);
}

14

36

2

28

8

8

1

6

6

1

2

6

3

0

a

b

a%b

Content

  • DP
  • Tower of Hanoi
  • Knapsack problem

Dynamic Programming

想像你是電腦，正在計算費式數列的第n項......

f(6)

f(4)

f(5)

f(2)

f(3)

f(4)

f(3)

f(2)

f(1)

f(1)

f(2)

f(2)

f(3)

f(1)

f(2)

好多東西都重複算喔......可不可以記下結果？

可以喔~我們可以把計算過的先放在陣列中記起來，這就是簡單的DP

long long a[100000];
long long Fibonacci(long long n){
	a[1]=1,a[2]=1;
	for(int i=2;i<=n;i++){
	    a[i]=a[i-1]+a[i-2];
	}
	return a[n];
}
1 1 2 3 5 8 13 21 34 55

Tower of Hanoi

Legend

  1. 把第一根柱子上的圓盤移到第三根上
  2. 大的圓盤不可以疊在小圓盤上
  3. 一次從上面移動一個圓盤

Code

想法：

  1. 把n-1個圓盤移動到第2根柱子上面
  2. 把第n個圓環移動到第3根柱子上面
  3. 把n-1個圓盤移動到第3根柱子上面 
void hanoi(int from, int to, int temp, int n)
{
  if(n==1){
      cout<<"Ring "<<n<<" from "<<from<<" to "<<to<<'\n';
      return;
  }
  hanoi(from,temp,to,n-1);
  cout<<"Ring "<<n<<" from "<<from<<" to "<<to<<'\n';
  hanoi(temp,to,from,n-1);
}

Exercise 1

請輸出n個圓盤從第一根柱子移動到第三根柱子的最少步驟，並且輸出總共幾步。

找找看n和步數之間的關係~

Knapsack Problem

Reference: 資訊之芽語法班2021_遞迴二

What is knapsack problem?

你有一個限制重量W的背包，眼前有n個價值分別為vi、重量為wi的物品，請問你最高可以帶走多少價值的東西？

(假如W=9，跟旁邊的同學討論一下吧~)

W

w (重量) v (價值)
貓頭鷹玩偶 5 30
天使吊飾 3 25
遙控車 6 45
撲克牌 2 20

在找尋過程中，每個物品有「拿」和「不拿」兩種選項，因此如果有n個物品，則有      種可能

2^n

Yes

No

要不要拿

第1個物品？

參數：(拿到第幾個物品, 目前重量, 目前價值)

終止條件： 看完所有物品 || 重量超過背包限制

要不要拿

第2個物品？

Yes

No

Yes

No

要不要拿

第3個物品？

Yes

Yes

Yes

Yes

No

No

No

No

好慢，有沒有什麼可以改良的地方呢？

rec(i,w)定義成可以拿第0到i號的物品，回傳背包w可以裝得下的最大價值

rec(n-1, W)就是答案

rec(i, w)

可拿0~i號，限重w

不拿第i號

拿第i號

rec(i-1, w)

rec(i-1, w-wi)+vi

忽略第i個物品

可裝重量-wi，

答案價值+vi

編號 (i) 0 1 2
重量 (w) 1kg 1kg 2kg
價值 (v) $2 $1 $2

假設W=3，則遞迴樹如下

rec(i,w)定義成可以拿第0到i號的物品，回傳背包w可以裝得下的最大價值

rec(2,3)

rec(1,1)+2

rec(1,3)

rec(0,0)+1

rec(0,1)

rec(0,3)

rec(0,2)+1

rec(0,0)+1

放不了0號

rec(-1,0)

rec(-1,0)+2

rec(-1,1)

rec(-1,1)+2

rec(-1,2)

rec(-1,2)+2

rec(-1,3)

1

2

2

3

3

4

4

int w[MAXN], v[MAXN];
int dp[MAXN][MAXM+1] = {0};

int rec(int i, int W) {
    if (i == -1)
        return 0;
    if (dp[i][W] > 0) 
        return dp[i][W];
    if ( W-w[i] >= 0 ) {
        dp[i][W] = max(rec(i-1, W), rec(i-1, W - w[i]) + v[i]);
    } 
    else {
        dp[i][W] = rec(i-1, W);
    }
    return dp[i][W];
}

Code

DP加上背包問題

More about knapsack problem

類型 大概意思
0/1 背包問題 每個物品只有放和不放兩種選擇
完全背包問題 每個物品可以拿很多個
有限背包問題 物品有數量上的限制

延伸閱讀：Knapsack Problem 演算法筆記

作業：0/1背包問題_zerojudge 開心的金明

詳解：演算法筆記

N-queen

Problem

皇后攻擊範圍是他所在的行和列以及斜線。請問n*n的方格最多可以放下幾個皇后？(0<n<12)

Code

int nq(int n){
  int p[14], total=0;
  for(int i=0;i<n;i++){
    p[i]=i;
  }
  do{
    bool valid=true;
    for(int i=0;i<n;i++){
      for(int j=i+1;j<n;j++){
        if(abs(p[j]-p[i])==j-i){
          valid=false;
          break;
        }
      }
    }
    if(valid){
      total++;
    }
  }while(next_permutation(p,p+n));
  return total;
}

Challenge

今天就決定以這個取代kahoot了~好欸

Competition Rules

請跟旁邊的好同學一起互相討論，達成任務!

(A.) Pascal triangle

(B.) Catalan number

  1. 請從上面題目中選一題，寫好程式，並抓一位學姊，和他解釋你們的想法~~
  2. 最快通過認證的組別可以獲得最新採購的零食！

Pascal triangle

Catalan number

1

1

1

1

2

1

1

3

3

1

1

1

1

1

4

4

6

5

5

10

10

輸入：n 和 m

輸出：第n列，第m個數是什麼？

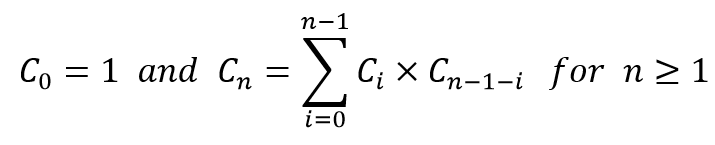
下面是卡特蘭數的遞迴型定義

輸入：n

輸出：第n項是多少？

Made with Slides.com