入營考前練習
結果已經有國手做這樣的簡報了qq
你應該要會的東西
1. 實作能力
熟記的語法:
- algorithm 裡面常用的東西
- stack, queue, deque (也可以陣列實作)
- set, map, priority queue(加自定義運算子)
- string 的操作
- math.h 的一些東西
一些技巧:
- 寫遞迴
- 位元運算子
- 枚舉
2. 演算法的部分 (基礎)
(其實現在補有點太晚了)
- Greedy 的思路(排序)
- 基本動態規劃 (計數,取極值問題)
- 二分搜答案
- 單調隊列
- 前綴與差分
- DFS, BFS
3. 演算法 (進階)
這些也算是重要的
- 樹上演算法(樹直徑、重心)
- 快速冪,矩陣快速冪,模質數的模逆元
- 排列組合,找到 \(C(n, m)\)
- Dijkstra, MST
- BIT 的使用
- 基本線段樹
這幾天建議以「複習」和「加強觀念」為主,不要學了新東西然後中毒ww
好的解題順序
時間複雜度(x
總共三小時五題
可能的時間分佈
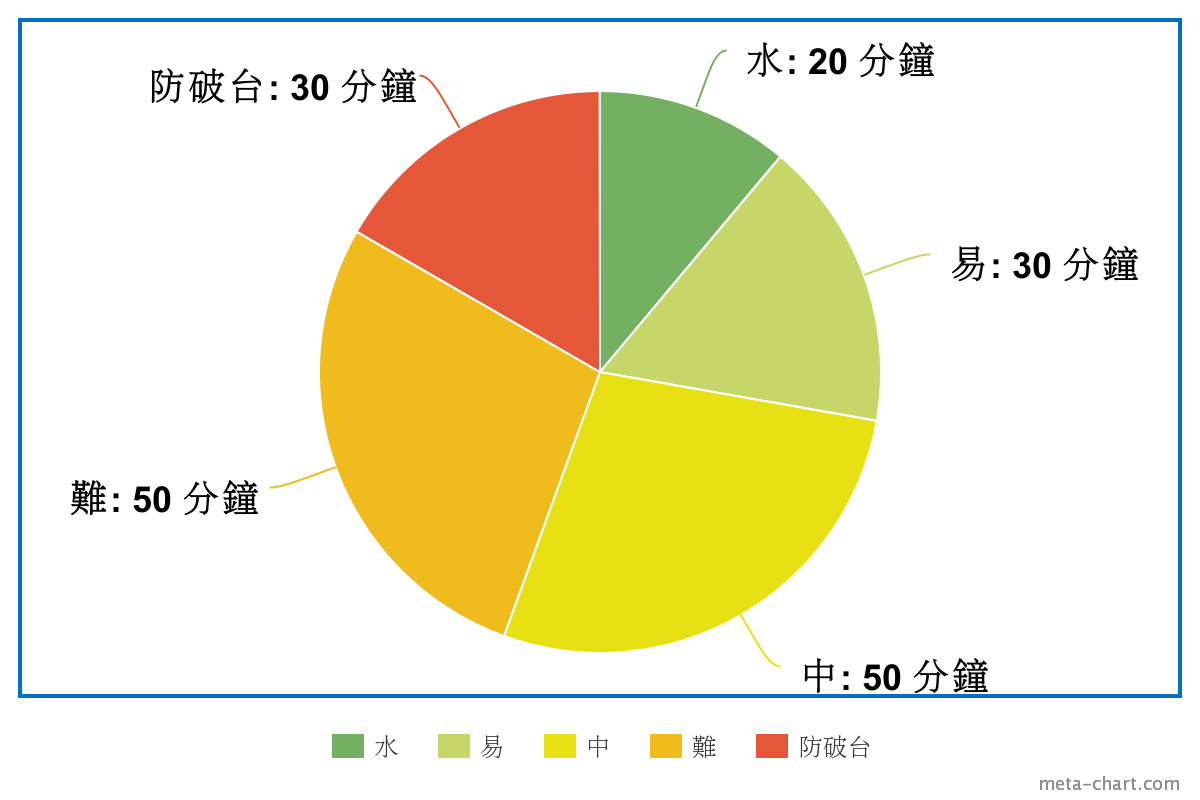
如何辨認題目難度
- 水題通常一眼就看得出做法,只有一點實作
- 實際上,判斷題目難度非常難,但是花個5~10分鐘想過會比較理解題目的難點在哪。
- 不一定要看整題的難度,把每個子問題難度分出來看!
如何辨認題目難度
TOI 專用
有些題目會是數學閱讀題,不要因為題敘很長就完全不看,試著看穿他的廢話ww
我的寫題策略
前15~20分鐘看懂所有題目,紀錄每題大致的內容和已經會做的子問題。
之後在寫的時候知道「哪一些可以拿的部分分還沒拿」
讀題練習!
Mashup Time
(註:以下題目比初選難)
pA. 雪球
在一個下雪的數線上有\(n\)個雪球,一開始第\(i\)個雪球在座標\(x_i\)上(都在不同位置)。對於所有的整數\(i\),在\([i, i + 1)\)的區間積了一單位的雪。
之後會有\(Q\)個事件,每次事件會有數值\(W_i\)的風吹過,使得所有雪球從原本位置移動\(W_i\)格(可以是負數)。每個雪球一開始質量為\(0\),經過有積雪的地方會吸收那邊的雪並增加質量,而該處的雪會消失。
問在所有事件後每個雪球的質量是多少。
pA. 雪球
子問題一:\(n, q \leq 2000\) (33%)
子問題二:\(n, q \leq 2 \times 10^5\) (67%)
對於所有測資,\(\mid x_i \mid, \mid w_i \mid \leq 10^{12}\)
pB. 捷運月票
給你一張\(n\)點\(m\)邊無向連通圖,每條邊有邊權(代價),再給你\(s, t, u, v\)。你必須選擇某一條\(s\) 到\(t\)的最短路(邊權總和最小),而將那條路上的每一條邊權改成\(0\)。請輸出改完邊之後,從\(u\)到\(v\)的最小路徑代價和。
pB. 捷運月票
對於所有測資:
\(n \leq 10^5, m \leq 2 \times 10^5\)
邊權 \(c_i \leq 10^9\)
子問題一:\(s = u\) (18%)
子問題二:\(s\)到\(t\)的最短路唯一 (15%)
子問題三:\(n \leq 300\) (24%)
子問題四:無其他限制 (45%)
pC. 數數列
給定\(x, y\),找出有多少個正整數序列\(A\) (每一項都是正整數),使得每一項的最大公因數是\(x\)且總和為\(y\)。
pC. 數數列
對於所有測資:
\(x, y \leq 10^9\)
子問題一:\(y\)是質數(14%)
子問題二:\(x, y \leq 10^6\) (30%)
子問題三:無其他限制 (56%)
pD. 走迷宮
給你一個字串,每個字元是 'L', 'R',請構造出一個簡單多邊形(邊不能在非頂點的地方相交),且每條邊平行 \(x\) 軸或\(y\)軸,
使得你從多邊形的一個頂點開始逆時針走,依序遇到的第\(i\)個轉角方向和第字串第\(i\)個字元相同(往左轉->L, 右轉->R)
保證有解。
pD. 走迷宮
子問題一:\( \mid S \mid \leq 5000\) (50%)
子問二:\( \mid S \mid \leq 10^5\) (50%)
pE. 圖書館
有\(n\)個學生和\(m\)個教授要去圖書館看一本書(現場看完),每個人有他到圖書館的時間\(t_i\)和他閱讀一本書需要的時間 \(w_i\)。每個人可以在 \( \geq t_i \)的時間開始閱讀,並且一次就要讀完 \( w_i\)。學生可以跟其他人一起看,但是教授必須全程自己看。請問所有人看完的最小時間是多少?
pE. 圖書館
對於所有測資:
\(n, m \leq 3000\)
\(t_i \leq 10^7, w_i \leq 10^5\)
子問題一:\(n, m \leq 10\)(22%)
子問題二:\(n, m \leq 300\) (35%)
子問題三:無其他限制 (43%)
實作/除蟲能力
平常就要練的實作
-
程式碼可讀性
-
變數名稱
-
使用函式、類別
-
- 常用模板的熟練度
- 可以練到每次都寫的幾乎一樣
- 保持頭腦清楚
- 用紙筆幫助思考
- 在實作前先想實作細節!
除蟲的時候
-
重新讀一次題目,確定你沒有理解錯題意,並注意數字範圍、long long、取模等問題
-
把程式碼分成一個個部分看,檢查完一個部分之後相信他是對的,並轉移焦點(不要一直盯著同一個地方)
- 對拍 (#jassorz)
- 重寫一遍 (不推薦)
- 不要de太久,先去寫別題!
注意時間!
@全國賽燒雞
在開始寫一題之前告訴自己:我大概會寫多久
超過這個時間太多就強制跳過