MAA5: Analyyttinen geometria 3/5
SUORA
SUORAN SUUNTA
SUORAN YHTÄLÖ
SUORIEN LEIKKAUSPISTE
SUORIEN VÄLINEN KULMA
SUORIEN KOHTISUORUUS
Suoran suunta

Kulmakerroin
Pisteiden
ja
kautta kulkevan suoran kulmakerroin on
HUOM! Pystysuoralla suoralla ei ole kulmakerrointa.
Suoran suuntavektori
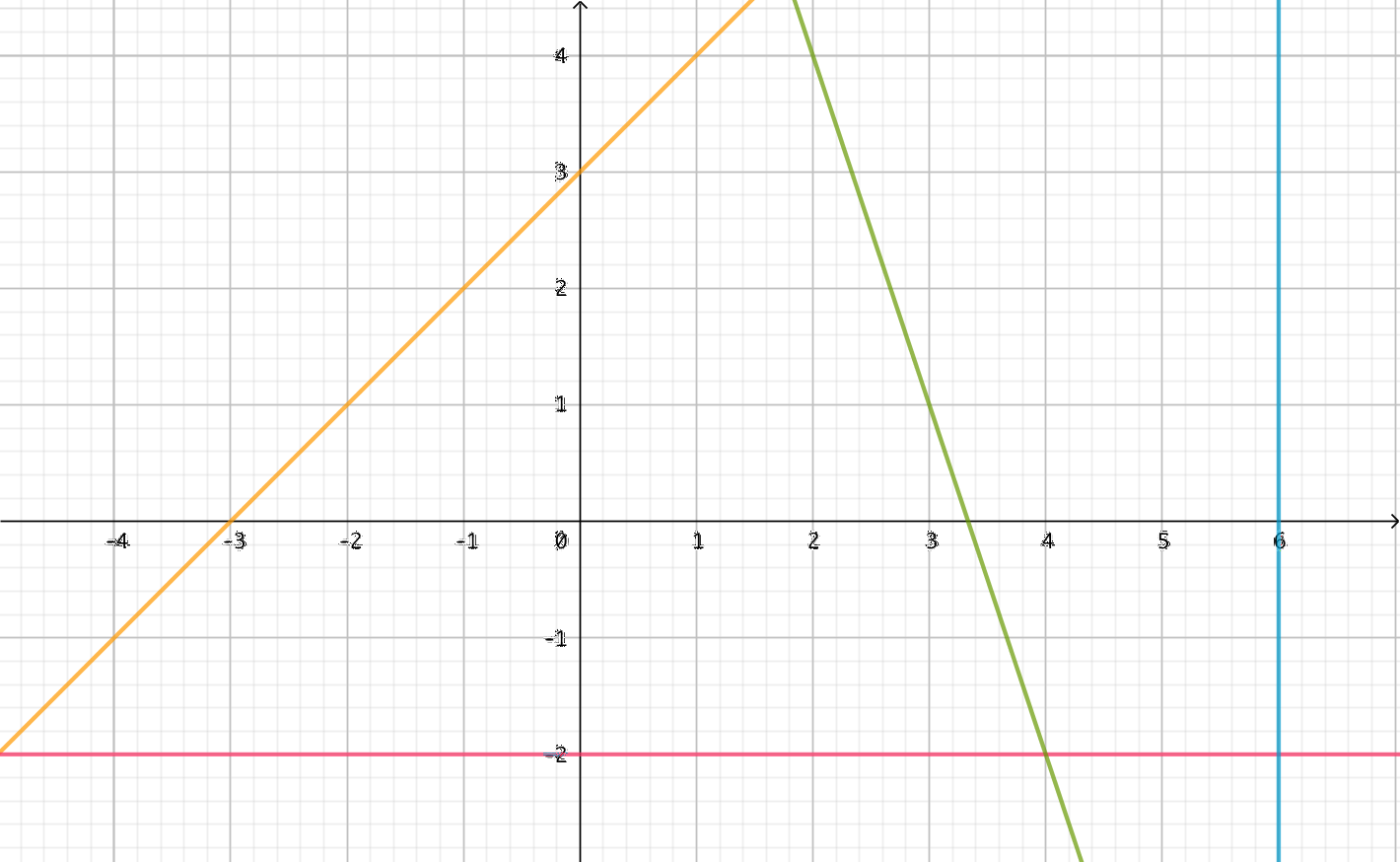
Määritä kullekin suoralle jokin suuntavektori.
Suuntakulma
Tason suoran suuntakulma on suoran ja x-akselin positiivisen suunnan välinen kulma, jonka etumerkki määritetään seuraavasti:

Nouseva suora
Laskeva suora
Vaakasuora
Pystysuora
Lause
Suoran kulmakerroin k on suuntakulman tangentti eli
Lause
Suorat ovat yhdensuuntaiset, jos ja vain jos
- niillä on sama kulmakerroin
- molemmat suorat ovat y-akselin suuntaisia.
Suoran yhtälö
Lause
Jos suora kulkee pisteen kautta ja sen kulmakerroin on k, suoran yhtälö on
Suoran yhtälön ratkaistu muoto
Suoran yhtälön normaalimuoto

Suora leikkaa y-akselin pisteessä (0, b)
Harjoittele suoran yhtälön määrittämistä kulmakertoimen ja vakiotermin avulla:
Määritä suoran yhtälö kahden pisteen avulla. Tarkista ratkaisusi syöttämällä suoran yhtälö vastauskenttään. Saat malliratkaisun näkyville klikkaamalla Ratkaisu-painiketta.
Suorien leikkauspiste
- Suorien leikkauspisteellä tarkoitetaan sitä pistettä, jossa suorat leikkaavat. Kyseisessä pisteessä molempien suorien x- ja y-koordinaatit ovat samat.
- Suorien leikkauspiste voidaan ratkaista
- graafisesti eli piirtämällä
-
algebrallisesti eli laskemalla.
- Kuvasta katsomalla ei saada selville leikkauspisteen tarkkoja koordinaatteja, joten leikkauspiste täytyy selvittää laskemalla!
- Leikkauspisteen koordinaatit saadaan selville yhtälöparin avulla
Yhtälöparin ratkaiseminen
- sijoitusmenetelmä
- yhteenlasku- eli eliminointimenetelmä
-
CAS-laskenta
- GeoGebra: Ratkaise(<Yhtälölista>,<muuttujalista>)
Suorien välinen kulma
Lause
Jos suorat m ja n eivät ole kohtisuorassa toisiaan vastaan, niiden välinen kulma toteuttaa yhtälön
Suorien kohtisuoruus
Lause
Suorat ovat kohtisuorassa toisiaan vastaan, jos ja vain jos niiden kulmakertoimien tulo on -1 tai suorat ovat koordinaattiakselien suuntaiset.
Pisteen etäisyys suorasta
Pisteen etäisyys suorasta on