MAB6: Talousmatematiikka 1/5

TALOUS-MATEMATIIKKA

MAB6: Talousmatematiikka

Talousmatematiikan kurssin tavoitteena on, että

  • oppisit ymmärtämään paremmin talouselämässä käytettyjä käsitteitä,
  • saisit matemaattisia valmiuksia oman taloutesi suunnitteluun,
  • saisit laskennallisen pohjan yrittäjyyden ja taloustiedon opiskeluun sekä
  • oppisit soveltamaan tilastollisia menetelmiä aineistojen käsittelyyn.

Arviointi

  • koe
    • ​saatava vähintään 30 % pisteistä
  • käsitetestit (2 kpl)
  • projektityö
  • tehdyt kirjan tehtävät
    • ​tehtävä vähintään 30 % annetuista tehtävistä
  • arvioitavat tehtävät

Kurssin eteneminen

Kurssin aloitus:

  • tavoitteet ja sisällöt
  • kurssin käytännöt ja arviointi
  • Talousmatematiikka
  • prosenttilaskennan kertausta

OSIO 3: RAHA

  • hintakehitys
  • rahan arvo
  • indeksilaskenta
  • valuutat

OSIO 2: VEROTUS

  • ansiotuloverotus
  • pääomatuloverotus
  • perintö- ja lahjaverotus
  • arvonlisävero

OSIO 4: LAINAT JA LUOTOT

  • lainan hakeminen
  • tasalyhennyslaina
  • tasaerälaina
  • muut lainat ja luotot

OSIO 5: SÄÄSTÄMINEN JA SIJOITTAMINEN

  • pankkitalletukset
  • osakkeet ja sijoitusrahastot

OSIO 1: TALOUS

  • yksilön talous: prosenttilaskennan kertaus
  • yrityksen talous: katetuottolaskenta

KERTAUS

TALOUS

Yksilön talous

Yrityksen talous

Mitä tarkoittaa talous?

  • Talous on ilmiö, jonka lähtökohtana on ihmisen tarve, jonka jokin toinen taho pyrkii täyttämään tuottamalla tarvetta vastaavan hyödykkeen.
  • Talous on tarpeeseen perustuvaa ihmisten välistä kanssakäymistä, joka liittyy hyödykkeiden tuotantoon, jakeluun, vaihtoon ja kulutukseen
  • Talouden toimiminen on elinehto ihmiskunnalle!​
  • Taloustilannetta kuvataan erilaisten tunnuslukujen avulla.
  • Taloustilannetta tarkasteltaessa puhutaan usein talouskasvusta.

Talousmatematiikka

Taloudellisia ilmiöitä voidaan tarkastella kolmesta eri näkökulmasta:

  1. Julkinen talous
  2. Yrityksen talous
  3. Yksilön talous

Julkinen talous

= Kunnan tai valtion tulot ja menot

  • menot:
    • julkiset palvelut: terveyden huolto, koulujärjestelmä, kirjastot, vesihuoltojärjestelmä, tieverkosto, rautatiet, lentokentät, poliisi, palokunta
    • tulonsiirrot: työttömyyskorvaukset, asumistuki, opintoraha, kansaneläke, lapsilisät
    • palkat

Yhteiskuntaoppi

MAB6: OSIO 2

  • tulot:
    • verot ja veronluonteiset tulot
    • lainat
    • pääomatulot
    • muut tulot

Yrityksen talous

= yrityksen tulot ja menot

  • investointikulut
  • verot ja verojen kaltaiset maksut
  • myyntituotto

Yksilön talous

  • verotus
  • sijoittaminen
  • lainaaminen
  • oman talouden suunnitteleminen
    • ​tulot
    • kiinteät menot
    • muuttuvat menot

OSIO 1

OSIO 2

OSIO 4

OSIO 5

Oman talouden suunnitteleminen

  • Laadi budjetti.
  • Säästä.
    • Pidä säästämäsi rahat eri tilillä kuin päivittäisiin menoihin tarkoitettu käyttötilisi.
    • Siirrä saamistasi tuloista säästettävä osuus (esim. 20 %) heti säästötilille.
  • Varaudu yllättäviin menoihin ja elinkustannusten nousuun. ○ Varatilillä on hyvä olla käteistä usean kuukauden menojen verran.
    • Meneekö taloutesi sekaisin, jos esimerkiksi jääkaappi ja pesukone menevät yhtä aikaa rikki?
    • Sijoita tuottavasti.
    • Huolehdi, että vakuutuksesi ovat kunnossa.
    • Lainanottotilanteessa laske ennakkoon, miten suuren lainan voit ottaa.
    • Kilpailuta lainat, sähkö, puhelinliittymä ja vakuutukset.
    • Pidä huolta kyvystäsi ansaita. Huolehdi siis omasta terveydestäsi ja kehitä osaamistasi.

Yksilön talous

Yksilön talous

Prosenttilaskennan kertaus

Vuonna 2017 opiskelijan oli mahdollista saada opintorahaa 250,28 €/kk, opintolainaa 650 €/kk ja yleistä asumistukea 80 % hyväksyttävien asumismenojen määrästä. Olga opiskelee Jyväskylässä ja asuu soluasunnossa, jonka vuokra on 251 €/kk. Kuinka paljon Olgalle jää rahaa vuokran jälkeen käytettäväksi kuukaudessa, kun hän ei käy töissä ja nostaa opinto- ja asumistukien lisäksi opintolainan maksimimäärän?

Esimerkki 1

LibreOffice Calc

  • Esimerkiksi kustannuslaskelmissa, verotuksessa ja korkolaskennassa pitää hallita prosenttilaskentaa.

Prosenttilaskennan kertaus

Kuinka paljon on p % luvusta a?

Kuinka paljon on 12 % luvusta 140?

\frac{p}{100}\cdot a
\frac{12}{100}=0,12
1\ \%=\frac{1}{100}=0,\!01

Prosenttikertoimen muodostaminen

80\ \%=\frac{80}{100}=0,\!80
120\ \%=\frac{120}{100}=1,\!20
0,\!12\cdot 140=16,\!8

Kuinka monta prosenttia a on luvusta b?

Kuinka monta prosenttia 14 on luvusta 80?

\frac{a}{b}\cdot 100\ \%
2) \ \frac{14}{80}\cdot 100\ \%=17,\!5 \ \%
1) \ \frac{14}{80}=0,\!175=17,\!5 \ \%

Kuinka monta prosenttia suurempi luku a on kuin luku b?

Kuinka monta prosenttia suurempi luku 150 on kuin 140?

\frac{a-b}{b}\cdot 100\ \%
1)\ \frac{150-140}{140}=0,\!0714...\approx 7,\!1 \ \%
2) \ \frac{150-140}{140}\cdot 100\ \%\approx 7,\!1 \ \%

Prosenttilaskennan kertaus

Kuinka monta prosenttia pienempi luku a on kuin luku b?

Kuinka monta prosenttia pienempi 45 on kuin 55?

\frac{a-b}{a}\cdot 100\ \%
1)\ \frac{55-45}{55}=0,\!1818..\approx 18,\!2 \ \%
2) \ \frac{55-45}{55}\cdot 100\ \%\approx 18,\!2 \ \%

Luku a kasvaa p %. Mikä on muuttunut arvo?

Luku 200 kasvaa 13 %.

\frac{100+p}{100}\cdot a
100\ \%+13\ \%=113\ \%=1,\!13
1,\!13\cdot 200=226

Luku a pienenee p %. Mikä on muuttunut arvo?

Luku 200 pienenee 13 %.

\frac{100-p}{100}\cdot a
100\ \%-13\ \%=87\ \%=0,\!87
0,\!87\cdot 200=174

Perus: 4, 5, 6

Luku 1:

Harjoitukset

Luku 1.1:

Perus: 1, 2, 4, 5

Taitaja: 9

Yrityksen talous

 

  • Kannattaako toiminta lyhyellä aikavälillä tarkasteltuna?
    • ​Kannattavuuteen vaikuttavat tulot ja menot.
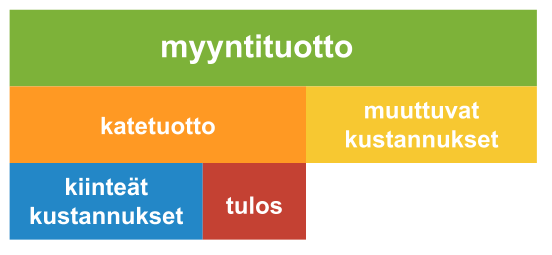
  • Myyntituotto
    • ​Lasketaan kaikkien myytyjen tuotteiden arvonlisäverottomat hinnat yhteen

Myyntituotto = arvonlisäveroton myyntihinta ∙ myyntimäärä

  • Kokonaiskustannukset jaotellaan muuttuviin ja kiinteisiin kustannuksiin.​
    • Muuttuvat kustannukset
      • ​muuttuvat samassa suhteessa myynnin tai tuotannon määrän kanssa.
      • myytävien tuotteiden ostohinnat, raaka-ainekustannukset, koneiden energiankulutus
    • Kiinteät kustannukset
      • eivät välittömästi muutu tuotannon tai myynnin määrän muuttuessa
      • tila- ja laitevuokrat, kiinteät palkat, markkinointikustannukset, hallinnon kustannukset, lämmitys-, siivous-, tietoliikenne- ja edustuskulut

Katetuottolaskenta

Katetuotto = myyntituotto – muuttuvat kustannukset

  • Katetuottoprosentti (KTP)
    • ​ ilmoittaa prosentteina, kuinka suuri osuus yrittäjälle jää tuotteen myyntihinnasta, kun siitä on vähennetty tuotteen muuttuvat kustannukset.
  • Tulos kertoo
    • onko yritys kannattava.
    • Tulokseen vaikuttaa myyntihinta, muuttuvat kustannukset, kiinteät kustannukset ja myyntimäärä.

Tulos = katetuotto – kiinteät kustannukset

  • Katetuotto
    • saadaan, kun myyntituotosta vähennetään kiinteät kustannukset

Kriittinen piste

  • On toiminta-aste, jossa myyntituotot ja kokonaiskustannukset ovat yhtä suuret.
    • ei synny voittoa eikä tappiota
  • Ilmoitetaan joko myyntituottona (€) tai tuotemääränä (kpl)

Perus: 2, 4, 5, 6

Luku 1.2:

Harjoitukset

Esimerkki 2

Jäätelökioskilla yhden irtojäätelöpallon veroton hinta on 2,90 €. Jäätelökioskilla myydään kesäkuun aikana 2300 yhden jäätelöpallon annosta. Muuttuvat kustannukset ovat 0,85 €/annos ja kiinteät kustannukset 2150 euroa. Kuinka suuren tuloksen jäätelökioski tekee kesäkuussa?

Ratkaisu:

1) Lasketaan jäätelökioskin kesäkuun myyntituotto:

2300\cdot2{,}90\ €=6670\ €

2) Lasketaan jäätelökioskin kesäkuun muuttuvat kustannukset:

2300\cdot 0{,}85\ €=1955\ €

3) Lasketaan jäätelökioskin kesäkuun katetuotto:

Katetuotto = Myyntituotto - Muuttuvat kustannukset

4) Jäätelökioskilla on kesäkuussa kiinteitä kustannuksia 2150 €.

6670\ €-1955\ €=4715\ €

5) Lasketaan jäätelökioskin kesäkuun tulos:

Tulos = Katetuotto - Kiinteät kustannukset

4715\ €-2150\ €=2565\ €

Vastaus:  Jäätelökioskin kesäkuun tulos on 2 565 €