組合賽局
- 兩位玩家輪流操作(通常我們習慣叫他們L和R)
- 資訊完全:雙方都知道現在的遊戲狀態也知道他們兩方可以移動到的狀態
-
雙方的行動是決定性的:操作是確定性的,無隨機成分。
-
結局分為勝、敗(、平手)
定義
通常一個狀態G會寫成\lbrace G^L\mid G^R\rbrace \\
其中G^L是L操作後能到的狀態的集合
分類
| 雙方合法操作異同 | 無偏(Impartial) | 有偏(Partial) |
| 有限步內結束與否 | 無環(Loopfree) | 有環(Loopy) |
| 玩法(不只有這兩種) | 標準(Normal) | 匱乏(Misère) |
接下來預設都是無篇無環標準
ZERMELO'S THEOREM
對於一個無環的組合賽局,以下敘述必恰有一條成立
- 先手有必勝策略
- 後手有必勝策略
- 雙方皆有必不敗策略(如果結局可能為平手)
GAME GRAPH
把遊戲中的每個狀態當成一個點
有兩種有向邊表示L和R分別能走的路
無偏無環標準
因為是無偏的所以勝敗只和先後手有關係
把狀態分成N(next 先手勝)和P(previous 後手勝)的型別
可以發現
N一定能走一步到一個P
P一定走一步只能到N
⇧這是充要的,但只會有一種分法嗎
N和P
會出現兩個人都不想走出去的時候,
我們把它稱為D(draw)
發現D要能走一步到一個D然後沒有一個P
有環了
所以要怎麼算
出度為0的點就會知道他是P
一直拔出度為0的點標成P
戳到P的都標成N然後拔掉
剩下都是D
有偏了
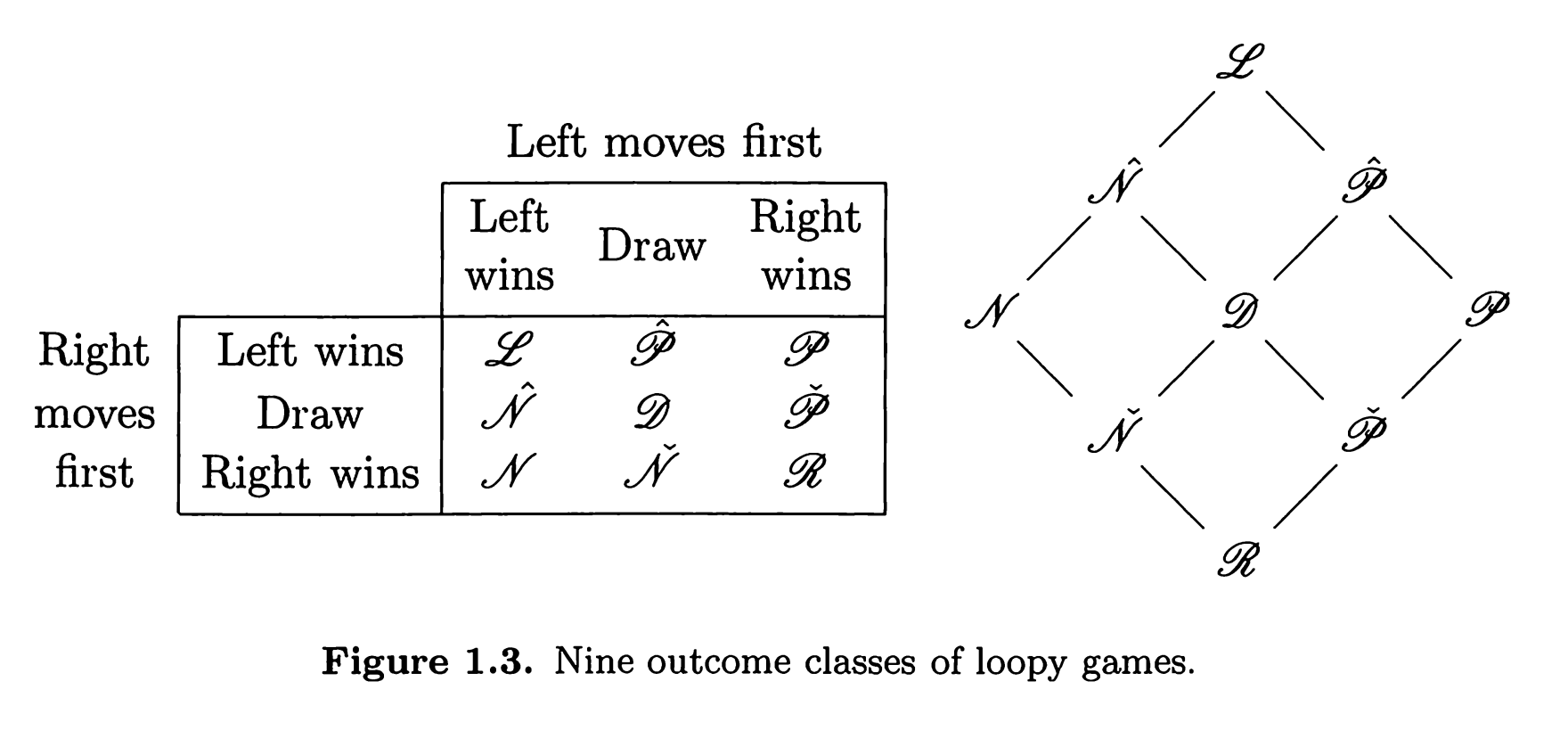
by combinatorial game theory
拿石頭
有若干堆石頭,每堆數量不一
雙方在自己的回合可以選擇其中一個非空的石堆
並拿取若干顆石頭(至少一顆)
拿走最後一顆石頭的人贏
NIm
把一個狀態賦值成每堆石頭xor起來
是P↔賦值是0
亂配對
賽局和和等價類
一個賽局玩不夠 那就玩兩個
有兩個賽局G和H\\
定義賽局G+H就是把他們放在一起\\
操作就是選一邊動一步\\
\\
和nim很像
有交換律和結合律
等價賽局
G,H型別相同記為G\approx H\\
\\
我們說G_1和G_2等價若且唯若對所有賽局H\\
有G_1+H\approx G_2+H\\
記作G_1\simeq G_2
等價賽局
P+P\approx P\\
N+P\approx N\\
G+G\approx P\\
所有P相互等價\\
G+H\approx P\Longleftrightarrow G\simeq H
對於一狀態�G
遞迴定義其SG value為
該狀態可轉移到的所有點之SG value取mex
設只有一堆x個石頭的nim叫
那有 (SPRAGUE-GRUNDY THEOREM)
證明就來看 的型別
然後就能發現P的SG value 都是0
SG value
N_x
G\simeq N_{SG(G)}
G+N_{SG(G)}
就我們可以開心地把兩個賽局加起來
然後只要把SG value xor 起來就好
加起來
匱乏
G是N若且唯若G不能動了或G能走到一個P
P/N
策略:
- 若各堆石頭數都只剩0 or 1顆,則只剩奇數/偶數顆時後手/先手必勝
- 若只剩一堆有超過1顆石頭,那就拿到剩下奇數個每堆1顆的石頭
- 否則應將各堆顆數的xor sum變成0
2只在xor sum 非零時會出現
匱乏nim
題目
參考資料
Combinatorial Game Theory by Aaron N. Siegel
有人要揪一起讀嗎
延伸閱讀
如果還有時間就抓數讀講義講或來看hackenbush