排列組合

Lecturer：20516 陳亮延

前導

1.排列組合很吃天分

2.排列組合思維很自由

3.大多數人不會用這個思維上課

4.大多數人聽不懂這個思維

Index

排列

組合

基本定理

跳過上次ㄉ邏輯與集合

1

什麼是排列組合

2

樹狀圖（窮舉法）

3

加法原理

5

階乘( ! )

4

乘法原理

1

什麼是排列組合

次序性

可能性

just排列

選擇

1

什麼是排列組合

次序性

just排列

選擇的結果

選擇

可能性

1

什麼是排列組合

just排列

選擇的結果

選擇的過程

次序性

選擇

選擇的結果

選擇的過程

次序性

選擇的過程

選擇

1

什麼是排列組合

2

樹狀圖

把所有結果列舉出來！

\begin{cases} \ A\ \begin{cases} \ B\ -\ C\\ \ C\ -\ B\\\end{cases}\\ \ B\ \begin{cases} \ A\ -\ C\\ \ C\ -\ A\\\end{cases}\\ \ C\ \begin{cases} \ A\ -\ B\\ \ B\ -\ A\\\end{cases}\\ \end{cases}

\begin{Bmatrix} (A,B,C),(A,C,B),\\ (B,A,C),(B,C,A),\\ (C,A,B),(C,B,A)\end{Bmatrix}

Ｑ: 請列舉 A, B, C 排列的結果（元素不可重複使用）

總共六種結果

什麼是排列組合

把所有結果列舉出來！

Ｑ:甲乙隊打比賽（五戰三勝），請問有幾種勝負過程？

甲\begin{cases} 甲\begin{cases} 甲\\ 乙\begin{cases} 甲\\ 乙\begin{cases} 甲\\乙 \end{cases} \end{cases} \end{cases}\\ 乙\begin{cases} 甲\begin{cases} 甲\\ 乙\begin{cases} 甲\\乙 \end{cases} \end{cases}\\ 乙\begin{cases} 甲\begin{cases} 甲\\乙 \end{cases}\\ 乙 \end{cases} \end{cases} \end{cases}

甲一開始獲勝，有10種結果

乙一開始獲勝與甲一開始獲勝等價

（起始狀態相同、競爭公平）

共有10+10=20種過程

樹狀圖的對稱性(元素狀態等價)

2

樹狀圖

什麼是排列組合

怎麼用程式模擬樹狀圖的繪製？

Sol：遞迴！

e.g. 請列舉出A, B, C, D所有排列的結果

#include <iostream>
#include <set>
#include <vector>
using namespace std;

set<char>temp;
string u={"ABCD"};
int size=4;
vector<char>resalt;
void f(int step)
{
  if(step==size)
  {
    for(auto i:resalt)cout<<i;
    cout<<'\n';
    return;
  }
  for(int n=0;n<size;n++)
  {
    if(temp.count(u[n]))continue;
    resalt.push_back(u[n]);
    temp.insert(u[n]);
    f(step+1);
    temp.erase(u[n]);
    resalt.pop_back();
  }
  return;
}
int main()
{
  f(0);
}

#include <set> //引入

set<type>a; //宣告

a.insert(x); //插入x (將x加入集合a)

a.erase(x); //刪除x (將x移出集合a)

a.count(x) //檢測x是否屬於a

a.size() //n(a)

a.empty() //集合a是否為空集合

※補充 set就是集合用法如下演算法會教

2

樹狀圖

什麼是排列組合

怎麼用程式模擬樹狀圖的繪製？

Sol：遞迴！

※補充 map是可以自訂索引值型態的STL

　有點像自訂索引值型別ㄉ陣列

#include <map> //引入

map<key_type,type>a; //宣告(儲存值皆預設0)

a[x]=123; //a裡面x對應的值設為123

a[-1]=123; //負數也能當索引值

#include <iostream>
#include <map>
#include <vector>
using namespace std;

map<string,int>temp;
string u[2]={"甲","乙"};
int size=2;
vector<string>resalt;
void f(int step)
{
  if(temp["甲"]==3||temp["乙"]==3)
  {
    for(auto i:resalt)cout<<i;
    cout<<'\n';
    return;
  }
  for(int n=0;n<size;n++)
  {
    //if(temp[u[n]])continue;
    resalt.push_back(u[n]);
    temp[u[n]]++;
    f(step+1);
    temp[u[n]]--;
    resalt.pop_back();
  }
  return;
}
int main()
{
  f(0);
}

e.g.請列出甲乙隊打比賽（五戰三勝）可能過程？

Try Try See NEOJ 2024

試試遞迴作法ㄅ

2

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

陳亮延要怎麼去上資芽語法班？

公車：棕22
公車轉公車：630+1
公車轉捷運：630 / 12 / 212直 / 中山幹線+綠線
YouBike：河濱公園
還沒蓋好的捷運：萬大線轉綠線

方法數 = 1 + 1 + 4 + 1 + 1 = 8種

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

1	7	28	84	210	462	924	1716	3003
1	6	21	56	126	252	462	792	1287
1	5	15	35	70	126	210	330	495
1	4	10	20	35	56	84	120	165
1	3	6	10	15	21	28	36	45
1	2	3	4	5	6	7	8	9
1	1	1	1	1	1	1	1	1

從Ａ走到Ｂ的

最短路徑量？

走到B=走到C+走到D

設定好邊界路徑量=1

每點值＝左值＋下值

一層一層向內

即可推斷解答

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

ZeroJudge d212 東東爬樓梯

可以選擇走一層或兩層

走到第 n 層的方法數，即走到 n-1 的方法數+走到 n-2 的方法數

⇒ 遞迴？

#include <iostream>
using namespace std;
int f(int a)
{
  if(a<=1)return 1; //邊界
  return f(a-1)+f(a-2);
}
int main()
{
  int x;
  while(cin>>x)cout<<f(x)<<'\n';
}

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

同樣的東西重複計算

[5]

[4]

[3]

[2]

[1]

[0]

[1]

[2]

[1]

[0]

[3]

[2]

[1]

[0]

把算過的東西記下來?

[5]共計算了14次

記憶化(memoization)！

(或DP (Dynamic Programming))

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

[0]	[1]	[2]	[3]	[4]	[5]
1	1

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

[0]	[1]	[2]	[3]	[4]	[5]
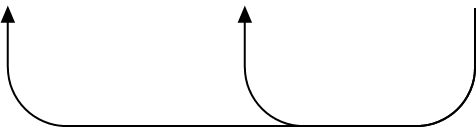
1	1	2

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

[0]	[1]	[2]	[3]	[4]	[5]
1	1	2	3

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

[0]	[1]	[2]	[3]	[4]	[5]
1	1	2	3	5

樹狀圖

什麼是排列組合

3

加法原理

把所有選擇加起來！

#include <iostream>
using namespace std;
int main()
{
  long long a[101]; //index為階數
  a[0]=1; //邊界
  a[1]=1; //邊界
  for(int n=2;n<101;n++)a[n]=a[n-1]+a[n-2];
  int x;
  while(cin>>x)cout<<a[x]<<'\n';
}

類題：

警報器長響 2s、短響 1s，

每響間間隔 1s，

響到第15秒有幾種響法？

A: 37種

樹狀圖

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

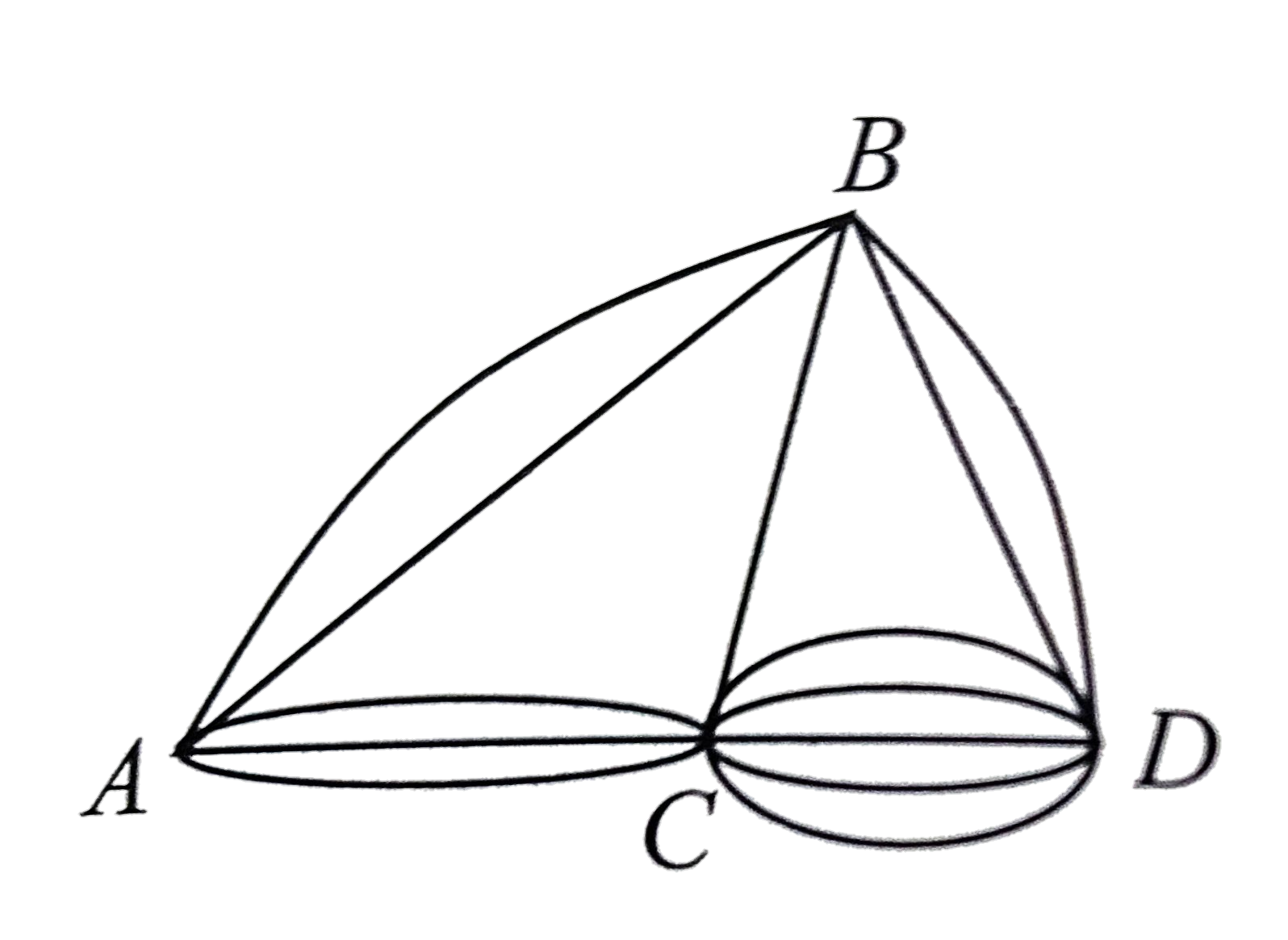
Ａ走到Ｄ，不重複過點，

共有　　　種走法？

2\times1\times5=10

2\times2=4

3\times5=15

3\times1\times2=6

10+4+6+15=35_\#

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

求540之因數內

個數？
和？
完全平方數個數？
完全平方數和？
為12的倍數而非5的倍數個數？
為12的倍數而非5的倍數和？

540=2^2+3^3+5^1

質因數相乘 = 因數

因數個數 = 質因數取捨

|S|=3\times4\times2=24

S=\{2^0,2^1,2^2\}\times\{3^0,3^1,3^2,3^3\}\times\{5^0,5^1\}

\begin{aligned} 和&=(2^0+2^1+2^2)(3^0+3^1+3^2+3^3)(5^0+5^1)\\ &=(1+2+4)(1+3+9+27)(1+5)\\ &=7\times40\times6\\ &=1680 \end{aligned}

(分配律)

A: 24

A: 1680

A: 4

A: 50

A: 3

A: 156

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

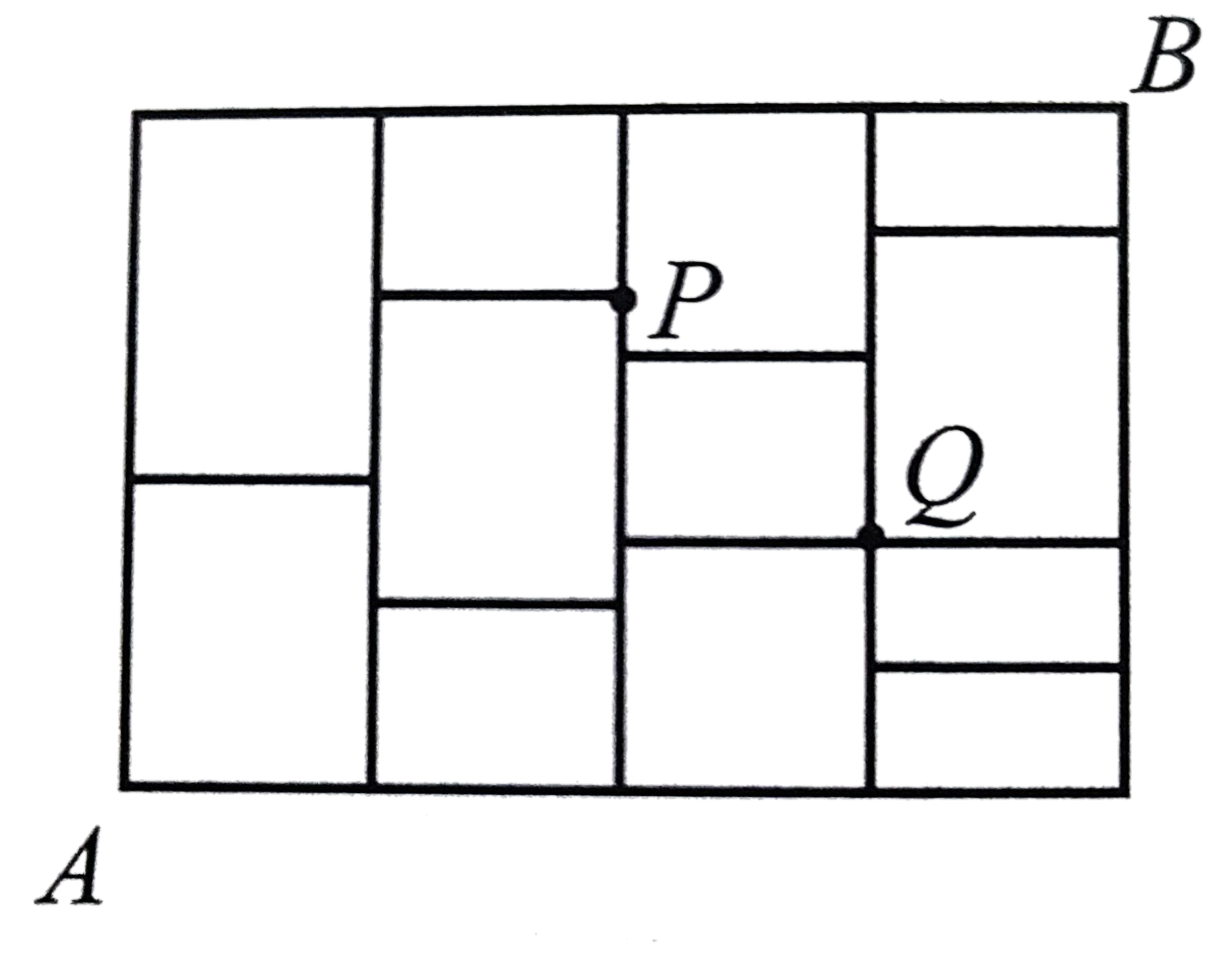
由A走到B，只能→、↑、↓

(1) 走法有　　　種

把縱線想為陸，橫線想為橋

3\times4\times4\times5=240

240

↓

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

由A走到B，只能→、↑、↓

(2) 不過P的走法有　　　種

向上

向下

3\times1\times1\times5=15

3\times2\times3\times5=90

105

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

由A走到B，只能→、↑、↓

(3) 必過P的走法有　　　種

向上

(I)

向下

(III/IV)

3\times1\times3\times5=45

3\times2\times1\times5=30

135

III

過P

(II)

過P

3\times1\times4\times5=60

Sol 2: 必過P = 全 - 不過P = 240 - 105 = 135

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

由A走到B，只能→、↑、↓

(4) 不過P也不過Q的走法有　　　種

向上

向下

3\times1\times1\times2=6

3\times2\times1\times2=12

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

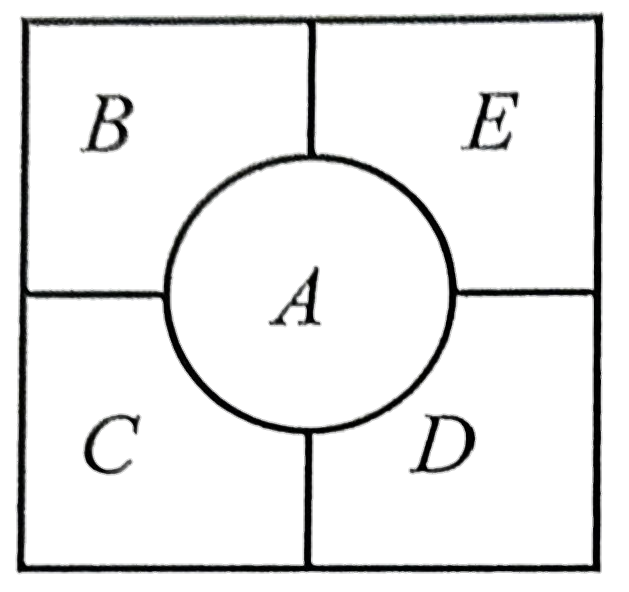
4種顏色，相鄰不同色，有幾種塗法？

從影響範圍大至小下手

A\rightarrow B\rightarrow D\rightarrow C\rightarrow E

4\rightarrow 3\rightarrow \begin{cases} 2\rightarrow 1\rightarrow 1\\ 1\rightarrow 2\rightarrow 2 \end{cases}

BD不同色，CE皆僅剩一色可塗

BD同色，CE皆剩二色可塗

4\times3\times[(2\times1\times1)+(1\times2\times2)]=72_\#

什麼是排列組合

樹狀圖

加法原理

把選擇過程相乘！

4

乘法原理

5種顏色，相鄰不同色，有幾種塗法？

A: 1200

什麼是排列組合

樹狀圖

加法原理

乘法原理

5

階乘( ! )

x!=1\times2\times\dots\times(x-1)\times x=\displaystyle\prod_{k=1}^xk=x\times(x-1)!

0!=1

用處：

直線排列ｎ個獨立物

定義：

設定：

1!	1	5!	120
2!	2	6!	720
3!	6	7!	5040
4!	24	8!	40320

Index

基本定理

排列

組合

排列

排列組合的運算

以獨立元素為本：×／÷（正運算／逆運算）

賦予／消除次序性（獨立性）

e.g.排字母，特定字母相鄰

將特定字母綑綁為獨立元素排列，在對相鄰組計算內排列

以結果為本：+／-

集合運算

e.g. 必過 A = 全 - 不過 A

~~所以排組其實就是分數的四則運算而已~~

1

P(直線排列)

2

錯排問題&排容原理

3

相鄰不相鄰

4

同物排列

1

　Ｐ(直線排列)

P^n_m=\frac{n!}{(n-m)!}

讀作：P n 取 m
意義：在 n 個物品(選項)中取 m 個來排列的結果（從 n 往後乘 m 次）
不要用，這很冗

e.g.\ P^8_6

$$8!排列範圍$$

$$欲排列範圍$$

$$2!排列範圍$$

\{1,2,3,4,5,6\}\Leftarrow\begin{cases} \{1,2,3,4,5,6,7,8\}\\ \{1,2,3,4,5,6,8,7\}\end{cases}

以除法歸納後兩位可能性

×　　 × 　　×　　 ×　　 ×　　 ×　　×

1

　Ｐ(直線排列)

P^n_m=\frac{n!}{(n-m)!}

在 a , b , c , d , e 裡取三個排列，共有　　種結果

\begin{aligned}P^5_3=\frac{5!}{2!}=\underbrace{5\times4\times3}_3\end{aligned}

若P^{2n}_3=28P^n_2，n=?

\begin{aligned} &(2n)(2n-1)(2n-2)=28n(n-1)\\ &\Rightarrow 8n^3-12n^2+4n=28n^2-28n\\ &\Rightarrow 8n^3-40n^2+32n=0\\ &\Rightarrow n^2-5n+4=(n-4)(n-1)0\\ &\Rightarrow n=4\lor n=1\ (不合n>1) \end{aligned}

A: n=4

2

　Ｐ

0 , 1 , 2 , 3 , 4 , 5 , 6 排列，共有　　　種七位數結果

4320

　錯排問題&排容原理

\begin{aligned} Sol\ 1(正面解):&\\ &第一格可能性為6(去掉0)，\\ &其餘格數可能性為6,5,4,3,2,1(0與剩下5數直線排列)\\ &\Rightarrow 6\times6!=6\times720=4320 \end{aligned}

\begin{aligned} Sol\ 2(集合解):&\\ &撇除七位數要求，\\ &總共有7!種可能性\\ &首位為0則有1\times6!種可能性\\ &\Rightarrow 7!-6!=6\times720=4320 \end{aligned}

2

　Ｐ

排列"builder"，字首字尾排母音，共有　　　種結果

720

　錯排問題&排容原理

\begin{aligned} &共有'u'、'i'、'e'三個母音\\ &排在字首字尾，共有3\times2=6種可能性(P^3_2)，\\ &剩下五種字母排列，共有5!=120種可能性，\\ &總可能性為120\times6=720 \end{aligned}

2

　Ｐ

　錯排問題&排容原理

排列"abcdefg"，'a'不排首，'b'不排尾，求有　　　種排列

\begin{aligned} Sol\ 1:&\\ &首位不排'a'，有6種可能性；\\ &尾位不排'b'，有6種可能性。\\ &方法數=6\times6\times5!=4320 \end{aligned}

如果首排'c'，尾位只剩5種可能性

\begin{aligned} Sol\ 2(集合解):&\\ &全部有7!=5040種方法\\ &'a'排首有6!=720種方法\\ &'b'排尾有6!=720種方法\\ &'a'排首且'b'排尾有5!=120種方法\\ &A\cap B=(A'\cup B')'=7!-2\cdot6!+5!=5040-1440+120=3720 \end{aligned}

\begin{aligned} Sol\ 3(正面解):&\\ &'a'在尾，'b'在首=5!=120\\ &只有'a'在尾=只有'b'在首=5\times5!=600\\ &'a','b'皆不在首尾=5\times4\times5!=2400\\ &方法數=120+2\times600+2400=3720 \end{aligned}

3720

\begin{aligned} Sol\ 4(集合解):&\\ &'a'不排首有6\times6!=4320種方法\\ &'a'不排首且'b'排尾有5\times5!=600種方法\\ &方法數=4320-600=3720 \end{aligned}

2

　Ｐ

　錯排問題&排容原理

排容原理(限制=其中一元素不能排某一位置)

一個限制= n ! - ( n - 1 ) !

兩個限制= n ! - 2 ( n - 1 ) ! + ( n - 2 ) !

三個限制= n ! - 3 ( n - 1 ) ! + 3 ( n - 2 ) ! - ( n - 3 )!

係數成巴斯卡係數，正負相間、階乘遞減

1 , 2 , 3 , 4 , 5 , 6 ，第 n 個元素不排第 n 位，有　　　種方法

　Ｐ

排列"fanceis"，'a' , 'e'相鄰，共有　　　種結果

1440

　錯排問題

\begin{aligned} &'a','e'相鄰，則視兩者為一個元素\\ &此元素內共有2!=2種可能性("ae","ea")，\\ &剩下五個字母與此元素排列，共有6!=720種可能性，\\ &總可能性為720\times2=1440 \end{aligned}

　 相鄰不相鄰

3

相鄰者視為一物，並把排列結果乘以內排列可能性

　Ｐ

排列"fanceis"，'a' , 'e'不相鄰，共有　　　種結果

3600

\begin{aligned} Sol\ 1(集合解):&\\ &'a','e'相鄰，有1440種排法，\\ &全部共有7!=5040種排法，\\ &'a','e'不相鄰，即全部-相鄰=5040-1440=3600\\ \end{aligned}

　 相鄰不相鄰

3

不相鄰者排列完用插空法

\begin{aligned} Sol\ 2(正面解):&\\ &先抽離'a','e'，剩下共有5!=120種排法，\\ &'a','e'不相鄰，即'a','e'中間必有其他字母，\\ &將'a','e'插入120種排法中，共有6個空格可以插入，\\ &其中不得插入相同空格，則有6\times5\times120=3600種解法 \end{aligned}

　錯排問題

　Ｐ

　 相鄰不相鄰

　 同物排列（不盡相異物）

4

排列"success"，共有　　　種組合

\begin{aligned} &先不管元素重複，共有7!=5040種可能性，\\ &把's'抽離來看，得進行3!的逆運算，\\ &把'c'抽離來看，得進行2!的逆運算，\\ &共有\frac{7!}{3!\cdot2!}=420種可能性 \end{aligned}

以success來說，\\ 共有\{s_1ucces_2s_3,s_2ucces_3s_1,s_3uccesss_1s_2,s_1ucces_3s_2,s_3ucces_2s_1,s_2ucces_1s_3\}種組合\\ 而不需考慮s_1,s_2,s_3的排列，則除以3!，c亦此理

420

同物除以內排列

　錯排問題

　Ｐ

　 相鄰不相鄰

　 同物排列（不盡相異物）

4

從左下到右上最快速路徑有　　　種

\begin{aligned} &總共有六次\uparrow，八次\rightarrow\\ &方法數=\frac{14!}{6!\cdot8!}=3003種 \end{aligned}

3003

　錯排問題

Index

基本定理

排列

組合

1

C(組合)

2

分組分堆

3

巴斯卡定理

4

二項式定理

\begin{aligned}C^n_m=\dbinom{n}{m}=\frac{P^n_m}{m!}=\frac{n!}{(n-m)!\cdot m!}\end{aligned}

讀作： C n 取 m
意義：在 n 個數中取 m 個出來的組合數

⇒消除 P n 取 m 的次序性

在紅橙黃綠藍靛紫球中取三顆，共有幾種結果

\begin{aligned}C^7_3=\frac{7\times6\times5}{3!}=7\times5=35\end{aligned}

A: 35種

1

　C(組合)

\begin{aligned}C^n_m=\dbinom{n}{m}=\frac{P^n_m}{m!}=\frac{n!}{(n-m)!\cdot m!}\end{aligned}

1

　C(組合)

在 n 個物品中取 x 個 = 在 n 個物品中剃除 ( n - x ) 個

C^n_m=C^n_{(n-m)}

C^{24}_4=6C^{23}_n，n=?

A: n=3,20

\begin{aligned}C^{23}_n=\frac{C^{24}_4}{6}=\frac{24\times23\times22\times21}{4!\cdot6}=\frac{23\times22\times21}{3!}=C^{23}_3=C^{23}_{20}\end{aligned}

\begin{aligned}C^n_m=\dbinom{n}{m}=\frac{P^n_m}{m!}=\frac{n!}{(n-m)!\cdot m!}\end{aligned}

1

　C(組合)

有五對夫妻選出四位出任委員會，夫妻不能同時當，有幾種組合？

剩下可能性=2^4=16

排除一對夫妻=5種可能性

總共=5\times16=80

A: 80

\begin{aligned}C^n_m=\dbinom{n}{m}=\frac{P^n_m}{m!}=\frac{n!}{(n-m)!\cdot m!}\end{aligned}

1

　C(組合)

有五對夫妻選出四位出任委員會，恰一對夫妻，有幾種組合？

A: 120

5 男 4 女選出四位出任委員，男女皆至少一人，有幾種組合

A: 80

10 選 4 出任班長、副班長、風紀、衛生，有兩人不能同時當，有幾種結果？

A: 4368

\begin{aligned}C^n_m=\dbinom{n}{m}=\frac{P^n_m}{m!}=\frac{n!}{(n-m)!\cdot m!}\end{aligned}

1 ~ 10 取三數且任兩數不連續，有幾種取法？

A: 120

某冰淇淋店最少需準備 n 桶不同口味的冰淇淋，才能滿足廣告所稱「任選兩球不同口味冰淇淋的組合數超過 100 種」。

試問來店顧客從 n 桶中任選兩球（可為同一口味）共有幾種方法？

A: 56

1

　C(組合)

2

　分組分堆

分組分堆思維：

12本書，依4,4,4分成三堆，有幾種分法？

12	11	10	9

8	7	6	5

4	3	2	1

逆運算

三大堆(無次序性)逆運算

\begin{aligned}\frac{12!}{(4!\cdot4!\cdot4!)\cdot3!}=\frac{11\times10\times9\times8\times7\times6\times5}{24\times6\times2}=11\times5\times3\times7\times5=5775\end{aligned}

A: 5775

　C(組合)

2

　分組分堆

12本書，依3,4,5分成三堆，有幾種分法？

\begin{aligned}\frac{12!}{3!\cdot4!\cdot5!}=27720\end{aligned}

A: 27720

12本書，依3,3,6分成三堆，有幾種分法？

\begin{aligned}\frac{12!}{(3!\cdot3!\cdot6!)\cdot2!}=9240\end{aligned}

A: 9240

　C(組合)

2

　分組分堆

12本書，3給甲，3本給乙,6本給丙，有幾種分法？

\begin{aligned}\frac{12!}{(3!\cdot3!\cdot6!)}=18480\end{aligned}

A: 18480

12本書，依4,4,4分給甲乙丙三人，有幾種分法？

\begin{aligned}\frac{12!}{4!\cdot4!\cdot4!}=34650\end{aligned}

A: 34650

12本書，依3,3,6分給甲、乙、丙，有幾種分法？

\begin{aligned}\frac{12!}{(3!\cdot3!\cdot6!)}\times3=55440\end{aligned}

A: 55440

　C(組合)

　分組分堆

3

　巴斯卡定理

\begin{aligned}C^n_m=C^{n-1}_m+C^{n-1}_{m-1}\end{aligned}

n 取 m =不挑 k +必挑 k

C^2_2+C^3_2+C^4_2+\dots+C^{20}_2=?

\begin{aligned} &=C^3_3+C^3_2+C^4_2+\dots+C^{20}_2\\ &=C^4_3+C^4_2+C^5_2+\dots+C^{20}_2\\ &=C^{20}_3+C^{20}_2=C^{21}_3=\frac{21\times20\times19}{3!}=1330 \end{aligned}

C^6_2+C^6_3+C^7_4+\dots+C^{20}_{17}=?

\begin{aligned} &=C^6_4+C^6_3+C^7_3+\dots+C^{20}_3\\ &=C^7_4+C^7_3+C^8_3+\dots+C^{20}_3\\ &=C^{20}_4+C^{20}_3=C^{21}_4=\frac{21\times20\times19\times18}{4!}=6985 \end{aligned}

A: 1330

A: 6985

　C(組合)

　分組分堆

　巴斯卡定理

4

　二項式定理

(x+y)^n=C^n_0x^n+C^n_1x^{n-1}y^1+C^n_2x^{n-2}y^2+\dots+C^n_{n-1}x^1y^{n-1}+C^n_ny^n

\begin{aligned} e.g.(x+y)^3&=(x+y)(x+y)(x+y)\\ &x^3=\{xxx\}\\ &x^2y^1=\{xxy,xyx,yxx\}\Rightarrow \frac{3!}{2!}=C^3_1\\ &x^1y^2=\{xyy,yxy,yyx\}\Rightarrow \frac{3!}{2!}=C^3_2\\ &y^3=\{yyy\} \end{aligned}

x=1，(1+x)^n為係數和

　C(組合)

4

　二項式定理

x=1，(1+x)^n為係數和

\begin{aligned} &C^n_0+C^n_1+\dots+C^n_n=2^n\\ &C^n_1+C^n_2+\dots+C^n_n=2^n-C^n_0=2^n-1\\ &C^n_0+C^n_2+\dots=C^n_1+C^n_3+\dots=\frac{2^n}{2}=2^{n-1} \end{aligned}

　分組分堆

　巴斯卡定理