Aula 09

Introdução à Física Clássica II

Prof. Ronai Lisbôa

Não compreendeu algo? Algo está esquisito? Comente!

Objetivos

Ao final dessa aula você deve se capaz de:

Bibliografia

Sears & Zemansky - Vol. 2 - 14a. edição.

Capítulo 16 - Som e Audição

Seções: 16.4, 16.5

Perceber o efeito do timbre sonoro.

Obter as ondas estacionárias em tubos sonoros.

Calcular os modos normais de vibração das ondas estacionárias.

Perceber o efeito da altura sonora.

Perceber o fenômeno de ressonância sonora.

Homenagem à Rita Lee!

Ondas sonoras:

Rapidez de propagação

Fonte: Sears & Zemansky

Golfinhos emitem ondas sonoras com frequências elevadas (da ordem de 100000 Hz) e usam o eco para se guiar e caçar. O comprimento de onda correspondente na água é igual a 1,48 cm. com esse sistema de “sonar” de alta frequência, eles conseguem detectar a presença de objetos tão pequenos quanto o comprimento de onda (porém não muito menores).

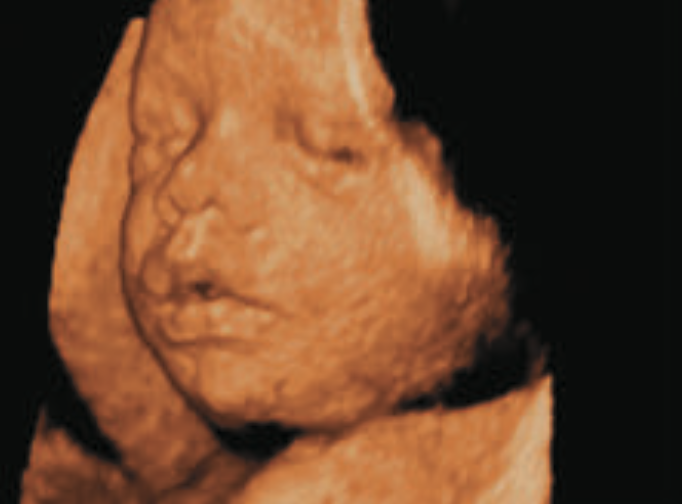
Fonte: Giphy

As ondas sonoras com frequências muito elevadas e comprimentos de onda muito pequenos, chamadas de ultrassom, percorrem o corpo humano, e os “ecos” oriundos do interior do organismo são usados para criar uma imagem. Para um ultrassom com frequência igual a 5 Mhz = 5 x \(10^6\) Hz, o comprimento de onda na água (o constituinte principal do corpo humano) é igual a 0,3 mm, e características com dimensões até essa ordem de grandeza podem ser discernidas na imagem

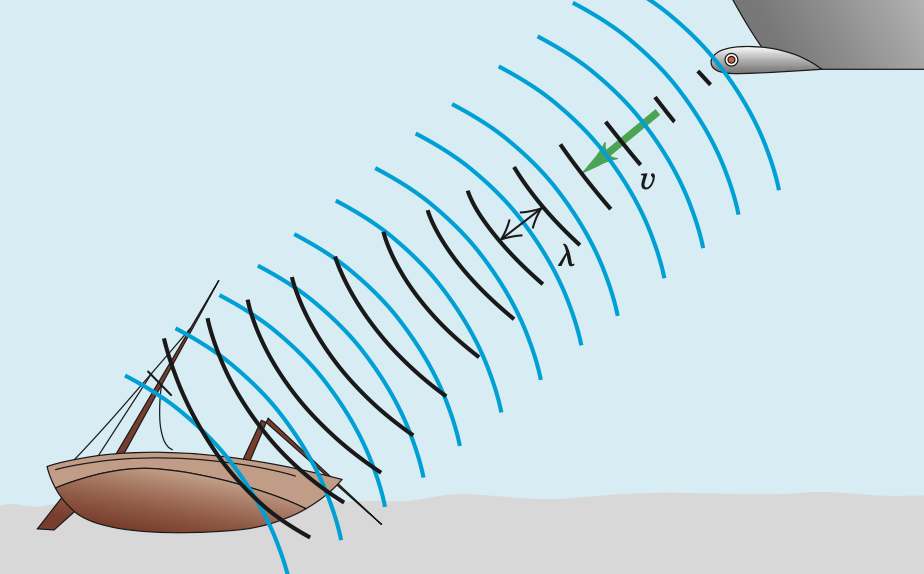
Fonte: Sears & Zemansky

v = \lambda f

constante em um mesmo meio

variam para manter \(v\) constante

Os seres humanos podem ouvir frequências no intervalo de 20 Hz a 24000 Hz, mas isso depende da altura e também da idade! Ou em comprimentos de onda de 20 m a 2,0 cm (no ar).

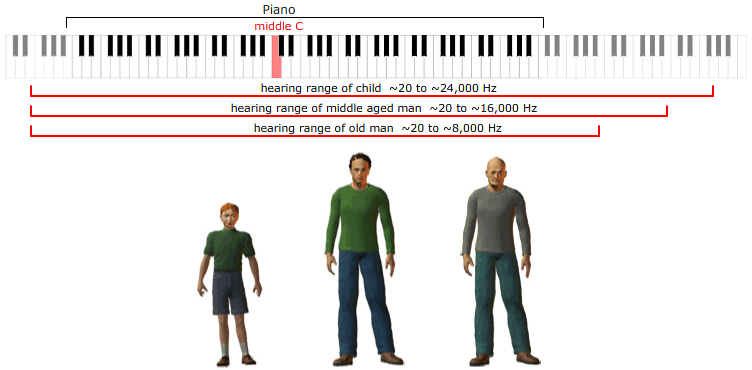
Fonte: https://www.animations.physics.unsw.edu.au/

Humanos podem ouvir aproximadamente 10 oitavas. Mas podem cantar apenas 4 (Fred e Tyler).

Fonte: https://www.animations.physics.unsw.edu.au/

v=\lambda f

v_{som,ar} = 340\text{ m/s}

Infra-sons: \(f < 20\) Hz e (\(\lambda > 20\) m).

\rightarrow \lambda=\frac{v}{f}

Ultra-sons: \(f > 20\) kHz e (\(\lambda < 2,0\) cm).

Ondas sonoras:

Rapidez de propagação

Ondas sonoras:

Rapidez de propagação

Fonte: Sears & Zemansky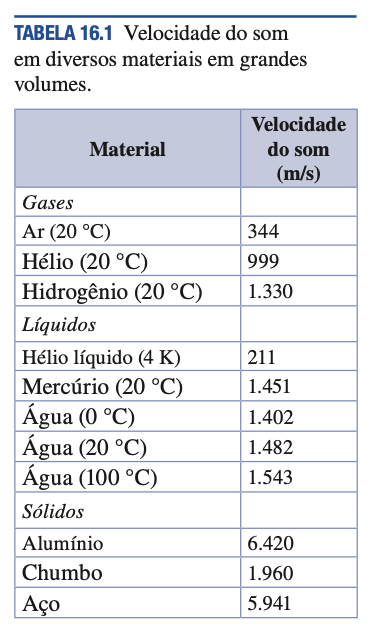

A rapidez das ondas sonoras na água:

\beta = 2,2\times 10^9 \text{ N/m}^2

\rho= 1,0\times 10^3\text{ kg/m}^3

v=\sqrt{\frac{B}{\rho}}=1482\text{ m/s}

A rapidez das ondas sonoras no ar: Veja aqui.

R= 8,314\text{ J/mol.K}

T= 293\text{ K}

M= 29\times 10^{-3}\text{ Kg/mol}

v=\sqrt{\frac{\gamma RT}{M}}=342\text{ m/s}

Se \(\beta = \rho v^2\), a velocidade de propagação da onda sonora no gás:

v=\sqrt{\frac{\beta}{\rho_0}}

\lambda_{agua} =5,65\text{ m}

O comprimento de onda do som na água é maior do que no ar para uma mesma frequência, por exemplo 262 Hz:

\lambda=\frac{v}{f}

\lambda_{agua} =1,30\text{ m}

Modos normais em um tubo

Quando ondas longitudinais (sonoras) se propagam em um fluido no interior de um tubo, elas são refletidas e a superposição das ondas que se propagam em sentidos opostos forma uma onda estacionária.

Fonte: https://youtu.be/r-Fy58ZzE78

As regiões com acúmulo de partículas são os nós da onda estacionária gerada porque não há vibração.

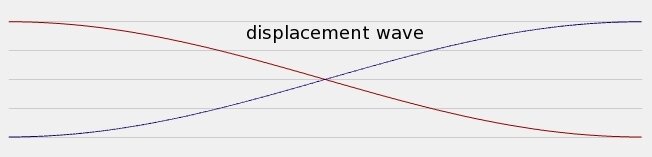
Os termos nó de deslocamento e ventre de deslocamento designam os pontos onde as partículas do fluido possuem deslocamento igual a zero e deslocamento máximo (há vibração).

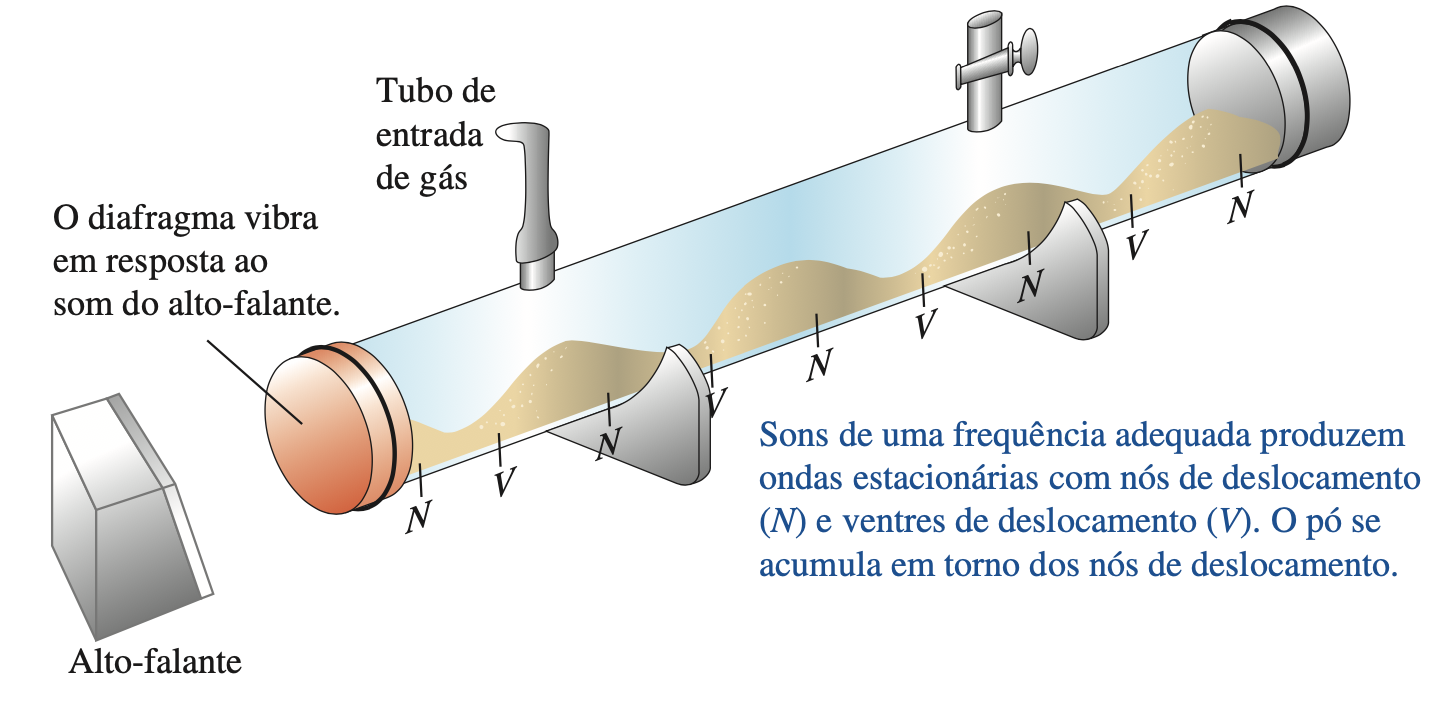
Fonte: Sears & Zemansky

Tubo de Kundt: a densidade e a pressão do gás atingem valores máximos e mínimos nos nós de deslocamento.

v=\lambda f

Modos normais em um tubo

Uma partícula em um nó de deslocamento (N) não se move.

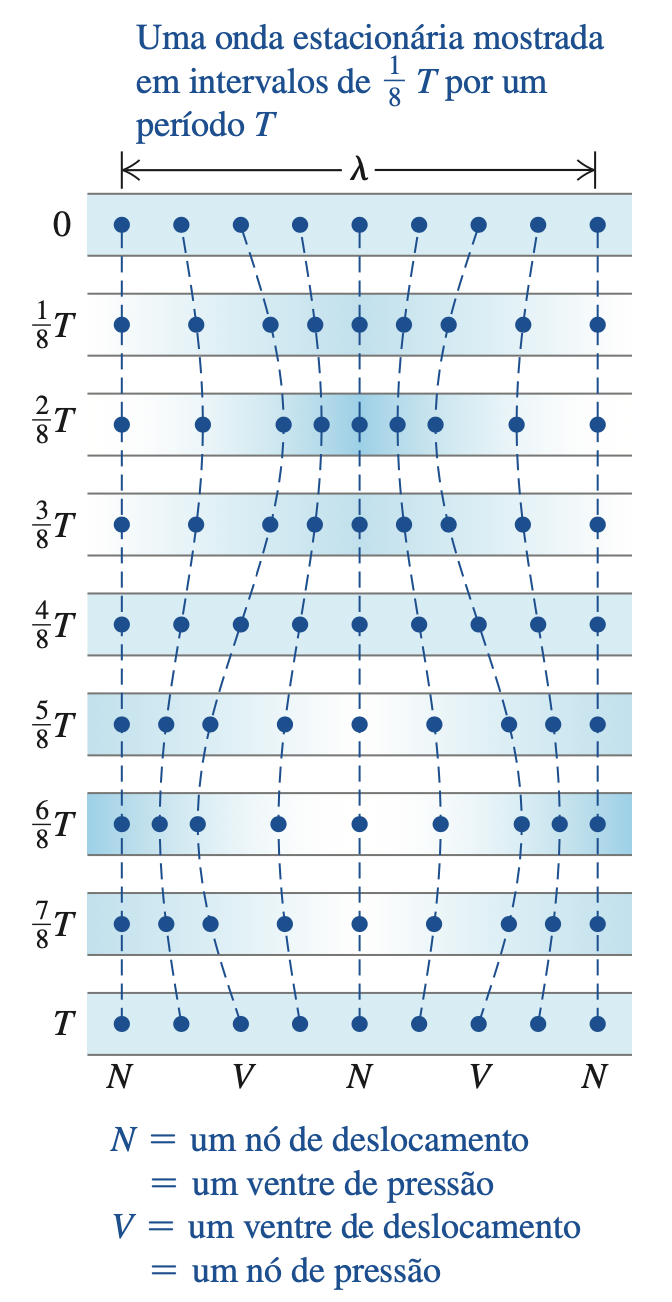
Fonte: Sears & Zemansky

Uma partícula em um ventre de deslocamento (V) oscila com amplitude máxima, em MHS.

As partículas em lados opostos do nó de deslocamento vibram em fases opostas.

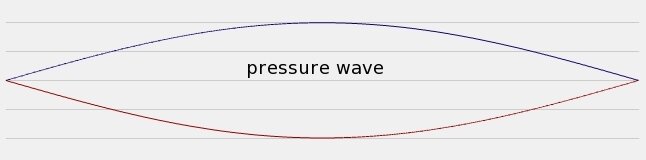
Na aproximação, o gás entre é comprimido e a pressão aumenta;

No afastamento, o gás entre é expandido e a pressão diminui;

dp=\beta\frac{d\rho}{\rho_0}

Um nó de pressão corresponde sempre a um ventre de deslocamento, e um ventre de pressão corresponde sempre a um nó de deslocamento.

densidade e pressão não variam

densidade e pressão atingem valores máximos

dp=-\beta \frac{\partial y}{\partial x}

Modos normais em um tubo

Quando ocorre reflexão na extremidade fechada de um tubo, o deslocamento das partículas nessa extremidade é sempre igual a zero. Há um nó de deslocamento e um ventre de pressão.

Fonte: http://newt.phys.unsw.edu.au/

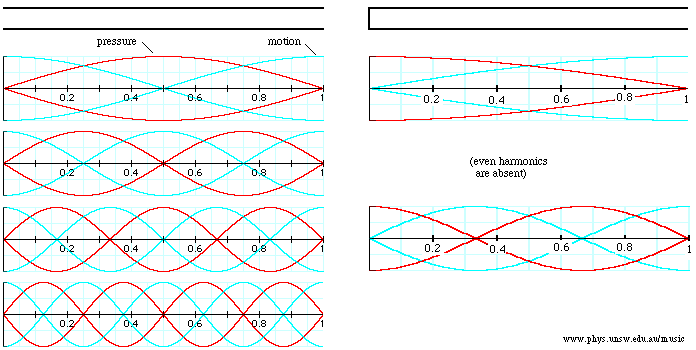
Fonte: https://youtu.be/N5Ch2NThFvY

As partículas não se movem, porém, a variação da pressão é máxima.

Fonte: https://www.acs.psu.edu/drussell/Demos/SWR/SWR.html

Uma extremidade aberta de um tubo é um nó de pressão porque ela está aberta para a atmosfera, onde a pressão permanece constante. Uma extremidade aberta é sempre um ventre de deslocamento e um nó de pressão.

As partículas se deslocam com amplitude máxima, mas a pressão não varia.

p=-\beta \frac{\partial y}{\partial x}

Modos normais em um tubo

A aplicação mais importante das ondas longitudinais estacionárias é a produção de tons musicais.

O tom depende do material, do comprimento e das extremidades do instrumento: abertas e/ou fechadas, de como a vibração (sinal) é produzida e claro do músico.

Fonte: https://youtu.be/MICCl0ke058

Usando os dedos, podemos abrir ou fechar os buracos, alterando o comprimento efetivo L da coluna de ar e, portanto, fazendo variar a altura/frequência do som.

aberto

fechado

Flauta transversal

Clarineta

Tubo de órgão

Modos normais em um tubo

Um tubo com uma das extremidades fechadas (Condições de contorno de Dirichlet/Neumann).

y_r(x,t)=b\text{ cos}[kx]\cos[\omega t]

y_r(L,t)=0

Aplicando (1), número de onda (\(k\)) é quantizado:

b\neq 0

\Rightarrow\quad kL=(2n-1)\frac{\pi}{2},\quad\forall t

E assume somente valores discretos,

k_n=(2n-1) \frac{\pi}{2L}

\lambda_n=\frac{4L}{2n-1}

\omega_n=\frac{(2n-1)\pi}{2L}v

para os modos normais: \(n=1,2,3,\cdots\).

\frac{\partial y_r(0,t)}{\partial x}=0

Fonte: https://www.geogebra.org/m/gm9k6hkg

aberto

fechado

sinal

O ar no tubo pode vibrar em certos modos normais:

Ventre de deslocamento

Nó de pressão

Nó de deslocamento

Ventre de pressão

(1)

(2)

f_n =\frac{(2 n-1)}{4L}v

(1)

(2)

Modos normais em um tubo

Na série harmônica somente os harmônicos ímpares são permitidos.

A frequência fundamental é:

para \(n=1,2,3,\cdots\).

f_n =(2 n-1)f_1

f_1=\frac{v}{4L}

Um tubo com uma das extremidades fechadas (Condições de contorno de Dirichlet/Neumann).

f_{n'} =n'f_1

para \(n'=1,3,5\cdots\).

Fonte: https://www.compadre.org/osp/EJSS/4492/277.htm?F=1

L=n'\frac{\lambda_{n'}}{4}

\lambda_{n'}=\frac{4L}{n'}

f_{n'}=\frac{n'}{4L}v

Fonte: Sears & Zemansky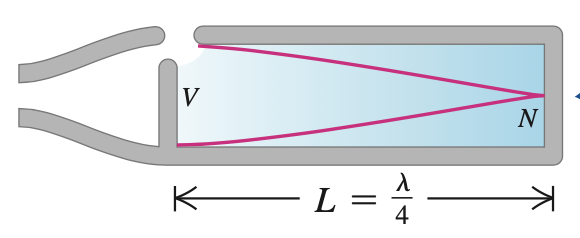

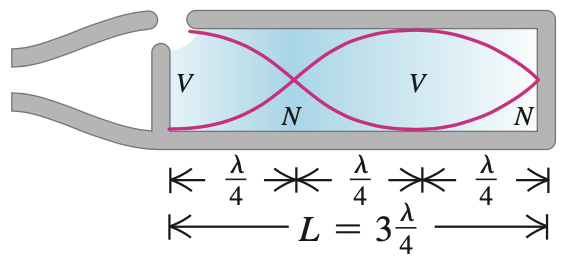
f_1=\frac{1}{4L}v

f_2=3f_1

f'_3=3f_1

f_3=5f_1

f'_5=5f_1

f_1 = 42,5 \text{ Hz}

f_2 = 127,5 \text{ Hz}

f_3 = 212,5 \text{ Hz}

f'_3 = 3f_1

f'_5 = 5f_1

\lambda_1=4L

\lambda'_3=\frac{1}{3}4L

\lambda'_5=\frac{1}{5}4L

Modos normais em um tubo

Um tubo com duas extremidades abertas (Condições de contorno de Neumann/Neumann).

y_r(x,t)=b\text{ sen}[kx]\cos[\omega t]

O ar no tubo pode vibrar em certos modos normais:

O número de onda (\(k\)) é quantizado:

E assume somente valores discretos,

para os modos normais: \(n=1,2,3,\cdots\).

Fonte: https://www.geogebra.org/m/tsufws72

k_n=\frac{n\pi}{L}

\lambda_n=\frac{2L}{n}

\omega_n=\frac{n\pi}{L}v

\frac{\partial y_r(0,t)}{\partial x}=0

\frac{\partial y_r(L,t)}{\partial x}=0

b\neq 0

\Rightarrow\quad kL=n\pi,\quad\forall t

aberto

sinal

f_n =\frac{n}{2L}v

Ventre de deslocamento

Nó de pressão

Ventre de deslocamento

Nó de pressão

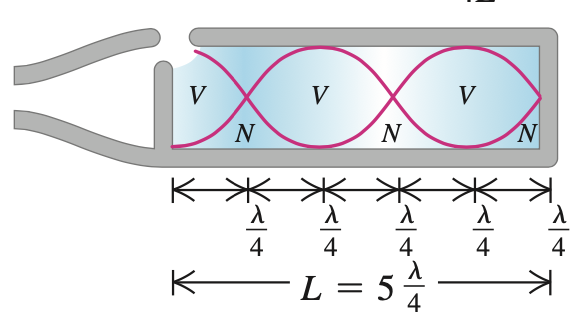
Modos normais em um tubo

A série harmônica é dada por:

A frequência fundamental é:

para \(n=1,2,3,\cdots\).

f_n =nf_1

f_1=\frac{v}{2L}

Um tubo com duas extremidades abertas (Condições de contorno de Dirichlet/Neumann).

Fonte: https://www.compadre.org/osp/EJSS/4492/277.htm?F=1

\lambda_3 =\frac{1}{3}2L

f_3=3f_1

\lambda_2 = \frac{1}{2} 2L

f_2=2f_1

\lambda_1 = 2L

f_1=v/\lambda_1

L=n\frac{\lambda_{n}}{2}

\lambda_{n}=\frac{2L}{n}

f_{n}=\frac{n}{2L}v

f_1 = 85 \text{ Hz}

f_2 = 170 \text{ Hz}

f_3 = 255 \text{ Hz}

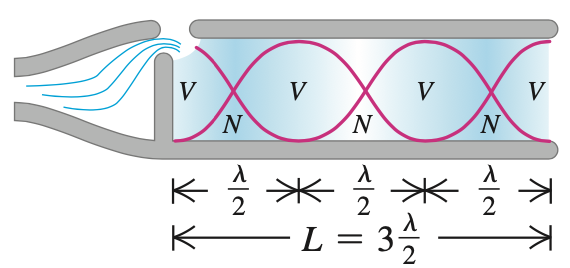
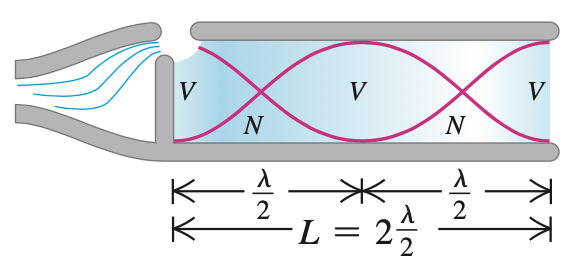
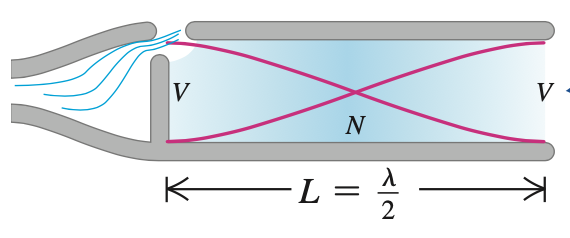
Modos normais em um tubo

Na linguagem muusical, a altura de um tubo fechado é uma oitava a menos (um fator de dois na frequência) do que a de um tubo aberto de mesmo comprimento.

T_{fechado}=\frac{4L}{v}

f_{fechado}=\frac{v}{4L}

f_{aberto}=\frac{v}{2L}

T_{aberto}=\frac{2L}{v}

Fonte: https://www.youtube.com/watch?v=N5Ch2NThFvY&t=50s

L=0,60\text{m} \Rightarrow f_1=140\text{ Hz}

L=0,60\text{m} \Rightarrow f_1=280\text{ Hz}

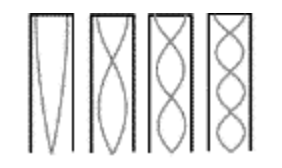
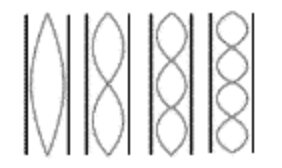
Série: = 140 Hz, 420 Hz, 700 Hz, ...

Série: = 280 Hz, 560 Hz, 840 Hz, ...

Fonte: https://www.youtube.com/watch?v=N5Ch2NThFvY&t=50s

f_n=nf_1

f_{n'}=n'f_1

Somente harmônicos ímpares da frequência fundamental

Tods harmônicos da frequência fundamental

n'=1,3,5,\cdots

n=1,2,3,\cdots

Ressonância e som

Ao variar o comprimento ou fechar os buracos dos instrumentos é possível alterar a frequência fundamental. As colunas de ar possuem uma série infinita de modos normais.

Fonte: https://www.youtube.com/embed/1z5T4S1iMPk?enablejsapi=1

Neste experimento, o ar no interior do tubo é forçado a oscilar com a mesma frequência \(f\) da força propulsora produzida pelo alto-falante.

Quando a frequência \(f\) da força propulsora tiver um valor próximo ao de uma das frequências dos modos normais, o ar no interior do tubo oscilará com a mesma frequência desse modo normal e a amplitude aumentará consideravelmente.

O tubo é do tipo fechado ou aberto?

Repare que os comprimentos (\(L\)), em centímetros, são os da coluna de ar entre o autofalante (a esquerda) e o êmbolo móvel.

Qual o comprimento (\(L\)) do tubo? Qual o modo fundamental, n?

A frequência é fixa e sempre vale 900 Hz. Para isto acontecer o modo normal (n) deve variar bem como o comprimento do tubo (\(L\)). Sendo assim, qual a velocidade do som no ar dentro do tubo no experimento realizado pela cientista?

Como \(v=\lambda_n f_n\), e neste experimento \(f_n = 900\) Hz, sempre, qual o comprimento de onda \(\lambda_n\)?

Você pode responder a estas perguntas. Veja link para turma no Google Classroom disponível no SIGAA.

Ressonância e som

Se a frequência da força propulsora for exatamente igual a uma das frequências dos modos normais, o sistema está em ressonância, e a amplitude da oscilação forçada atingirá seu valor máximo.

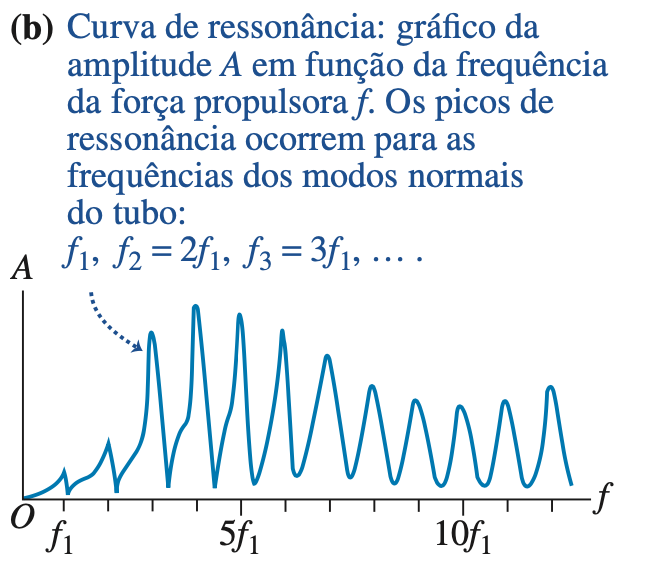
Fonte: https://www.youtube.com/embed/jfQitoRuxfI?enablejsapi=1

Fonte: Sears & Zemansky

Fonte: https://youtu.be/_cpC4dtvVjI?si=S5WNGG3Ey72nN35c

Em todos estes experimentos note que o som depende da altura da coluna do fluido, neste caso, da coluna de ar.

Verifique aqui.

Atividade 1 - Opcional

Na página original: LINK.

A animação mostra uma onda estacionária em uma corda (a posição é dada em centímetros e o tempo é dado em segundos). Se esta corda estiver em um instrumento musical, que comprimento de onda é produzido pela onda estacionária?

Esta atividade vai auxilar a solução das atividades a partir da terceira.

Nestes simuladores há cronômetros embutidos (time) e as coordenadas das grandezas nos eixos (x,y) podem ser lidas com o mouse ao clicar com o botão esquerdo. Por exemplo, neste gráfico o eixo x é a posição de um ponto da corda e o eixo vertical é o valor da perturbação (aqui chamada de F de função). Com estas informações torna-se possível medir (virtualmente) o período e o comprimento de onda.

Envie suas respostas:

aqui,

mas você deve ter um e-mail institucional da UFRN e estar logado no seu navegador nesta conta.

Atividade 2 - Opcional

Na página original: LINK.

A animação mostra uma onda estacionária em um instrumento musical de cordas (a posição é dada em centímetros e o tempo é dado em segundos). Se a tensão nesta corda for dobrada e a corda permanecer em seu modo fundamental, que frequência o som é produzido pela nova onda estacionária?

Esta atividade vai auxilar a solução das atividades a partir da terceira.

Envie suas respostas:

aqui,

mas você deve ter um e-mail institucional da UFRN e estar logado no seu navegador nesta conta.

Atividade 3 - Opcional

Na página original: LINK

Usando um alto-falante, uma onda sonora estacionária foi configurada dentro de um tubo. Um microfone móvel fica dentro do tubo (a posição é dada em metros e o tempo é dado em segundos). O gráfico mostra o som gravado pelo microfone em função do tempo. Mova o microfone para frente e para trás para estudar a amplitude variável do som que ele detecta.

a) Para qual(is) posição(s) do microfone a amplitude do som vai para zero? Como se chama esse local?

b) Para qual(is) posição(ões) do microfone a amplitude do som é máxima? Como se chama esse local?

c) A partir dos locais dos nós, determine o comprimento de onda das ondas sonoras.

d) A partir do gráfico, determine a frequência das ondas sonoras.

e) Usando o comprimento de onda e a frequência, encontre a velocidade das ondas sonoras no tubo.

Ao clicar com o mouse terá as coordenadas de amplitude (vertical) e tempo (horizontal).

Você deve arrastar o microfone que está a frente do autovalente e observar os máximos e/ou mínimos.

Envie suas respostas:

aqui,

mas você deve ter um e-mail institucional da UFRN e estar logado no seu navegador nesta conta.

Atividade 4 - Opcional

Na página original: LINK

Esta animação mostra uma onda estacionária em um tubo aberto (a posição é dada em centímetros e o tempo é dado em segundos).

a) Em qual harmônico, n, o ar no tubo está oscilando?

b) Determine a frequência do tom musical produzido pelo tubo nesta situação.

c) Determine a frequência fundamental do tubo (mais baixa frequência de ressonância).

Ao clicar com o mouse há duas coordenadas (x,y). Aquela que importa é a coordenada horizontal porque a onda é longitudinal.

Observe que há um contador de tempo (time). Você precisa saber ler as amplitudes, comprimentos de onda e períodos.

Se você não está entendendo este conceito é porque não lembra desta aula: https://slides.com/d/RR3uklU/live#/6.

Envie suas respostas:

aqui,

mas você deve ter um e-mail institucional da UFRN e estar logado no seu navegador nesta conta.

Atividade 5 - Opcional

Na página original: LINK.

A animação mostra uma onda estacionária em um tubo aberto (a posição é dada em centímetros e o tempo é dado em segundos).

a) Em qual harmônico, n, o ar no tubo está oscilando?

b) Determine a frequência \(f_n\) do tom produzido pelo tubo nesta situação.

c) Determine a frequência do oitavo harmônico \(f_8\).

d) Determine a velocidade do som v.

Ao clicar com o mouse há duas coordenadas (x,y). Aquela que importa é a coordenada horizontal porque a onda é longitudinal.

Observe que há um contador de tempo (time). Você precisa saber ler as amplitudes, comprimentos de onda e períodos.

Se você não está entendendo este conceito é porque não lembra desta aula: https://slides.com/d/RR3uklU/live#/6.

Envie suas respostas:

aqui,

mas você deve ter um e-mail institucional da UFRN e estar logado no seu navegador nesta conta.

Atividade 6 - Opcional

Na página original: LINK

Esta animação mostra uma onda estacionária em um tubo fechado (a posição é dada em centímetros e o tempo é dado em segundos).

a) Determine a frequência \(f_n\) do tom produzido pelo tubo nesta situação.

b) Agora o tubo é cortado em dois pedaços de igual comprimento. Determine a frequência fundamental de cada uma das duas partes.

Ao clicar com o mouse há duas coordenadas (x,y). Aquela que importa é a coordenada horizontal porque a onda é longitudinal.

Observe que há um contador de tempo (time). Você precisa saber ler as amplitudes, comprimentos de onda e períodos.

Se você não está entendendo este conceito é porque não lembra desta aula: https://slides.com/d/RR3uklU/live#/6.

Envie suas respostas:

aqui,

mas você deve ter um e-mail institucional da UFRN e estar logado no seu navegador nesta conta.

Atividade 7 - Opcional

Na página original: LINK

Esta animação mostra uma onda estacionária em um tubo fechado (a posição é dada em centímetros e o tempo é dado em segundos).

a) Em qual harmônico, n, o ar no tubo está oscilando?

b) Determine o comprimento de onda para essa oscilação.

Ao clicar com o mouse há duas coordenadas (x,y). Aquela que importa é a coordenada horizontal porque a onda é longitudinal.

Observe que há um contador de tempo (time). Você precisa saber ler as amplitudes, comprimentos de onda e períodos.

Se você não está entendendo este conceito é porque não lembra desta aula: https://slides.com/d/RR3uklU/live#/6.

Envie suas respostas:

aqui,

mas você deve ter um e-mail institucional da UFRN e estar logado no seu navegador nesta conta.

A altura sonora está associada aos sons:

Propriedades do som:

Graves - baixa frequência.

Frequência e Altura.

Agudos - alta frequência.

A escala cromática temperada* tem sua oitava dividida em 12 intervalos (semitons temperados):

Fonte: https://www.geogebra.org/m/azhqswhe

1 oitava

(*) Sebastian Bach (1685-1750 ) & Simon Stevin (1548 a 1620).

i^{12}=2\rightarrow i=1,0595

do#

re#

fa#

sol

sol#

la#

261,63\text{ Hz}

523,25\,\text{Hz}

Na escala cromática temperada, a oitava é dividida em 12 intervalos (semitons temperados)

i^{12}=2\rightarrow i=1,0595

Fonte: Wolfgang & Bauer

Propriedades do som:

A diferença entre quaisquer duas notas adjacentes é a mesma!

Fonte: https://www.geogebra.org/m/ABEUQCQr

1,0595^{1}(130,81)

1,0595^{0/12}(130,81)

1,0595^{2}(130,81)

1,0595^{3}(130,81)

1,0595^{5}(130,81)

1,0595^{4}(130,81)

1,0595^{6}(130,81)

1,0595^{7}(130,81)

1,0595^{8}(130,81)

1,0595^{9}(130,81)

1,0595^{10}(130,81)

1,0595^{11 }(130,81)

1,0595^{12 /12}(130,81)

1,0595^{17 /12}(130,81)

1,0595^{21 /12}(130,81)

1,0595^{22 /12}(130,81)

Aumentar a frequência também aumenta o volume e o timbre muda. Portanto, a frequência tem um grande efeito no tom, mas também afeta o volume e o timbre.

Frequência e Altura.

\Delta f_8=1

\Delta f_{12}=12

O aumento da frequência aumenta o tom e uma duplicação da frequência é um aumento de uma oitava.

\Delta f_8 = \log_2\left( \frac{f_2}{f_1} \right)

\Delta f_{12} = 12\log_2\left( \frac{f_2}{f_1} \right)

E entre frequências quaisquer:

Um som com mesma intensidade (fraco/forte) e altura (grave/agudo) pode diferir pelo timbre.

A mesma nota é tocada com instrumentos diferentes ( \(f_1 = 440\) Hz):

Os espectros de amplitudes são diferentes, mas elas guardam o mesmo período (T). Logo, mesma frequência (f = 1/T). O timbre pode ser rico ou pobre em harmônicos.

Propriedades do som:

Envelope espectral e Timbre.

Teste: https://www.compadre.org/

O timbre é uma percepção da riqueza do som.

Fonte: https://youtu.be/zTO41jP0OrM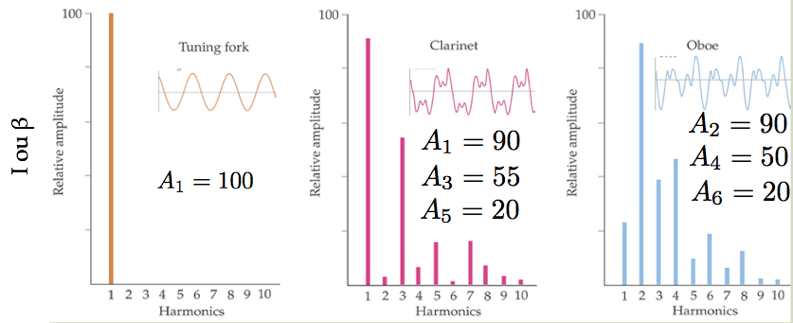

Fonte: Tipler

O diapasão produz um som de um único harmônico fundamental.

f_1 =440\text{ Hz}

y_1(x,t)=A_1\text{ sen}[k_1x]\cos[2\pi f_1 t]

Frequência fundamental

Modo normal

Um instrumento musical e até mesmo a voz humana vibram como uma superposição de vários harmônicos permitidos:

y_r(x,t)=\sum_n A_n\text{ sen}[k_nx]\cos[2\pi f_n t]

Propriedades do som:

Envelope espectral e Timbre.

Fonte: https://www.compadre.org/books/?ID=46&FID=45043

Função triangular:

f_1

f_3

f_5

f_7...

A_1

A_3

A_5

A_7\cdots

Função quadrada:

f_1

f_3

f_5

f_7...

A_1

A_3

A_5

A_7\cdots

Função dente de serra:

f_1

f_2

f_3

f_4...

A_1

A_2

A_3

A_4\cdots

Função seno:

f_1

A_1

y_r(x,t)=\sum_n A_n\text{ sen}[k_nx]\cos[2\pi f_n t]

Os harmônicos dominantes dependem do instrumento (tipo) e de como ele é tocado.

A amplitude \(A_n\) indica qual harmônico é dominante.

Propriedades do som:

Envelope espectral e Timbre.

A_n =\frac{2}{L}\int _0^L \,f(x)\,\text{sen}(k_n\,x)dx

Fonte: https://youtu.be/hTLjAl8MGvw

Fonte: https://youtu.be/XWKWY4Rjmkg

O ouvido humano é capaz de fazer uma análise de Fourier identificando o timbre.

Teste: https://www.compadre.org/

y_r(x,t)=\sum_n A_n\text{sen}[2\pi f_n t]\text{ sen}[k_nx]

Propriedades do som:

Envelope espectral e Timbre.

Fonte: https://www.animations.physics.unsw.edu.au/

A_n =\frac{2}{L}\int _0^L \,f(x)\,\text{sen}(k_n\,x)dx

A intensidade é proporcional ao quadrado da amplitude.

Fonte: PHET

Motivação

Manutenção de órgãos. Uma tarefa difícil. Onde estão os profissionais?

O ar é fornecido por foles ou ventoinhas na extremidade inferior do tubo. Uma corrente de ar emerge da abertura estreita na extremidade da superfície horizontal e a seguir é direcionada para a parte superior da abertura, chamada de boca do tubo. A coluna de ar no tubo começa a vibrar e ocorrem diversos modos normais possíveis. Mas cada tubo possui apenas um único nota e possivelmente algumas oitavas.

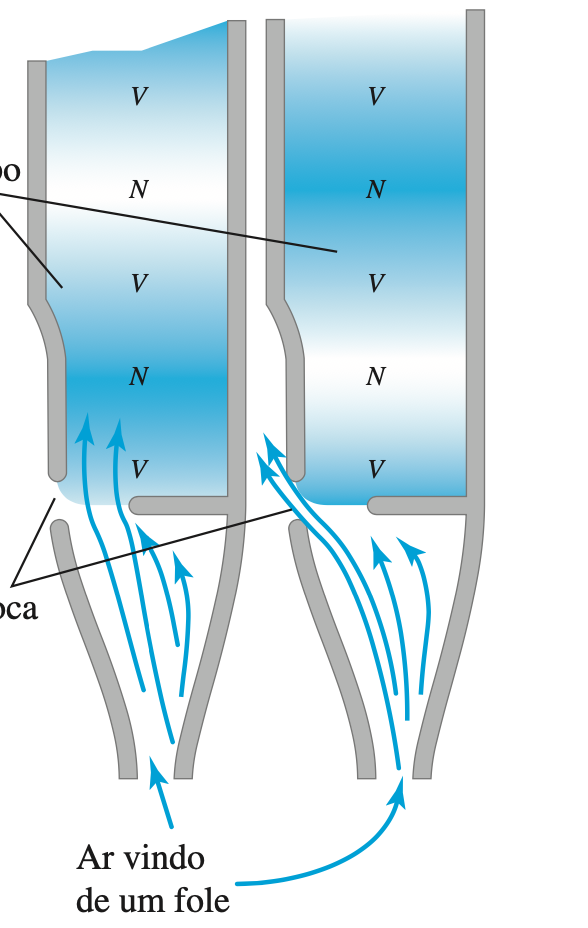
Um tubo muito fino produz uma onda sonora rica em harmônicos superiores; um tubo grosso produz basicamente o harmônico fundamental.

Questão 1

O tubo de órgão A, com as duas extremidades abertas, tem uma frequência fundamental de 300 Hz. O terceiro harmônico do tubo de órgão B, com uma extremidade aberta, tem a mesma frequência que o segundo harmônico do tubo A. Qual é o comprimento:

(a) do tubo A e

(b) do tubo B?

H17-42 (8a)

Questão 2

O nível de água em um tubo de vidro vertical com 1,00 m de comprimento pode ser ajustado em qualquer posição dentro do tubo. Um diapasão vibrando a 686 Hz é mantido acima da extremidade aberta do tubo para gerar uma onda sonora estacionária na parte superior do tubo, onde existe ar. Essa parte superior cheia de ar se comporta como um tubo com uma extremidade aberta e outra fechada.

(a) Para quantas posições diferentes do nível de água o som do diapasão produz uma ressonância na parte do tubo cheia de ar?

(b) Quais são a menor altura e a segunda menor altura da água no tubo para as qual ocorre ressonância?

H17-44 (8a)

Questão 3

Uma das frequências harmônicas do tubo A, que possui duas extremidades abertas, é 325 Hz. A frequência harmônica seguinte é 390 Hz.

(a) Qual é a frequência harmônica que se segue à frequência harmônica de 195 Hz?

(b) Qual é o número desse harmônico?

Uma das frequências harmônicas do tubo B, com apenas uma extremidade aberta, é 1080 Hz. A frequência harmônica seguinte é 1320 Hz.

(d) Qual é o número desse harmônico?

H17-46 (8a)

Questão 4

Uma onda sonora estacionária produzida no interior de um tubo sonoro é dada por y(x, t) = A sen(5x) cos(ωt), onde ω = 27,4κ. Na extremidade em x = L a condição de contorno é dada por ∂ y(x,t)/∂ x= 0, para x = L.

Qual o comprimento mínimo do tubo sonoro?