https://introml.mit.edu/

Lecture 7: Neural Networks II, Auto-encoders

 

Shen Shen

October 11, 2024

Intro to Machine Learning

(slides adapted from Phillip Isola)

Outline

  • Recap, neural networks mechanism
  • Neural networks are representation learners
  • Auto-encoder:
    • ​Bottleneck
    • Reconstruction
  • Unsupervised learning
  • (Some recent representation learning ideas)
x^{(1)}
y^{(1)}
f^1

linear combination

nonlinear activation

\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
g^{(1)}

\(\dots\)

f^2\left(\hspace{2cm}; \mathbf{W}^2\right)
f^1(\mathbf{x}^{(i)}; \mathbf{W}^1)
f^L\left(\dots \hspace{3.5cm}; \dots \mathbf{W}^L\right)

Forward pass: evaluate, given the current parameters,

  • the model output \(g^{(i)}\) =  
  • the loss incurred on the current data \(\mathcal{L}(g^{(i)}, y^{(i)})\)
  • the training error \(J = \frac{1}{n} \sum_{i=1}^{n}\mathcal{L}(g^{(i)}, y^{(i)})\)
\mathcal{L}(g^{(1)}, y^{(1)})
\mathcal{L}(g, y)
\mathcal{L}(g^{(n)}, y^{(n)})
\underbrace{\quad \quad \quad \quad \quad } \\ n
\dots
\dots
\dots

loss function

Recap:

compositions of ReLU(s) can be quite expressive

in fact, asymptotically, can approximate any function!

(image credit: Phillip Isola)

\sigma_1 = \sigma(5 x_1 + -5 x_2 + 1)
\sigma_2 = \sigma(-5 x_1 + 5 x_2 + 1)

some weighted sum

Recap:
  • Randomly pick a data point \((x^{(i)}, y^{(i)})\)
  • Evaluate the gradient \(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\) 
  • Update the weights \(W^2 \leftarrow W^2 - \eta \nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)}})\) 
x^{(i)}
y^{(i)}
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
g^{(i)}

\(\dots\)

\mathcal{L}(g^{(i)}, y^{(i)})
\mathcal{L}(g, y)
\mathcal{L}(g^{(n)}, y^{(n)})
\underbrace{\quad \quad \quad \quad \quad } \\ n
\dots
\dots
\dots

Backward pass: run SGD to update the parameters, e.g. to update \(W^2\)

\(\nabla_{W^2} \mathcal{L(g^{(i)},y^{(i)})}\) 

Recap:
x

\(\dots\)

y
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}
\underbrace{\hspace{4.7cm}}
\frac{\partial Z^2}{\partial W^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}
Recap:

back propagation: reuse of computation

\underbrace{\hspace{6.5cm}}
\frac{\partial Z^2}{\partial A^{1}}
\frac{\partial A^1}{\partial Z^{1}}
\frac{\partial Z^1}{\partial W^{1}}
x

\(\dots\)

y
f^1
\begin{aligned} & W^1 \\ \end{aligned}
\begin{aligned} & W^2 \\ \end{aligned}
\begin{aligned} & W^L \\ \end{aligned}
f^2
f^L
\mathcal{L}(g,y)
g
Z^L
A^2
Z^2
A^1
Z^1
\frac{\partial \mathcal{L}(g,y)}{\partial g}
\frac{\partial g}{\partial Z^{L}}
\frac{\partial Z^3}{\partial A^{2}}\frac{\partial A^4}{\partial Z^{3}} \dots \frac{\partial Z^L}{\partial A^{L-1}}
\frac{\partial A^2}{\partial Z^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial Z^2}
\underbrace{\hspace{4cm}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^1}
\underbrace{\hspace{4.7cm}}
\frac{\partial Z^2}{\partial W^{2}}
\frac{\partial \mathcal{L}(g,y)}{\partial W^2}

back propagation: reuse of computation

Recap:

Outline

  • Recap, neural networks mechanism
  • Neural networks are representation learners
  • Auto-encoder:
    • ​Bottleneck
    • Reconstruction
  • Unsupervised learning
  • (Some recent representation learning ideas)

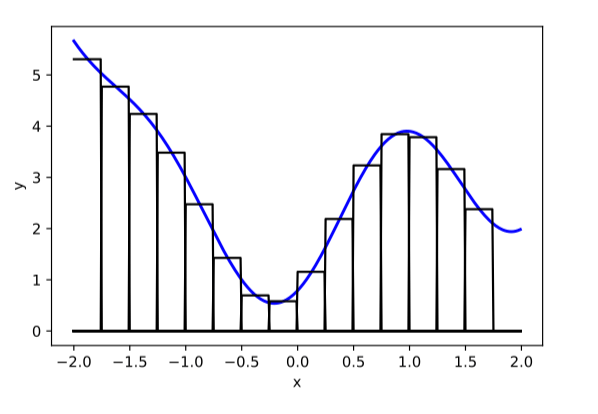
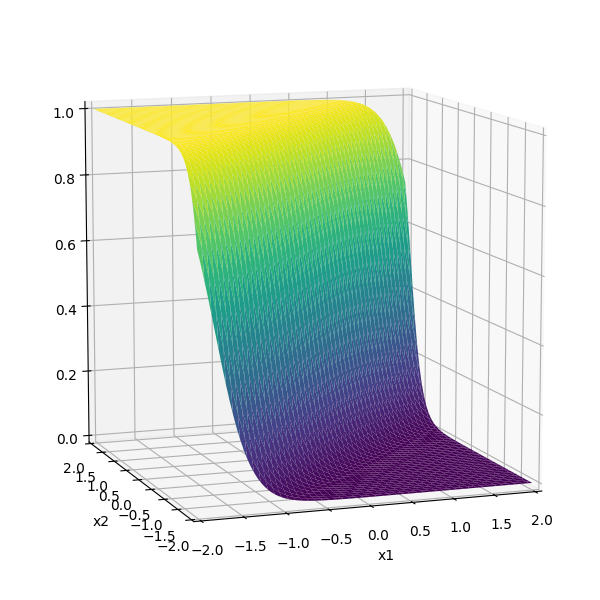
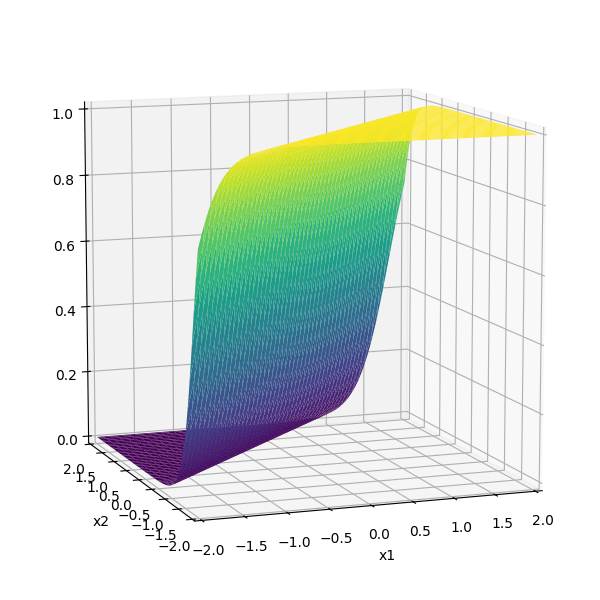
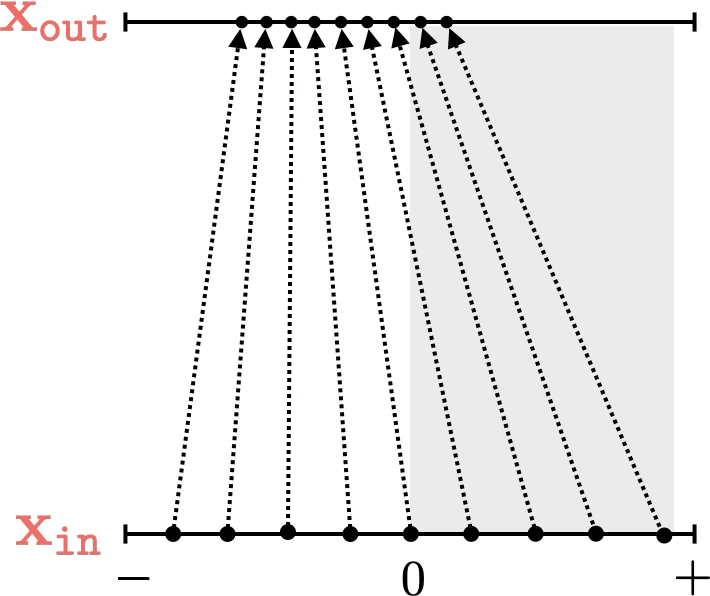
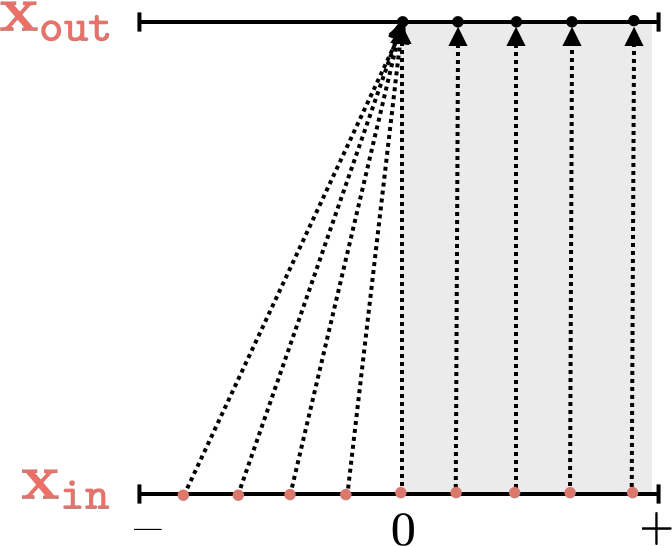
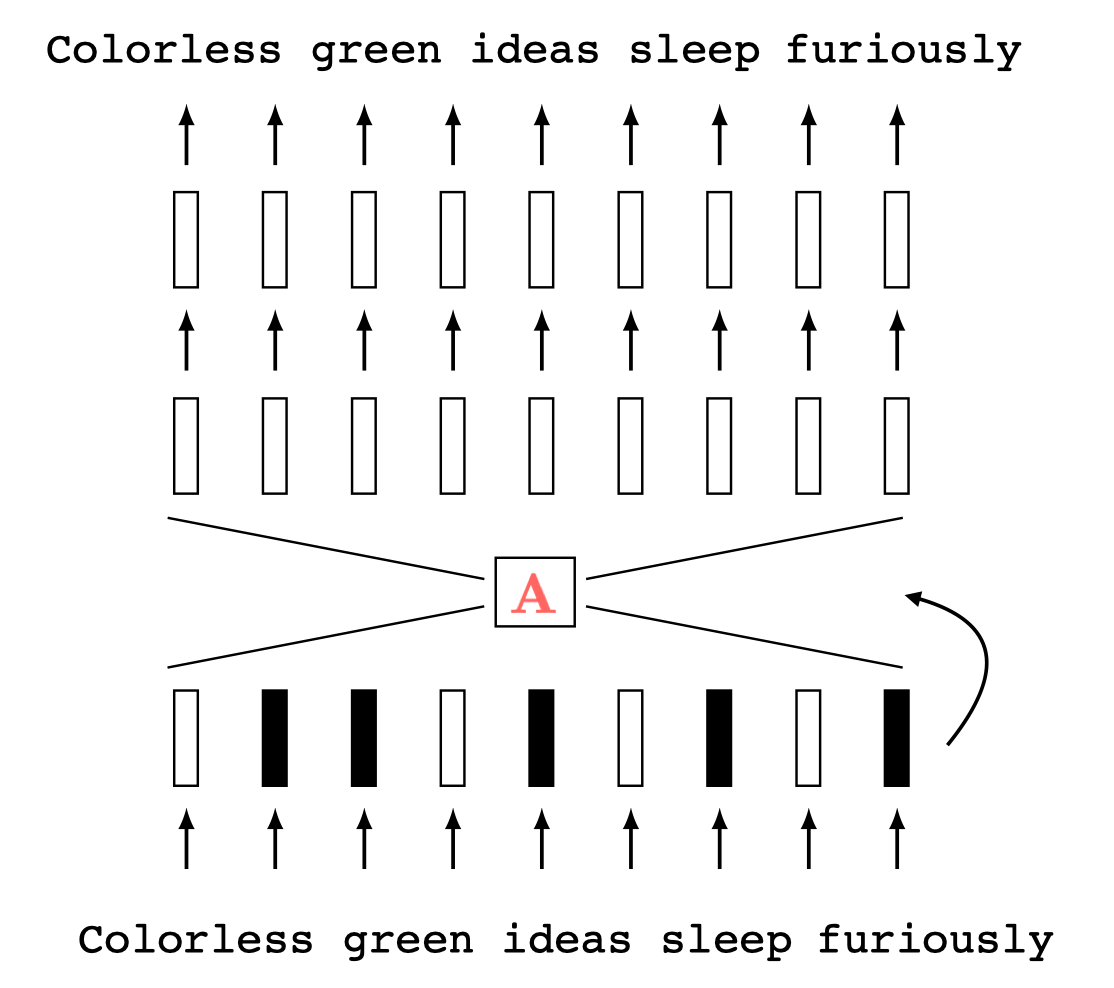
Two different ways to visualize a function

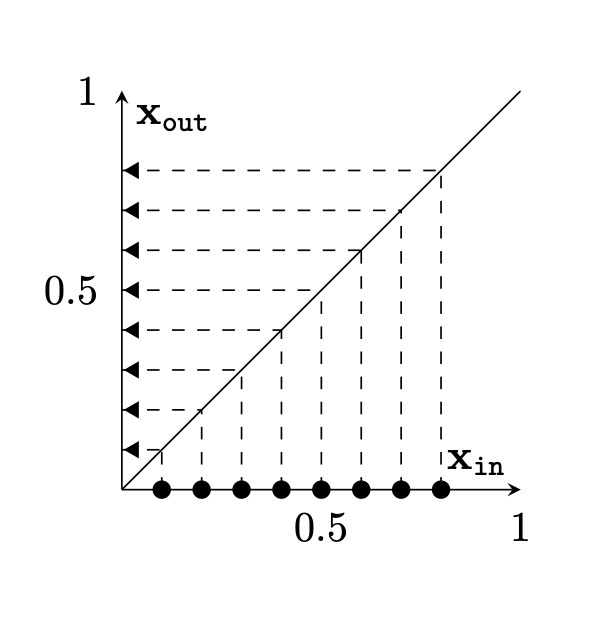
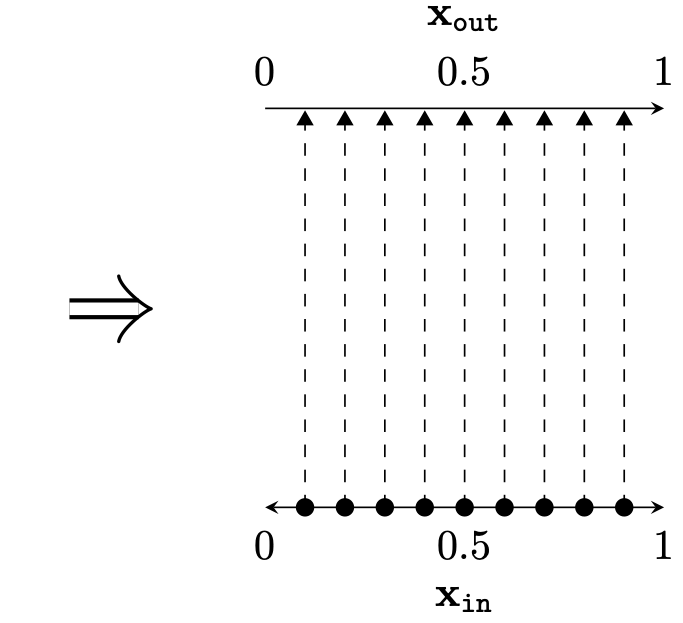
Two different ways to visualize a function

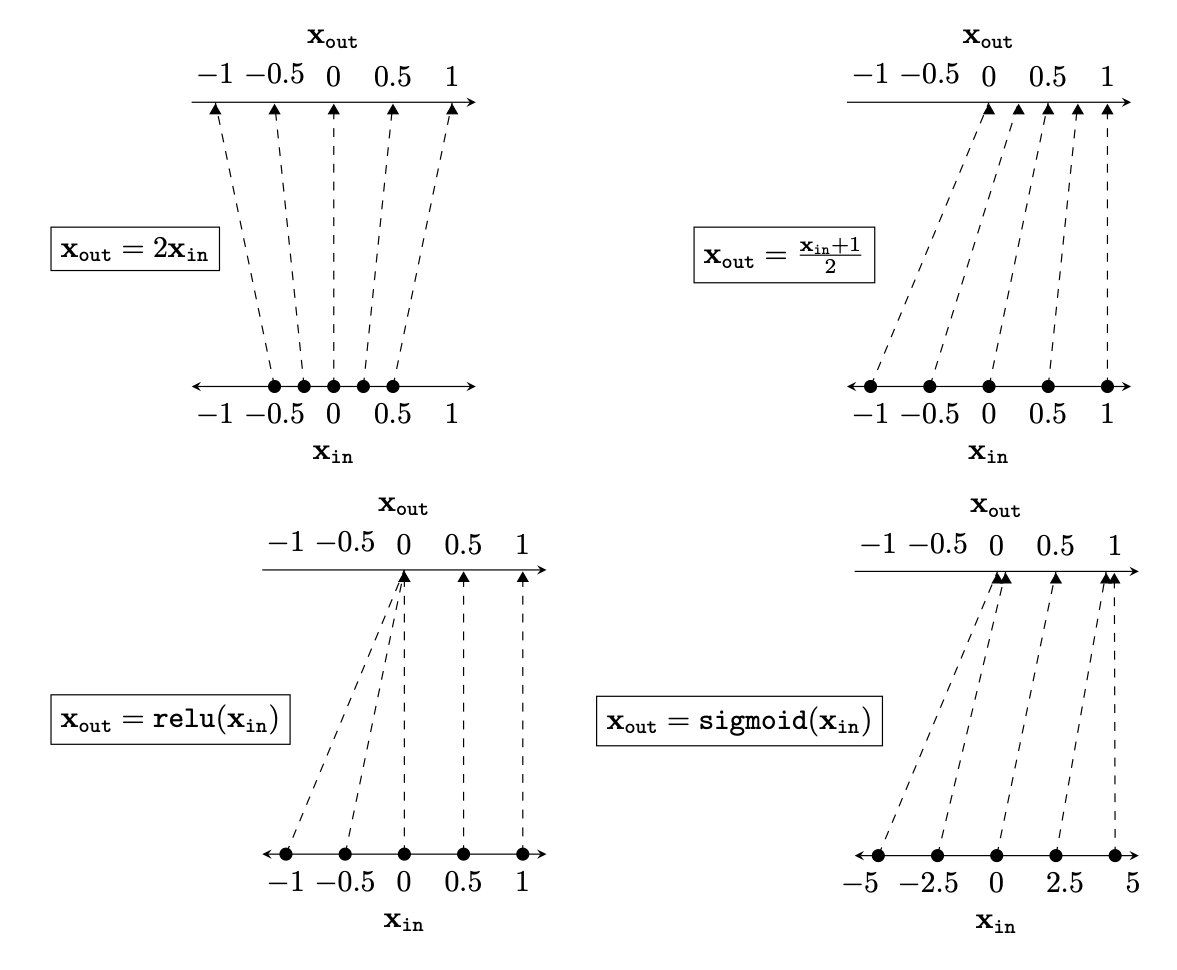
Representation transformations for a variety of neural net operations

and stack of neural net operations

)

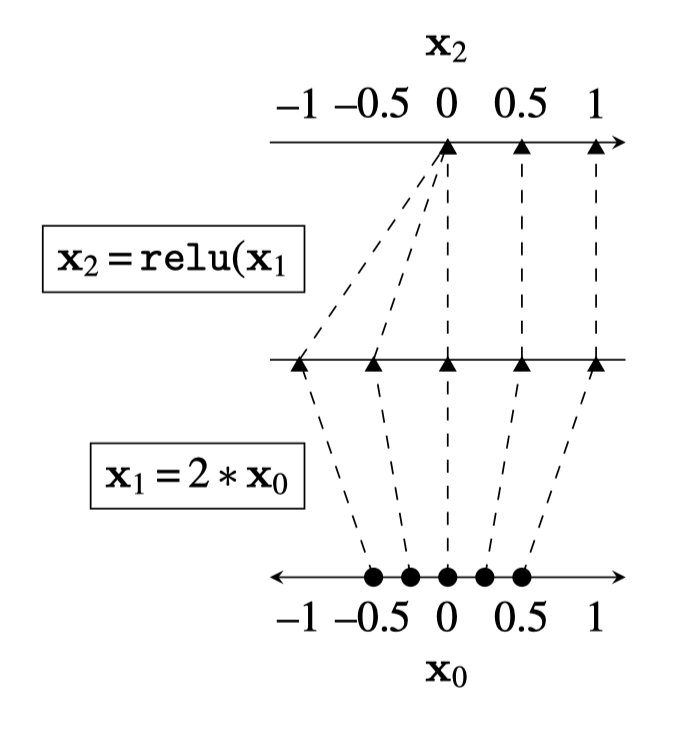
wiring graph

equation

mapping 1D

mapping 2D

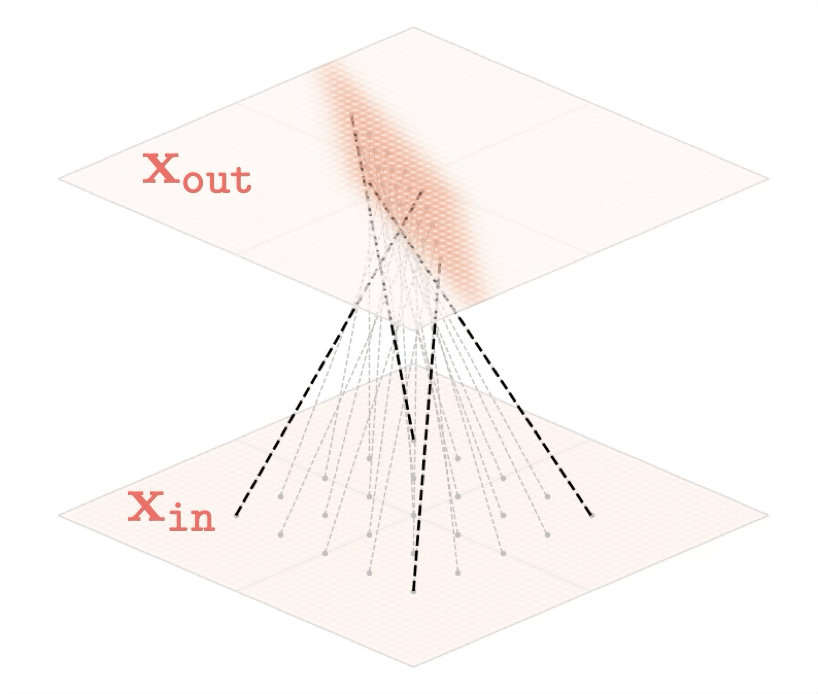
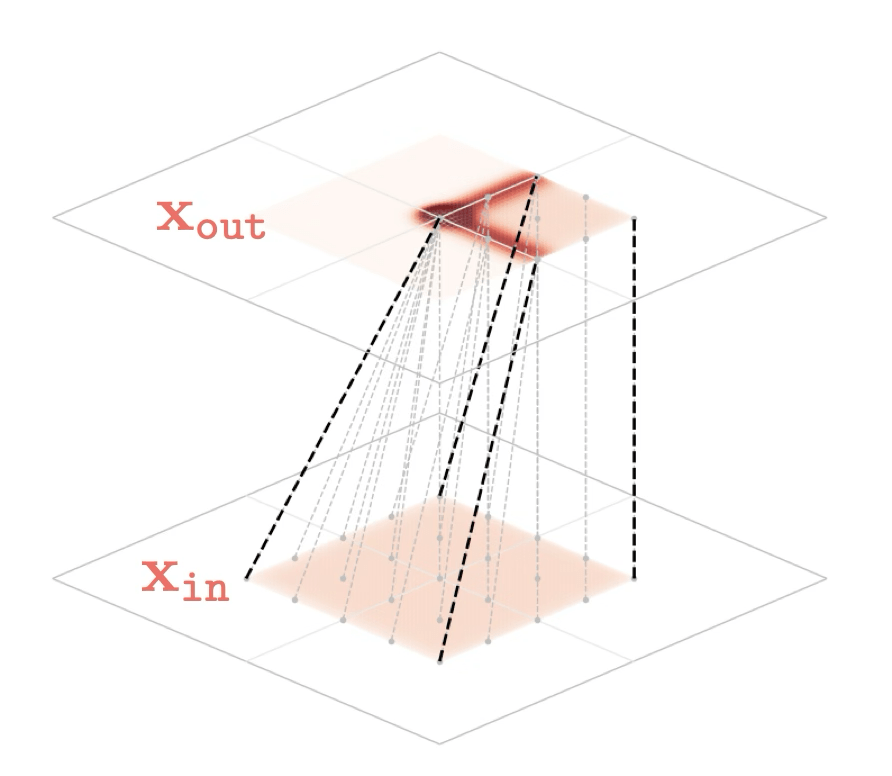
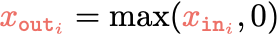
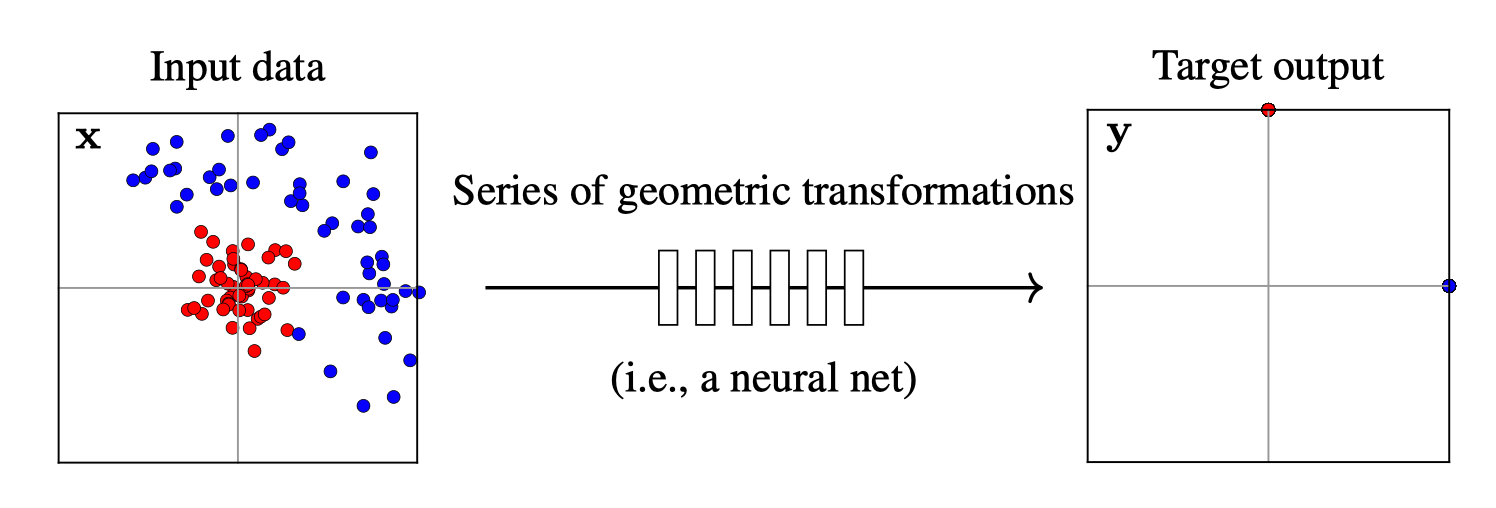
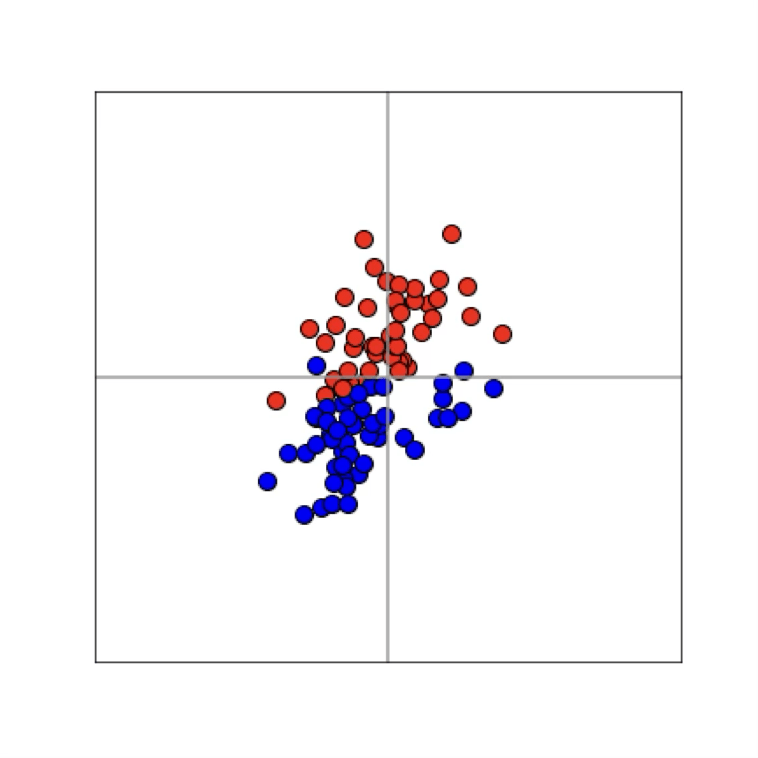
Training data

x
z_1
a_1
z_2
g
{z}_1=\text { linear }(x)
{a}_1=\text { ReLU}(z_1)
g=\text {softmax}(z_2)
{z}_2=\text { linear }(a_1)
x\in \mathbb{R^2}

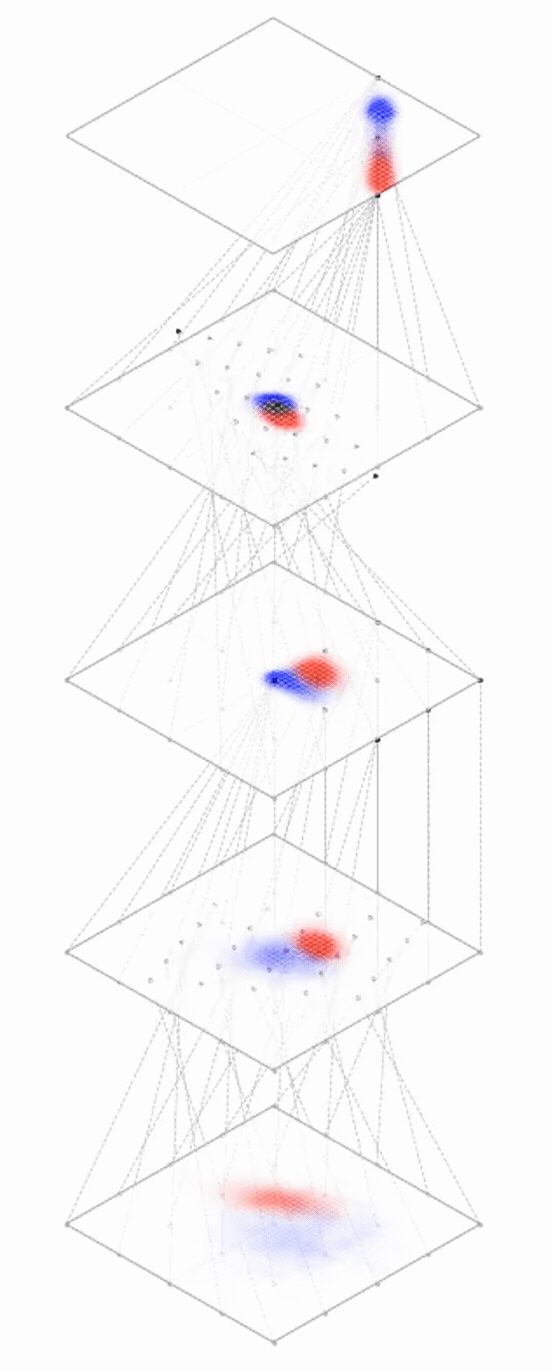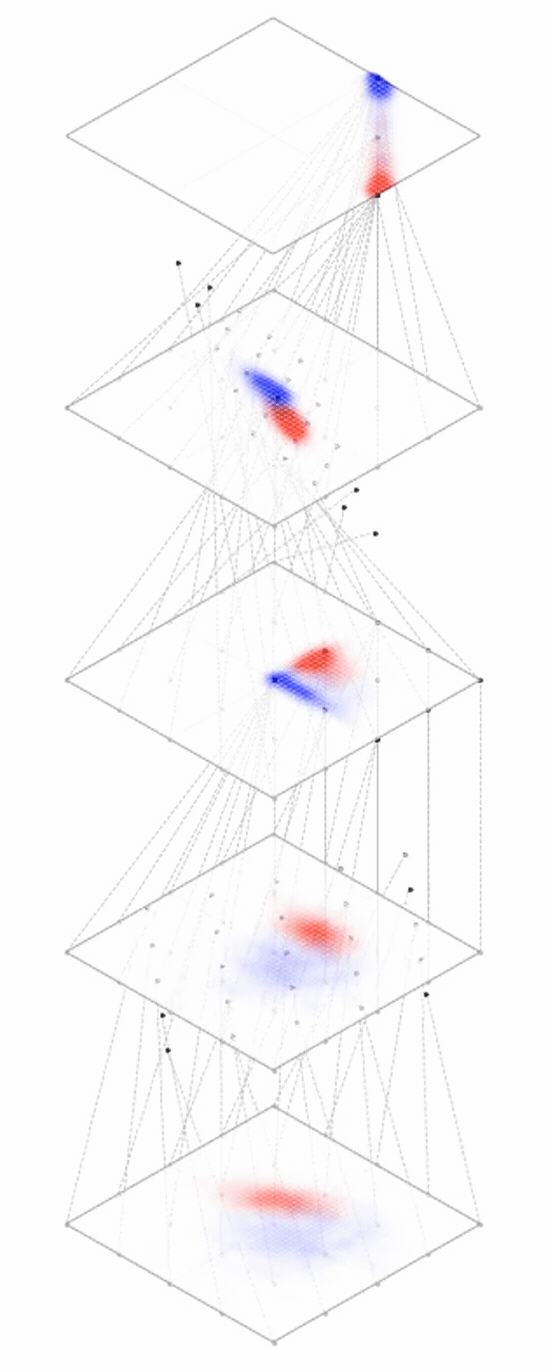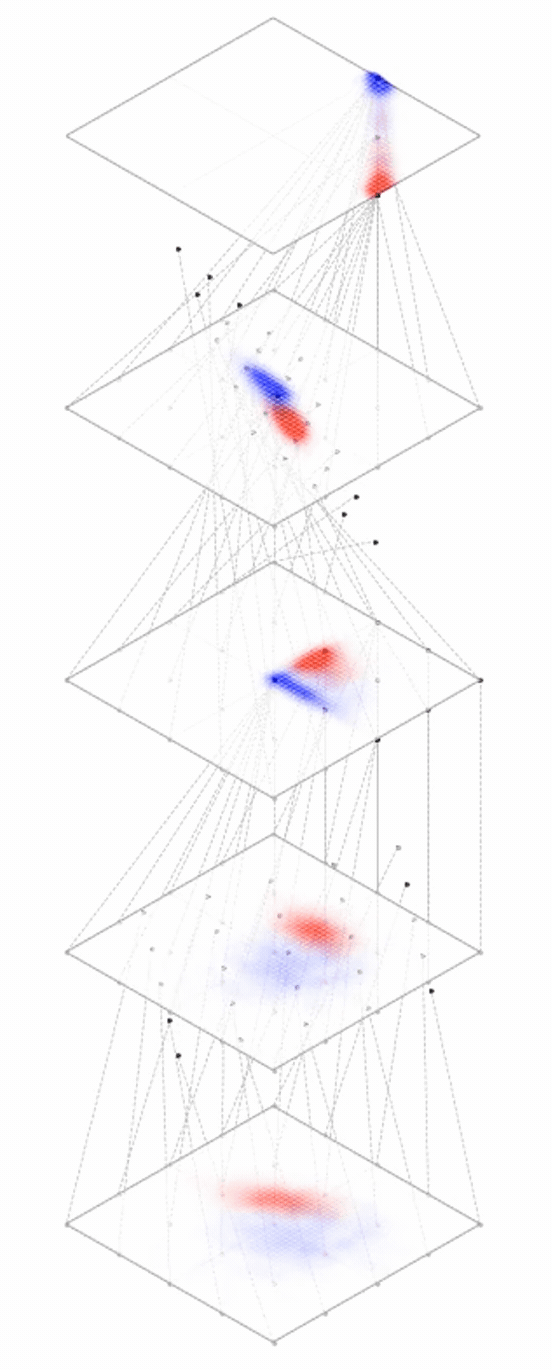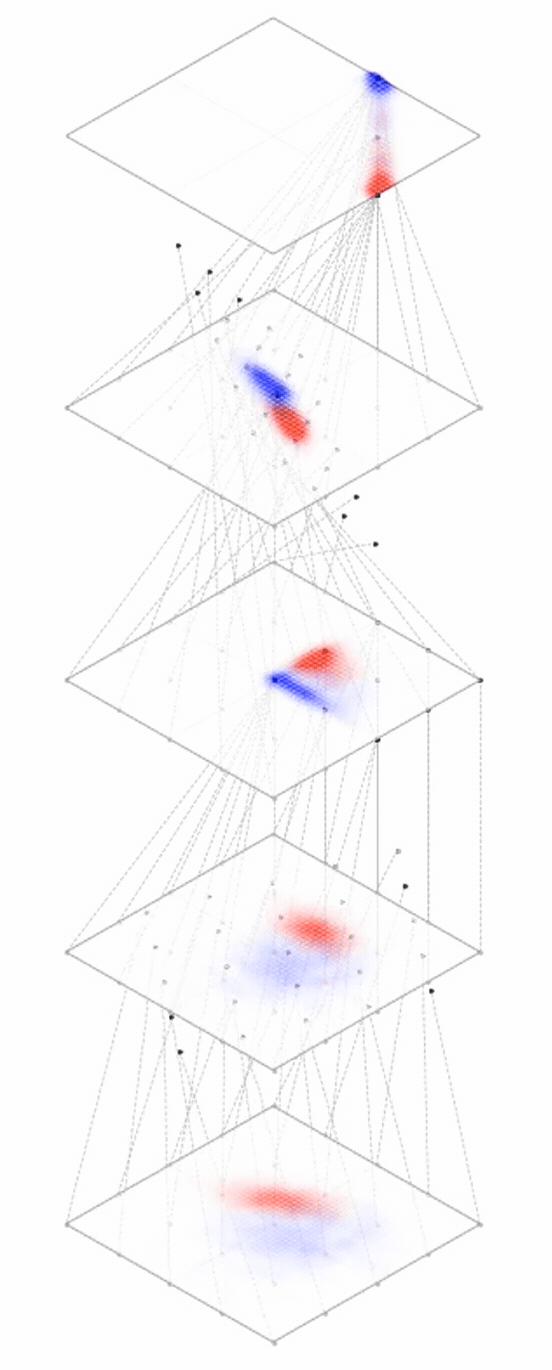
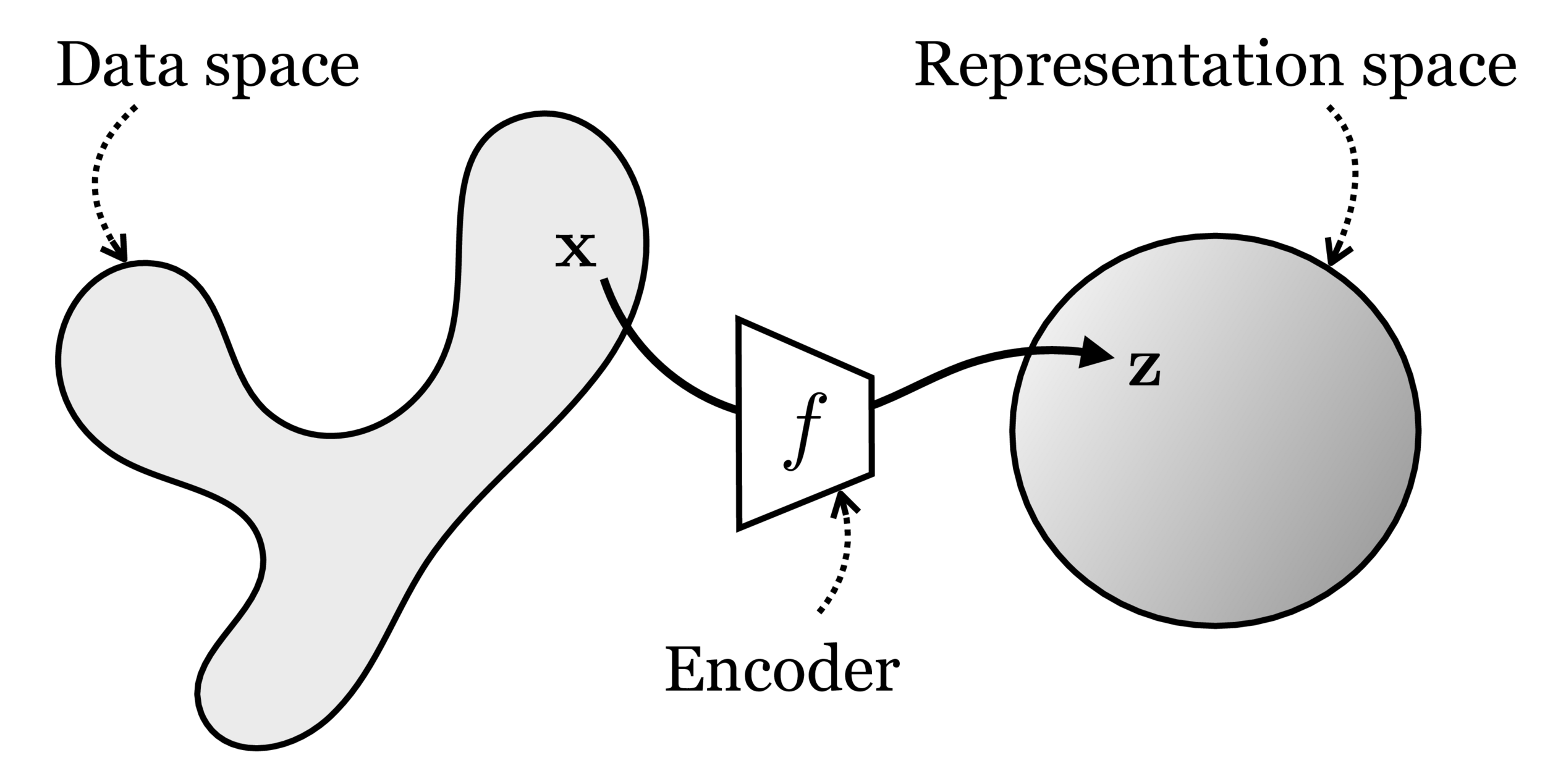
maps from complex data space to simple embedding space

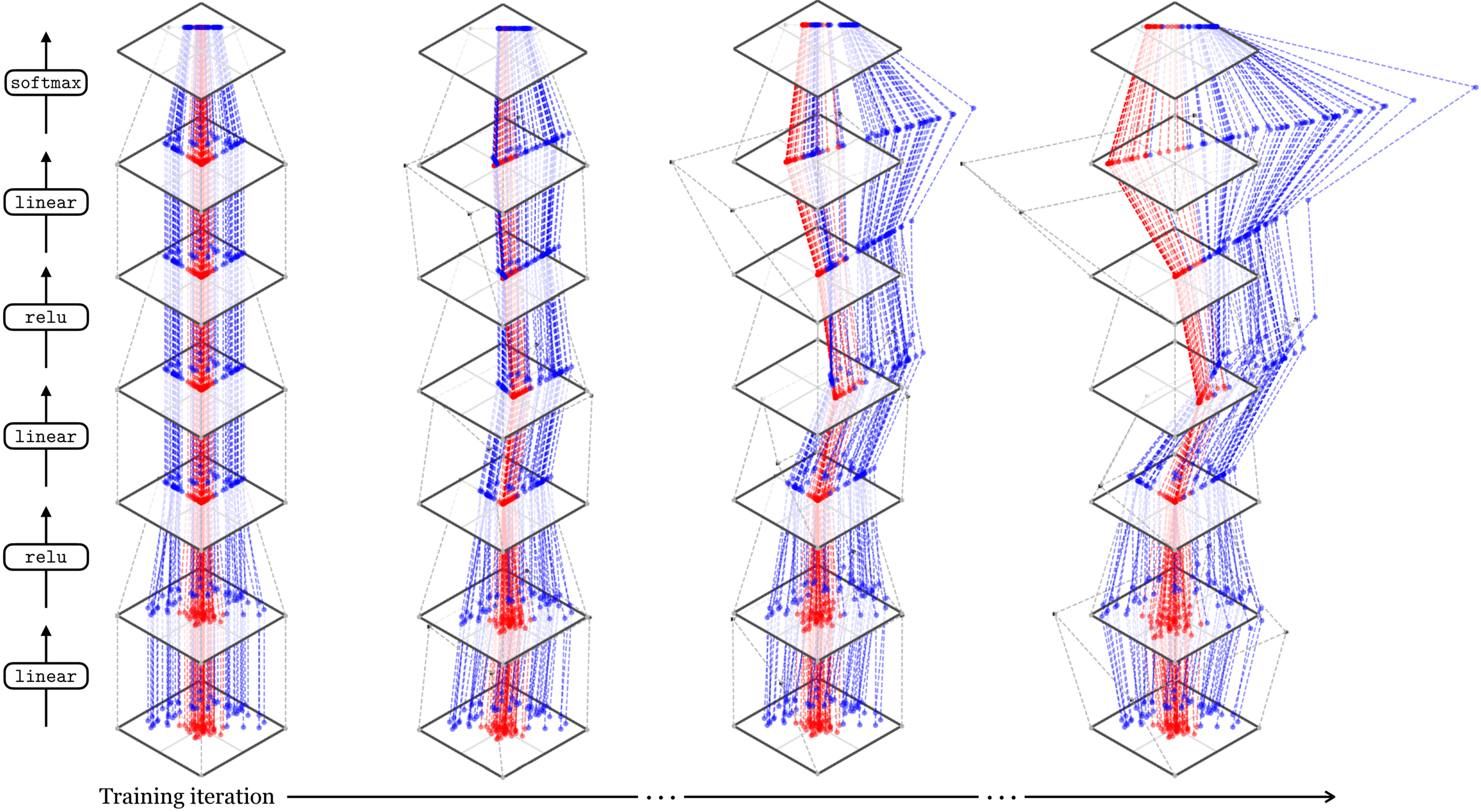
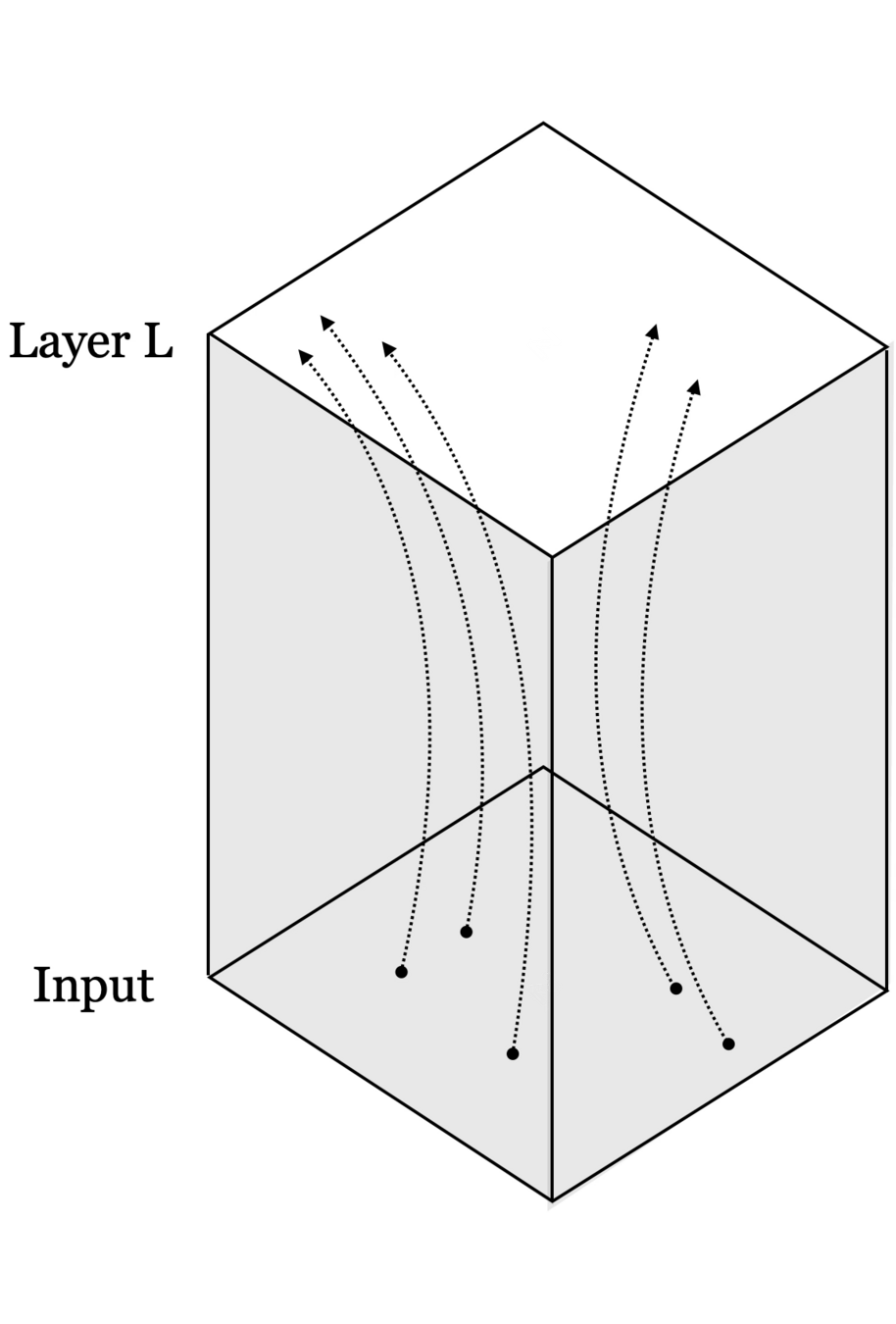
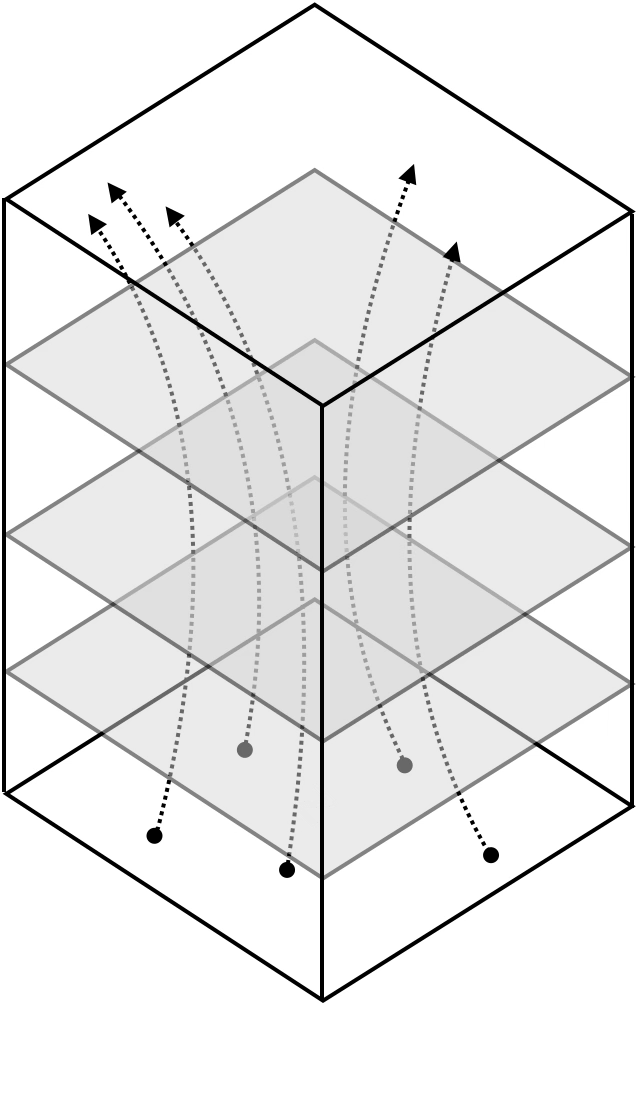
Neural networks are representation learners 

 Deep nets transform datapoints, layer by layer
 Each layer gives a different representation (aka embedding) of the data

🧠

humans also learn representations

"I stand at the window and see a house, trees, sky. Theoretically I might say there were 327 brightnesses and nuances of colour. Do I have "327"? No. I have sky, house, and trees.”

— Max Wertheimer, 1923

Good representations are:

  • Compact (minimal)
  • Explanatory (roughly sufficient)

[See “Representation Learning”, Bengio 2013, for more commentary]

[Bartlett, 1932]
[Intraub & Richardson, 1989]

[https://www.behance.net/gallery/35437979/Velocipedia]

Outline

  • Recap, neural networks mechanism
  • Neural networks are representation learners
  • Auto-encoder:
    • ​Bottleneck
    • Reconstruction
  • Unsupervised learning
  • (Some recent representation learning ideas)

 

  • Compact (minimal)
  • Explanatory (roughly sufficient)
  • Disentangled (independent factors)
  • Interpretable
  • Make subsequent problem solving easy

[See “Representation Learning”, Bengio 2013, for more commentary]

Auto-encoders try to achieve these

\left\{ \begin{array}{l} \\ \\ \end{array} \right.
\left\{ \begin{array}{l} \\ \\ \\ \end{array} \right.

these may just emerge as well

Good representations are:

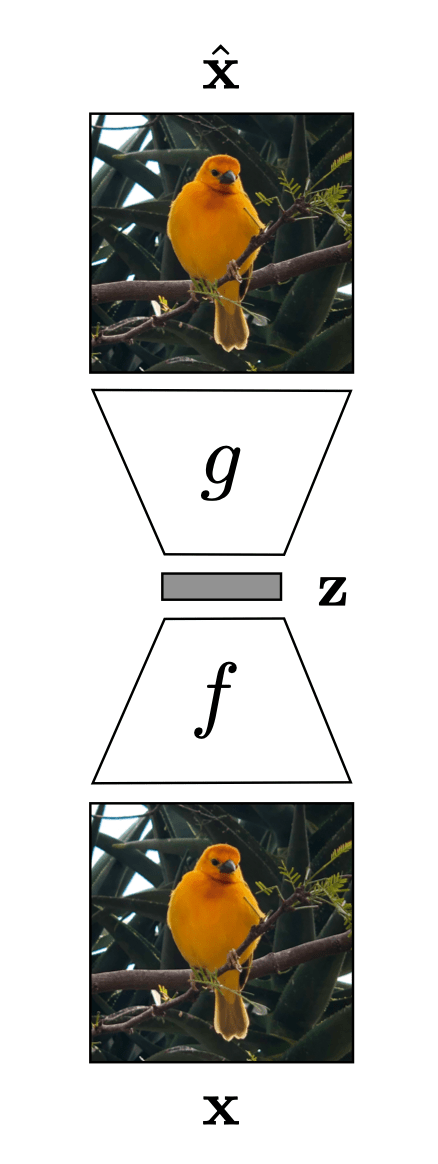
compact representation/embedding

Auto-encoder

Auto-encoder

"What I cannot create, I do not understand." Feynman

Auto-encoder

\underbrace{\hspace{1cm}}
\underbrace{\hspace{1cm}}

encoder

decoder

bottleneck

Auto-encoder

x
\tilde{x}=\text{NN}(x;W)
\min_{W} ||x - \tilde{x}||^2

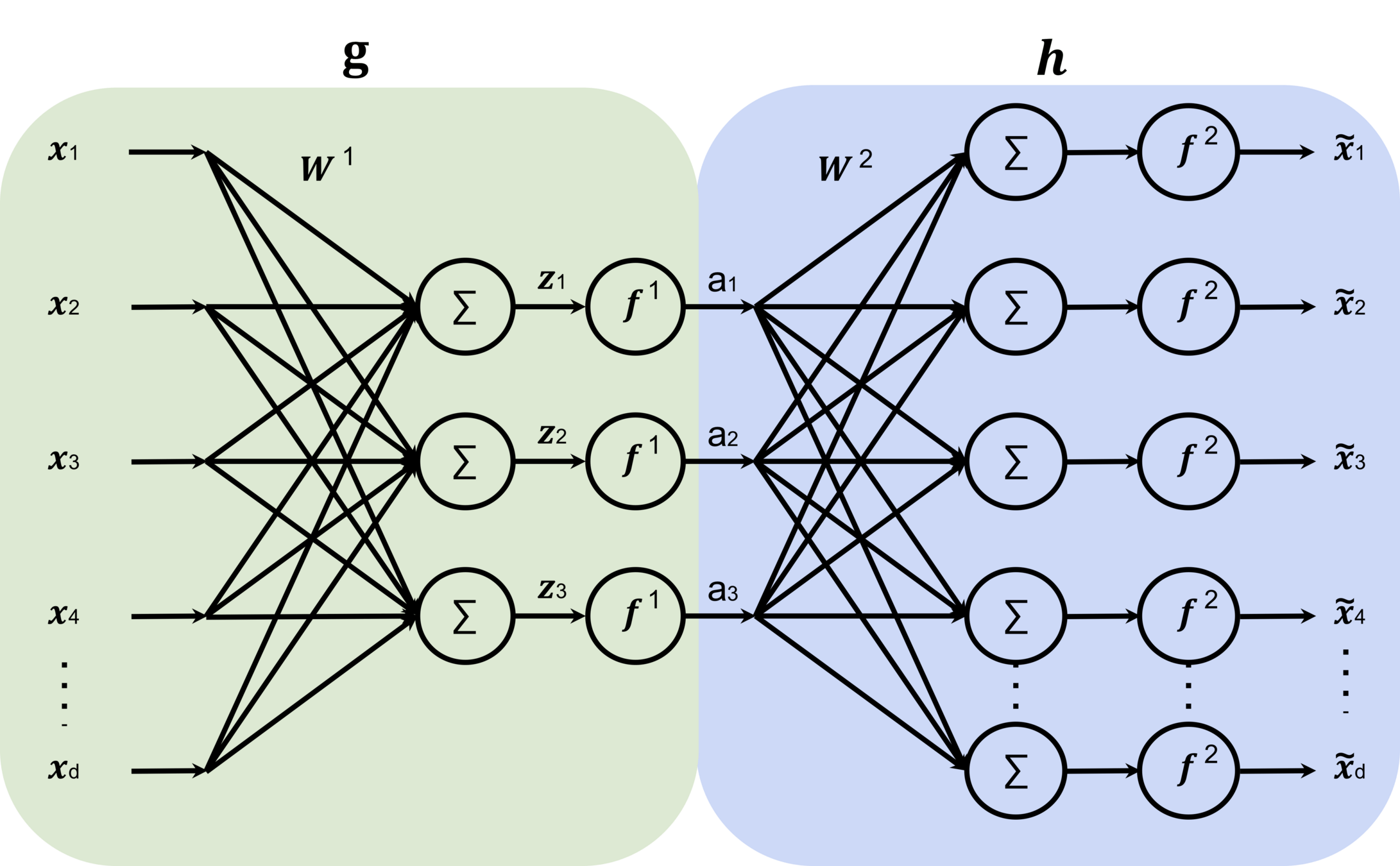
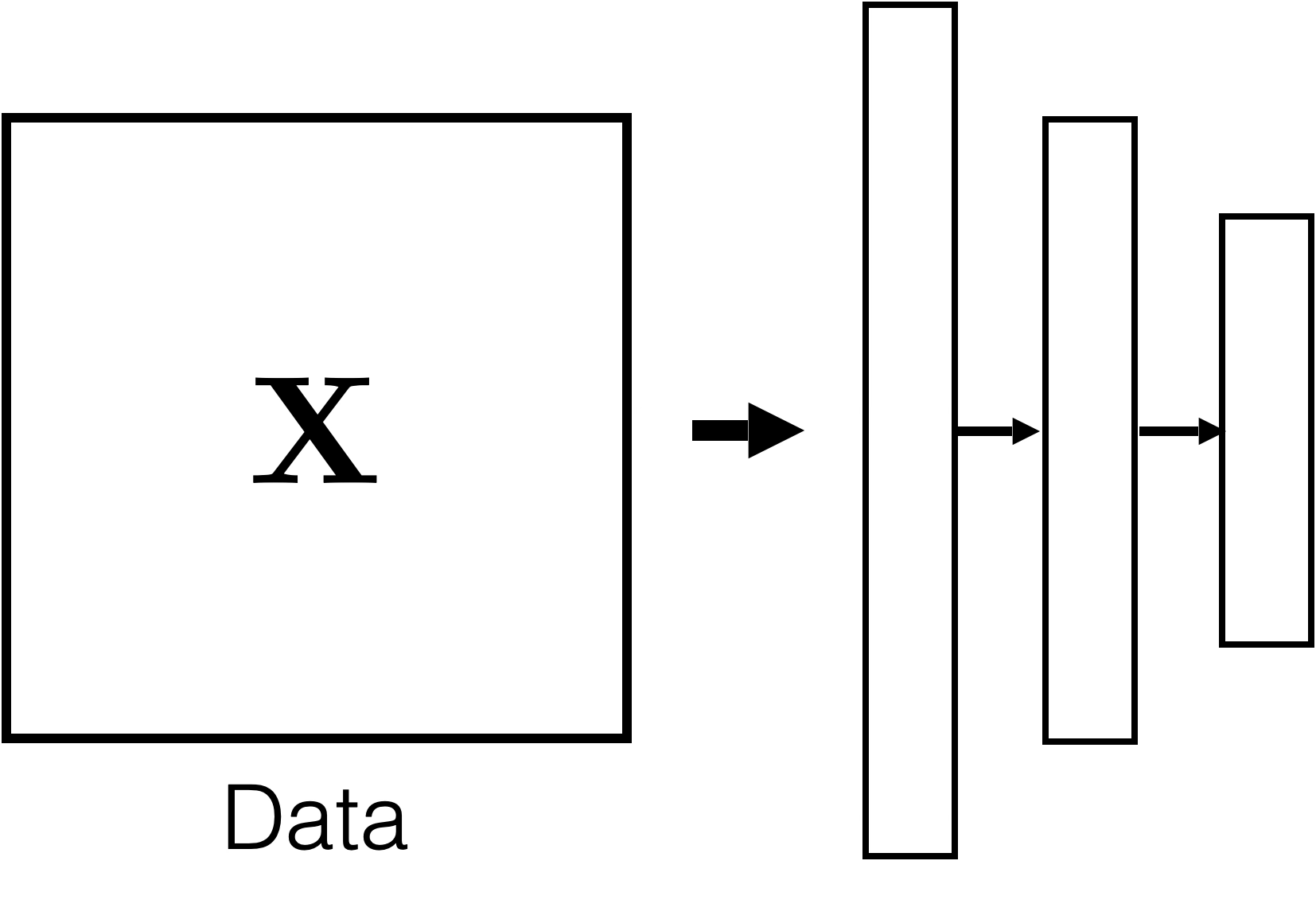
input \(x \in \mathbb{R^d}\)

output \(\tilde{x} \in \mathbb{R^d}\)

\dots

bottleneck

typically, has lower dimension than \(d\)

Auto-encoder

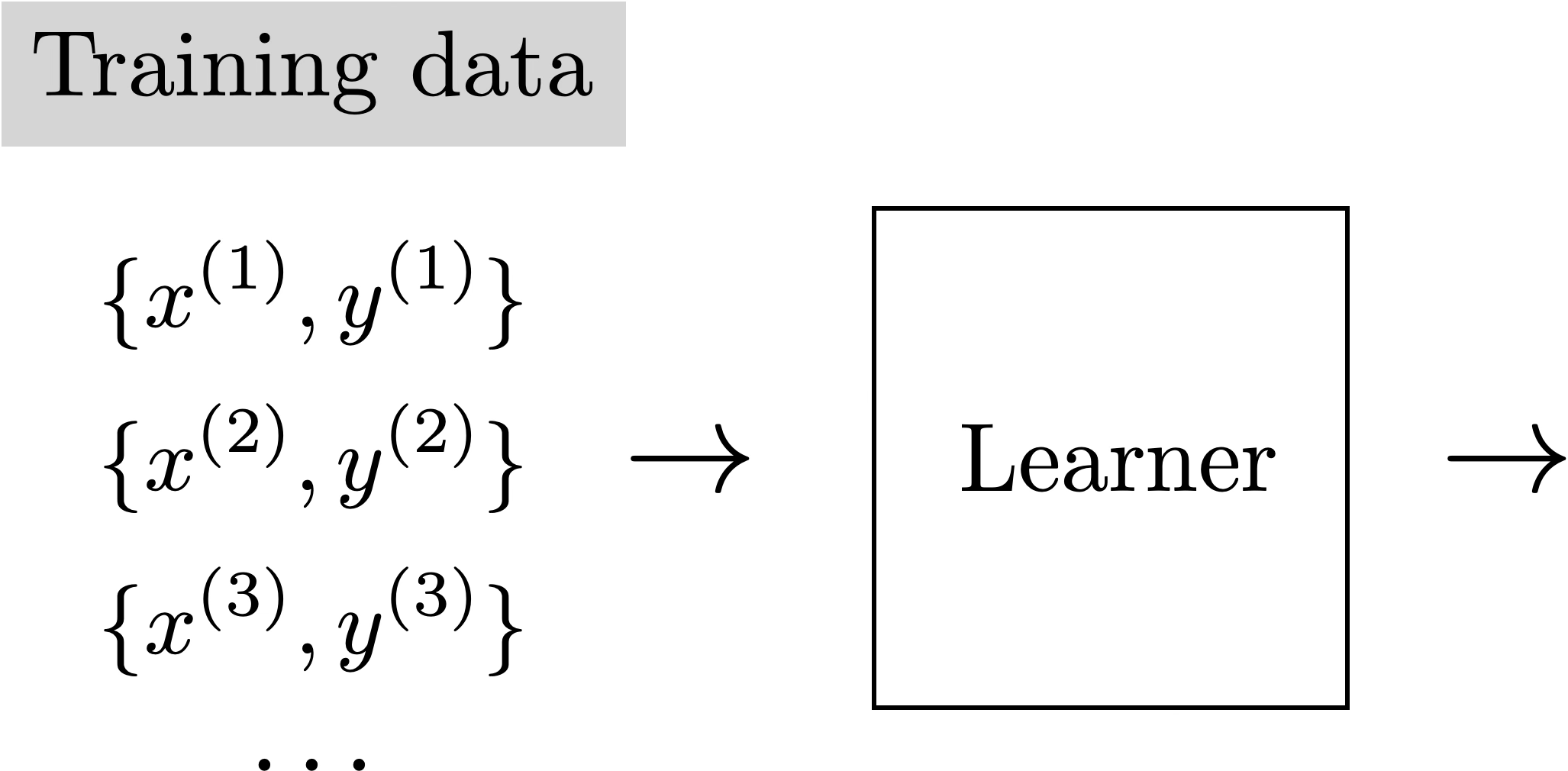
Training Data

\left\{{x}^{(i)}\right\}_{i=1}^n

loss/objective

\mathcal{L}(F(\mathbf{x}), \mathbf{x})=\|F(\mathbf{x})-\mathbf{x}\|^2

hypothesis class

A model

\(f\)

F=g \circ h: \mathbb{R}^d \rightarrow \mathbb{R}^m \rightarrow \mathbb{R}^d
h
g

\(m<d\)

\(f: X \rightarrow Y\) 

Supervised Learning

"Good"

Representation

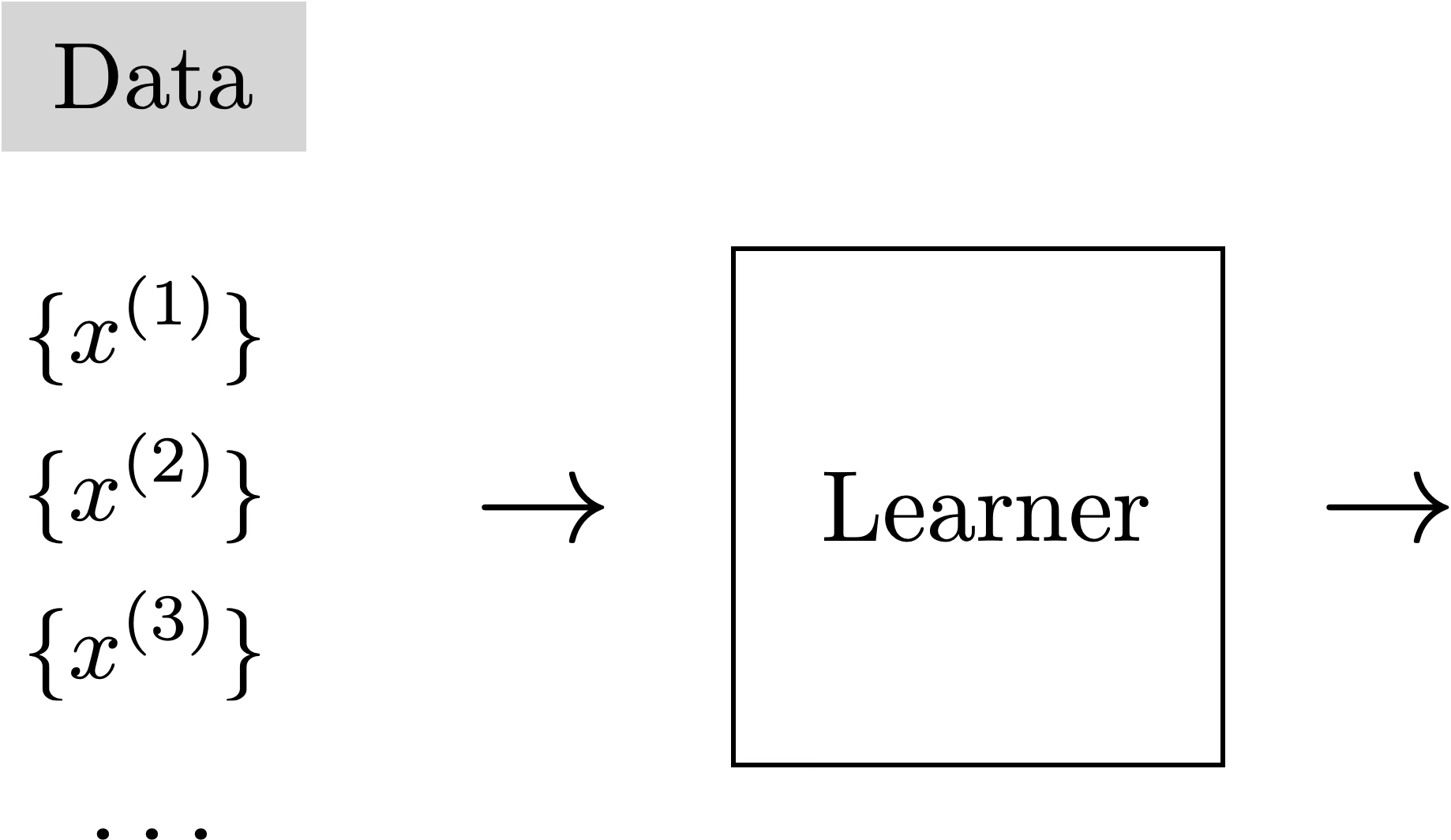
Unsupervised Learning

Training Data

Word2Vec

https://www.tensorflow.org/text/tutorials/word2vec

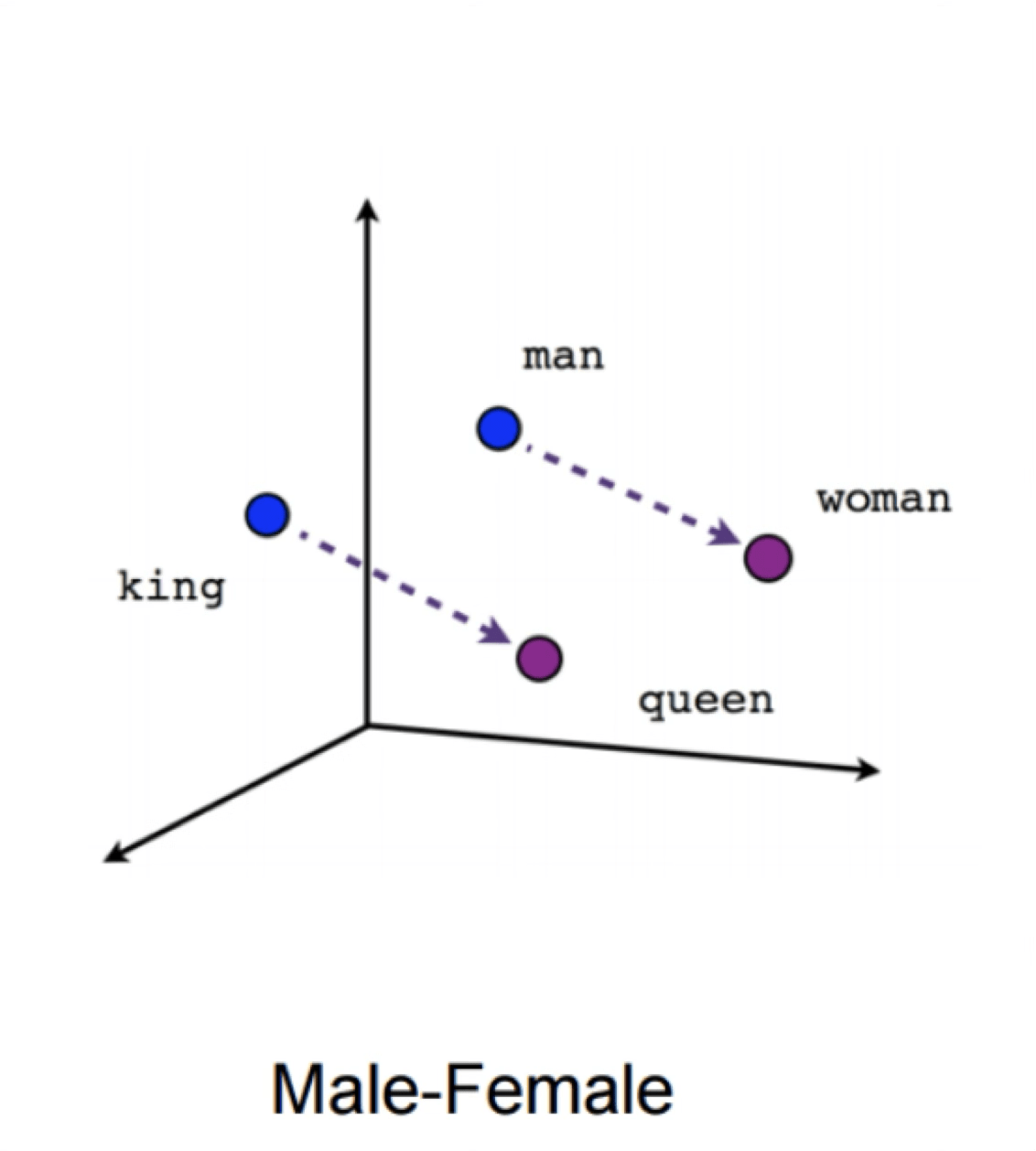
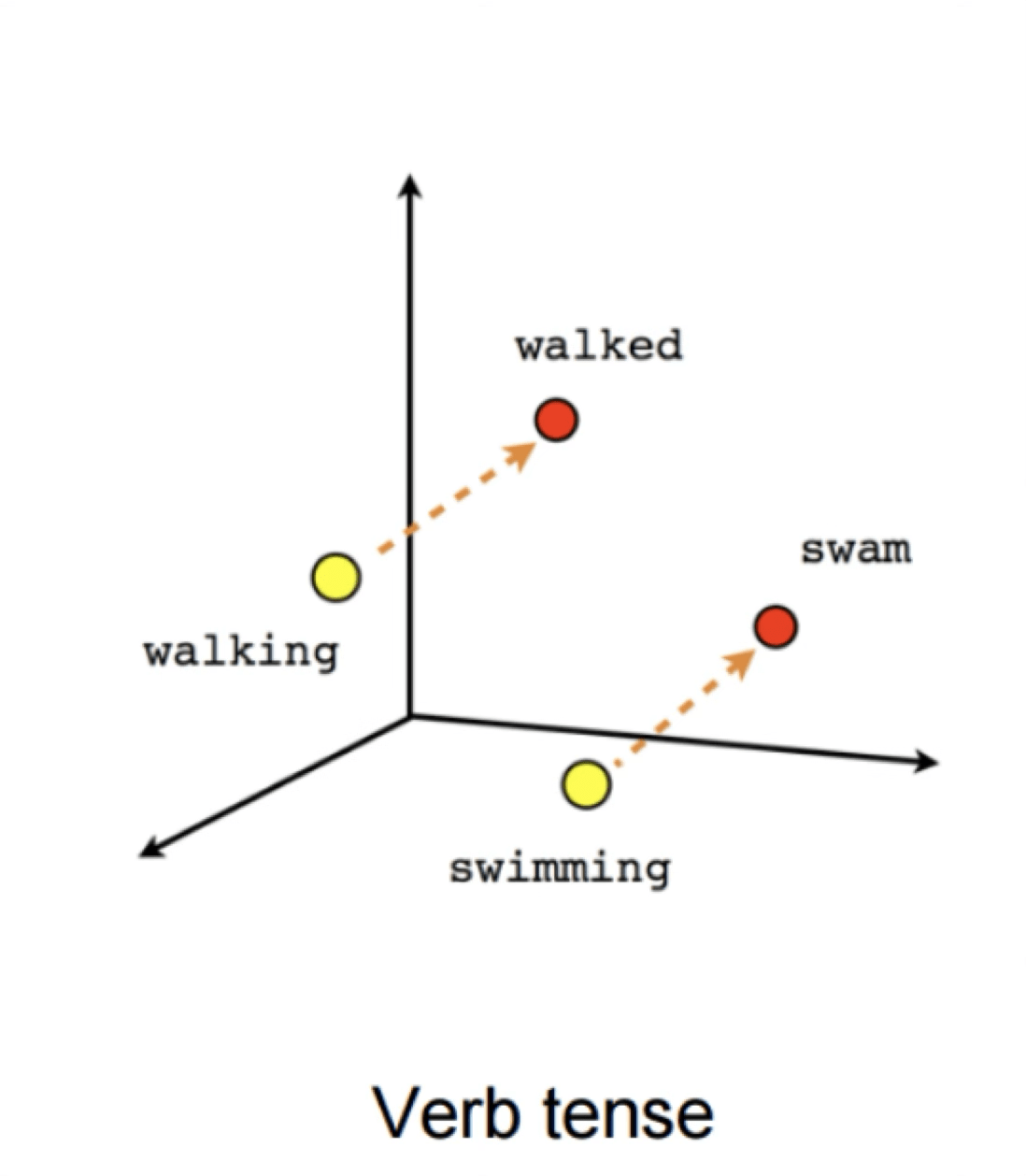
Word2Vec

verb tense

gender

X = Vector(“Paris”) – vector(“France”) + vector(“Italy”) \(\approx\) vector("Rome")

“Meaning is use” — Wittgenstein

Can help downstream tasks:

  • sentiment analysis
  • machine translation
  • info retrieval 

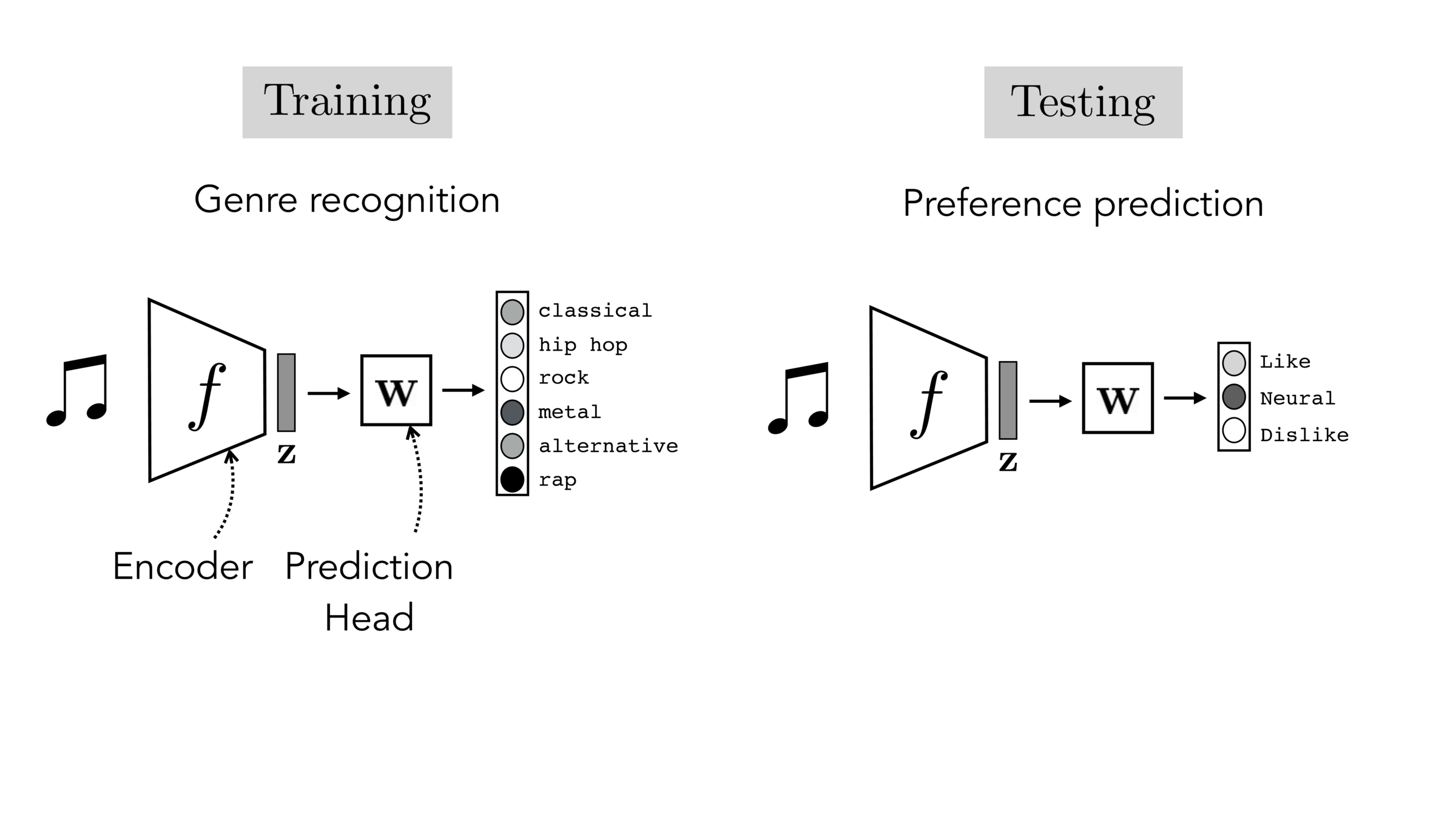
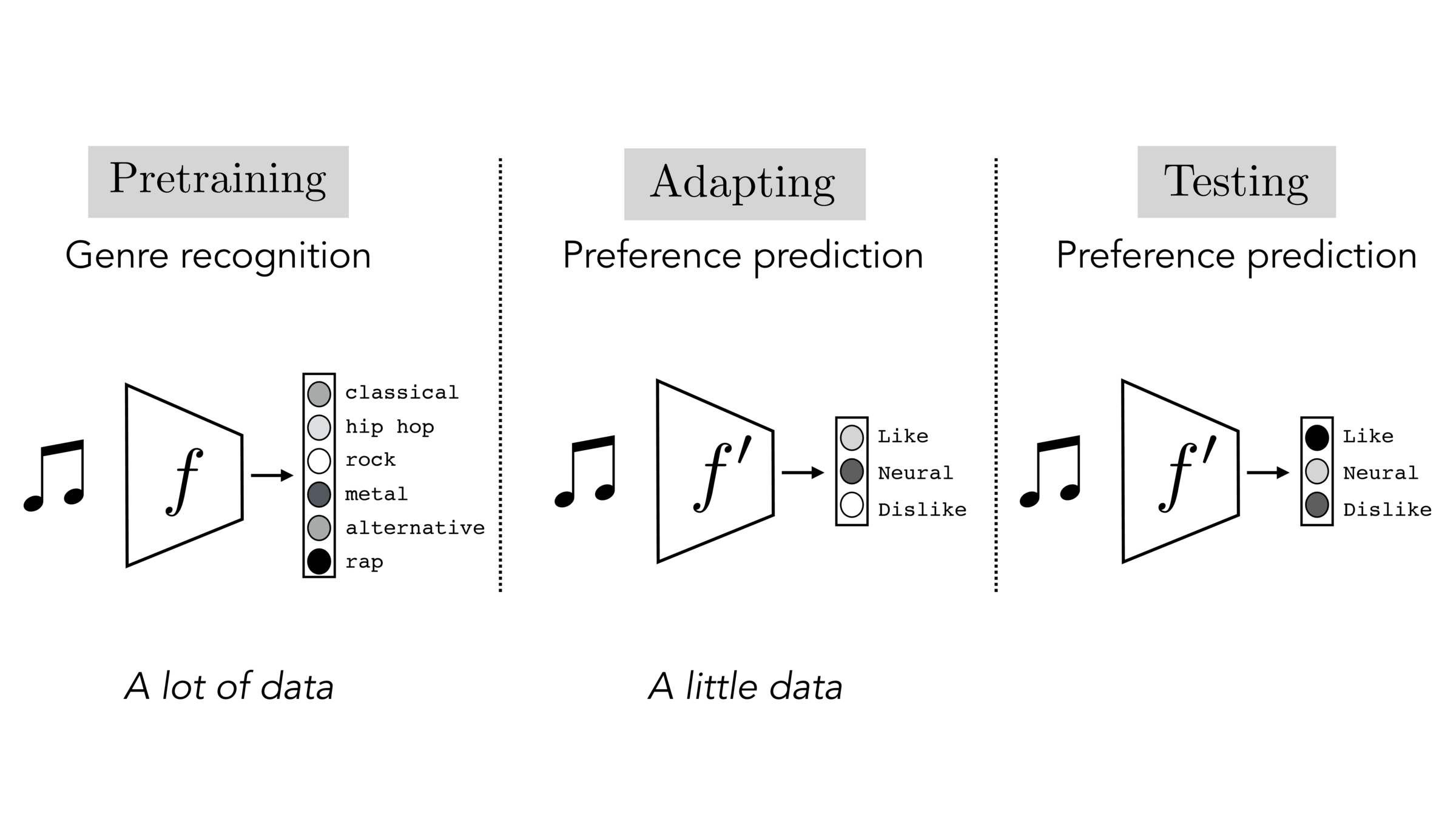
Often, what we will be “tested” on is not what we were trained on.

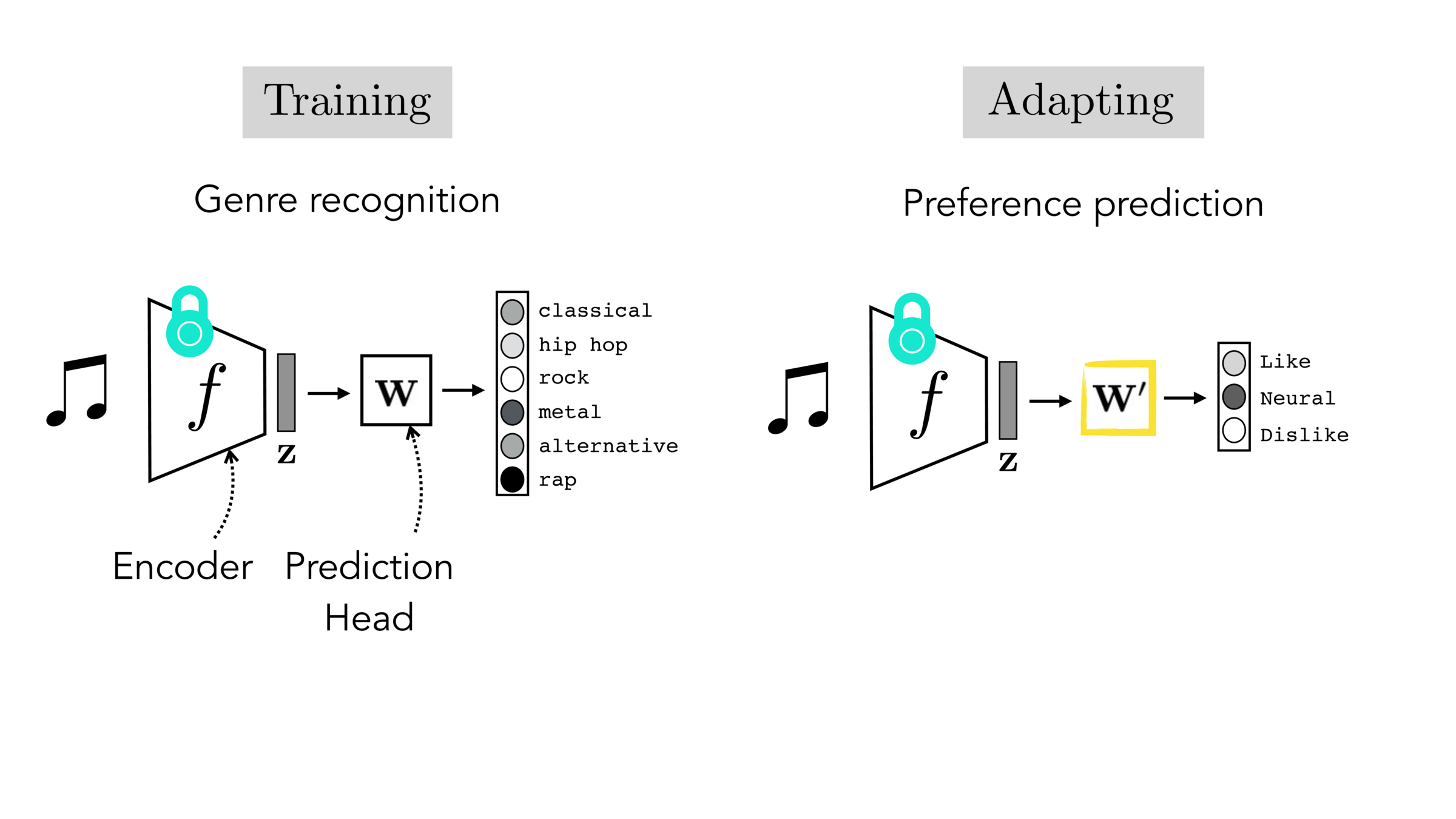
Final-layer adaptation: freeze \(f\), train a new final layer to new target data

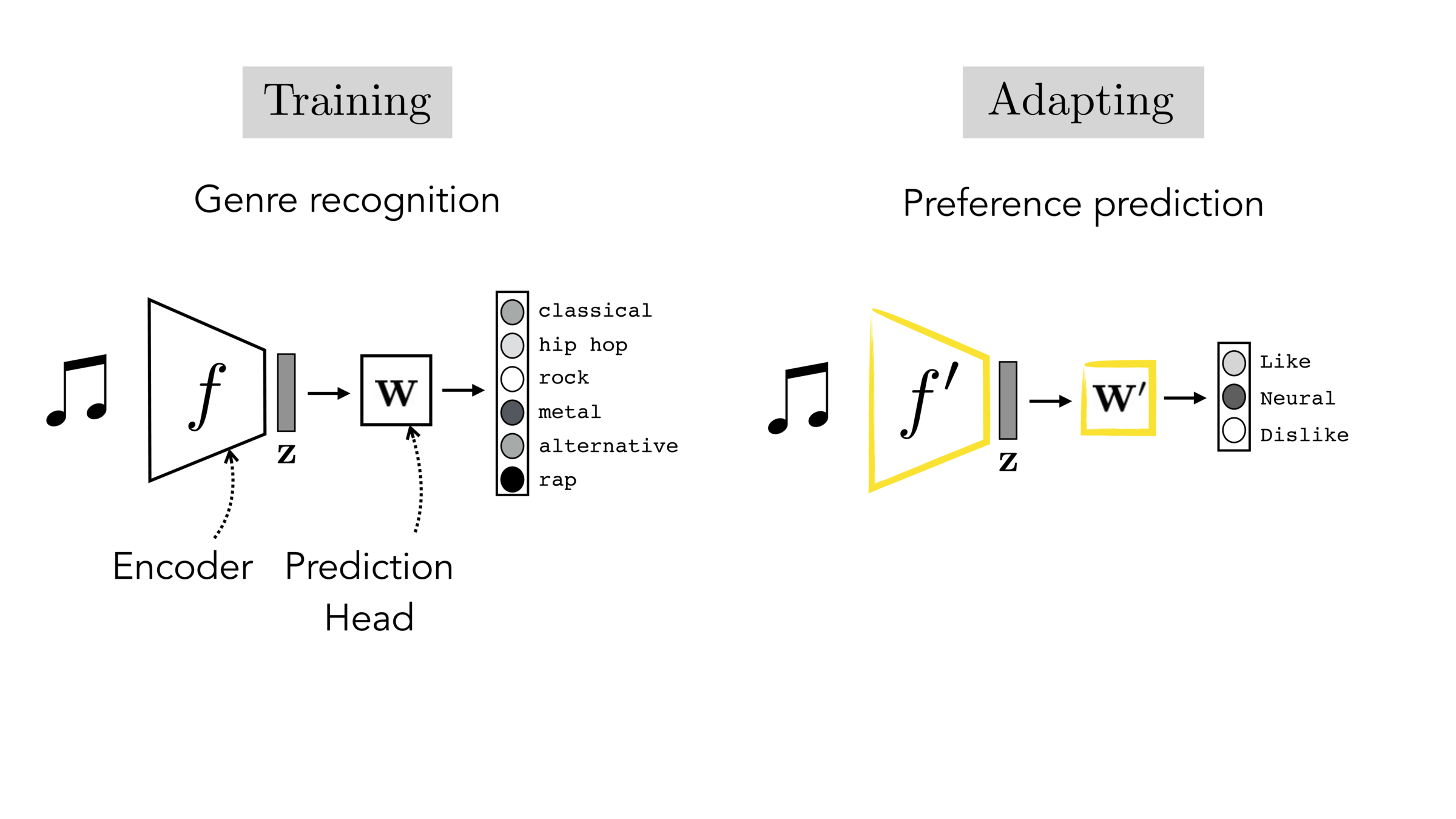
Finetuning: initialize \(f’\) as \(f\), then continue training for \(f'\) as well, on new target data

Outline

  • Recap, neural networks mechanism
  • Neural networks are representation learners
  • Auto-encoder:
    • ​Bottleneck
    • Reconstruction
  • Unsupervised learning
  • (Some recent representation learning ideas)
\left( \begin{array}{l} \\ \\ \\ \\ \\ \\ \end{array} \right.

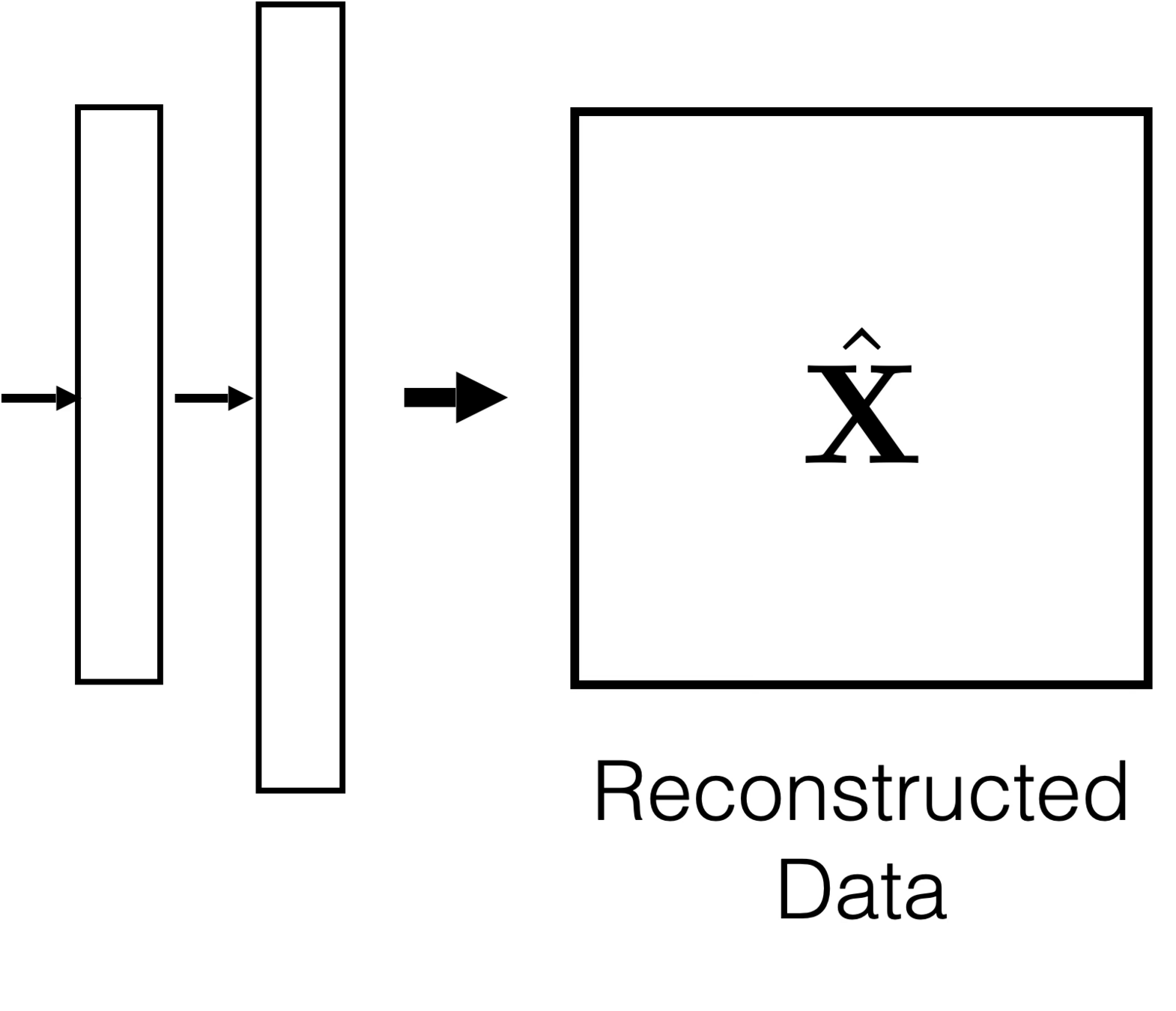
Feature reconstruction (unsupervised learning)

Features

Reconstructed Features

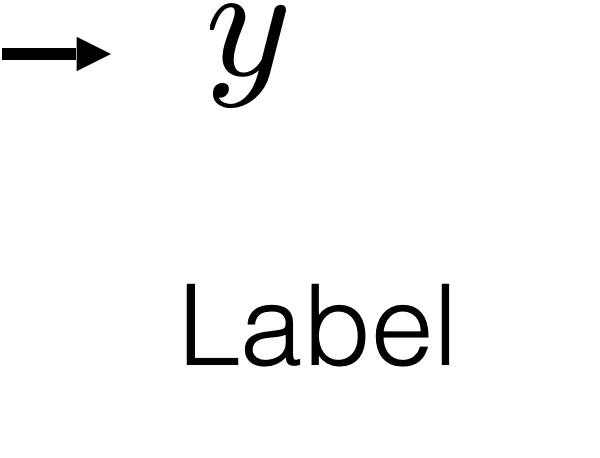
Label prediction (supervised learning)

Features

Label

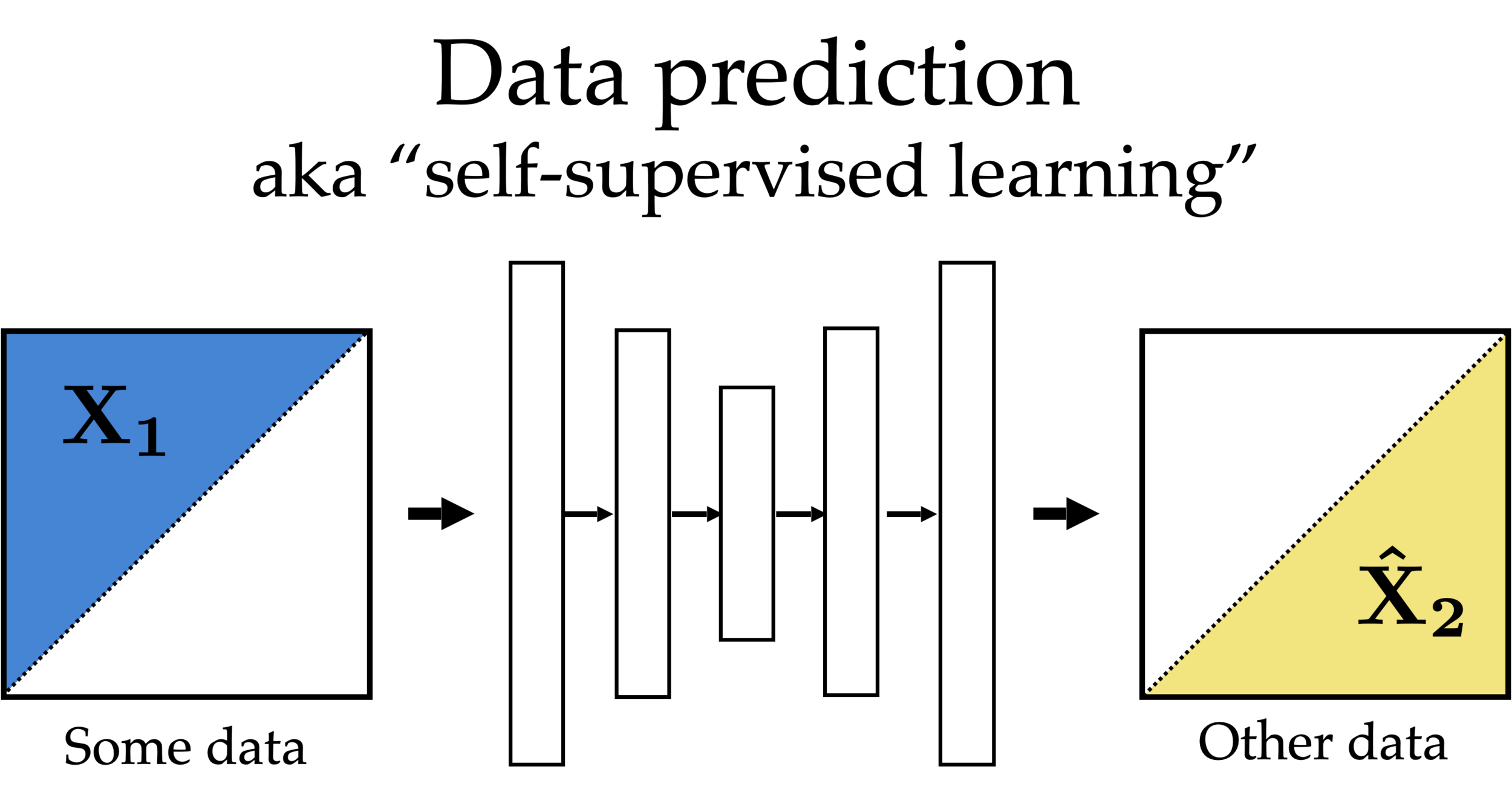
Partial

features

Other partial

features

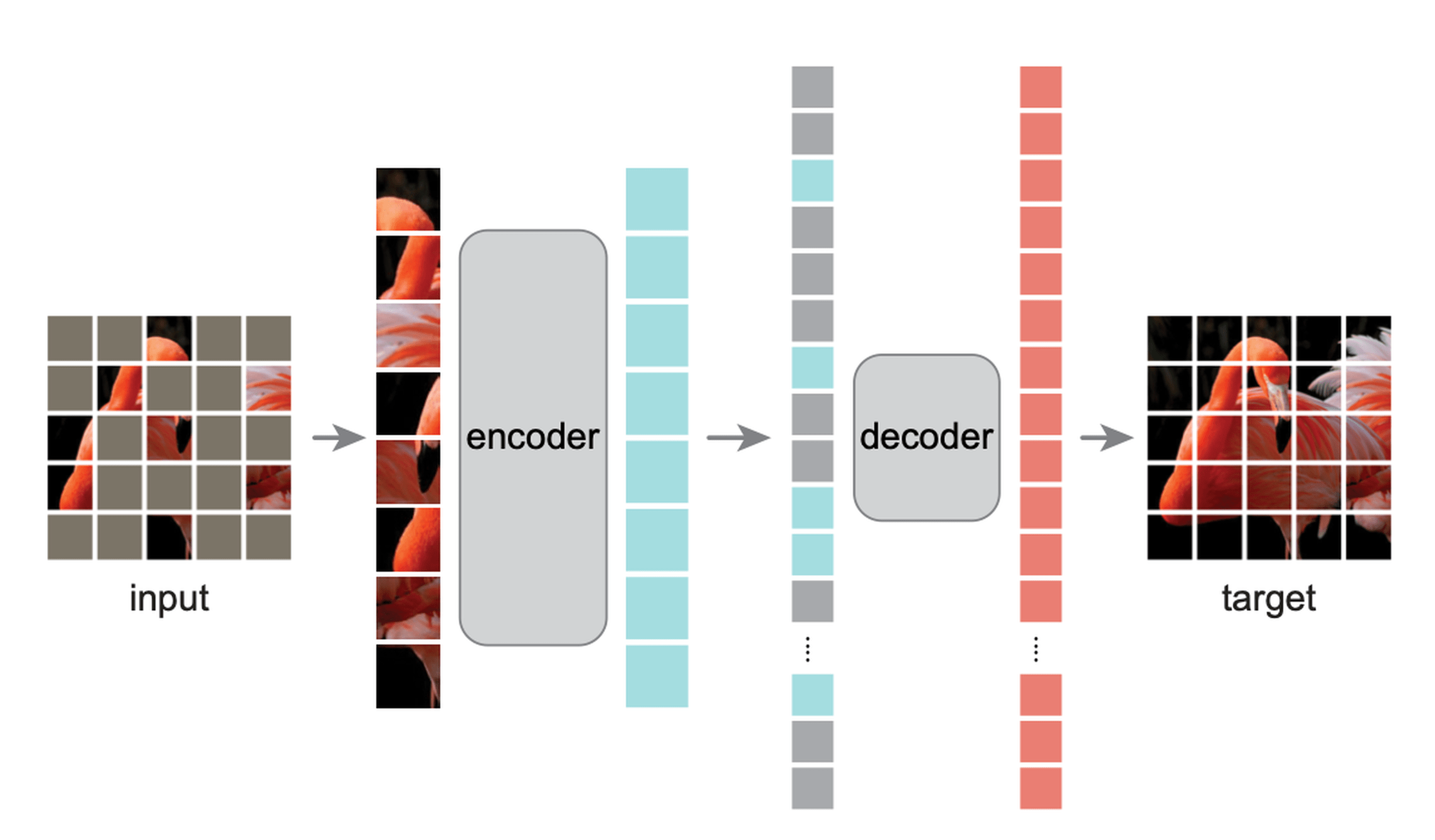
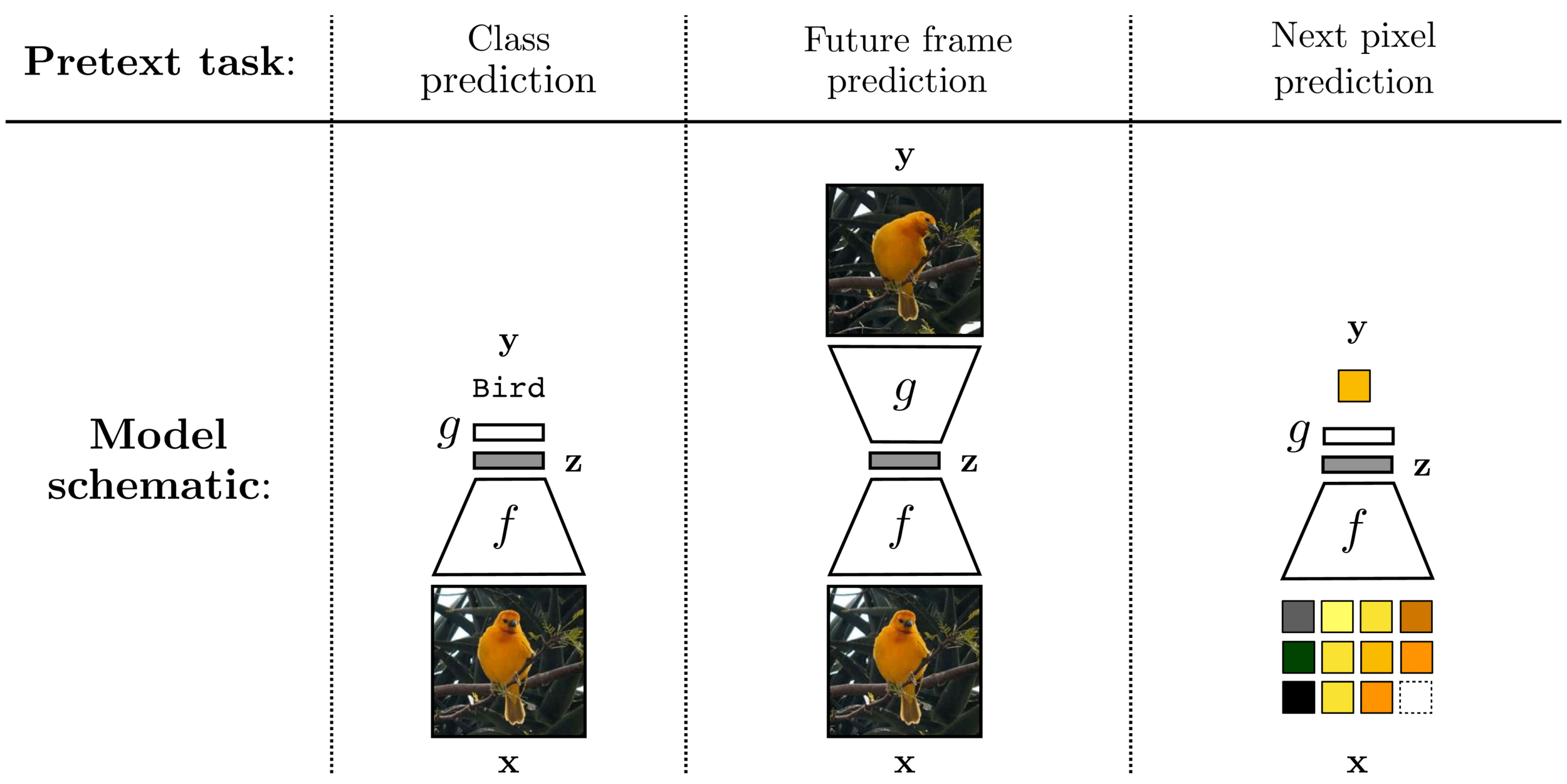
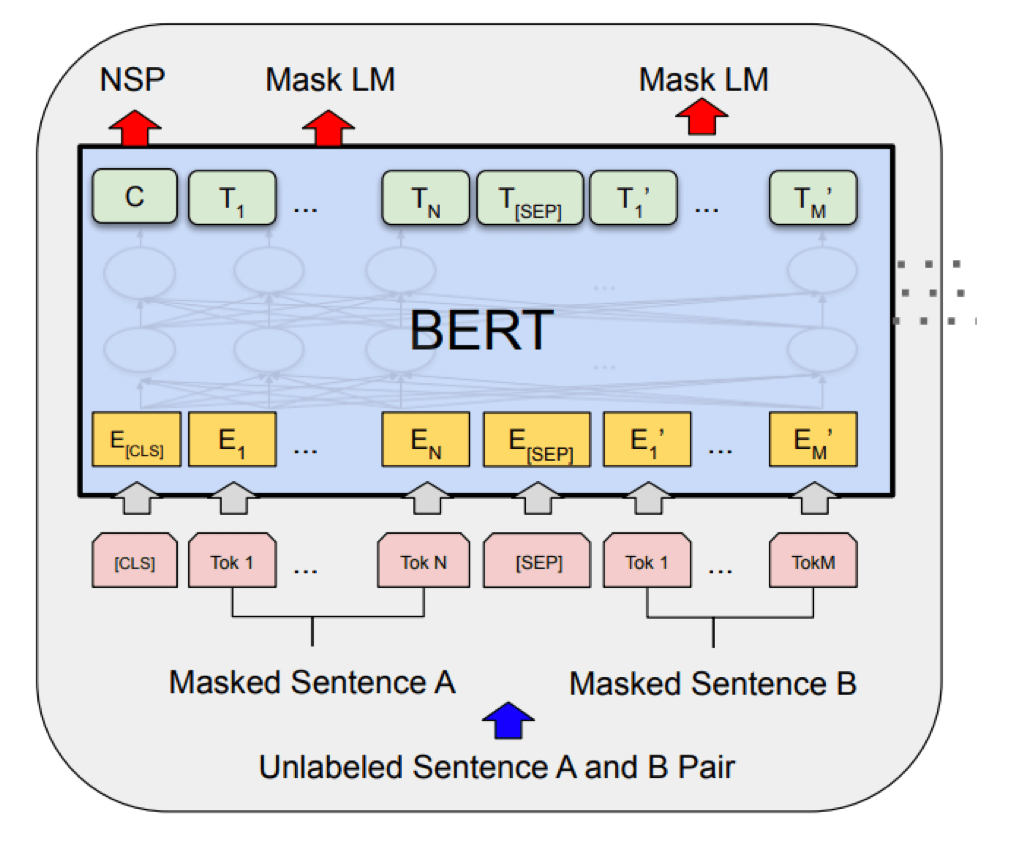
Masked Auto-encoder

[He, Chen, Xie, et al. 2021]

Masked Auto-encoder

[Devlin, Chang, Lee, et al. 2019]

[Zhang, Isola, Efros, ECCV 2016]

predict color from gray-scale

[Zhang, Isola, Efros, ECCV 2016]

Self-supervised learning

Common trick: 

  • Convert “unsupervised” problem into “supervised” setup
  • Do so by cooking up “labels” (prediction targets) from the raw data itself — called pretext task

The allegory of the cave

[Slide credit: Andrew Owens]

[Owens et al, Ambient Sound Provides Supervision for Visual Learning, ECCV 2016]

[Slide credit: Andrew Owens]

[Owens et al, Ambient Sound Provides Supervision for Visual Learning, ECCV 2016]

What did the model learn?

[Slide credit: Andrew Owens]

[Owens et al, Ambient Sound Provides Supervision for Visual Learning, ECCV 2016]

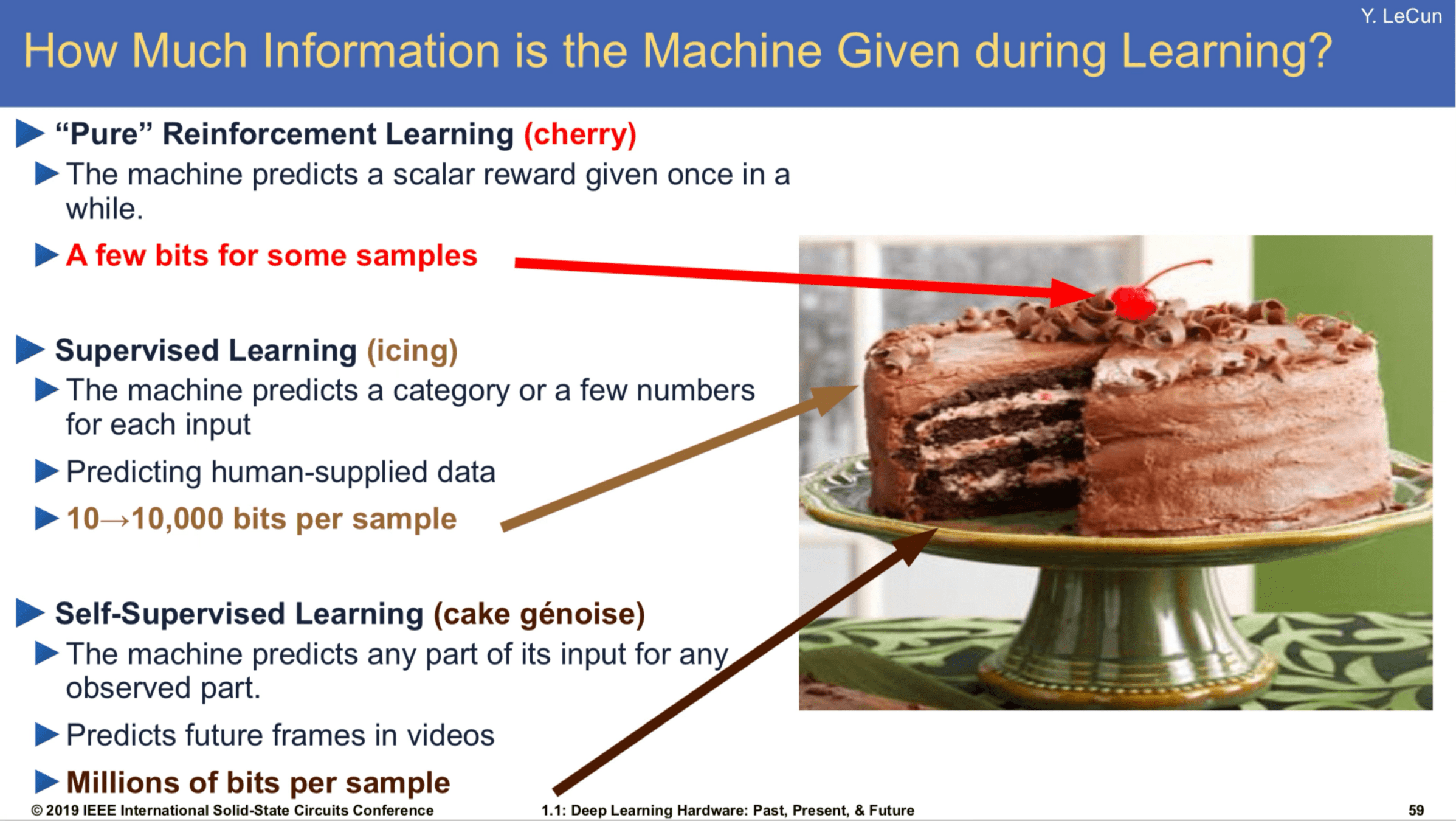
[Slide Credit: Yann LeCun]

Contrastive learning 

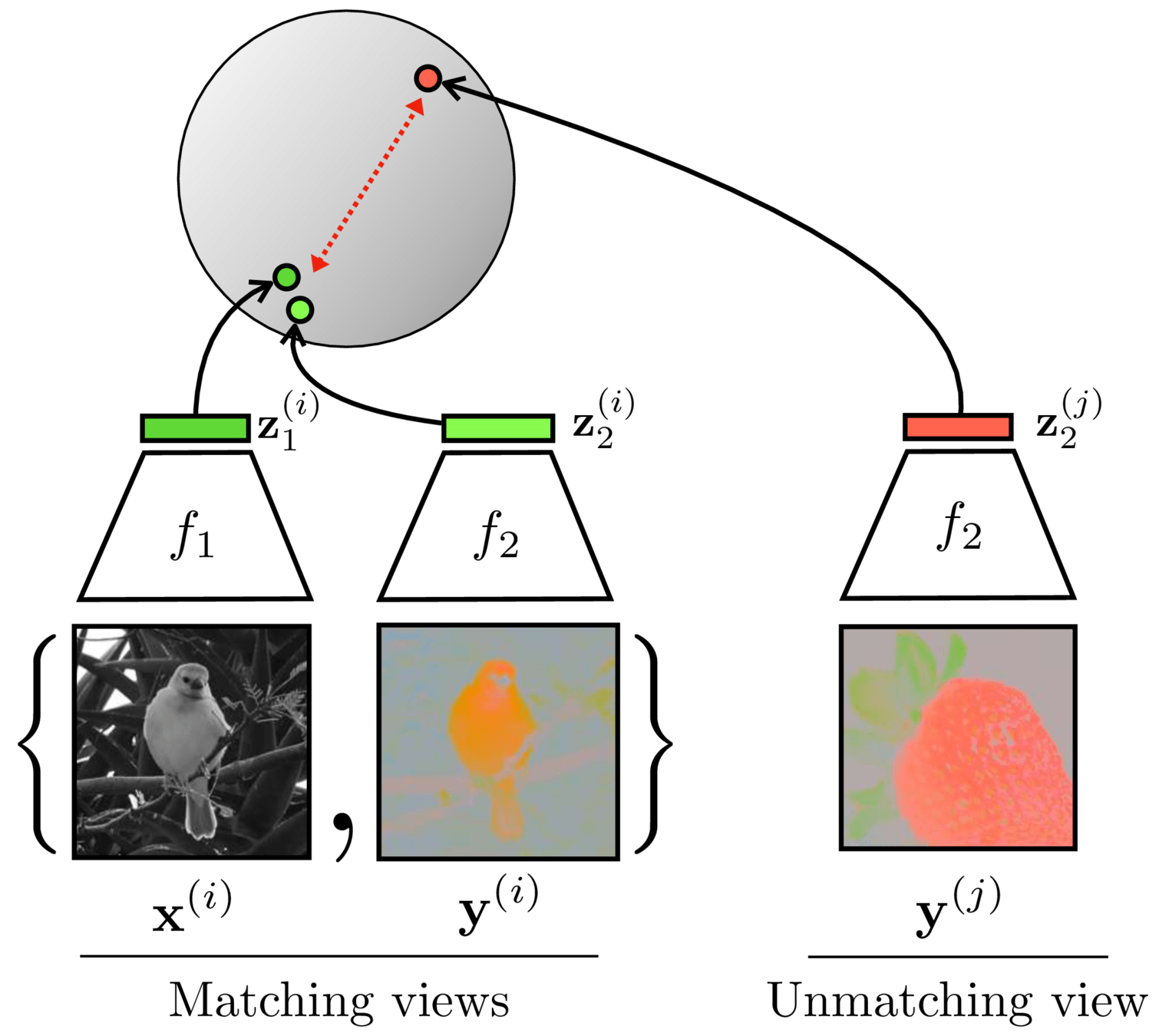
Contrastive learning 

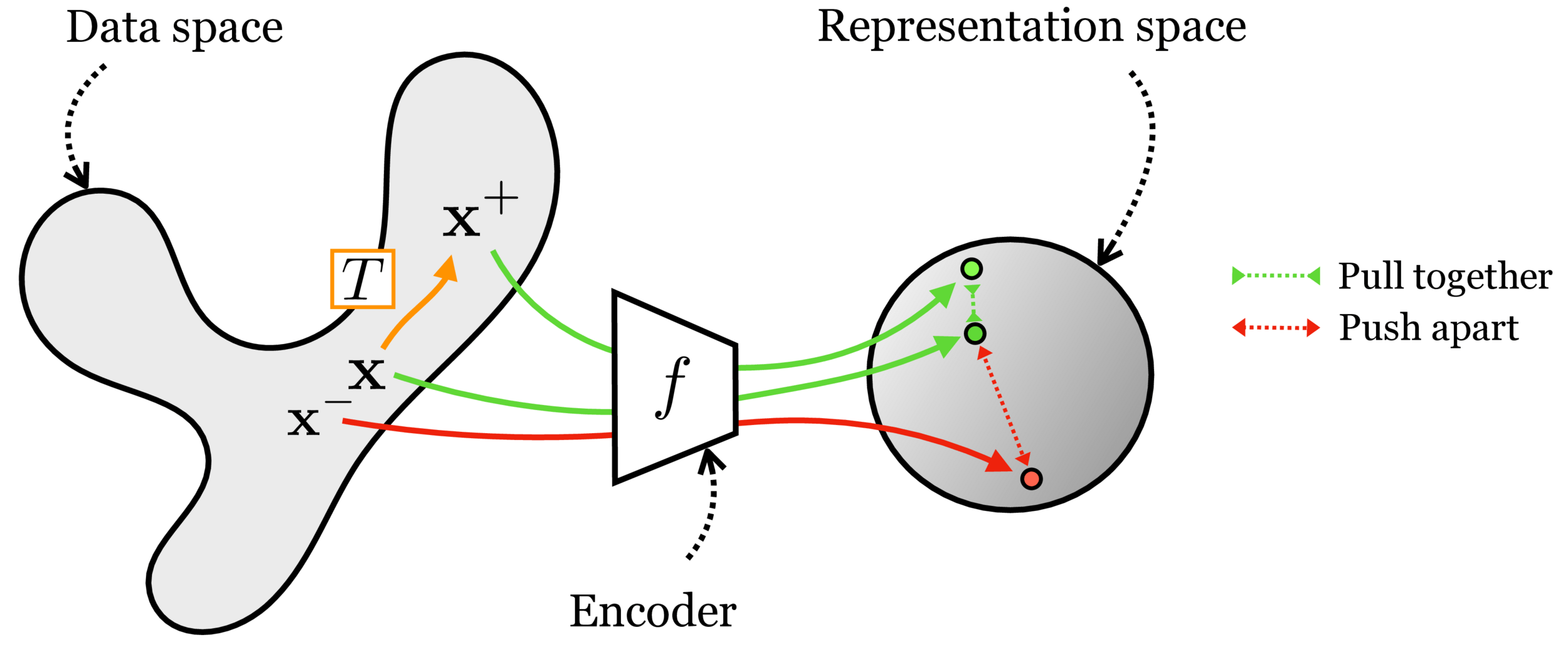
[Chen, Kornblith, Norouzi, Hinton, ICML 2020]

[https://arxiv.org/pdf/2204.06125.pdf]

DallE

\left) \begin{array}{l} \\ \\ \\ \\ \\ \\ \end{array} \right.

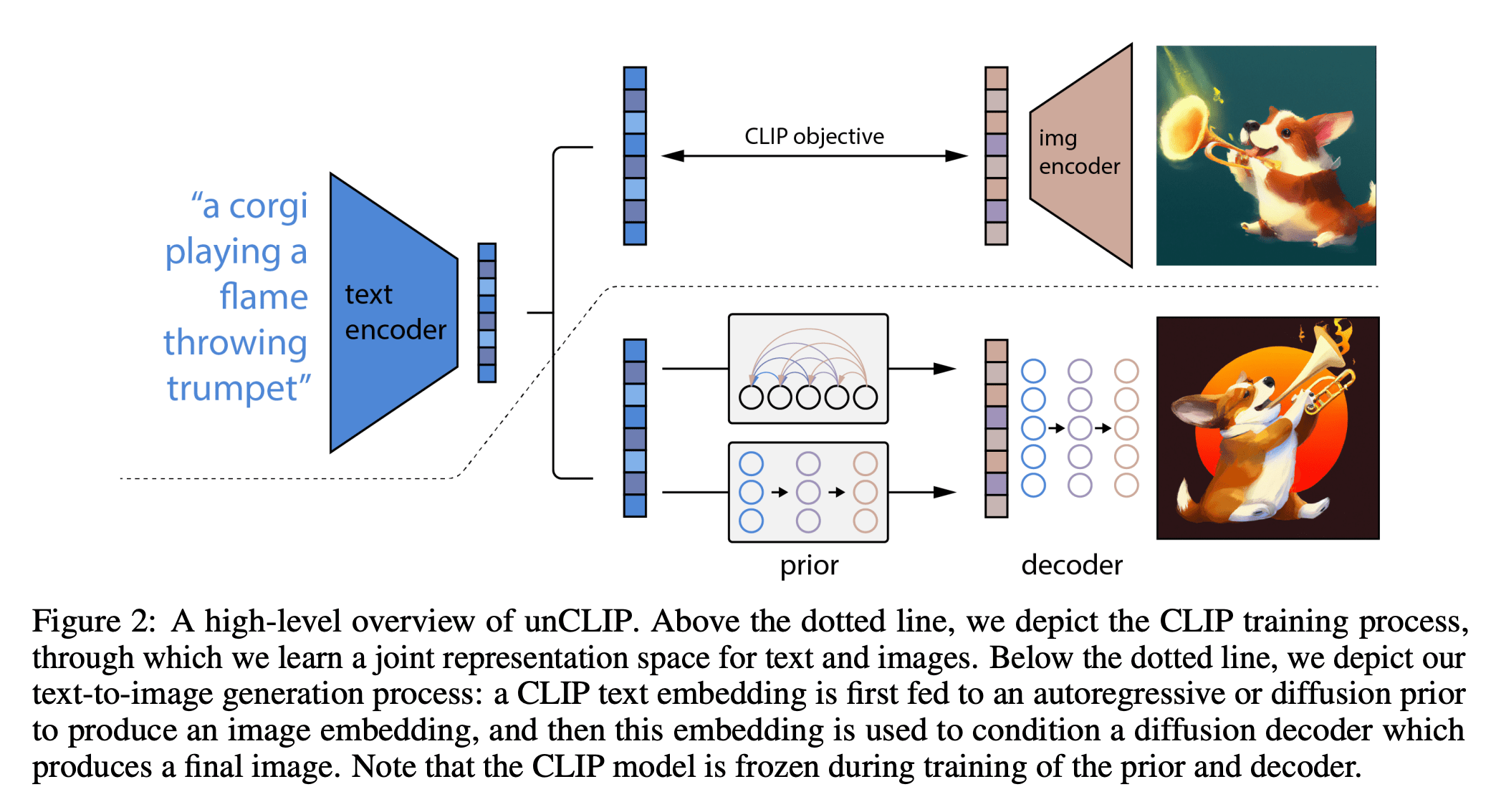
Summary

  • We looked at the mechanics of neural net last time. Today we see deep nets learn representations, just like our brains do.
  • This is useful because representations transfer — they act as prior knowledge that enables quick learning on new tasks.
  • Representations can also be learned without labels, e.g. as we do in unsupervised, or self-supervised learning. This is great since labels are expensive and limiting.
  • Without labels there are many ways to learn representations. We saw today:
    • representations as compressed codes, auto-encoder with bottleneck
    • (representations that are shared across sensory modalities)
    • (representations that are predictive of their context)

Thanks!

We'd love to hear your thoughts.