機器學習
Machine Learning
講師介紹
-
227郭彥聖
-
yennnn
-
建中資訊 外交長
-
想學習機器學習所以才來教機器學習
-
FB:郭彥聖

0. 課程介紹
課程資訊
-
每週四18:00~19:00
-
段考週、段考前一週停課
-
線上Google Meet
-
電教二
上課方式
-
自由參加,不須請假
-
歡迎提問討論
-
中文授課,但專有名詞會用英文
-
以理論為主,實作為輔
-
Keras

課程安排
| 日期 | 課程內容 |
|---|---|
| 3/10 | 課程介紹、AI初探、先備知識 |
| 4/7 | 神經元、激勵函數、類神經網路 |
| 4/14 | 損失函數、梯度下降、反向傳播 |
| 4/21 | 過適、卷積神經網路 |
| 4/28 | 卷積神經網路實作 |
課程安排
| 日期 | 課程內容 |
|---|---|
| 5/26 | 遞迴神經網路 |
| 6/2 | 遞迴神經網路實作 |
| 6/9 | 遞迴神經網路實作 |
| 6/16 | 生成對抗網路、Transformer |
*實際課程依進度滾動調整
能力要求
-
Python語法
-
物件導向概念
-
看函式庫文件
-
國中數學
-
國中英文

能力奢求
-
矩陣與線性代數
-
微分與偏微分
-
認識神經網路
學習資源



1. 什麼是AI?
AI
-
Artificial Intelligent
-
人工智慧
-
人類製造出來的機器所展現的智慧
-
機器能模仿人類感知、思考、決策、學習的能力
也許你們想像的AI

但目前人類做得到的AI

Strong AI
-
強人工智慧
-
就像是一個人類一樣
-
能做到人類可以做到的所有事情
Weak AI
-
弱人工智慧
- 只具備一部份人類智慧的能力
- 目前的研究範疇
說了那麼多
但我們這堂課不是叫機器學習嗎?
事實上是這樣的
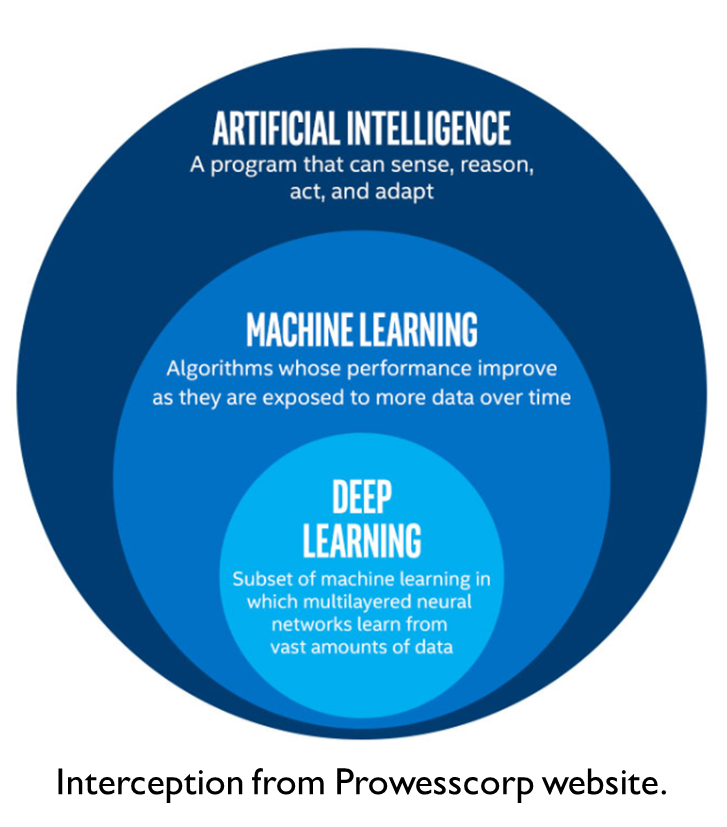
Machine Learning
-
機器學習
-
一種實現人工智慧的方法
-
利用大量資料訓練,讓機器學會某項技能
-
送機器去補習班
廢物機器
有用機器
資料
氣溫、濕度
風速、雨量
熱食部營業額
新增病例數
隔天是否下雨
ML演算法
支持向量機
迴歸模型
類神經網路
判斷隔天會不會下雨
要怎麼實現機器學習呢?
類神經網路
支持向量機
K-近鄰演算法
蒙地卡羅搜尋
線性判別分析
但這門課其實我們只會教類神經網路
類神經網路
- Neural Network
- 模仿生物神經系統的計算模型
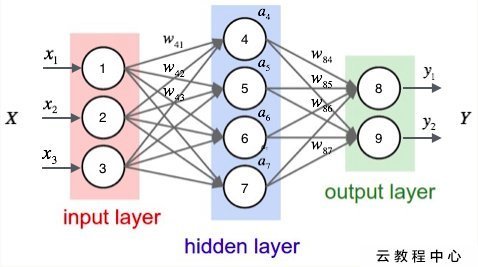
來玩玩看
2. 先備知識
這節課你會學到
-
機器學習開發環境
-
矩陣的運算
-
微分與偏微分的概念
ML實作的兩個流派


-
2015年發布
-
Google 開發
-
穩定性較佳
-
業界普遍使用
-
語法較艱澀

-
建立於tensorflow框架上
-
簡化語法

kernel = tf.Variable(tf.truncated_normal([3, 3, 64, 64], type=tf.float32, stddev=1e-1), name='weights')
conv = tf.nn.conv2d(self.conv1_1, kernel, [1, 1, 1, 1], padding='SAME')
biases = tf.Variable(tf.constant(0.0, shape=[64], dtype=tf.float32), trainable=True, name='biases')
out = tf.nn.bias_add(conv, biases)
self.conv1_2 = tf.nn.relu(out, name='block1_conv2')x = Convolution2D(64, 3, 3, activation='relu', border_mode='same', name='block1_conv2')(x)-
2016年發布
-
Facebook 開發
-
學術界愛用
-
語法較簡單

開發環境有兩種
-
線上
-
本機
| 線上 | 本機 |
|---|---|
| 不用安裝 | 安裝麻煩 |
| 不吃本地資源 | 占用本機資源 |
| 依賴網路 | 可離線開發 |
| 設定自由度低 | 設定自由度高 |
嗯嗯 聽起來非常麻煩是吧?

矩陣
長得像這樣的數學物件
舉個例子
矩陣的大小
\( 2 \times 3 階矩陣 \)
\( 3 階方陣 \)
- 矩陣的階(Order)和問題的維度(Dimension)常有密切相關
矩陣可以幹嘛?
-
解方程組
-
算機率
-
算幾何
-
算物理
-
簡化表達方式
-
矩陣常常代表一種轉移關係
矩陣的運算
加法
- 一樣大才能加
- 對應項相加
減法
- 一樣大才能減
- 對應項相減
和實數的乘法
- 又叫係數積
- 直接把每一項乘以 \(r \)
和矩陣的乘法
- 把A的列的每一個元素和B的對應行的每一個元素的積的和
- \( c_{i, j} = \sum_{k=1}^{n} a_{i,k} \times b_{k,j} \)
具體的做法
具體的做法
具體的做法
具體的做法
矩陣乘法的條件
-
\(若A 為 m \times n階、B為k \times p階 \)
-
\(矩陣可乘若且唯若 n = k\)
-
\( 乘完會變 m \times p階 \)
微分與偏微分
斜率
直線的傾斜程度
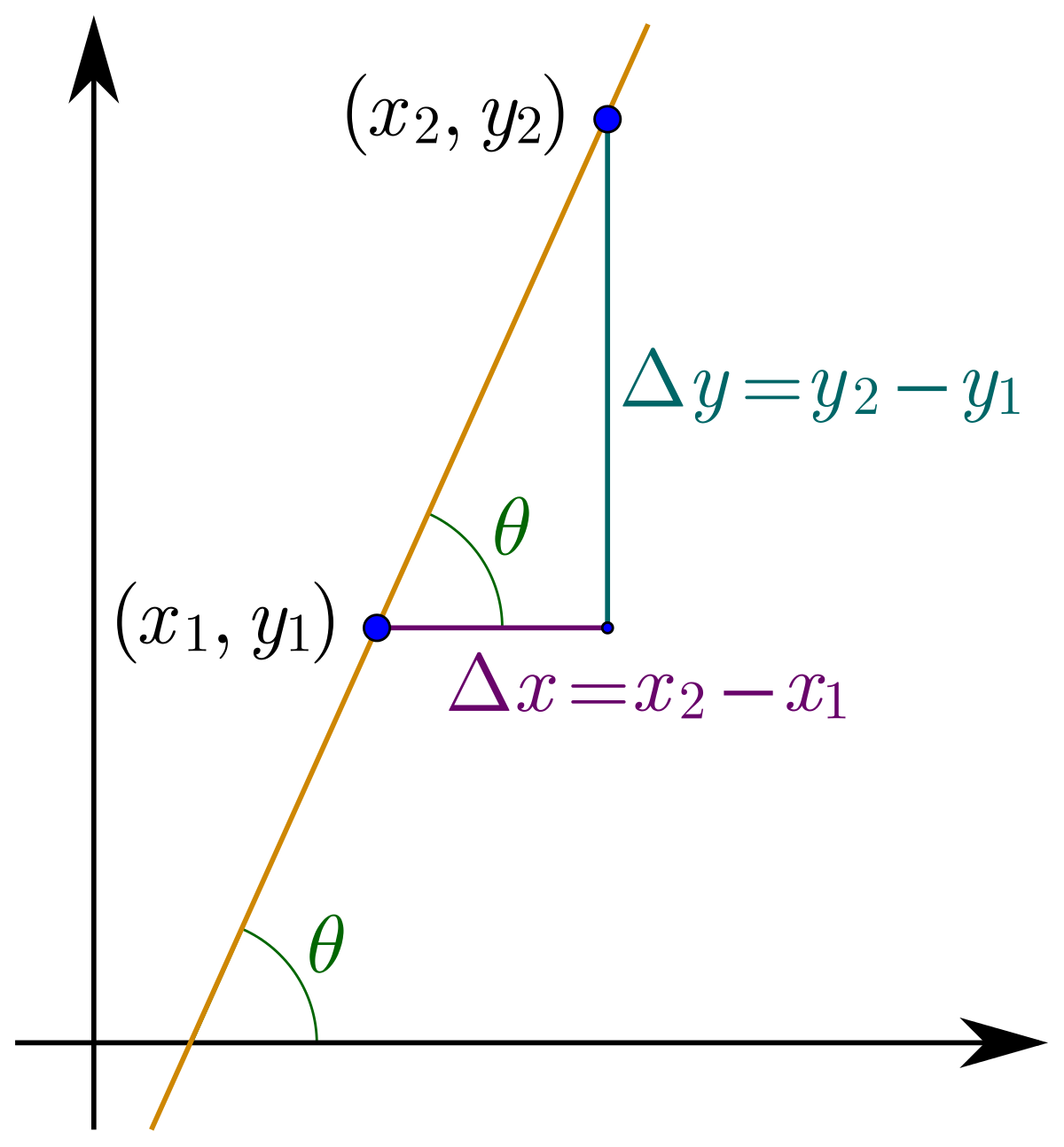
割線斜率
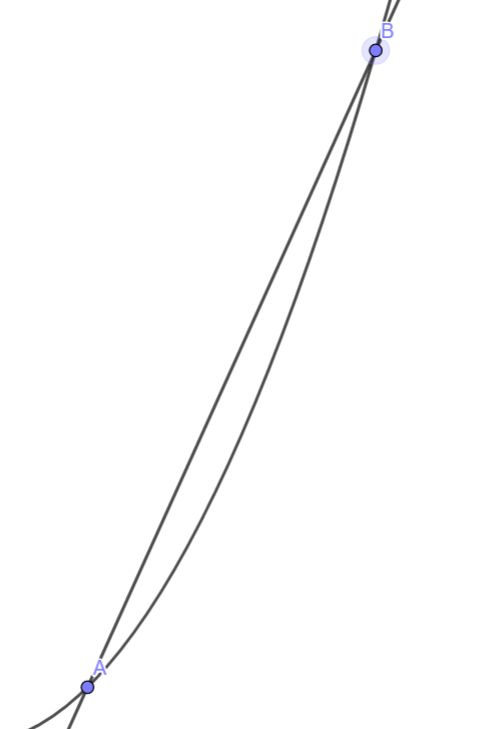
如果我們把B靠近A?

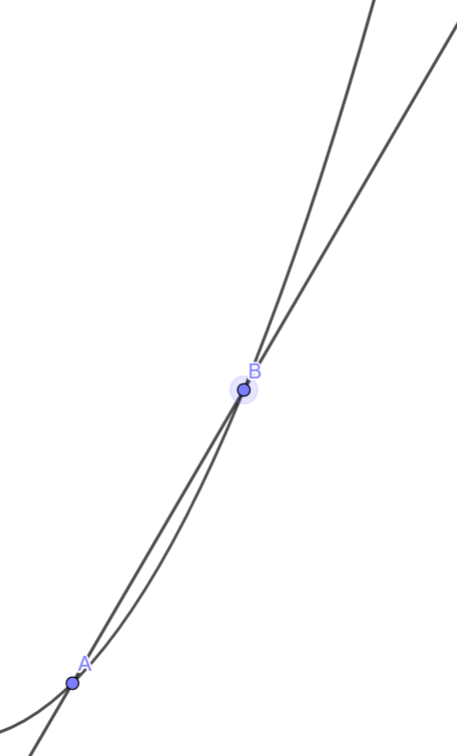
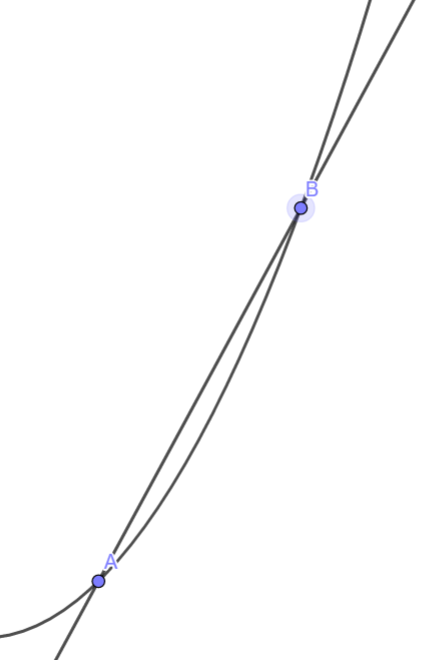
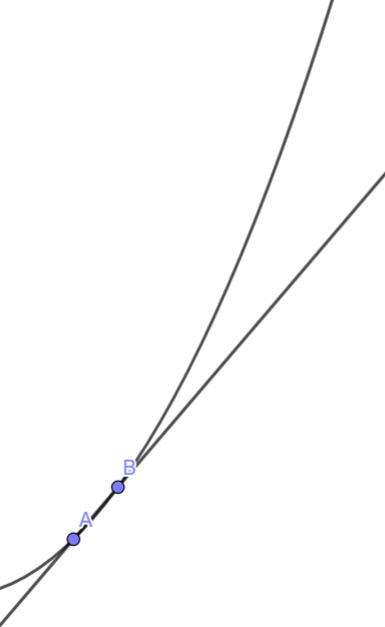

它就變成切線了耶
切線斜率
-
代表B很靠近A時的斜率
-
\(稱為f(x) 在 x = a時的導數\)
-
\(記作f'(a)\)
導函數
-
\(把f(x)在每一個點的導數收集起來變成一個函數\)
-
求導函數的方法:微分
微分法則
-
常數函數微分
-
多項式微分
舉例
-
常數函數微分
-
多項式微分
微分法則
-
加減法
-
係數積
舉例
-
加減法
-
係數積
微分法則
-
乘法
-
前微後不微+後微前不微
舉例
-
乘法
微分法則
-
除法
-
母平分之子微母減母微子
舉例
-
除法
微分法則
-
鏈鎖律
換個寫法更漂亮
舉例
-
鏈鎖律
偏微分
\(如果f是個多變數函數?\)
\(f(x,y) = x^2 +xy + y^2\)
怎麼做微分?
把其他變數固定當常數就好啦
偏微分
-
算偏導函數的工具
-
記作 \( \frac{ \partial f}{ \partial x} \)
-
舉例:
偏微分法則
-
加減法
-
係數積
偏微分法則
-
乘法
-
除法
偏微分法則
-
鏈鎖律
那偏導數代表什麼意義
如果我們把微分推廣到更高維度
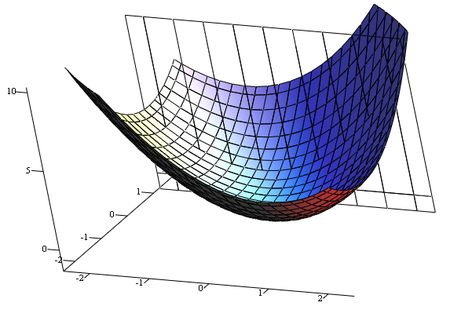
怎麼定義斜率?
梯度
-
是一個向量
-
記作 \( \nabla f\)
-
梯度的方向指向曲面上升最快的方向
-
梯度的大小代表曲面的單位上升率


梯度的算法
\(f(x,y)對x作偏微分可以得到梯度在x方向的分量大小\)
\(f(x,y)對y作偏微分可以得到梯度在y方向的分量大小\)
\(\vdots\)
把每個方向的分量合起來就是梯度
梯度的應用
梯度指向上升最快的地方
往梯度的反方向走下降最快
逆著梯度走我們就可以找到局部最小值!
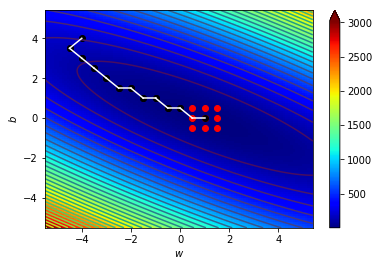

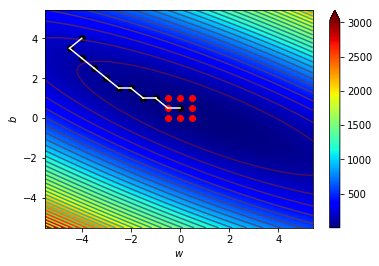
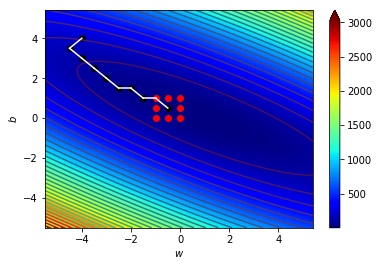
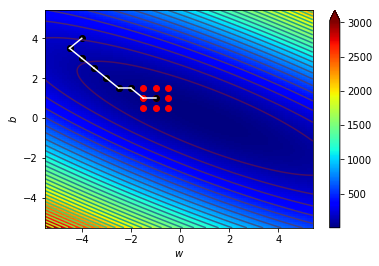
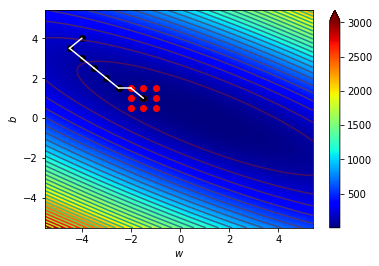
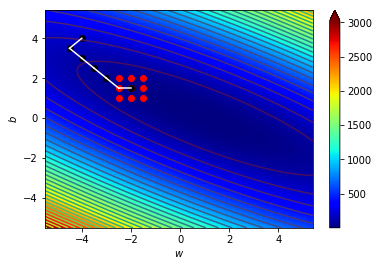
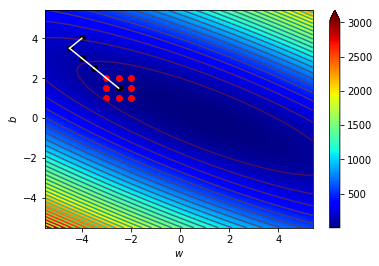
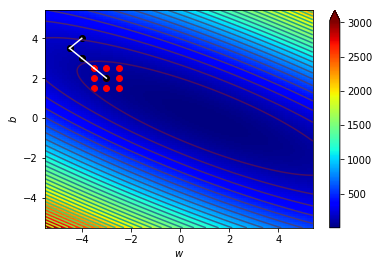
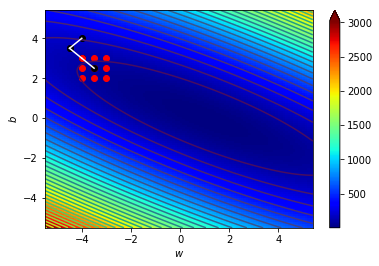
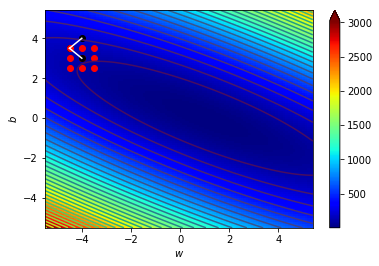
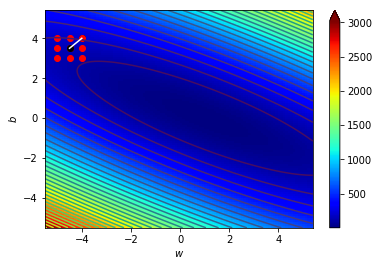
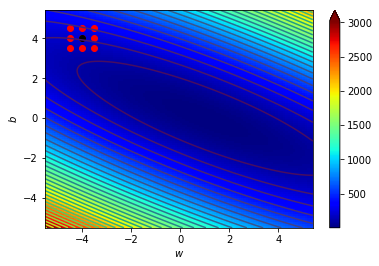
梯度下降!
結語
-
聽得懂很好
-
聽不懂也沒關係
-
數學可以給你不一樣的觀點
-
希望大家還是願意來下一堂課
-
下堂課會比今天簡單很多
3. 神經元
Neurons
先來看看生物學的神經元
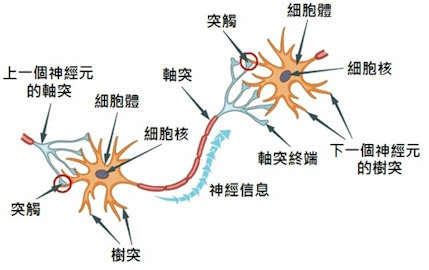
神經元是怎麼運作的?
把生物學的想法延伸到資訊上

\(x_1\)
\(x_2\)
\(x_3\)
\(y\)
神經元
- 就像是一個函數
- 每個神經元會提取某種特徵
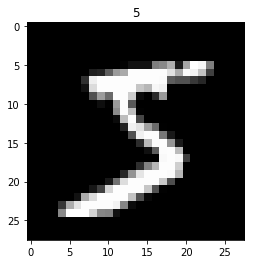
怎麼處理輸入?
每個輸入的重要性可能不相同
所以幫每個輸入乘個權重(weight)好了
\(x_1\)
\(x_2\)
\(x_3\)
\(y\)
\(w_1\)
\(w_3\)
\(w_2\)
每個神經元判斷的區域可能不相同
所以幫每個神經元加個偏值(bias)好了
\(x_1\)
\(x_2\)
\(x_3\)
\(y\)
\(w_1\)
\(w_3\)
\(w_2\)
\(b\)
我們建立了一種方法用數學模擬神經元
但這還不是最後的輸出

不是所有的刺激都可以引發神經衝動
不是所有的輸入都值得繼續傳遞下去
激勵函數!
4. 激勵函數
Activation Function
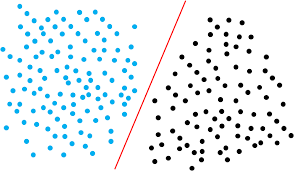
線性可分 v.s. 線性不可分


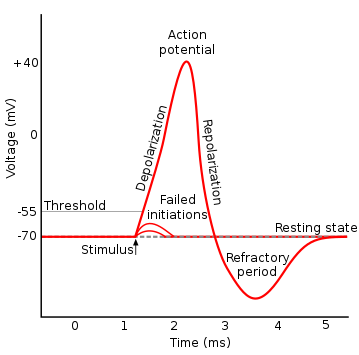
Action Potential
Activation Function
激勵函數的特性
- 不是線性
- 可以微分
- 有單調性
- 在某個閾值前後的函數值差異很大
常見的一些激勵函數
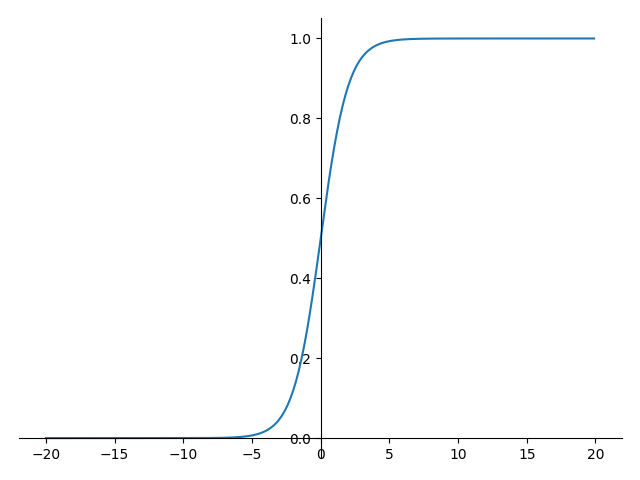
Sigmoid
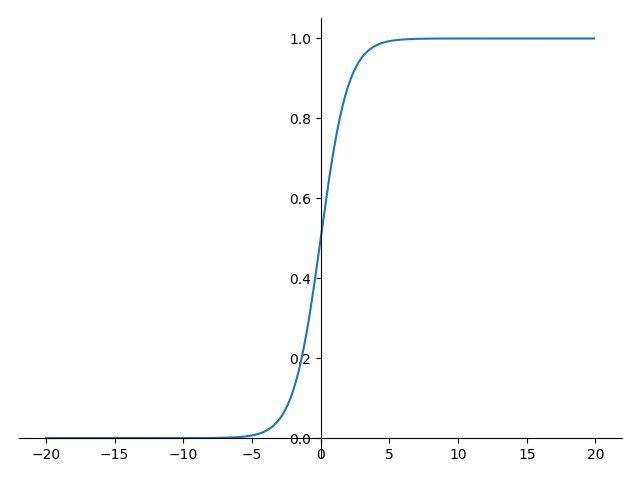
tanh
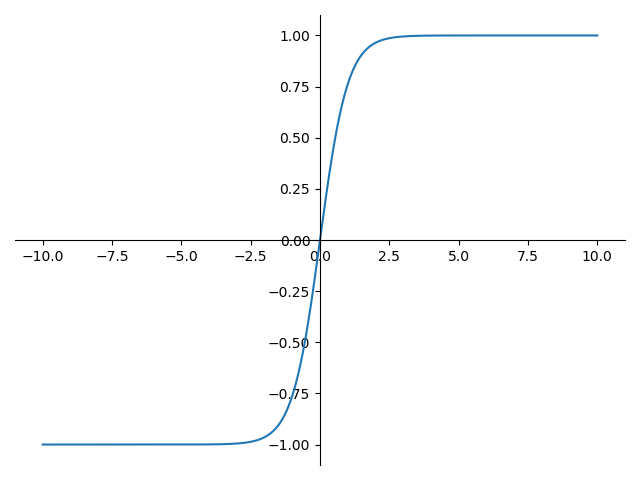
ReLU
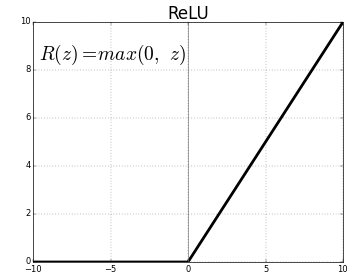
Leaky Relu
我們終於完整的了解神經元在幹嘛了
5. 類神經網路的結構
The Structure of Neural Network
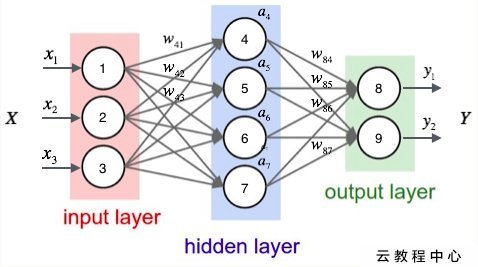
一個類神經網路長這樣
層(Layer)
輸入層
Input Layer
隱藏層
Hidden Layer
輸出層
Output Layer
\(a^{(0)}\)
\(a^{(2)}\)
\(a^{(1)}\)
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(0)}_2\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(1)}_3\)
\(a^{(2)}_0\)
\(a^{(2)}_1\)
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(0)}_2\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(1)}_3\)
\(a^{(2)}_0\)
\(a^{(2)}_1\)
\(w^{(1)}_{0, 0}\)
\(w^{(1)}_{1, 0}\)
\(w^{(1)}_{2, 0}\)
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(0)}_2\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(1)}_3\)
\(a^{(2)}_0\)
\(a^{(2)}_1\)
\(w^{(1)}_{0,1}\)
\(w^{(1)}_{1,1}\)
\(w^{(1)}_{2,1}\)
我們現在先只關注第(1)層的權重和輸入的關係就好
對應項相乘?
那其實就是這樣?
加權重?
最後一起丟進activaton function
我們就把資料的運算往右推一層了!
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(0)}_2\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(1)}_3\)
\(a^{(2)}_0\)
\(a^{(2)}_1\)
一層hidden layer好少喔
可以多幾層嗎?
深度學習!
Deep Learning
算法差不多
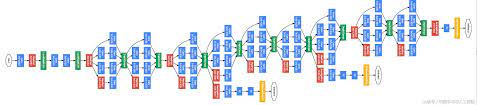
一些奇聞軼事
Google Net (2014)
22 Layers
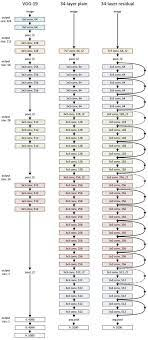
Residual Net (2015)
152 layers
6. 損失函數
Loss Function
Loss Function
- 評估目前的學習成效
神經網路的輸出
理想的輸出
0.0
0.1
0.4
0.8
0.5
0.4
0.3
0.1
0.1
0.9
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
神經網路的輸出
理想的輸出
0.0
0.1
0.4
0.8
0.5
0.4
0.3
0.1
0.1
0.9
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
定義Loss = \(\sum{(\hat y-y)^2}\)
\(\hat y\)
\( y\)
2.14
損失函數:L
輸入:神經網路的所有參數 \(\theta\)
輸出:一個數字(Loss值)
Loss Function
- Loss 越大,成效越差
- 我們想要讓Loss 盡量小
Loss Function
梯度下降
課後閱讀
7. 梯度下降
Gradient Descent
先定義一下我們想要解決的問題
Loss Function
- Loss代表神經網路的學習結果與理想的差異
- Loss 越大,成效越差
- 我們想要讓Loss 盡量小
Loss Function
- \(L (\omega) 和 \hat y, y有關係\)
- \(y 和 W, B, input 有關係\)
- \(\hat y, input是不能改的\)
- \(我們可以藉由調整W, B 最小化 L(\omega)\)
\(L( \omega ) 和 所有的w_{i, j}^{(k)}, b_{n}^{(m)} 有關\)
\(可以把L(\omega) 想成 L(w_{0, 0}^{(0)}, w_{1, 0}^{(0)}, \dots, w_{i, j}^{(k)}, b_0^{(0)}, b_1^{(0)}, \dots, b_n^{(m)})\)
接下來瞧瞧函數的形狀
0個變數的函數
- \(f(x) = 7122\)
- 一維直線上的一點

1個變數的函數
- \(f(x) = 7x^2 + 12x + 2\)
- \(x軸上的每一點都對應到一個y\)
- 二維平面上的一曲線
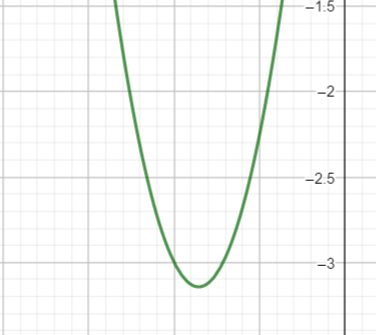
2個變數的函數
- \(f(x, y) = 7x^2 + y^2 + 2x + 2y\)
- \(xy平面上的每一點都對應到一個z\)
- 三維空間中的一曲面
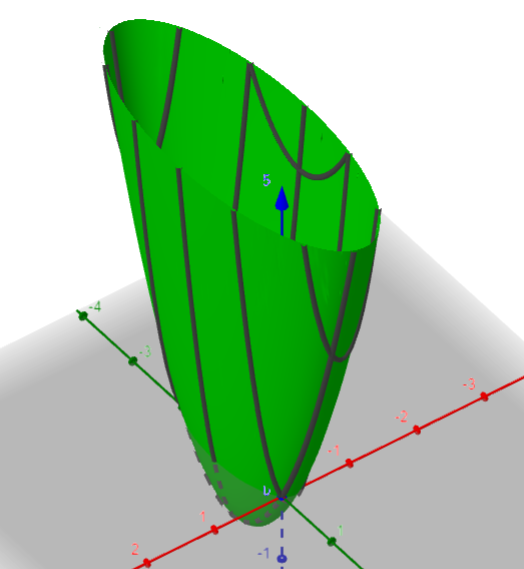
n個變數的函數
- \(f(X) = 7x_1^2 + x_2^2 + 2x_3 + 2x_4 + \dots\)
- \(X 是一個n維的輸入向量\)
- \(給定每一個(x_1, x_2, \dots, x_n)都對應到一個z\)
- \((n + 1)維空間中的一n維超曲面\)(hypersurface)

\(L(\omega)是一個n變數函數\)
\(n = 神經網路的參數數量\)
\(最小化L(\omega) \Leftrightarrow 找一個n維超曲面的極小點\)
可以把一個超曲面想成一座山


\( \Leftrightarrow \)
\(找一個n維超曲面的極小點\)
\(找山谷的極低點\)
一直往山下走
\(一直往L(\omega)低的地方走\)
怎麼找\(L(\omega)\)低的方向?
想起我們之前教過的梯度
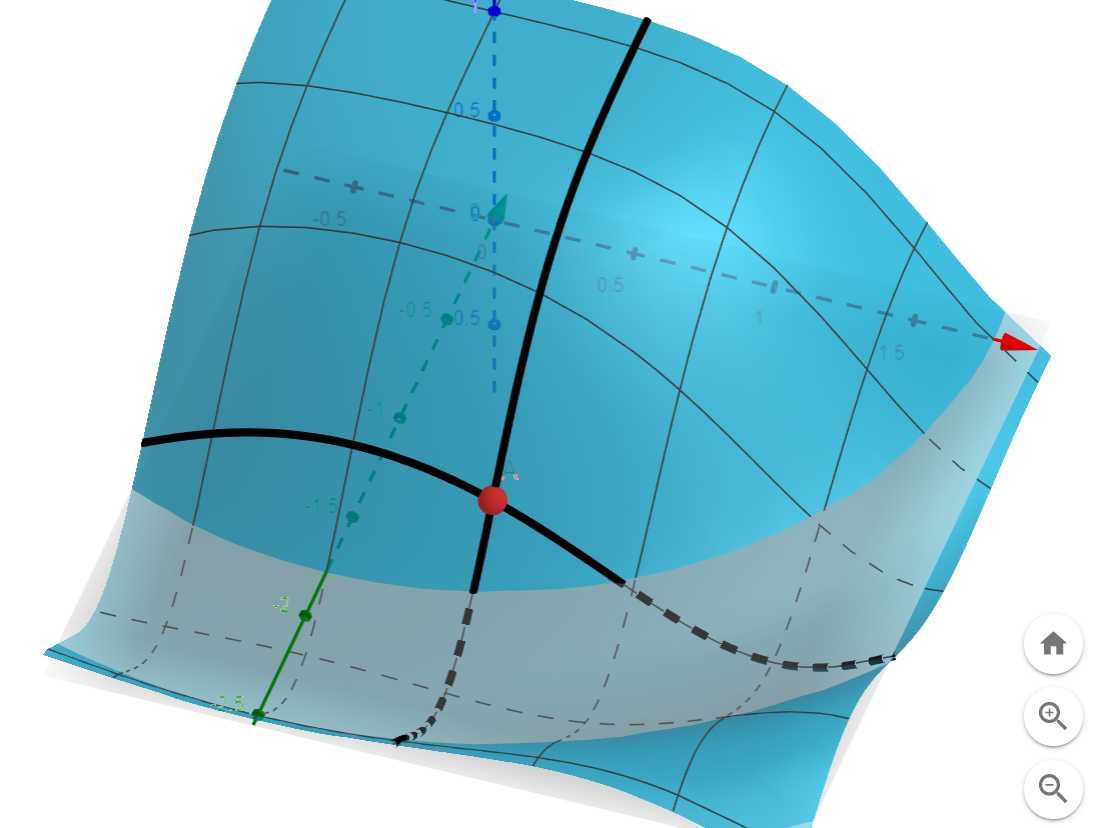
梯度 = \(\nabla F =( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n})\)
梯度指向超曲面上升最快的方向
往反方向走可以快速下降
往超曲面的極小點靠近
更新參數
\( \omega = (w_1, w_2, \dots, w_n, b_1, b_2, \dots, b_m)\)
\( \omega \rightarrow \omega - \mu \nabla L\)
也就是
\(w_i \rightarrow w_i - \mu \frac{\partial L}{\partial w_i}\)
\(b_j \rightarrow b_j - \mu \frac{\partial L}{\partial b_j}\)
\(\mu : \) Learning rate,一個不大的正數
用這個方法慢慢調整參數
就可以走到Loss最低的地方
這就是梯度下降
BTW. 其實梯度下降不是只有這種調整方法
這種梯度下降方法叫做隨機梯度下降
(Stochastic Gradient Descent, SGD)
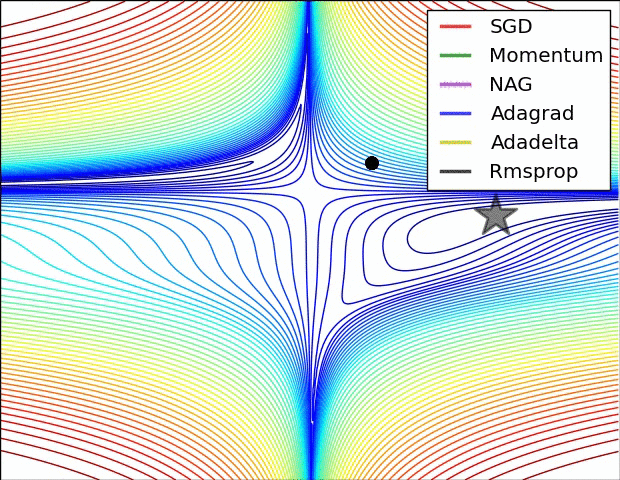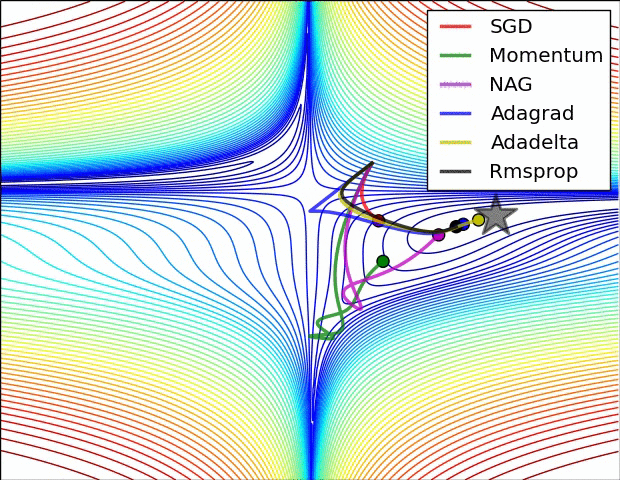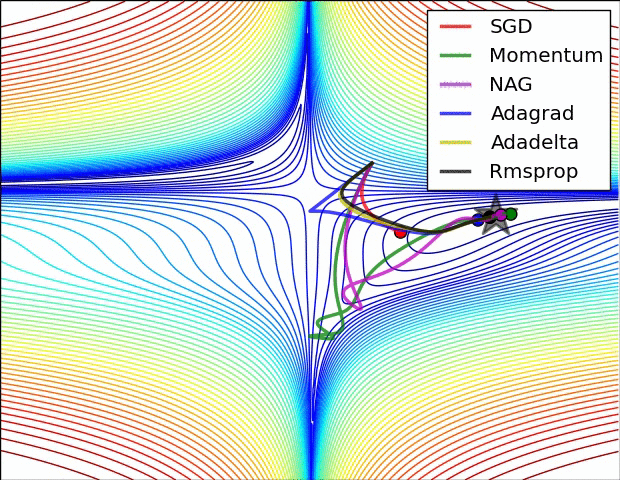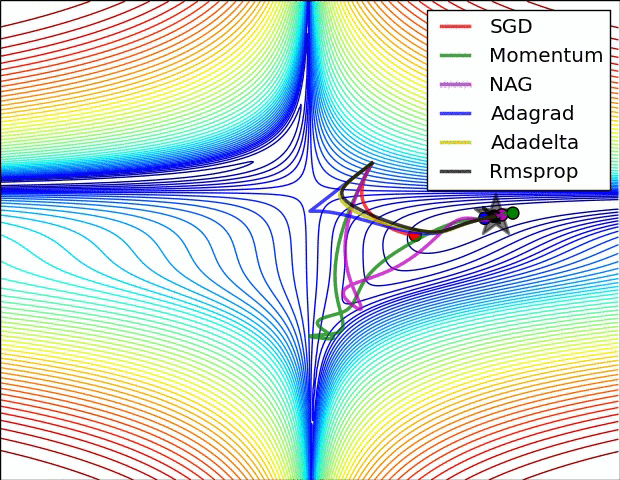
優化器 Optimizer
- 神經網路更新參數的方法
- SGD (stochastic gradient decent, 隨機梯度下降)
- Adam
- Adagrad
- RMSprop
- .....
- Optimizer的選擇會影響Loss的收斂性和收斂速度
8. 反向傳播
Backpropagation
反向傳播
- 從後面往前更新參數
- 計算\(\frac{\partial L}{\partial w_i}\)的流程
回顧一下之前教過神經網路怎麼計算的
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(0)}_2\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(1)}_3\)
\(a^{(2)}_0\)
\(w^{(1)}_{0, 0}\)
\(w^{(1)}_{1, 0}\)
\(w^{(1)}_{2, 0}\)
\(w^{(2)}_{0, 0}\)
\(w^{(2)}_{1, 0}\)
\(w^{(2)}_{2, 0}\)
\(w^{(2)}_{3, 0}\)
\(a^{(2)}_1\)
先看一層
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(1)}_3\)
\(a^{(2)}_0\)
\(w^{(2)}_{0, 0}\)
\(w^{(2)}_{1, 0}\)
\(w^{(2)}_{2, 0}\)
\(w^{(2)}_{3, 0}\)
\(我們想要利用L更新W^{(2)}\)
\(要求\frac{\partial L}{\partial W^{(2)}}\)
先看一層
我們沒辦法直接算\(\frac{\partial L} {\partial W}\)
但我們可以算
也就是
利用鏈鎖律
再推到上一層
依此類推
於是我們就找到一種計算Loss對各參數的梯度的方法了
這個算法稱為反向傳播演算法
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(0)}_2\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(1)}_3\)
\(a^{(2)}_0\)
\(a^{(2)}_1\)
前向傳播,利用\(W和B\)計算\(y與Loss\)
反向傳播,利用\(Loss\)計算\(梯度\),修正\(W和B\)
9. 過適
Overfit

補習
理想情況
考古題庫


補習
實際上...
考古題庫
只會寫看過的題目QQ
機器學習
理想情況
訓練資料
適應所有情況
機器學習
實際上...
訓練資料
只會判斷訓練資料QQ

機器過度適應於訓練資料
簡稱 過適 Overfit
參數
Parameters
超參數
Hyperparameters
v.s.
- 模型內部的參數
- 機器自己在訓練過程中學習到的
- 權重 weights
- 偏值 bias
- 決定模型結構與訓練方式的參數
- 訓練之前人工設定的
- 層數
- 神經元數量
- Learning rate
- batch_size
- epoch
關於資料
- 資料有限
- 分類資料用在不同用途
- 訓練集 ( Training dataset )
- 驗證集 ( Validation dataset )
- 測試集 ( Testing dataset )
- 彼此不可有交集
- 資料分布盡量平均、隨機
Training dataset
Validation dataset
Testing
dataset
Training dataset
Validation dataset
Testing
dataset
訓練集
- 給機器調參數
- 需要比較大量
- 回家作業
驗證集
- 驗收訓練成果
- 讓人調超參數
- 小考
測試集
- 檢驗最終模型
- 非到最後關頭不用測試集
- 段考
普適化
generalization
最佳化
optimization
機器學習想要做到的兩件事
- 讓模型在訓練資料上獲得最好的表現
- 對於沒看過的資料的預測能力
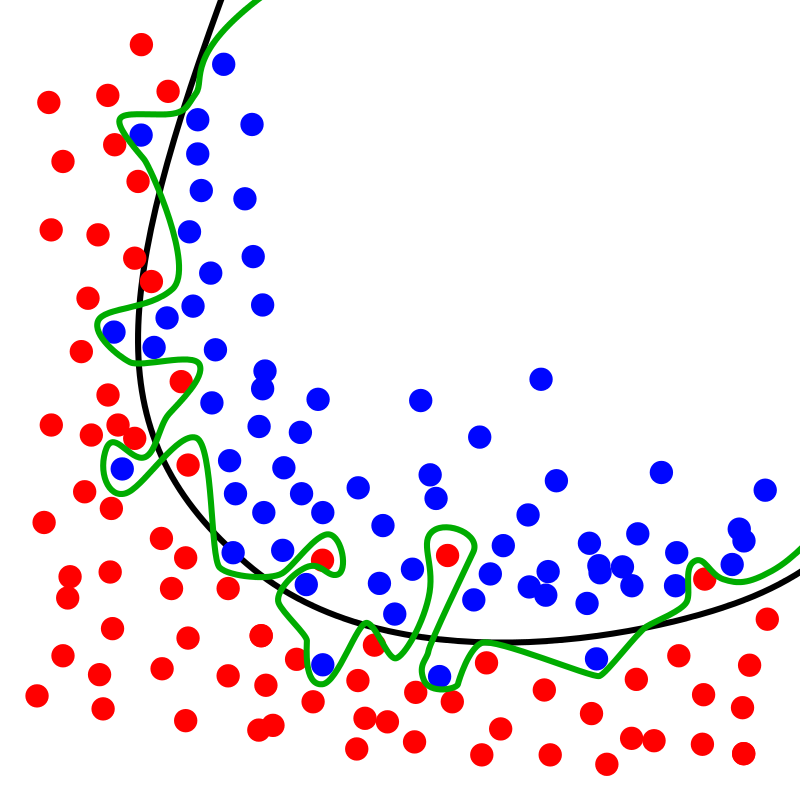
黑線:
worse optimization
better generalization
綠線:
better optimization
worse generalization
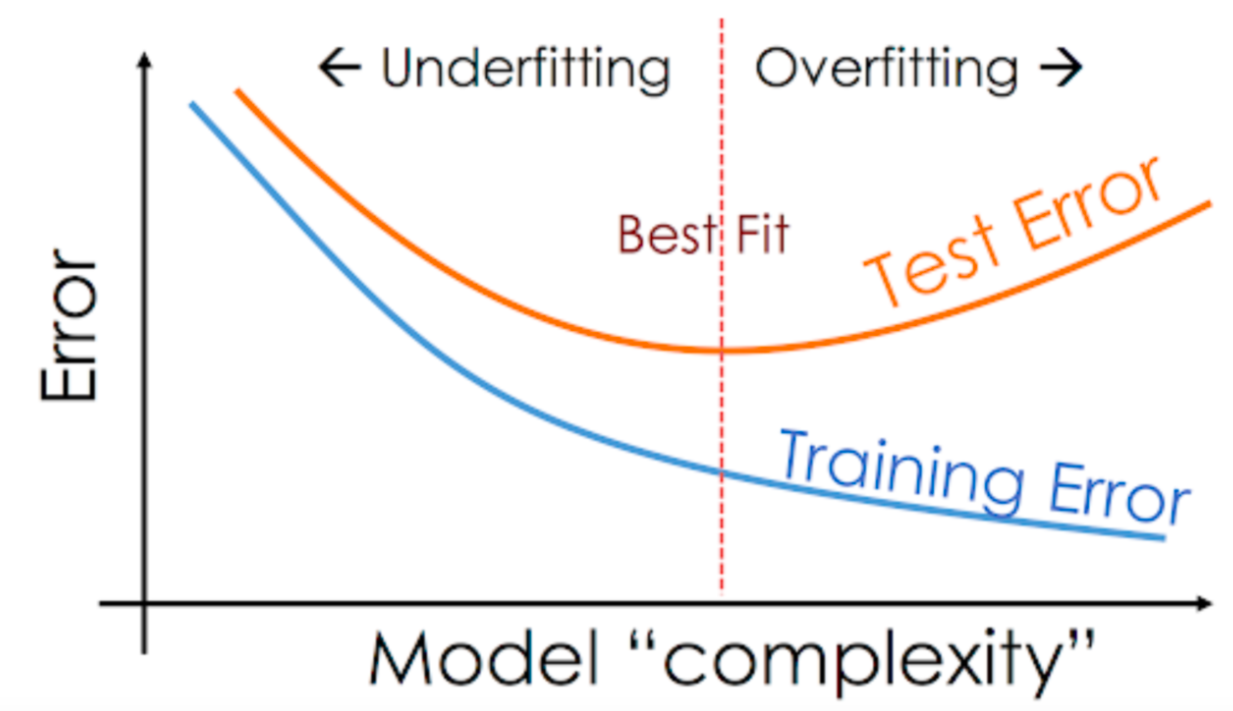
過適
- 我們只用training dataset訓練模型
- 訓練初期
- 模型學習資料集顯著的特徵
- optimization與generalization均提升
- 訓練後期
- 模型開始學習資料集細微特徵,可能是訓練集特有的
- optimization提升
- 但generalization開始下降
- 模型開始overfit
解決過適的方法
- 更多的訓練資料
- 減少神經網路容量
- 權重正則化
- 丟棄法
更多的訓練資料
- 刷更多題目就會寫更多題目拉
- 生資料不容易
- 資料永遠生不完
減少神經網路容量
- 神經網路有越多參數就可以記越多東西
- 函數有越多變數就可以有越多曲折
- 適度減少容量可以避免overfit
- 但也不能太少XD
權重正則化
regularization
- 我們希望可以讓權重小一點
- 讓Loss大一點,加上代價項
- eg : \( L'(\omega) = L(\omega) + \lambda \sum w_i^2\)
丟棄法
Dropout
- 訓練時隨機丟棄layer的一些輸出值
- 就像是把某些神經元關閉
- 測試時不會丟棄任何數據
- 可以看成加入某種雜訊
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(2)}_0\)
\(a^{(2)}_1\)
丟棄法
Dropout
- 訓練時隨機丟棄layer的一些輸出值
- 就像是把某些神經元關閉
- 測試時不會丟棄任何數據
- 可以看成加入某種雜訊
\(a^{(0)}_0\)
\(a^{(0)}_1\)
\(a^{(1)}_0\)
\(a^{(1)}_1\)
\(a^{(1)}_2\)
\(a^{(2)}_0\)
\(a^{(2)}_1\)
今天是二段前最後一堂課喔
下次上課是12/8
開始會帶實作
10. Keras實作
Implementation
手寫數字辨識
ML界的Hello World
輸入:
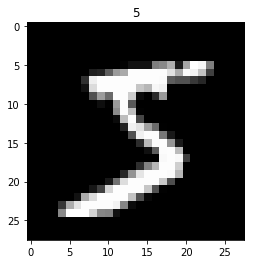
輸出:
" 5 "
圖片
文字
訓練資料怎麼來?
已經有人都幫你寫好標好拉
直接下載來用就好!

MNIST database
-
Modified National Institute of Standards and Technology database
-
含有大量已標記的手寫數字圖片
-
60000筆 training data
-
10000筆 testing data
-
由美國普查局員工和高中生寫的

開發工具
小提醒:記得用私人帳號登入喔!
Step 1:
使用tensorflow搭建keras
%env KERAS_BACKEND=tensorflow Step 2:
引入函式庫 numpy、matplotlib
%matplotlib inline
import numpy
import matplotlib.pyplotnumpy可以進行矩陣等數學運算
matplotlib可以幫助我們畫圖
Step 3:
下載MNIST
#download MNIST
from keras.datasets import mnist
(train_data, train_ans), (test_data, test_ans) = mnist.load_data()keras都幫我們做好了XD
我們下載下來的MNIST到底長怎麼樣咧?
來試看看!
|
|
|---|




\(\dots\)
train_data
x60000
each image is 28x28
| 4 | 1 | 7 | 0 |
|---|
\(\dots\)
train_ans
x60000
|
|
|---|




\(\dots\)
test_data
x10000
| 0 | 4 | 8 | 7 |
|---|
\(\dots\)
test_ans
x10000
Step 4:
調整輸入圖片形狀
train_data = train_data.reshape(60000, 784) #28 * 28 = 784
test_data = test_data.reshape(10000, 784)keras都幫我們做好了XD
把二維圖片壓成一維陣列
Step 5:
設定輸出格式
#output data settings
from keras.utils import np_utils
train_ans = np_utils.to_categorical(train_ans, 10)
test_ans = np_utils.to_categorical(test_ans, 10)把答案轉換成one hot encoding的格式
One Hot Encoding
- 獨熱編碼(?
- 用於有限個選項的分類問題
- 用一個陣列存每個選項是對的機率
5
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.]
前面五步主要在處理資料,方便我們後續神經網路的運作
這個過程叫做資料預處理(Preprocessing)
Step 6:
引入keras類神經網路模型函式庫
from keras.models import Sequential # model物件
from keras.layers import Dense, Activation, Dropout #Dense:設定layer的neuron數 Acitvation:激勵函數
from tensorflow.keras.optimizers import SGD #載入stochastic gradient decent的optimzer- Sequential : 神經網路模型物件
- Dense : 全連接層相關的東西
- Activation : 激勵函數
- Dropout : 丟棄
- SGD : 反向傳播的優化器(Optimizer)
優化器 Optimizer
- 神經網路更新參數的方法
- SGD (stochastic gradient decent, 隨機梯度下降)
- Adam
- Adagrad
- RMSprop
- .....
- Optimizer的選擇會影響Loss的收斂性和收斂速度

Step 7:
建立神經網路物件
model = Sequential() # 建立神經網路物件- 開始進入黑盒子的部分:D
Step 8:
加入第一層Hidden Layer
layer1_size = 800
model.add(Dense(layer1_size, input_dim = 784)) #新增一個hidden layer(含800個神經元, 輸入維度784)
model.add(Activation('sigmoid')) #新增layer1的activation : sigmoid
model.add(Dropout(0.4))- layer1_size : 第一層的神經元數量
- Dense(output_dim, input_dim) : 加入全連接層
- (output_dim : 輸出維度,input_dim : 輸入維度)
- Activation('') : 加入激勵函數
- Dropout(rate) : 加入丟棄層 (rate : 丟棄率 )
Step 9:
加入第二層Hidden Layer
layer2_size = 800
model.add(Dense(layer2_size, input_dim = layer1_size))#新增一個hidden layer(含800個神經元, 輸入維度800)
model.add(Activation('sigmoid')) #新增layer2的activation : sigmoid
model.add(Dropout(0.4))- layer2_size : 第一層的神經元數量
- Dense(output_dim, input_dim) : 加入全連接層
- (output_dim : 輸出維度,input_dim : 輸入維度)
- Activation('') : 加入激勵函數
- Dropout(rate) : 加入丟棄層 (rate : 丟棄率 )
Step 10:
加入Output Layer
output_size = 10
model.add(Dense(output_size, input_dim = layer2_size))
model.add(Activation('softmax')) #新增output layer的activation : sigmoid- output_size : 輸出數量
- Dense(output_dim, input_dim) : 加入全連接層
- (output_dim : 輸出維度,input_dim : 輸入維度)
- Activation('') : 加入激勵函數softmax
SoftMax
- 我們想要把神經網路算出來的結果轉化成每個選項的機率
- 類似概念,但我們在做機器學習的時候會把他丟到指數函數去做
Step 11:
把神經網路組裝起來
#設定loss function : mse(平方平均), optimzer : SGD, learing_rate = 0.1, 評比標準:accuracy
model.compile(loss = 'mse', optimizer = SGD(learning_rate = 0.1), metrics = ['accuracy'])- model.compile()
- loss : 計算Loss的方式
- optimizer : 優化器
- Learning Rate : 學習率(\(\mu\))
- metrics : 評比標準
Step 12:
model.summary()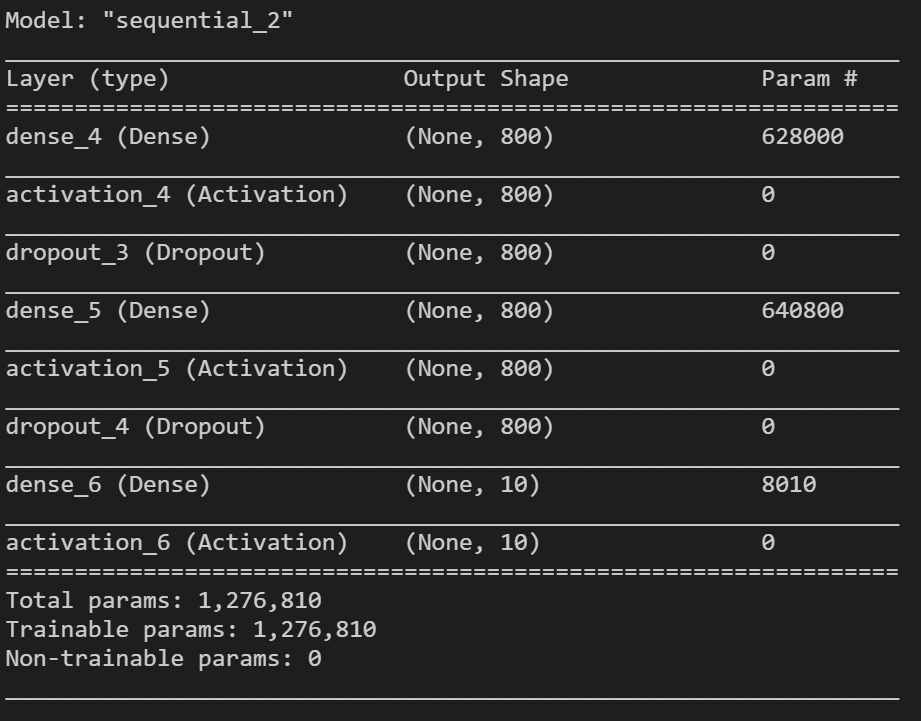
看看神經網路的模樣
Step 13:
#train NN
model.fit(train_data, train_ans, batch_size = 50, epochs = 40)訓練神經網路嚕!
- model.fit()
- 需要等上一陣子
- 先來講講batch_size和epoch吧:D
訓練時兩個重要的超參數
Batch_size
Epoch
- 批次大小
- 一次訓練的樣本數目
- 看好幾筆資料以後再一次一起調參數
- 影響模型的收斂速度
- 加快訓練速度
- 影響訓練效果
- 訓練時期數/次數
- 把整個資料集跑過幾次
- 影響訓練效果
- Epoch太小underfit
- Epoch太大overfit
選取好的batch_size搭配適當的Epoch訓練出最好的模型
Step 14:
score = model.evaluate(test_data, test_ans)
print("loss : ", score[0])
print("acc : ", score[1])驗收一下訓練結果
- model.evaluate()
- 檢視剛剛fit的成果
- 成果不好的話回去調超參數
Step 15:
#show results
from ipywidgets import interact_manual再引入一個好工具ipywidgets
- 顯示學習結果的好工具
Step 16:
def test(index) :
matplotlib.pyplot.imshow(test_data[index].reshape(28, 28), cmap = "Greys")
print("神經網路判斷為:", predict[index])定義test函式
- test函式用來顯示神經網路的判斷結果
Step 17:
predict = model.predict(test_data)應用model去預測未知的圖片
- model.predict(輸入圖片陣列)
- 回傳值為model的預測結果
- 回傳值以one-hot encoding格式儲存
Step 18:
predict = numpy.argmax(predict, axis = -1)將one-hot encoding格式轉換成整數
- numpy.argmax(a, axis=None, out=None)
- 以某個維度為比較基準,回傳該維度最大值所在的index
numpy.argmax
Step 19:
interact_manual(test, index = (0, 9999))互動式呈現預測結果
- 一個簡單的滑桿與按鈕互動介面
Step 20:
#save model and parameters
model.save("handwriting_model.h5")儲存訓練好的模型與參數
- 把模型的結構、超參數、與訓練好的參數存到.h5檔裡面
Step 20-1:
from keras.models import load_model
model2 = load_model("handwriting_model.h5")開啟訓練好的模型與參數
- 用keras.models的load_model直接讀進來就好
- 一模一樣的結構
- 梯度下降過的參數
11. 卷積神經網路
Convolution Neural Network



卷積
神經網路
卷積神經網路
卷積神經網路
- Convolution Neural Network
- CNN
美國有線電視新聞網- 一種類神經網路的變形
- 利用卷積與池化操作提升學習效果
- 在電腦視覺方面表現優異
- 用更少參數、更少資料訓練出更高準確率
卷積神經網路的結構
- 先做特徵擷取
- 卷積層
- 池化層
- 分類
- 小型的全連接層
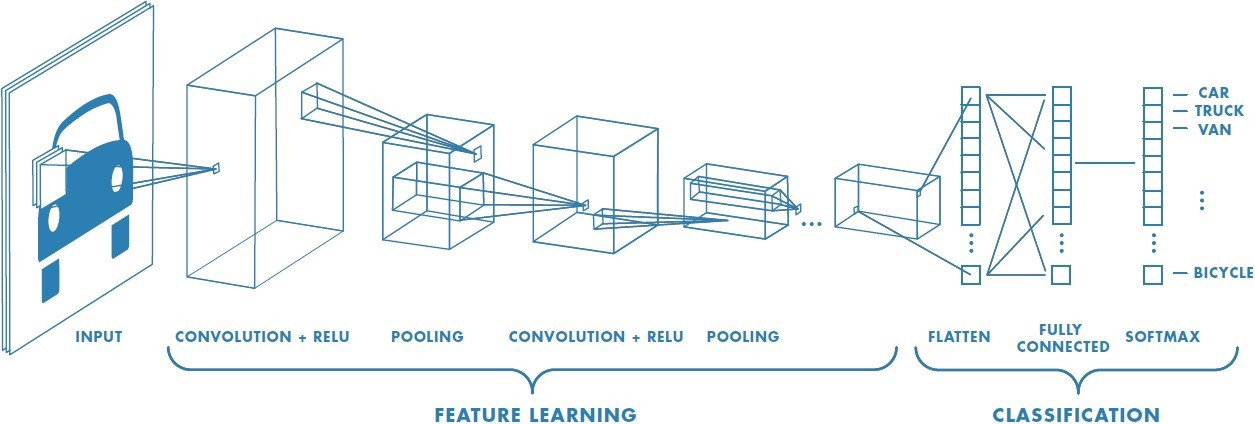
12. 卷積
Convolution
卷積是一種特徵擷取的方式
什麼是卷積?
什麼意思呢?
來看個例子!

有玩過Where is wally嗎?
圖片這麼大、這麼複雜,怎麼找?
逐一掃描比對


搜尋的圖片
要找的目標
逐一掃描比對


逐一掃描比對


逐一掃描比對


逐一掃描比對


逐一掃描比對


逐一掃描比對


逐一掃描比對


逐一掃描比對


逐一掃描比對


逐一掃描比對

整張圖掃描完以後就會發現他在這邊
試想:要如何在圖片上找到水平線段呢?

先定義好我們要找的目標特徵

\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
- 可以用矩陣表達這個特徵
- 卷積核 (Convolution Kernel)
開始比對

怎麼量化他們的相似程度?


\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(0\)
\(0\)
\(0\)

\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(\ast\)
\(0\)
\(0\)
\(29\)
\(0\)
\(170\)
\(255\)
\(0\)
\(86\)
\(255\)
\(0\)


\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(0\)

\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(0\)
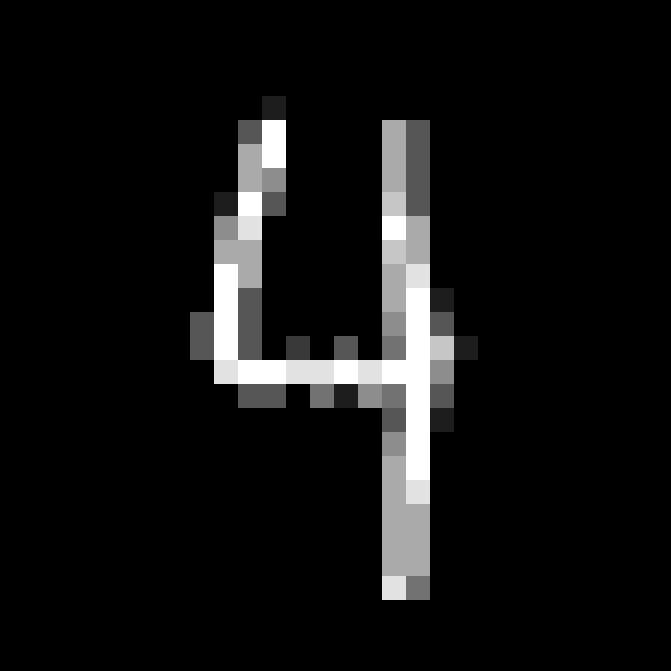
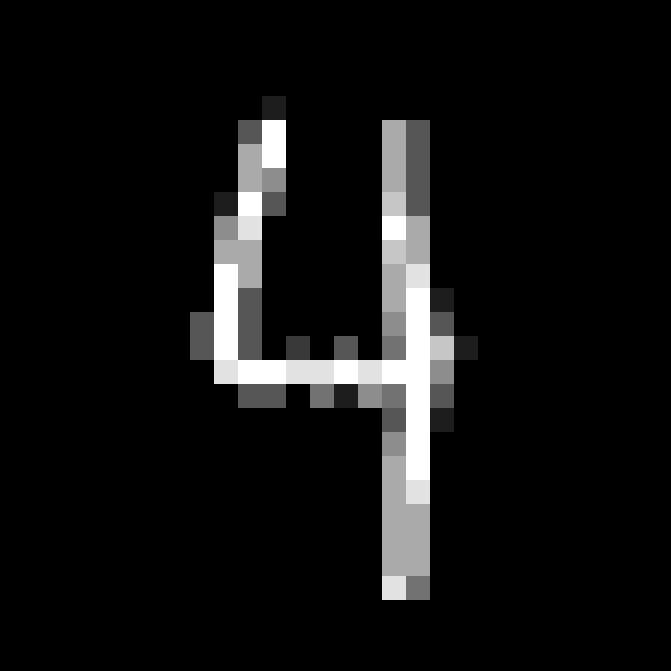

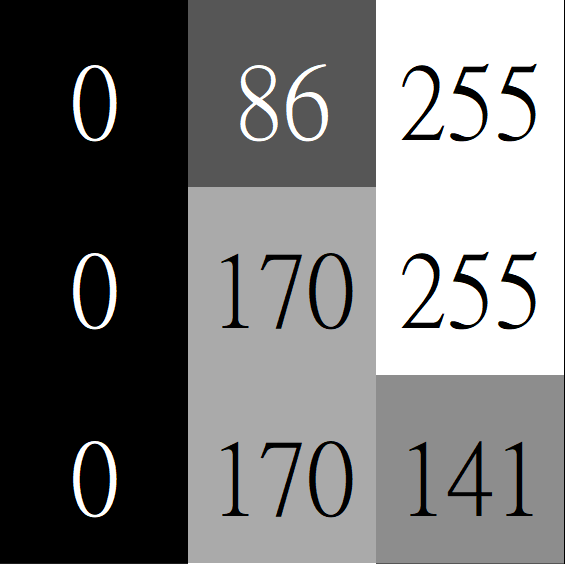

\(0\)
\(0\)
\(0\)
\(0\)
\(0\)
\(1\)
\(1\)
\(1\)
\(0\)
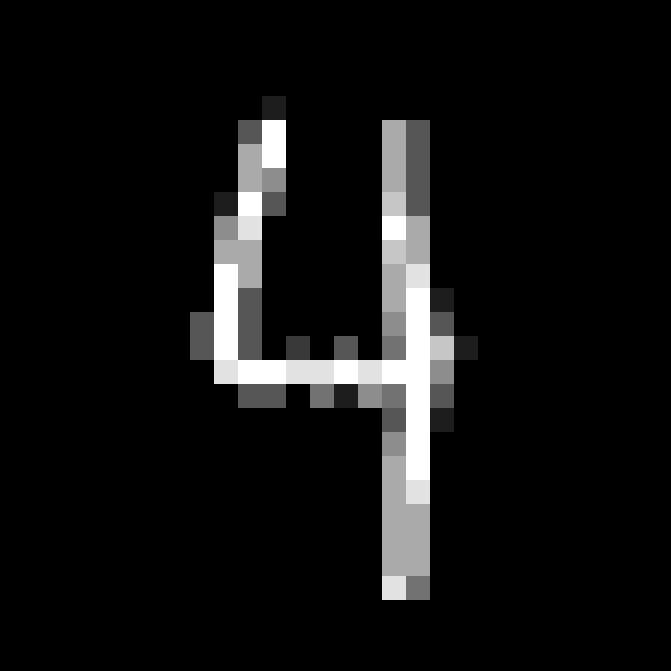

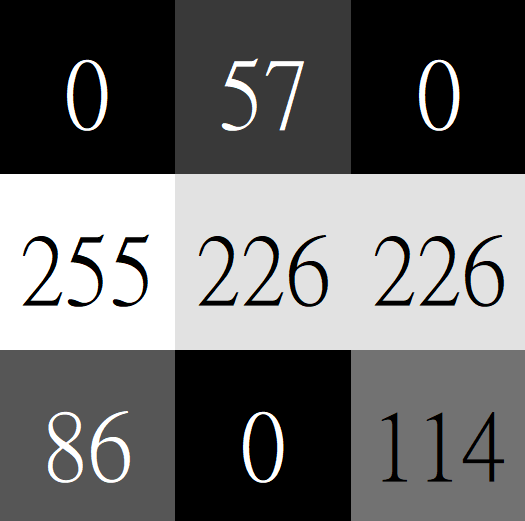
滑動

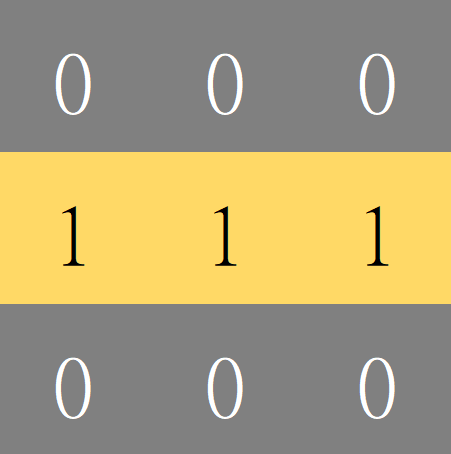
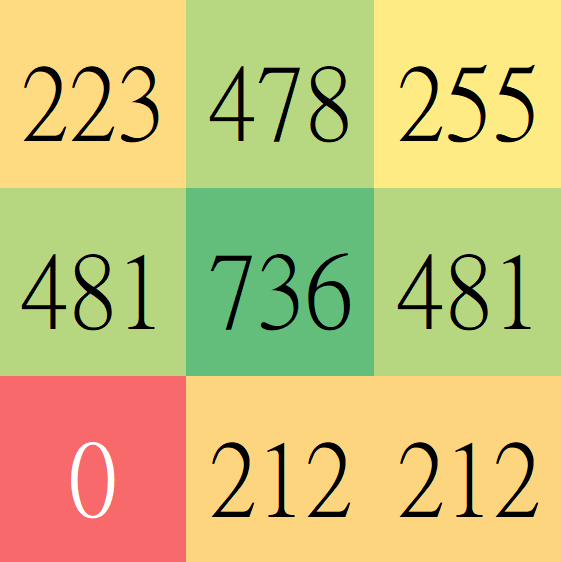
滑動

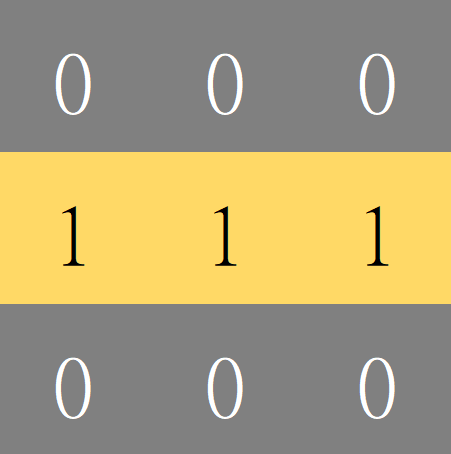

滑動

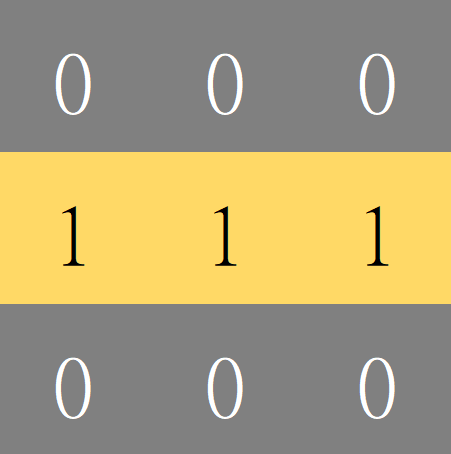

滑動

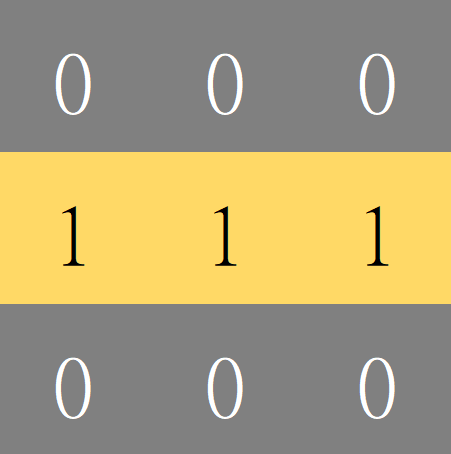

滑動

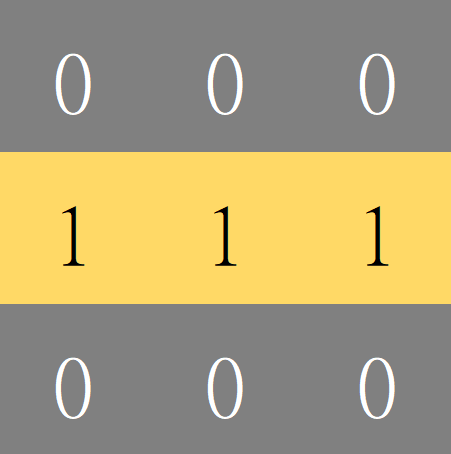

滑動

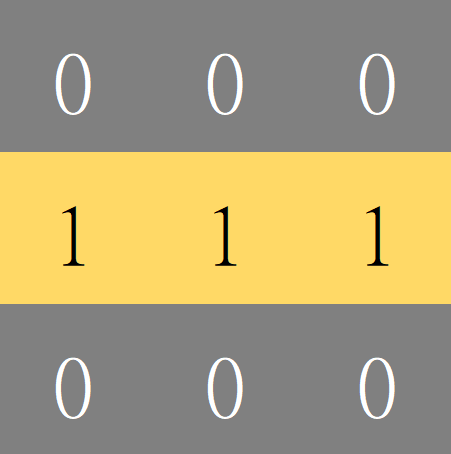

滑動

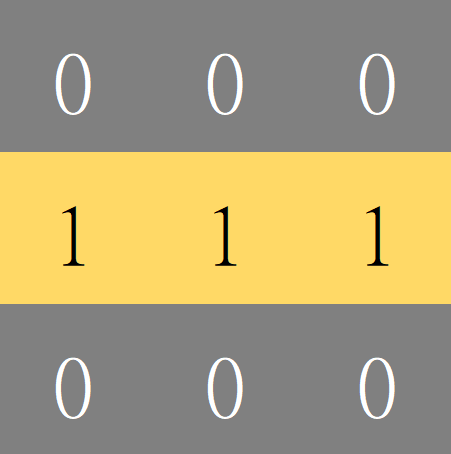

滑動

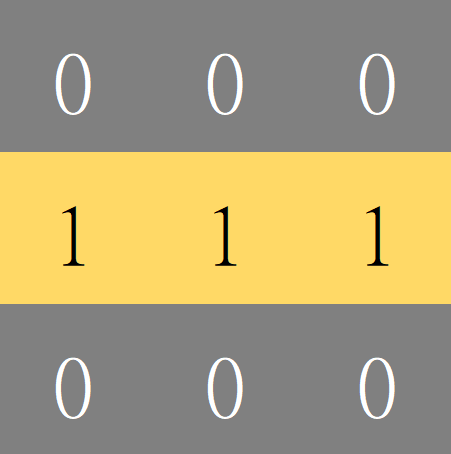

滑動

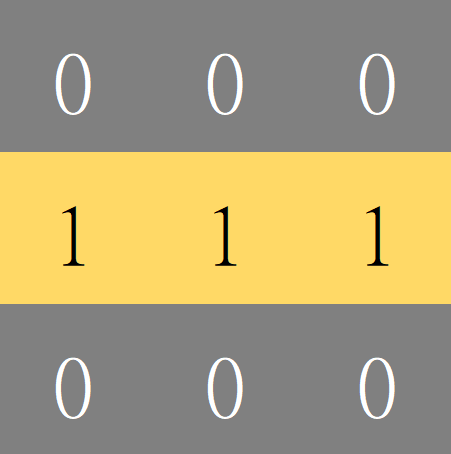

滑動

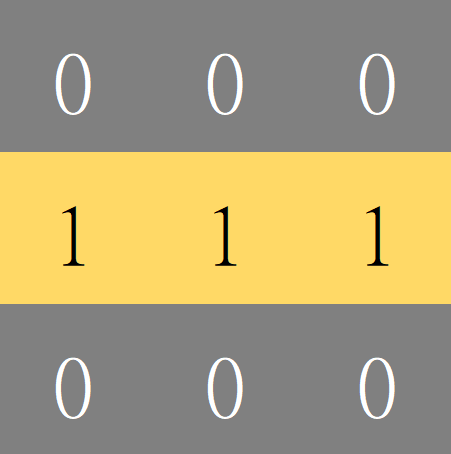


Feature map
- 特徵映射圖
- 每個網格值代表該處和卷積核的契合度
- 網格值愈高代表圖上出現和卷積核越相似的特徵
More about Conv Layer
卷積層
全連接層
- 學習局部特徵
- 學習到的特徵可平移辨識
- 可以用較少資料訓練好
- 學習全域特徵
- 特徵移動後就要重新學習
More about Conv Kernel
- Kernel的權重也是用梯度下降學習的
- 一個Conv Layer中會拿多個Kernel去卷積
- 每個Kernel都可以卷積出一張Feature map
- 一層Conv Layer的輸出是 (Kernel數) 張Feature map
- 實際上 Kernel、Conv Layer的輸入、輸出都是三維張量
- Kernel的尺寸也不一定要是\(3 \times 3\)
- 每次Kernel也不一定要往右滑1
多核卷積
- 一個Conv Layer內會用多個Kernel分別做卷積
- 每個Kernel會辨識不同的特徵
多層卷積
- 一個CNN內會包含多個Conv Layer
- 越後面的Layer會辨識越高階、複雜的特徵
直線段
橫線段
卷積層一
斜線段
十字
叉叉
卷積層三
圓
左彎
右彎
上彎
卷積層二
輸出尺寸
- 圖片在卷積後通常會輸出尺寸較小的Feature Map
- 影響輸出尺寸的因素:
- Kernel尺寸
- 步長
Kernel尺寸


\(5 \times 5\)
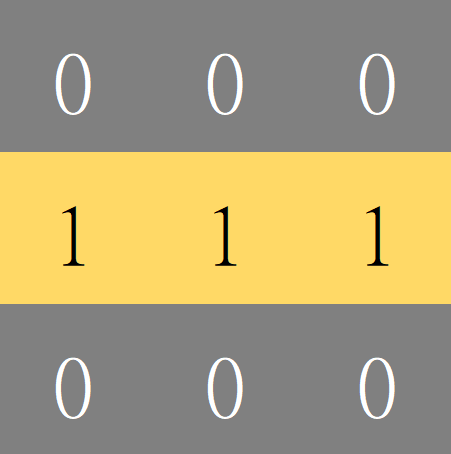
\(3 \times 3\)
\(3 \times 3\)
Kernel尺寸


\(5 \times 5\)
\(1 \times 1\)
\(5 \times 5\)
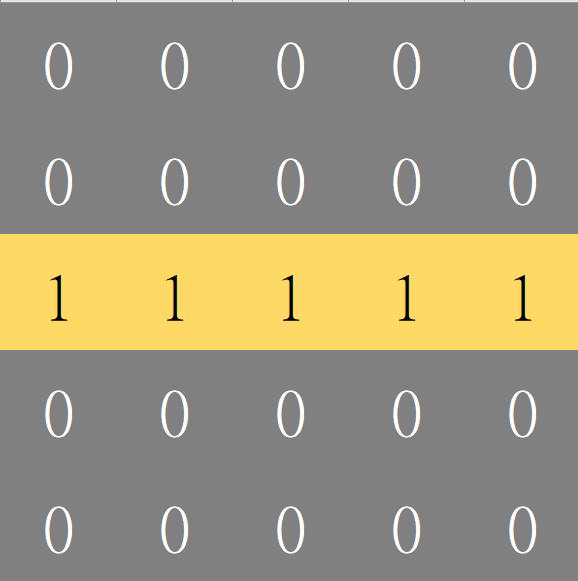
步長
Strides
- Kernel每次滑動的距離
- 預設1
Strides = 2

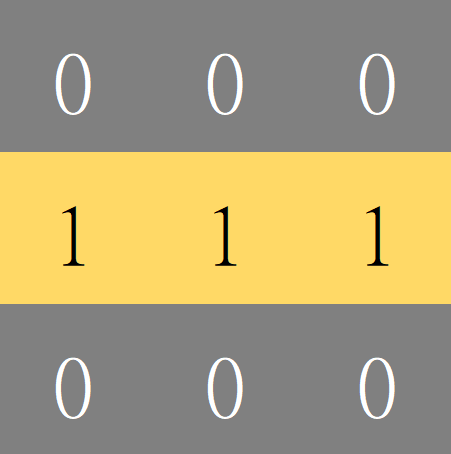
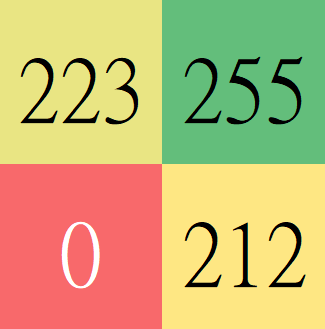
Strides = 2

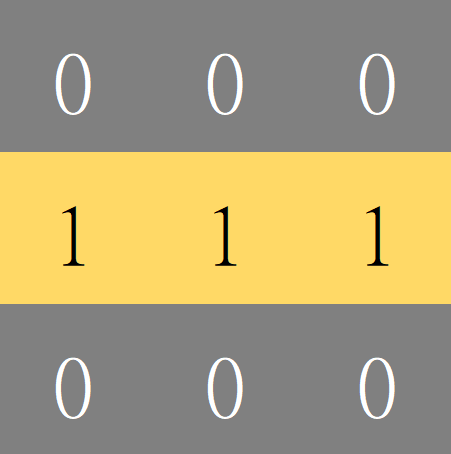
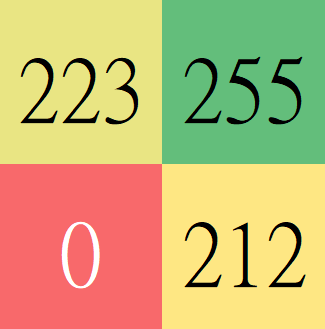
Strides = 2

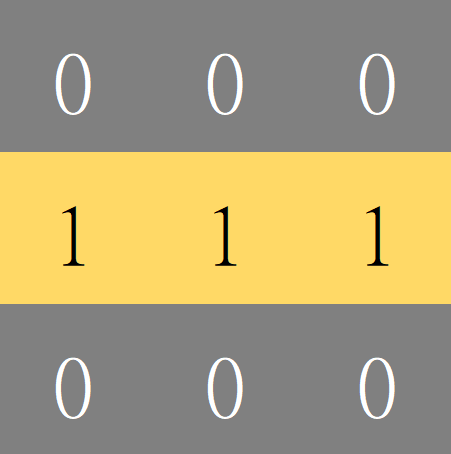
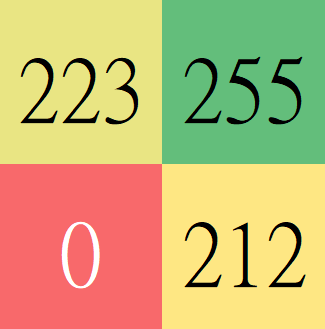
Strides = 2

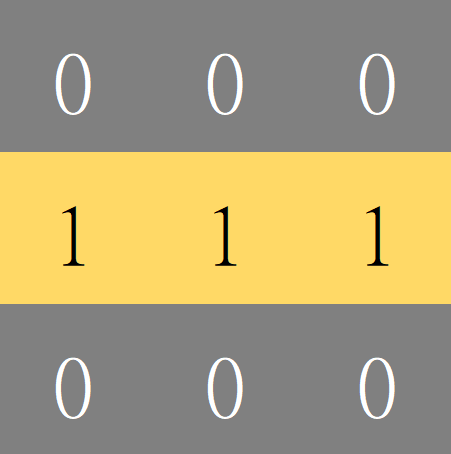
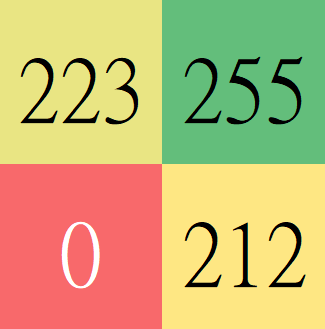
- 運算減少
- Feature Map變小
填補
Padding
- 卷積以後尺寸會縮小
- 在輸入外圍填零擴大輸入圖
- 維持輸出圖和原輸入一樣大
- 讓Kernel充分掃描到圖的每個邊緣


13. 池化
Pooling
池化是一種資料壓縮的方式
- 我們想要用較少的資料量來表示原本的圖片
- 只保留最重要、最有特色的資料
- 取最大值(?
怎麼壓縮?


最大池化 Maximum Pooling
其實也可以做平均池化拉,只是效果可能沒那麼好
滑動
- 作法跟卷積層很像
- 但是視窗通常取\( 2 \times 2\)
- 步長通常取2

滑動
- 作法跟卷積層很像
- 但是視窗通常取\( 2 \times 2\)
- 步長通常取2


滑動
- 作法跟卷積層很像
- 但是視窗通常取\( 2 \times 2\)
- 步長通常取2


滑動
- 作法跟卷積層很像
- 但是視窗通常取\( 2 \times 2\)
- 步長通常取2


滑動
- 作法跟卷積層很像
- 但是視窗通常取\( 2 \times 2\)
- 步長通常取2


滑動


一張\(n \times n \)的圖
經過\( 2 \times 2 ,步長2\)的池化層後
輸出 \( \frac{n}{2} \times \frac{n}{2}\)的圖
為什麼要池化?
- 減少參數數量
- 擴大卷積核對原圖的視野
減少參數數量
試想:
- 原本輸入\(28 \times 28 \)的圖
- 經過一個有\(20\)個Kernel的卷積層
- 變成\(20張 28 \times 28的\)Feature Map
- 資料量瞬間變\(20\)倍
- 經過池化層後變成\(20張 14 \times 14\)的圖
- 資料量只增加\(5\)倍
擴大卷積核對原圖的視野
- 不做池化:


Feature Map上一格只代表 \(3 \times 3 區域\)
卷積
擴大卷積核對原圖的視野
- 做池化:


Feature Map上一格代表 \(4 \times 4 區域\)
卷積
池化

有利於學習更廣域的特徵!
14. 卷積神經網路實作
CNN Implementation
手寫數字辨識
ML界的Hello World
輸入:
輸出:
" 5 "
圖片
文字
Training Database

開發工具
Step 1:
使用tensorflow搭建keras
%env KERAS_BACKEND=tensorflow Step 2:
引入函式庫 numpy、matplotlib
%matplotlib inline
import numpy
import matplotlib.pyplotnumpy可以進行矩陣等數學運算
matplotlib可以幫助我們畫圖
Step 3:
下載MNIST
#download MNIST
from keras.datasets import mnist
(train_data, train_ans), (test_data, test_ans) = mnist.load_data()keras都幫我們做好了XD
我們下載下來的MNIST到底長怎麼樣咧?
來試看看!
print(train_data.shape)
print(test_data.shape)
# (60000, 28, 28)
# (10000, 28, 28)|
|
|---|




\(\dots\)
train_data
x60000
each image is 28x28
| 4 | 1 | 7 | 0 |
|---|
\(\dots\)
train_ans
x60000
|
|
|---|




\(\dots\)
test_data
x10000
| 0 | 4 | 8 | 7 |
|---|
\(\dots\)
test_ans
x10000
Step 4:
調整輸入圖片形狀
#reshape_data:
train_data = train_data.reshape(60000, 28, 28, 1)
test_data = test_data.reshape(10000, 28, 28, 1)這次不是要壓成一維!
我們還是保持他二維的形狀,這樣才能做卷積
只是把他擴展一個維度,代表這筆輸入資料只有一張圖片
Step 5:
設定輸出格式
#output data settings
from keras.utils import np_utils
train_ans = np_utils.to_categorical(train_ans, 10)
test_ans = np_utils.to_categorical(test_ans, 10)把答案轉換成one hot encoding的格式
One Hot Encoding
- 獨熱編碼(?
- 用於有限個選項的分類問題
- 用一個陣列存每個選項是對的機率
5
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.]
Step 6:
引入keras類神經網路模型函式庫
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Flatten
from tensorflow.keras.layers import Conv2D, MaxPooling2D
from tensorflow.keras.optimizers import SGD- Sequential : 神經網路模型物件
- Dense : 全連接層相關的東西
- Activation : 激勵函數
- Flatten : 把資料壓平成一維的工具
- Conv2D:二維卷積層
- MaxPooling2D:二維池化層
- SGD : 反向傳播的優化器(Optimizer)
Step 7:
建立神經網路物件
model = Sequential() # 建立神經網路物件- 開始進入黑盒子的部分:D
Step 8:
加入第一層卷積層
#加入卷積層1
model.add(Conv2D(32, (3, 3), padding = "same", input_shape = (28, 28, 1)))
model.add(Activation("relu"))- Conv2D(filter數量, filter形狀, 卷積後的形狀padding(same:和輸入形狀相同), 輸入形狀)
- filter形狀:n*m(n, m)
- 輸入形狀input_shape = (n, m, l)
- Activation('') : 加入激勵函數
Step 9:
加入第一層池化層
#加入池化層1
model.add(MaxPooling2D(pool_size = (2, 2)))- MaxPooling2D(pool_size)
- pool_size:池化單位形狀 = (n, m)
Step 10:
加入第二層卷積層
#加入卷積層2
model.add(Conv2D(64, (3, 3), padding = "same"))
model.add(Activation("relu"))- Conv2D(filter數量, filter形狀, 卷積後的形狀padding(same:和輸入形狀相同), 輸入形狀)
- filter形狀:n*m(n, m)
- 輸入形狀input_shape = (n, m, l)(中間層可省略此參數)
- Activation('') : 加入激勵函數
Step 11:
加入第二層池化層
#加入池化層2
model.add(MaxPooling2D(pool_size = (2, 2)))- MaxPooling2D(pool_size)
- pool_size:池化單位形狀 = (n, m)
Step 12:
加入第三層卷積層
#加入卷積層3
model.add(Conv2D(128, (3, 3), padding = "same"))
model.add(Activation("relu"))- Conv2D(filter數量, filter形狀, 卷積後的形狀padding(same:和輸入形狀相同), 輸入形狀)
- filter形狀:n*m(n, m)
- 輸入形狀input_shape = (n, m, l)(中間層可省略此參數)
- Activation('') : 加入激勵函數
Step 13:
加入第三層池化層
#加入池化層3
model.add(MaxPooling2D(pool_size = (2, 2)))- MaxPooling2D(pool_size)
- pool_size:池化單位形狀 = (n, m)
Step 14:
加入壓平層
#把卷積後的二維矩陣壓平成一維
model.add(Flatten())- Flatten()
- 沒有參數,酷吧XD
- 把卷積後的二維矩陣壓平成一維
- 以便送進後續的Dense層
Step 15:
加入全連接層
#丟入全連接層
model.add(Dense(200, input_dim = 28 * 28))
model.add(Activation("relu"))- Dense(output_dim, input_dim) : 加入全連接層
- (output_dim : 輸出維度,input_dim : 輸入維度)
- Activation('') : 加入激勵函數
Step 16:
加入輸出層
#輸出層
model.add(Dense(10, input_dim = 200))
model.add(Activation("softmax"))- Dense(output_dim, input_dim) : 加入全連接層
- (output_dim : 輸出維度,input_dim : 輸入維度)
- Activation('') : 加入激勵函數
SoftMax
- 我們想要把神經網路算出來的結果轉化成每個選項的機率
- 類似概念,但我們在做機器學習的時候會把他丟到指數函數去做
Step 17:
把神經網路組裝起來
#設定loss function : mse(平方平均), optimzer : SGD, learing_rate = 0.008, 評比標準:accuracy
model.compile(loss = 'mse', optimizer = SGD(learning_rate = 0.008), metrics = ['accuracy'])- model.compile()
- loss : 計算Loss的方式
- optimizer : 優化器
- Learning Rate : 學習率(\(\mu\))
- metrics : 評比標準
Step 18:
model.summary()看看神經網路的模樣
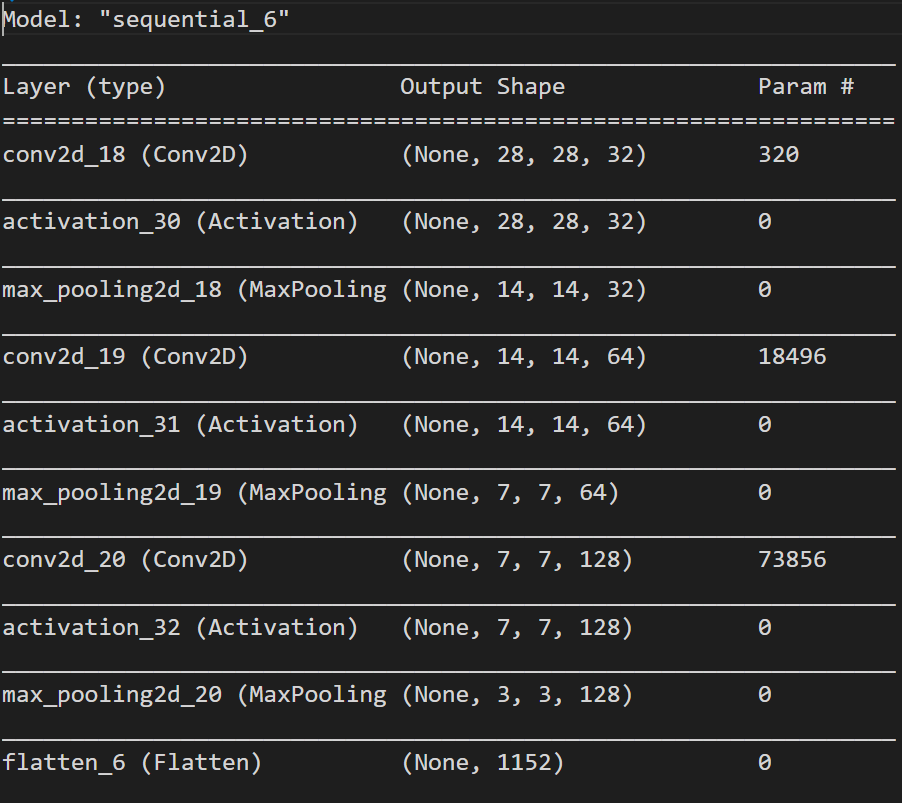
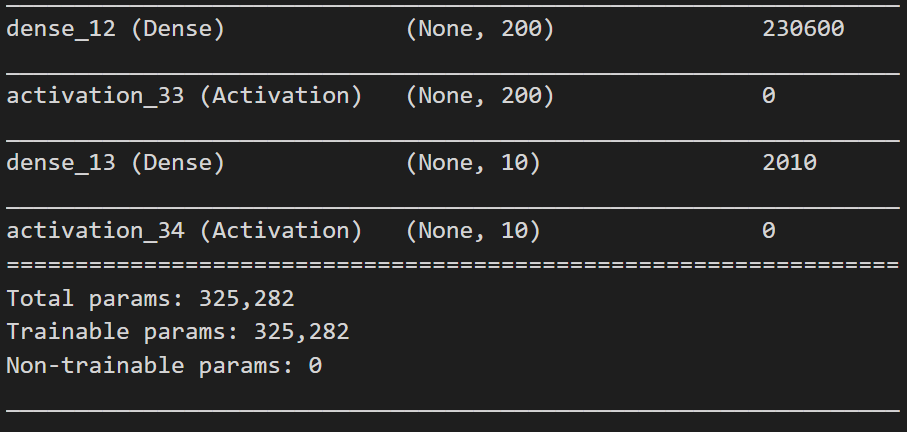
Step 19:
#train CNN
model.fit(train_data, train_ans, batch_size = 50, epochs = 20)訓練神經網路嚕!
- model.fit()
- 需要等上一陣子
- 先來講講batch_size和epoch吧:D
訓練時兩個重要的超參數
Batch_size
Epoch
- 批次大小
- 一次訓練的樣本數目
- 看好幾筆資料以後再一次一起調參數
- 影響模型的收斂速度
- 加快訓練速度
- 影響訓練效果
- 訓練時期數/次數
- 把整個資料集跑過幾次
- 影響訓練效果
- Epoch太小underfit
- Epoch太大overfit
選取好的batch_size搭配適當的Epoch訓練出最好的模型
Step 20:
score = model.evaluate(test_data, test_ans)
print("loss : ", score[0])
print("acc : ", score[1])驗收一下訓練結果
- model.evaluate()
- 檢視剛剛fit的成果
- 成果不好的話回去調超參數
Step 21:
predict = model.predict(test_data)應用model去預測未知的圖片
- model.predict(輸入圖片陣列)
- 回傳值為model的預測結果
- 回傳值以one-hot encoding格式儲存
Step 22:
predict = numpy.argmax(predict, axis = -1)將one-hot encoding格式轉換成整數
- numpy.argmax(a, axis=None, out=None)
- 以某個維度為比較基準,回傳該維度最大值所在的index
Step 23:
def test(index) :
matplotlib.pyplot.imshow(test_data[index].reshape(28, 28), cmap = "Greys")
print("神經網路判斷為:", predict[index])定義test函式
- test函式用來顯示神經網路的判斷結果
Step 24:
from ipywidgets import interact_manual
interact_manual(test, index = (0, 9999))互動式呈現預測結果
- 一個簡單的滑桿與按鈕互動介面
Step 25:
#save model and parameters
model.save("handwriting_model.h5")儲存訓練好的模型與參數
- 把模型的結構、超參數、與訓練好的參數存到.h5檔裡面
15. 遞迴神經網路
Recursive Neural Network
簡介一下RNN
-
遞迴神經網路 (Recursive Neural Network, RNN)
-
遞迴:重複的利用自己
-
在 自然語言處理領域 的王者
自然語言處理?
-
Natural Learning Processing
-
NLP
-
自然語言:人類日常溝通使用的語言
-
Eg : 中文、英文、日文、西班牙文、德文\( \dots \)
-
教機器學會認知、理解、生成自然語言
-
語音識別、機器翻譯、文字情感分析、聊天機器人\( \dots \)
文字情感分析
- 輸入一段英文電影評論,判斷這段評論是正面或是負面
The movie is fantastic.
What a horrible film.
機器
Positive
Negative
其實這算是RNN的入門經典問題啦,
網路上有個資料集叫IMDB,有興趣可以做做看
用我們以前的想法?
但這樣只能處理固定長度的文本輸入QQ
(也只能輸出固定長度的輸出TAT)
引入RNN!
我們要打破輸入&輸出維度的限制
不如不要一次輸入整個句子
改成一次輸入一個詞輸入很多次
RNN
RNN
RNN
RNN
RNN
The
movie
is
fantastic
<end>
Positive
但是這樣記不住啊啊啊~我們需要讓RNN有記憶!
引入記憶!
把先前的輸入打包成一個記憶存起來
輸入下個詞的時候,把記憶也視為輸入的一部份一起處理
每次處理完輸出一份新的記憶
RNN
RNN
RNN
RNN
RNN
The
movie
is
fantastic
<end>
Positive
.
(Memory)
(Memory)
(Memory)
(Memory)
記憶的雛型
Simple RNN
每個神經元都有自己的記憶
要讓整個RNN有記憶就從個別的神經元下手
記憶的雛型
Simple RNN
回想我們基本神經元的構造:
\( \sigma(x) \)
\(x_1\)
\(x_2\)
\(x_3\)
\(y\)
\(w_1\)
\(w_3\)
\(w_2\)
\(b\)
讓他有記憶:\(h\)
用下標t表示不同時間的記憶:\(h_t\)
\(h\)
\(h_t\)
記憶的雛型
Simple RNN
\( \sigma(x) \)
\(x_1\)
\(x_2\)
\(x_3\)
\(y\)
\(w_1\)
\(w_3\)
\(w_2\)
\(b\)
\(h_t\)
同時,輸入也多了前一個時刻的記憶\( h_{t-1} \)
\(h_{t-1}\)
\(u_1\)
記憶的雛型
Simple RNN
\( \sigma(x) \)
\(x_1\)
\(x_2\)
\(x_3\)
\(y\)
\(w_1\)
\(w_3\)
\(w_2\)
\(b\)
\(h_t\)
\(h_{t-1}\)
\(u_1\)
於是,計算方式從
擴展成
只是這原本作為輸出\(y\),
但現在改作為新記憶\(h_t\)
\(h_t\)
記憶的雛型
Simple RNN
\(h_{t-1}\)
\(u_1\)
為了避免混淆,我們將\(X與Y也加上時間下標t\)
並將\(W, U, b, \sigma \)加上下標\(h\)表示這是計算\(h\)的權重、偏值與激勵函數
\(h_t\)
\( \sigma(x) \)
\(x_1\)
\(x_2\)
\(x_3\)
\(w_1\)
\(w_3\)
\(w_2\)
\(b\)
\(b_h\)
\( \sigma_h(x) \)
記憶的雛型
Simple RNN
而輸出\(y_t\)則是將記憶\(h_t\)再做一次線性變換後丟進\( \sigma(x) \)裡面
注意這邊的\(W_y, b_y, \sigma_y和W_h, b_h, \sigma_h是不同的\)
\(h_{t-1}\)
\(u_1\)
\(h_t\)
\(x_1\)
\(x_2\)
\(x_3\)
\(w_1\)
\(w_3\)
\(w_2\)
\(b_h\)
\( \sigma_h(x) \)
\(w_y\)
\(b_y\)
\( \sigma_y(x) \)
\(y_t\)
記憶的雛型
Simple RNN
\(h_{t-1}\)
\(u_1\)
\(h_t\)
\(x_1\)
\(x_2\)
\(x_3\)
\(w_1\)
\(w_3\)
\(w_2\)
\(b_h\)
\( \sigma_h(x) \)
\(w_y\)
\(b_y\)
\( \sigma_y(x) \)
\(y_t\)
\(x_1\)
\(x_2\)
\(x_3\)
\(w_1\)
\(w_3\)
\(w_2\)
\(u_1\)
\(h_{t+1}\)
\(b_h\)
\( \sigma_h(x) \)
\(w_y\)
\(b_y\)
\( \sigma_y(x) \)
\(y_{t+1}\)
到此,我們已經學會了一種最基本的RNN記憶模型
Simple RNN
- RNN發展早期提出來的模型
- 最原始的記憶
- 記不住太久遠以前的東西
- 梯度爆炸
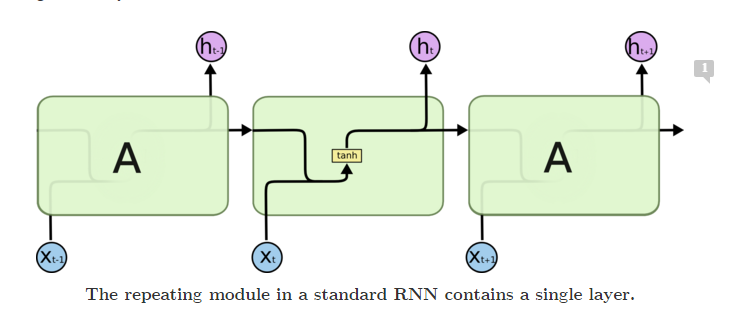
所以現在大家比較常用的是
LSTM
- Long Short-Term Memory
- 長短期記憶
- 效果比simple RNN好很多
- 當代RNN最常用的記憶模型
- 由input gate, output gate, forget gate四個閘控制輸入、輸出與記憶資訊的流動
LSTM
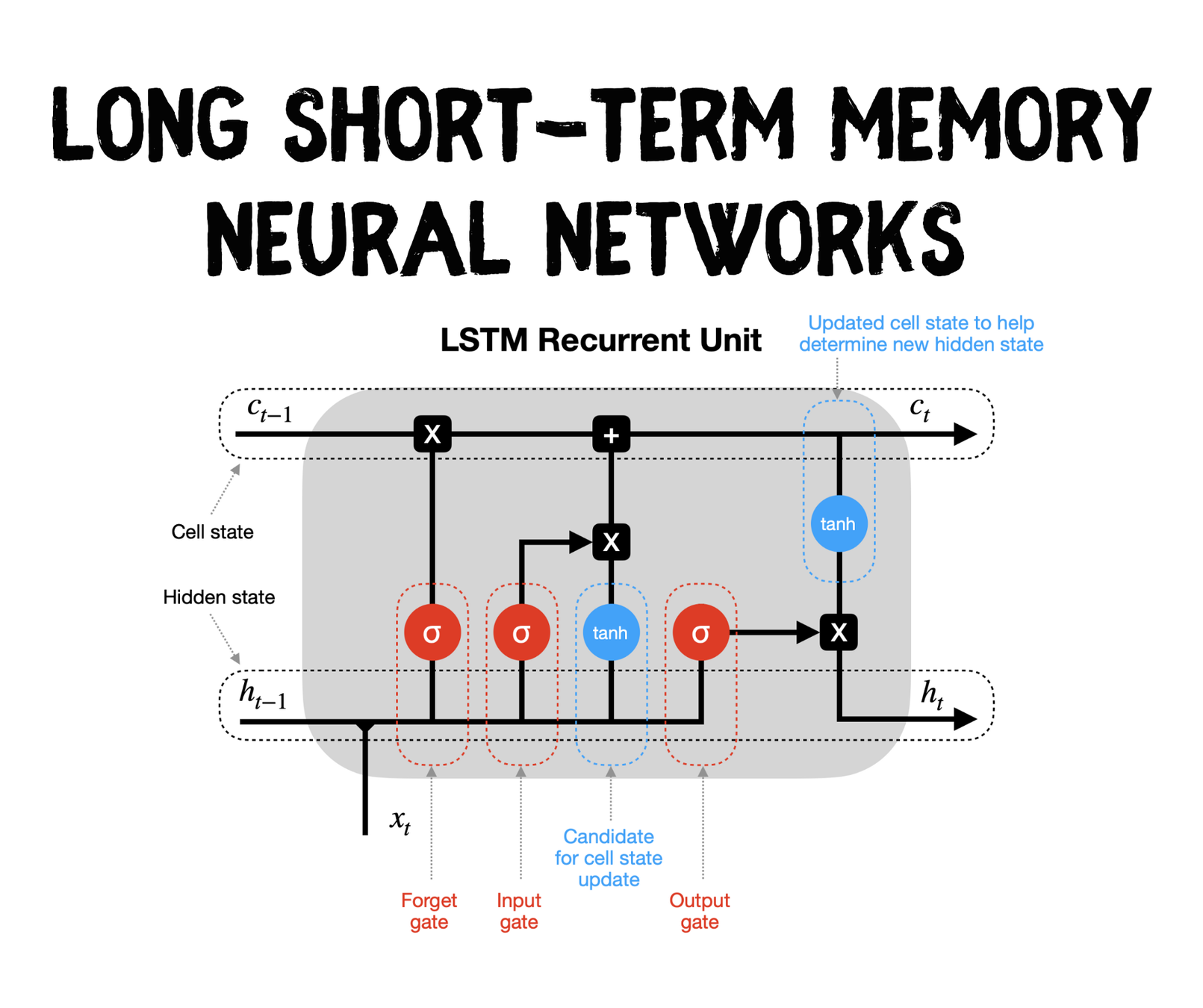
李弘毅教授講解RNN與LSTM
個人覺得講得非常好,有興趣深入了解LSTM的人可以去看
16. 結語



