Study on Geometric Construction in Dynamic Geometry Environments

- day ## month 2024  -

Academic stay at the Department of Mathematics

at the University of Bari, Italy 🇮🇹

Sergio Rubio-Pizzorno | 🇲🇽🇨🇱

Phd student (last year) in Science with specialization in Mathematics Education

Center for Research and Advanced Studies (Cinvestav) - México 🇲🇽

Department of Mathematics Education

Créditos












Taller "Herramientas GeoGebra para la Educación en línea" por Sergio Rubio-Pizzorno se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Basada en una obra en https://slides.com/zergiorubio/2020-taller-11eical .

BY

NC

Overview

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Dynamic Geometry Environments (DGE) have brought changes in Geometry Education both in research and teaching and learning:

Dynamic Geometry changes the game

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

The applications of geometry range widely, and increasingly so, given developments in computer-based visualization and modeling. The emergence of dynamic, digital images has not only revived the discipline of mathematics, it has radically changed the way it is being taught and learned in schools today.

(Sinclair et al., 2017, p. 457).

INTRODUCTION

Research gap with some central geometric notions using DGE

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Technology in geometry education has become mainstream; but there is still not enough research into its specific effects.

(Sinclair et al., 2016, p. 704)

Little research has focused on geometric constructions, despite their central role in geometry.

(Sinclair et al., 2017, p. 480)

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Common functional constructive approach [of DGE] (where geometric configurations must be expressed in terms of sequential constructions).

(Sinclair et al., 2016, p. 704)

Why geometric constructions are important on the use of DGE?

[In DGE], during dragging, a figure maintains all the properties according to which it was constructed and all the consequences that the construction entails in Euclidean Geometry.

 (Leung, 2015, p. 467)

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Central theme in Euclidean Geometry.

Why consider geometric constructions in DGE for researching?

Possibility of studying it using only geometric registers (not algebraic or numerical).

Suitability of DGE to study of geometric constructions.

It fits with the trend in geometry education research to move to a more active meaning-making orientation to geometry (Sinclair & Bruce, 2015).

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Interest is the inherent characteristics of
geometric construction in DGE

Scopus, WoS, and Redalyc

37 results

36 papers tangentially mention geometric construction.

1 paper addresses the inherent characteristics of geometric construction.

They refer mainaly to dragging.

Talmon & Yerushalmy (2004). Understanding dynamic behavior: Parent–Child relations in dynamic geometry environments.

LITERATURE REVIEW

The gap shown in specialized literature is confirm with literature review.

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Papers included in Literatura review

Talmon, V., & Yerushalmy, M. (2004). Understanding dynamic behavior: Parent–Child relations in dynamic geometry environments. Educational Studies in Mathematics, 57(1), 91–119. https://doi.org/10.1023/B:EDUC.0000047052.57084.d8

Jones, K. (2001). Providing a Foundation for Deductive Reasoning: Students’ Interpretations when Using Dynamic Geometry Software and Their Evolving Mathematical Explanations. Educational Studies in Mathematics, 44, pp. 55–85. https://doi.org/10.1023/A:1012789201736

Hölzl, R., Healy, L., Hoyles, C., & Noss, R. (1994). Geometrical relationships and dependencies in Cabri. Micromath, 10(3).

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

What do we get from Literature review?

Characteristics of geometric construction in a DGE

Dynamic behavior

Dependency relations

Construction order

Geometric relations

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Objectives of the study

Objective 1: Propose a characterization of the geometric construction in DGE.

Objective 2: Operationalize such characterization with a view to having a more active approach when working with geometric construction in DGE.

Base on these objectives and adding the considerations from theoretical framework, the research questions of this study will be proposed.

OBJECTIVES

OF THE STUDY

Objective of the study

Con base en estos puntos, en esta tesis se pretende investigar los haceres que constituyen las prácticas relacionadas con la construcción geométrica, que estén mediados por los AGD, y los nexos de tales prácticas. Todo esto con el propósito de explicar, comprender e interpretar el fenómeno de enseñar y aprender geometría —específicamente lo relativo a la construcción geométrica en AGD— como una articulación de prácticas.

1. Objective of the study

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

In simple words, doings are what people do with their bodies and extensions of their bodies.

Practices are defined as a set of human doings which are embodied and materially mediated (Schatzki, 2005).

Thus, doings are the basic unit of organization and analysis of practices (Schatzki, 2002).

Practices and doings

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Design-based research (DBR)
(Bakker, 2018; Camargo Uribe, 2021; Cobb et al., 2003; Swan, 2014)

Phase 1: Design elaboration

Phase 2: Design implementation

Phase 3: Retrospective analysis

Trajectory of Hypothetical Learning

Ongoing analysis, this is, design could be modified

Three levels analysis (Simon, 2018)

Design as a research instrument

METHODOLOGY

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Design-based research (DBR)

Design as a research instrument

Elaborated design

(Phase 1)

Implemented design

(Phase 2)

  • 4 Moments.
  • 17 Activities.
  • 5 Moments.
  • 30 Activities.

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

General information on data production

Screen recording of each student

Teacher screen recording

Classroom recording

Students' answers (in GeoGebra Classroom)

Data logging

Five students in their third year of the Bachelor's Degree in Mathematics Teaching

Design implementation

Universidad Autónoma de Baja California, Mexico

The design was implemented in the Digital Practices for Future Mathematics Teachers course

Five classes were considered: the first two were face-to-face and the last three were online.

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno (Phd student) | sergio.rubio@cinvestav.mx

1. Introduction

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Data organization

Sesion 1

Sesion 2

Sesion 3

Sesion 4

Sesion 5

Private

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

6. Data analysis

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Case of study: María

Design

Level 1

RQ1: What geometric doings are involved as we develop geometric construction activities in DGE?

Three levels of analysis

Level 2

Level 3

  1. What does María do?
  2. How does María do?
  3. What does María say?
  1. Contrast local hypotheses.
  2. Are the proposed theoretical doings recognized?
  3. Do new doings emerge?
  4. Is an organization of doings identified?

RQ2: How do these geometric doings organize as we develop geometric construction activities in DGE?

Tasks and Activities
(line-by-line analysis)

Moments

Explanations throw theoretical framework.

DATA ANALYSIS:

An example (phase 3)

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

6. Data analysis

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Activity 3

Tasks

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

6. Data analysis

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Activity 3

Level 1

What does María do?

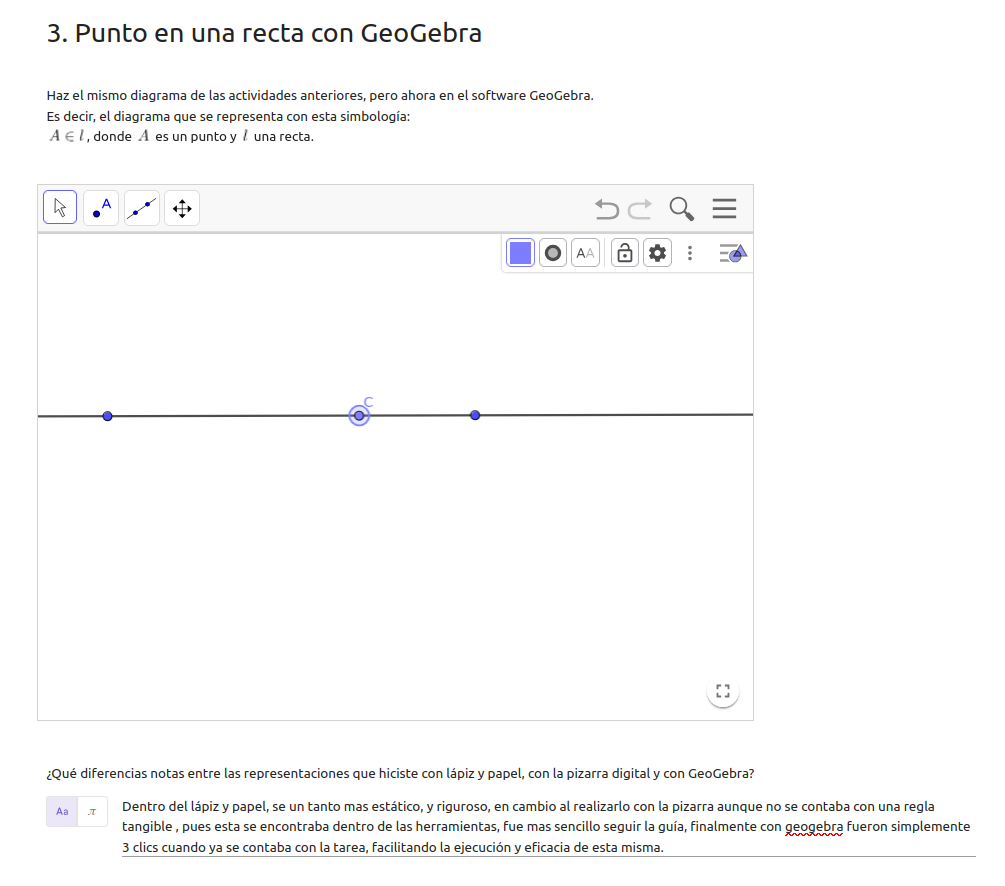
Construct a line through two points.
Then construct a third point on the line.

How does María do?

  1. Use the Line tool and create a point A and then a point B, with which you completely determine the line.
  2. Select the Point tool and construct a point C on the line.
  3. Drag point C on the line.
  4. Hide the name label of points A and B.
  5. After a moment, drag points A and B.
  6. Answer the open-ended question about the differences in the three records.

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

6. Data analysis

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Activity 3

Level 1

What does María say?

Written answer

With pencil and paper, it is a bit more static and rigorous.
On the other hand, when doing it with the blackboard, although there was no tangible ruler - since it was found within the [GeoGebra Notes] tools - it was easier to follow the guide.
Finally, with GeoGebra it was just three clicks when the task was ready, facilitating the execution and efficiency of the task.

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

6. Data analysis

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Activity 3

Level 1

What does María say?

Discussion between María and the teacher about the number of points used in each representation

 

Teacher: Why does GeoGebra require two points as opposed to paper and pencil or a digital whiteboard which only require one point?
María: In GeoGebra, at least two points are required to define a line since two distinct points determine a line. In contrast, with pencil and paper or on a digital whiteboard, you can draw a line by simply drawing an initial point and extending it in the desired direction without explicitly specifying a second point.

Cinvestav - México 🇲🇽

Sergio Rubio-Pizzorno  (Phd student) | sergio.rubio@cinvestav.mx

6. Data analysis

2. Literature review

3. Research questions

4. Theoretical framework

5. Methodology

Activity 3

Level 2

Are the proposed theoretical doings recognized?

When students are asked to justify how they did solve a task (regardless of whether the solution is correct), they express geometric relationships, dependency relationships, or geometric properties to validate their doings.

Sinclair et al. (2017) han identificado algunos temas geométricos que han tenido muy poco desarrollo en la investigación, entre los cuales destaca la “poca investigación que se ha enfocado en las construcciones geométricas, a pesar de su rol central en la geometría” (p. 480).

2. Revisión de literatura

¿Construcción geométrica?

Construcción geométrica en AGD

REVISIÓN DE LITERATURA

Construcción geométrica con tecnologías físicas

Articulación del AGD con tecnologías físicas

2. Revisión de literatura

Construcción geométrica en AGD

Comportamiento dinámico

Relación de dependencia

Orden de construcción

Relación geométrica

2. Revisión de literatura

Articulación del AGD con tecnologías físicas

Alternancia en el uso de las tecnologías

Valor epistémico de cada tecnología

Articulación del valor epistémico de cada tecnología

Falta de investigación sobre construcciones geométricas en AGD, a pesar de ser un objeto de suma relevancia para la geometría euclidiana.

3. Planteamiento

Caracterizar prácticas geométricas híbridas asociadas a la construcción geométrica, específicamente utilizando AGD y papel y lápiz, al trabajar con estudiantes de formación docente.

PLANTEAMIENTO

Se han identificado elementos que dan cuenta del valor epistémico de los AGD relativos a la construcción geométrica, por lo que ahora es necesario ponerlos a prueba e investigarlos.

Perspectiva de investigación que pone el énfasis en lo propio de cada tecnología –valor epistémico– y propicia su articulación.

Objetivo de investigación

4. Marco teórico

MARCO TEÓRICO

Modelo de
 Trabajo  Práctica Geométrica

Ecosistemas Educativos Híbridos

Enfoques de práctica social

Objeto concreto

Objeto teórico

Representación

(Rubio-Pizzorno, 2018, pp. 67 - 104)

Abstracción

Construcción

Bosquejo

  • General
  • Particular

Intuición empírica

Intuición sofisticada

  • Interpretación
  • Reconocimiento
  • Identificación

Modelo de Trabajo Práctica Geométrica

Plano concreto

Plano teórico

Representación

Abstracción

Modelo de Trabajo Práctica Geométrica
para la construcción geométrica

Manipulación*

Práctica geométrica de Manipulación* para la construcción geométrica en AGD

  1. Propiedad geométrica: resultado de la geometría euclidiana que fundamenta y guía la construcción geométrica.

  2. Relación geométrica: vínculo intrafigural específico (no es general) entre dos objetos geométricos de un mismo diagrama. Tal vínculo expresa una propiedad geométrica establecida mediante un proceso de construcción. O, dicho en palabras simples, es la propiedad geométrica que vincula a dos objetos de una misma construcción.

  3. Orden de construcción: organización secuencial de las acciones necesarias para construir un diagrama.

  4. Relación de dependencia: vínculo jerárquico y funcional entre dos objetos de una construcción geométrica, determinado por el proceso de construcción.

  5. Comportamiento dinámico: tipos de cambios de los objetos geométricos de una construcción al momento de arrastrar alguno de ellos.

References

 

  • Sinclair, N., Bartolini Bussi, M. G., de Villiers, M., Jones, K., Kortenkamp, U., Leung, A., & Owens, K. (2016). Recent research on geometry education: an ICME-13 survey team report. ZDM - Mathematics Education, 48(5), 691–719. https://doi.org/10.1007/s11858-016-0796-6

  • Sinclair, N., Cirillo, M., & de Villiers, M. (2017). The Learning and Teaching of Geometry. In J. Cai (Ed.), Compendium for Research in Mathematics Education (pp. 457–489). Abingdon, Oxon; New York: The National Council of Teachers of Mathematics Education.

  •  

Made with Slides.com