向量、矩陣
Lecturer: 立葉
建北電資運算思維小社課 Lesson 5
Index
-
基礎定義
-
空間概念(帶過)
-
斜坐標系
-
向量內積
-
柯西不等式(好東西)
平面向量(vECTOR)
話說上兩次的運算思維小社課,我們提到了特殊三角比...
STORY TIME!
STORY TIME!
而在下課之後,我們可愛的酥育根跟章程+說:「你怎麼沒有教37-53-90的特殊三角比啊,這樣他們會像我一樣在物理課耍智障欸」
STORY TIME!
陳諒妍表示,這個東西只是估計值硬要講而已;章程甲也表示,這只會出現在物理,啊我又不教物理。

STORY TIME!
「啊我又不教物理?」

這個論述要破滅ㄌ
向量與我們的物理學息息相關ㄋ
雖然這堂課重心不會放在那 故事是白講ㄌ
What is 向量?
這是一個點。
當然,它本身並沒有所謂大小;有形狀只是為了讓你能看的到。
這是一條直線,它會無限延伸。
當然,它本身並沒有所謂寬度,有也只是為了讓你能看的到。
這是一條射線。
它會以一點作為起點,並往另一邊無限延伸。
這是一條線段。
它有兩個端點,但是沒有方向性。
最後就是我們這堂課要交的:向量!
它是一個有起點和終點,具有方向性的線段。
向量的基本性質!
- 向量由其 大小 和 方向 決定,不在意起點與終點。
- 向量的圖示:在起點和終點上面畫一個箭頭來表示,如:\(\overrightarrow{AB}\)。為了方便表示,也可以一個字母如 \(\overrightarrow{a}\) 來表示。
- 向量的量值:以\(|\overrightarrow{AB}|\)來表示。
- 特殊的向量:
- 反向量:若一向量與另一向量的量值相同而方向相反,則稱其互為反向量。
- 零向量:量值為零的向量,記為 \(\overrightarrow{0}\) 。其可視作任意方向。
- 在生活(aka 物理)上的應用:包括位移、速度、加速度、力等等,都是向量!
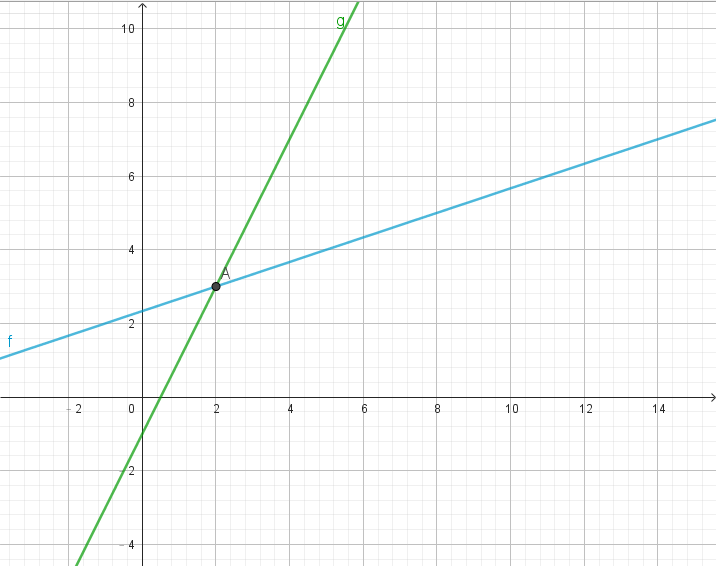
平面座標系上的向量
- 一般來說,我們會令一平面上的向量 \(\overrightarrow{a}\) 的起點為\((0, 0)\)
- 在這樣的情況時,令它的終點為\((x, y)\)
- 則我們可以將其表示為 \(\overrightarrow{a} = (x, y)\) 了呢!
- 當然,如果原點不是起點,那麼該向量為 (終點座標 - 起點座標)
- 從這種表示方式也可以很輕易地發現,一個向量的量值是\(\sqrt{x^2+y^2}\) 。
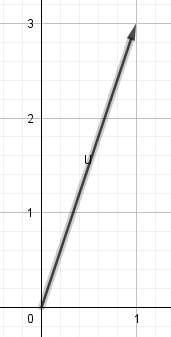
- 以左圖這個向量為例
- \(\overrightarrow{u} = (1, 3)\)
- \(|\overrightarrow{u}| = \sqrt{10}\)
向量的加減運算與係數積
- 設兩個向量 \(\overrightarrow{a} = (x_1, y_1), \overrightarrow{b} = (x_2, y_2)\) ,則:
- \(\overrightarrow{a} + \overrightarrow{b} = (x_1 + x_2, y_1+ y_2)\)
- \(\overrightarrow{a} - \overrightarrow{b} = (x_1 - x_2, y_1- y_2)\)
- \(r\overrightarrow{a} = (ra_1, ra_2)\),其中\(r\)為實數
- 向量與向量的「乘法」?後面會提到!
向量加減的幾何意義
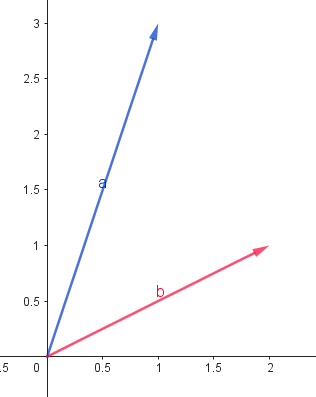
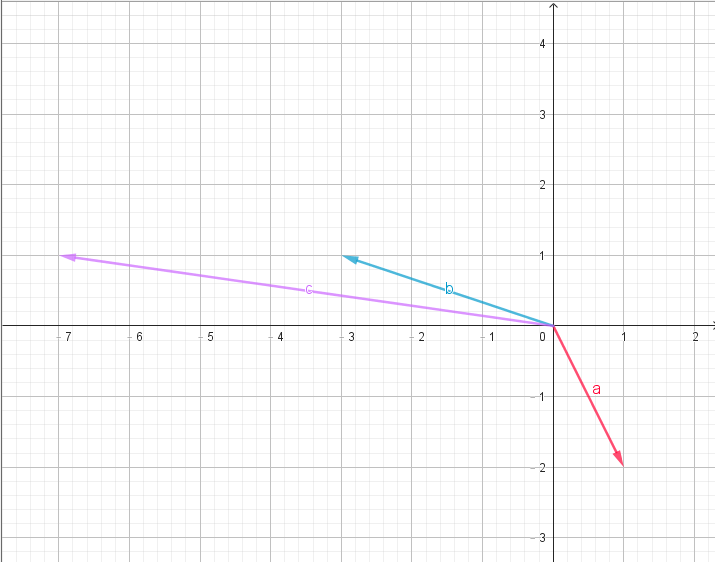
- 設兩個向量 \(\overrightarrow{a} = (1, 3), \overrightarrow{b} = (2, 1)\) 。我們來把它具象化一下:
- 而我們由上頁對於向量的加減定義可得知:
- \(\overrightarrow{a} + \overrightarrow{b} = (3, 4)\)
- \(\overrightarrow{a} - \overrightarrow{b} = (-1, 4)\)
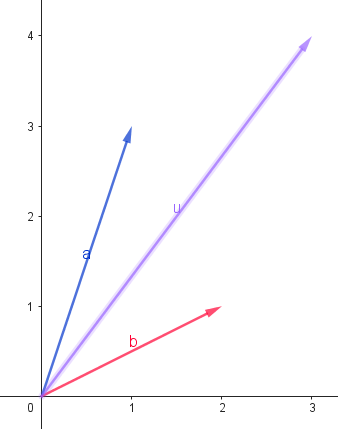
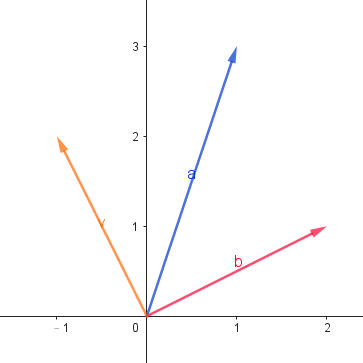
向量加減的幾何意義
- 仔細觀察它們的圖形,你可以發現:
- 兩個向量的加法就是物理課所謂「三角形平移法」或「四角形對角線法」的實現!(對名字我亂掰的
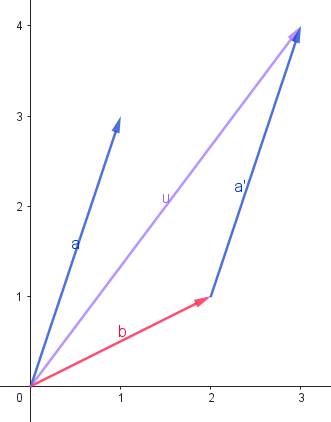
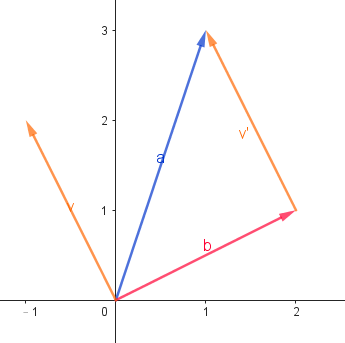
- 至於向量的減法,對於初學者可能較不直觀,但其實真的很直觀
- 設\(\overrightarrow{v} = \overrightarrow{a} - \overrightarrow{b}\),我們稍微將這個式子平移一下,得到\(\overrightarrow{a} = \overrightarrow{b} + \overrightarrow{v}\)
- 所以這樣就變直觀ㄌ!
小小的例題
- 一個質點以速率 30 m/s的速度碰撞牆壁,並在 0.2 s 內以相同速率反射出去,如圖所示。請求出這顆球碰撞牆壁時所受到的加速度量值?
\(30\)
\(30\)
黃色線段 = \(\sqrt{30^2+30^2-2\times30\times30\times\cos120\degree} \\ = 30\sqrt{3}\)
ans: \(150\sqrt{3} m/s^2\)
向量間的關係
- 平行向量:
- 設兩個向量\(\overrightarrow{a} = (x_1, y_1), \overrightarrow{b} = (x_2, y_2)\)
- 則\(\overrightarrow{a} // \overrightarrow{b} \Leftrightarrow \overrightarrow{a} = r\overrightarrow{b} \)
- 單位向量(長度為1的向量):
- \(\overrightarrow{a} = \pm |\overrightarrow{a}|\overrightarrow{e}\)
- \(\overrightarrow{e} = \pm\frac{\overrightarrow{a}}{|\overrightarrow{a}|}\)
向量的線性組合特性
- 在一平面座標上,設兩個向量\(\overrightarrow{a},\overrightarrow{b}\),若此兩向量不平行,則任一向量\(\overrightarrow{c}\)都可以 \(r\overrightarrow{a} + s\overrightarrow{b} \) 表示!
- 例如:
- 將向量\(\overrightarrow{c} = (-7, -1)\)表示成兩不平行向量\(\overrightarrow{a} = (1, -2)\)與\(\overrightarrow{b} = (-3, 1)\)的線性組合。
ans: \(\overrightarrow{c} = 2\overrightarrow{a} + 3\overrightarrow{b}\)
我們可以設 \(\overrightarrow{c} = r\overrightarrow{a} + s\overrightarrow{b}\)
接下來列二元一次聯立方程式,得到
解方程式,得到 r=2, s=3
向量的線性組合
- 接下來,我們一樣把上一頁的東西具象化:
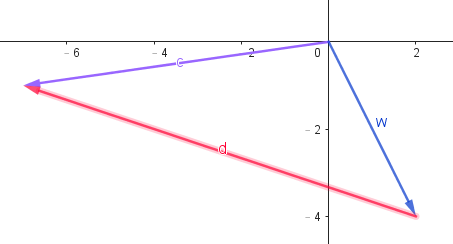
- 我們把它們分別改成 \(2\overrightarrow{a}\) 和 \(3\overrightarrow{b}\) ,並把\(3\overrightarrow{b}\) 稍微平移一下,就可以發現我們已經成功用這兩個向量表示\(\overrightarrow{c}\)了呢!
其實這頁目前沒什麼要講的,只是要告訴你它很漂亮順便埋個伏筆
向量與斜座標系統
- 事實上,我們可以使用兩個不平行的向量來創立一個新的斜座標系統!
- 令 \(\overrightarrow{a} = (1, 0),\overrightarrow{b} = (0, 1)\)
- 那麼這時候 \(\overrightarrow{c} = x\overrightarrow{a} + y\overrightarrow{b}\) 的座標就是 \((x, y)\)
- 也可以從這個角度去發現 \(x\overrightarrow{a} + y\overrightarrow{b}\) 可以表示出平面上任一向量
- 不知道也不太會怎麼樣,但知道了會很有用

畫出來就像這樣!
小小的例題
- 以下是一個正六邊形ABCDEF,請以 \(\overline{AB} = \overrightarrow{a}\) 和 \(\overline{BC} = \overrightarrow{b}\) 表示 \(\overline{AE}\) 和 \(\overline{EC}\)。
A
B
C
D
E
F
O
ans:
\(\overrightarrow{AE} = -\overrightarrow{a} + 2\overrightarrow{b}\)
\(\overrightarrow{EC} = 2\overrightarrow{a} - \overrightarrow{b}\)
多維空間ㄉ向量
我原本想塞一點空間概念,但我沒時間- 對於一個 n 維的向量 \(\overrightarrow{v}\),我們可以寫作 \(\overrightarrow{v} = R^n\)
- 然後對於這個向量 \(\overrightarrow{v}\),它的座標是 \((a_1, a_2, \dotsb, a_n)\),
量值是 \(\sqrt{\displaystyle\sum_{i=1}^{n} {a_i}^2}\)
向量內積
- 也就是「點積」!
- 向量內積是一個純量。
- 定義為 \(\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|\cos\theta = a_1b_1 + a_2b_2\)
- 對於超過三維的向量,我們只能以\(\overrightarrow{a} \cdot \overrightarrow{b} = \displaystyle\Sigma_{i=1}^{n} a_ib_i\)表示
- 在物理課中學到的功,就是力和位移的內積!
- 內積也是 \(\overrightarrow{a}\) 投影到 \(\overrightarrow{b}\) 的量值乘以 \(|\overrightarrow{b}|\)!
- 將 \(\overrightarrow{a}\) 投影到 \(\overrightarrow{b}\),則:
- 其投影的向量量值為 \(\left(\frac{\overrightarrow{a} \cdot \overrightarrow{b} }{|\overrightarrow{b}|}\right)\)
- 其投影的向量本人為 \(\left(\frac{\overrightarrow{a} \cdot \overrightarrow{b} }{|\overrightarrow{b}|^2}\right)\overrightarrow{b}\)
小小的例題
- 已知三角形 ABC 的三邊長為 \(\overline{AB} = 7, \overline{BC}=5, \overline{CA} = 8\),求
- \(\overrightarrow{AB} \cdot \overrightarrow{AC}\)
- \(\overrightarrow{AB} \cdot \overrightarrow{BC}\)
ans: 44; -5
忘記餘弦定理的點我(雖然那邊的簡報我做的很懶蛋)
柯西不等式
- 向量形式:
- \(|\overrightarrow{a}||\overrightarrow{b}| \geq |\overrightarrow{a} \cdot \overrightarrow{b}| = |\overrightarrow{a}||\overrightarrow{b}|\cos\theta\)
- 實數形式:
- \(({a_1}^2+{a_2}^2)({b_1}^2+{b_2}^2) \geq (a_1b_1 + a_2b_2)^2\)
- 其中等式成立於\(\frac{a_1}{a_2} = \frac{b_1}{b_2}\)
- 也能推廣到多維!
- \((\displaystyle\sum_{i=1}^{n} x_iy_i)^2\ \leq (\displaystyle\sum_{i=1}^{n} {x_i}^2)(\displaystyle\sum_{i=1}^{n} {y_i}^2)\)
- 等式成立於\(\frac{x_1}{y_1} = \frac{x_2}{y_2} = \dotsb = \frac{x_n}{y_n}\)
用柯西不等式來證明相關係數 \(r\) 的範圍!?
- 忘記相關係數的點我
- 我們知道 \(-1 \leq r \leq 1\)
- 我們的證明方式可以土法煉鋼,把所有東西展開(有時間我在之前的簡報會放證明)
- 而這邊可以用柯西不等式!
小小的例題
- 設兩向量 \(\overrightarrow{a} = (x, y)\) 與 \(\overrightarrow{b} = (p, q)\),若 \(|\overrightarrow{a}| = 2, |\overrightarrow{b}| = 6\),求 \(px + qy\) 的最大值。
- 設 \(P(x, y) 為直線 \(L: 3x + 5y - 4 = 0\) 上的任一點,求 \(3x^2 + 5y^2\) 之最小值及此時數對 \((x, y)\)。
ans: 12
ans: 2;\((\frac{1}{2}, \frac{1}{2})\)
- 求 \(y = \sqrt{2x-1} + \sqrt{5-3x}\) 的最大值及此的 \(x\) 值。
ans: \(\sqrt{\frac{35}{6}}\);\(x = \frac{29}{30}\)
向量的應用:重心公式
- 想必各位應該都還記得重心是什麼吧:)
- 我們從向量的角度去探討重心
- 三角形 ABC,我們設 \(A(a_1, a_2), B(b_1, b_2), C(c_1, c_2)\),並設其重心為點G。
1)
2)
3)
向量的應用:兩向量所張的平行四邊形的面積
- 從之前學到的正弦定理,我們知道
- 三角形 ABC 的面積為 \(\frac{1}{2} bc\sin\theta\)
- 從另一個角度來看,我們可以把其中兩個邊長設為 \(\overrightarrow{AB}, \overrightarrow{AC}\)
- 那麼,由這兩個向量所張出的平行四邊形面積就是 \(bc \sin \theta\)!
- 那麼就會有以下的式子:
\(|\overrightarrow{a}||\overrightarrow{b}|\sin\theta\)
= \(|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-\cos^2\theta}\)
= \(\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-|\overrightarrow{a}|^2|\overrightarrow{b}|^2\cos^2\theta}\)
= \(\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a} \cdot \overrightarrow{b})^2}\)
-
二階與三階行列式
-
二 / 三元一次方程式克拉瑪公式
-
向量外積
-
平行四面形 / 平行六面體
行列式
二階行列式
- 一些雜七雜八性質:
- 行列互換,值不變
- 兩行 / 兩列互換,值變號
- 任一行 / 列,可提出公因數
- 任一行 / 列乘以 \(r\) 並加到另一行 / 列,其值不變
- 可以拆項
小小的例題
- 請算出以下行列式的值:
1)
2)
- 若
,求
?
ans: 2015
行列式的應用:平行四邊形的面積
- 設向量 \(\overrightarrow{a} = (a_1, a_2), \overrightarrow{b} = (b_1, b_2)\),則由 \(\overrightarrow{a}\) 和 \(\overrightarrow{b}\) 所張成的平行四邊形面積為:
對ㄚ我就懶得排版
要看ㄉ自己看
二元一次聯立方程式克拉瑪公式
- 我們在此定義三個東西:
- 使用 \(\Delta\) 來判斷x, y的解情況!
- \(\Delta \neq 0\),則x, y有唯一解
- \(\Delta = 0\),則再分成兩種情況:
- \(\Delta_x, \Delta_y = 0\),則x, y有無限多組解
- \(\Delta_x, \Delta_y\)有任一不為0,則x, y無解
- 若 \(\Delta \neq 0\),則:
- \(x = \frac{\Delta_x}{\Delta}\)
- \(y = \frac{\Delta_y}{\Delta}\)
三階行列式
三階行列式的性質
- 基本上都跟二階行列式一樣
- 三階行列式降階成為二階:依據某一行 / 列!
變號的時候要依據這張表格
用處?
計算形如
的三階行列式會方便很多
三元一次聯立方程式克拉瑪公式
- 我們在此定義四個東西:
- 使用 \(\Delta\) 來判斷x, y, z的解情況!
- \(\Delta \neq 0\),則x, y, z有唯一解
- \(\Delta = 0\),則再分成兩種情況:
- \(\Delta_x, \Delta_y, \Delta_z = 0\),則x, y, z 可能無解,也可能無限多組解
- \(\Delta_x, \Delta_y\, \Delta_z\)有任一不為0,則x, y, z 無解
- 若 \(\Delta \neq 0\),則:
- \(x = \frac{\Delta_x}{\Delta}\)
- \(y = \frac{\Delta_y}{\Delta}\)
- \(z = \frac{\Delta_z}{\Delta}\)
結論:使用克拉瑪公式解聯立方程式不一定比較方便。
但它判斷解數的情況比較快速
向量外積
- 是一個向量,只有在空間中才有辦法定義!
- 寫法為 \(\times\)
- 為 \(\overrightarrow{a}\) 和 \(\overrightarrow{b}\) 的公垂向量,姑且設它為 \(\overrightarrow{n} = (x, y, z)\)
- 根據內積,我們可以得到下面這個聯立方程式:
- 然後根據上面二元一次方程式的克拉瑪公式,整理可得到:
- 向量外積定義為 \(k=1\) 時的 \(\overrightarrow{n}\)
- 方向性:右手法則
- 物理課學到的力矩,就是一種外積!
空間中兩向量所張成的面積
- 在前面,我們有提到兩向量所張成的平行四邊形面積
- 而在空間中,我們可以把這個式子化成
- 然後你就會發現 :flushed:
\(\overrightarrow{a}\)
\(\overrightarrow{b}\)
\(\overrightarrow{a} \times \overrightarrow{b}\)
空間中三向量所張成的平行六面體體積
- 延續上頁,所以我們的平行四邊形面積其實可以一個向量 \(\overrightarrow{t} = \overrightarrow{a} \times \overrightarrow{b}\) 表示
- 這時候,體積 = 底面積 \(\times\) 高
- 我們的高可以 \(|\overrightarrow{c}| \cos\theta\) 表示
\(\overrightarrow{a}\)
\(\overrightarrow{b}\)
\(\overrightarrow{c}\)
- 體積 =\(||\overrightarrow{t}||\overrightarrow{c}|\cos\theta| = |\overrightarrow{t} \cdot \overrightarrow{c}| = |(\overrightarrow{a} \times \overrightarrow{b}) \cdot \overrightarrow{c}|\)
- 然後把所有的行列式都帶進來,你可以得到:
-
What is 線性代數?
-
矩陣的基本定義與運算
-
各種矩陣
矩陣
線性代數
- 用個前面放的二元一次聯立方程式
- 它有兩種幾何意義:
列的圖像
行的圖像
線性代數

行的圖像
線性組合
矩陣
- 把一群數字 / 文字排成矩形陣列
- 表示法:
或簡記為
其中在第 \(i\) 列和第 \(j\) 行的元素為 \(a_{ij}\)
- 同階矩陣:列數、行數皆相同的兩個矩陣
- 矩陣相等:列數、行數相同,且所含元素也相同
各種矩陣
- 方陣:列數、行數相同
- 列矩陣: \(m=1\) / 行矩陣:\(n=1\)
- 轉置矩陣:將 A 行列互換,記為 \(A^T\)
- 對稱方陣:\(A = A^T\)
- 反對稱方陣:\(A = -A^T\)
- 三角矩陣:上三角、下三角、對角
2 x 2 方陣
3 x 3 方陣
列矩陣 / 行矩陣可以視為列向量 / 行向量
如右圖所示
它是三維向量
也是 3 x 1 的矩陣
\(R^n = R^{n\times1}\)
可以把矩陣視為向量的組合體!
列向量 \(\overrightarrow{A_1}\)
列向量 \(\overrightarrow{A_2}\)
列向量 \(\overrightarrow{A_3}\)
可以寫成這樣!
上三角矩陣
下三角矩陣
對角矩陣
矩陣加法
- 當兩個矩陣的行數、列數相同時,加法才具有意義!
- 做法:將每個相同位置的元素加起來
- 減法當然就是反過來囉
- 係數積:rA 的每個元素都是 A 裡面每個元素的 r 倍
小小的例題
ans:
矩陣乘法
- 對於 A x B,其中A為 \(m \times p\),B為 \(q \times n\),則我們定義
- 當 \(p = q\),也就是 A 的列數恰為 B 的行數, A x B 才有意義
- 有意義時,A x B 為 \(m \times n\) 的矩陣!
- 作法如下:
\(c_{11} = 1\times7 + 2\times(-1) = 5 \)
\(c_{12} = 1\times3 + 2\times1 = 5\)
對於 \(C = A \times B\),
\(c_{ij} = (A的第i列) \cdot (B的第j行) = \displaystyle\sum_{k=1}^{n} a_{ik}b_{kj}\)
矩陣乘法
- 有兩個矩陣 A, B 如下,則
- \(A \times B \in R^{2 \times 2}\)
- \(B \times A \in R^{3 \times 3}\)
- 看到這邊相信各位已經體悟到,矩陣乘法沒有交換律ㄛ
方程的矩陣形式
- 有了矩陣乘法,我們就可以把以下的方程組寫成矩陣了:
- 將這 9 個係數提出來變成矩陣,成為我們的係數矩陣 A
- 然後 x, y, z 三個未知數也形成了行向量 x
- 三行的解則形成了行向量 b
- 根據矩陣乘法的定義,我們可以很簡潔的將上面的方程組寫成:
單位矩陣
- 我們來介紹一個矩陣:
- 對於此矩陣\(I\),\(AI = A, IB = B\) 恆成立
單位矩陣
- 單位矩陣就是形如下面的方陣:
- 其中,我們可以 \(I_n\) 來表示 \(I\) 是 \(n\)的方陣
逆矩陣
- 對於實數,我們稱 \(a\) 和 \(\frac{1}{a}\) 互為倒數,其中 \(a \cdot \frac{1}{a} = 1\)
- 對於矩陣,如果我們有一個矩陣 B,可以使 \(AB = I\),其中 \(I\) 為單位矩陣,那麼 B 稱為 A 的逆矩陣,記為 \(A^{-1}\)
- 從上面的定義可以發現,只有方陣才有逆矩陣
- 經過運算,你可以發現 \(AB = I\) 且 \(BA = I\)
- 事實上,若一方陣 \(A\) 的逆矩陣為 \(B\),則 \(B\) 的逆矩陣也會是 \(A\)
- \((A^{-1})^{-1} = A\)
逆矩陣
- 一些逆矩陣的特性與存在的條件:
- 一個矩陣若有逆矩陣,則它是唯一的。
- 若 \(A\) 可逆,則 \(Ax = b\) 的唯一解是 \(x = A^{-1}b\)
- 若有一非零向量使 \(Ax = 0\),則 \(A\) 不可逆
- 對於一個 2 x 2 的矩陣,它的逆矩陣存在條件與計算:
- 對於實數,如果 \(a = 0\),那麼它沒有倒數
- 那矩陣呢?除了是方陣以外還有什麼限制?
如果 \(ad - bc \neq 0\),則此逆矩陣存在
逆矩陣
- 對於一個對角矩陣,如果它對角線上的元素皆不為零,則它有逆矩陣。
小小的例題
- 設 \(a \in \{-1, 1, 2, 3\} 且 \(b \in \{0, -1, 1, 2}\),試問
矩陣
無反方陣的機率?
ans: \(\frac{3}{8}\)

好欸沒ㄌ 感謝聆聽
- 如果各位對線性代數超級有興趣,推薦高二多元選修選這門課(但你可能要祈禱不要像我一樣選到第六志願的法語)
- 超級感謝多元選修就是選線性代數的格瑞格秋。就算他需要複習,還是願意每週都借我線性代數學資讓我參考。我好愛他,可以跟他原地結婚ㄇㄚ
- python 有一個 module 叫做 numpy,是一個可以操作向量與矩陣運算的模組,有興趣可以自己玩玩看!下學期的 python 課會有一堂課是在教這個,期待一下啦
- 有沒有發現用這個模板廢話會變超級多