向量、矩陣
Lecturer: 立葉
建北電資運算思維小社課 Lesson 5
Index
-
基礎定義
-
空間概念（帶過）
-
斜坐標系
-
向量內積
-
柯西不等式（好東西）
平面向量(vECTOR)
話說上兩次的運算思維小社課，我們提到了特殊三角比...
STORY TIME!
STORY TIME!
而在下課之後，我們可愛的酥育根跟章程+說：「你怎麼沒有教37-53-90的特殊三角比啊，這樣他們會像我一樣在物理課耍智障欸」
STORY TIME!
陳諒妍表示，這個東西只是估計值硬要講而已；章程甲也表示，這只會出現在物理，啊我又不教物理。
STORY TIME!
「啊我又不教物理？」
這個論述要破滅ㄌ
向量與我們的物理學息息相關ㄋ
雖然這堂課重心不會放在那 故事是白講ㄌ
What is 向量？
這是一個點。
當然，它本身並沒有所謂大小；有形狀只是為了讓你能看的到。
這是一條直線，它會無限延伸。
當然，它本身並沒有所謂寬度，有也只是為了讓你能看的到。
這是一條射線。
它會以一點作為起點，並往另一邊無限延伸。
這是一條線段。
它有兩個端點，但是沒有方向性。
最後就是我們這堂課要交的：向量！
它是一個有起點和終點，具有方向性的線段。
向量的基本性質！
- 向量由其 大小 和 方向 決定，不在意起點與終點。
- 向量的圖示：在起點和終點上面畫一個箭頭來表示，如：\(\overrightarrow{AB}\)。為了方便表示，也可以一個字母如 \(\overrightarrow{a}\) 來表示。
- 向量的量值：以\(|\overrightarrow{AB}|\)來表示。
- 特殊的向量：
- 反向量：若一向量與另一向量的量值相同而方向相反，則稱其互為反向量。
- 零向量：量值為零的向量，記為 \(\overrightarrow{0}\) 。其可視作任意方向。
- 在生活(aka 物理)上的應用：包括位移、速度、加速度、力等等，都是向量！
平面座標系上的向量
- 一般來說，我們會令一平面上的向量 \(\overrightarrow{a}\) 的起點為\((0, 0)\)
- 在這樣的情況時，令它的終點為\((x, y)\)
- 則我們可以將其表示為 \(\overrightarrow{a} = (x, y)\) 了呢！
- 當然，如果原點不是起點，那麼該向量為 (終點座標 - 起點座標)
- 從這種表示方式也可以很輕易地發現，一個向量的量值是\(\sqrt{x^2+y^2}\) 。
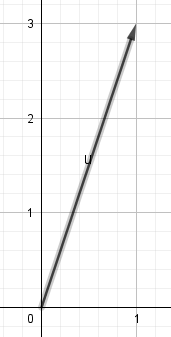
- 以左圖這個向量為例
- \(\overrightarrow{u} = (1, 3)\)
- \(|\overrightarrow{u}| = \sqrt{10}\)
向量的加減運算與係數積
- 設兩個向量 \(\overrightarrow{a} = (x_1, y_1), \overrightarrow{b} = (x_2, y_2)\) ，則：
- \(\overrightarrow{a} + \overrightarrow{b} = (x_1 + x_2, y_1+ y_2)\)
- \(\overrightarrow{a} - \overrightarrow{b} = (x_1 - x_2, y_1- y_2)\)
- \(r\overrightarrow{a} = (ra_1, ra_2)\)，其中\(r\)為實數
- 向量與向量的「乘法」？後面會提到！
向量加減的幾何意義
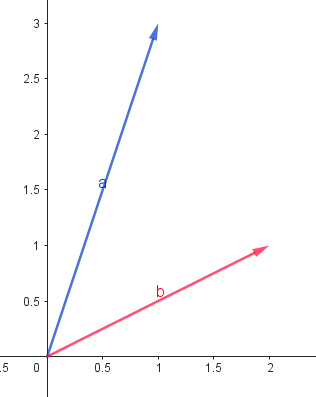
- 設兩個向量 \(\overrightarrow{a} = (1, 3), \overrightarrow{b} = (2, 1)\) 。我們來把它具象化一下：
- 而我們由上頁對於向量的加減定義可得知：
- \(\overrightarrow{a} + \overrightarrow{b} = (3, 4)\)
- \(\overrightarrow{a} - \overrightarrow{b} = (-1, 4)\)
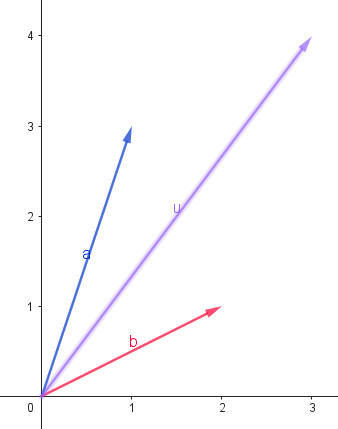
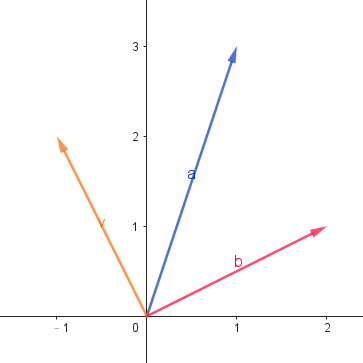
向量加減的幾何意義
- 仔細觀察它們的圖形，你可以發現：
- 兩個向量的加法就是物理課所謂「三角形平移法」或「四角形對角線法」的實現！(對名字我亂掰的
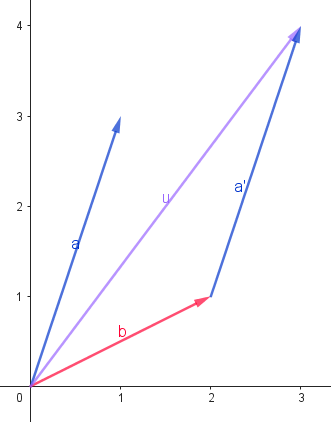
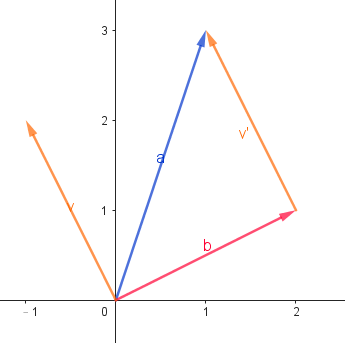
- 至於向量的減法，對於初學者可能較不直觀，但其實真的很直觀
- 設\(\overrightarrow{v} = \overrightarrow{a} - \overrightarrow{b}\)，我們稍微將這個式子平移一下，得到\(\overrightarrow{a} = \overrightarrow{b} + \overrightarrow{v}\)
- 所以這樣就變直觀ㄌ！
小小的例題
- 一個質點以速率 30 m/s的速度碰撞牆壁，並在 0.2 s 內以相同速率反射出去，如圖所示。請求出這顆球碰撞牆壁時所受到的加速度量值？
\(30\)
\(30\)
黃色線段 = \(\sqrt{30^2+30^2-2\times30\times30\times\cos120\degree} \\ = 30\sqrt{3}\)
ans: \(150\sqrt{3} m/s^2\)
向量間的關係
- 平行向量：
- 設兩個向量\(\overrightarrow{a} = (x_1, y_1), \overrightarrow{b} = (x_2, y_2)\)
- 則\(\overrightarrow{a} // \overrightarrow{b} \Leftrightarrow \overrightarrow{a} = r\overrightarrow{b} \)
- 單位向量(長度為1的向量)：
- \(\overrightarrow{a} = \pm |\overrightarrow{a}|\overrightarrow{e}\)
- \(\overrightarrow{e} = \pm\frac{\overrightarrow{a}}{|\overrightarrow{a}|}\)
向量的線性組合特性
- 在一平面座標上，設兩個向量\(\overrightarrow{a}，\overrightarrow{b}\)，若此兩向量不平行，則任一向量\(\overrightarrow{c}\)都可以 \(r\overrightarrow{a} + s\overrightarrow{b} \) 表示！
- 例如：
- 將向量\(\overrightarrow{c} = (-7, -1)\)表示成兩不平行向量\(\overrightarrow{a} = (1, -2)\)與\(\overrightarrow{b} = (-3, 1)\)的線性組合。
ans: \(\overrightarrow{c} = 2\overrightarrow{a} + 3\overrightarrow{b}\)
我們可以設 \(\overrightarrow{c} = r\overrightarrow{a} + s\overrightarrow{b}\)
接下來列二元一次聯立方程式，得到
\begin{aligned}
\begin{cases}
r-3s = -7 \\
-2r+s = -1 \\
\end{cases}
\end{aligned}
解方程式，得到 r=2, s=3
向量的線性組合
- 接下來，我們一樣把上一頁的東西具象化：
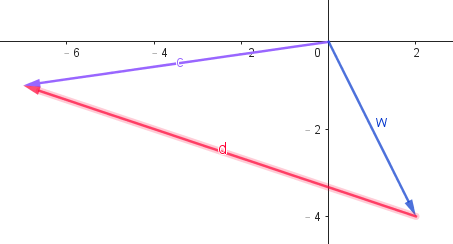
- 我們把它們分別改成 \(2\overrightarrow{a}\) 和 \(3\overrightarrow{b}\) ，並把\(3\overrightarrow{b}\) 稍微平移一下，就可以發現我們已經成功用這兩個向量表示\(\overrightarrow{c}\)了呢！
其實這頁目前沒什麼要講的，只是要告訴你它很漂亮順便埋個伏筆
向量與斜座標系統
- 事實上，我們可以使用兩個不平行的向量來創立一個新的斜座標系統！
- 令 \(\overrightarrow{a} = (1, 0)，\overrightarrow{b} = (0, 1)\)
- 那麼這時候 \(\overrightarrow{c} = x\overrightarrow{a} + y\overrightarrow{b}\) 的座標就是 \((x, y)\)
- 也可以從這個角度去發現 \(x\overrightarrow{a} + y\overrightarrow{b}\) 可以表示出平面上任一向量
- 不知道也不太會怎麼樣，但知道了會很有用
畫出來就像這樣！
小小的例題
- 以下是一個正六邊形ABCDEF，請以 \(\overline{AB} = \overrightarrow{a}\) 和 \(\overline{BC} = \overrightarrow{b}\) 表示 \(\overline{AE}\) 和 \(\overline{EC}\)。
A
B
C
D
E
F
O
ans:
\(\overrightarrow{AE} = -\overrightarrow{a} + 2\overrightarrow{b}\)
\(\overrightarrow{EC} = 2\overrightarrow{a} - \overrightarrow{b}\)
多維空間ㄉ向量
我原本想塞一點空間概念，但我沒時間- 對於一個 n 維的向量 \(\overrightarrow{v}\)，我們可以寫作 \(\overrightarrow{v} = R^n\)
- 然後對於這個向量 \(\overrightarrow{v}\)，它的座標是 \((a_1, a_2, \dotsb, a_n)\)，
量值是 \(\sqrt{\displaystyle\sum_{i=1}^{n} {a_i}^2}\)
向量內積
- 也就是「點積」！
- 向量內積是一個純量。
- 定義為 \(\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|\cos\theta = a_1b_1 + a_2b_2\)
- 對於超過三維的向量，我們只能以\(\overrightarrow{a} \cdot \overrightarrow{b} = \displaystyle\Sigma_{i=1}^{n} a_ib_i\)表示
- 在物理課中學到的功，就是力和位移的內積！
- 內積也是 \(\overrightarrow{a}\) 投影到 \(\overrightarrow{b}\) 的量值乘以 \(|\overrightarrow{b}|\)！
- 將 \(\overrightarrow{a}\) 投影到 \(\overrightarrow{b}\)，則：
- 其投影的向量量值為 \(\left(\frac{\overrightarrow{a} \cdot \overrightarrow{b} }{|\overrightarrow{b}|}\right)\)
- 其投影的向量本人為 \(\left(\frac{\overrightarrow{a} \cdot \overrightarrow{b} }{|\overrightarrow{b}|^2}\right)\overrightarrow{b}\)
小小的例題
- 已知三角形 ABC 的三邊長為 \(\overline{AB} = 7, \overline{BC}=5, \overline{CA} = 8\)，求
- \(\overrightarrow{AB} \cdot \overrightarrow{AC}\)
- \(\overrightarrow{AB} \cdot \overrightarrow{BC}\)
ans: 44; -5
忘記餘弦定理的點我(雖然那邊的簡報我做的很懶蛋)
柯西不等式
- 向量形式：
- \(|\overrightarrow{a}||\overrightarrow{b}| \geq |\overrightarrow{a} \cdot \overrightarrow{b}| = |\overrightarrow{a}||\overrightarrow{b}|\cos\theta\)
- 實數形式：
- \(({a_1}^2+{a_2}^2)({b_1}^2+{b_2}^2) \geq (a_1b_1 + a_2b_2)^2\)
- 其中等式成立於\(\frac{a_1}{a_2} = \frac{b_1}{b_2}\)
- 也能推廣到多維！
- \((\displaystyle\sum_{i=1}^{n} x_iy_i)^2\ \leq (\displaystyle\sum_{i=1}^{n} {x_i}^2)(\displaystyle\sum_{i=1}^{n} {y_i}^2)\)
- 等式成立於\(\frac{x_1}{y_1} = \frac{x_2}{y_2} = \dotsb = \frac{x_n}{y_n}\)
用柯西不等式來證明相關係數 \(r\) 的範圍!?
- 忘記相關係數的點我
- 我們知道 \(-1 \leq r \leq 1\)
- 我們的證明方式可以土法煉鋼，把所有東西展開（有時間我在之前的簡報會放證明）
- 而這邊可以用柯西不等式！
(\displaystyle\sum_{i=1}^{n} x_iy_i)^2\ \leq (\displaystyle\sum_{i=1}^{n} {x_i}^2)(\displaystyle\sum_{i=1}^{n} {y_i}^2) \\
\frac{(\displaystyle\sum_{i=1}^{n} x_iy_i)^2}{(\displaystyle\sum_{i=1}^{n} {x_i}^2)(\displaystyle\sum_{i=1}^{n} {y_i}^2) } \leq 1 \\
-1 \leq \frac{\displaystyle\sum_{i=1}^{n} x_iy_i}{\displaystyle\sum_{i=1}^{n} {x_i}\displaystyle\sum_{i=1}^{n} {y_i}} = \frac{S_{XY}}{\sqrt{S_{XX}}\sqrt{S_{YY}}} \leq 1 \\
小小的例題
- 設兩向量 \(\overrightarrow{a} = (x, y)\) 與 \(\overrightarrow{b} = (p, q)\)，若 \(|\overrightarrow{a}| = 2, |\overrightarrow{b}| = 6\)，求 \(px + qy\) 的最大值。
- 設 \(P(x, y) 為直線 \(L: 3x + 5y - 4 = 0\) 上的任一點，求 \(3x^2 + 5y^2\) 之最小值及此時數對 \((x, y)\)。
ans: 12
ans: 2；\((\frac{1}{2}, \frac{1}{2})\)
- 求 \(y = \sqrt{2x-1} + \sqrt{5-3x}\) 的最大值及此的 \(x\) 值。
ans: \(\sqrt{\frac{35}{6}}\)；\(x = \frac{29}{30}\)
向量的應用：重心公式
- 想必各位應該都還記得重心是什麼吧：）
- 我們從向量的角度去探討重心
- 三角形 ABC，我們設 \(A(a_1, a_2), B(b_1, b_2), C(c_1, c_2)\)，並設其重心為點G。
G(\frac{a_1+b_1+c_1}{3}, \frac{a_2+b_2+c_2}{3}) \\
\overrightarrow{OG} = \frac{1}{3}\overrightarrow{OA} + \frac{1}{3}\overrightarrow{OB} + \frac{1}{3}\overrightarrow{OC} \\
\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0} \\
1)
2)
3)
向量的應用：兩向量所張的平行四邊形的面積
- 從之前學到的正弦定理，我們知道
- 三角形 ABC 的面積為 \(\frac{1}{2} bc\sin\theta\)
- 從另一個角度來看，我們可以把其中兩個邊長設為 \(\overrightarrow{AB}, \overrightarrow{AC}\)
- 那麼，由這兩個向量所張出的平行四邊形面積就是 \(bc \sin \theta\)！
- 那麼就會有以下的式子：
\(|\overrightarrow{a}||\overrightarrow{b}|\sin\theta\)
= \(|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-\cos^2\theta}\)
= \(\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-|\overrightarrow{a}|^2|\overrightarrow{b}|^2\cos^2\theta}\)
= \(\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a} \cdot \overrightarrow{b})^2}\)
-
二階與三階行列式
-
二 / 三元一次方程式克拉瑪公式
-
向量外積
-
平行四面形 / 平行六面體
行列式
二階行列式
\begin{vmatrix}
a & b \\
c & d \\
\end{vmatrix}
= ad - bc
- 一些雜七雜八性質：
- 行列互換，值不變
- 兩行 / 兩列互換，值變號
- 任一行 / 列，可提出公因數
- 任一行 / 列乘以 \(r\) 並加到另一行 / 列，其值不變
- 可以拆項
\begin{vmatrix}
a_1 & b_1 \\
a_2 & b_2 \\
\end{vmatrix}
=
\begin{vmatrix}
a_1 + rb_1 & b_1 \\
a_2 + rb_2 & b_2 \\
\end{vmatrix}
\begin{vmatrix}
a_1 & b_1 \\
a_2 & b_2 \\
\end{vmatrix}
=
\begin{vmatrix}
a_1 + ra_2 & b_1 + rb_2 \\
a_2 & b_2 \\
\end{vmatrix}
\begin{vmatrix}
a_1 & b_1 + c_1 \\
a_2 & b_2 + c_2 \\
\end{vmatrix}
=
\begin{vmatrix}
a_1 & b_1 \\
a_2 & b_2 \\
\end{vmatrix}
+
\begin{vmatrix}
a_1 & c_1 \\
a_2 & c_2 \\
\end{vmatrix}
小小的例題
\begin{vmatrix}
2021 & 110 \\
2022 & 111 \\
\end{vmatrix}
- 請算出以下行列式的值：
\begin{vmatrix}
\sqrt{5}+\sqrt{11}+\sqrt{17} & \sqrt{11} \\
\sqrt{5}+\sqrt{11}-\sqrt{17} & \sqrt{5}+\sqrt{17} \\
\end{vmatrix}
1)
2)
\begin{vmatrix}
2021 & 110 \\
2022 & 111 \\
\end{vmatrix}
= 1911
\begin{vmatrix}
\sqrt{5}+\sqrt{11}+\sqrt{17} & \sqrt{11} \\
\sqrt{5}+\sqrt{11}-\sqrt{17} & \sqrt{5}+\sqrt{17} \\
\end{vmatrix}
= -23
- 若
\begin{vmatrix}
a & b \\
c & d \\
\end{vmatrix}
= 2015
，求
\begin{vmatrix}
2a & 2b \\
2c & 2d \\
\end{vmatrix}
+
\begin{vmatrix}
c & 2c + 3d \\
a & 2a + 3b \\
\end{vmatrix}
？
ans: 2015
行列式的應用：平行四邊形的面積
- 設向量 \(\overrightarrow{a} = (a_1, a_2), \overrightarrow{b} = (b_1, b_2)\)，則由 \(\overrightarrow{a}\) 和 \(\overrightarrow{b}\) 所張成的平行四邊形面積為：
|\begin{vmatrix}
a_1 & b_1 \\
a_2 & b_2 \\
\end{vmatrix}|
對ㄚ我就懶得排版
\begin{aligned}
\begin{matrix}
& = \sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2 - (\overrightarrow{a} \cdot \overrightarrow{b})^2} \\
& = \sqrt{({a_1}^2+{a_2}^2)({b_1}^2+{b_2}^2)-(a_1a_2+b_1b_2)^2} \\
& = \sqrt{({a_1}^2{a_2}^2+{a_1}^2{b_2}^2+{a_2}^2{b_1}^2+{a_2}^2{b_2}^2)-({a_1}^2{a_2}^2+2a_1a_2b_1b_2+{b_1}^2{b_2}^2)} \\
& = \sqrt{{a_1}^2{b_2}^2-{a_2}^2{b_1}^2-2a_1a_2b_1b_2} \\
& = \sqrt{(a_1b_2-a_2b_1)^2} \\
& = |\begin{vmatrix}
a_1 & b_1 \\
a_2 & b_2 \\
\end{vmatrix}
| \\
\end{matrix}
\end{aligned}
要看ㄉ自己看
二元一次聯立方程式克拉瑪公式
- 我們在此定義三個東西：
\begin{aligned}
\begin{cases}
a_1x + b_1y = c_1 \\
a_2x + b_2y = c_2 \\
\end{cases}
\end{aligned}
\Delta =
\begin{vmatrix}
a_1 & b_1\\
a_2 & b_2\\
\end{vmatrix}
\Delta_x =
\begin{vmatrix}
c_1 & b_1\\
c_2 & b_2\\
\end{vmatrix}
\Delta_y =
\begin{vmatrix}
a_1 & c_1\\
a_2 & c_2\\
\end{vmatrix}
- 使用 \(\Delta\) 來判斷x, y的解情況！
- \(\Delta \neq 0\)，則x, y有唯一解
- \(\Delta = 0\)，則再分成兩種情況：
- \(\Delta_x, \Delta_y = 0\)，則x, y有無限多組解
- \(\Delta_x, \Delta_y\)有任一不為0，則x, y無解
- 若 \(\Delta \neq 0\)，則：
- \(x = \frac{\Delta_x}{\Delta}\)
- \(y = \frac{\Delta_y}{\Delta}\)
三階行列式
\begin{vmatrix}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3 \\
\end{vmatrix}
\\ = a_1b_2c_3 + b_1c_2a_3 + c_1a_2b_3
\\ - a_3b_2c_1 - b_3c_2a_1 - c_3a_2b_1
\begin{matrix}
a_1 & b_1 & c_1 & a_1 & b_1 \\
a_2 & b_2 & c_2 & a_2 & b_2 \\
a_3 & b_3 & c_3 & a_3 & b_3 \\
\end{matrix}
三階行列式的性質
- 基本上都跟二階行列式一樣
- 三階行列式降階成為二階：依據某一行 / 列！
\begin{vmatrix}
+ & - & + \\
- & + & - \\
+ & - & + \\
\end{vmatrix}
\begin{vmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{vmatrix}
\begin{vmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{vmatrix}
=
-4\begin{vmatrix}
2 & 3 \\
8 & 9 \\
\end{vmatrix}
\begin{vmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{vmatrix}
=
-4\begin{vmatrix}
2 & 3 \\
8 & 9 \\
\end{vmatrix}
+
5\begin{vmatrix}
1 & 3 \\
7 & 9 \\
\end{vmatrix}
\begin{vmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{vmatrix}
=
-4\begin{vmatrix}
2 & 3 \\
8 & 9 \\
\end{vmatrix}
+
5\begin{vmatrix}
1 & 3 \\
7 & 9 \\
\end{vmatrix}
-6\begin{vmatrix}
1 & 2 \\
7 & 8 \\
\end{vmatrix}
變號的時候要依據這張表格
用處？
計算形如
\begin{vmatrix}
0 & 1 & 3 \\
0 & 2 & 4 \\
1001 & 107 & 789 \\
\end{vmatrix}
的三階行列式會方便很多
三元一次聯立方程式克拉瑪公式
- 我們在此定義四個東西：
\begin{aligned}
\begin{cases}
a_1x + b_1y + c_1z = d_1 \\
a_2x + b_2y + c_2z= d_2 \\
a_3x + b_3y + c_3z = d_3 \\
\end{cases}
\end{aligned}
\Delta =
\begin{vmatrix}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_3 \\
a_3 & b_3 & c_3 \\
\end{vmatrix}
- 使用 \(\Delta\) 來判斷x, y, z的解情況！
- \(\Delta \neq 0\)，則x, y, z有唯一解
- \(\Delta = 0\)，則再分成兩種情況：
- \(\Delta_x, \Delta_y, \Delta_z = 0\)，則x, y, z 可能無解，也可能無限多組解
- \(\Delta_x, \Delta_y\, \Delta_z\)有任一不為0，則x, y, z 無解
- 若 \(\Delta \neq 0\)，則：
- \(x = \frac{\Delta_x}{\Delta}\)
- \(y = \frac{\Delta_y}{\Delta}\)
- \(z = \frac{\Delta_z}{\Delta}\)
\Delta_x =
\begin{vmatrix}
d_1 & b_1 & c_1 \\
d_2 & b_2 & c_3 \\
d_3 & b_3 & c_3 \\
\end{vmatrix}
\Delta_y =
\begin{vmatrix}
a_1 & d_1 & c_1 \\
a_2 & d_2 & c_3 \\
a_3 & d_3 & c_3 \\
\end{vmatrix}
\Delta_z =
\begin{vmatrix}
a_1 & b_1 & d_1 \\
a_2 & b_2 & d_3 \\
a_3 & b_3 & d_3 \\
\end{vmatrix}
結論：使用克拉瑪公式解聯立方程式不一定比較方便。
但它判斷解數的情況比較快速
向量外積
- 是一個向量，只有在空間中才有辦法定義！
- 寫法為 \(\times\)
- 為 \(\overrightarrow{a}\) 和 \(\overrightarrow{b}\) 的公垂向量，姑且設它為 \(\overrightarrow{n} = (x, y, z)\)
- 根據內積，我們可以得到下面這個聯立方程式：
\begin{aligned}
\begin{cases}
x_1x + y_1y + z_1z = 0 \\
x_2x + y_2y + z_2z = 0 \\
\end{cases}
\end{aligned}
- 然後根據上面二元一次方程式的克拉瑪公式，整理可得到：
\begin{aligned}
\begin{cases}
x_1x + y_1y = -z_1z \\
x_2x + y_2y = -z_2z \\
\end{cases}
\end{aligned}
x:y:z
=\begin{vmatrix}
y_1 & z_1 \\
y_2 & z_2 \\
\end{vmatrix}
:\begin{vmatrix}
z_1 & x_1 \\
z_2 & x_2 \\
\end{vmatrix}
:\begin{vmatrix}
x_1 & y_1 \\
x_2 & y_2 \\
\end{vmatrix}
\overrightarrow{n}
=k(\begin{vmatrix}
y_1 & z_1 \\
y_2 & z_2 \\
\end{vmatrix}
, \begin{vmatrix}
z_1 & x_1 \\
z_2 & x_2 \\
\end{vmatrix}
, \begin{vmatrix}
x_1 & y_1 \\
x_2 & y_2 \\
\end{vmatrix})
- 向量外積定義為 \(k=1\) 時的 \(\overrightarrow{n}\)
- 方向性：右手法則
- 物理課學到的力矩，就是一種外積！
空間中兩向量所張成的面積
- 在前面，我們有提到兩向量所張成的平行四邊形面積
- 而在空間中，我們可以把這個式子化成
- 然後你就會發現 :flushed:
\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2 - (\overrightarrow{a} \cdot \overrightarrow{b})^2} \\
=\sqrt{(\begin{vmatrix}
y_1 & z_1 \\
y_2 & z_2 \\
\end{vmatrix})^2
+ (\begin{vmatrix}
z_1 & x_1 \\
z_2 & x_2 \\
\end{vmatrix})^2
+ (\begin{vmatrix}
x_1 & y_1 \\
x_2 & y_2 \\
\end{vmatrix})^2
}
\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2 - (\overrightarrow{a} \cdot \overrightarrow{b})^2}
\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2 - (\overrightarrow{a} \cdot \overrightarrow{b})^2} \\
=\sqrt{(\begin{vmatrix}
y_1 & z_1 \\
y_2 & z_2 \\
\end{vmatrix})^2
+ (\begin{vmatrix}
z_1 & x_1 \\
z_2 & x_2 \\
\end{vmatrix})^2
+ (\begin{vmatrix}
x_1 & y_1 \\
x_2 & y_2 \\
\end{vmatrix})^2
} \\
= |\overrightarrow{a} \times \overrightarrow{b}|
\(\overrightarrow{a}\)
\(\overrightarrow{b}\)
\(\overrightarrow{a} \times \overrightarrow{b}\)
空間中三向量所張成的平行六面體體積
- 延續上頁，所以我們的平行四邊形面積其實可以一個向量 \(\overrightarrow{t} = \overrightarrow{a} \times \overrightarrow{b}\) 表示
- 這時候，體積 = 底面積 \(\times\) 高
- 我們的高可以 \(|\overrightarrow{c}| \cos\theta\) 表示
\(\overrightarrow{a}\)
\(\overrightarrow{b}\)
\(\overrightarrow{c}\)
|(\overrightarrow{a} \times \overrightarrow{b}) \cdot \overrightarrow{c}|
\\ = |(\begin{vmatrix}
y_1 & z_1 \\
y_2 & z_2 \\
\end{vmatrix}
, \begin{vmatrix}
z_1 & x_1 \\
z_2 & x_2 \\
\end{vmatrix}
, \begin{vmatrix}
x_1 & y_1 \\
x_2 & y_2 \\
\end{vmatrix})
\cdot
(x_3, y_3, z_3)|\\
= |\begin{vmatrix}
x_1 & y_1 & z_1 \\
x_2 & y_2 & z_2 \\
x_3 & y_3 & z_3 \\
\end{vmatrix}|
- 體積 =\(||\overrightarrow{t}||\overrightarrow{c}|\cos\theta| = |\overrightarrow{t} \cdot \overrightarrow{c}| = |(\overrightarrow{a} \times \overrightarrow{b}) \cdot \overrightarrow{c}|\)
- 然後把所有的行列式都帶進來，你可以得到：
-
What is 線性代數?
-
矩陣的基本定義與運算
-
各種矩陣
矩陣
線性代數
- 用個前面放的二元一次聯立方程式
\begin{aligned}
\begin{cases}
x-3y = -7 \\
-2x+y = -2
\end{cases}
\end{aligned}
- 它有兩種幾何意義：
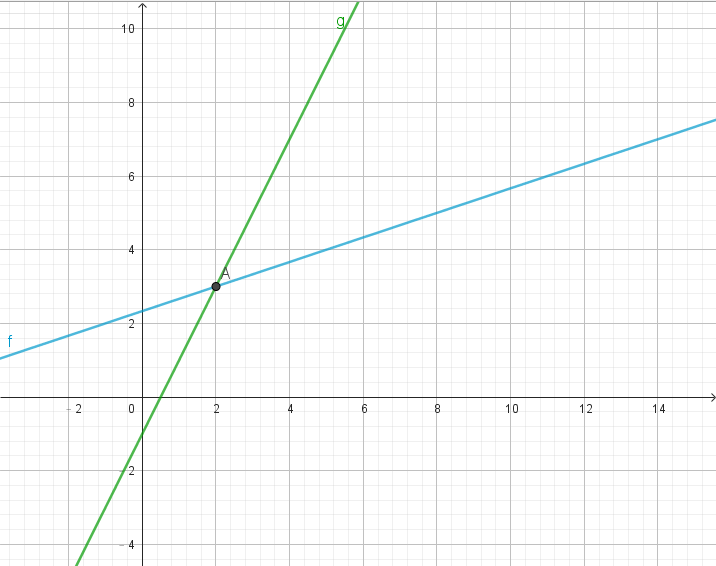
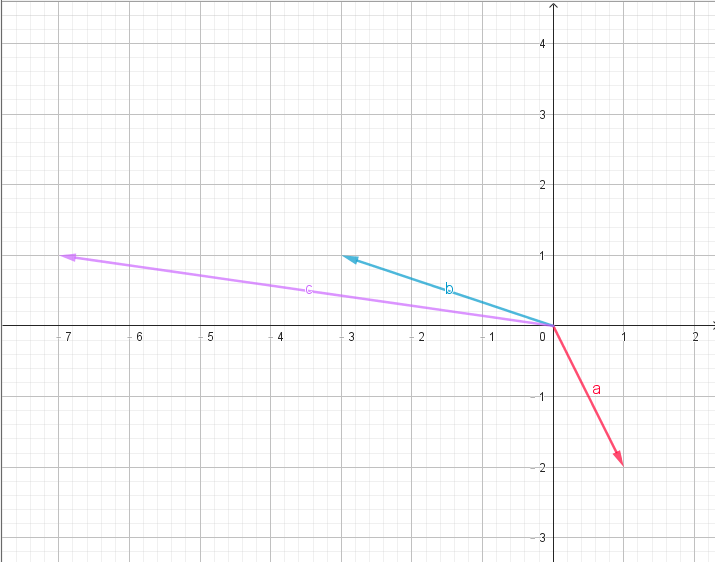
列的圖像
行的圖像
線性代數
\begin{aligned}
\begin{cases}
x-3y = -7 \\
-2x+y = -2
\end{cases}
\end{aligned}
行的圖像
x\begin{bmatrix}
1 \\
-2 \\
\end{bmatrix}
+y\begin{bmatrix}
-3 \\
1 \\
\end{bmatrix}
=\begin{bmatrix}
-7 \\
2 \\
\end{bmatrix}
線性組合
矩陣
- 把一群數字 / 文字排成矩形陣列
- 表示法：
A = \begin{bmatrix}
a_{11} & a_{12} & \dotsb & a_{1n} \\
a_{21} & a_{22} & \dotsb & a_{2n} \\
\dotsb & \dotsb & & \dotsb \\
a_{m1} & a_{m2} & \dotsb & a_{mn} \\
\end{bmatrix}
或簡記為
A = [a_{ij}]_{m \times n}
其中在第 \(i\) 列和第 \(j\) 行的元素為 \(a_{ij}\)
- 同階矩陣：列數、行數皆相同的兩個矩陣
- 矩陣相等：列數、行數相同，且所含元素也相同
各種矩陣
- 方陣：列數、行數相同
- 列矩陣： \(m=1\) / 行矩陣：\(n=1\)
- 轉置矩陣：將 A 行列互換，記為 \(A^T\)
- 對稱方陣：\(A = A^T\)
- 反對稱方陣：\(A = -A^T\)
- 三角矩陣：上三角、下三角、對角
\begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{bmatrix}
2 x 2 方陣
3 x 3 方陣
v = \begin{bmatrix}
11 \\
21 \\
31 \\
\end{bmatrix}
列矩陣 / 行矩陣可以視為列向量 / 行向量
如右圖所示
它是三維向量
也是 3 x 1 的矩陣
\(R^n = R^{n\times1}\)
v = \begin{bmatrix}
11 & 12 & 13\\
21 & 22 & 23\\
31 & 32 & 33\\
\end{bmatrix}
可以把矩陣視為向量的組合體！
列向量 \(\overrightarrow{A_1}\)
列向量 \(\overrightarrow{A_2}\)
列向量 \(\overrightarrow{A_3}\)
v = \begin{bmatrix}
\overrightarrow{A_1}\\
\overrightarrow{A_2}\\
\overrightarrow{A_3}\\
\end{bmatrix}
可以寫成這樣！
A = \begin{bmatrix}
1 & 2 \\
3 & 4 \\
5 & 6 \\
\end{bmatrix}
A^T = \begin{bmatrix}
1 & 3 & 5 \\
2 & 4 & 6 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 5 \\
2 & 0 & 7 \\
5 & 7 & 8 \\
\end{bmatrix}
\begin{bmatrix}
0 & 2 & 5 \\
-2 & 0 & 7 \\
-5 & -7 & 0 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 3 \\
0 & 4 & 5 \\
0 & 0 & 6 \\
\end{bmatrix}
上三角矩陣
\begin{bmatrix}
1 & 0 & 0 \\
2 & 3 & 0 \\
4 & 5 & 6 \\
\end{bmatrix}
下三角矩陣
\begin{bmatrix}
1 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 3 \\
\end{bmatrix}
對角矩陣
矩陣加法
- 當兩個矩陣的行數、列數相同時，加法才具有意義！
- 做法：將每個相同位置的元素加起來
- 減法當然就是反過來囉
- 係數積：rA 的每個元素都是 A 裡面每個元素的 r 倍
\begin{bmatrix}
1 & 5 \\
4 & 7 \\
\end{bmatrix}
+
\begin{bmatrix}
2 & 5 \\
7 & -2 \\
\end{bmatrix}
=
\begin{bmatrix}
3 & 10 \\
11 & 5 \\
\end{bmatrix}
3\begin{bmatrix}
1 & 5 \\
4 & -7 \\
\end{bmatrix}
=
\begin{bmatrix}
3 & 15 \\
12 & -21 \\
\end{bmatrix}
小小的例題
A = [a_{ij}]_{2\times2}，a_{ij} = i+j\\
B = [b_{ij}]_{2\times2}，b_{ij} = i-j\\
C = [c_{ij}]_{2\times2}，c_{ij} = i\times j\\
A + B - C = ? \\
ans:
\begin{bmatrix}
1 & 0 \\
2 & 0 \\
\end{bmatrix}
矩陣乘法
- 對於 A x B，其中A為 \(m \times p\)，B為 \(q \times n\)，則我們定義
- 當 \(p = q\)，也就是 A 的列數恰為 B 的行數， A x B 才有意義
- 有意義時，A x B 為 \(m \times n\) 的矩陣！
- 作法如下：
\begin{bmatrix}
1 & 2 \\
3 & -2 \\
5 & 1 \\
\end{bmatrix}
\begin{bmatrix}
7 & 3 \\
-1 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
5 & 5 \\
23 & 7 \\
34 & 16 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 \\
3 & -2 \\
5 & 1 \\
\end{bmatrix}
\begin{bmatrix}
c_{11} & c_{12} \\
c_{21} & c_{22} \\
c_{31} & c_{32} \\
\end{bmatrix}
\begin{bmatrix}
7 & 3 \\
-1 & 1 \\
\end{bmatrix}
\(c_{11} = 1\times7 + 2\times(-1) = 5 \)
\(c_{12} = 1\times3 + 2\times1 = 5\)
對於 \(C = A \times B\)，
\(c_{ij} = (A的第i列) \cdot (B的第j行) = \displaystyle\sum_{k=1}^{n} a_{ik}b_{kj}\)
矩陣乘法
- 有兩個矩陣 A, B 如下，則
A = \begin{bmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32} \\
\end{bmatrix}
B = \begin{bmatrix}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23} \\
\end{bmatrix}
- \(A \times B \in R^{2 \times 2}\)
- \(B \times A \in R^{3 \times 3}\)
- 看到這邊相信各位已經體悟到，矩陣乘法沒有交換律ㄛ
方程的矩陣形式
- 有了矩陣乘法，我們就可以把以下的方程組寫成矩陣了：
\begin{aligned}
\begin{cases}
1x + 2y + 3z = 6 \\
2x + 5y + 2z = 4 \\
6x - 3y + 1z = 2 \\
\end{cases}
\end{aligned}
A = \begin{bmatrix}
1 & 2 & 3 \\
2 & 5 & 2 \\
6 & -3 & 1\\
\end{bmatrix}
x= \begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
- 將這 9 個係數提出來變成矩陣，成為我們的係數矩陣 A
- 然後 x, y, z 三個未知數也形成了行向量 x
- 三行的解則形成了行向量 b
- 根據矩陣乘法的定義，我們可以很簡潔的將上面的方程組寫成：
b = \begin{bmatrix}
6 \\
4 \\
2 \\
\end{bmatrix}
Ax = b
單位矩陣
- 我們來介紹一個矩陣：
I = \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
- 對於此矩陣\(I\)，\(AI = A, IB = B\) 恆成立
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
4 \\
5 \\
6 \\
\end{bmatrix}
=
\begin{bmatrix}
4 \\
5 \\
6 \\
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
4 \\
5 \\
6 \\
\end{bmatrix}
單位矩陣
- 單位矩陣就是形如下面的方陣：
I = \begin{bmatrix}
1 & 0 & \dotsb & 0 \\
0 & 1 & \dotsb & 0 \\
\dotsb & \dotsb & \ddots & \dotsb \\
0 & 0 & \dotsb & 1 \\
\end{bmatrix}
- 其中，我們可以 \(I_n\) 來表示 \(I\) 是 \(n\)的方陣
I_1 = \begin{bmatrix}
1 \\
\end{bmatrix}
,
I_2 = \begin{bmatrix}
1 & 0 \\
0 & 1 \\
\end{bmatrix}
,
I_3 = \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
, \dotsb
逆矩陣
- 對於實數，我們稱 \(a\) 和 \(\frac{1}{a}\) 互為倒數，其中 \(a \cdot \frac{1}{a} = 1\)
- 對於矩陣，如果我們有一個矩陣 B，可以使 \(AB = I\)，其中 \(I\) 為單位矩陣，那麼 B 稱為 A 的逆矩陣，記為 \(A^{-1}\)
- 從上面的定義可以發現，只有方陣才有逆矩陣
A = \begin{bmatrix}
2 & 3 \\
5 & 7 \\
\end{bmatrix}
B = \begin{bmatrix}
-7 & 3 \\
5 & -2 \\
\end{bmatrix}
- 經過運算，你可以發現 \(AB = I\) 且 \(BA = I\)
- 事實上，若一方陣 \(A\) 的逆矩陣為 \(B\)，則 \(B\) 的逆矩陣也會是 \(A\)
- \((A^{-1})^{-1} = A\)
逆矩陣
- 一些逆矩陣的特性與存在的條件：
- 一個矩陣若有逆矩陣，則它是唯一的。
- 若 \(A\) 可逆，則 \(Ax = b\) 的唯一解是 \(x = A^{-1}b\)
- 若有一非零向量使 \(Ax = 0\)，則 \(A\) 不可逆
- 對於一個 2 x 2 的矩陣，它的逆矩陣存在條件與計算：
- 對於實數，如果 \(a = 0\)，那麼它沒有倒數
- 那矩陣呢？除了是方陣以外還有什麼限制？
\begin{bmatrix}
a & b \\
c & d \\
\end{bmatrix}
=
\frac{1}{ad-bc}
\begin{bmatrix}
d & -b \\
-c & a \\
\end{bmatrix}
如果 \(ad - bc \neq 0\)，則此逆矩陣存在
逆矩陣
- 對於一個對角矩陣，如果它對角線上的元素皆不為零，則它有逆矩陣。
A = \begin{bmatrix}
d_1 & & \\
& \dotsb & \\
& & d_n
\end{bmatrix}
, d_1, d_2, \dotsb, d_n \neq 0\\，則
A^{-1} =
\begin{bmatrix}
\frac{1}{d_1} & & \\
& \dotsb & \\
& & \frac{1}{d_n} \\
\end{bmatrix}
\begin{bmatrix}
2 & 0 \\
0 & 3 \\
\end{bmatrix}^{-1}
= \begin{bmatrix}
\frac{1}{2} & 0 \\
0 & \frac{1}{3} \\
\end{bmatrix}
小小的例題
\begin{bmatrix}
a & a^2 \\
b^2 & b \\
\end{bmatrix}
- 設 \(a \in \{-1, 1, 2, 3\} 且 \(b \in \{0, -1, 1, 2}\)，試問
矩陣
無反方陣的機率？
ans: \(\frac{3}{8}\)
好欸沒ㄌ 感謝聆聽
- 如果各位對線性代數超級有興趣，推薦高二多元選修選這門課（但你可能要祈禱不要像我一樣選到第六志願的法語）
- 超級感謝多元選修就是選線性代數的格瑞格秋。就算他需要複習，還是願意每週都借我線性代數學資讓我參考。我好愛他，可以跟他原地結婚ㄇㄚ
- python 有一個 module 叫做 numpy，是一個可以操作向量與矩陣運算的模組，有興趣可以自己玩玩看！下學期的 python 課會有一堂課是在教這個，期待一下啦
- 有沒有發現用這個模板廢話會變超級多