圖論[2]

Graph Theory[2]

INFOR 36th. @小海_夢想特急_夢城前

Index

連通性

連通分量

講師

225 賴柏宇
海之音、小海或其他類似的
美術能力見底
表達能力差，不懂要問
INFOR 36th 學術長
~~這頁是偷來的~~
不會圖論所以來當圖論講師

BrineTW 的簡報

Reference

8e7 的簡報

FHVirus 的簡報

劉澈的簡報

資芽

維基百科

本次的講師很弱
本次提供的範例 Code 可能有誤，請見諒
為了提高可讀性，拆成很多函式以及回傳值處理，有時會導致常數較大，請自行修改
表達能力很差，所以聽不懂一定一定要問
講師永遠不會放棄你 ~~啊對保有最終解釋權人很ㄐㄅ不在此範圍~~
簡報或我的觀念可能有誤，歡迎隨時糾正
有些奇怪的連結是我推薦的歌.jpg (不是 Rickroll...)

聲明

連通性

Connectivity.

剛剛用最小生成樹架出來的網路只要一條線斷了就沒了喔
或者，只要一個點爛掉就什麼都沒了
耐受性 / 連通強度？
- 如果損失幾個據點，其他點仍能連通
- 損失幾條邊，所有點仍能連通

繼續架網路

剛剛用最小生成樹架出來的網路只要一條線斷了就沒了喔
或者，只要一個點爛掉就什麼都沒了
耐受性 / 連通強度？
- 如果損失幾個據點，其他點仍能連通
  - 點連通度
- 損失幾條邊，所有點仍能連通
  - 邊連通度

繼續架網路

一般情況下，我們希望連通度
但某些情況下連通度 = 1
每個點 / 邊被拔掉都會使此圖不連通嗎？
我們希望有演算法能找出這些弱點

找出弱點

\geq 2

割
- 沿用前面的定義，將一個點集分割成多個不連通的子集
割點：點使點集分割成多個不連通的子集
又稱關節點
如何求所有的割點？

割點 Cut Vertex

「我是你今晚的噩夢。」

「參加這社團就別想逃過我的魔爪。」

Tarjan

– Robert Endre Tarjan,
沒有說過

「不少他發明的算法都以他的名字命名，以至於有時會讓人混淆幾種不同的算法。」

– 維基百科

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？

DFS Tree

首先介紹一個討論連通度時強大的工具 - DFS Tree
什麼是 DFS Tree？
看出來了嗎？
DFS 的軌跡不會經過相同的點，無環是樹

為邊做分類

樹邊：DFS Tree 中的邊

返祖邊：剩下不是樹邊的邊

觀察性質

看完邊後來看點和邊的關係
割點在哪裡？

觀察性質

看完邊後來看點和邊的關係
割點在哪裡？

觀察性質

思考「被拔除後會變成多個不連通塊」的性質
不連通代表不能從一邊走到令一邊
子樹只能透過它的根走到另一邊
- 什麼情況下不會發生？
- 返祖邊！

如何尋找返祖邊？
思考 DFS 的過程
- 如果戳到的是新的點，一定是樹邊
- 如果戳到的是重複的點，一定是返祖邊
要怎麼利用返祖邊？

返祖邊

什麼情況下返祖邊能發揮作用？
只要子樹中的所有點都能走到圖的另一個部分，這個點就不是割點，否則它是割點

返祖邊

因為左邊沒有邊能不經過紅點到達右邊，所以它是割點

因為左右邊所有點都能不經過紅點到達彼此，所以它不是割點

以紅點為根的子樹中，左邊一定要經過紅點到達其他部分

所以紅點是割點

以紅點為根的子樹中所有點都可以不經由紅點連到其他部分，所以它不是割點

如何利用以上性質？
暴力？
- 對於子樹中的每個點都確認一次是否連通？
- 想太多，單點複雜度就
我們可以考慮 ~~樹 DP~~ 記錄一些事情

實作

O(|V|^2+|V||E|)

一條返祖邊可能會改變哪些點是割點的性質？
- 較高者/深度較淺者到另一者間的點

再次觀察

這些點在 DFS Tree 上有什麼特性？
- 出點一定在出較低點後，入點一定在較低點前
- 換句話說，我們一定能在遞迴返回的時候更新到它們

再次觀察

所以，有必要急著更新嗎？
我們不如把子樹處理完再處理較高的點吧
現在滿足怎樣的情況這點會變得不是割點？
- 子樹能連到比自己時間戳還小的點
- 那我們記錄子樹時間戳最小能連到哪吧
子樹處理完後怎麼轉移回子樹的根節點
- 對於根節點來說，從分支挑一個最小的就行了
- 注意不能用親代的樹邊更新

Tarjan 割點算法

剛剛講得好像很有道理，但有一個例外
- 根節點
- 這個點是我們選定的，所以好像很正常？
- 怎麼判斷？再做一次 DFS 嗎？

例外

不是割點的情況：所有分支都相連？
- 在 DFS 的過程中，回到根時所有點都已經被拜訪過一次了
- 所以它只會往下一次 / 只有一個子節點

Case: root

你會發現，你的 DFS 樹應該長這樣

而非這樣

DFS，對每點記錄 DFS 序 (dfn)
- 對於每個子樹，記錄它能走到的最小 dfn (low)
  - 對於每條邊，更新自己的 low
- 使用每個分支的答案更新自己的答案
特判根節點的子節點數
對於每個點 u，如果 low(u) < dfn(u)，則它不是割點
複雜度同 DFS，

總結過程

O(|V|+|E|)

using Graph = vector<vector<int>>;

vector<bool> cut_vertex(const Graph &graph) {
    int n = graph.size();
    vector<int> dfn(n, 0), low(n, 0);
    vector<bool> result(n, false);
    int time = 0;

    auto dfs = [&](int cur, int pre, auto &&dfs) -> void {
        dfn[cur] = low[cur] = ++time;
        for (const int &nxt : graph[cur]) {
            if (nxt == pre) continue;

            if (dfn[nxt]) {
                low[cur] = min(low[cur], dfn[nxt]);
            }
            else {
                dfs(nxt, cur, dfs);
                if (low[nxt] >= dfn[cur]) result[cur] = true;
                low[cur] = min(low[cur], dfn[nxt]);
            }
        }
    };

    int child_count = 0;
    dfn[0] = ++time;
    for (const auto &child : graph[0]) {
        if (dfn[child]) continue;
        child_count++;
        dfs(child, 0, dfs);
    }
    if (child_count > 1) result[0] = true;

    return result;
}

剛剛討論完被拔掉點會不連通的割點，現在我們想要被拔掉會不連通的邊
這種邊我們叫橋
聽起來就很像割點，有關係嗎？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？

Edge

看不出來？
弄成 DFST 的樣子？
　　：割點、割邊
　　：其他點、樹邊
　　：返祖邊

Edge

你會發現，它和割點具有的性質簡直一模一樣
對，所以基本上照抄割點的就行了，還不用特判根節點
一個小地方要改掉：low(u) > dfn(u) 才能保證它是橋，其中 u 是起點
一樣注意在更新 low 的時候不能用它的親代更新

相似？

連通分量

Components.

一張圖可以互相連在一起的部分就叫連通分量
如果不能再向外連更多點，稱為極大連通分量，一般都討論極大連通分量
某些定義在有向圖上可能需要調整或有多種定義，所以先記得它是圖的某部分就行

連通分量

就是一般的連通分量，用前面教的 DSU 就做完了，沒要求加邊也可以用 DFS

單連通分量

「我是你今晚的噩夢。」

「參加資讀就別想逃過我的魔爪。」

Tarjan

– Robert Endre Tarjan,
沒有說過

「不少他發明的算法都以他的名字命名，以至於有時會讓人混淆幾種不同的算法。」

– 維基百科

Bridge Connected Components, BCC
記得前面講的連通度嗎？
- 連通度 > 1 時網路可抗破壞！
我們不如把這些拔掉任一點都還是連通的子區域劃分在同一個連通分量！
怎麼找？
- 找到橋後將所有東西分開
- 把連通分量的點們「縮起來」

邊雙連通分量

這簡單，把橋標記起來之後，對每個點做一次 DFS
遇到橋就不要走，剩下在同一次 DFS 戳到的點就把它標記在同一個連通分量裡

怎麼做

你會發現縮完之後是沒有環的
- 如果有環，上面任一邊都不是橋，表示一定會被縮在一起
很多時候我們不喜歡環。如果把這張圖變成一棵樹 /森林就會好處理很多

用途？

BiConnected Components, BCC
對，又是 BCC
你知道該請出誰了吧

點雙連通分量

「我是你今晚的噩夢。」

「參加這社團就別想逃過我的魔爪。」

Tarjan

– Robert Endre Tarjan,
沒有說過

「不少他發明的算法都以他的名字命名，以至於有時會讓人混淆幾種不同的算法。」

– 維基百科

和剛剛邊雙連通分量很像，拔掉分量內的任一點都保持連通
我們這次好像不能像邊雙連通分量一樣標記然後不走了欸
- 為什麼？
- 看圖
- 這要怎麼縮？

點雙連通分量

和剛剛邊雙連通分量很像，拔掉分量內的任一點都保持連通
我們這次好像不能像邊雙連通分量一樣標記然後不走了欸
- 為什麼？
- 看圖
- 這要怎麼縮？

點雙連通分量

234

012

「等等，那個 2 剛剛是不是出現了三次」

是，又是一個學長不講的東西了
簡單來說，既然依定義縮起來很麻煩，那就別縮
不如我們把在同一個連通分量的點指向一個新節點，以後要操作都對新節點操作
忽略原圖的邊
- 圓點：原本圖上的點
- 方點：代表一個點雙連通分量的點

圓方樹

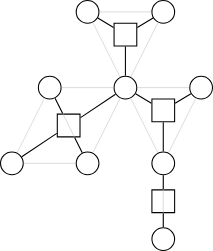
首先它一定是一棵樹
點數小於 2n，自己證，這很顯然
如果原圖不連通，那新的圓方樹會是森林
一個方點接到的圓點實際上就是一個 BCC

圓方樹的性質

套用 Tarjan 割點算法再魔改下
這裡把 low 的定義改成可以用連向親代的樹邊更新一次
當 low[nxt] == dfn[cur] 時代表找到割點
- 找到割點時，相關的 BCC 點應該在哪？
  - 在剛剛你經過的 DFS 路徑裡啊！
我們用一個 Stack 維護 DFS 的路徑，如果找到一個割點就把還沒用過的、在割點底下的點縮進去
- 割點以外的點只存在於一個 BCC
- 割點不能被視為「用過」，因為它可能存在兩個內

建樹

←當你到這裡時，會發現 low[nxt] = dfn[cur]

cur

nxt

cur

nxt

這是剛剛經過的子樹

cur

nxt

將它連起來

cur

nxt

接著是來到這裡

cur

nxt

這是我們 BCC 還沒用過的點 / stack 還剩下的範圍

cur

nxt

建方點，連起來

cur

nxt

還有一個

cur

nxt

還有一個

完成圓方樹

vector<vector<int>> block_cut_tree(const vector<vector<int>> &graph) {
    int dfs_clock = 0;
    stack<int> path;
    vector<vector<int>> result;
    result.reserve(graph.size() * 2);
    vector<int> dfn(graph.size(), 0);
    vector<int> low(graph.size(), INF);

    auto dfs = [&](int cur, auto &&dfs) -> void {
        low[cur] = dfn[cur] = ++dfs_clock;
        path.push(cur);
        for (const auto &nxt : graph[cur]) {
            if (!dfn[nxt]) {
                dfs(nxt, dfs);
                low[cur] = min(low[cur], dfn[nxt]);
                if (low[nxt] == dfn[cur]) {	 // find cut vertex / BCC
                    result.push_back(vector<int>(0));
                    int square = result.size() - 1;
                    for(int v = -1; v != nxt; path.pop()) {
                        v = path.top();
                        result[v].push_back(square);
                        result[square].push_back(v);
                    }
                    result[square].push_back(cur);
                    result[cur].push_back(square);
                }
            }
            else {
                low[cur] = min(low[cur], dfn[nxt]);
            }
        }
    };

    dfs(0, dfs);
    return result;
}

其實邊雙連通也可以用 stack 喔

這兩種方式~~都叫 BCC~~ 都在縮點變樹，差別在哪
邊雙連通分量是以「邊」為主體
點雙連通分量是以「點」為主體
具體來說，看題目想要你怎麼區分

差別

終於要來講有向圖了
前面提到圖有強連通、弱連通
同理，有向圖也有強連通分量、弱連通分量
- 強連通分量 (SCC)：對連通分量內每個 (u, v)，u 可以走到 v、v 也可以走到 u
- 弱連通分量 (WCC)：對連通分量內每個 (u, v)，至少滿足 u 可以走到 v 或 v 可以走到 u
注意弱連通分量的定義和弱連通圖不同

有向圖上的 CC

不過有向圖反而有比較簡單的演算法(蛤
我們可以不要再 Tarjan 了嗎
- 不行。
- 經過剛剛一番折磨，你應該知道為什麼這個演算法能被稱做「Tarjan 演算法」，它能應用的情況太多了

有向圖上

Strongly Connected Components
裡面實際上就是一堆有向環
引用拓撲排序說的：「這樣會沒辦法好好轉移」
把環縮起來就沒事了
縮起來後就是 DAG，你想拓撲排序或幹嘛都行

SCC

Strongly Connected Components
裡面實際上就是一堆有向環
引用拓撲排序說的：「這樣會沒辦法好好轉移」
把環縮起來就沒事了
縮起來後就是 DAG，你想拓撲排序或幹嘛都行

SCC

「我是你今晚的噩夢。」

「參加這社團就別想逃過我的魔爪。」

Tarjan

– Robert Endre Tarjan,
沒有說過

「這傢伙讓我做簡報做到腦中風。」

– 海之音

你會天真地以為 Tarjan 的那棵 DFS Tree 只能用在無向圖上嗎
顯然否吧他可是 Tarjan 欸
所以在有向圖上會發生什麼事

拓展 DFS Tree

在有向圖的情況下，會有新種類的邊產生
樹邊 (tree edge)：戳到新點的邊
返祖邊 (back edge)：從子孫連回祖先
前向邊 (foward edge)：從祖先連向非兒子的子孫
交錯邊 (cross edge)：連向非祖先、已經經過的點

Tarjan's SCC

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

遇到前向邊時會發生什麼？

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

怎麼處理前向邊？
- 不用處理啊
- 如果今天底下還有一個子樹，那它因為已經被樹邊戳過了，沒差
- 正常轉移就好了

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

返祖邊和交錯邊都是戳到時間戳較小的點
但你會發現返祖邊可以縮點，但是交錯邊不見得能
所以我們可能要判斷
1. 這條邊是否是交錯邊
2. 這條邊是否可以拿來被縮點

返祖邊 Vs. 交錯邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

交錯邊具有什麼性質？
可以對於指向的情況討論

判斷交錯邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

樹邊

子樹 0

返祖

前向

交錯

子樹 1

子樹 2

超級源點

Case 1: 指到的已經被分派 SCC

已經找到對應「割點」

樹邊

返祖

前向

交錯

分支 0

分支 1

子樹根

Case 2: 指到的還沒被分派 SCC

但之後會縮點

Case 3: 指到的還沒被分派 SCC

且之後不會縮點

Case 1: 指到的點已經被分派 SCC
- 已經找到對應的分割點了，表示指到的點過不來，無法構成強連通分量
- 對於 Case 1，保證是交錯邊
- 並且，對於這種情況，不能用交錯邊更新

情況的分別

Case 2: 指到後會縮點
- 對於這種情況，就算是交錯邊，用那條交錯邊更新也沒有差別，反正都會縮
Case 3: 指到後不會縮點
- 真的有這種情況嗎？
- 你想想，不會縮點表示下面一定是分割點嘛
- 所以它已經被指派 SCC 了

情況的分別

你仔細看就會發現我有要唬爛你的意思(

所以...交錯邊？

所以我們對於交錯邊的結論是：如果指到的被分派 SCC 那就別用它更新
否則使用它更新自己的 low 值
記錄已分派 SCC 本身其實可以用 SCC 的編號來記錄，一舉兩得
- 當找到新的 SCC 時，++scc_id, scc[...] = scc_id;
- 否則 scc[i] 應設為 0

結論

DFS, 記錄每點的 dfn, low
- 把自己加入 stack
- 對於每個 u 附近的點 v
  - 如果 v 已經被分派 scc，continue
  - 如果 v 還沒被拜訪過，dfs(v)，更新自己的 low
  - 如果 v 被拜訪過，更新自己的 low
- 判斷是否 dfn[u] = low[u]，是的話把目前 stack 在 u 以下的東西縮進 SCC，記錄編號

整體過程

vector<int> tarjan_SCC(const vector<vector<int>> &graph) {
    vector<int> scc(graph.size(), 0);
    vector<int> dfn(graph.size(), 0);
    vector<int> low(graph.size(), INF);
    stack<int> path;
    int dfs_clock = 0;
    int scc_id = 0;

    auto dfs = [&](int cur, auto &&dfs) -> void {
        low[cur] = dfn[cur] = ++dfs_clock;
        path.push(cur);

        for (const auto &nxt : graph[cur]) {
            if (scc[nxt]) continue;

            if (!dfn[nxt]) dfs(nxt, dfs), low[cur] = min(low[cur], low[nxt]);
            else low[cur] = min(low[cur], dfn[nxt]);
        }

        if (dfn[cur] == low[cur]) {
            ++scc_id;
            for (int v = -1; v != cur; path.pop()) {
                v = path.top();
                scc[v] = scc_id;
            }
        }
    };

    for (int v = 0; v < graph.size(); v++)
        if (!dfn[v]) dfs(v, dfs);

    return scc;
}

另一個連通分量超人
我的超人
他想出了一個超好寫 SCC 的方法
- 太神奇了，他不是 Tarjan 欸
- 但這個方法常數比較大
- 但他不是 Tarjan 欸
- 他並沒有以此發表論文
- 但他不是 Tarjan 欸

Kosaraju

這個算法的核心在「反圖」
點相同，所有邊相反的圖
反圖具有什麼性質？
SCC 在反圖下具有什麼性質？

反圖

這個算法的核心在「反圖」
點相同，所有邊相反的圖
反圖具有什麼性質？
SCC 在反圖下具有什麼性質？

反圖

SCC 在反圖下具有什麼性質？
- SCC 在反圖下是點相同的
- 因為在原圖 u 可以走到 v，v 可以走到 u，反圖上反過來 v 可以走到 u，u 可以走到 v

反圖

在原圖上 DFS 如果有 u → v
在反圖上只要確認 u → v
這樣代表原圖上的 u → v，v -> u 都確認過了
這聽起來感覺有一點像拓撲排序，拓撲排序在有向環有什麼性質？

怎麼利用？

先把 SCC 當成一個群體來看
拓撲排序出來會依照群體排序，原先輩分較大會被排在前面，輩分小的不能往輩分大的走
今天反向圖會讓輩分順序反過來，會讓原先輩分大的不能走向輩分小的
這時，我們將由反向後輩分小點的開始搜尋，可以發現走不到其他群體
所以，這樣我們可以確定群體範圍

感性理解

原先 A > B > C

A 可以單向走到 B，B 可以單向走到 C

原先 A > B > C

反向後 A 走不到 B，B 走不到 C

這時如果在 A 裡面不管怎麼走都不會走到 B

B 可能會走到 A，但走不到 C

在走 B 前確認完 A 有哪些人，不要碰

對原圖每點 DFS，確定拓撲排序 (時間戳)
對反圖依照原拓撲排序大到小每點 DFS，點用過就「封鎖」，標記 visited
就這樣，超好理解

算法流程

vector<int> KosarajuSCC(const vector<vector<int>> &graph) {
    vector<vector<int>> hparg(graph.size());
    for (int u = 0; u < graph.size(); u++)
        for (const auto &v : graph[u])
            hparg[v].push_back(u);

    vector<int> sort_result;
    sort_result.reserve(graph.size());
    vector<bool> visited(graph.size(), false);

    auto dfs = [&](int cur, auto &&dfs) -> void {
        visited[cur] = true;
        for (const auto &nxt : graph[cur])
            if (!visited[nxt]) dfs(nxt, dfs);
        sort_result.push_back(cur);
    };
    for (int v = 0; v < graph.size(); v++)
        if (!visited[v]) dfs(v, dfs);

    vector<int> scc(graph.size(), 0);
    int scc_id = 0;
    auto sfd = [&](int cur, auto &&sfd) -> void {
        scc[cur] = scc_id;
        for (const auto &nxt : hparg[cur])
            if (!scc[nxt]) sfd(nxt, sfd);
    };
    for (auto v_pt = scc.rbegin(); v_pt != scc.rend(); v_pt++)
        if (!scc[*v_pt]) ++scc_id, sfd(*v_pt, sfd);
}

會這麼長是因為建反圖等等的都在裡面

實際上算法本體不到 20 行

重點是他不是 Tarjan ，他很直觀

TIOJ 2319 / 建中 2023 校內賽複試 PA

Thanks for your Listening！

有人要猜猜看總簡報頁數嗎

Graph Theory[2]

Index

講師

Reference

聲明

連通性

繼續架網路

繼續架網路

找出弱點

割點 Cut Vertex

Tarjan

DFS Tree

DFS Tree

DFS Tree

DFS Tree

DFS Tree

DFS Tree

DFS Tree

DFS Tree

DFS Tree

DFS Tree

為邊做分類

觀察性質

觀察性質

觀察性質

返祖邊

返祖邊

實作

再次觀察

再次觀察

Tarjan 割點算法

例外

Case: root

總結過程

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

Edge

相似？

連通分量

連通分量

單連通分量

Tarjan

邊雙連通分量

怎麼做

用途？

點雙連通分量

Tarjan

點雙連通分量

點雙連通分量

圓方樹

圓方樹的性質

建樹

差別

有向圖上的 CC

有向圖上

SCC

SCC

Tarjan

拓展 DFS Tree

更多分類

Tarjan's SCC

前向邊

前向邊

前向邊

前向邊

前向邊

前向邊

前向邊