樹

TREE

Index

介紹

樹上 DFS

樹 DP

樹直徑

Index

LCA

樹壓平

樹鍊剖分

樹重心

other

樹上啟發式合併

樹同構

Link-Cut Tree

重心分治/重心剖分/重心樹

other

樹上背包

樹分塊

各種怪東西

建中 225 賴柏宇
海之音 / 小海或其他類似的
表達能力差，不懂要問
INFOR 36th 學術長
不會樹論所以來當樹論講師

講師

慣用詞

#include <iostream>
#include <vector>
#incldue <functional>
#incldue <utility>
// ...可能有其他的

int n;     // 點數
int m;     // 邊數
int cur;   // 當前節點編號
int pre;   // 上一個節點，通常是父節點
int nxt;   // 下一個節點，通常是子節點
int depth; // 深度
int size;  // 大小，通常是子樹大小

const int null = -1;
const int MOD = 1e9 + 7;
const int INF = 2e9;

template <typename T>
using vec = std::vector<T>;

using pii = std::pair<int, int>;
using std::min;
using std::max;
using std::cin;
using std::cout;

ReSOURCES

註：編譯器使用 g++ , std=c++20

介紹

Introduction

〞

樹是一種無向圖，其中任意兩個頂點間存在唯一一條路徑。

或者說，只要沒有環的連通圖就是樹。

– Wikipedia

樹的定義 & 特性

一種特殊的圖
連通圖
通常無向
無環
- 邊數 = 點數 - 1
- 兩點間路徑唯一
反過來說，只要 m = n - 1 的圖就是樹

1

0

2

3

4

5

6

7

8

9

樹的相關名詞

以 0 為根
- 資訊圈的樹都是反著長的

1

0

2

3

4

5

6

7

8

9

樹的相關名詞

1

0

2

3

4

5

6

7

8

9

以 0 為根
輩分關係：上 > 下
- 0, 1 有父子關係　
- 0 是父節點，1 是子節點
- 看離根遠近

樹的相關名詞

1

0

2

3

4

5

6

7

8

9

以 0 為根
輩分關係：上 > 下
- 0 是 5 的祖先
- 5 是 0 的子孫
- 看離根遠近

樹的相關名詞

1

0

2

3

4

5

6

7

8

9

以 0 為根
輩分關係：上 > 下
深度：根到某節點的距離
- 5 的深度為 2

d = 0

d = 1

d = 2

d = 3

樹的相關名詞

1

0

2

3

4

5

6

7

8

9

以 0 為根
輩分關係：上 > 下
深度：根到某節點的距離
樹高：樹的層數
- 這棵樹樹高為 4

height = 4

樹的相關名詞

1

0

2

3

4

5

6

7

8

9

以 0 為根
輩分關係：上 > 下
深度：根到某節點的距離
樹高：樹的層數
葉節點：度數 = 1 的節點
- 4, 5, 7, 8, 9 是葉節點

樹的相關名詞

1

0

2

3

4

5

6

7

8

9

以 0 為根
輩分關係：上 > 下
深度：根到某節點的距離
樹高：樹的層數
葉節點：沒有子節點的節點
子樹：節點底下的所有節點
- 2 的子樹如右圖
- 有些人定義不包含自身

樹的相關名詞

1

0

2

3

4

5

6

7

8

9

以 0 為根
輩分關係：上 > 下
深度：根到某節點的距離
樹高：樹的層數
葉節點：沒有子節點的節點
子樹：節點底下的所有節點
注意以上是在有根的情況下
- 樹不一定要有根
- 根不一定唯一

樹的相關名詞

0

3

9

以 3 為根
輩分關係：上 > 下
深度：根到某節點的距離
樹高：樹的層數
葉節點：沒有子節點的節點
子樹：節點底下的所有節點
注意以上是在有根的情況下
- 樹不一定要有根
- 根不一定唯一

1

4

5

2

6

7

8

樹的用途

樹論作為圖的延伸，有很多特性能用
- 其實很多植物都和圖有關：森林、仙人掌...
很多圖論題要用樹的方式解
- 圖可以用 Tarjan 演算法變成樹，然後解掉
樹論題包裝成圖論題
...

樹的儲存

一般來說我們會用鄰接串列
如果要儲存的東西比較多，我會用下述方式存

struct Edge {
	// edge data
};

struct Node {
    // node data
    vec<Edge> edges;
};

using Tree = vec<Node>;

// 或者如果你想用 for (auto &nxt : tree[cur]) 遍歷

struct Node {
    // node data
    vec<Edge> edges;
    
    auto begin() {
        return edges.begin();
    }
    
    auto end() {
        return edges.end();
    }
};

樹上 DFS

DFS on Tree

樹的 DFS

樹有什麼特性？
- 連通
- 無環
有什麼能用的地方？

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

拜訪重複節點

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

圖可能有環，需記錄 Visited
樹無環，只需記錄 Parent

1

0

2

1

0

2

i

當前拜訪節點

i

前個拜訪節點

# 一般圖 DFS

# 樹上的 DFS

樹的 DFS

void dfs(int cur, int pre, vec<vec<int>> &tree) {
    for (int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        dfs(nxt, cur, tree);
    }
}

遍歷順序

運作的順序上雖然按照前面的模板，但處理順序可以不同
二元樹中有三種處理方式
- 前序遍歷：中節點 -> 左節點 -> 右節點
- 中序遍歷：左節點 -> 中節點 -> 右節點
- 後序遍歷：左節點 -> 右節點 -> 中節點

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：
中序遍歷：
後序遍歷：

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3
中序遍歷：
後序遍歷：

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1
中序遍歷：
後序遍歷：

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0
中序遍歷：0
後序遍歷：0

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0
中序遍歷：0, 1
後序遍歷：0

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2
中序遍歷：0, 1, 2
後序遍歷：0, 2

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2
中序遍歷：0, 1, 2
後序遍歷：0, 2, 1

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2
中序遍歷：0, 1, 2, 3
後序遍歷：0, 2, 1

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7
中序遍歷：0, 1, 2, 3
後序遍歷：0, 2, 1

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5
中序遍歷：0, 1, 2, 3
後序遍歷：0, 2, 1

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5, 4
中序遍歷：0, 1, 2, 3, 4
後序遍歷：0, 2, 1, 4

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5, 4
中序遍歷：0, 1, 2, 3, 4, 5
後序遍歷：0, 2, 1, 4

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5, 4, 6
中序遍歷：0, 1, 2, 3, 4, 5, 6
後序遍歷：0, 2, 1, 4, 6

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5, 4, 6
中序遍歷：0, 1, 2, 3, 4, 5, 6
後序遍歷：0, 2, 1, 4, 6, 5

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5, 4, 6
中序遍歷：0, 1, 2, 3, 4, 5, 6, 7
後序遍歷：0, 2, 1, 4, 6, 5, 7

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5, 4, 6
中序遍歷：0, 1, 2, 3, 4, 5, 6, 7
後序遍歷：0, 2, 1, 4, 6, 5, 7, 3

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

處理順序

i

當前拜訪節點

前序遍歷：3, 1, 0, 2, 7, 5, 4, 6
中序遍歷：0, 1, 2, 3, 4, 5, 6, 7
後序遍歷：0, 2, 1, 4, 6, 5, 7, 3

i

已拜訪節點

1

3

0

2

7

5

4

6

#遍歷順序

遍歷順序

#define lchild first
#define rchild second

void preorder(int cur, vec<pii> &tree) {
    if (cur == null) return;
    process(cur);
    preorder(tree[cur].lchild, tree);
    preorder(tree[cur].rchild, tree);
}

void inorder(int cur, vec<pii> &tree) {
    if (cur == null) return;
    inorder(tree[cur].lchild, tree);
    process(cur);
    inorder(tree[cur].rchild, tree);
}

void postorder(int cur, vec<pii> &tree) {
    if (cur == null) return;
    postorder(tree[cur].lchild, tree);
    postorder(tree[cur].rchild, tree);
    process(cur);
}

輸出

#include <iostream>
#include <utility>
#include <vector>

#define lchild first
#define rchild second

template <typename T>
using vec = std::vector<T>;

using pii = std::pair<int, int>;

const int null = -1;

void process(int node) {
    std::cout << node << " ";
}

void preorder(int cur, vec<pii> &tree) {
    if (cur == null) return;
    process(cur);
    preorder(tree[cur].lchild, tree);
    preorder(tree[cur].rchild, tree);
}

void inorder(int cur, vec<pii> &tree) {
    if (cur == null) return;
    inorder(tree[cur].lchild, tree);
    process(cur);
    inorder(tree[cur].rchild, tree);
}

void postorder(int cur, vec<pii> &tree) {
    if (cur == null) return;
    postorder(tree[cur].lchild, tree);
    postorder(tree[cur].rchild, tree);
    process(cur);
}

int main() {
    vec<pii> tree = {{-1, -1}, {0, 2}, {-1, -1}, {1, 7}, {-1, -1}, {4, 6}, {-1, -1}, {5, -1}};
    int root = 3;
    preorder(root, tree);
    std::cout << "\n";
    inorder(root, tree);
    std::cout << "\n";
    postorder(root, tree);
    std::cout << "\n";
}

3 1 0 2 7 5 4 6 
0 1 2 3 4 5 6 7 
0 2 1 4 6 5 7 3

Undo

樹上 DFS 的過程有「前進」還有「後退」
我們可以好好利用這個特性做一些事
舉個例子，重複利用資料

樹上LIS

樹上 LIS：找尋所有分支的 LIS
以右圖來說，就是 3, 5, 6 節點
LIS 做法：維護可能尾端的單調隊列
怎麼應用在樹上？

i

LIS 所在節點

LIS 所在分支

i

1

3

2

7

5

4

6

0

#樹上LIS

樹上LIS

一種做法是在每個節點都維護到那點的可能尾端
從父節點複製一份來給當前節點用
這麼做顯然不切實際，時空耗費太大
有沒有一種可能，不用複製？

1

3

0

2

7

5

4

6

可能的尾端

[...]

[3]

[1]

[0]

[1, 2]

[3, 7]

[3, 5]

[3, 4]

[3, 4, 6]

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[1]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[0]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[1]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[1, 2]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[1]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3, 7]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3, 5]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3, 4]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3, 5]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3, 5, 6]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3, 5]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3, 7]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[3]

i

當前拜訪節點

#樹上LIS

樹上LIS

我們常常用「回到上一步」這個功能
可以把想法用在這裡
不用複製，只要前一個分支用完恢復成用之前的樣子就好了！

1

3

0

2

7

5

4

6

當前節點可能的尾端

[...]

[]

i

當前拜訪節點

#樹上LIS

樹上LIS

怎麼恢復？
記錄修改的位置以及修改以前的值
遞迴用 stack 記錄會比較方便

樹上 LIS

struct LIS {
    vec<int> mono;
    std::stack<pii> trace;
    void add_number(int n) {
        if (mono.empty() || n > mono.back()) {
            mono.push_back(n);
            trace.push({-1, n});
        }
        else {
            auto pos = std::lower_bound(mono.begin(), mono.end(), n);
            trace.push({pos - mono.begin(), *pos});
            *pos = n;
        }
    }
    void undo() {
        auto [pos, val] = trace.top();
        trace.pop();
        if (pos == -1) mono.pop_back();
        else mono[pos] = val;
    }
};

int max_len = 0;

void tree_lis(int cur, int pre, LIS &lis, const vec<int> &nums, const vec<vec<int>> &tree) {
    lis.add_number(nums[cur]);
    max_len = max(max_len, lis.mono.size());
    for (const int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        tree_lis(nxt, cur, lis, nums, tree);
    }
    lis.undo();
}

題單

TIOJ 2277

CF #756 pE1

2024 學術上機考 B2

樹 DP

DP on Tree

Dynamic Programming

記得 DP 在做什麼嗎？
- 分治優化
- 把小狀態記錄下來，優化重複使用的效率
樹具有相當良好的分治結構

樹分治

從分治的例子看起
- CSES 1674 - Subordinates
- 求子樹大小總和（不含自身）
分、治
- 分：對每個子節點求解
- 治：所有子節點加上自己

3

8

1

4

3

1

#子樹大小

子樹大小

vec<int> sub_sizes;

int get_sub_size(int cur, const vec<vec<int>> &tree) {
	// 這題的測資輸法不會有環
	for (const int &nxt : tree[cur])
		sub_sizes[cur] += get_sub_size(nxt, tree);

	return sub_sizes[cur] + 1; // 回傳時記得加上自己
}

int main() {
	std::ios_base::sync_with_stdio(0), std::cin.tie(0);

	int n;
	cin >> n;

	sub_sizes.resize(n, 0);
	vec<vec<int>> tree(n);

	for (int i = 1; i < n; i++) {
		int parent;
		cin >> parent;
		parent--;
		tree[parent].push_back(i);
	}

	get_sub_size(0, tree);

	for (const int &sub_size : sub_sizes)
		cout << sub_size << " ";
}

樹分治

因為樹本身的結構，所以在樹上做分治的特點有：
- 分要想辦法拆成子樹能處理的
- 合併也是透過子樹答案合併
- 到葉節點時中止遞迴
之前的線段樹做的也是種樹分治
而一般來說，樹分治的各個子節點可以獨立處理

樹DP

樹分治可以不用記錄值，但有時候會需要存起來
但其實沒有那麼明顯的分別，參考就好

樹DP

例題：樹上最大匹配（CSES 1130）
樹上鄰近兩點湊一對，最多可以湊幾對？
思路：對於每個子節點可以分成兩種情況
- 該子節點根有配對，該分支的最大匹配
- 該子節點沒配對，該分支的最大匹配

樹DP

令 (dp0, dp1) 分別為不選取、選取該點時子樹的最大匹配
dp0 顯然就是各子節點的最大值加起來
dp1 表示當前節點一定要和某個子節點匹配，且該子節點不能匹配

(0, 0)

(0, 1)

(0, 0)

(0, 1)

(1, 1)

(2, 3)

#(dp0, dp1)

樹上最大匹配

vec<pii> dp;
// dp[i].first: 不選當前節點的最大值
// dp[i].second: 選當前節點的最大值

void max_match(int cur, int pre, const vec<vec<int>> &tree) {
    for (const int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        max_match(nxt, cur, tree);
        dp[cur].first += max(dp[nxt].first, dp[nxt].second);
        // 不選當前節點：所有分支的最大值和
    }
    for (const int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        int nxt_ans = max(dp[nxt].first, dp[nxt].second);
        dp[cur].second = max(dp[cur].first - nxt_ans + dp[nxt].first + 1, dp[cur].second);
        // 選當前節點：其中一個分支必須沒有選才能接當前節點
    }
}

int main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);

    int n;
    cin >> n;
    vec<vec<int>> tree(n);
    dp.resize(n);
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        std::cin >> u >> v;
        u--, v--;
        tree[u].push_back(v);
        tree[v].push_back(u);
    }
    max_match(0, null, tree);
    cout << std::max(dp[0].first, dp[0].second) << "\n";
}

換根DP

顧名思義，dp 的過程中換根
有些時候題目並沒有明確說哪個節點是根，是我們自己定的
例題：CSES 1133 - Tree Distances II
- 求一個節點各節點的深度和

換根DP

從固定某個點想起，然後思考怎麼轉移到其他點
不妨先設 0 為根，計算 0 的答案

int sub_depth_sum(int cur, int pre, int cur_depth, const vec<vec<int>> &tree) {
    int cur_depth_sum = cur_depth;
    for (const int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        cur_depth_sum += sub_depth_sum(nxt, cur, cur_depth + 1, tree);
    }
    return cur_depth_sum;
}

換根DP

怎麼轉移到鄰近的點？

12

?

#轉移

換根DP

在那棵子樹以外的其他點距離都會 +1

12

?

#轉移

換根DP

相反地，在那棵子樹的點距離會 -1

12

?

#轉移

換根DP

換根 dp 大致可以歸納出以下重點
- 在預處理時順便處理子樹大小
- 之後用根的答案轉移到每個點
預處理的資訊通常會有子樹大小或深度什麼的

Tree Distance II

#define int long long
vec<int> sub_size;
int preprocess(int cur, int pre, int cur_depth, const vec<vec<int>> &tree) {
    int cur_depth_sum = cur_depth;
    sub_size[cur] = 1;
    for (const int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        cur_depth_sum += preprocess(nxt, cur, cur_depth + 1, tree);
        sub_size[cur] += sub_size[nxt];
    }
    return cur_depth_sum;
}

vec<int> depth_sums;
void trans_from_root(int cur, int pre, const vec<vec<int>> &tree) {
    for (const int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        depth_sums[nxt] = depth_sums[cur] - sub_size[nxt] + (tree.size() - sub_size[nxt]);
        trans_from_root(nxt, cur, tree);
    }
}

signed main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);
    int n;
    cin >> n;
    vec<vec<int>> tree(n);
    sub_size.resize(n);
    depth_sums.resize(n);
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        tree[u].push_back(v);
        tree[v].push_back(u);
    }
    depth_sums[0] = preprocess(0, 0, 0, tree);
    trans_from_root(0, 0, tree);
    for (const auto &sum : depth_sums)
        cout << sum << " ";
}

題單

AtCoder DP P

CF #722 pA

CF #800 pD

樹直徑

Diameter

樹直徑

圓的直徑其實就是圓上最長的一條弦
樹直徑同理，是樹上最長的一條路徑
樹直徑有可能有很多條

#樹直徑

樹直徑

圓的直徑其實就是圓上最長的一條弦
樹直徑同理，是樹上最長的一條路徑
樹直徑有可能有很多條

#樹直徑

樹直徑

至於如何找到樹直徑？
其實意料之外地簡單
隨便選某個點 O，找到那點的最遠點 A
然後找 A 的最遠點 B ，AB 就是樹直徑的兩端
證明

樹直徑

或者你可以樹 dp
對於每個節點存往下的最長路徑長以及次長路徑長
- 注意最長路徑以及次長路徑必須從不同子樹得到答案
- 確保無公共邊
所有點中最長 + 次長 - 1 中最大者即為樹直徑

(2, 2)

(4, 3)

(1, 1)

(3, 1)

(2, 2)

(1, 1)

#(最長, 次長)

樹直徑

這麼做的好處是有負邊時也行
相較於上個做法比較不唬爛（

(2, 2)

(4, 3)

(1, 1)

(3, 1)

(2, 2)

(1, 1)

#(最長, 次長)

樹直徑

int diameter_len = 0;
int get_longest_path(int cur, int pre, const vec<vec<int>> &tree) {
    int l1 = 1, l2 = 1;
    for (const int &nxt : tree[cur]) {
        if (nxt == pre) continue;
        int nxt_longest = get_longest_path(nxt, cur, tree) + 1;
        if (nxt_longest >= l1) {
            l2 = l1;
            l1 = nxt_longest;
        }
        else if (nxt_longest >= l2) {
            l2 = nxt_longest;
        }
    }
    diameter_len = max(diameter_len, l1 + l2 - 1);
    return l1;
}

int main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);
    int n;
    cin >> n;
    vec<vec<int>> tree(n);
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        tree[u].push_back(v);
        tree[v].push_back(u);
    }
    get_longest_path(0, 0, tree);
    cout << diameter_len - 1;
}

題單

CSES 1131

CSES 1132

TIOJ 2189 / TOI 2020 初選 pB

TOI 2023 初選 pC

TIOJ 2215

CF #495 pE

LCA

Lowest Common Ancestor

LCA

What is LCA?
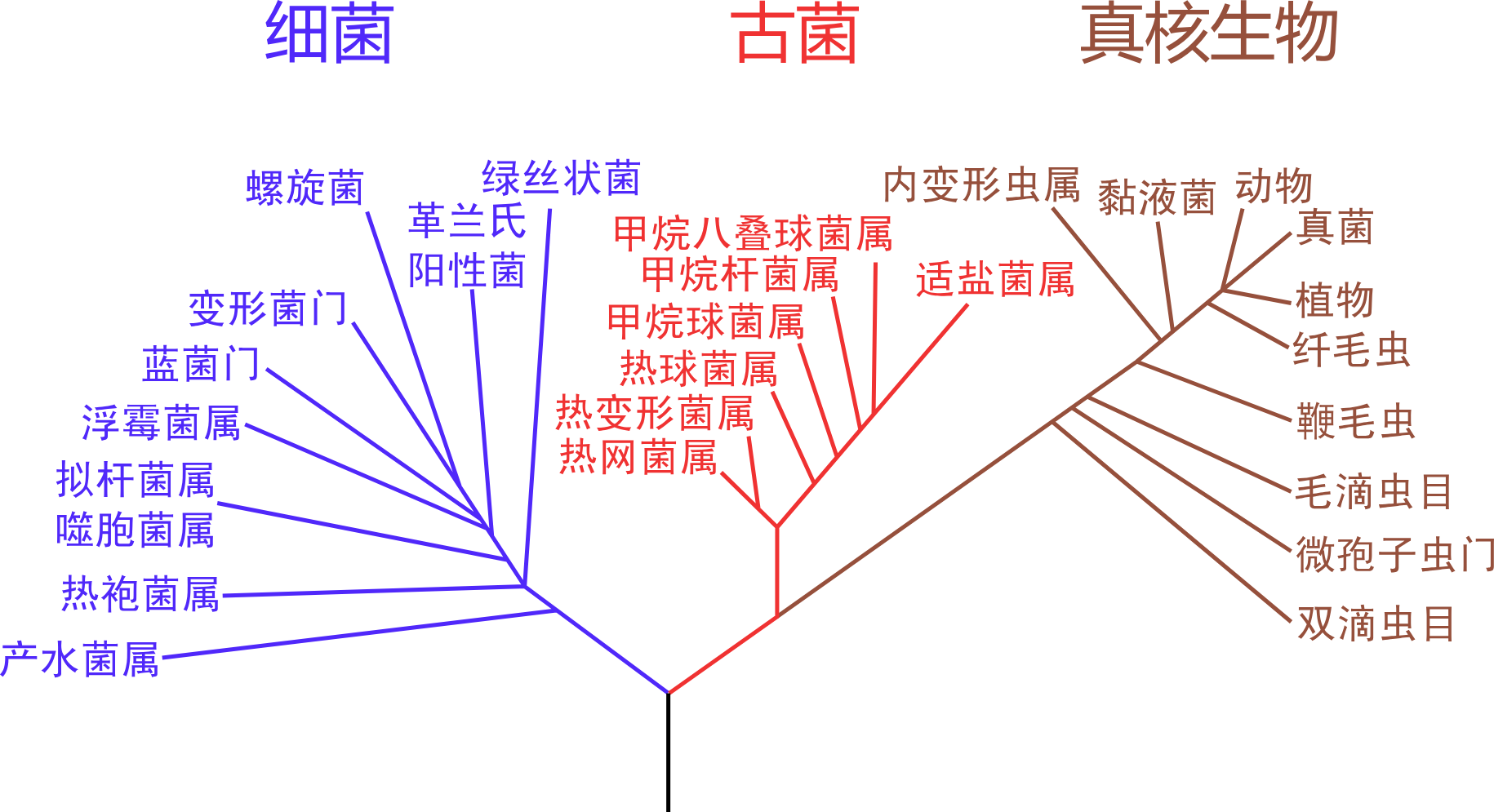
最低共同祖先
在演化樹上，就是距離兩種生物最近的共同祖先

LCA

在資訊學上，就是兩點的共同祖先中，深度最大的

1

0

2

3

4

5

6

7

8

9

d = 0

d = 1

d = 2

d = 3

LCA

這是 5 的祖先

1

0

2

3

4

5

6

7

8

9

d = 0

d = 1

d = 2

d = 3

LCA

這是 9 的祖先

1

0

2

3

4

5

6

7

8

9

d = 0

d = 1

d = 2

d = 3

LCA

這是 5, 9 的共同祖先

1

0

2

3

4

5

6

7

8

9

d = 0

d = 1

d = 2

d = 3

LCA

再舉個例子，這是 7 的祖先

1

0

2

3

4

5

6

7

8

9

d = 0

d = 1

d = 2

d = 3

LCA

這是 8 的祖先

1

0

2

3

4

5

6

7

8

9

d = 0

d = 1

d = 2

d = 3

LCA

這是他們的共同祖先，最低的就是 6

1

0

2

3

4

5

6

7

8

9

d = 0

d = 1

d = 2

d = 3

LCA

CSES 1688 (Company Queries II)
LCA 可以拿來求樹上最短路
樹上的其他問題也可能用到 LCA

倍增法

對，又是你倍增法
上次提到是在資結的 sparse table
這次要怎麼和倍增扯上關聯？

倍增法

先考慮暴力做法
對於每個點預處理祖先是誰
兩個點同時往上爬
兩個點相遇時就是答案

1

3

0

2

7

5

4

6

#LCA(2, 5)

倍增法

先考慮暴力做法
對於每個點預處理祖先是誰
兩個點同時往上爬
兩個點相遇時就是答案

1

3

0

2

7

5

4

6

#LCA(2, 5)

倍增法

先考慮暴力做法
對於每個點預處理祖先是誰
兩個點同時往上爬
兩個點相遇時就是答案

1

3

0

2

7

5

4

6

#LCA(2, 5)

倍增法

先考慮暴力做法
對於每個點預處理祖先是誰
兩個點同時往上爬
兩個點相遇時就是答案
然而，深度不同時不可行
所以要預處理深度，低的先爬到深度相同的位置再開始一起爬

1

3

0

2

7

5

4

6

#LCA(1, 5)

倍增法

先考慮暴力做法
對於每個點預處理祖先是誰
兩個點同時往上爬
兩個點相遇時就是答案
然而，深度不同時不可行
所以要預處理深度，低的先爬到深度相同的位置再開始一起爬

1

3

0

2

7

5

4

6

#LCA(1, 5)

倍增法

先考慮暴力做法
對於每個點預處理祖先是誰
兩個點同時往上爬
兩個點相遇時就是答案
然而，深度不同時不可行
所以要預處理深度，低的先爬到深度相同的位置再開始一起爬

1

3

0

2

7

5

4

6

#LCA(1, 5)

倍增法

你會發現，這方法慢得很，單次查詢
但造成速度慢的主要原因也很明顯：爬的過程
很顯然一次爬一步太慢，所以我們一次爬多一點

O(n)

倍增法

假設目標是向上爬 n 步
n 可以拆成二進位：例如 n = 26 = 16 + 8 + 2
開一個表格，儲存每個節點的代祖先
類似稀疏表

2^i

倍增法

類似於稀疏表，令為的代祖先
一個節點的代祖先相當於代祖先的代祖先
所以
建層，每層格，複雜度

2^{i+1}

2^i

ancestors[i][u]

u

2^i

ancestors[i + 1][u] = ancestors[i][ancestors[i][u]]

\lfloor log_2n + 1\rfloor

n

O(n\ log\ n)

倍增法

現在沒有所謂「範圍大小」了，怎麼查詢？
範圍如果不確定那就搜尋啊！
先找表裡有的最低祖先，如果是共祖就向下找
找到不是共祖的祖先就向上爬
結果是不是共祖的點裡最高的

1

3

0

2

7

5

4

6

2 的 2 代祖先為 3

5 的 2 代祖先為 3

3 為 2, 5 共祖

#LCA(2, 5)

倍增法

現在沒有所謂「範圍大小」了，怎麼查詢？
範圍如果不確定那就搜尋啊！
先找表裡有的最低祖先，如果是共祖就向下找
找到不是共祖的祖先就向上爬
結果是不是共祖的點裡最高的

1

3

0

2

7

5

4

6

2 的 1 代祖先為 1

5 的 1 代祖先為 7

非共祖

#LCA(2, 5)

倍增法

現在沒有所謂「範圍大小」了，怎麼查詢？
範圍如果不確定那就搜尋啊！
先找表裡有的最低祖先，如果是共祖就向下找
找到不是共祖的祖先就向上爬
結果是不是共祖的點裡最高的

1

3

0

2

7

5

4

6

結束

結果為 1 (或 7) 的父節點 3

#LCA(2, 5)

倍增法

如果每次都從表中最高的祖先開始找複雜度是
還可以再優化
可以保證，向上走的步長只會愈來愈小
只會跑過 2 的冪次的步長，複雜度

O(log^2n)

O(log\ n)

倍增法 LCA

namespace BinaryLifting {
    vec<vec<int>> ancestors;
    vec<int> depths;

    void dfs(int cur, int pre, int cur_depth, const vec<vec<int>> &tree) {
        depths[cur] = cur_depth;
        ancestors[0][cur] = pre;
        for (const int &nxt : tree[cur])
            if (nxt != pre)
                dfs(nxt, cur, cur_depth + 1, tree);
    }

    void build_ancestor_table(const vec<vec<int>> &tree) {
        depths.resize(tree.size());
        ancestors.resize(std::__lg(tree.size()) + 1);
        for (auto &_list : ancestors) _list.resize(tree.size());
        dfs(0, 0, 0, tree);

        for (int i = 0; i < ancestors.size() - 1; i++)
            for (int u = 0; u < tree.size(); u++)
                ancestors[i + 1][u] = ancestors[i][ancestors[i][u]];
    }

    int LCA(int u, int v) {
        if (depths[v] > depths[u]) std::swap(u, v);

        for (int diff = depths[u] - depths[v], i = 0; diff; diff >>= 1, i++)
            if (diff & 1)
                u = ancestors[i][u];

        if (u == v) return u;

        for (int i = ancestors.size() - 1; i >= 0; i--)
            if (ancestors[i][u] != ancestors[i][v])
                u = ancestors[i][u], v = ancestors[i][v];

        return ancestors[0][u];
    }
}

int main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);
    int n, q;
    cin >> n >> q;
    vec<vec<int>> tree(n);
    for (int i = 1; i < n; i++) {
        int u;
        cin >> u;
        u--;
        tree[u].push_back(i);
    }
    BinaryLifting::build_ancestor_table(tree);
    for (int i = 0; i < q; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        cout << BinaryLifting::LCA(u, v) + 1 << "\n";
    }
}

「我是你今晚的噩夢。」

「參加這社團就別想逃過我的魔爪。」

Tarjan

– Robert Endre Tarjan,
沒有說過

「為什麼，到底為什麼。」

– 維基百科上大概沒有

Tarjan LCA

我還需要說什麼
之前關於連通性的 Tarjan 算法都是基於 DFS 延伸
這次也是，幾乎把 DFS 玩到極致了

Tarjan LCA

找 LCA 相當於找某個子樹的根
在 DFS 某個子樹時一定會在兩個點走過之後才離開

#LCA子樹

Tarjan LCA

找 LCA 相當於找某個子樹的根
在 DFS 某個子樹時一定會在兩個點走過之後才離開

#LCA子樹

Tarjan LCA

找 LCA 相當於找某個子樹的根
在 DFS 某個子樹時一定會在兩個點走過之後才離開

#LCA子樹

Tarjan LCA

任務變成「在離開兩點之前，抵達最高的點」
在每點維護一個值，代表在離開一點後抵達的最高點
假設要求 LCA(A, B)
- 離開 A 點抵達 B 點後，A 的值就是 LCA
那麼，要如何維護每個點離開後抵達的最高點？

Tarjan LCA

不如我們在離開後就把點向上合併吧
向上合併符合我們說「記錄離開後到達的最高點」
處理合併的資料結構：併查集

struct DSU {
    vec<int> master;

    DSU(int n)
        : master(n) {
        for (int i = 0; i < n; i++)
            master[i] = i;
    }

    int find(int n) {
        return (master[n] == n) ? n : (master[n] = find(master[n]));
    }

    void combine(int a, int b) {
        a = find(a), b = find(b);
        master[b] = a;
    }
};

Tarjan LCA

當前拜訪節點

LCA

在離開一點後合併該點和它的父節點

目標：到 B 點時記錄 A 所在子樹的根

B

A

i

LCA 目標節點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

i

LCA 目標節點

LCA

在離開一點後合併該點和它的父節點

目標：到 B 點時記錄 A 所在子樹的根

B

A

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

在離開一點後合併該點和它的父節點

目標：到 B 點時記錄 A 所在子樹的根

B

A

i

LCA 目標節點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

在離開一點後合併該點和它的父節點

目標：到 B 點時記錄 A 所在子樹的根

B

A

i

LCA 目標節點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

在離開一點後合併該點和它的父節點

目標：到 B 點時記錄 A 所在子樹的根

A

B

i

LCA 目標節點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

在離開一點後合併該點和它的父節點

目標：到 B 點時記錄 A 所在子樹的根

A

B

i

LCA 目標節點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

在離開一點後合併該點和它的父節點

目標：到 B 點時記錄 A 所在子樹的根

A

B

i

LCA 目標節點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

到達 B 節點

此時從 A 向上找（合併）

A

B

i

LCA 目標節點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

A

B

i

LCA 目標節點

到達 B 節點

此時從 A 向上找（合併）

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

A

B

i

LCA 目標節點

到達 B 節點

此時從 A 向上找（合併）

因此結果就是 A 此時指向的點

#LCA(A, B)

Tarjan LCA

當前拜訪節點

LCA

i

LCA 目標節點

再示範一個 A' B'

A'

B'

#LCA(A', B')

Tarjan LCA

當前拜訪節點

LCA

i

LCA 目標節點

在離開一點後合併該點和它的父節點

目標：到 B' 點時記錄 A' 所在子樹的根

A'

B'

#LCA(A', B')

Tarjan LCA

當前拜訪節點

LCA

i

LCA 目標節點

在離開一點後合併該點和它的父節點

目標：到 B' 點時記錄 A' 所在子樹的根

A'

B'

#LCA(A', B')

Tarjan LCA

當前拜訪節點

LCA

i

LCA 目標節點

在離開一點後合併該點和它的父節點

目標：到 B' 點時記錄 A' 所在子樹的根

A'

B'

#LCA(A', B')

Tarjan LCA

當前拜訪節點

LCA

i

LCA 目標節點

在離開一點後合併該點和它的父節點

目標：到 B' 點時記錄 A' 所在子樹的根

A'

B'

#LCA(A', B')

Tarjan LCA

當前拜訪節點

LCA

i

LCA 目標節點

到達 B' 節點

此時從 A' 向上找（合併）

A'

B'

#LCA(A', B')

Tarjan LCA

當前拜訪節點

LCA

i

LCA 目標節點

到達 B' 節點

此時從 A' 向上找（合併）

因此結果就是 A' 此時指向的點

A'

B'

#LCA(A', B')

Tarjan LCA

至此我們也可以看出 Tarjan LCA 的另一個特性：離線
雖然 DFS 一次要，但查詢更多次是可以在同一次 DFS 完成的
它的複雜度是其中是查詢次數
為什麼不帶？
- 併查集特殊用法
- 每條邊只會在 DFS 被使用以及在查詢時被使用

O(n)

O(n + q)

q

\alpha (n)

Tarjan LCA

namespace Tarjan_LCA {
    struct Node {
        vec<int> neighbors;
        vec<pii> LCA_target;  // LCA partner, index in query queue
    };

    vec<Node> tree;
    vec<bool> visited;
    vec<int> master;
    vec<int> LCAs;
    int root;

    void set_size(int n, int q) {
        tree.resize(n);
        visited.resize(n, false);
        master.resize(n);
        LCAs.resize(q);
        for (int i = 0; i < n; i++)
            master[i] = i;
    }

    void set_root(int index) {
        root = index;
    }

    void add_edge(int u, int v) {
        tree[u].neighbors.push_back(v);
        tree[v].neighbors.push_back(u);
    }

    void add_query(int u, int v) {
        static int cnt = 0;
        tree[u].LCA_target.push_back({v, cnt});
        tree[v].LCA_target.push_back({u, cnt});
        ++cnt;
    }

    void solve() {
        auto find = [&](int n, auto &&find) -> int {
            return (n == master[n]) ? n : (master[n] = find(master[n], find));
        };

        auto combine = [&](int a, int b) -> void {
            a = find(a, find), b = find(b, find);
            if (a == b) return;
            master[b] = a;
        };

        auto dfs = [&](int cur, int pre, auto &&dfs) -> void {
            visited[cur] = true;

            for (const auto &[target, index] : tree[cur].LCA_target)
                if (visited[target])
                    LCAs[index] = find(target, find);

            for (const auto &nxt : tree[cur].neighbors) {
                if (nxt == pre) continue;
                dfs(nxt, cur, dfs);
            }

            combine(pre, cur);
        };

        dfs(root, root, dfs);
    }
}  // namespace Tarjan_LCA

int main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);

    int n, q;
    cin >> n >> q;
    Tarjan_LCA::set_size(n, q);
    Tarjan_LCA::set_root(0);

    for (int u = 1; u < n; u++) {
        int v;
        cin >> v;
        v--;
        Tarjan_LCA::add_edge(u, v);
    }
    for (int i = 0; i < q; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        Tarjan_LCA::add_query(u, v);
    }

    Tarjan_LCA::solve();

    for (const auto &ans : Tarjan_LCA::LCAs)
        cout << ans + 1 << "\n";
}

Tarjan LCA 真的很美，這邊寫長只是因為方便當模板

OTher

倍增法複雜度比較差一點，但有些時候會用到它的性質
還有其他 LCA 的求法，等等會講
- 樹鏈剖分
- 樹壓平

題單

CSES 1687

CSES 1688

CSES 1135

CSES 1136

TIOJ 2196 / TOI 初選 2021 pD

CF #881 F2

CSA Root LCA Queries

TIOJ 2172

樹壓平

Tree Serialization

樹壓平

看中文比較難懂，英文翻成中文叫作「樹的序列化」
顧名思義，就是將一棵樹轉變成序列操作的演算法
序列化不只用在樹，也可以用在圖片等其他資料結構

樹壓平

而一棵樹要怎麼變成序列？
變成序列後最好還要是我們有辦法利用的樣子
於是我們想到了 DFS 序

DFS 序

DFS 序有什麼特徵？
或者說，入點時間戳和出點時間戳有什麼特徵？

(3, 4)

(5, 6)

(2, 7)

(10, 11)

(12, 13)

(9, 14)

(8, 15)

(1, 16)

#(入點, 出點)

DFS 序

DFS 序有什麼特徵？
或者說，入點時間戳和出點時間戳有什麼特徵？

(3, 4)

(5, 6)

(2, 7)

(10, 11)

(12, 13)

(9, 14)

(8, 15)

(1, 16)

#(入點, 出點)

DFS 序

DFS 序有什麼特徵？
或者說，入點時間戳和出點時間戳有什麼特徵？

(3, 4)

(5, 6)

(2, 7)

(10, 11)

(12, 13)

(9, 14)

(8, 15)

(1, 16)

#(入點, 出點)

DFS 序

DFS 序有什麼特徵？
或者說，入點時間戳和出點時間戳有什麼特徵？
你會發現，同一棵子樹的編號是連續的
這樣就可以對子樹砸資結！

(3, 4)

(5, 6)

(2, 7)

(10, 11)

(12, 13)

(9, 14)

(8, 15)

(1, 16)

#(入點, 出點)

DFS 序

不光是入點+出點，只看入點也是連續的

1

2

3

4

5

6

7

8

#入點時間戳

DFS 序

依照編號將節點填入序列中就完成序列化了，長度 2n

struct Node {
    vec<int> neighbors;
    int start, end;
};

vec<int> serialized_tree;

void serialize(int cur, int pre, const vec<Node> &tree) {
    static int time = 0;
    serialized_tree[time] = cur;
    tree[cur].start = time++;
    for (const int &nxt : tree[cur].neighbor) {
        if (nxt == pre) continue;
        serialize(nxt, cur, tree);
    }
    serialized_tree[time] = cur;
    tree[cur].end = time++;
}

DFS 序

僅入點時間戳，長度 n

struct Node {
    vec<int> neighbors;
    int start, end;
};

vec<int> serialized_tree;

void serialize(int cur, int pre, const vec<Node> &tree) {
    static int time = 0;
    serialized_tree[time] = cur;
    tree[cur].start = time++;
    for (const int &nxt : tree[cur].neighbor) {
        if (nxt == pre) continue;
        serialize(nxt, cur, tree);
    }
    tree[cur].end = time;
}

樹壓平

舉個例子：CSES 1137 (Subtree Queries)
子樹和帶修改
子樹在入點時間戳裡面是連續的一個區間
找出這個區間然後求和就好了
修改可以套用線段樹或 BIT 之類的

樹壓平

怎麼找到這個區間？
沒有出點時間戳就沒有右界
僅在入點時改動，在出點時不改動時間戳的話，就可以記錄到子樹的右界

(3, 4)

(4, 5)

(2, 5)

(7, 8)

(8, 9)

(6, 9)

(5, 9)

(1, 9)

#(入點, 出點)

子樹和

struct Node {
    vec<int> neighbors;
    int start, end;
    int val;
};

vec<Node> tree;
vec<int> serialized_tree;

void serialize(int cur, int pre) {
    static int time = 0;
    serialized_tree[time] = cur;
    tree[cur].start = time++;

    for (const int &nxt : tree[cur].neighbors) {
        if (nxt != pre)
            serialize(nxt, cur);
    }

    tree[cur].end = time;
}

struct Stree {
    vec<int> data;
    int size;

    Stree() {
        size = tree.size();
        data.resize(size << 1);
        for (int i = 0; i < size; i++)
            data[i + size] = tree[serialized_tree[i]].val;
        for (int i = size - 1; i > 0; i--)
            data[i] = data[i << 1] + data[i << 1 | 1];
    }

    void modify(int node, int new_val) {
        int pos = tree[node].start;
        pos += size;
        data[pos] = new_val;
        for (; pos > 1; pos >>= 1)
            data[pos >> 1] = data[pos] + data[pos ^ 1];
    }

    int query(int root) {
        int l = tree[root].start, r = tree[root].end;
        int result = 0;
        for (l += size, r += size; l < r; l >>= 1, r >>= 1) {
            if (l & 1) result += data[l++];
            if (r & 1) result += data[--r];
        }
        return result;
    }
};

signed main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);

    int n, q;
    cin >> n >> q;
    tree.resize(n);
    serialized_tree.resize(n);

    for (int i = 0; i < n; i++)
        cin >> tree[i].val;

    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        tree[u].neighbors.push_back(v);
        tree[v].neighbors.push_back(u);
    }

    serialize(0, 0);
    Stree stree;

    for (int i = 0; i < q; i++) {
        int t;
        cin >> t;
        if (t == 1) {
            int s, x;
            cin >> s >> x;
            s--;
            stree.modify(s, x);
        }
        else {
            int s;
            cin >> s;
            s--;
            cout << stree.query(s) << "\n";
        }
    }
}

樹壓平

來看另一種壓法的應用
路徑和帶修改，怎麼用上樹壓平？

1

2

3

4

5

6

7

8

#路徑和

樹壓平

簡化一下問題
CSES 1138 (Path Quries)
如何求根到某點的路徑和？

1

2

3

4

5

6

7

8

#根到點路徑和

樹壓平

求根到某點的路徑和，可以想成根的某個子樹剪掉一些分枝
把不必要的分枝抵消掉
在離開戳記順便抵消該點
由於點在離開後被抵銷，因此只會算到一條分枝

1

2

3

4

5

6

7

8

#根到點路徑和

樹壓平

求根到某點的路徑和，可以想成根的某個子樹剪掉一些分枝
把不必要的分枝抵消掉
在離開戳記順便抵消該點

1

2

3

4

5

6

7

8

#根到點路徑和

樹壓平

求和時應該會包含右邊圈起來的值
離開戳的位置記錄負值，在求和時就會消掉

(3, -3)

(4, -4)

(2, -2)

(7, -7)

(8, -8)

(6, -6)

(5, -5)

(1, -1)

#(入點, 出點資料)

樹壓平

回到原本的問題，你會發現其實就是上面稍微改下
假設要求 d(A, B)
d(A, B) = d(root, A) + d(root, B) - 2 * d(root, LCA(A, B)) + val(LCA(A, B))

d(root, A)

root

LCA

A

B

#路徑和求法

樹壓平

回到原本的問題，你會發現其實就是上面稍微改下
假設要求 d(A, B)
d(A, B) = d(root, A) + d(root, B) - 2 * d(root, LCA(A, B)) + val(LCA(A, B))

d(root, A) + d(root, B)

root

LCA

A

B

#路徑和求法

樹壓平

回到原本的問題，你會發現其實就是上面稍微改下
假設要求 d(A, B)
d(A, B) = d(root, A) + d(root, B) - 2 * d(root, LCA(A, B)) + val(LCA(A, B))

d(root, A) + d(root, B) - 2 * d(root, LCA(A, B))

root

LCA

A

B

#路徑和求法

樹壓平

回到原本的問題，你會發現其實就是上面稍微改下
假設要求 d(A, B)
d(A, B) = d(root, A) + d(root, B) - 2 * d(root, LCA(A, B)) + val(LCA(A, B))

d(root, A) + d(root, B) - 2 * d(root, LCA(A, B)) + val(LCA(A, B))

root

LCA

A

B

#路徑和求法

路徑和

const int root = 0;

struct Node {
    vec<int> neighbors;
    int start, end;
    int val;
};

vec<Node> tree;
vec<int> serialized_tree;

void serialize(int cur, int pre) {
    static int time = 0;
    serialized_tree[time] = tree[cur].val;
    tree[cur].start = time++;

    for (const int &nxt : tree[cur].neighbors) {
        if (nxt != pre)
            serialize(nxt, cur);
    }

    serialized_tree[time] = -tree[cur].val;
    tree[cur].end = time++;
}

struct Stree {
    vec<int> data;
    int size;

    Stree() {
        size = tree.size() << 1;
        data.resize(size << 1);
        for (int i = 0; i < size; i++)
            data[i + size] = serialized_tree[i];
        for (int i = size - 1; i > 0; i--)
            data[i] = data[i << 1] + data[i << 1 | 1];
    }

    void modify(int node, int new_val) {
        int pos = tree[node].start;
        pos += size;
        data[pos] = new_val;
        for (; pos > 1; pos >>= 1)
            data[pos >> 1] = data[pos] + data[pos ^ 1];

        pos = tree[node].end;
        pos += size;
        data[pos] = -new_val;
        for (; pos > 1; pos >>= 1)
            data[pos >> 1] = data[pos] + data[pos ^ 1];
    }

    int query(int node) {
        int l = tree[root].start, r = tree[node].start + 1;
        int result = 0;
        for (l += size, r += size; l < r; l >>= 1, r >>= 1) {
            if (l & 1) result += data[l++];
            if (r & 1) result += data[--r];
        }
        return result;
    }
};

signed main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);

    int n, q;
    cin >> n >> q;
    tree.resize(n);
    serialized_tree.resize(n << 1);

    for (int i = 0; i < n; i++)
        cin >> tree[i].val;

    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        tree[u].neighbors.push_back(v);
        tree[v].neighbors.push_back(u);
    }

    serialize(root, root);
    Stree stree;

    for (int i = 0; i < q; i++) {
        int t;
        cin >> t;
        if (t == 1) {
            int s, x;
            cin >> s >> x;
            s--;
            stree.modify(s, x);
        }
        else {
            int s;
            cin >> s;
            s--;
            cout << stree.query(s) << "\n";
        }
    }
}

LCA

最後還有一種特殊的壓法，用在 LCA 上
不只在入點時記錄，也在每次回到點時記錄！

1

0

2

序列：

#LCA 樹壓平

LCA

最後還有一種特殊的壓法，用在 LCA 上
不只在入點時記錄，也在每次回到點時記錄！

1

0

2

序列：0

#LCA 樹壓平

LCA

最後還有一種特殊的壓法，用在 LCA 上
不只在入點時記錄，也在每次回到點時記錄！

1

0

2

序列：0, 1

#LCA 樹壓平

LCA

最後還有一種特殊的壓法，用在 LCA 上
不只在入點時記錄，也在每次回到點時記錄！

1

0

2

序列：0, 1, 0

#LCA 樹壓平

LCA

最後還有一種特殊的壓法，用在 LCA 上
不只在入點時記錄，也在每次回到點時記錄！

1

0

2

序列：0, 1, 0, 2

#LCA 樹壓平

LCA

最後還有一種特殊的壓法，用在 LCA 上
不只在入點時記錄，也在每次回到點時記錄！

1

0

2

序列：0, 1, 0, 2, 0

#LCA 樹壓平

LCA

最後還有一種特殊的壓法，用在 LCA 上
不只在入點時記錄，也在每次回到點時記錄！

1

0

2

序列：0, 1, 0, 2, 0

#LCA 樹壓平

LCA

在兩點之間路徑的點會出現在兩點時間戳間
LCA 就在尋找兩路徑間深度最低的點
記錄各點深度，然後用 Sparse Table 或線段樹之類的求
問題：這樣序列不會有太多點嗎？
- 每個點在入點時有一次
- 一個點同時還會有它子節點數量的次數
- 長度 = n + (n - 1) = 2n - 1
這個方法運行時間表現還不錯，寫起來也算方便

不排除是我 Tarjan 寫太爛

LCA

struct Node {
    vec<int> neighbors;
    int start, depth;
};

vec<Node> tree;
vec<pii> serialized_tree;

void serialize(int cur, int pre, int depth) {
    static int time = 0;
    serialized_tree[time] = {depth, cur};
    tree[cur].start = time++;
    for (const int &nxt : tree[cur].neighbors) {
        if (nxt == pre) continue;
        serialize(nxt, cur, depth + 1);
        serialized_tree[time++] = {depth, cur};
    }
}

struct Stree {
    vec<pii> data;
    int size;

    Stree() {
        size = serialized_tree.size();
        data.resize(size << 1);
        for (int i = 0; i < size; i++)
            data[i + size] = serialized_tree[i];

        for (int i = size - 1; i > 0; i--)
            data[i] = min(data[i << 1], data[i << 1 | 1]);
    }

    int query(int a, int b) {
        pii ans = {INF, -1};
        int l = tree[a].start + size, r = tree[b].start + size;
        if (l > r) std::swap(l, r);
        for (++r; l < r; l >>= 1, r >>= 1) {
            if (l & 1) ans = min(ans, data[l++]);
            if (r & 1) ans = min(ans, data[--r]);
        }
        return ans.second;
    }
};

int main() {
    std::ios_base::sync_with_stdio(0), std::cin.tie(0);
    int n, q;
    cin >> n >> q;
    tree.resize(n);
    serialized_tree.resize((n << 1) - 1);

    for (int i = 1; i < n; i++) {
        int u;
        cin >> u;
        u--;
        tree[u].neighbors.push_back(i);
    }

    serialize(0, 0, 0);
    Stree LCA;

    for (int i = 0; i < q; i++) {
        int a, b;
        cin >> a >> b;
        a--, b--;
        cout << LCA.query(a, b) + 1 << "\n";
    }
}

題單

CSES 1135

CSES 1136

CSES 1137

TIOJ 2257 / 2021 全國賽 pG

CF #756 pE2

CSES 1688

樹鍊剖分

Heavy-light Decomposition, HLD

樹鍊剖分

顧名思義，樹鍊剖分是把樹剖分成好幾條鍊的演算法
其實還有幾種剖分方法
- 輕重鍊剖分
- 實虛鍊剖分
- 長鍊剖分
這份簡報集中在常見的輕重鍊剖分，也就是 HLD

樹鍊剖分

把樹變成鍊有什麼好處？
鍊可以套用常見的資結，例如線段樹
- 你沒聽錯，樹上有樹
HLD 一般拿來處理路徑相關問題
- 路徑問題？為什麼不用樹壓平

樹鍊剖分

例子：CSES 2134 (Path Quries II) 路徑最大值帶修改
現在最大值沒有辦法抵消了，樹壓平行不通
這種時候專門處理路徑問題的樹鍊剖分就能用了

樹鍊剖分

就算要把樹切成鍊，也要切得有性質能利用
舉個例子，希望讓需要處理的鍊的數量少一點
這就是輕重鍊剖分的目標

樹鍊剖分

如何在處理更少鍊的情況下將樹剖成鍊？
一個想法：將一個點和它最大的子樹相連

#HLD

樹鍊剖分

如何在處理更少鍊的情況下將樹剖成鍊？
一個想法：將一個點和它最最大的子樹相連

#HLD

樹鍊剖分

和最大子樹相連的邊稱為重邊
連接鍊之間的邊稱為輕邊

#重邊

樹鍊剖分

和最大子樹相連的邊稱為重邊
連接鍊之間的邊稱為輕邊

#輕邊

樹鍊剖分

鍊頂端的節點稱為輕子節點
其餘稱為重子節點

#輕子節點

樹鍊剖分

鍊頂端的節點稱為輕子節點
其餘稱為重子節點

#重子節點

樹鍊剖分

可以證明，透過這種拆法，點到根路徑間切換鍊的次數是的
最壞情況下，從該點往根跳轉鍊子樹大小至少會變成兩倍
經過次跳轉後子樹大小故

O(log\ n)

k

2^k \geq n

k \in O(log\ n)

樹鍊剖分

而根據定義，實作就很簡單了
預處理子樹大小，找出重兒子並記錄
根據需求進行樹壓平、開資結等等操作

樹鍊剖分

struct Node {
    vec<int> neighbors;	 // 另一種做法是讓第零個為重子節點
    int hson = null;	 // 重子節點，子樹（含本身）大小
};

vec<Node> tree;

int preprocess(int cur, int pre) {	// 回傳子樹大小
    int sub_size = 1;
    int max_son_size = 0;
    for (const int &nxt : tree[cur].neighbors) {
        if (nxt == pre) continue;
        int nxt_size = preprocess(nxt, cur);
        sub_size += nxt_size;
        if (nxt_size > max_son_size) {
            max_son_size = nxt_size;
            tree[cur].hson = nxt;
        }
    }
    return sub_size;
}

樹鍊剖分

現在問題來了：怎麼利用這些鍊？
先從更簡單的 LCA 看起
類似倍增法，在往上爬的過程中看深度相不相同

樹鍊剖分

與倍增法不同的是向上爬是直接爬到鍊頂的父節點
決定誰向上爬是用鍊頂的深度決定
鍊頂相同代表較高者為 LCA

A

B

此時 A, B 鍊頂相同說明在同條鍊

所以深度較淺者 B 為 LCA

#HLD LCA

樹鍊剖分

與倍增法不同的是向上爬是直接爬到鍊頂的父節點
決定誰向上爬是用鍊頂的深度決定
鍊頂相同代表較高者為 LCA

A'

B'

此時 B' 的鍊頂比較深

B' 向上爬

#HLD LCA

樹鍊剖分

與倍增法不同的是向上爬是直接爬到鍊頂的父節點
決定誰向上爬是用鍊頂的深度決定
鍊頂相同代表較高者為 LCA

A'

B'

此時 A' 的鍊頂比較深

A' 向上爬

#HLD LCA

樹鍊剖分

與倍增法不同的是向上爬是直接爬到鍊頂的父節點
決定誰向上爬是用鍊頂的深度決定
鍊頂相同代表較高者為 LCA

A'

B'

此時 A' 的鍊頂比較深

A' 向上爬

#HLD LCA

樹鍊剖分

與倍增法不同的是向上爬是直接爬到鍊頂的父節點
決定誰向上爬是用鍊頂的深度決定
鍊頂相同代表較高者為 LCA

A'

B'

A', B' 鍊頂相同，較淺者 A' 為 LCA

#HLD LCA

樹鍊剖分

類似地，如果要找路徑上最小值可以對每條鍊開線段樹
或者...?

A'

B'

A', B' 鍊頂相同，較淺者 A' 為 LCA

#HLD LCA

樹鍊剖分

其實可以直接開一棵大的線段樹
利用樹壓平的想法，將鍊拆分成線段樹上的片段

路徑最小值

#include <stdio.h>

#include <functional>
#include <vector>
using std::vector;
const int max_n = 2e5 + 1;
const int INF = 2e9;
struct node {
	int parent = 1, size = 1, hson = 0, depth = 0, top = 1, dfn = -1;
	int value;
	vector<int> neighbor;
} graph[max_n];

struct stree {
	inline static int tree[max_n << 1];
	int size;
	inline void build() {
		for (int i = size - 1; i > 0; i--) {
			tree[i] = std::max(tree[i << 1], tree[i << 1 | 1]);
		}
		return;
	}
	inline int query(int l, int r) {
		int ans = -INF;
		for (l += size, r += size; l < r; l >>= 1, r >>= 1) {
			if (l & 1) ans = std::max(ans, tree[l++]);
			if (r & 1) ans = std::max(ans, tree[--r]);
		}
		return ans;
	}
	inline void modify(int pos, int x) {
		for (pos += size, tree[pos] = x; pos > 1; pos >>= 1) {
			tree[pos >> 1] = std::max(tree[pos], tree[pos ^ 1]);
		}
		return;
	}
} max;
void dfs1(int cur) {
	static int depth = 0;
	graph[cur].depth = ++depth;
	int max_size = 0;
	for (const auto& next : graph[cur].neighbor) {
		if (!graph[next].depth) {
			graph[next].parent = cur;
			dfs1(next);
			graph[cur].size += graph[next].size;
			if (graph[next].size > max_size) {
				max_size = graph[next].size;
				graph[cur].hson = next;
			}
		}
	}
	--depth;
	return;
}
void dfs2(int cur) {
	static int dfn = 0;
	graph[cur].dfn = dfn;
	max.tree[dfn + max.size] = graph[cur].value, dfn++;
	if (graph[cur].hson) {
		graph[graph[cur].hson].top = graph[cur].top;
		dfs2(graph[cur].hson);
	}
	else {
		return;
	}
	for (const auto& next : graph[cur].neighbor) {
		if (next != graph[cur].parent && next != graph[cur].hson) {
			graph[next].top = next;
			dfs2(next);
		}
	}
	return;
}
int main() {
	int n, q;
	scanf("%d%d", &n, &q);
	max.size = n;
	for (int i = 1; i <= n; i++) scanf("%d", &graph[i].value);
	int u, v;
	for (int i = 0; i < n - 1; i++) {
		scanf("%d%d", &u, &v);
		graph[u].neighbor.push_back(v);
		graph[v].neighbor.push_back(u);
	}
	dfs1(1);
	dfs2(1);
	max.build();
	int type, x, ans;
	while (q--) {
		scanf("%d", &type);
		if (type == 1) {
			scanf("%d%d", &v, &x);
			max.modify(graph[v].dfn, x);
		}
		else {
			ans = -INF;
			scanf("%d%d", &u, &v);
			// LCA
			while (graph[u].top != graph[v].top) {
				if (graph[graph[u].top].depth < graph[graph[v].top].depth) std::swap(u, v);
				ans = std::max(ans, max.query(graph[graph[u].top].dfn, graph[u].dfn + 1));
				u = graph[u].top;
				u = graph[u].parent;
			}
			if (graph[u].dfn > graph[v].dfn) std::swap(u, v);
			ans = std::max(ans, max.query(graph[u].dfn, graph[v].dfn + 1));
			printf("%d\n", ans);
		}
	}
	return 0;
}

題單

CSES 1135

CSES 1136

CSES 1137

TIOJ 2257 / 2021 全國賽 pG

CF #756 pE2

CSES 1688

樹重心

Tree Centroid

重心

說到重心，你會想到什麼？
- 作用於質心的力不會造成力矩（被打）
- 三角形中三中線的交點（幾何中心）

重心

無論如何，它們都都具有類似的性質
以三角形來說，重心和平分面積有很大的關係
以重心為界，兩邊似乎具有某種對稱性

樹重心

以樹來說，最簡單的性質就是子樹大小
所以重心定義為任何一個子樹都不超過 n/2 的點
- 有可能有兩個點嗎?
- 有可能，最簡單的例子就是兩個點連在一起

樹重心

有了定義後，找重心就很簡單了
預處理每個子樹的大小
再 DFS 一次，確定每個子樹的大小都不超過 n/2
- 每個子樹包含父節點那個子樹，用 n 去扣剩下的
如果有個點符合，那它就是重心

樹重心

樹重心就只講這樣，剩下的性質太多講不完
可以參考簡報前面的補充

路徑最小值

#include <stdio.h>
 
#include <utility>
#include <vector>
using std::pair;
using std::vector;
const int max_n = 2e5 + 1;
struct node {
	int size = 1;
	vector<int> neighbor;
} tree[max_n];
int tree_size;
void pre_size(int cur, int parent) {
	for (const auto &next : tree[cur].neighbor) {
		if (next != parent) pre_size(next, cur), tree[cur].size += tree[next].size;
	}
	return;
}
int get_centroid(int cur, int parent) {
	for (const auto &next : tree[cur].neighbor) {
		if (next != parent) {
			if (tree[next].size > (tree_size >> 1)) return get_centroid(next, cur);
		}
	}
	return cur;
}
int main() {
	scanf("%d", &tree_size);
	int u, v;
	for (int i = 0; i < tree_size - 1; i++) {
		scanf("%d%d", &u, &v);
		tree[u].neighbor.push_back(v);
		tree[v].neighbor.push_back(u);
	}
	pre_size(1, 1);
	printf("%d", get_centroid(1, 1));
	return 0;
}

題單

CSES 2079