樹論
講師:張秉中
今天要講的
好像有點多...
- what is 樹
- 樹直徑
- 樹DP
- 樹重心
- LCA
- 樹壓平
- 輕重鍊剖分
- 重心剖分
- 關於樹,你還可以學的
What is 樹(tree)
- 沒有環的圖->共有n-1條邊
- 每個點對有唯一最短路徑
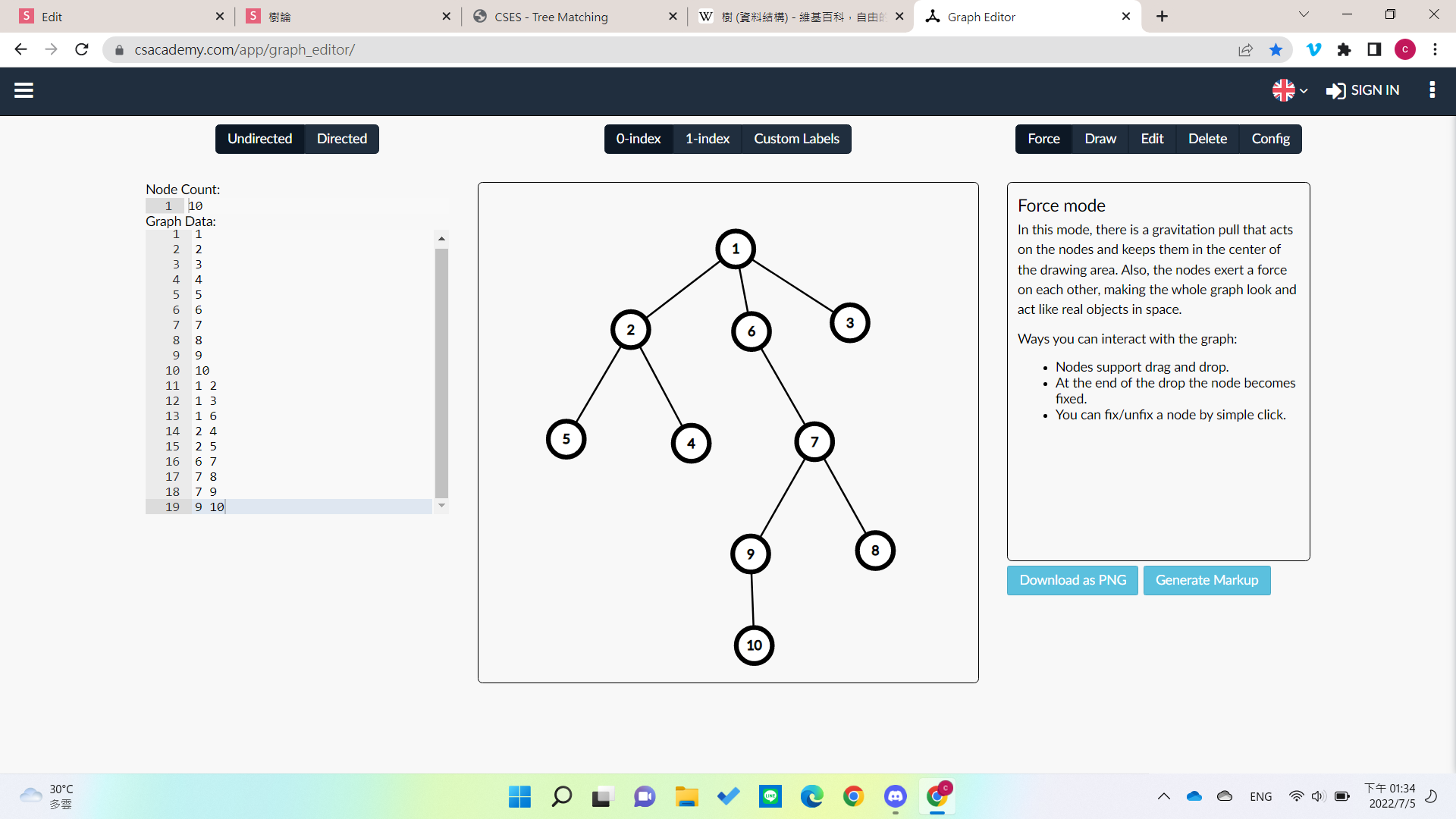
一些名詞
以1為根結點
- 1是2的父節點(parent)
- 2是1的子節點(child)

7的子樹
subtree
5的祖先
ancestor
一些名詞
以1為根結點
深度(degree):
根結點到此節點的最短距離

0
1
2
3
4
一些名詞
以1為根結點
葉節點:沒有子節點的節點

樹直徑 & DFS
diameter
樹上距離最遠的點對
How to 找直徑?
- DFS/BFS
- 樹DP
DFS/BFS
- 隨便選一個點BFS/DFS找最遠點
- 從最遠點BFS/DFS一次最遠點即為直徑
例子
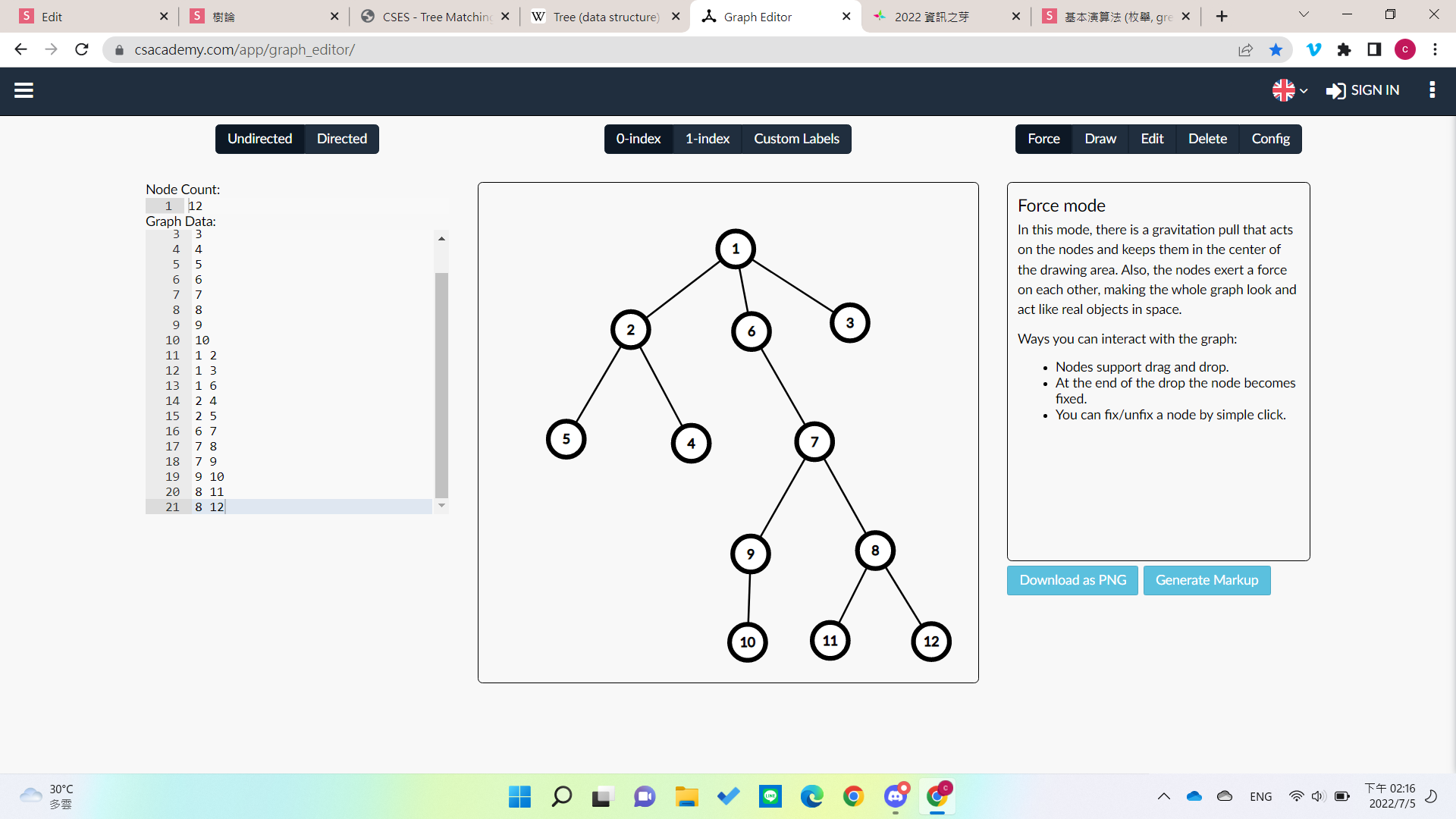
0
1
1
1
2
2
2
2
3
4
5
5
例子

0
1
2
2
3
4
5
5
3
6
6
6
例子

0
1
2
2
3
4
5
5
3
6
6
6
樹DP之後會講到
題目(DFS+BFS)
樹DP
DP on tree
樹DP
- 基本上就是跑DFS時先計算子節點答案,在反推回父節點
- 在節點紀錄其子樹的答案
簡單的範例
給一棵以節點1為根大小為N(N<2e5)的樹,求樹上各點子樹大小-1
解題思路
- DFS子節點
- 當節點為葉節點時,答案為1
- 否則,節點答案為其子節點大小總和+1
- 注意此題最後輸出答案時要-1,因為要去掉自己
code
#include <bits/stdc++.h>
using namespace std;
const int mxn = 2e5+10;
vector<int> childs[mxn];
int sz[mxn] = {};
int n;
void dfs(int now){
sz[now] = 1;
for(auto nxt:childs[now]){
dfs(nxt);
sz[now] += sz[nxt];
}
return;
}
int main(){
cin>>n;
for(int i = 2;i<=n;i++){
int p;
cin>>p;
childs[p].push_back(i);
}
dfs(1);
for(int i = 1;i<=n;i++)cout<<sz[i]-1<<' ';
return 0;
} 回到樹直徑
- 定根,然後DFS
- 在節點紀錄:
- 若為葉節點: 則記錄{1}
- 各子節點為一端之最長路徑+1
- 則答案為所存之所有節點中DP之(最大值+次大值-1)中最大的
圖示

{1}
{1}
{1}
圖示

{1}
{1}
{1}
{2}
{2,2}
圖示

{1}
{1}
{1}
{2}
{2,2}
{max({2})+1,
max({2,2})+1}
圖示

{1}
{1}
{1}
{2}
{2,2}
{3,3}
{max({3,3})+1}
圖示

{1}
{1}
{1}
{2}
{2,2}
{3,3}
{4}
圖示

{1}
{1}
{1}
{2}
{2,2}
{3,3}
{4}
{1}
{1}
{1}
{2,2}
{3,5,2}
在DFS一次
如果只有一個子節點則答案為
max(目前答案,該節點值)
否則答案為
max(目前答案,該節點最大值+次大值-1)

{1}
{1}
{1}
{2}
{2,2}
{3,3}
{4}
{1}
{1}
{1}
{2,2}
{3,5,2}

{1}
{1}
{1}
{2}
{2,2}
{3,3}
{4}
{1}
{1}
{1}
{2,2}
{3,5,2}
3+5-1=7
1
4
2+2-1=3
1
1
1
1
2
1
2+2-1=3
3+3-1=5

{1}
{1}
{1}
{2}
{2,2}
{3,3}
{4}
{1}
{1}
{1}
{2,2}
{3,5,2}
3+5-1=7
1
4
2+2-1=3
1
1
1
1
2
1
2+2-1=3
3+3-1=5
如果好好做的話,時間複雜度為O(n)
題目
樹重心
centroid
性質
- 去除後所有子樹大小不超過總節點數/2
- 一棵樹最多有兩個重心,若且唯若兩重心相鄰
how to 找重心
(對不起我只會一種作法)
- 隨便選一個點當根,並且預處理所有點的子樹大小(用樹DP)
- 跑dfs,如果有一個子節點大小>節點數/2->重心在那棵子樹
- 如果找不到則此節點就是重心
code
#include <bits/stdc++.h>
using namespace std;
struct node{
int par,sz;
vector<int> childs;
node(){
par = -1,sz = 1;
}
};
int n;
vector<node> tree;
void get_sz(int now){
for(auto nxt:tree[now].childs){
if(nxt == tree[now].par)continue;
tree[nxt].par = now;
get_sz(nxt);
tree[now].sz += tree[nxt].sz;
}
return;
}
int get_centroid(int now){
for(auto nxt:tree[now].childs){
if(nxt == tree[now].par)continue;
if(tree[nxt].sz>n/2)return get_centroid(nxt);
}
return now;
}
int main(){
cin>>n;
tree = vector<node>(n+1,node());
for(int i = 0;i<n-1;i++){
int a,b;
cin>>a>>b;
tree[a].childs.push_back(b);
tree[b].childs.push_back(a);
}
get_sz(1);
cout<<get_centroid(1);
}題目
樹壓平
tree flattening
樹壓平
- 就是把DFS的順序壓時間戳
- 壓法1:只在進點跟出點時壓時間戳
- 可以發現進出點之間的時間戳就是其子樹
- 壓法2:在每次遞迴時壓出發點的時間戳
- 優點是一個節點在其子節點之間穿插出現
- 因此找LCA會變成找兩時間戳之間深度最淺的點
- 壓法1:只在進點跟出點時壓時間戳
題目
輕重鍊剖分
樹鍊剖分
heavy-light decomposition(HLD)
功能
- 處理有關「路徑」的問題
- 可以在樹上套資料結構(eg:線段樹)
概念
- 每次找大小最大的子節點連成一條鍊
- 其他子節點接出別條鍊
- 修改節點時,修改鍊上的點,以及接到這條鍊的區間
OI wiki的圖
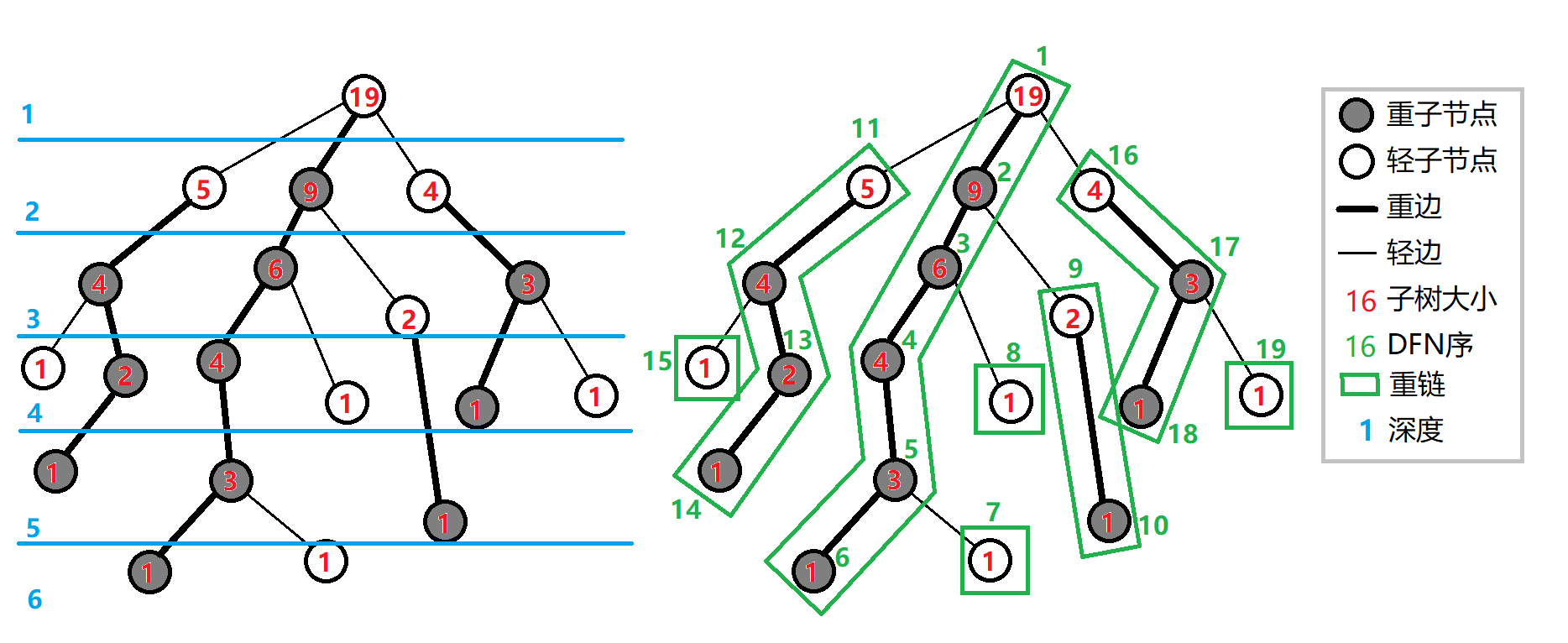
實作LCA
- 定根,dfs第一次,算子樹大小
- dfs第二次,往最大子樹走時鍊頂不動,否則鍊頂設為子節點,壓時間戳
- 找lca時,當兩者鍊頂不同,將鍊頂較深的節點往上跳到鍊頂的父節點
- 當鍊頂相同時則比較節點深度,較淺者為LCA
code
#include <bits/stdc++.h>
using namespace std;
struct node{
int link_top,depth,sz,par,big_son;
vector<int> childs;
node(){
link_top = -1;
depth = -1;
sz = 1;
big_son = -1;
}
};
vector<node> tree;
vector<int> time_stamp;
void dfs1(int now){
for(auto nxt:tree[now].childs){
if(nxt == tree[now].par)continue;
tree[nxt].par = now;
tree[nxt].depth = tree[now].depth+1;
dfs1(nxt);
if(tree[now].big_son == -1 || tree[tree[now].big_son].sz<tree[nxt].sz)tree[now].big_son = nxt;
tree[now].sz += tree[nxt].sz;
}
return;
}
void dfs2(int now,int top){
time_stamp.push_back(now);
tree[now].link_top = top;
if(tree[now].big_son != -1)dfs2(tree[now].big_son,top);
for(auto nxt:tree[now].childs){
if(nxt == tree[now].par||nxt == tree[now].big_son)continue;
dfs2(nxt,nxt);
}
return;
}
int lca(int a,int b){
int ta = tree[a].link_top,tb = tree[b].link_top;
while(ta != tb){
if(tree[ta].depth>tree[tb].depth){
swap(ta,tb);
swap(a,b);
}
//update link
b = tree[tb].par;
tb = tree[b].link_top;
cout<<a<<' '<<b<<endl;
}
if(tree[a].depth>tree[b].depth){
swap(a,b);
}
//update link(更新同鏈上的兩節點)
return a;
}
int main(){
int n;
cin>>n;
tree = vector<node>(n+1,node());
for(int i = 1;i<=n-1;i++){
int a,b;
cin>>a>>b;
tree[a].childs.push_back(b);
tree[b].childs.push_back(a);
}
dfs1(1);
dfs2(1,1);
}HLD複雜度
O(log(n))
- 可以證明,每次詢問最多跳log(n)條鍊
題目
實作題
重心剖分
centroid decomposition
總之建一棵重心樹
- 找重心,設為根節點
- 把重心「拔掉」(可以用一個bool表示)
- 對所有剩下的子樹找重心
網路上的圖
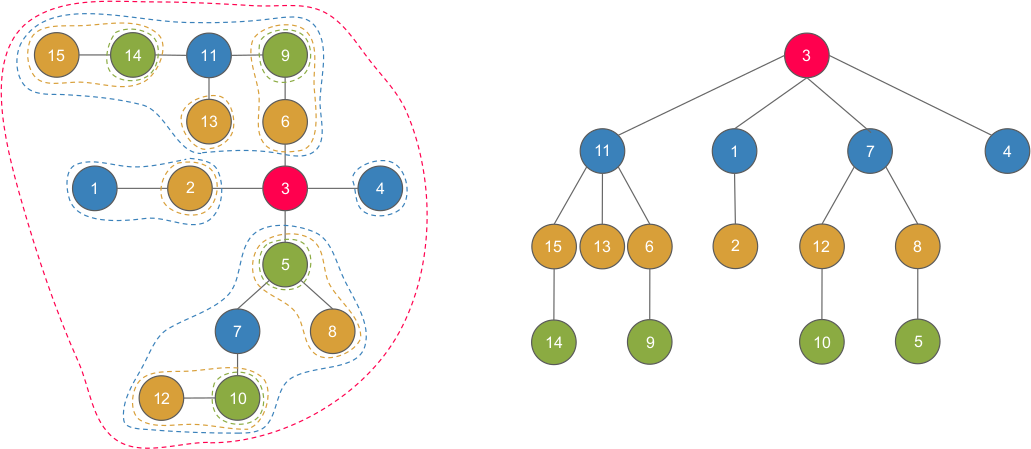
code
#include <bits/stdc++.h>
using namespace std;
struct node{
int sz;
int parent;
bool del;
int val;
vector<int> childs;
node(){
parent = -1;
del = false;
val = -1;
}
};
vector<node> tree;
vector<node> centree;
void get_sz(int now,int par){
tree[now].sz = 1;
for(auto nxt:tree[now].childs){
if(nxt == par||tree[nxt].del)continue;
get_sz(nxt,now);
tree[now].sz += tree[nxt].sz;
}
return;
}
int find_centroid(int now,int par,int tar){
for(auto nxt:tree[now].childs){
if(nxt == par||tree[nxt].del)continue;
if(tree[nxt].sz>tar)return find_centroid(nxt,now,tar);
}
return now;
}
int cendfs(int now,int par){
get_sz(now,now);
int cen = find_centroid(now,now,tree[now].sz/2);
tree[cen].del = true;
centree[par].childs.push_back(cen);
centree[cen].parent = par;
for(auto nxt:tree[cen].childs){
if(tree[nxt].del)continue;
cendfs(nxt,cen);
}
return cen;
}
int main(){
int n;
cin>>n;
tree = vector<node>(n+1,node());
centree = vector<node>(n+1,node());
for(int i = 0;i<n-1;i++){
int a,b;
cin>>a>>b;
tree[a].childs.push_back(b);
tree[b].childs.push_back(a);
}
int root = cendfs(1,0);
dfs(root,root);
}
重心樹的性質
- 深度不超過log(n)
- 重心樹上兩點LCA在兩點最短路徑上
- 思考一下
作法
- 總之先建重心樹
- 重心樹根節點開始,計算經過節點的答案,然後拔掉節點
- how to 算一棵樹經過根的答案?
- 紀錄每個子節點各深度的節點數cnt,之後經過點i時,該點答案為cnt[k-depth[i]]
- (注意depth在跑重心樹時需要重新計算)
- 繼續遞迴
作法

O(n)
作法

O(size(11))
作法

O(size(15))
作法

O(size(14))
經過觀察
- 複雜度為:O(sum(size(i)))
- 又重心樹上同一深度的節點數量和為深度-1
- 重心樹深度不超過log(n)
- 所以複雜度為O(nlog(n))
好像沒有用到重心樹的另一個性質耶
- 就是兩點最短路經過LCA的性質
- 重心剖分經典題 : Xenia and Tree
留給讀者自行思考
複雜度O(nlog(n)+qlog(n)log(n))或O((n+q)log(n))
看有沒有優化LCA
題目
經過這堂課,你學到了
- 樹直徑
- 樹DP
- 樹重心
- LCA
- 樹壓平
- 輕重鍊剖分
- 重心剖分
關於樹,你還可以學的
其實是講師不會的
- 樹背包問題
- 換根DP
- 樹分塊
- link cut tree(這應該算樹吧)
謝謝大家
樹論
By ck1100890張秉中
樹論
- 760

