更多樹

講師:張秉中

目錄

 

  • 重心樹
  • 樹同構
  • 換根DP
  • 樹背包問題
  • 淺談LCT

重心樹

上次講太少了QQ

圖

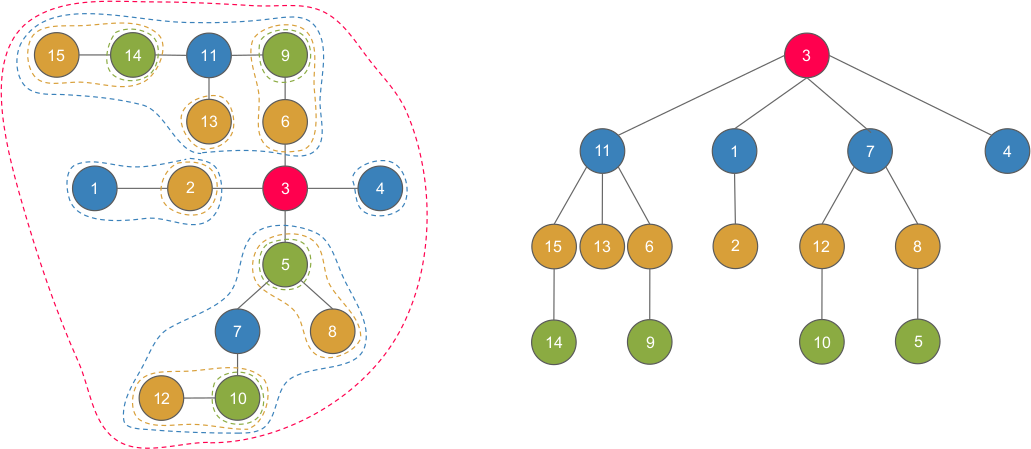
性質

  • 深度log(n)
  • 重心樹上兩點LCA必定在其路徑上

Xenia and Tree

  • 蓋重心樹，在各點記錄到紅點的最短距離，令其為\(ans[u]\)
  • 修改\(v\)時沿著重心樹往上改，並且更新最短距離
    • 各點距離最近的紅點變為\(min(ans[u],dist(u,v))\)
  • 查詢\(v\)時沿著重心往上走，並且計算答案為
    • \(shortest =min(shortest,ans[u]+dist(u,v))\) 

還可以記錄其他資訊

  • 像是該連通塊各點到重心的距離之類的
    • 這樣只需要 \(O(NlogN)\)的記憶體

樹同構

問題(cses1700)

  • 給兩個有根樹，判斷其是否可以將根結點以外的點重新編號使兩樹長一樣

Hash

ll dfs(vector<int> tree[],int now,int par){
	vector<ll> tmp;
	for(auto nxt:tree[now]){
		if(nxt == par)continue;
		tmp.push_back(dfs(tree,nxt,now));
	}
	sort(tmp.rbegin(),tmp.rend());
	ll re = 1;
	for(auto &i:tmp){
		re*= p;
		re += i;
		re %= mod;
	}
	return re;
}

重新編號

map<vector<int>,int> mp;
int idx = 0;
void dfs1(int now,int par){
    vector<int> tmp;
    for(auto nxt:tree[now]){
        if(nxt == par)continue;
        dfs1(nxt,now);
        tmp.push_back(dp[nxt]);
    }
    sort(tmp.begin(),tmp.end());
    if(!mp[tmp]){
        dp[now] = mp[tmp] = ++idx;
    }
    else dp[now] = mp[tmp];
    return;
}

無根樹呢?

  • 所有點當根試一輪?
  • 有一些特殊點數量很少?

無根樹呢?

  • 所有點當根試一輪?
  • 有一些特殊點數量很少?
  • 選重心當根!(一棵樹最多只有兩個重心)

換根DP

直接看題目

CSES Tree Distances II/ABC 220F

先處理單點的距離和

  • 顯然樹DP
  • 以要求的點為根且深度為0，答案就是各點深度和
  • DP時在各點紀錄深度大小
  • 複雜度O(N)

暴力作法

  • 對每個點為根都樹DP一次算答案
  • 複雜度 O(N^2)，爛掉了

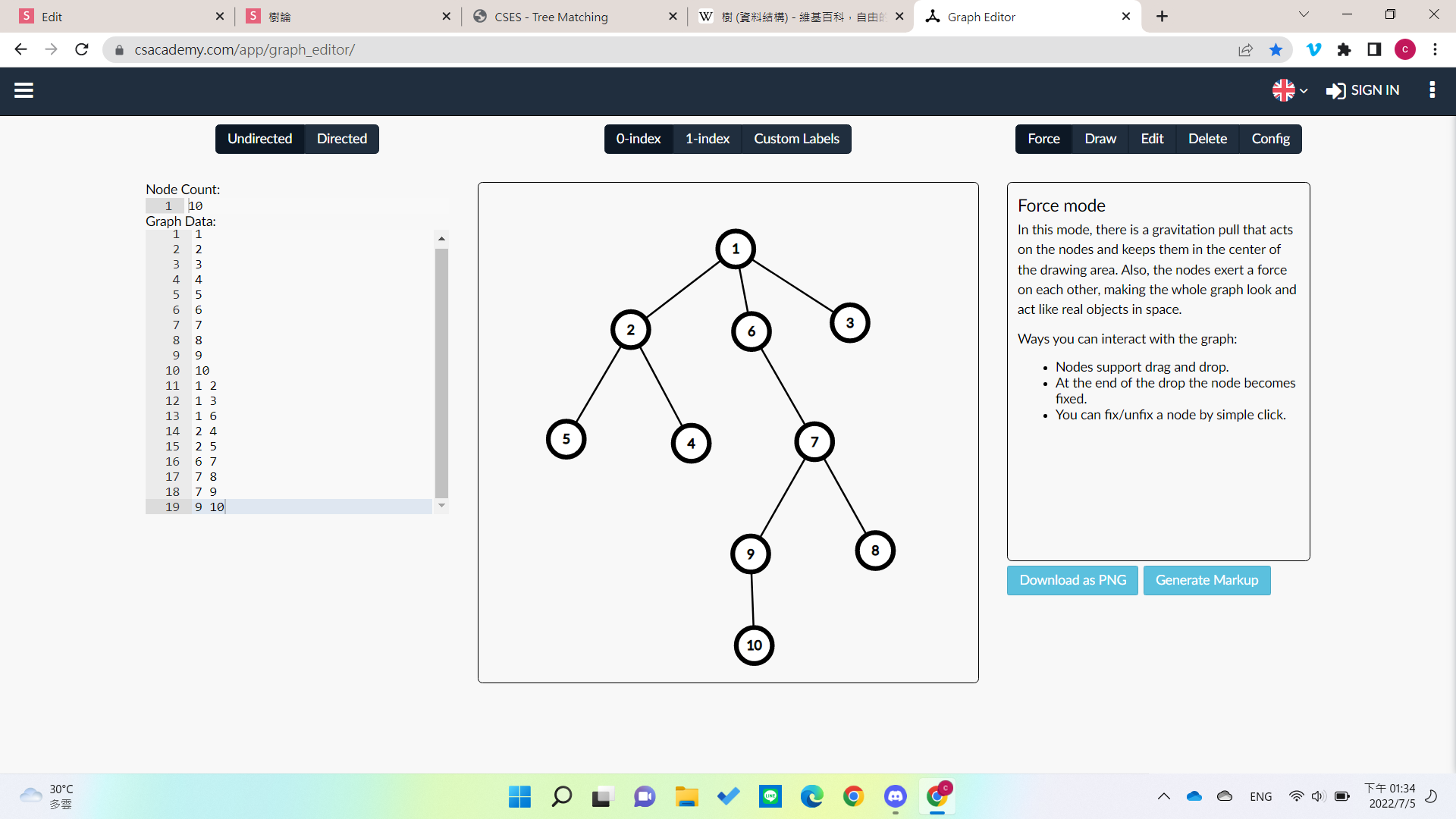
觀察

  • 假如現在已經以1為跟算完答案了
  • 我們以和1相鄰的點算的答案比較
  • 以2為例

1

1

1

2

2

2

3

3

4

0

觀察

  • 假如現在已經以1為跟算完答案了
  • 我們以和1相鄰的點算的答案比較
  • 以2為例

0

2

2

1

3

1

4

4

5

1

觀察

  • 假如現在已經以1為跟算完答案了
  • 我們以和1相鄰的點算的答案比較
  • 以2為例

0

2

2

1

3

1

4

4

5

1

觀察

  • 當我們把根從u變成v時，以u為根時v的子樹所有點深度會-1，其他點的深度會+1
  • 令f(u)表示以u為根時的深度和
  • 可以推得，f(v) = f(u)-size(v)+(n-size(v))

於是，我們得到一個算法

  • 先以任意點為根(通常選1)樹DP一次，算一個點的答案以及各點子樹大小
  • DFS第二次
  • 第二次DFS經過點u時用u的父節點的答案計算u的答案

流程

3

1

5

1

4

1

2

1

1

10

19

流程

3

1

5

1

4

1

2

1

1

10

19

19-3+(10-3) = 23

23

流程

3

1

5

1

4

1

2

1

1

10

19

23-1+(10-1) = 31

23

31

流程

3

1

5

1

4

1

2

1

1

10

19

23-1+(10-1) = 31

23

31

31

流程

3

1

5

1

4

1

2

1

1

10

19

19-5+(10-5) = 19

23

31

31

19

流程

3

1

5

1

4

1

2

1

1

10

19

19-5+(10-5) = 19

23

31

31

19

21

27

36

27

28

做完了!

  • 複雜度:O(N)

其他換根DP

樹背包問題

先看題目

luogu P2014

一些觀察

  • 會形成一棵樹，節點的父節點是直接先修課
  • 把沒有直接先修課的點想成接到0號點
  • 所求就是以0為根大小為m+1的樹的最大權重和

考慮樹DP

  • 另DP(u,i)表示u的子樹選<=i個包含u的最大權重和
  • 令u為v的父節點
  • dfs的同時計算個節點的DP(u,i) for 1<=i<=m+1

考慮樹DP

0,5,5,5,5,5

令DP(u,i)表示u的子樹選<=i個包含u的最大權重和\newline dfs的同時計算個節點的DP(u,i) for 1<=i<=m+1

考慮樹DP

0,5,5,5,5,5

令DP(u,i)表示u的子樹選<=i個包含u的最大權重和\newline dfs的同時計算個節點的DP(u,i) for 1<=i<=m+1\newline 合併子樹的答案時，用類似背包問題的方法對每個子樹分別處理

0,4,4,4,4,4

0,2,7,7,7,7

考慮樹DP

0,5,5,5,5,5

令DP(u,i)表示u的子樹選<=i個包含u的最大權重和\newline dfs的同時計算個節點的DP(u,i) for 1<=i<=m+1\newline 合併子樹的答案時，用類似背包問題的方法對每個子樹分別處理

0,4,4,4,4,4

0,2,7,11,11,11

code 大概長這樣

const int mxn = 303;
vector<int> tree[mxn];
int dp[mxn][mxn]
void dfs(int now,int par){
    for(auto nxt:tree[now]){
        if(nxt == par)continue;
        dfs(nxt,now);
        for(int i = mxn-1;i>=2;i--){
            for(int j = 1;j<i;j++){
                dp[now][i] = max(dp[now][i],dp[now][i-j]+dp[nxt][j]);
            }
        }
    }
}

複雜度

有n個節點，每個節點內要跑m \times m的迴圈\newline 複雜度為O(N \times M^2) \newline 如果今天N,M \leq 2000?

優化

sz紀錄目前的子樹大小

const int mxn = 1010;
vector<int> tree[mxn];
int dp[mxn][mxn];
int sz[mxn];

void dfs(int now,int par){
    sz[now] = 1;
    for(auto nxt:tree[now]){
        if(nxt == par)continue;
        dfs(nxt,now);
        sz[now] += sz[nxt];
        for(int i = sz[now];i>=2;i--){
            for(int j = max(i-sz[now]+sz[nxt],0);j<=min(i-1,sz[nxt]);j++){
                dp[now][i] = max(dp[now][i],dp[now][i-j]+dp[nxt][j]);
            }
        }
    }
}

另一種寫法

sz紀錄目前的子樹大小

const int mxn = 1010;
vector<int> tree[mxn];
int dp[mxn][mxn];
int sz[mxn];

void dfs(int now,int par){
    sz[now] = 1;
    for(auto nxt:tree[now]){
        if(nxt == par)continue;
        dfs(nxt,now);
        for(int i = sz[now];i>=2;i--){
            for(int j = 1;j<=sz[nxt];j++){
                dp[now][i+j] = max(dp[now][i+j],dp[now][i]+dp[nxt][j]);
            }
        }
        sz[now] += sz[nxt];
    }
}

複雜度估算

令T(u)表示u的子樹DP的複雜度\newline T(葉節點) = O(1)\newline T(u) = \Sigma_{son}T(v)+t(u)\newline t(u) = 1+(sz[v_1]+1)\times sz[v_1]+(1+sz[v_1]+sz[v_2])*sz[v_2]+...\newline t(u) = 1+sz[v_1]^2+sz[v_1] \times sz[v_2]+sz[v_1] \times sz[v_3]+...\newline +sz[v_2]^2+sz[v_2] \times sz[v_3]+sz[v_2] \times sz[v_4]+.. \newline \leq 1+(sz[v_1]+sz[v_2]+sz[v_3]+...)^2 = sz[u]^2\newline

複雜度估算

T(u) = \Sigma_{son}T(v)+sz[u]^2\newline = \Sigma_{son}sz[v]^2+sz[u]^2 \leq 2 \times sz[u]^2\newline 因此複雜度為O(N^2)

題目

Splay

 

簡介

又是Tarjan弄的\newline 一顆用轉動來維持複雜度的二元樹\newline 維持中序遍歷不改變\newline 特色是在每次做完詢問之後會做splay操作把剛使用過的節點轉到根結點

旋轉

  • 把自己深度-1
  • 分為左旋、右旋

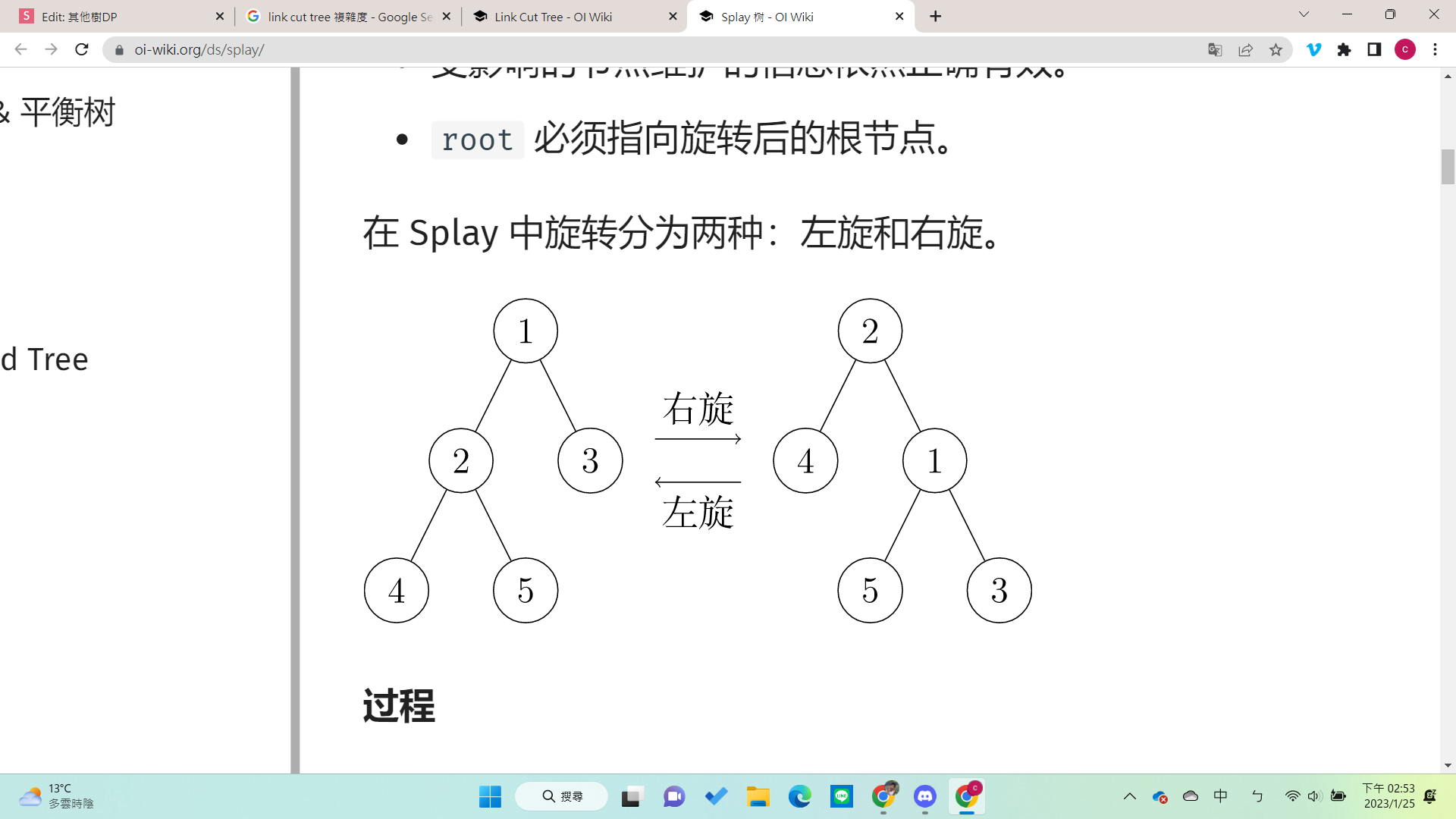
左旋

  • rc不動
  • f 的右邊變成lc
  • p的左邊變成f

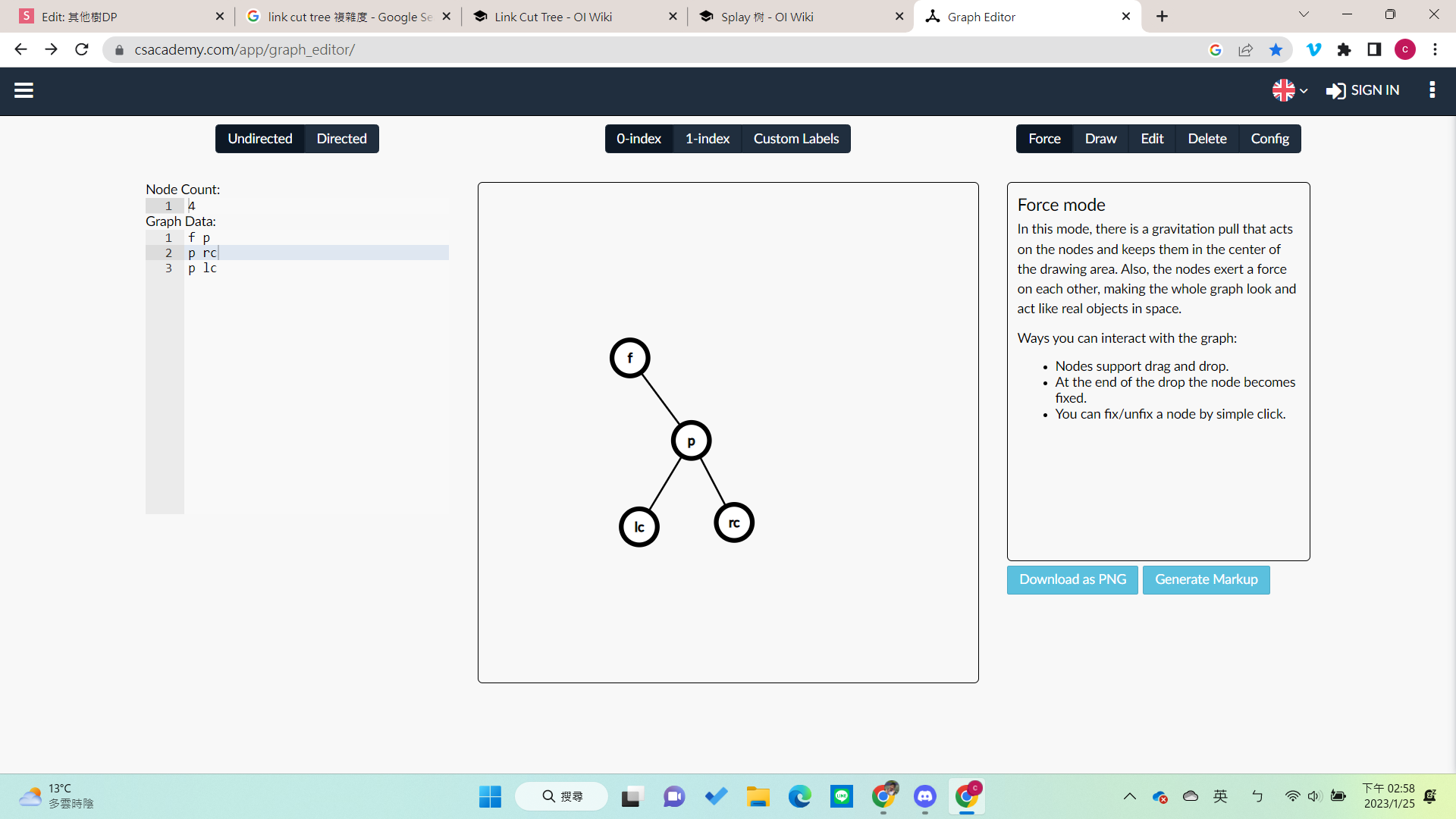
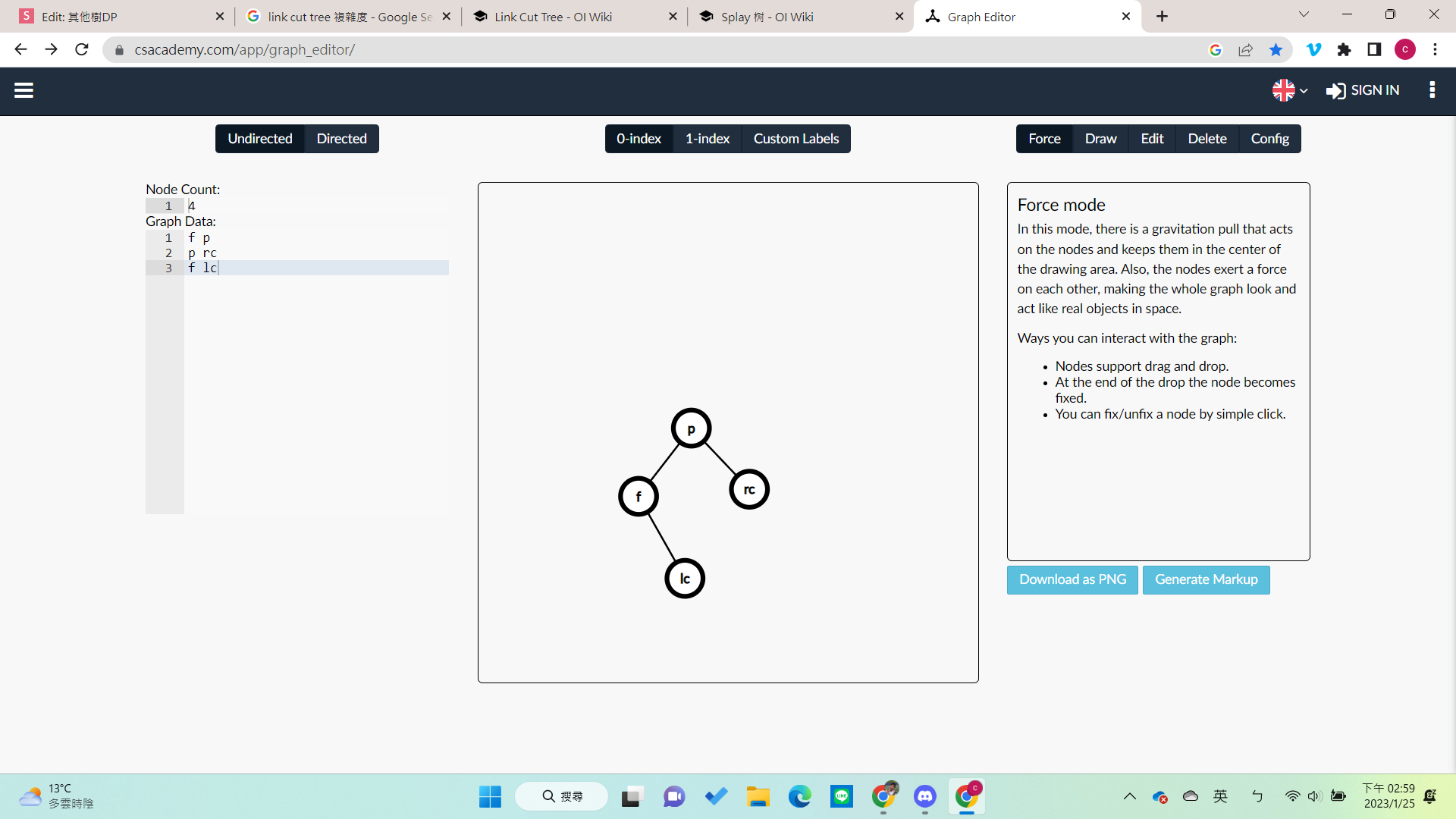
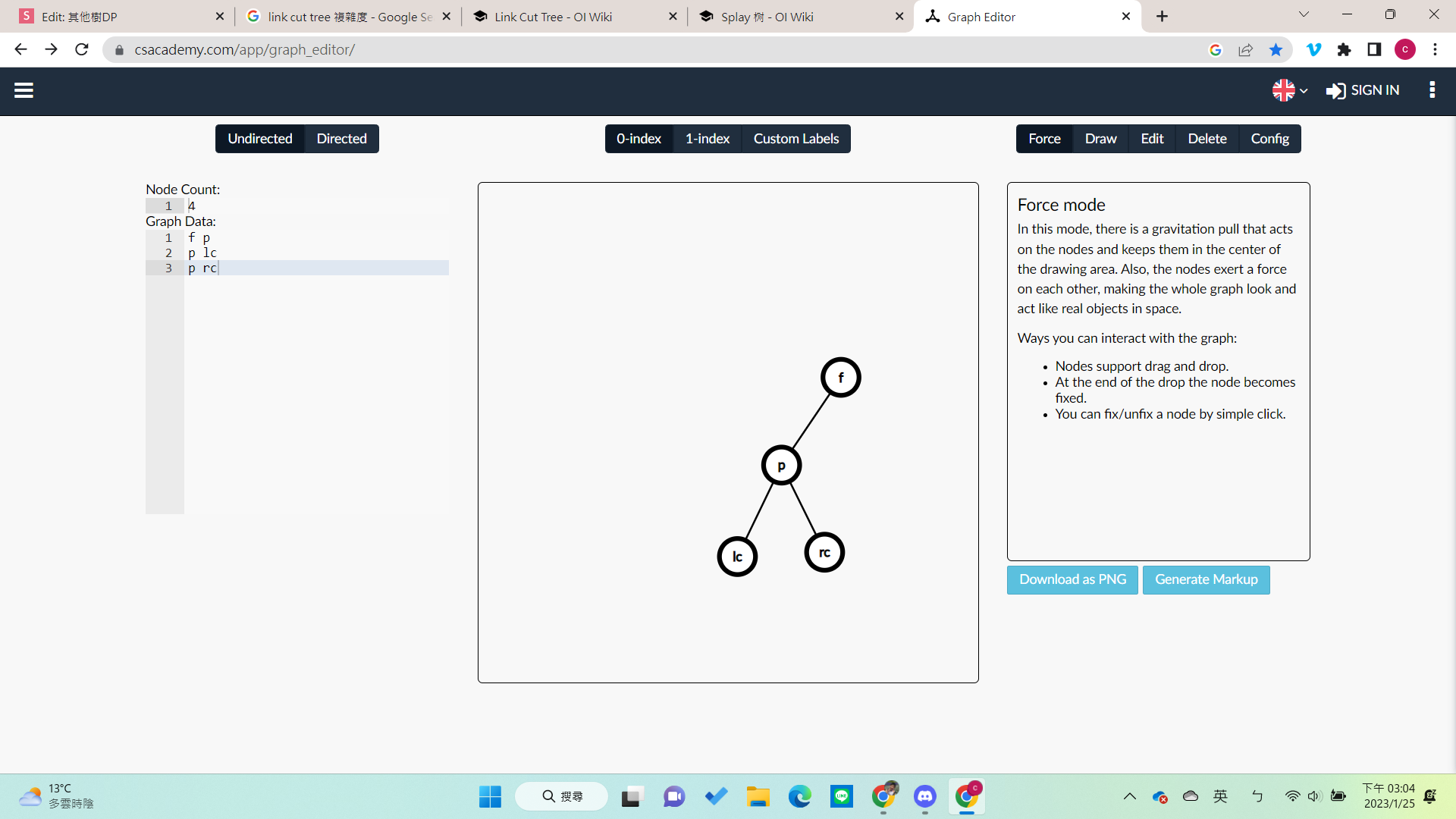
右旋

  • lc不動
  • f 的左邊變成rc
  • p的右邊變成f

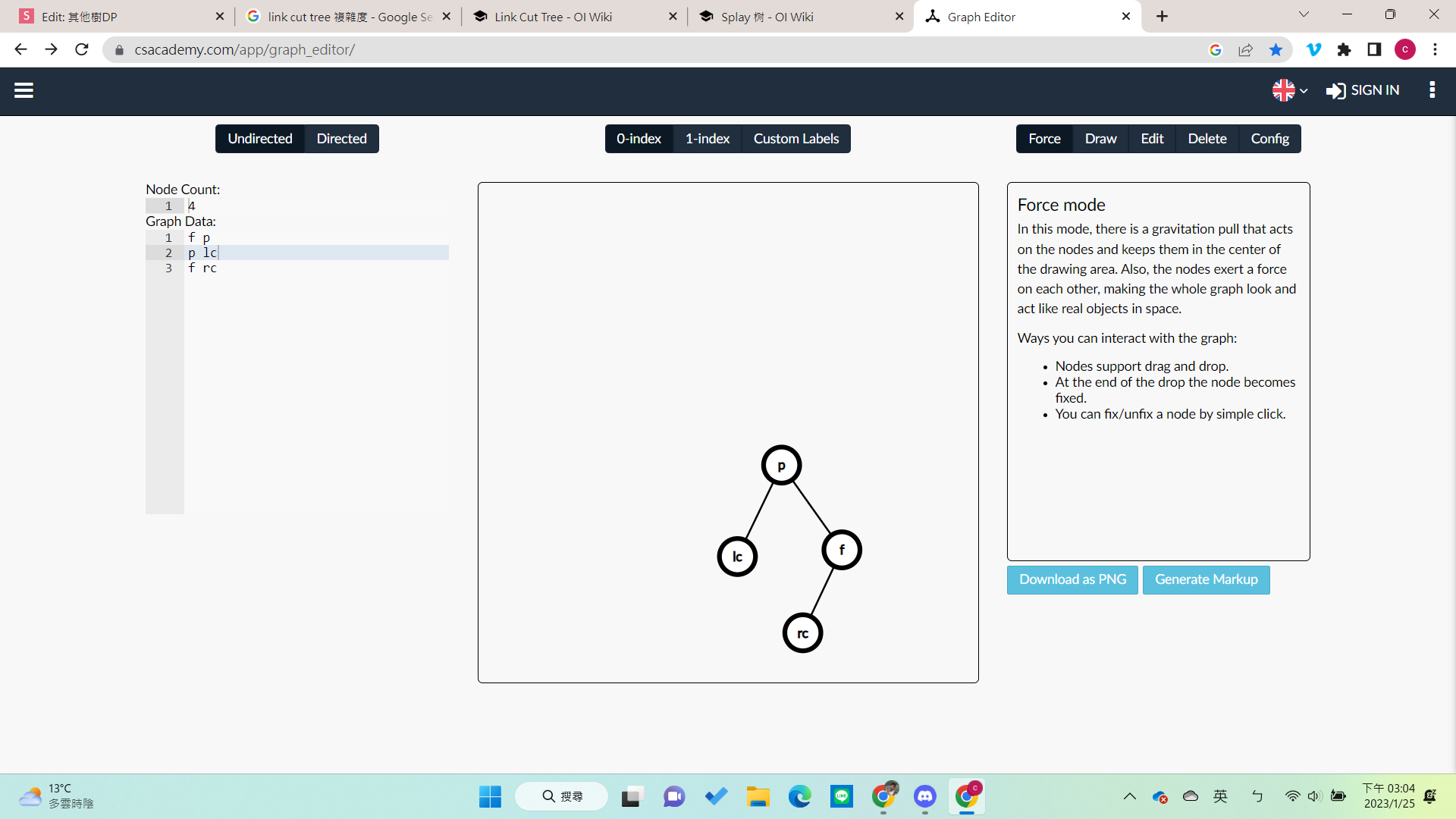
code

#include <bits/stdc++.h>
using namespace std;
const int mxn = 2e5+10;
int childs[mxn][2];
int par[mxn];
bool get(int id){
    if(!id||!par[id])return 0;
    if(childs[par[id]][0] == id)return 0;
    else if(childs[par[id]][1] == id)return 1;
    else{
    cout<<"ERROR "<<id<<endl;
    return 0;
    }
}
void rotate(int id){
    push(par[id]);
    push(id);
    int lr = get(id);
    int p = par[id];
    int g = par[par[id]];
    childs[g][get(p)] = id;
    par[id] = g;
    childs[p][lr] = childs[id][lr^1];
    par[childs[id][lr^1]] = p;
    childs[id][lr^1] = p;
    par[p] = id;//注意pull的順序
    pull(p);
    pull(id);
    pull(g);
    return;
}

splay

  • splay的轉動主要就是左右旋這兩種組合成的
  • 主要是判自己，父親跟祖父三代的關係來轉
  • 分case!

Case 1:沒有祖父

zig

  • 直接左旋或右旋把自己變成根結點

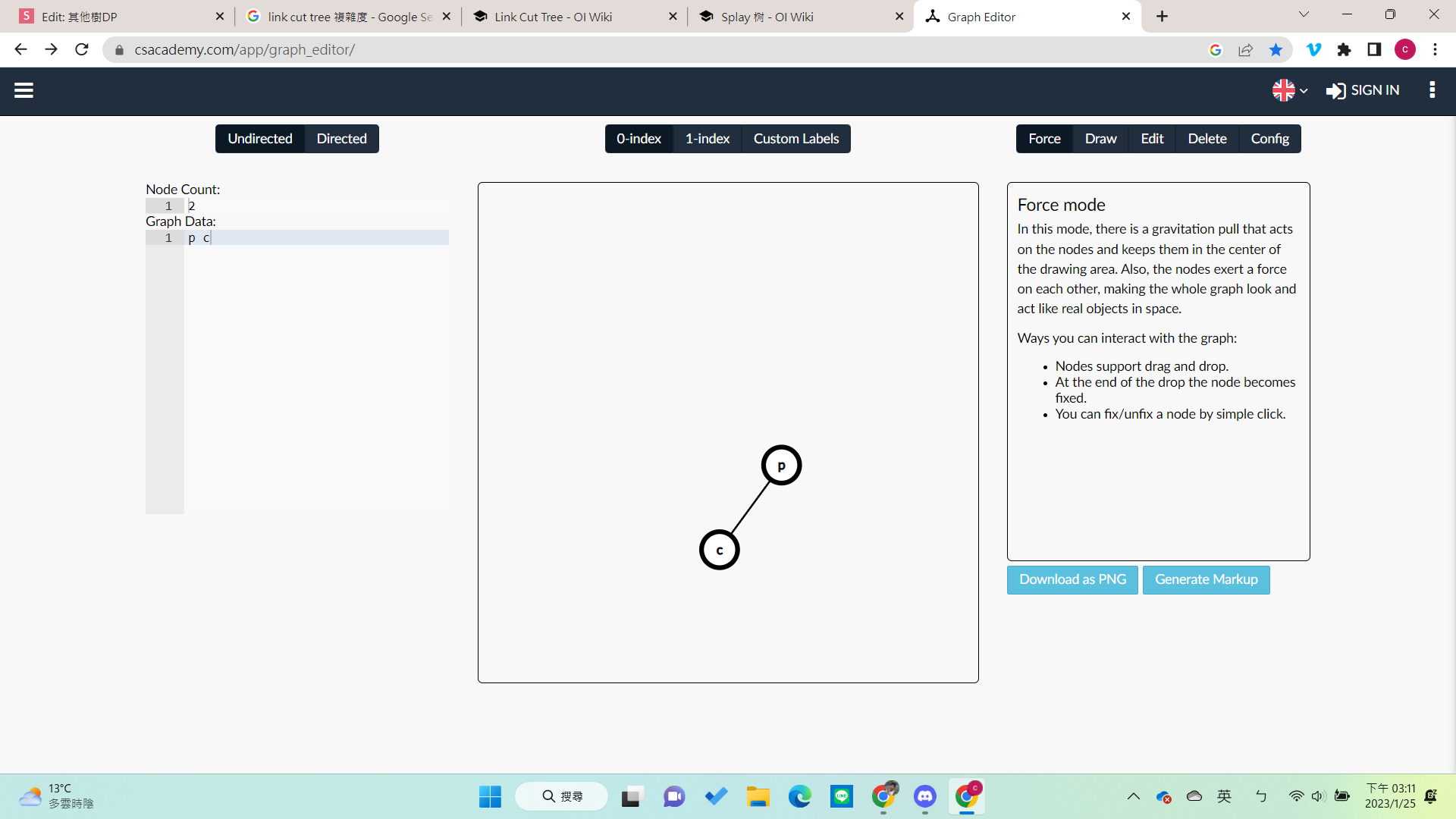
Case 2:祖父跟父親方向相同

zig-zig

  • 先轉父親再轉自己

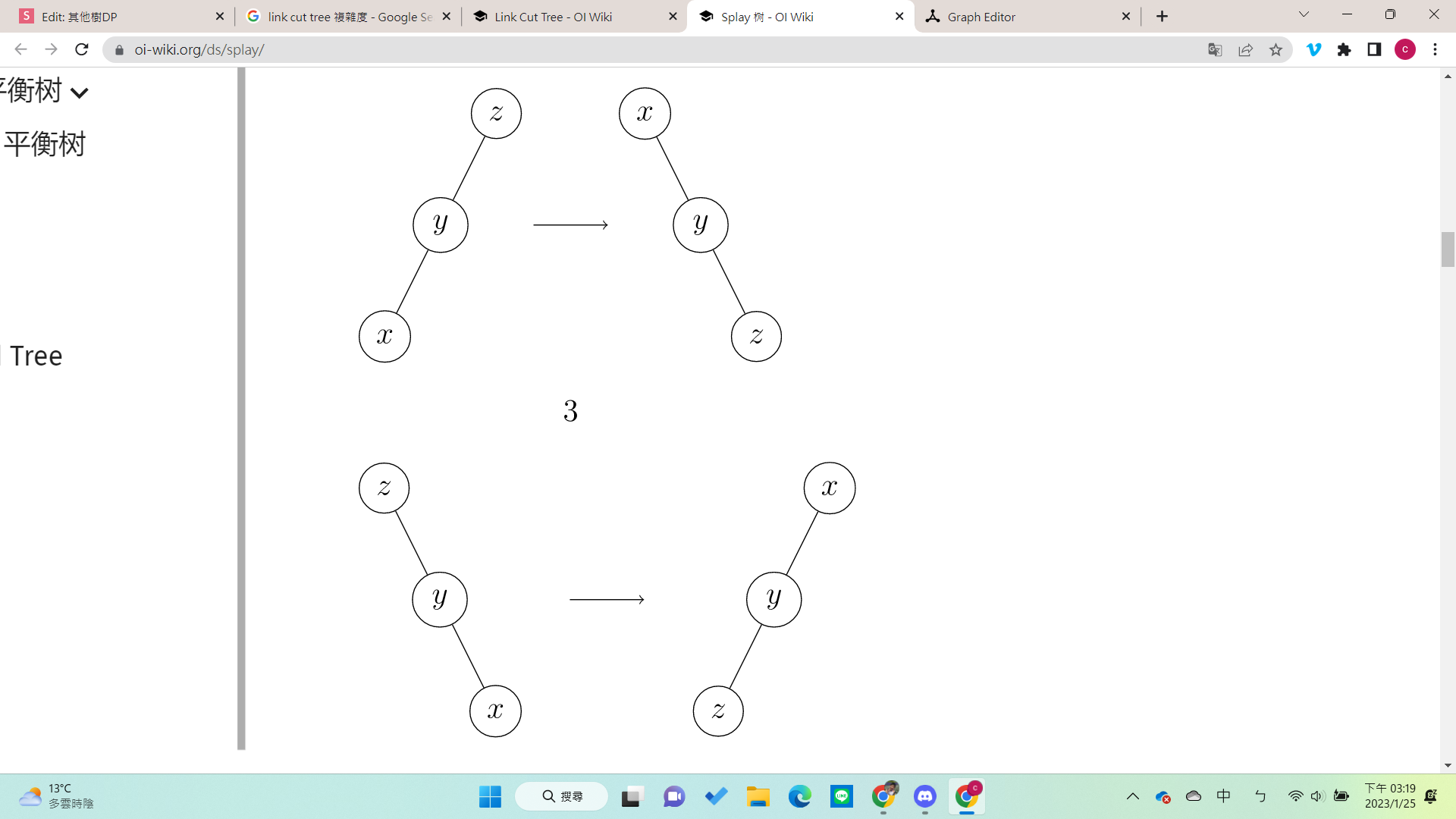
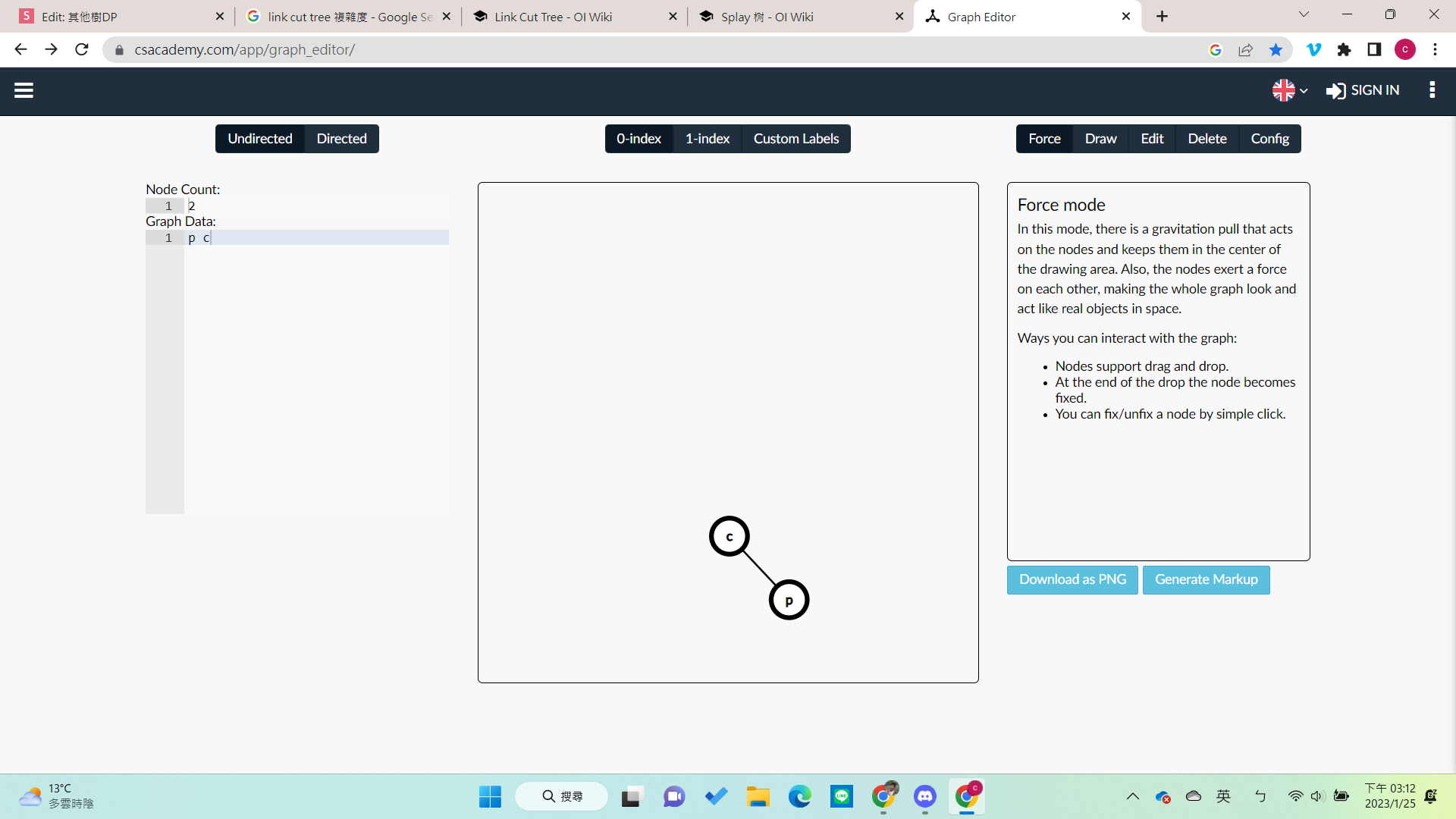
Case 3:祖父跟父親方向相反

zig-zag

  • 自己轉兩次

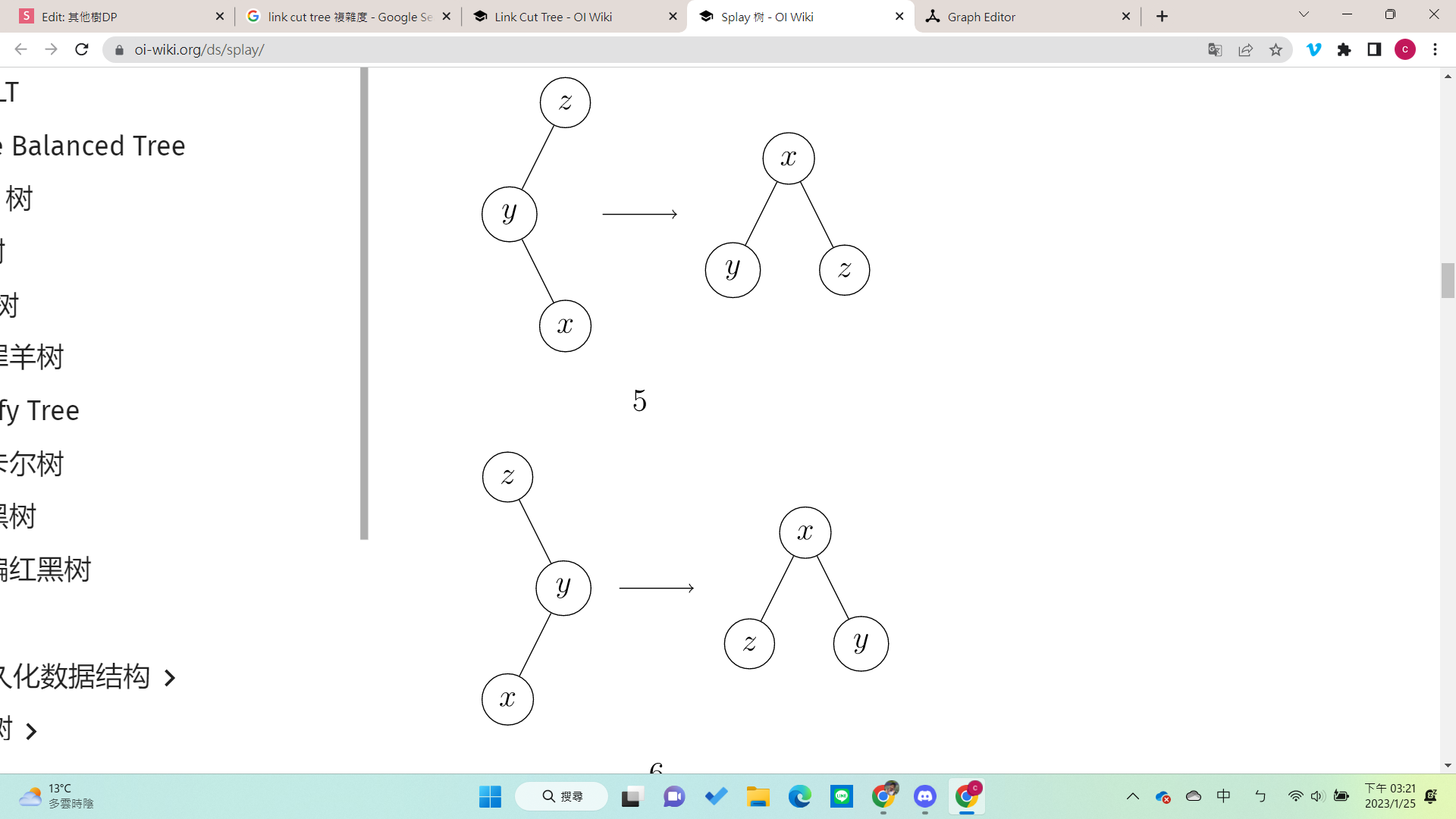
code

    void splay(int id){
        if(!id)return;
        while(par[id]){
            if(par[par[id]])push(par[par[id]]);
            push(par[id]);
            push(id);
            if(!par[par[id]]){
                rotate(id);
                return;
            }
            if(get(par[id]) == get(id))rotate(par[id]);
            else rotate(id);
            rotate(id);
        }
    }

然後pull跟push要記得做

其他性質

  • 可以上懶標(轉動的同時push+pull)
  • 可以merge,split
  • 基本上treap可以做的他應該都行
  • 做完所有操作要記得splay一下

複雜度證明

勢能分析

  • \(x\)代表一個樹的狀態(長相)
  • 令第i次操作所花費的時間為\(c_i(x)\)
  • 先假設一個函數\(\Phi_i(x)\)
  • 使得\(c'_i(x) = c_i(x)+\Phi_i(x)-\Phi_{i-1}(x)\)
  • 則\(\sum_0^t c'_i(x) \ge \sum_0^t c_i(x)\) 的條件為 \(\Phi_{t}(x)-\Phi_0(x) \ge 0\)

複雜度證明

勢能分析

  • 在這裡，我們通靈出\(\Phi(x)=\sum log|x|\)(\(|x|\)為子樹大小)
  • 然後，我們開始分析三種操作的\(c(x)+\Phi(x)-\Phi'(x)\)

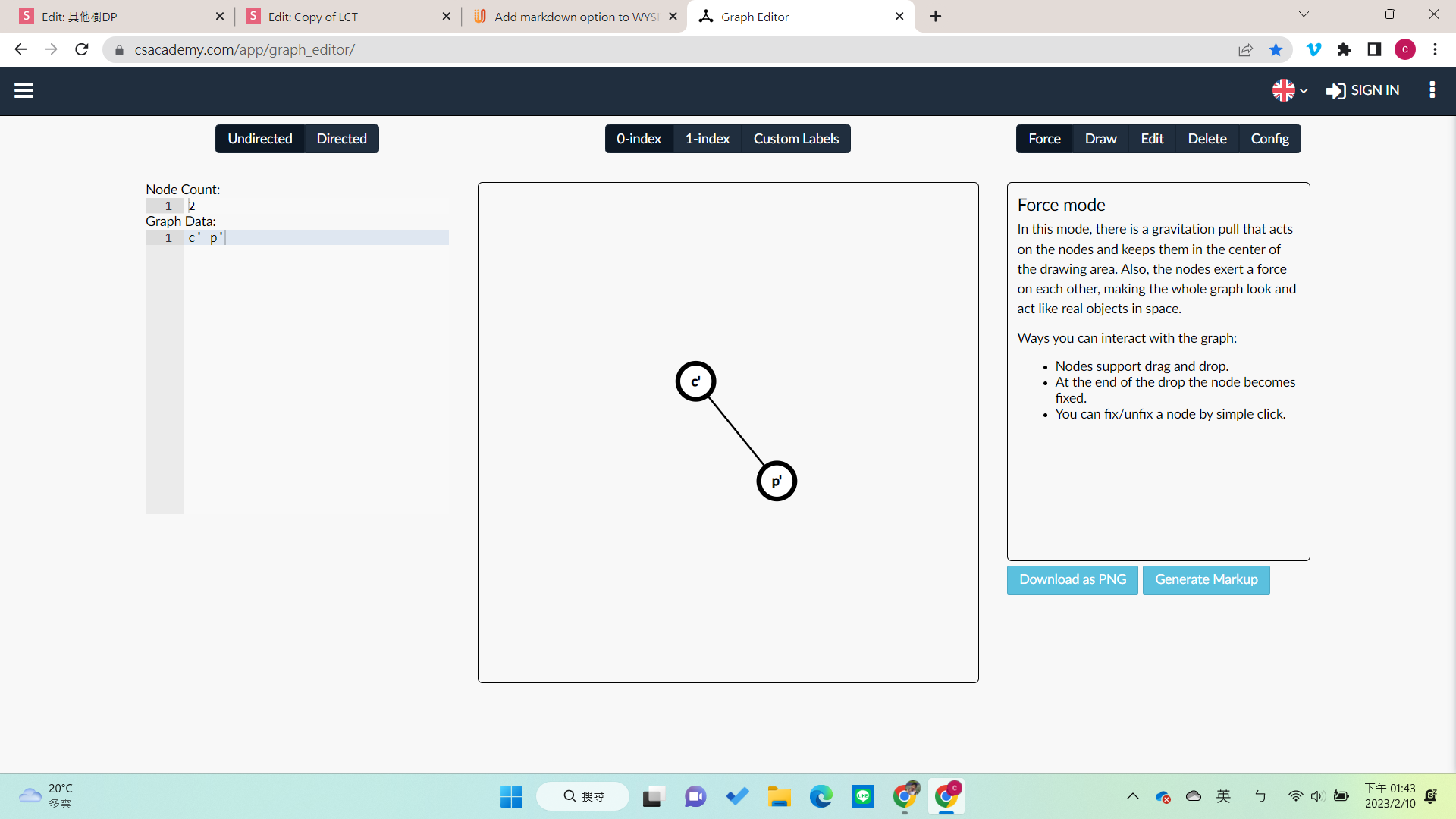
Case 1

zig

\(c(x) = 1\)

\(\Delta\Phi(x) = log|c'|+log|p'|-log|p|-log|c|\)

\(=log|p'|-log|c|(|p|=|c'|)\)

\( \le log|c'|-log|c|(|p'|\le|c'|)\)

\(c(x)+\Delta \Phi(x) \le 1+log|c'|-log|c| \le 3\times (log|c'|-log|c|)+1\)

Case 2:祖父跟父親方向相同

zig-zig

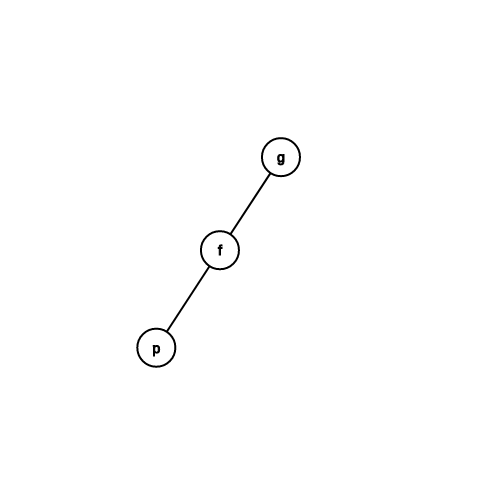
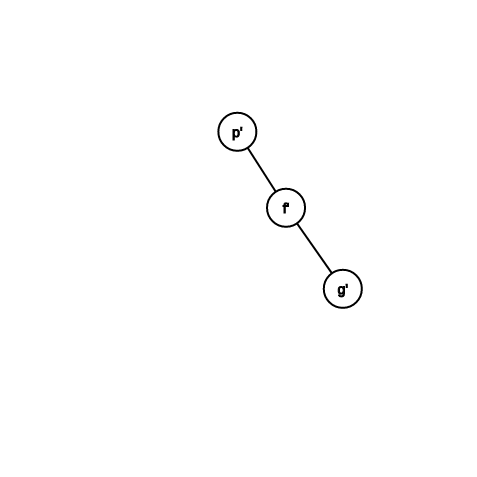
\(c(x) = 2\)

\(\Delta\Phi(x) = log|p'|+log|f'|+log|g'|-log|g|-log|f|-log|p|\)

\(=log|f'|+log|g'|-log|f|-log|p|(|g|=|p'|)\)

\(\le log|p'|+log|g'|-2\times log|p| (|p|\le |f| ,  |f'|\le |p'|)\)

\(又log|g'|+log|p| \le 2\times log \frac{|g'|+|p|}{2}\le 2\times (log|p'|-1)\)

\(因此log|g'| \le 2\times (log|p'|-1)-log|p|\)

\(c(x)+\Delta \Phi(x) \le 3\times (log|p'|-log|p|)\)

Case 3:祖父跟父親方向相同

zig-zag

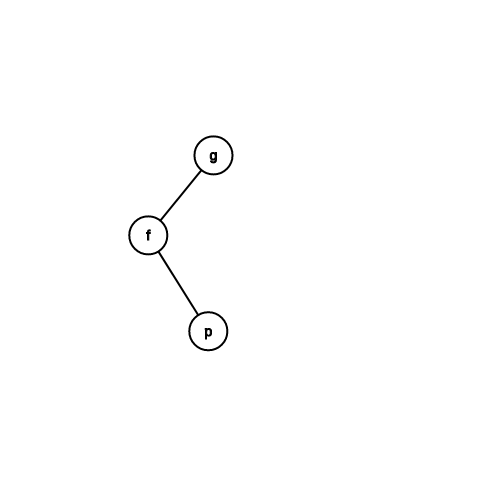
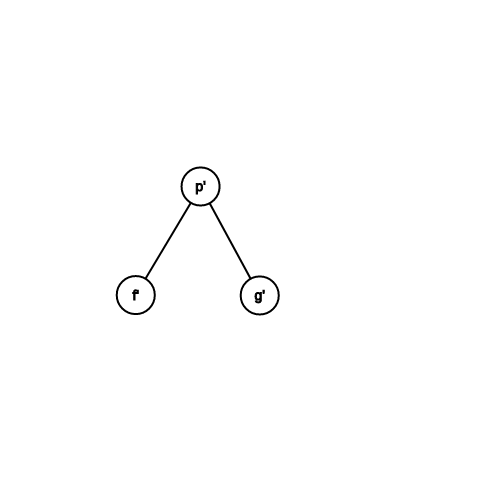
\(c(x) = 2\)

\(\Delta\Phi(x) = log|p'|+log|f'|+log|g'|-log|g|-log|f|-log|p|\)

\(=log|f'|+log|g'|-log|f|-log|p|(|g|=|p'|)\)

\(\le log|p'|+log|g'|-2\times log|p| (|p|\le |f| ,  |f'|\le |p'|)\)

\(\le 2\times (log|p'|-1)-2\times log|p|(因為log|f'|+log|g'| \le log \frac{|f'|+|g'|}{2} \times 2)\)

\(c(x)+\Delta \Phi(x) \le 2\times (log|p'|-log|p|) \le 3\times (log|p'|-log|p|)\)

複雜度證明

勢能分析

  • 每一次splay為多次zig-zig,zig-zag+一次zig
  • \(c'_i(x) = 3\times (log|p'|-log|p|)\)+[is zig]
  • \(\sum c'(x) = 3\times(log|p'|-log|p_0|)+(zig count \le 1) \ge c(x)=\)實際時間 
  • 因此複雜度為log(n)

merge

  • merge可以先把左樹的最大跟右樹的最小分別splay
  • 然後直接把左樹的右節點設成右樹
  • 記得懶標
    void merge(int a,int b){
         if(!a||!b)return;
         splay(a);
         splay(b);
         push(a);
         push(b);
         while(childs[a][1]){
            a = childs[a][1];
            push(a);
         }
         while(childs[b][0]){
            b = childs[b][0];
            push(b);
         }
         splay(a);
         push(a);
         splay(b);
         childs[a][1] = b;
         par[b] = a;
         pull(a);
         return;
    }

find rank

  • 直接在樹上找第k小
  • 然後可能要splay
    int find(int head,int k){
        if(!k)return 0;
        splay(head);
        while(head&&k){
            push(head);
            int ls = childs[head][0],rs = childs[head][1];
            if(sz[ls]+1 == k){
                splay(head);
                return head;
            }
            else if(sz[ls]+1<k){
                k -= sz[ls]+1;
                head = rs;
            }
            else head = ls;
        }
        splay(head);
        return head;
    }

split

  • 可以把第k大的點splay
  • 然後切斷根與右節點
    pair<int,int> split(int head,int k){
        if(k == 0){
            splay(head);
            return make_pair(0,head);
        }
        head = find(head,k);
        splay(head);
        int tmp = childs[head][1];
        childs[head][1] = par[tmp] = 0;
        pull(tmp);
        pull(head);
        return make_pair(head,tmp);
    }

code

  • 講師刻不出來QQ

練習

Link Cut Tree

回顧一下HLD

  • 在HLD，我們用子樹大小來分鍊

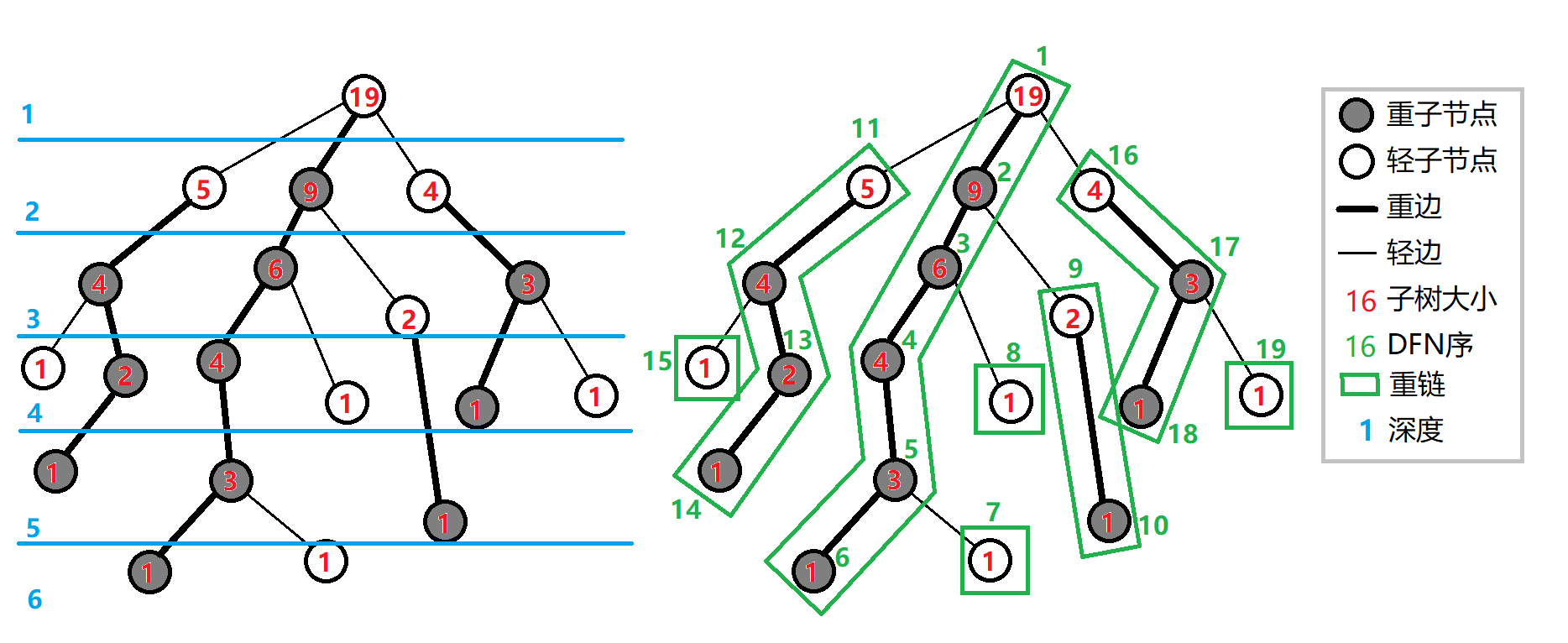
實虛鍊剖分

  • 實鍊虛鍊是我們自己訂的，可以任意變動

實

虛

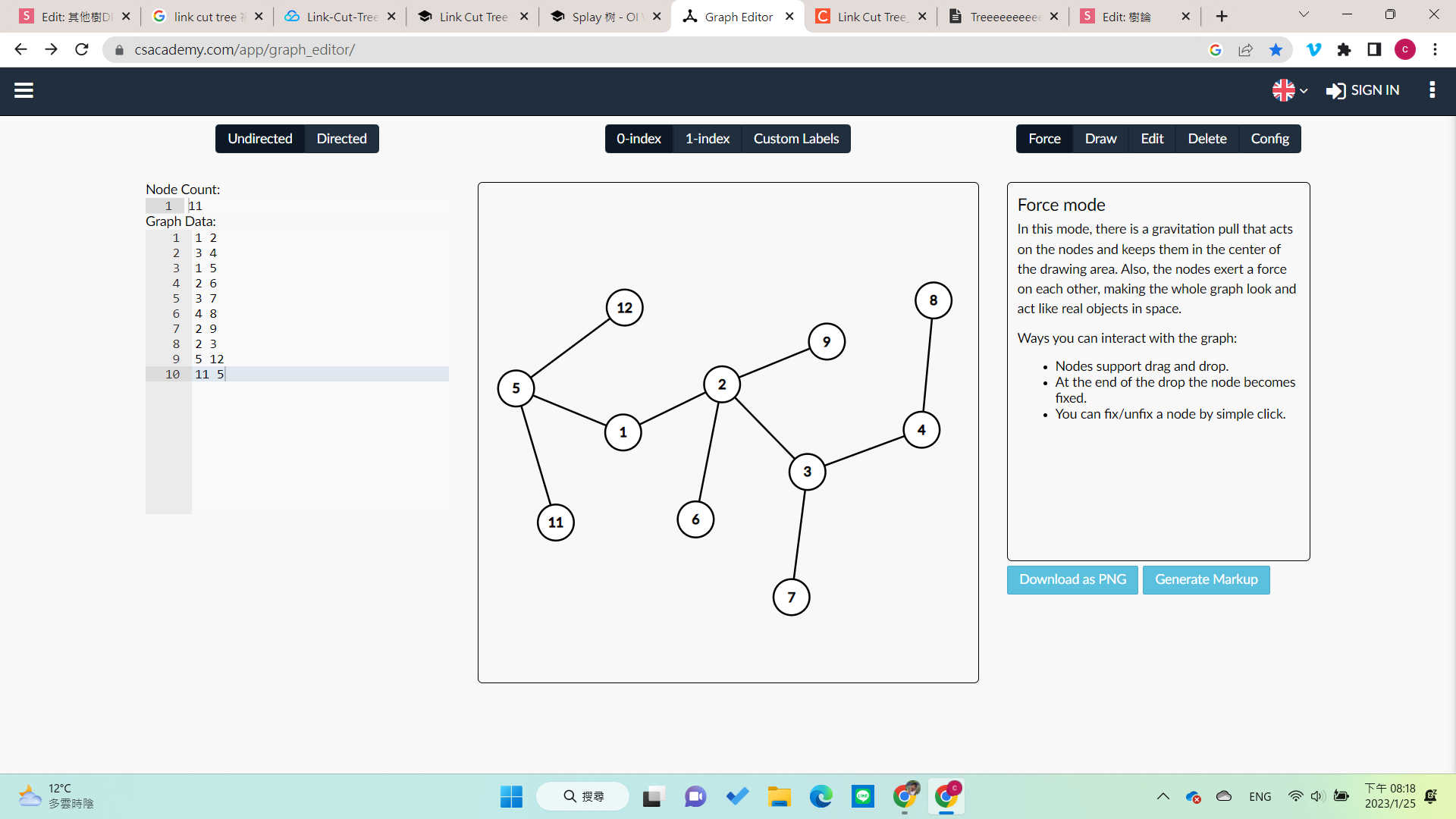
實虛鍊剖分

  • 對於實鍊，我們用splay維護資訊

實

虛

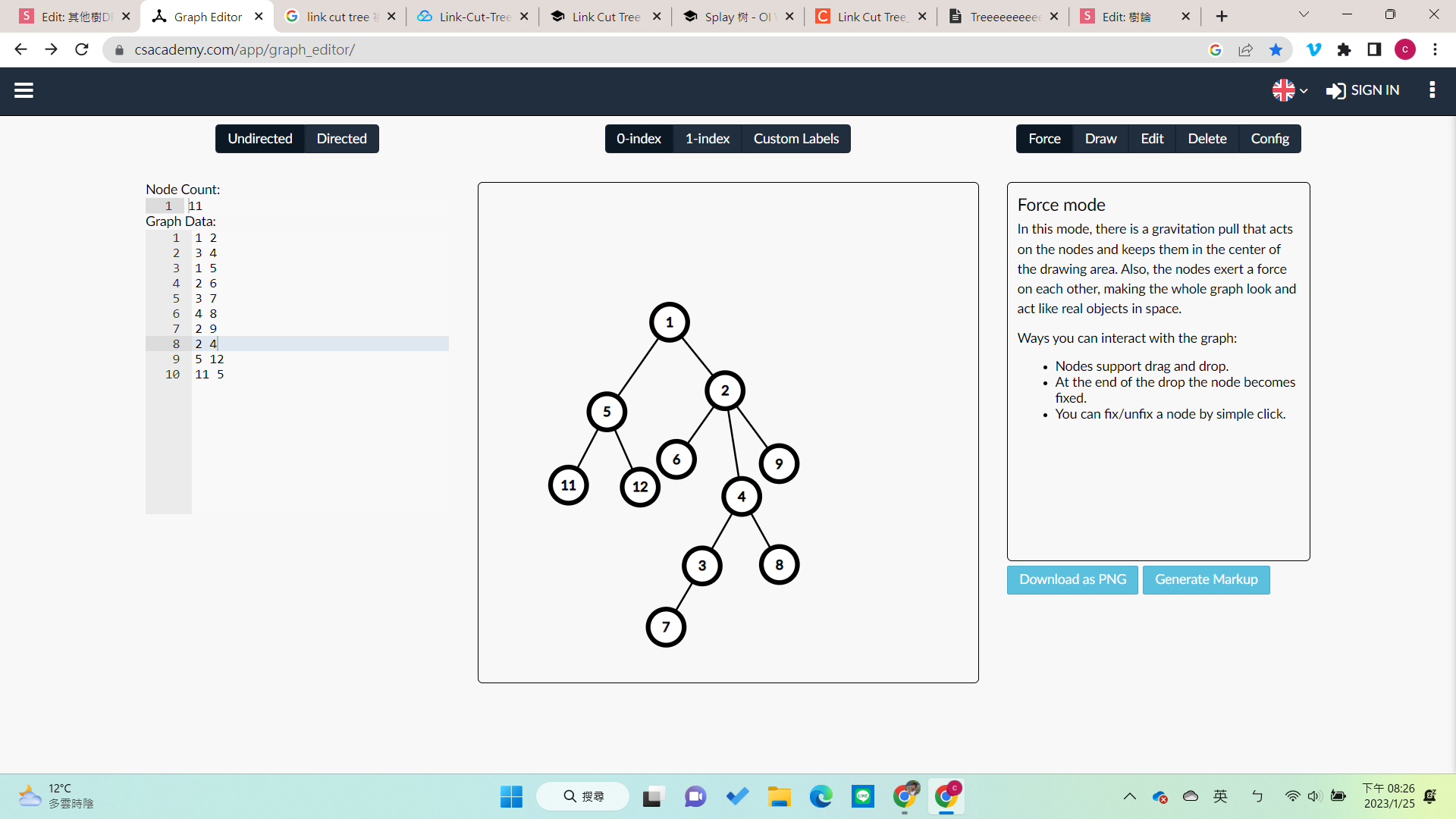
串接

  • LCT最重要的功能
  • 把某個點到根節點之間的邊都變成實鍊
  • 偷一下圖(我畫不出來QQ)

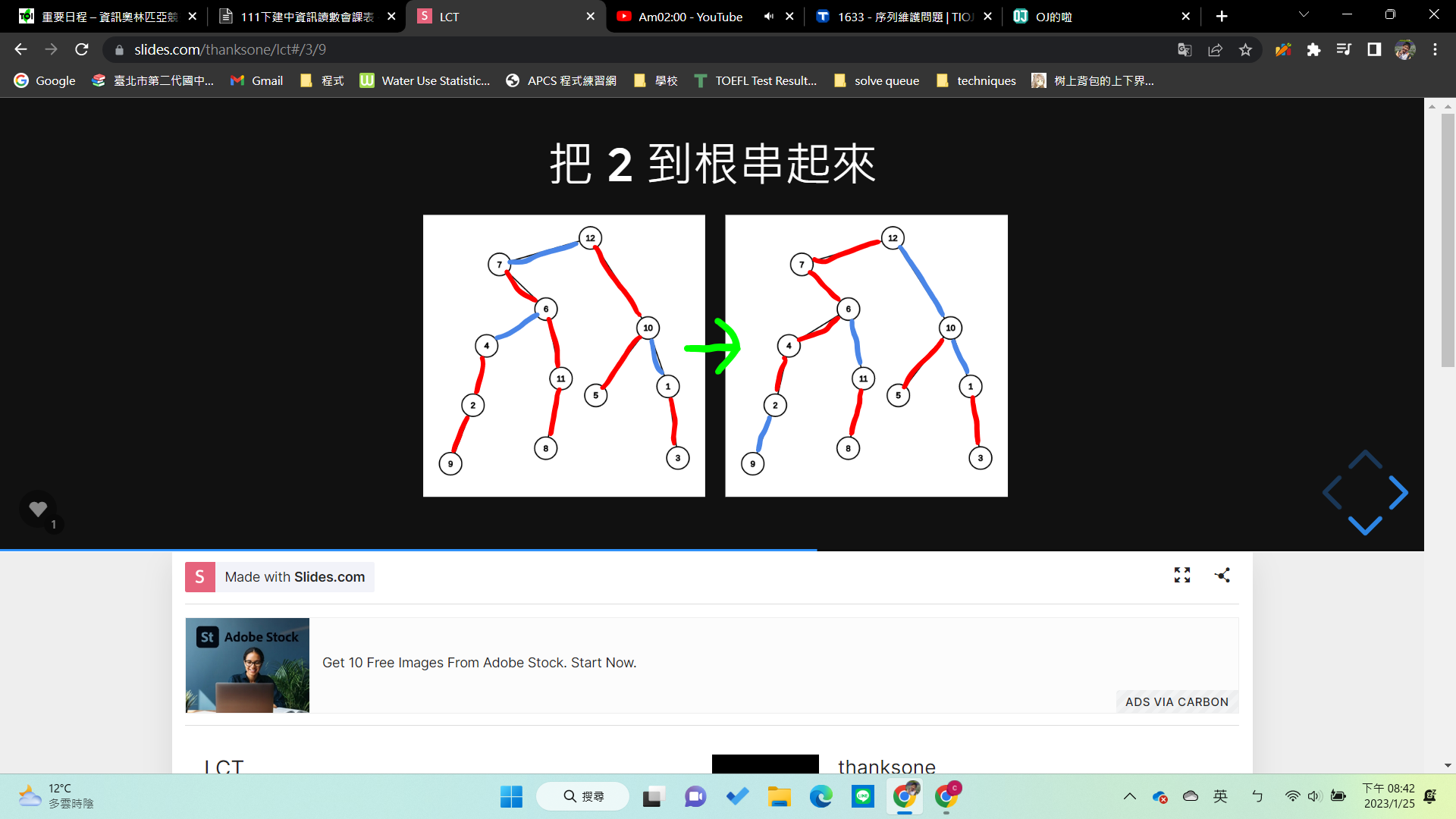
串接

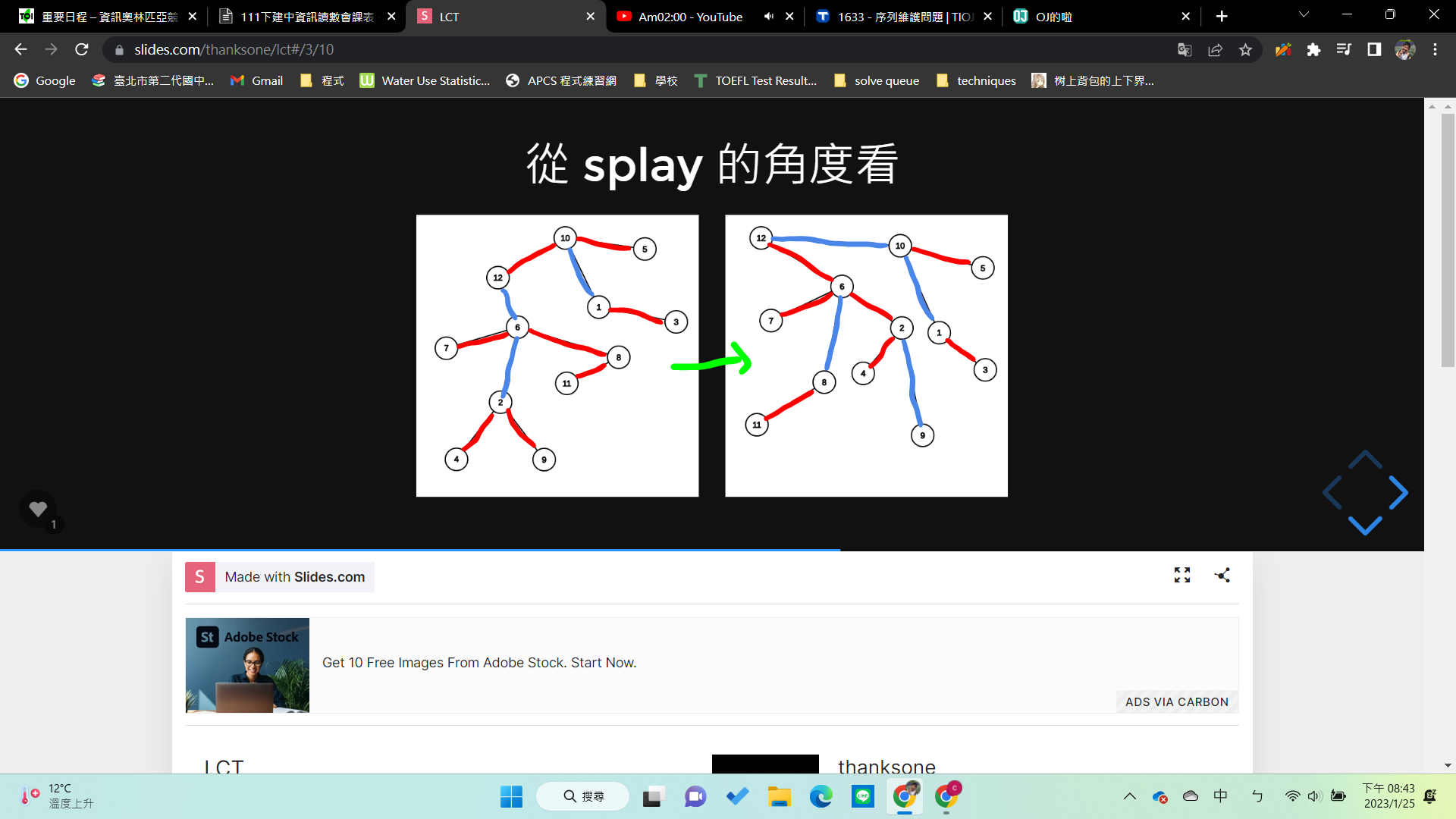
其他操作

換根

makeroot

  • access之後翻轉
    void makeroot(int now){
        access(now);
        splay(now);
        rev[now] ^=1;
        return;
    }

找根

findroot

  • access之後一直往左子節點走
  • 可以用來判連通性
    int findroot(int now){
        access(now);
        splay(now);
        while(childs[now][0])now = childs[now][0];
        return now;
    }

連接兩不連通的點

link

  • 先判連通性
  • 把兩點轉到根之後接起來
    void link(int a,int b){
        if(findroot(a) == findroot(b))return;
        edges.insert({min(a,b),max(a,b)});
        makeroot(a);
        makeroot(b);
        par[b] = a;
    }

斷開兩連通的點

cut

    void cut(int a,int b){
        if(findroot(a) != findroot(b))return;
        if(a>b)swap(a,b);
        if(edges.find({a,b}) == edges.end())return;
        edges.erase({a,b});
        makeroot(a);
        access(b);
        splay(b);
        par[childs[b][0]] = 0;
        childs[b][0] = 0;
        pull(b);
        return;
    }

複雜度

  • 可以證明用splay為\(O(logN)\)
  • 用其他二元樹(merge-split treap)為\(O(log^2N)\)

更多樹

  • 支配樹
  • 樹分塊

更多樹

By ck1100890張秉中

Made with Slides.com

更多樹

  • 237

More from ck1100890張秉中