進階樹論
建國中學 賴昭勳
Euler Tour & DFS
樹壓平
樹的DFS順序 - 1
1
2
3
4
5
6
7
8
9
10
前序遍歷:
1, 2, 9, 5, 8, 7, 6, 10, 3, 4
性質:進入一個節點後,走完該子樹的所有節點之後才會離開。
他的用處:用序列表示樹
1
2
3
4
5
6
7
8
9
10
紀錄每個點的左界和右界,代表該點的子樹的區間。
int ti = 0;
int lef[maxn], rig[maxn]; //[lef, rig)
void dfs(int n, int par) {
lef[n] = ti++;
for (int v:adj[n]) {
if (v != par) {
dfs(v, n);
}
}
rig[n] = ti;
}考慮這種問題
樹上每個點上有一個數值\(a_i\),
處理 \(q\) 筆操作。
- 改變某個點的值
- 詢問以\(v\)為子樹的數值和
變成線段樹!
在樹上歐拉遍歷 - 2
進去和離開點時都把點加到序列裡面,
也就是說序列長度為\(2n\)
1
2
3
4
5
6
7
8
9
10
進入:1, 2, 9, 5, 8, 7, 6, 10, 3, 4,
離開: 9, 8, 5, 7, 2, 3, 10, 4, 6, 1
解決路徑相關的問題!
尋找根到任意節點的路徑
1
2
3
4
5
6
7
8
9
10
\(\text{In}\):1, 2, 9, 5, 8, 7, 6, 10, 3, 4,
\(\text{Out}\): 9, 8, 5, 7, 2, 3, 10, 4, 6, 1
考慮區間\([in[1], in[v]]\)
所有只出現一次\(in\)的點都在\((1, v)\)的路徑上,\(in\)跟\(out\)都出現的點應該被「抵銷」掉。
如果題目求的數值是可以用扣的(ex.路徑和),那可以將\((u, v)\)拆成
\((1, u) + (1, v) - 2 * (1, lca(u, v))\)
還有一種樹壓平-3
在歐拉遍歷時每次遇到一個點就把他紀錄下來。
額外紀錄一個深度陣列
1
2
4
5
6
8
7
3
\(arr\): 1, 2, 7, 7, 2, 5, 8, 8, 5, 2, 1, 6, 3, 3, 6, 4, 4, 6, 1
\(dep\): 0, 1, 2, 2, 1, 2, 3, 3, 2, 1, 0, 1, 2, 2, 1, 2, 2, 1, 0
用這種方法找路徑
1
2
4
5
6
8
7
3
\(arr\): 1, 2, 7, 7, 2, 5, 8, 8, 5, 2, 1, 6, 3, 3, 6, 4, 4, 6, 1
紀錄每個點的首次出現(\(in\))和最後一次出現(\(out\))時間
對於兩個節點\(u, v \ (in[u] < in[v])\):
1. \(v\)在\(u\)的子樹內 (ex. 1-8)
\([in[u], in[v]]\)
2. \(v\) 不在\(u\)的子樹內 (ex. 5-4)
\([out[u], in[v]]\)
用樹壓平做\(O(n \log n)/ O(1)\) LCA
一樣定義\(in[v], out[v]\)分別為點\(v\)第一個、最後一個出現在序列的位置
1
2
4
5
6
8
7
3
\(arr\): 1, 2, 7, 7, 2, 5, 8, 8, 5, 2, 1, 6, 3, 3, 6, 4, 4, 6, 1
\(dep\): 0, 1, 2, 2, 1, 2, 3, 3, 2, 1, 0, 1, 2, 2, 1, 2, 2, 1, 0
Sparse Table!
對於兩個點\(u, v\),\(lca(u, v)\)會位於
\(in[u], in[v]\)中間,且\(in[u], in[v]\)必定在\([in[lca(u, v)], out[lca(u, v)]]\)中間
也就是說\(lca(u, v)\)是\([in[u], in[v]]\)中間深度最小的一個!
以下是練習題
大家自己判斷要怎麼樹壓平!
給你一棵樹,每個點上有值\(v_i\),對於每個點\(u\),找出他子樹內有幾個點\(v\)值比\(u\)大。
\(n \leq 10^5, v_i \leq 10^9\)
給你一棵樹,每個點上有值\(a_i\),有\(q\)筆詢問,每次問兩個點\(u, v\)的路徑間的\(xor\)和。
\(n, q \leq 10^5, a_i \leq 10^9\)
給一棵有根樹,上面每個點是 1 或 0 (一開始全部是0),接下來有\(q\)筆操作。
1. 改一個子樹裡面每個點的值 (0變1, 1 變 0)
2. 詢問一個點的值
\(n, q \leq 10^5\)
給你兩棵有\(n\)個節點的樹\(T_1, T_2\),
請找出有多少對邊\(e_1 \in T_1, e_2 \in T_2\),使得當我們分別把這兩條邊拔掉後,兩棵樹上所製造的兩個連通塊點集可以一一對應。
1
2
2
3
3
5
4
1
4
5
如左圖有三組解:
\(n \leq 10^5\)
註:想想看確定性(不用random/hash)的解
例題5:數樹問題
樹DP/樹分治
在樹上DP有什麼特別的?
- 通常需要考慮不定數量個轉移點(例如子節點數量)
- 有根樹 vs 無根樹
- 有時候他根本不是DP,而是分治或Greedy
- 有不同的應用/變形
樹DP常見的想法:
把根拔掉,拆成一棵棵的子樹
簡單的例題:樹上最大匹配
給定一棵樹,選出一個邊的集合\(S\),使得\(S\)裡面任兩條邊都沒有共用點,並且\(|S|\)盡量大。
\(O(n)\)
1
2
3
4
5
6
7
8
9
10
解一:DP
令\(dp[0][v]\)代表以\(v\)為根的子樹中,不把\(v\)連到子節點的最大邊數。
\(dp[1][v]\)代表把\(v\)連到其中一個子節點的最大邊數。
\(dp[0][v] = \sum max(dp[0][u], dp[1][u])\)
\(dp[1][v]\)要怎麼辦?
解一:DP
所有子節點\(u\)中,至少要有一個使用\(dp[0][u]\),其他的可以用\(max(dp[0][u], dp[1][u])\)
也就是說:
把\(u\)跟\(v\)配對所付出的「代價」
解二:其實Greedy就好了
從葉節點開始選,如果可以配對就配對,並把配對的兩個節點拔掉。
1
2
3
4
5
6
7
8
9
10
為什麼是對的?
選那一條邊的答案 \(\geq\)不選
(如果不選就等同於那個葉節點不存在)
其實樹DP大概就這樣
但他超難><
以下的題目會有某些 OI 題的雷
給你一棵樹,每個節點上面有一個人,現在每個人都必須去一個不同的節點,而且每個節點最後只能有一個人,問所有人移動距離的最小總和(並輸出移動方法)。
\(n \leq 10^5\)
例題2: Appleman and Tree
給你一棵樹,每個節點是黑色或白色,問有多少種方法把樹分成任意多個連通塊,使得每個連通塊內洽有一個黑點。
(答案模\(10^9 + 7\))
\(n \leq 10^5\)
給你一棵\(n\)個節點的樹和距離\(D\),請選出最多個點,使得任兩點的距離至少為\(D\)。
全方位木DP
なに
在大部份的樹DP問題,我們都可以直接選根
但有時候我們必須考慮所有可能的根
要怎麼有效率的做這件事呢?
來看一個裸題
在一棵樹上,點有點權\(a_i\),請找出一個點\(v\),使得\(\sum_{1 \leq i \leq n} dist(i, v) \cdot a_i\) 最大
\(n \leq 2 \times 10^5\)
\(O(n^2)\)顯然可做,但是要怎麼優化?
優化暴力?
先隨便選一個點DFS,用一個變數紀錄答案,並對每個點存兩個值:
- 子樹大小
- 子樹內的\(a_i\)總和
當我要從目前的根\(u\)移動到相鄰的點\(v\)為根時...
u
v
4
5
6
7
8
9
10
只會改到\(u, v\)的資訊!
\(O(1)\)更新
並維護答案
我們做得到的事
在\(O(1)\)內把根往一條邊移動
這樣就夠了
對樹做歐拉遍歷,每經過一條邊就改變根的位置,總共改變\(O(n)\)次,而且每個點都會被看到。
這就是全方位木DP,又稱Rerooting Technique
例題1: TIOJ 魔法鏈
給你一棵樹,你每次可以選一個葉子(只有連到一個點)的節點,把他的編號紀錄在一個序列,並拔掉那個點。問可以形成的序列數。
註:本題的\(n \leq 2000\),但其實可以做到\(n \leq 2 \times 10^5\)
2
5
7
8
9
合法序列有:
9, 8, 5, 7, 2
7, 8, 5, 2, 9
...
不合法序列有:
9, 5, 8, 7, 2
給你一棵樹,點有點權\(a_i\),一個「好的」根節點\(v\)會符合,對於任意一條從\(v\)到點\(u\)的路徑,路徑上都不會有權值相同的點。問有幾個好的根節點。
\(n \leq 2 \times 10^5\)
Binary Jumping
倍增法
還記得倍增法的LCA怎麼做嗎?
對每個點維護他的\(1, 2, 4, ..., 2^k\)倍祖先,即可以在\(O(\log n)\)時間內找到一個點的\(x\)倍祖先。
其實,這個技巧不一定要在樹上也可以做。
一個常見的變形是:一個點指向另一個(可能有環)
你有一個 1~n 的排列\(p\)和一個長度為\(m\)的序列\(a\),
保證\(1 \leq a_i \leq n\)。
接著有\(q\)筆詢問,每次問區間\([l, r]\),回答\(a\)裡面是否存在一個在\([l, r]\)內的子序列,是排列\(p\)的某個循環移位 (Cyclic shift)
\(n, m, q \leq 2 \times 10^5\)
假設我固定子序列的第一項,如果他是答案的話,考慮最後一項....
提示->
倍增法還可以做什麼
把一條路徑分成\(\log n\)條不重疊的路徑!
當我們在處理可合併的東西的時候(ex. min, max, sum, gcd, ...),在做倍增表的時候就可以一邊紀錄這個東西,並用相同的方法在\(O(\log n * 合併時間)\)找答案。
LCA 的一個(有點廢話的)性質
-
每一對點會有恰好一個LCA,因此可以用枚舉LCA的方式枚舉路徑
- 其實我原本要寫更多性質的但我想不到了
給你一張圖,邊有邊權,對於每一條邊,找到包含那條邊的最小生成樹權值。
\(n, m \leq 2 \times 10^5\),圖連通
給你一棵樹,有\(q\)筆詢問,每次問三個點\(a, b, c\),回答有多少點\(d\),使得如果你把\(d\)當根節點,\(lca(a, b) = c\)。
\(n, q \leq 10^5\),
補充:強強的LCA
使用\(O(n)\)記憶體和預處理時間,一樣\(O(\log n)\)跳\(k\)倍祖先
然後其實倍增表能做到的所有事情他都可以做到(因為路徑一樣可以被拆解)。
Small to large Merging
啟發式合併
啟發式合併?
簡單來說,就是當我們要合併兩個大小為\(a, b \ (a \geq b)\)的資料結構(可以是序列,set,map...)時,把小的合併到大的。
他跟樹上問題的關係?
1
2
3
4
5
6
7
8
9
10
假設我對一個子樹必須維護\(O(子樹大小)\)的東西
那在合併子樹答案的時候就可以用這個方法。
他的複雜度是...?
什麼?多一個 log 而已
有\(n\)個點,每次合併大小為\(a, b\)的連通塊時需要\(O(min(a, b))\)的時間。
考慮一個點所在的連通塊大小,每次他「被合併到其他連通塊」時,這個大小會增加為原本的至少\(2\)倍,也就是說一個點只會被算到\(O(\log n)\)次。
有\(n\)個點,所以總共合併 \(O(n \log n)\)次
給你一棵有根樹,每個點上有顏色\(c_i\),一個子樹內的顏色為「重要」的,代表沒有其他顏色在那個子樹內出現比該顏色更多次(也就是說可能有多個重要的顏色)。
對於每個點,找到該子樹所有重要顏色的編號(\(c_i\))總和。
\(n \leq 10^5\)
例題:忍者調度問題
給你一棵有根樹以及預算上限\(M\),每個點上是一個忍者,有出動費用\(c_i\)和領導值\(l_i\),如果你選了\(v\)為領導人,則他的滿意度為
\(l_v \times 預算內能在v子樹內出動的忍者數量\)
請找出最大的滿意度。
\(n \leq 10^5, M, c_i, l_i \leq 10^9\)
給你一棵\(n\)個葉節點的二元樹,每個葉子上有一個值\(a_i\),且所有\(a_i\)形成一個排列。
你可以選擇任意個非葉節點並把他們的左右小孩交換。在交換之後,我們用前序遍歷這棵二元樹並上葉節點上的值紀錄成一個序列,
求這個序列最少的逆序數對數。
\(n \leq 2 \times 10^5\)
Heavy Light Decomposition
樹鏈剖分
Binary Jumping 的問題
一個點會被\(O(n)\)個區間覆蓋到,所以如果點上要修改,會有\(O(n)\)個值改變。
我們需要把樹上路徑切成\(O(\log n)\)條不相交的路徑,而且每個點都只被一個紀錄的路徑覆蓋到。
所以就有樹鏈剖分了
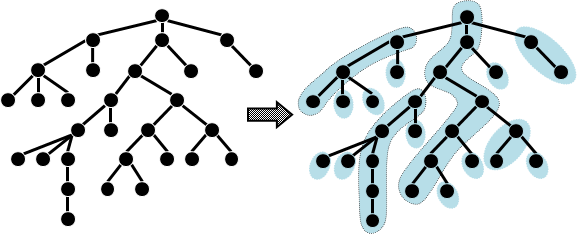
每個點都屬於一條樹鏈
考慮點\(v\)所在的樹鏈\(d(v)\)和他所有的小孩\(u\)。
子樹大小最大的一個小孩會有\(d(u) = d(v)\)。
其他的小孩屬於一條新的樹鏈。
這樣的複雜度

定義\(up(v)\)為點\(v\)所在樹鏈的「頂端」的節點。
那考慮一個點\(v\)走到根的路徑中,依序經過的樹鏈頂端的子樹大小。
跳到另一個樹鏈時,樹鏈頂端的子樹大小至少會加倍。
至多只會經過\(O(\log n)\)條樹鏈
那樹鏈剖分之後呢?
任意一條路徑可以被拆成\(O(\log n)\)條樹鏈組成的路徑
把一條樹鏈當成序列的一個區間,一條路徑會變成\(O(\log n)\)個區間,可以用線段樹維護。
那我們就會做這種問題
給你一棵樹,點有點權\(a_i\),處理\(q\)筆操作。
- 把點\(v\)的值改成\(x\)
- 詢問\(u\)到\(v\)路徑的最大\(a_i\)值
\(n, q \leq 10 ^5\)
More (hard) Problems
以下有很多 OI 題
很多我曾經會的題
跟很多我不會的題
卡常
在一個\(n\)個點的有根樹上,每個點有顏色\(1 \leq c_i \leq K\),接著有\(q\)筆操作:
1. 把一個點的顏色改為\(x\)
2. 詢問以\(v\)為根的子樹有多少種不同的顏色
\(n \leq 5 \times 10^5, q \leq 3 \times 10^5, SLOW JUDGE\)
這題有兩種解法w
進階樹論 (資讀)
By justinlai2003
進階樹論 (資讀)
- 1,697



