DP2與DP優化
講者 : 卡特藍數
澄清
是真的不會DP優化才教DP優化的,就跟不會String教String一樣
我偷了很多簡報
偷誰的沒有一定標準,只是個人喜好
然後我不敢偷IOIC
如果有原作者希望我拿掉,我會拿掉的
DP2
大綱
- Digit DP(又稱數位DP)
- 插頭DP(又稱輪廓線DP)
- 其它
Digit DP
#偷 #芒國手
辣個男人太強了
來點比較溫和的習題
- 剛剛那題
- CF 1036C(也有排組做法、暴力作法)
- luogu P2657 (for LOJ愛好者)
- CF 919B但要\(k=10^{12}\)(題解)
- CF 628D
- 2024 AA競程TOI模擬賽II pD (可能需要fatman87878個資)
插頭 DP
我用的狀態可能會和某些題解有些出入,但概念是一樣的
\(n*m\)的網格有幾種被 \(1*2\) 與\(2*1\) 的骨牌完全覆蓋的方式
- \(min(n,m)\leq 10\)
- \(max(n,m)\leq 1000\)
粉的是決策完了
藍的是正要決策(放骨牌或已有)
黃色稱作輪廓線,上面有插頭
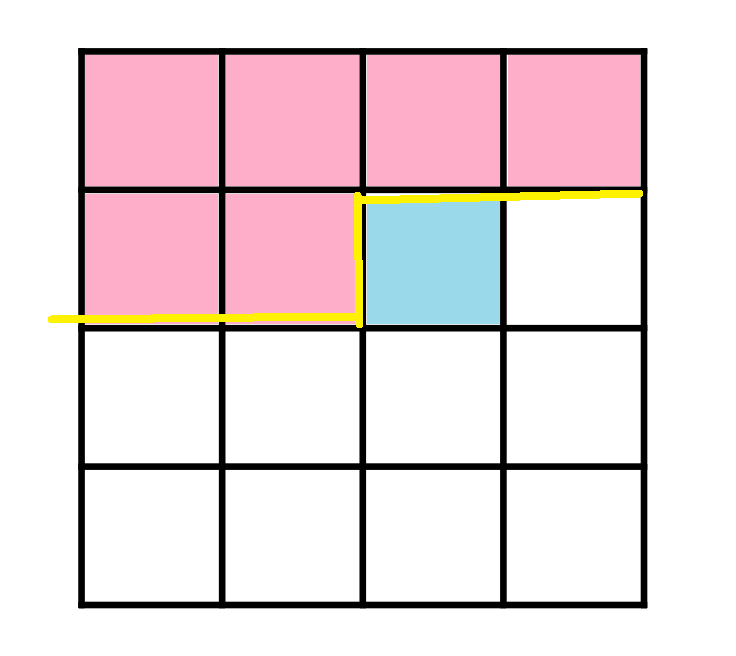
粉的是決策完了
藍的是正要決策(放骨牌或已有)
黃色稱作輪廓線,上面有插頭
就是綠色那些
對藍色這格
朝下的箭頭是上插頭
朝右的箭頭是左插頭
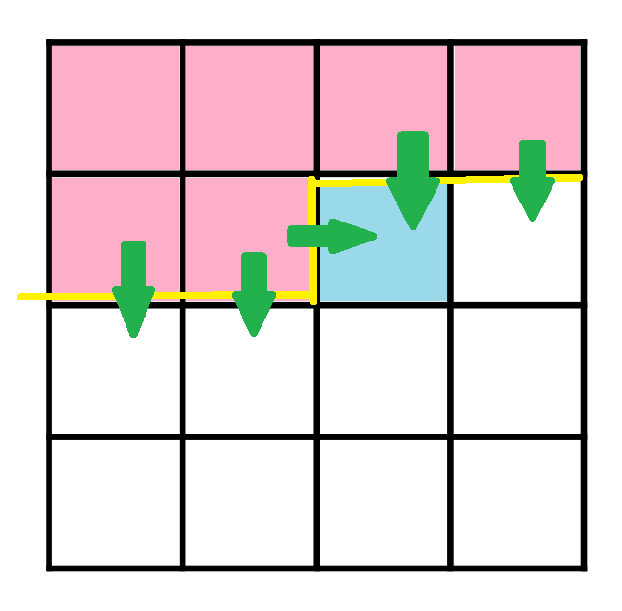
如果上面有覆蓋骨牌的話
那這個插頭的狀態就是1
左圖的輪廓線的狀態就是0,1,0,1,1
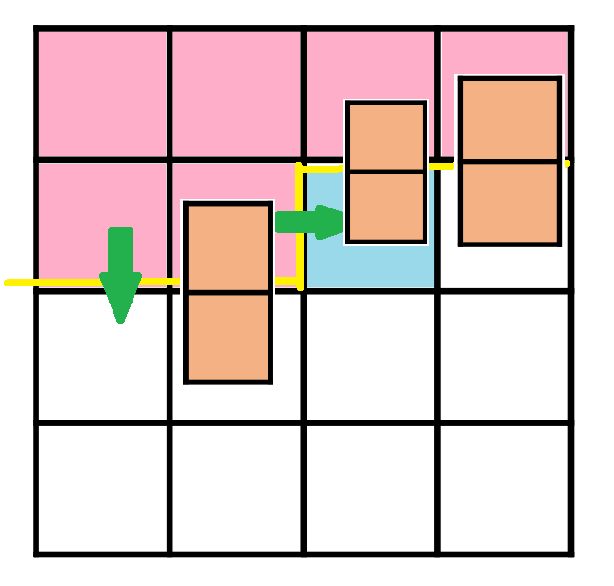
狀態間怎麼互相轉移呢?
(正常會一次做完一個橫排,每個橫排都是由左往右做)

Case 1
沒有左箭頭也沒有上箭頭:
可以放骨牌上去

Case 1
沒有左箭頭也沒有上箭頭:
可以放骨牌上去
放的是橫的話
那(0,0)變成(0,1)

Case 1
沒有左箭頭也沒有上箭頭:
可以放骨牌上去
放的是直的話
那(0,0)變成(1,0)

Case 2
沒有左箭頭但有上箭頭:
這格被上一橫排的骨牌蓋到

Case 2
沒有左箭頭但有上箭頭:
這格被上一橫排的骨牌蓋到
放不了骨牌上去
(0,1)變(0,0)

Case 2-2
有左箭頭但沒有上箭頭:
這格被同一橫排的骨牌蓋到

Case 2-2
有左箭頭但沒有上箭頭:
這格被同一橫排的骨牌蓋到
放不了骨牌上去
(1,0)變(0,0)

Case 3
有左箭頭也有上箭頭:

Case 3
有左箭頭也有上箭頭:
假的
一個格子不會被兩個骨牌蓋
這個case根本不存在
那我做完一橫排了
怎麼換到下個橫排?

最後一個根本沒用
不可能會有再往右的骨牌
根本不存在的待轉移格子

最後一個根本沒用
不可能會有再往右的骨牌
把他踢掉,並在最前面放個新插頭

最後一個根本沒用
不可能會有再往右的骨牌
把他踢掉,並在最前面放個新插頭
新插頭也一定是0
1,1,0,1,0變成0,1,1,0,1了
習題
你還可以學...
DP優化
大綱
- 資料結構優化 - 單調隊列、BIT
- 轉移點單調優化(分治優化)
- 四邊形優化(1D/1D凸凹)
- 2D/1D凸
- 矩陣相關
- 斜率優化(凸包優化)
- Slope trick
(臻斜率優化) - Aliens
轉移點單調
函數性值
xD/yD指的是?
xD指的是子狀態數為\(O(n^x)\)
yD指的是轉移次數是\(O(n^y)\)
費式數列,則為1D/0D
區間DP,通常為2D/1D
DP優化的本質
DP優化的本質就是觀察性質,
再利用這些性質去找好的方式(如資料結構、分治)以較快的速度
"維護最佳轉移點"
或是
"從很多轉移點同時轉移並取最佳值"
或是
"利用函數的好性質把不好算的東西挖出來"
DP優化到最後會發現其實跟本重點不在DP
DP本來就是種思想
不是種科技
單調隊列優化
#偷 #Caido
多重背包問題
$$有n種物品,每種重w_i,價值v_i,有a_i個$$
你現在有一個容量\(W\)的大背包,問可以拿取的最大價值
多重背包問題
現在假設你考慮完了前\(n-1種\)物品,現在只考慮第\(n\)種物品
$$設dp[i]代表背包用掉i容量的所拿取的最大價值,$$
$$ldp[i]代表背包只看前n-1種物品時用掉i容量所拿取的最大價值$$
$$dp_i =\max_{0\le x \le a[i]}{ldp[i - x * w[n]] + x * v[n]}$$
多重背包問題
現在假設你考慮完了前\(n-1種\)物品,現在只考慮第\(n\)種物品
$$設dp[i]代表背包用掉i容量的所拿取的最大價值,$$
$$ldp[i]代表背包只看前n-1種物品時用掉i容量所拿取的最大價值$$
$$dp_i =\max_{0\le x \le a[i]}{ldp[i - x * w[n]] + x * v[n]}$$
$$i只從和自己同餘w[n]的j(<i)轉移過去!!$$
多重背包問題
$$i只從和自己同餘w[n]的j(<i)轉移過去!!$$
$$對0\le i < w[n]做一次單調隊列優化,每次都只讓O(\lfloor\frac{n}{w}\rfloor)個點互相轉移$$
多重背包問題
$$i只從和自己同餘w[n]的j(<i)轉移過去!!$$
$$對0\le i < w[n]做一次單調隊列優化,每次都只讓O(\lfloor\frac{n}{w}\rfloor)個點互相轉移$$
$$單次O(\lfloor\frac{W}{w[i]}\rfloor) ,每個物品i用O(w[i])次$$
$$O(n)種物品$$
$$總時間複雜度O(nW)$$
RMQ相關優化
題意
在长度为 �n 的数列 �a 中,求出长度为 �m 的严格上升子序列的个数
答案对 109+7\(10^9+7\) 取模
- $$1\le m \le n \le 1000$$
- $$1\le a[i] \le 10^9$$
轉移式與naive solution
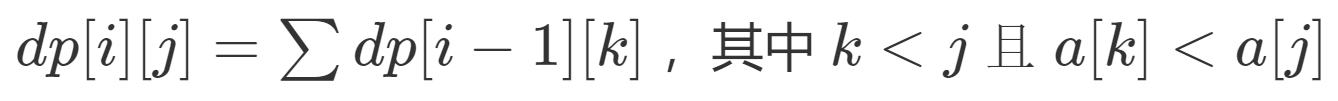

长度为 \(i\) 的子序列的数量。
$$暴力乱做O(mn^2),TLE$$
加上BIT
$$在算dp[i][j]時可以轉移的k是在j前面且a[k]<a[j]$$
要怎麼知道哪些數\(<a[j]\)?
加上BIT
$$在算dp[i][j]時可以轉移的k是在j前面且a[k]<a[j]$$
要怎麼知道哪些數\(<a[j]\)?
離散化 + BIT!
$$先對a離散化$$
$$然後枚舉i來算dp[i]$$
$$dp[i][j] = bit[i - 1].query(a[j] - 1)$$
$$然後在更新BIT[i]$$
總時間複雜度\(O(mn log n)\)
習題
轉移點單調優化
不論是支語還是英文,都是分治優化
和四邊形優化的關聯
可以先了解一下甚麼是凸單調,什麼是凹單調(看下一頁)
凸單調一定可以用轉移點單調優化做
反向則不然
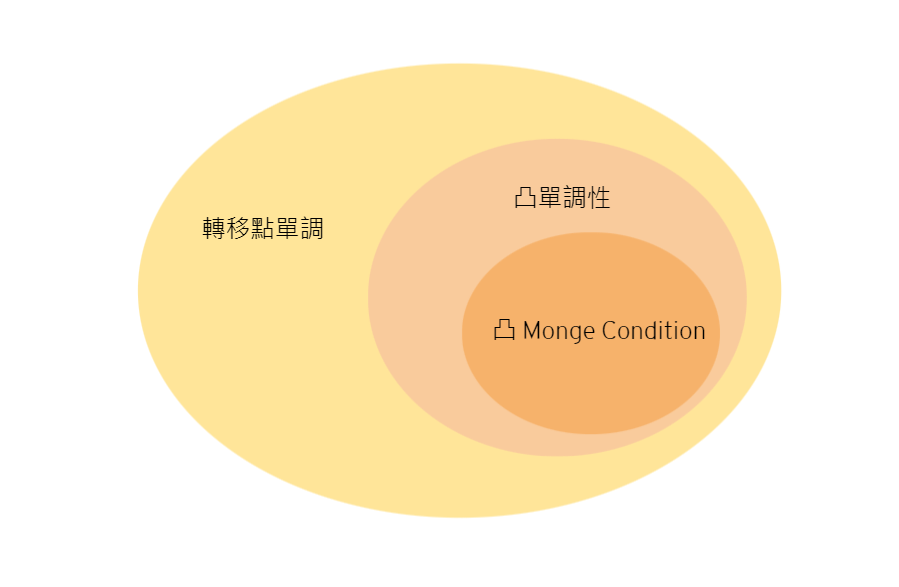
什麼是轉移點單調
$$cost[i][j]為i轉移到j的代價,以下我們假設cost[i][j]為已知$$
$$求dp[r]=\min_{l<r}a[l][r] = \min_{l<r}(dp[l - 1] + cost[l][r])$$
$$如果dp[i]由dp[k-1]轉移過去最好,那我們稱K[i]=k為i的最佳轉移點$$
$$轉移點單調指的是\forall i < j,K[i]\le K[j]$$
然後這樣可以分治做
$$O(n^2)變O(n log n)$$
CDQ分治套轉移點單調優化
有時轉移來源無法先預處理出來,(\(cost[i][j]\)仰賴\(dp[i-1]\))
這時要用CDQ分治套轉移點單調做
也就是算到[L,R]時先做出[L,mid]的DP值
接著做分治(轉移點單調優化),用[L,mid]來更新[mid,R]
再做出[mid,R]的DP值
由主定理證得時間複雜度為\(O(n log^2 n)\)
CDQ分治套轉移點單調優化
//轉移點單調優化也可以做"題目是要求min,然後cost有凸性值"
...
int dp[N];
int cost (int l, int r) {
...
}
void dc (int fromL, int fromR, int L, int R) { //[L, R]由[fromL, fromR]轉移,試試看mid從[fromL,fromR]轉移
if (L > R) return;
int mid = (L + R), opt = INT_MAX, optid = fromL;
for (int i = fromL; i <= min(fromR, L); i++) {
int woo = cost(i, mid);
if (woo < opt) opt = woo, optid = i;
}
dp[mid] = opt;
if (L == R) continue;
dc(fromL, optid, L, mid - 1);
dc(optid, fromR, mid + 1, R);
}
void cdq (int L, int R) {
if (L == R) return;
int mid = (L + R) >> 1;
cdq(L, mid);
dc(L, mid, mid + 1, R);
cdq(mid + 1, R);
}
int main () {
...
cdq(1, n);
...
}四邊形優化
適用於\(1D/1D\)求\(min/max\)
凸完全單調性
-
對於所有轉移點\(i,j(i < j)\)都存在一個\(k\),使的在\(k\)前從\(i\)轉移比較好,\(k\)後從\(j\)轉移比較好。
可想成新同學都會優超 - 求\(dp[r] =min\{a[l][r]\}\)時,$$$$ \(當i < j時,若a[i][x] \ge a[j][x],則對於所有y > x,有a[i][y] \ge a[j][y]\)
- \(dp[r] =max\{a[l][r]\}\),相當於\(-dp[r]=min(-a[l][r])\),所以變號變成\(a[i][x] \le a[j][x]\)推得\(a[i][y] \le a[j][y]\)
- 最佳轉移點會遞增
- 可以用轉移點單調優化做
凹完全單調性
- 對於所有轉移點\(i,j(i < j)\)都存在一個\(k\),使的在\(k\)前從\(j\)轉移比較好,\(k\)後從\(i\)轉移比較好。
- 求\(dp[r] =min\{a[l][r]\}\)時,$$$$ \(當i < j時,若a[i][x] \le a[j][x],則對於所有y > x,有a[i][y] \le a[j][y]\)
- 求\(dp[r] =max\{a[l][r]\}\)時,$$$$ \(當i < j時,若a[i][x] \ge a[j][x],則對於所有y > x,有a[i][y] \ge a[j][y]\)
- 最佳轉移點會遞減
- 可能可以用轉移點優化來做(但要反過來寫)(沒人這樣,但應該要可以)
更多說明與例題(#偷 #Caido)
$$註:藍線左端是pre_{l1/2},紅線是pre_i-L_i-K,兩者相減就是我們要的$$
四邊形不等式
- $$\forall i_1 \le i_2, j_1 \le j_2,f[i_1][j_1]+f[i_2][j_2]\le f[i_1][j_2] + f[i_2][j_1]$$
求\(min時,a\)符合這個不等式便有凸完全單調性。不符合不代表不單調
也可以看\(cost\)符不符合,正常狀況下,\(cost\)符合則\(a\)符合
看是不是凹要變號,如果是求\(max\)也要變號
Monge Codition
- $$\forall i, j,f[i][j]+f[i+1][j+1]\le f[i][j+1] + f[i+1][j]$$
等價於
不會證時可以\(O(n^2)\)打表\(O(n^2)\)確認!
可以記"交叉比包含好"這個口訣
習題
- #zck
- 某些被分在轉移單單調優化的題目
Knuth-Yao Speedup
適用於有\(2D/1D\)凸性質的DP
Knuth-Yao Speedup
適用於有\(2D/1D\)凸性質的DP
和四邊形優化有關,但跟剛才講的是不同東西
題意
有一個長度為\(n\)的陣列\(a\)。
你每次(共\(n - 1\)次)可以選一個長度\(\ge 2\)的子陣列,
然後把他切成兩個非空子陣列。
花費的代價是原本子陣列的和。
問切成\(n\)個陣列的最小花費。
- \(1 \le n \le 5000\)
轉移式與naive solution
令\(dp[i][j]代表把[i,j]切成j - i + 1塊的最小代價\)
$$有dp[i][j] = (\sum_{k = i}^{j}a_k) + (\min_{i\le k < j}dp[i][k] + dp[k + 1][j])$$
可以枚舉區塊長度,然後枚舉左界,再枚舉轉移點
時間複雜度\(O(n^3)\)
顯(通)然(靈)
感覺上對一個大區間和一個小區間加一相同新東西,大的增加較多代價
$$對i_1<i_2 \le j,有dp[i_1][j+1] - dp[i_1][j] \ge dp[i_2][j+1] - dp[i_2][j]$$
$$假設我們已知dp[l][r]切成dp[l][k]+dp[k + 1][r]最好$$
$$我們來看一下[l,r+1]從k'(<k)轉移和從k轉移哪個比較好$$
$$1.k是[l,r]最佳轉移點:dp[l][k']+dp[k'+1][r]\ge dp[l][k] + dp[k+1][r]$$
$$2.最上面那條:dp[k'+1][r+1]-dp[k'+1][r] \ge dp[k+1][r+1]-dp[k+1][r]$$
$$於是有dp[l][k']+dp[k'+1][r+1]\ge dp[l][k]+dp[k+1][r+1]$$
$$進而得到[l,r+1]的最佳轉移點不比[l,r]的最佳轉移點k小$$
從顯(通)然(靈)得到的性質
$$令K[i][j]是[i,j]的最佳轉移點,便是說[i,j]切成[i,K[i][j]]和[K[i][j]+1,j]最好$$
$$從上一頁結論與其對稱性知K[i][j]\le K[i][j+1]和K[i-1][j]\le K[i][j]$$
$$進而推得K[i][j-1] \le K[i][j]\le K[i+1][j]$$
最後得到
$$K[i-2][j-1]\le K[i-1][j-1] \le K[i][j-1] \le K[i][j]\le K[i+1][j] \le K[i+1][j+1]$$
從顯(通)然(靈)得到的性質
$$令K[i][j]是[i,j]的最佳轉移點,便是說[i,j]切成[i,K[i][j]]和[K[i][j]+1,j]最好$$
$$從上一頁結論與其對稱性知K[i][j]\le K[i][j+1]和K[i-1][j]\le K[i][j]$$
$$進而推得K[i][j-1] \le K[i][j]\le K[i+1][j]$$
最後得到
$$K[i-2][j-1]\le K[i-1][j-1] \le K[i][j-1] \le K[i][j]\le K[i+1][j] \le K[i+1][j+1]$$
ㄟˊ 對於相同的\(j-i\),\(K[i][j]\)單調!
作法
一樣先枚舉長度(\(j-i\)),再枚舉左界\(i\)(也得到\(j=i+長度-1\))
$$接著枚舉K[i+1][j]\le k\le K[i][j-1],$$
$$試著轉移並找到[i,j]最好的轉移點,記作K[i][j]$$
因為單調,對於同個\(j-i\),最多只要看過\(n\)個轉移點
$$又只有n種j-i$$
所以時間複雜度是\(O(n^2)\),比原本少一個\(n\)
這樣的技巧就叫作Knuth-Yao Speedup(也叫Knuth's Optimization)
作法
一樣先枚舉長度(\(j-i\)),再枚舉左界\(i\)(也得到\(j=i+長度-1\))
$$接著枚舉K[i+1][j]\le k\le K[i][j-1],$$
$$試著轉移並找到[i,j]最好的轉移點,記作K[i][j]$$
因為單調,對於同個\(j-i\),最多只要看過\(n\)個轉移點
$$又只有n種j-i$$
所以時間複雜度是\(O(n^2)\),比原本少一個\(n\)
這樣的技巧就叫作Knuth-Yao Speedup(也叫Knuth's Optimization)
可以看dp符不符合Monge Condition(交叉比包含小)來判斷凸性
4頁前的那個靠感覺得出的式子,移項後其實也符合Monge Condition
dp
參考code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 5010;
int n, a[N];
ll pre[N], dp[N][N], opt[N][N]; //opt存最佳轉移點
int main () {
cin >> n;
pre[0] = 0;
for (int i = 1; i <= n; i++) {
cin >> a[i];
pre[i] = a[i] + pre[i - 1];
opt[i][i] = i;
dp[i][i] = 0;
}
for (int len = 2; len <= n; len++) {
for (int i = 1, j = len; j <= n; i++, j++) {
dp[i][j] = LLONG_MAX;
for (int k = opt[i][j - 1]; k <= opt[i + 1][j]; k++) {
if (dp[i][k] + dp[k + 1][j] < dp[i][j]) {
dp[i][j] = dp[i][k] + dp[k + 1][j];
opt[i][j] = k;
}
}
dp[i][j] += pre[j] - pre[i - 1];
}
}
/*
//驗算有沒有monge condition,可以自己載cses測資試試看
bool y = 1;
for (int i = 1; i <= n; i++) for (int j = i; j + 1<= n; j++) {
if (dp[i][j] + dp[i+1][j+1] > dp[i][j+1] + dp[i+1][j] ) y = 0;
}
if (y == 0) cout << "No monge condion!";
*/
cout << dp[1][n] << '\n';
return 0;}不一定只能用在區間DP喔
題意
$$你要在一條有n個房子(a[1]\le a[2]\le... \le a[n])的大街上蓋m間學校$$
$$這n間房子的都裡都住著一個人$$
每個人都會走去離自己最近的郵局
你想要讓大家走的總距離最小
小觀察1
先想想看只蓋一棟郵局時答案是甚麼?
答案就是把郵局蓋在房子位置的中位數
小觀察1的口糊證明
$$我們假設n = 2 mid + 1$$
$$如果我今天不把郵局蓋在a[mid],而是蓋在a[mid - 1]呢?$$
$$那前mid - 1的人可以少走a[mid]-a[mid - 1],$$
$$但第mid到第n個人都要多走a[mid] - a[mid - 1]$$
$$總距離比原本多a[mid] - a[mid - 1],還是放在mid比較好$$
\(n\)是偶數的話放在兩個中位數之間的任何一處皆好,此略
naive solution
$$dp[i][r]代表在[1, r]蓋i棟房子時,[1,r]的人走的最小總距離$$
$$先隨便處理好cost[i][j]代表[i,j]的人都往其中位數跑的總距離$$
$$則dp[1][i] = cost[1][i]$$
$$然後有轉移式dp[i][r] = \min_{k<r}(dp[i-1][k] + cost[k + 1][r])$$
$$可以枚舉i(2到m),然後枚舉右界r,再枚舉轉移點k$$
時間複雜度 \(O(mn^2) \le O(n^3)\) ,TLE
回到中位數
要求\(O(n^3)\)的話,\(cost\)可以隨便求
要證這題的性質就需要知道\(cost\)怎麼\(O(n^2)\)
$$結論就是 cost[l][r] = cost[l][r-1] + a[r] - a[\lfloor\frac{l + r}{2}\rfloor],然後cost[i][i]=0$$
每次多加一個東西進來,如果目前有奇數個東西,那中位數變成兩個;
[l,r-1]繼續走到較小那個中位數,r走到較大那個中位數。
如果目前有偶數的東西,那我會拔掉較小的那個中位數;
原本走到較小那個中位數的會改去較大那個中位數,可以證明\(cost\)同,
然後再加上\(r\)走到新中位數(原本較大得那個)的距離。
回到中位數
$$結論就是 cost[l][r] = cost[l][r-1] + a[r] - a[\lfloor\frac{l + r}{2}\rfloor],然後cost[i][i]=0$$
可能會發現\(cost\)符合不等式,我們這裡假設不符合來反證看看
$$cost[i][j] + cost[i+1][j+1] > cost[i+1][j] + cost[i][j+1]$$
$$左邊展開:cost[i][j]+(cost[i+1][j]+a[j+1]-a[\lfloor\frac{i+j+2}{2}\rfloor])$$
$$右邊展開:cost[i+1][j]+(cost[i][j]+a[j+1]-a[\lfloor\frac{i+j+1}{2}\rfloor])$$
$$消一消變證a[\lfloor\frac{i+j+2}{2}\rfloor]<a[\lfloor\frac{i+j+1}{2}\rfloor],顯然是錯的,矛盾。$$
回到中位數
$$結論就是 cost[l][r] = cost[l][r-1] + a[r] - a[\lfloor\frac{l + r}{2}\rfloor],然後cost[i][i]=0$$
可能會發現\(cost\)符合不等式,我們這裡假設不符合來反證看看
所以\(cost\)符合Monge Condition,
進而得到\(dp[i][r]=\min_{k<r}(dp[i-1][k]+cost[k+1][r])\)min裡那串也符合
$$最後得到\forall i,dp[i]有凸單調性$$
好ㄟ
$$所以現在\forall i,dp[i]都有凸單調性$$
可以做\(m\)次1D/1D凸優化或分治優化,時間複雜度是\(O(mn log n)\)
更好ㄟ
$$所以現在\forall i,dp[i]都有凸單調性$$
可以做\(m\)次1D/1D凸優化或分治優化,時間複雜度是\(O(mn log n)\)
但
$$1.剛剛我們推出來K[i][j] \le K[i][j+1]$$
$$2.顯然地,蓋越多郵局越好,所以有K[i-1][j] \le K[i][j]$$
$$這樣就有K[i][j-1] \le K[i][j]\le K[i+1][j]$$
可以用Kuth-Yao Speedup!\(O(n^2)\)做完!
然後這題其實還有困難版,要用到Aliens
比一比
1D/1D凸時間複雜度比較
- 暴力 : \(O(n^2)\)
- 轉移點優化 : \(O(n log n)\) or \(O(n log^2 n)\)
- 1D/1D凸 : \(O(n log n)\)
2D/1D凸時間複雜度比較
- 暴力 : \(O(n^3)\)
- 轉移點優化 : \(O(n^2 log n)\) or \(O(n^2 log^2 n)\)
- 1D/1D凸優化 : \(O(n^2 log n)\)
- Knuth-Yao Speedup: \(O(n^2)\)
轉移點優化、1D/1D凸優化指的是做\(n\)次,
2D/1D凹沒有Knuth's Optimization可用,只能1D/1D凹優化做\(n\)次
但我不知道為什麼QQ
矩陣相關
矩陣快速冪
你應該已經會了
但我還是幫大家(還有笨我)複習一下 (偷自這)
費式數列
$$f(n) = f(n - 1) + f(n - 2)$$
費式數列
$$f(n) = f(n - 1) + f(n - 2)$$
\(\begin{vmatrix}f(n)&f(n - 1)\end{vmatrix}\) = \(\begin{vmatrix}f(n - 1)&f(n - 2)\end{vmatrix}\) \(\begin{vmatrix}1 &1\\1 &0\end{vmatrix}\)
\(\begin{vmatrix}f(n)&f(n - 1)\end{vmatrix}\) = \(\begin{vmatrix}f(1)&f(0)\end{vmatrix}\) \(\begin{vmatrix}1 &1\\1 &0\end{vmatrix}^{n-1}\)
加上常數項\(k\)
$$f(n) = f(n - 1) + f(n - 2) + k$$
加上常數項\(k\)
$$f(n) = f(n - 1) + f(n - 2) + k$$
\(\begin{vmatrix}f(n)&f(n - 1)&k\end{vmatrix}\) = \(\begin{vmatrix}f(n - 1)&f(n - 2)&k\end{vmatrix}\) \(\begin{vmatrix}1 &1&0\\1 &0&0\\1&0&1\end{vmatrix}\)
加上\(n\)
$$f(n) = f(n - 1) + f(n - 2) + n$$
加上\(n\)
$$f(n) = f(n - 1) + f(n - 2) + n$$
\((n - 1) + 1 = n\)好好維護喔
加上\(n\)
$$f(n) = f(n - 1) + f(n - 2) + n$$
\((n - 1) + 1 = n\)好好維護喔
要記得維護\(1\)喔
加上\(n\)
$$f(n) = f(n - 1) + f(n - 2) + n$$
\((n - 1) + 1 = n\)好好維護喔
要記得維護\(1\)喔
\(\begin{vmatrix}f(n)&f(n - 1)&n&1\end{vmatrix}\) = \(\begin{vmatrix}f(n - 1)&f(n - 2)&n-1&1\end{vmatrix}\) \(\begin{vmatrix}1 &1&0&0\\1&0&0&0\\1&0&1&0\\1&0&1&1\end{vmatrix}\)
求和
$$f(n) = f(n - 1) + f(n - 2)$$
$$S(n) = \sum_{1\leq i\leq n} f(i)$$
求和
$$f(n) = f(n - 1) + f(n - 2)$$
$$S(n) = \sum_{1\leq i\leq n} f(i)$$
\(\begin{vmatrix}f(n)&f(n - 1)&S(n-1)\end{vmatrix}\) = \(\begin{vmatrix}f(n - 1)&f(n - 2)&S(n-2)\end{vmatrix}\) \(\begin{vmatrix}1 &1&1\\1&0&0\\0&0&1\end{vmatrix}\)
矩陣快速冪
經典題&小技巧
有張簡單有向圖有\(n\)點
給你一個數字\(k\)
問從\(1\)號點走到\(n\)號點花恰好\(k\)步有幾種走法?(要取模)
- \(n\leq 100\)
- \(k\leq 10^9\)
\(k\)很小怎麼做?
\(k\)很小怎麼做?
\(dp[i][u]\)代表走了\(i\)步停在\(u\)的走法
則如果\(u\)有條邊連向\(v\),\(dp[i][u]\)可轉移至\(dp[i+1][v]\)
\(dp[k][n]\)即為所求
\(k\)很大呢?
\(k\)很大呢?
你已經知道了
我們可以把轉移式用矩陣寫出來(我討厭latex)
\(\begin{vmatrix}dp_{i,1} & dp_{i,2} &\cdots& dp_{i,n}\end{vmatrix}\) = \(\begin{vmatrix}dp_{i-1,1} & dp_{i-1,2} &\cdots& dp_{i-1,n}\end{vmatrix}\) \(\begin{vmatrix}w_{1,1} & w_{1,2} &\cdots& w_{1,n}\\w_{2,1}&w_{2,2}&\cdots&w_{2,n}\\\vdots&\ddots&&\vdots\\\vdots&&\ddots&\vdots\\w_{n,1}&w_{n,2}&\cdots&w_{n,n}\end{vmatrix}\)
其中\(w_{i,j}\)代表\(i\)有無連一條邊到\(j\)
\(k\)很大呢?
所以就可以矩陣快速冪了,時間複雜度\(O(n^3 log\ k)\)
\(\begin{vmatrix}dp_{k,1} & dp_{k,2} &\cdots& dp_{k,n}\end{vmatrix}\) = \(\begin{vmatrix}1 & 0 &\cdots& 0\end{vmatrix}\) \(\begin{vmatrix}w_{1,1} & w_{1,2} &\cdots& w_{1,n}\\w_{2,1}&w_{2,2}&\cdots&w_{2,n}\\\vdots&\ddots&&\vdots\\\vdots&&\ddots&\vdots\\w_{n,1}&w_{n,2}&\cdots&w_{n,n}\end{vmatrix}^k\)
$$有一個n*n矩陣A和一整數k$$
$$求A^1 + A^2+...+A^k (要取模)$$
- \(n\leq 40\)
- \(k \leq 10^9\)
分治!!!!!!
$$注意到\sum_{1\leq i \leq k}A_i = (1+A_{mid})\sum_{1\leq i \leq mid}A_i$$
可以先算出\(A_mid\),再切成一半,遞迴左半邊,右半邊就由左半邊得到
當然\(k\)是奇數時會稍微不一樣
分治!!!!!!
$$注意到\sum_{1\leq i \leq k}A_i = (1+A_{mid})\sum_{1\leq i \leq mid}A_i$$
可以先算出\(A_mid\),再切成一半,遞迴左半邊,右半邊就由左半邊得到
當然\(k\)是奇數時會稍微不一樣
總共遞迴\(log\ k\)次,每次\(O(n^3 log\ k)\)
總時間複雜度\(O(n^3 log^2k)\)
現在有一個變形的費式數列
$$f(i) = f(i - k) + f(i - k + 1) + ... + f(i - 1)$$
求\(Q\)次\(f(n)\)
- \(k \leq 16\)
- \(n \leq 10^{18}\)
- \(Q \leq 10 ^ 5\)
我會,矩陣快速冪!
令\(A=\begin{vmatrix}1&1&0&\cdots&0\\1&0&1&\cdots&0\\1&0&0&\cdots&0\\\vdots&&\ddots&&\vdots\\1&0&0&\cdots&1\\1&0&0&\cdots&0\end{vmatrix}\)
\(\begin{vmatrix}f(n)&f(n-1)&\cdots&f(n-k+1)\end{vmatrix}\) \(\ =\ \begin{vmatrix}f(n-1)&f(n-2)&\cdots&f(n-k)\end{vmatrix}\ A\)
\(\begin{vmatrix}f(n)&f(n-1)&\cdots&f(n-k+1)\end{vmatrix}\) \(\ =\ \begin{vmatrix}f(k-1)&f(k-2)&\cdots&f(0)\end{vmatrix}\ A ^{n- k +1}\)
$$中間算A的冪次時是k*k矩陣互乘,$$
$$時間複雜度O(Q k^3 log \ C)$$
我會,矩陣快速冪!
$$O(Q k^3 log \ C)$$
TLE了...
(乘起來高達\(2.5*10^{10}\))
考慮預處理
可以先做出\(A^1,A^2,A^4,...\)共\(log\ C\)個矩陣
$$A^{2^x}可直接仰賴A^{2^{x-1}},所以只要一個log$$
對於單一\(k\)的時間複雜度為\(O(k^3 log\ C)\)
\(k\)會變的話就是\(O(k^4 log\ C)\)
考慮預處理
對於一個詢問我就只要讓
\(\begin{vmatrix}f(k-1)&f(k-2)&\cdots&f(0)\end{vmatrix}\)
一直乘\(A\)的冪次就好
最多乘\(log C\)次,每次都是\(1*k\)和\(k*k\)的矩陣相乘
單次詢問時間複雜度\(O(k^2 log\ C)\)
整題的總時間複雜度為\(O((k^2 log\ C)(Q+k^2))\)
習題
斜率優化
#偷 #caido
Slope trick
維護線段和轉折點,是真正的斜率優化
Slope-trick-able
當一個連續的凸/凹函數,可以被切成很多段直線時
我們稱這個函數Slope-trick-able
Slope-trick-able
當一個連續的凸/凹函數,可以被切成很多段直線時
我們稱這個函數Slope-trick-able
左邊的凸函數就是一個例子
Slope-trick-able
當一個連續的凸/凹函數,可以被切成很多段直線時
我們稱這個函數Slope-trick-able
左邊的凸函數就是一個例子
可以用斜率、轉折點存所有資訊
Slope-trick-able
當一個連續的凸/凹函數,可以被切成很多段直線時
我們稱這個函數Slope-trick-able
左邊的凸函數就是一個例子
可以用斜率、轉折點存所有資訊
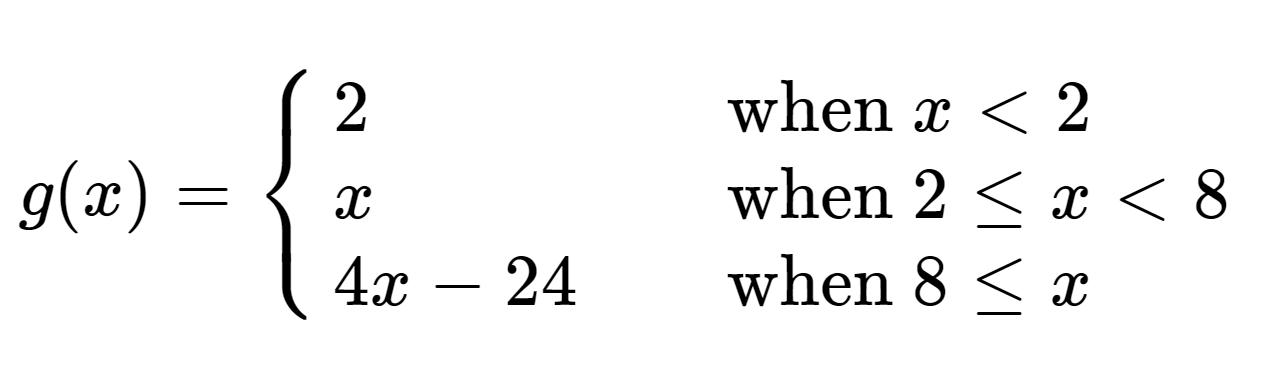
上面這個和左圖無關
Slope-trick-able
當一個連續的凸/凹函數,可以被切成很多段直線時
我們稱這個函數Slope-trick-able
左邊的凸函數就是一個例子
可以用斜率、轉折點存所有資訊
常常會用multiset之類的來存
如果斜率一次變不只1
那就加同個點很多次
Slope-trick-able
兩個凹凸性同的slope-trick-able的函數相加依然slope-trick-able
然後新函數的斜率分割點是兩者的分割點取交集後,把一些丟掉
+1和-1抵銷之類的
你有一個長度為\(n\)的數列\(a\)
你每次操作可以使隨便一個數\(+1或-1\)
問最少的操作次數使得\(x\)非嚴格遞增
- \(n \leq 2*10^5\)
- \(a_i \leq 10^9\)
\(O(nC)\)DP解
令\(dp[i][x]\)代表使得\(a_i\)\(\leq\)x時的答案
有轉移式
$$dp[i][j]=\min(dp[i][x-1],\ \ |x-a_i|+\min_{1\leq k \leq x}dp[i-1][k])$$
\(dp[n][C]即為所求\)
\(O(nC)\)DP解
令\(dp[i][x]\)代表使得\(a_i\)\(\leq\)x時的答案
有轉移式
$$dp[i][j]=\min(dp[i][x-1],\ \ |x-a_i|+\min_{1\leq k \leq x}dp[i-1][k])$$
\(dp[n][C]即為所求\)
穩TLE
小觀(通)察(靈)
一定存在一個最佳解,
使得最後的陣列裡的所有數字都是原陣列裡出現過的數字
小觀(通)察(靈)
一定存在一個最佳解,
使得最後的陣列裡的所有數字都是原陣列裡出現過的數字
小觀察的證明
留給讀者作為練習
\(O(nC)\)DP解
令\(dp[i][x]\)代表使得\(a_i\)\(\leq\)x時的答案
有轉移式
$$dp[i][j]=\min(dp[i][x-1],\ \ |x-a_i|+\min_{1\leq k \leq x}dp[i-1][k])$$
套用小觀察就會知道有用的\(x\)只有\(n\)個
所以時間複雜度就變\(O(n^2)\)
會過CF 713C
\(O(nC)\)DP解
令\(dp[i][x]\)代表使得\(a_i\)\(\leq\)x時的答案
有轉移式
$$dp[i][j]=\min(dp[i][x-1],\ \ |x-a_i|+\min_{1\leq k \leq x}dp[i-1][k])$$
套用小觀察就會知道有用的\(x\)只有\(n\)個
所以時間複雜度就變\(O(n^2)\)
會過CF 713C
更好的做法?
$$dp[i][j]=\min(dp[i][x-1],\ \ |x-a_i|+\min_{1\leq k \leq x}dp[i-1][k])$$
把\(dp_i,dp_i-1\)當成函數來想
每次算\(dp_i(x)\)的時候就相當於先讓\(dp_{i-1}(x)\)加上\(|x-a_i|\)
再前綴取\(min\)
加上\(|x-a_1|\)
前綴取min
得到\(dp_1\)
\(加上|x-a_2|\)
\(加上|x-a_2|\)
前綴取min
得到\(dp_2\)
\(加上|x-a_3|\)
\(加完了|x-a_3|\)
前綴取min
得到\(dp_3\)
疑?
\(dp\)好像一直都是slope trick able,而\(|x-a_i|\)本來就是slope trick able
疑?
\(dp\)好像一直都是slope trick able,而\(|x-a_i|\)本來就是slope trick able
每次\(i\)變大,就是讓\(a_i\)左邊的線斜率減一,讓其右邊的線斜率加一
疑?
\(dp\)好像一直都是slope trick able,而\(|x-a_i|\)本來就是slope trick able
每次\(i\)變大,就是讓\(a_i\)左邊的線斜率減一,讓其右邊的線斜率加一
把原本最右的轉折點拔掉(如果\(a_i\)較大那就不拔)
同時在\(a_i\)這個位置,加兩個轉折點
疑?
\(dp\)好像一直都是slope trick able,而\(|x-a_i|\)本來就是slope trick able
每次\(i\)變大,就是讓\(a_i\)左邊的線斜率減一,讓其右邊的線斜率加一
把原本最右的轉折點拔掉(如果\(a_i\)較大那就不拔)
同時在\(a_i\)這個位置,加兩個轉折點
前綴取min就是把斜率剛從0變成1的整段拔掉
函數的最右邊還是保持水平線
作法出來了喔
我整個函數一直都是這種可以由轉折點、斜率紀錄的函數
又我們最後想要的答案\(dp_n(C)\)是\(dp_n\)中的水平線的\(y\)座標
也就是說我們只需要維護最右邊的轉折點及其y座標
作法出來了喔
我整個函數一直都是這種可以由轉折點、斜率紀錄的函數
又我們最後想要的答案\(dp_n(C)\)是\(dp_n\)中的水平線的\(y\)座標
也就是說我們只需要維護最右邊的轉折點及其y座標
可以開個priority_queue存轉移點,同時記錄答案
作法出來了喔
我整個函數一直都是這種可以由轉折點、斜率紀錄的函數
又我們最後想要的答案\(dp_n(C)\)是\(dp_n\)中的水平線的\(y\)座標
也就是說我們只需要維護最右邊的轉折點及其y座標
可以開個priority_queue存轉移點,同時記錄答案
每次加一個\(a_i\)進來,就先放兩個\(a_i\)進入pq,再把pq中最大值踢掉
踢掉時順便看一下答案的變化
時間複雜度 \(O(n log n)\)
習題(自caido簡報)
Aliens
變數要叫ufo
#偷 #caido
謝謝大家
好想進二階
然後揪資讀\(\frac{1}{3}\)馬拉松
(從建中跑到大湖公園站)