DP
alvingogo
DP 是什麼
DP
- dynamic programming
- 由小狀態的答案知道大狀態的答案
怎麼使用
定狀態+轉移式
基礎 DP
DP: 定狀態+轉移式
怎麼定狀態?
題目要求扣到 0 的最小步數
直接的想法可能是遞迴枚舉,把所有可能的過程都跑過一遍
這樣 TLE,不過我們可以優化
怎麼優化?
考慮兩個過程 39 -> 30 與 39 -> 36 -> 30
可以發現 30 這個狀態出現兩次,但後續是一樣的
於是就有個想法:只想讓一個狀態被算好一次
假設 dp[i] 表示從 i 開始,最少要用到多少次
以後又經過 i 的時候,是不是只要用 dp[i] 就好了
轉移式:dp[i] = min(dp[i-a])+1 其中 a 是 i 的任一個 digit
DP 問題的精髓:拿小問題的解推到大問題的解
code
#include <bits/stdc++.h>
#define fastio cin.tie(0);ios_base::sync_with_stdio(0);
using namespace std;
int main(){
fastio;
int n;
cin >> n;
vector<int> dp(n+1,10000000);
dp[0]=0;
for(int i=1;i<=n;i++){
int p=i;
while(p>0){
dp[i]=min(dp[i],dp[i-p%10]+1);
p/=10;
}
}
cout << dp[n] << endl;
return 0;
}題單
以下的東西都沒有難度順序,但我應該可以保證能只用目前的東西做出來,不過 mod 要學一下XD
背包問題
我有 n 本書可以買,每本書有各自的價格跟頁數,求在總價格不超過 x 的情況下頁數總和的最大值
n <= 1e4
x <= 1e5
怎麼定狀態?
假設 dp[i][j] 表示考慮前 i 本書,總價格恰好是 j 的情況下總頁數的最大值
dp[i+1][j] = max (dp[i][j], dp[i][j - w[i+1]] + v[i+1])
其中 w[i] 與 v[i] 分別表示第 i 本書的價格跟頁數
可以自己想一下
用兩層迴圈分別掃過 i 跟 j,更新 dp,結案
時間複雜度跟空間複雜度都是 O(nx)
最後的答案就是 max dp[n-1][j] (0-base)
小優化
注意到 dp[i][j] 只跟 dp[i-1][j] 以及 dp[i-1][j-w[i]] 有關
而 w[i] > 0
那麼可以捨棄掉 i 這個維度
具體上是第二層迴圈改成從大往小掃
那更新 dp[j] 的時候,就直接用 dp[j] 跟 dp[j-w[i]] 更新
這樣的空間複雜度會變 O(x)
code
#include <bits/stdc++.h>
#define fastio cin.tie(0);ios_base::sync_with_stdio(0);
using namespace std;
int main(){
fastio;
int n,x;
cin >> n >> x;
vector<int> w(n),v(n);
for(int i=0;i<n;i++){
cin >> w[i];
}
for(int i=0;i<n;i++){
cin >> v[i];
}
vector<int> kn(x+1);
for(int i=0;i<n;i++){
for(int j=x;j>=0;j--){
if(j-w[i]>=0){
kn[j]=max(kn[j],kn[j-w[i]]+v[i]);
}
}
}
cout << kn[x] << "\n";
return 0;
}無限背包
我有 n 本書可以買,每本書有無限個複製品,每本書有各自的價格跟頁數,求在總價格不超過 x 的情況下頁數總和的最大值
n <= 1e4
x <= 1e5
提示:把上面那個改一個地方就好了
注意到每個書都有無限個複製品
代表這次我們把價格從小掃到大就可以有效的處理每一種情況
優化也是一樣的方式
題單
LIS
Longest Increasing Subsequence
給你一個序列,你要求出最長的遞增子序列長度
n <= 2e5
一個初始的想法是考慮 \(dp_i \) 表示結尾是 j 的最大值,那這樣轉移式就是
$$dp_j = \underset { u < j }{ max } (dp_u) + 1$$
O(n^2)
考慮保存當前的轉移點位置,把它存成一個陣列, \( v_i \) 表示當 LIS 的長度為 i 的時候當前的末尾元素是多少
可以發現 v 一定是一個遞增數列
當我新增一個元素的時候,我在陣列裡面找出最小的 >= 他的元素,然後把它換成當前元素
例:v = {1,2,3,5,8,13} 我新增了 7
new_v = {1,2,3,5,7,13}
為什麼這樣是好的?
可以發現如果有多個點的 DP 值相同,那我們最後只需要原本的值最小的那個
所以更新的時候就是把後面那個改小就好
code
#include <bits/stdc++.h>
#define fastio cin.tie(0);ios_base::sync_with_stdio(0);
using namespace std;
int main(){
fastio;
int n;
cin >> n;
vector<int> v(n);
for(int i=0;i<n;i++){
cin >> v[i];
}
vector<int> dp;
dp.push_back(v[0]);
for(int i=1;i<n;i++){
auto r=lower_bound(dp.begin(),dp.end(),v[i]);
if(r==dp.end()){
dp.push_back(v[i]);
}
else{
dp[r-dp.begin()]=v[i];
}
}
cout << dp.size() << "\n";
return 0;
}輸出一組 LIS
前面留下來的陣列不一定是一個合法的 LIS
現在要輸出一組完整的 LIS
只需要在更新的時候順便存每個點的前一個是誰
最後從陣列的最後一個 DFS 回去就好
題單
Edit Distance
給你兩個字串 \(a, b\),我要花費最少次數把兩個字串變成相同
可選的操作是
1. 從第一個字串刪除任意一個字元
2. 從第一個字串插入任意一個字元
3. 從第一個字串更改任意一個字元
$$|a|,|b| \leq 5000$$
解法:考慮 dp[x][y] 表示至少要做多少次才能把 a 的前 x 個字跟 b 的前 y 個字變成相同
$$dp_{x,y} = min(dp_{x,y-1}+1,dp_{x-1,y}+1,dp_{x-1,y-1}+1[a_x \neq b_y])$$
其中 \(1[a_x \neq b_y]\) 的意思是如果 \(a_x \neq b_y\) 那就是 1,否則是 0
分別對應到三種情況:插入、刪除、修改
題單
Digit DP
給你兩個十進位的數字,問你有多少數字界在 a 跟 b 之間 (included),且任意兩個相鄰數位皆不相同
0 <= a <= b <= 1e18
- 假設我有一個函數可以算出有多少數字界在 0 跟 b 之間滿足題目條件,那麼 f(b) - f(a-1) 就是答案
- 考慮從左到右建構字串,假設目前的字串是 s,要加的字元是 c,那麼答案只跟以下四個相關:目前的位數、s 是不是原本字串的前綴、s 的最後一位、當前是不是前綴都是 0,這些東西相關
- 於是可以 dp[i][j][k][l] 表示目前走到第 i 位,s 的最後一位是j,k 表示目前 s 是不是原本字串的前綴,l 表示當前前綴是不是都是 0,共有多少種數字滿足前綴是 i
- 4. 可以採用遞迴的形式,轉移會類似 dp[i][j][][] += dp[i+1][p!=j][][] 之類的
題單
區間 DP
給你一堆數字,兩個人輪流拿,只能拿最邊邊的數字,數字被拿過之後就會消失,兩個人都想讓自己拿最多,問最後結果是多少
n <= 5000
- 觀察可以發現第二個人讓自己拿最多 <=> 讓第一個人拿最少,所以問題可以變成第二個人想要 minimize,第一個人要 maximize
- 考慮 \(dp_{l,r}\) 表示把 [l,r] 拿完,第一個人先拿的結果,\(dp2_{l,r}\) 表示第二個人先拿的結果,那麼
\(dp_{l,r} = max(dp2_{l+1,r}+v_l, dp2_{l,r-1}+v_r) \)
\(dp2_{l,r} = min(dp_{l,r-1},dp_{l+1,r})\) - 在刻的時候要注意,必須讓小區間先算好
有兩種刻法,一種是枚舉長度再枚舉左界,另一種是按左界從大到小枚舉,再右界從小到大枚舉
題單
位元 DP
男生跟女生各有 n 個,給你每對男女可不可以配對,問你最後有幾種讓每個人都配對到的方式
n <= 21
一開始的想法可能會是枚舉 n! 種個可能
$$21! \approx 5 \cdot 10^{19}$$
顯然 TLE
注意到假設 1->1 2->2
跟 1->2 2->1
對 3 來講是一樣的
假設 dp[i][j] 表示前 i 個人都選好了,目前被選過的集合是 j,j 可以用整數表示
那可以枚舉第 i+1 個人要選什麼來 dp
$$dp_{i+1,j}=\sum_{z \in j} dp_{i,j-\{z\}}$$
附帶一提,這種我有時候也會寫成遞迴
題單
SOS DP
給你一個陣列 \(v\),令 \( b_{mask} = \sum_{r \subseteq mask} v[r]\)
求 \(b_0 \cdots b_{2^n-1} \)
假設 \(v\) 的長度是 \(2\) 的冪次
最直覺的想法
枚舉 i 再枚舉 j,一一檢查 j 是不是 i 的 submask
\(O(2^n \cdot 2^n) = O(4^n)\)
小小觀察
這裡假設你們都會 C++ 的 mask 操作
枚舉 mask,x = mask & (x-1),那麼 x 從 mask 掃到 0 這樣可以掃過全部的 submask
for(int i=0;i<(1<<n);i++){
for(int j=i;j>=0;j=i&(j-1)){
}
}複雜度
恰有 i 個 bit 是 1 數字的有 C(n,i) 個,每個都要掃 \(2^i\) 次
合起來是 $$ \sum_{i=0}^n C^n_i \cdot 2^i = (1+2)^n = 3^n$$
(大概) 3^n 的題單
SOS DP
定義 dp[i][j] = 對當前的 i 我想要對每個 j<n 找出 sum if k 是 i 的 submask,且 i 跟 k 最高的相異位 <= j
例如 i = 1101011, j = 1 那 dp[i][1] 就是
k = 1101011, 1101010, 1101001, 1101000 的總和
SOS DP
假設按照上面的定義方法,那考慮 i 的第 j 個 bit
如果是 0 那麼就 = dp[i][j-1]
如果是 1 那麼除了 dp[i][j-1] 之外,還要考慮把第 j 個 bit 換成 0 的總和,所以就是
dp[i][j-1]+dp[i^(1<<j)][j-1]
code
vector<int> v(1<<n);
vector<vector<int> > dp(1<<n,vector<int>(n+1));
for(int i=0;i<(1<<n);i++){
dp[i][0]=v[i];
}
for(int i=0;i<(1<<n);i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i][j-1];
if((i>>(j-1))&1){
dp[i][j]+=dp[i^(1<<(j-1))][j-1];
}
}
}vector<int> v(1<<n);
vector<int> dp(1<<n);
for(int i=0;i<(1<<n);i++){
dp[i]=v[i];
}
for(int j=0;j<n;j++){
for(int i=0;i<(1<<n);i++){
if((i>>j)&1){
dp[i]+=dp[(i^(1<<j))];
}
}
}比較簡短的寫法
題單
資源
輪廓線 DP
請問 n*m 的網格有幾種被 1*2 與 2*1 的骨牌完全覆蓋的方式
\( n \leq 10 \)
\( m \leq 1000 \)
n 很小 => 可以枚舉 O(2^n)
要怎麼枚舉?
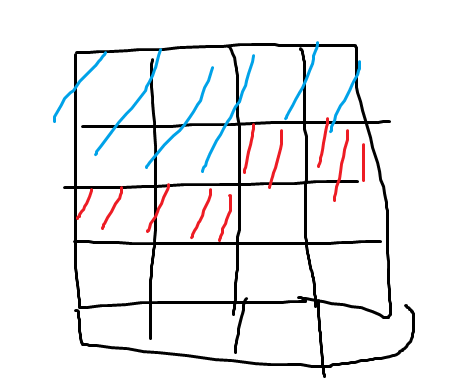
考慮右邊這張圖
假設已經放好藍色的部分了,紅色的部分待確定
可以發現藍色的部分就有點像子問題,於是可以 DP
\(dp_{i,j,s} \) 表示第 i 行第 j 列狀態為 s ,在藍色區域都放滿的情況下有幾種放法

左邊這張圖是第 1 行第 2 列
s 表示紅色區域每格分別有沒有被放過
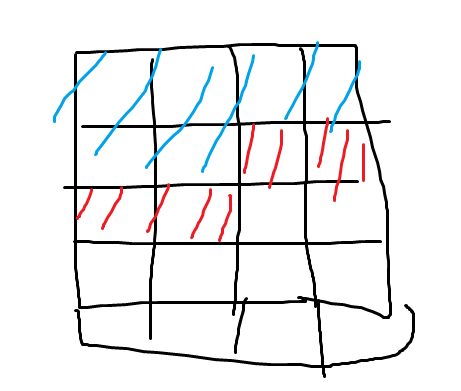
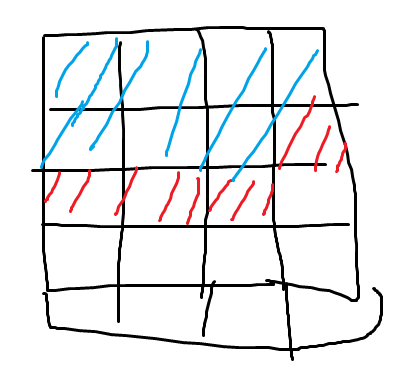
考慮從左邊到右邊的過程
轉移
因為它會變底下的藍色區域,所以一定要把這格放好,而我只能朝下放,因為朝右放會被重複計算到
這格還要考慮往左放的可能
這兩種情況考慮完的話就涵蓋到所有情況了
至於最後要取什麼?最後一行最後一列並且全部放滿就是答案
code
#include <bits/stdc++.h>
#define fastio cin.tie(0);ios_base::sync_with_stdio(0);
using namespace std;
int main(){
int n,m;
cin >> n >> m;
const int mod=1e9+7;
vector<long long> dp[2];
dp[0].resize(1<<n);
dp[1].resize(1<<n);
dp[0][(1<<n)-1]=1;
int now=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
for(int s=0;s<(1<<n);s++){
dp[now^1][s]=0;
}
for(int s=0;s<(1<<n);s++){
dp[now][s]%=mod;
if(s&(1<<j)){
dp[now^1][(s|(1<<j))^(1<<j)]+=dp[now][s];
}
else{
dp[now^1][s|(1<<j)]+=dp[now][s];
continue;
}
if(j==0){
continue;
}
if(!(s&(1<<(j-1)))){
dp[now^1][(s|1<<(j-1))|(1<<j)]+=dp[now][s];
}
}
now^=1;
}
}
cout << dp[now][(1<<n)-1]%mod << "\n";
return 0;
}tab 什麼的就算了
題單
DP
By alvingogo
DP
- 1,058



