DP 優化
becaido
講師介紹
- 建國中學 陳柏凱
- OJ handle:becaido
- 因為想學習 DP 優化所以當 DP 優化講師
單調隊列優化
給一個陣列 \(a_1\sim a_n\),問每個長度為 \(k\) 的區間最大值 (\(a_i\sim a_{i+k-1}\) 的最大值)?
我會線段樹!
\(O(n\log(n))\)
\(n=10^7\),被卡常

\(O(n)\) 的做法
維護一個 deque,代表一個長度為 \(k\) 的區間
最前段為區間最大值,後面的元素遞減
當最前面元素與目前位置距離 \(\geq k\),代表它不會被考慮到了
加入的元素可以把 deque 後端的元素淘汰掉
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7 + 5;
int n, k;
int a[N];
deque<int> dq;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
if (dq.size() && i - dq.front() >= k) dq.pop_front();
while (dq.size() && a[i] >= a[dq.back()]) dq.pop_back();
dq.push_back(i);
if (i >= k) cout << a[dq.front()] << ' ';
}
}用單調隊列優化多重背包問題
\(n\) 種物品,每種重量 \(w_i\),價值 \(v_i\),個數 \(a_i\),背包重量限制 \(W\)
用二進制做 01 背包
\(O(W\sum\log(a_i))\)
dp 式:
\(dp_{i,j}\):前 \(i\) 個物品重量為 \(j\) 以下能拿到的最大值
\(\rightarrow dp_{i,j}=\max\limits_{0\leq x\leq a_i}(dp_{i-1,j-x\times w_i}+x\times v_i)\)
令 \(k=j-x\times w_i\)
\(dp_{i,j}=\max\limits_{0\leq x\leq a_i}(dp_{i-1,k}+\frac{j-k}{w_i}\times v_i)\\=\max\limits_{0\leq x\leq a_i}(dp_{i-1,k}-\lfloor\frac{k}{w_i}\rfloor\times v_i)+\lfloor\frac{j}{w_i}\rfloor\times v_i\)
對 \(j\text{ mod }w_i\) 相同的做一遍單調隊列優化!
\(O(n\times W)\)
斜率優化
給 \(n,x,s_1\sim s_n(s_i\leq s_{i+1}),f_1\sim f_n(x\geq f_i\geq f_{i+1})\)
殺第 \(i\) 隻怪獸要花 \(s\times f\) 的時間,\(s\) 是現在這隻怪獸的 \(s_i\),\(f\) 是你目前的 \(f\) (初始值 \(f_0=x\)),殺了第 \(i\) 隻怪獸,\(f\) 會變 \(f_i\),可以選擇要殺或不殺這隻怪獸,問最少要花多少時間才能殺掉第 \(n\) 隻怪獸?
列出 DP 式,令 \(dp_i\) 是殺掉第 \(i\) 隻怪獸最少要花的時間,最後要求 \(dp_n\)
\(dp_i = \min\limits_{0\leq j<i}(dp_j + s_i\times f_j)\)
直接 \(O(n^2)\) 算
TLE
\(dp_i = \min\limits_{0\leq j<i}(dp_j + s_i\times f_j)\)
轉換一下式子
\(dp_i = \min\limits_{0\leq j<i}(f_j\times s_i+dp_j)\)
是不是很像一個東西?
\(dp_i = \min\limits_{0\leq j<i}(M_j\times x+K_j)\)
一條直線的樣子!
把第 \(j\) 隻怪獸用 \(L_j:y=M_j\times x+K_j\) 表示
這題還有什麼性質?
當 \(j\) 變大,\(M\) (斜率) 會遞減,\(x\) (查詢) 會遞增!
查詢的是很多直線在某個 \(x\) 的 \(\min\)
維護一個上凸包!
(實線代表目前 \(x\) 的 \(\min\) 在哪一條)
可以用 deque 維護凸包的直線
當要詢問某個 \(x\) 的最小值,可以比較最前面的兩條線
因為 \(x\) 會遞增,所以 \(L_1\) 在之後一定比 \(L_2\) 差,直接把 \(L_1\) pop 掉
繼續比,發現 \(L_2\) 比 \(L_3\) 好,
所以目前 \(x\) 值最好的直線是 \(L_2\)
現在我們算出 \(dp_i\) 了,代表我們有 \(L_i\) 這條直線了,要放入這個凸包
情況一
直接放在 deque 後面
情況二
\(L_3\) 好像不管怎樣都不會是最好的...
(\(L_3\) 不在凸包上 \(\Leftrightarrow\) \(L_3,L_i\) 交點的 \(x\) \(\leq\) \(L_3,L_2\) 交點的 \(x\))
這個時候 \(L_2\) 跟 \(L_i\) 會合力把 \(L_3\) 殺掉
算交點可以用數學處理(國中數學)
Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 5;
int n;
int s[N], f[N];
int M[N];
ll K[N], dp[N];
deque<int> dq;
ll cal_y(int i, int x) {
return 1ll * M[i] * x + K[i];
}
bool can_del(int i1, int i2, int i) {
/*
y = m1*x + k1, y = m2*x + k2
==> x = (k2-k1) / (m1 - m2)
x_{i1,i2} >= x_{i,i2}
==> (k[i2]-k[i1]) / (m[i1]-m[i2]) >= (k[i2]-k[i]) / (m[i]-m[i2])
==> (k[i2]-k[i1]) * (m[i]-m[i2]) <= (k[i2]-k[i]) * (m[i1]-m[i2])
*/
return (K[i2] - K[i1]) * (M[i] - M[i2]) <= (K[i2] - K[i]) * (M[i1] - M[i2]);
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> f[0];
for (int i = 1; i <= n; i++) cin >> s[i];
for (int i = 1; i <= n; i++) cin >> f[i];
M[0] = f[0];
dq.push_back(0);
for (int i = 1; i <= n; i++) {
int x = s[i];
while (dq.size() >= 2 && cal_y(dq[0], x) >= cal_y(dq[1], x)) dq.pop_front();
dp[i] = cal_y(dq[0], x);
M[i] = f[i], K[i] = dp[i];
while (dq.size() >= 2 && can_del(dq.end()[-2], dq.end()[-1], i)) dq.pop_back();
dq.push_back(i);
}
cout << dp[n] << '\n';
}
如果查詢是遞減不是遞增怎麼辦?
改用 stack!
Monster Game Ex
與原本問題相同,只是每 \(k\) 個怪獸必須要有一個被殺。
\(\Rightarrow\) 只能從 \(\max(0,i-k)\leq j<i\) 轉移
原本 \(L_2,L_i\) 會殺掉 \(L_3\),但是有可能 \(L_2\) 在被用到之前就過期了
原本 \(x_{L_3,L_i}\leq x_{L_3,L_2}\) 可以把 \(L_3\) pop 掉變成
\(x_{L_3,L_i}\leq \min(x_{L_3,L_2},\)過期點\()\)
練習題:TIOJ 1676
Monster Game ExEx
每個怪獸都有上一個轉移範圍 \(l_i,r_i\)
區間詢問...
可以線段樹嗎?
可以!
對每個線段樹節點開一個 deque
每次加入 \(L_i\),加入區間有包含 \(i\) 的 deque
每次查詢,可以對 \(O(\log(n))\) 個小區間做一次,最後取 \(\min\)
與原題相同,但 \(s_i,f_i\) 沒有遞增或遞減了
沒有遞增(減)性就不能好好維護凸包了...
有三個方法!
方法一:分治
沒有遞增(減)性,我們強制讓它有!
\(\text{divide}(l,r)\) 可以處理好在 \([l,r]\) 的所有轉移
呼叫 \(\text{divide}(l,mid)\) 把左邊的處理好,接著我們要處理從 \([l,mid]\) 轉移到 \([mid+1,r]\)
對 \([l,mid]\) 的斜率 \(\text{sort}\),對 \([mid+1,r]\) 的查詢 \(\text{sort}\),就可以直接 \(O(r-l+1)\) 做斜率優化了,之後呼叫 \(\text{divide}(mid+1,r)\) 處理右邊的
\(\text{sort}\) 的部分可以用 \(\text{merge sort}\) 的方法,時間、空間複雜度 \(O(n\times\log(n))\)
方法二:李超線段樹

對值域開一個動態開點線段樹
區間 \([L,R]\) 這個節點會存一條直線 \(line\),
代表 \(mid=\frac{L+R}{2}\) 在 \(line\) 及祖先節點的 \(line\) 中會有最小值
現在要插入一個線段,有兩種情況
第一種:此節點還沒有放任何線段
\(\Rightarrow\) 直接放
第二種:遇到此節點的 \(line\) 了
代入 \(x=mid\) 比較大小
把此節點的 \(line\) 設成較好的,繼續往下插入較不好的
要往左還是往右?
比斜率!
1. \(m\geq line.m\)
插左邊
2. \(m<line.m\)
插右邊
每次空間至多只會多 \(O(1)\)
空間複雜度 \(O(n)\),時間複雜度 \(O(n\times\log(C))\)
Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 5;
const int MAX = 1e6;
int n;
int s[N], f[N];
ll dp[N];
struct Line {
int m;
ll k;
Line() {}
Line(int m, ll k) : m(m), k(k) {}
ll operator () (const int &x) const {
return 1ll * m * x + k;
}
};
struct Node {
Line line;
int ls = 0, rs = 0;
Node() {}
Node(Line line) : line(line) {}
} node[N];
int root, sz;
int newnode(Line line) {
node[++sz] = Node(line);
return sz;
}
void ins(int &pos, int l, int r, Line line) {
if (pos == 0) {
pos = newnode(line);
return;
}
Node &nd = node[pos];
if (l == r) {
if (line(l) < nd.line(l)) nd.line = line;
return;
}
int mid = (l + r) / 2;
if (line(mid) < nd.line(mid)) swap(line, nd.line);
if (line.m >= nd.line.m) ins(nd.ls, l, mid, line);
else ins(nd.rs, mid + 1, r, line);
}
ll que(int pos, int l, int r, int x) {
if (pos == 0) return LLONG_MAX;
Node &nd = node[pos];
if (l == r) return nd.line(x);
int mid = (l + r) / 2;
return min(nd.line(x), x <= mid ? que(nd.ls, l, mid, x) : que(nd.rs, mid + 1, r, x));
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> f[0];
for (int i = 1; i <= n; i++) cin >> s[i];
for (int i = 1; i <= n; i++) cin >> f[i];
ins(root, 0, MAX, Line(f[0], 0));
for (int i = 1; i <= n; i++) {
dp[i] = que(root, 0, MAX, s[i]);
ins(root, 0, MAX, Line(f[i], dp[i]));
}
cout << dp[n] << '\n';
}
方法三:動態凸包
一樣是空間 \(O(n)\),時間 \(O(n\times\log(n))\)
但是講師不會 OAO
會的可以上來講
有轉移範圍的不單調斜率優化...
線段樹!
每個線段樹節點都開一棵李超線段樹
\(O(n\times\log(n)\times\log(C))\)
練習題:
ZJ f995:疊疊杯子蛋糕 - Extreme (\(n\leq 3\times 10^5\))
對於轉移範圍任意的,似乎就只能這樣了
那如果大小固定是 \(k\) 呢?
原本以為只能做到 \(O(n\times\log(n)\times\log(C))\)
直到...
TIOJ 2285:花花世界
給你 \(a_0\sim a_n,\ b_1\sim b_n,\ m_1\sim m_n\),
\(F_i = \max\limits_{\max(0, b_i - k + 1)\leq j \leq b_i}(F_j + (a_i - a_j + 1)\times m_i)\),請你輸出 \(\sum\limits_{i = 0}^n F_i\ (\text{mod }1020050909)\)
(校內賽寫線段樹套李超線段樹被卡...)
要想辦法優化到 \(O(n\times\log(C))\)
移一下式子,變成
\(F_i = (-a_j)\times m_i + F_j + (a_i + 1)\times m_i\)
每 \(k\) 個分一塊,那每個區間會蓋住恰好一個分界點
分界點往左跟往右的直線可以分開算
每個點記錄它在分界點的左(右)邊會轉移到哪一些點
練習題
ZJ i963:疊疊杯子蛋糕 ꝏ Extreme (\(n\leq 10^6\))
基本上是看完花花世界出的
矩陣優化
費式數列 \(f_0=0,f_1=1,f_i=f_{i-1}+f_{i-2}\)
求 \(f_n\ (\text{mod }M)\)
直接算
\(O(n)\)
\(n\leq 10^{18}\) 怎麼辦?
把轉移寫成矩陣乘法
令 \(A=\)
那
\(\times A\times A\times\dots\)
可以寫成 \(\times A^n\)
\(\Rightarrow\) 可以快速冪!
\(O(\log(n))\)
矩陣快速冪的時機
DP 轉移可以用矩陣表達
矩陣快速冪的優化
#include "moon.h"
\(f_1\sim f_k=1\) (\(k\leq 15\))
\(f_i=\sum\limits_{j=1}^k f_{i-j}\)
\(q\leq 10^5\) 次詢問,每次給 \(n\leq 10^{18}\),請求出 \(f_n\ (\text{mod }M)\)
費式數列 Ex
現在要考慮矩陣大小了,兩個 \(k\times k\) 矩陣相乘的複雜度是 \(O(k^3)\) (或是你可以用 \(O(k^{2.37188})\))
那 \(q\) 次詢問的總時間複雜度是 \(O(q\times k^3\times\log(C))\)
TLE 了
可以預處理
先算出 \(A^1,A^2,A^4,A^8\dots\),快速冪時可以直接用
把 \(k\times k\) 的矩陣改成 \(1\times k\)
複雜度 \(O(k^4\times\log(C)+q\times k^2\times\log(C))\)
給 \(f_0\sim f_{k-1}\),\(f_i=\sum\limits_{j=1}^k a_j\times f_{i-j}\) (\(k\leq 2000\))
求 \(f_n\) (\(n\leq 10^{18}\))
費式數列 ExEx
\(O(k^3\times\log(C))\) 太慢
似乎有一個多項式的做法
做法 (From OI-wiki)
令 \(F(\sum c_ix^i)=\sum c_if_i\) (把多項式的第 \(i\) 項乘 \(f_i\))
想求 \(F(x^n)=f_n\)
\(F(x^n)=F(\sum\limits_{i=1}^ka_ix^{n-i})\)
\(\Rightarrow\ F(x^n-\sum\limits_{i=1}^ka_ix^{n-i})=F(x^{n-k}(x^k-\sum\limits_{i=0}^{k-1}a_{k-i}x^i))=0\)
我們現在知道 \(F(x^k-\sum\limits_{i=0}^{k-1}a_{k-i}x^i)=0\)
\(\text{mod}\) 一次多項式要 \(O(k^2)\),加上快速冪,複雜度 \(O(k^2\times\log(C))\)
令 \(G(x)=x^k-\sum\limits_{i=0}^{k-1}a_{k-i}x^i\)
那求 \(F(x^n)\) 相當於求 \(F(x^n\ \text{mod }G(x))\)
費式數列 ExExEx
給 \(f_0\sim f_{k-1}\),\(f_i=\sum\limits_{j=1}^k a_j\times f_{i-j}\) (\(k\leq 3\times 10^4\))
求 \(f_n\) (\(n\leq 10^{18}\))
\(O(k^2\times\log(C))\) 也 TLE 了,要怎麼優化啊?
多項式...
NTT!
把 \(\text{mod }G(x)\) 從 \(O(k^2)\) 優化到 \(O(k\times\log(k))\) 了
複雜度 \(O(k\times\log(k)\times\log(C))\)
ZJ f013:\(k\leq 30,n\leq 2^{50},q\leq 10^4\),測資爛,\(O(k^3\times\log(C))\) 可過
ZJ f996:\(k\leq 15,n\leq 2^{60},q\leq 10^5\),\(O(k^4\times\log(C)+q\times k^2\times\log(C))\)
ZJ i001:\(k\leq 2000,n\leq 10^9\),\(O(k^2\times\log(n))\) 可過
ZJ i002:\(k\leq 3\times 10^4,n\leq 10^9\),\(O(k\times\log(k)\times\log(n))\)
ZJ j777:\(k\leq 2\times 10^5,n\leq 2^{24}\),有點卡常
一連串的費式數列題
練習題:
luogu P5808 (挑戰題!(我也不會))
Library Checker - Kth term of Linearly Recurrent Sequence (看別人寫的超快 code)
ZJ c490 (任意模數(好難...))
轉移點單調優化 / 分治優化
\(\text{val}(l,i)\) 代表從 \(l\) 轉移到 \(i\) 的數值,
並且可以直接算(不需要仰賴之前的結果)
\(\text{last}(i)\) 代表 \(i\) 最好的轉移點(極值會是 \(\text{val}(\text{last}(i),i)\))
現在如果 \(\text{last}(1)\leq\text{last}(2)\leq\dots\leq\text{last}(n)\)
要算出 \(\text{last}(1)\sim\text{last}(n)\),有沒有什麼快速的方法?
假設算一次 \(\text{val}(l,i)\) 要 \(O(f(n))\)
現在先令它是 \(O(1)\) (計算方便)
直接暴力算
\(O(n^2)\),TLE
嘗試優化
每次暴力的時候從 \(\text{last}(i-1)\) 開始枚舉 \(\dots\)
還是 \(O(n^2)\)
worst case:\(\text{last}(1)=\text{last}(2)= \dots =\text{last}(n)=1\)
要找到好的枚舉順序 \(\dots\)
每次對半切!
分治!
定義函數 \(\text{divide}(x,y,l,r)\)
要算 \(\text{last}(l)\sim\text{last}(r)\)
並且只能從 \([x,y]\) 這個區間轉移
\(mid=\lfloor\frac{l+r}{2}\rfloor\)(\([l,r]\) 的中點)
算出 \(mid\) 最好的轉移點 \(best=\text{last}(mid)\)
然後呼叫 \(\text{divide}(x,best,l,mid-1),\text{divide}(best,y,mid+1,r)\)
複雜度:
最多只會遞迴 \(O(\log(n))\) 層
每層最多只會跑 \(O(n)\)
\(O(n\log(n))\)!
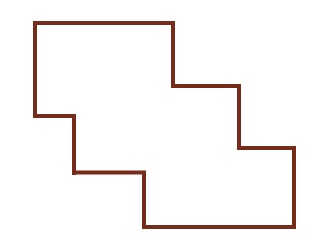
有一個頂點會往右、往下的框框,問你裡面面積最大的矩形。

看成把紅點轉移到藍點
直接對每個藍點看從哪個紅點轉移比較好
\(O(n^2)\)
看看有沒有轉移點單調
如果從 \(r_2\) 轉移到 \(b_1\) 比
從 \(r_1\) 轉移好 (紅色面積 > 藍色面積)
那 \(\dots\)
從 \(r_2\) 轉移到 \(b_2\) 也會從 \(r_1\) 轉移好!
Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
int n, m;
ll ans;
pair<ll, ll> a[N], b[N];
ll cal(int i, int j) {
if (a[i].first < b[j].first || a[i].second > b[j].second) return -1;
return (a[i].first - b[j].first) * (b[j].second - a[i].second);
}
void divide(int x, int y, int l, int r) {
if (l > r) return;
int mid = (l + r) / 2, best;
ll mx = -1;
for (int i = x; i <= y; i++) {
ll val = cal(mid, i);
if (val > mx) {
mx = val;
best = i;
}
}
ans = max(ans, mx);
divide(x, best, l, mid - 1);
divide(best, y, mid + 1, r);
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
n /= 2;
ll x = 0, y = 0;
for (int i = 1; i <= n; i++) {
int dx, dy;
cin >> dx >> dy;
x += dx;
a[i] = {x, y};
y += dy;
}
cin >> m;
m /= 2;
x = y = 0;
for (int i = 1; i <= m; i++) {
int dx, dy;
cin >> dy >> dx;
y += dy;
b[i] = {x, y};
x += dx;
}
divide(1, m, 1, n);
cout << ans << '\n';
}轉移點單調 Ex
\(\text{val}(l,i)\) 不能直接算了,要算出 \(\text{val}(i)\) 要仰賴 \(\text{val}(l)\)
強制讓他可以直接算!
\(\text{solve}(l,r)\) 要算出 \(\text{val}(l)\sim \text{val}(r)\)
\(mid=\lfloor\frac{l+r}{2}\rfloor\)
先呼叫 \(\text{solve}(l,mid)\) 算出左半部分
從左半部分轉移到右半部分的可以呼叫 \(\text{divide}(l,mid,mid+1,r)\)
最後呼叫 \(\text{solve}(mid+1,r)\) 處理右半部分的轉移
大致上來說就是套兩層分治
複雜度 \(O(n\log^2(n))\)
有沒有更快的方法啊?
四邊形優化
xD / yD 指的是狀態有 \(O(n^x)\),轉移有 \(O(n^y)\) 的 DP
\(dp_i=\min\limits_{0\leq l<i}(dp_l+\text{val}(l,i))\)
有 \(O(n)\) 個狀態,有 \(O(n)\) 個轉移,
所以是 1D / 1D
凸性優化
\(l_1<l_2\),
當從 \(l_2\) 轉移到 \(i\) 比從 \(l_1\) 轉移到 \(i\) 好,
那從 \(l_2\) 轉移到 \(i+1\) 會比從 \(l_1\) 轉移到 \(i+1\) 好
以上性質會有
\(\text{last}(1)\leq\text{last}(2)\leq\dots\leq\text{last}(n)\)
但反過來不一定
可以用一個 deque 維護每一個轉移點轉移到哪些範圍
詢問某個點 \(i\) 時,如果 deque 最前面的轉移點沒有包含它,那就 pop 掉
要加入 \(i\) 可以轉移到的範圍
比較 deque 後面線段的左端點 \(L\)
比較 \(dp_i+\text{val}(i,L)\) 與 \(dp_{p_4}+\text{val}(p_4,L)\) 的大小
如果從 \(i\) 轉移比較好,可以把 \(p_4\) 轉移到的範圍 pop 掉
再來看 \(p_3\) 的範圍,如果轉移到 \(p_3\) 的左端點 \(p_3\) 比 \(i\) 好
那 \(i\) 比 \(p_3\) 好的點會在 \(p_3\) 的線段中間
可以二分搜!!!
搜到 \(pos\) 後可以把 \(i\) 轉移到的範圍 push 在後面
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
int dp[N];
struct seg {
int p, L, R;
};
deque<seg> DQ;
int cal(int l, int i) {
// do something
}
int main() {
// init
DQ.push_back({0, 1, n});
for (int i = 1; i <= n; i++) {
while (DQ.size() && DQ[0].R < i) DQ.pop_front();
dp[i] = cal(DQ[0].p, i);
while (DQ.size() && cal(i, DQ.back().L) <= cal(DQ.back().p, DQ.back().L)) DQ.pop_back();
if (DQ.size() == 0) DQ.push_back({i, i + 1, n});
else {
auto [p, L, R] = DQ.back();
while (L < R) {
int mid = (L + R) / 2 + 1;
if (cal(p, mid) < cal(i, mid)) R = mid - 1;
else L = mid;
}
DQ.back().R = R;
if (R != n) DQ.push_back({i, R + 1, n});
}
}
}有一位偉人曾經說過:「有優超性就可以用李超線段樹耶!」
於是也可以用線段樹來做 1D / 1D 優化
Code (凸性):
/* adapted from PCC's code */
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
int dp[N];
int cal(int l, int i) {
// do something
}
int node[4 * N];
void ins(int pos, int l, int r, int p) {
if (l == r) {
if (cal(p, l) <= cal(node[pos], l)) node[pos] = p;
return;
}
if (p == node[pos]) return;
int mid = (l + r) / 2;
if (p >= mid) {
ins(pos << 1 | 1, mid + 1, r, p);
return;
}
if (cal(p, mid) <= cal(node[pos], mid)) swap(node[pos], p);
if (p < node[pos]) ins(pos << 1, l, mid, p);
else ins(pos << 1 | 1, mid + 1, r, p);
}
int que(int pos, int l, int r, int p) {
if (l == r) return cal(node[pos], p);
int mid = (l + r) / 2;
return min(cal(node[pos], p), p <= mid ? que(pos << 1, l, mid, p) : que(pos << 1 | 1, mid + 1, r, p));
}
int main() {
// init
for (int i = 1; i <= n; i++) {
dp[i] = que(1, 1, n, i);
ins(1, 1, n, i);
}
}給 \(N,K,P\),有 \(N\) 本書,每本書有寬度 \(A_i\)
要把書放在很多層書架,每層都是連續的書組成,如果 \(i\) 跟 \(i+1\) 放在同一層,中間要放 寬度 \(L_i\) 的隔板
一層總寬度 \(M\) 書架的代價是 \(|M-K|^P\)
問最小代價
令 \(\text{pre}_i=\sum\limits_{i=1}^n(A_i+L_i)\)
列出 DP 式:
\(dp_i=\min\limits_{0\leq l<i}(dp_l+|\text{pre}_i-\text{pre}_l-L_i-K|^P)\)
有凸單調性嗎?
\(\text{pre}_i-\text{pre}_{l_1}-L_i\):
\(\text{pre}_i-\text{pre}_{l_2}-L_i\):
想像有一條正在往右移的紅線
代價如果是(藍線左端點與紅線的距離)\(^P\)
那在紅線到某個點時從 \(l_2\) 轉移會比較好,
在這個點往右都會是 \(l_2\) 比較好
(初始減 \(K\) 是紅線往左 \(K\),從轉移到 \(i\) 變轉移到 \(i+1\) 是紅線往右)
用 deque 維護
數字可能很大,比較時可能會需要用 double
\(O(n\log(n)\log(P))\)
凹性優化
\(l_1<l_2\),
當從 \(l_1\) 轉移到 \(i\) 比從 \(l_2\) 轉移到 \(i\) 好,
那從 \(l_1\) 轉移到 \(i+1\) 會比從 \(l_2\) 轉移到 \(i+1\) 好
原本維護 deque
現在最好的轉移點與插入時都是從同一個地方看
\(\Rightarrow\) 用 stack 維護!
stack 頂端
一樣可以二分搜
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
int dp[N];
struct seg {
int p, L, R;
};
vector<seg> ST;
int cal(int l, int i) {
// do something
}
int main() {
// init
ST.push_back({0, 1, n});
for (int i = 1; i <= n; i++) {
while (ST.size() && ST.back().R < i) ST.pop_back();
dp[i] = cal(ST.back().p, i);
while (ST.size() && cal(i, ST.back().R) <= cal(ST.back().p, ST.back().R)) ST.pop_back();
if (ST.size() == 0) ST.push_back({i, i + 1, n});
else {
auto [p, L, R] = ST.back();
while (L < R) {
int mid = (L + R) / 2;
if (cal(p, mid) < cal(i, mid)) R = mid;
else L = mid + 1;
}
ST.back().L = L;
if (i + 1 <= L - 1) ST.push_back({i, i + 1, L - 1});
}
}
}#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
int dp[N];
int cal(int l, int i) {
// do something
}
int node[4 * N];
void ins(int pos, int l, int r, int p) {
if (l == r) {
if (cal(p, l) <= cal(node[pos], l)) node[pos] = p;
return;
}
if (p == node[pos]) return;
int mid = (l + r) / 2;
if (p >= mid) {
ins(pos << 1 | 1, mid + 1, r, p);
return;
}
if (cal(p, mid) <= cal(node[pos], mid)) swap(node[pos], p);
if (p < node[pos]) ins(pos << 1 | 1, mid + 1, r, p);
else ins(pos << 1, l, mid, p);
}
int que(int pos, int l, int r, int p) {
if (l == r) return cal(node[pos], p);
int mid = (l + r) / 2;
return min(cal(node[pos], p), p <= mid ? que(pos << 1, l, mid, p) : que(pos << 1 | 1, mid + 1, r, p));
}
int main() {
// init
for (int i = 1; i <= n; i++) {
dp[i] = que(1, 1, n, i);
ins(1, 1, n, i);
}
}線段樹(只跟凸性差一個地方)
選擇轉移點的唬爛方法
選一個數字 \(\text{magic}\)
只在 \([\max(0,i-\text{magic}),i-1]\) 找轉移點
複雜度:\(O(n\times\text{magic})\)
正確性:???


竟然有 IOI 題可以用這個過
Monge Condition
一個 \(n\times m\) 的矩陣 \(A\)
對所有 \(1\leq i_1<i_2\leq n,1\leq j_1<j_2\leq m\)
都有 \(A_{i_1,j_1}+A_{i_2,j_2}\leq(\geq)A_{i_1,j_2}+A_{i_2,j_1}\)
與對所有 \(1\leq i<n,1\leq j<m\)
\(A_{i,j}+A_{i+1,j+1}\leq(\geq)A_{i,j+1}+A_{i+1,j}\) 等價
紅色總和 \(\leq(\geq)\) 藍色總和
Knuth's Optimization
2D / 1D 的 DP 轉移
\(dp_{l,r}=\min\limits_{l\leq k<r}(dp_{l,k}+dp_{k+1,r}+\text{val}(l,r))\)
當 \(\text{val}\) 滿足以下條件:
區間包含單調:\(\text{val}(l_2,r_1)\leq\text{val}(l_1,r_2)\)
對任意 \(1\leq l_1\leq l_2\leq r_1\leq r_2\leq n\)
四邊形不等式:\(\text{val}(l_1,r_1)+\text{val}(l_2,r_2)\leq\text{val}(l_1,r_2)+\text{val}(l_2,r_1)\)
(跟 Monge Condition 的樣子長好像)
會有一個性質
令 \(\text{best}(l,r)\) 為 \(dp_{l,r}\) 最好的轉移點
也就是一個 \(k\) 使得從 \(\text{best}(l,r)=k\) 轉移會使 \(dp_{l,r}\) 有最小值
則 \(\text{best}(l,r-1)\leq\text{best}(l,r)\leq\text{best}(l+1,r)\)
證明:
The proof is left as an exercise for the reader.
由於證明有好多數字,講師不會數學,有興趣的人可以去 CP-Algorithm 看
每次要算 \(dp_{l,r}\) 的時候
原本轉移範圍是 \([l,r]\)
現在只要從 \([\text{best}(l,r-1),\text{best}(l+1,r)]\)
複雜度原本是 \(O(n^3)\),現在變成 \(\dots\)
\(O(n^2)\)!
\(\text{best}(1,1)\leq\text{best}(2,2)\leq\text{best}(3,3)\leq\dots\)
\(\text{best}(1,2)\leq\text{best}(2,3)\leq\text{best}(3,4)\leq\dots\)
\(\text{best}(1,3)\leq\text{best}(2,4)\leq\text{best}(3,5)\leq\dots\)
每一層 \(O(n)\),總共 \(n\) 層
有一個大小為 \(n\) 的陣列 \(x\)
剛開始只有一個大陣列 \(x_1\sim x_n\)
每次要把大陣列分成左右兩個小陣列
花費是陣列數字的總和
問把陣列分 \(n\) 個大小為 \(1\) 陣列的總花費?
設 \(dp_{l,r}\) 是把 \(x_l\sim x_r\) 分完後的最小花費
\(pre_i=\sum\limits_{j=1}^i x_j\)
\(dp_{l,r}=\min\limits_{l\leq k<r}(dp_{l,k}+dp_{k+1,r})+\text{pre}_r-\text{pre}_{l-1}\)
區間包含單調:\(\text{val}(l_2,r_1)\leq\text{val}(l_1,r_2)\)
四邊形不等式:\(\text{val}(l_1,r_1)+\text{val}(l_2,r_2)\leq\text{val}(l_1,r_2)+\text{val}(l_2,r_1)\)
發現 \(\text{val}(l,r)=\text{pre}_r-\text{pre}_{l-1}\)
可以優化!
Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5005;
int n;
int best[N][N];
ll pre[N], dp[N][N];
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> pre[i];
pre[i] += pre[i - 1];
best[i][i] = i;
}
for (int len = 2; len <= n; len++) {
for (int l = 1, r = len; r <= n; l++, r++) {
ll mn = LLONG_MAX;
for (int k = best[l][r - 1]; k <= min(r - 1, best[l + 1][r]); k++) {
if (dp[l][k] + dp[k + 1][r] < mn) {
mn = dp[l][k] + dp[k + 1][r];
best[l][r] = k;
}
}
dp[l][r] = mn + pre[r] - pre[l - 1];
}
}
cout << dp[1][n] << '\n';
}轉移點單調
凸單調性
凸 Monge Condition
Slope trick
有一個長這樣的函數
由很多個直線組成
紅色點是斜率改變的地方
除了把一段一段的直線跟分界點存起來
有沒有其他存法啊
觀察每一條線的斜率
發現只要存最右邊那條線跟所有斜率改變 \(1\) 的點就好了!
以這個函數為例,假設最右邊的直線是 \(y=2x+5\)
那我們就只要存 \(y=2x+5\) 與 \(\{p_1,p_1,p_2,p_3,p_4\}\) 就好了
注意到如果在同一點斜率改變超過 \(1\),那要放入這個點很多次
性質:
可以把兩個這樣子的函數合起來
假設 \(h(x)=f(x)+g(x)\)
那 \(h\) 最右邊的直線會是 \(f\) 最右邊的 \(+\ g\) 最右邊的
\(h\) 斜率改變 \(1\) 的點會是 \(f\) 與 \(g\) 的聯集!
應用
有 \(n\) 個整數 \(a_1\sim a_n\),每次可以花費 \(1\) 讓 \(a_i\) 減 \(1\) 或加 \(1\)
問最少要花費多少讓 \(a\) 非嚴格遞增?
\(O(nC)\) 的做法:
令 \(dp_{i,x}\) 是把 \(a_i\) 變成 \(x\) 所需最少的花費
那 \(dp_{i,x}=\min\limits_{x'\leq x}(dp_{i-1,x'})+|x-a_i|\)
這樣不夠快
雖然可以注意到 \(a_i\) 一定會變成原陣列的某個數
可以優化到 \(O(n^2)\)
但終究不是我們要的複雜度
我們讓 \(dp\) 變成一個函數
\(dp_{i,x}\Rightarrow dp_i(x)\)
同時我們設一個叫 \(mn_i(x)\) 的函數
這個函數是對 \(dp_i(x)\) 取前綴 \(\min\)
也就是 \(mn_i(x)=\min\limits_{x'\leq x}(dp_i(x'))\)
轉移式從原本的 \(dp_{i,x}=\min\limits_{x'\leq x}(dp_{i-1,x'})+|x-a_i|\)
變成 \(dp_i(x)=mn_{i-1}(x)+|x-a_i|\)
注意到 \(y=|x-a_i|\) 這個函數可以轉換成之前提到的形式
可以用數學歸納法證明 \(dp_i(x)\) 跟 \(mn_i(x)\)
也可以轉換成這種形式
\(mn_{i-1}(x)\) 會長這樣
最右邊的直線會是 \(y=K\) 的形式 (斜率 \(=0\))
\(dp_i(x)=mn_{i-1}(x)+|x-a_i|\) 會長這樣
最右邊的函數
會是 \(y=x-a_i+K\)
相當於在 \(mn_{i-1}(x)\) 裡加了 \(\{a_i,a_i\}\)
將 \(y=K\) 加上了 \(y=x-a_i\)
\(mn_i(x)\) 是對 \(dp_i(x)\) 取前綴 \(\min\)
\(dp_i(x)\)
其實就是把最右邊的紅點 \(R\) 移除
然後把最右邊那條線變成 \(y=R-a_i+K\)
\(mn_i(x)\)
最後想要求 \(dp_n(x)\) 的最小值
也就是 \(mn_n(x)\) 最右邊的地方
會發現答案是 \(y=K\) 的 \(K\)
實作上斜率改變點可以用 pq 維護!
Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 5;
int n;
ll ans;
int a[N];
priority_queue<int> pq;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
pq.push(a[i]);
pq.push(a[i]);
int R = pq.top();
ans += R - a[i];
pq.pop();
}
cout << ans << '\n';
}Aliens 優化
又叫做 wqs 二分搜或帶權二分
因為某一年 IOI 需要用到這個技巧而變有名
這是一個凹函數
\(dp(x)\)
這個函數的最大值可以用 \(dp\) 算
並且我們可以知道最大值的位置發生在哪裡
\((p_{mx},dp(p_{mx}))\)
\(dp(x)\)
如果把 \(dp(x)-\text{pen}\times x\) 會發生什麼事?
(pen = penalty = 罰款)
\((p_{mx},dp(p_{mx}))\)
\(-\text{pen}\times x\) 也是一個凹函數
兩個凹函數相加還是一個凹函數
\(dp(x)\)
\(-\text{pen}\times x\)
\(dp'(x)=dp(x)-\text{pen}\times x\)
\((p_{mx}',dp'(p_{mx}'))\)
最大值位置會改變!
得到 \(dp'(p_{mx}')\) 後,
可以加上 \(\text{pen}\times p_{mx}'\) 得到原本的 \(dp(p_{mx}')\)!
Aliens 優化的核心思想就是利用最大值可以快速求的特性,加或減 penalty 改變凹(凸)函數最大(小)值發生的位置,求出不容易求的值
可以二分搜 \(\text{pen}\) 來控制最大值發生的位置!
但有的時候 \(dp'(K-1)=dp'(K)=dp'(K+1)\)
沒辦法直接搜到 \(K\)
搜到的如果是 \(t\)
\(dp'(t)=dp(t)-\text{pen}\times t=dp(K)-\text{pen}\times K\)
\(\Rightarrow dp(K)=dp'(t)+\text{pen}\times K\)
所以不管搜到哪個點加上 \(\text{pen}\times K\) 就可以了
然後有的時候你很難證明題目的函數是凹(凸)函數
二分搜的時候要注意搜的方向
方向錯誤很可能就導致答案錯誤
有一種證法是把題目轉成 mincost flow 模型
流量每增加 \(1\),增加量會遞增
大部分的時候可以靠感覺 (〃∀〃)
有一個商品在 \(n\) 個時間點的價格是 \(a_1\sim a_n\)
當身上沒有商品時可以花 \(a_i\) 買
當身上有商品時可以以 \(a_i\) 賣掉
問最多買賣 \(k\) 次能賺到最多的錢
\(O(nk)\) 做法:
\(dp_{0,i,j},\ dp_{1,i,j}\) 代表第 \(i\) 個時間點,身上(沒)有東西,買賣 \(j\) 次最多能賺到的錢
\(dp_{0,i,j}=\max(dp_{0,i-1,j},dp_{1,i-1,j-1}+a_i)\)
\(dp_{1,i,j}=\max(dp_{1,i-1,j},dp_{0,i-1,j}-a_i)\)
觀察到它是凹函數
\(\Rightarrow\) Aliens 優化
用 pair 存 dp 值,存最大獲利與買賣次數
\(O(n\log(C))\)
Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e6 + 5;
int n, k;
int a[N];
pair<ll, int> better(pair<ll, int> a, pair<ll, int> b) {
if (a.first != b.first) return a.first > b.first ? a : b;
return a.second < b.second ? a : b;
}
pair<ll, int> cal(int pen) {
pair<ll, int> dp0, dp1;
dp0 = {0, 0};
dp1 = {-1e18, 0};
for (int i = 1; i <= n; i++) {
pair<ll, int> tmp = dp0;
dp0 = better(dp0, {dp1.first + a[i] - pen, dp1.second + 1});
dp1 = better(dp1, {tmp.first - a[i], tmp.second});
}
return dp0;
}
int main() {
ios::sync_with_stdio (false), cin.tie (0);
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
int l = 0, r = 1e9;
while (l < r) {
int mid = (l + r) / 2;
if (cal(mid).second > k) l = mid + 1;
else r = mid;
}
cout << cal(l).first + 1ll * l * k << '\n';
}有 \(N\) 個關卡,與 \(N\) 個正整數 \(t_1\sim t_N\),要分成 \(K\) 個連續的區段,想要一次一個區段去做練習,假設現在的區段為 \([l,r]\),已經練好了 \([l,i)\),這次想練關卡 \(i\),那練到關卡 \(i\) 的機率是 \(\frac{t_i}{\sum_{j = l}^{\ i}\ t_j}\),否則會練到已經練過的關卡,想要以最好的分法使總共練習次數的期望值最小。
每個區段可以分開算,先來看一個區段期望要練幾次
假設現在區段的 \(t\) 值為 \(t_l\sim t_r\),那輪到 \(t_i\) 的時候,設 \(x = \frac{\sum_{j = l}^{\ i - 1}\ t_j}{\sum_{j = l}^{\ i}\ t_j}\),\(y = \frac{t_i}{\sum_{j = l}^{\ i}\ t_j}\),那練一次的機率為 \(y\),練兩次的機率為 \(xy\),練三次的機率為 \(x^2y\)。
依此類推,那麼期望值就會是
\(y + 2xy + 3x^2y +\dots= y(1 + 2x + 3x^2+\dots) = \frac{y}{(1-x)^2}\),又 \(1 - x = y\),所以最後是 \(\frac{1}{y}\)。
令 \(\text{pre}_i = \sum\limits_{j = 1}^{i} t_j\),\(\text{p1}_i = \sum\limits_{j = 1}^{i} \frac{1}{t_j}\),\(\text{p2}_i = \sum\limits_{j = 1}^{i} \frac{\text{pre}_{j - 1}}{t_j}\)
\(\frac{1}{y}\) 可以寫成 \(\frac{\text{pre}_{i - 1} - \text{pre}_{l-1} + t_i}{t_i} = 1 + \frac{\text{pre}_{i-1}}{t_i} - \text{pre}_{l-1}\times \frac{1}{t_i}\),
那把 \(l\sim r\) 的 \(\frac{1}{y}\) 都加起來後會得到
\((r - l + 1) + (\text{p2}_r - \text{p2}_{l - 1}) - \text{pre}_{l-1}\times (\text{p1}_r - \text{p1}_{l-1})\)
如果要 \(dp\) 可以假設上一個區段結束的點為 \(l\),現在在 \(r\),那 \(dp_r = dp_l + (r-l) + (\text{p2}_r-\text{p2}_l) - \text{pre}_l\times (\text{p1}_r-\text{p1}_l) \\ = \max(-\text{pre}_l\times \text{p1}_r + dp_l - l - \text{p2}_l + \text{pre}_l\times \text{p1}_l) + r + \text{p2}_r \\= \max (m_l\times x_r + k_l) + C_r\)
可以使用一個斜率遞減,查詢遞增的 \(O(N)\) 斜率優化
現在已經知道要怎麼 \(dp\) 了,只差怎麼分 \(K\) 段
如果你的數學夠強,或是你的信仰夠深
那你可以相信這是一個凸函數
於是可以 \(O(N\log(C))\) Aliens 優化套斜率優化!
數線上有 \(n\) 個座標,要在其中 \(k\) 個設郵局,求每個座標到自己最近之郵局座標距離和最小值。
發揮信仰之力
相信它是凸函數
假設我們現在的 \(\text{pen}\) 是固定的
要來推 \(dp\) 式
假設 \(dp_i\) 是從 \(dp_j\) 轉移過來的
在 \([j+1,i]\) 的座標都跑到同一家郵局
那在 \([j+1,i]\) 的中位數設郵局是最好的
\(dp_i=\min\limits_{0\leq j<i}(dp_j+\text{dis}(j+1,i)+\text{pen})\)
\(\text{dis}(j+1,i)\) 代表 \([j+1,i]\) 到中位數的總距離,可以用前綴和算
目前推出的 \(dp\) 式是 \(O(n^2)\) 的
繼續觀察會發現它有凸單調性
\(\Rightarrow\) 可以凸四邊形優化
做一次要 \(O(n\log(n))\)
總共 \(O(n\log(n)\log(C))\)
有 \(n\) 個寶可夢,有 \(a\) 顆紅球跟 \(b\) 顆藍球,丟紅球抓到第 \(i\) 隻寶可夢的機率是 \(p_i\),丟藍球抓到第 \(i\) 隻寶可夢的機率是 \(u_i\),同一種球對一隻寶可夢最多只能丟一顆,也可以同時丟紅球跟藍球,這樣抓到的機率是 \(1-(1-p_i)(1-u_i)\)。
問抓到寶可夢數量最大的期望值。
\(dp_{i,x,y}\) 是到了第 \(i\) 隻寶可夢,共丟了 \(x\) 顆紅球、\(y\) 顆藍球能抓到的期望值
有四種情況:不丟、丟紅球、丟藍球、丟紅球跟藍球
網路上的解法幾乎都是說套兩層 Aliens
給紅球 \(\text{pen}_1\),給藍球 \(\text{pen}_2\)
複雜度 \(O(n\log^2(C))\)
但是好像這種寫法都有辦法 hack
在這篇 blog 的做法是三分搜
做 \(k\) 維的 Aliens 的複雜度是 \(O(n2^k\log^k(C))\)
類似題:ZJ f998
謝謝大家!
DP 優化
By becaido
DP 優化
- 1,391



