樹論
不是數論
Lecture : AaW
演算法小社 [14]
什麼是樹論勒?
- 樹論是圖論的一部分
- 只要看到植物幾乎都跟圖論有關
- 例如:森林、仙人掌
-
很多圖論的題目都和樹有關
-
看出一張圖為樹、套用樹的性質來解題是種常用的技巧
-
之後會學到的一堆 Tarjan 演算法就會教你把圖和樹變來變去,
但那是下個月ㄉ事了
什麼是一棵樹?
複習一下
什麼是一棵樹?

複習一下
什麼是一棵樹?

複習一下
什麼是一棵樹?

複習一下
什麼是一棵樹?
樹的定義:
定義:沒有環的連通圖
複習一下
樹的名詞解釋
複習一下
樹的名詞解釋
根
複習一下
樹的名詞解釋
根
樹葉
度數為一的點(不是根的那些)
選定一個點做「根」
複習一下
樹的名詞解釋
深度
0
3
4
3
2
2
2
2
1
1
1
複習一下
樹的名詞解釋
對於這一點來說
父節點
子樹
複習一下
樹的名詞解釋
對於這一點來說
沒有父節點
三棵子樹
複習一下
樹的名詞解釋
對於這一點來說
沒有父節點
三棵子樹
複習一下
樹的名詞解釋
對於這一點來說
沒有父節點
三棵子樹
複習一下
樹的名詞解釋
對於這一點來說
祖先(們)
複習一下
樹的根不唯一
複習一下
樹的根不唯一
改用這點當根
複習一下
樹的根不唯一
複習一下
樹的根不唯一
樹的性質
樹的性質
- 定義:沒有環的連通圖
- 任何一點都可以當作根
- 任兩點間恰有一條不經過重複點的路徑
- 一顆有 n 個點的樹,共有 n-1 條邊
-
如果有一張連通圖,
點樹為 n ,邊數為 n-1
-
一定是一棵樹!
-
proof is left as an exercise to the reader
-
樹的儲存
- 先用一般存圖的方式儲存
- 鄰接串列!
- DFS 將整張樹遍歷一遍之後,記錄每一點的父節點和子節點,就記錄完了
複習:
還記得怎麼 DFS 嗎?
vector<int> adj[maxn]; // 鄰接串列
bool visited[maxn]; // 是否到訪過
int dfs(int i) {
visited[i] = true;
// 在這裏做一些按照題目邊DFS邊要做的事情
for (auto v : adj[i]) {
if (!visited[v]) {
dfs(v);
}
}
}建議把模板背好喔
樹的儲存的 code
#include <bits/stdc++.h>
using namespace std;
vector<int> adj[maxn]; // 鄰接串列
vector<int> child[maxn]; // 記錄每個點的子節點為哪些
int father[maxn]; // 記錄每個點的父節點為何
void dfs(int i, int fa) {
father[i] = fa;
for (auto v : adj[i]) {
if (v == fa) continue;
child[i].push_back(v);
dfs(v, i);
}
}
int main() {
// input
// 假設共有n個點,編號 1~n,1為根
int n;
cin >> n;
for (int i = 0; i < n-1; ++i) { // n-1 條邊
int a, b;
cin >> a >> b;
adj[a].push_back(b); // 建立鄰接串列
adj[b].push_back(a);
}
int root = 1;
dfs(root, 0); // 根沒有父親,用0代表
}由於樹沒有環,
所以不用另外紀錄節點有沒有被走過
只要確定不要往回走即可
事實上
對於任意一張簡單圖(無自環、多重邊)
我們都可以透過DFS來將其轉變為類似樹的形式
但這是很久以後要講ㄉ ㄏㄏ
關於DFS
樹直徑
利用剛剛學的DFS技巧摟w
啥是樹直徑?
樹上距離最遠的兩點
要怎麼找直徑?
- DFS / BFS
- 樹 DP (等等會講)
用 DFS 找樹直徑
步驟:
從任意一個點當根,找到離根最遠的點 i從 i 當根,找到離 i 最遠的點 j- 路徑 (i, j) 就是直徑了
複雜度 O(v)
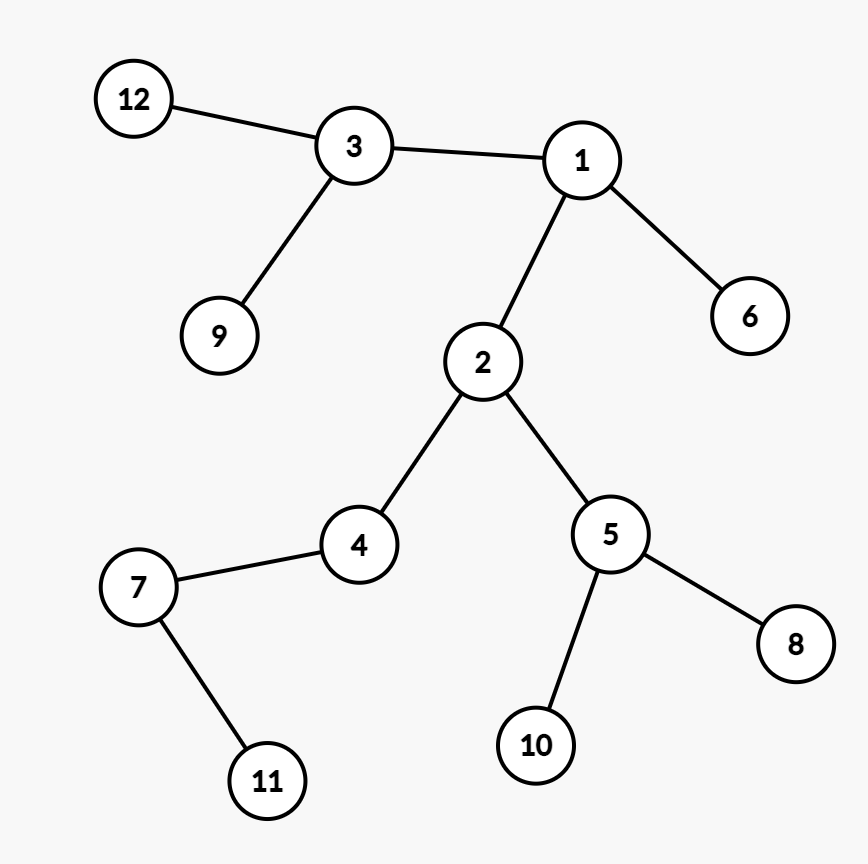
0
藍字為距離,假設我以一號點當 root
1
1
1
2
2
2
2
3
3
3
4

藍字為距離,改用11號點當root
4
4
5
5
5
5
6
6
0
1
2
3

0
藍字為距離,改用11號點當root
1
2
3
4
4
5
5
5
5
6
6
直徑
code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int maxn = 2e5+5;
vector<int> adj[maxn];
void dfs(int i, vector<int> & dep, vector<bool> & visited) {
visited[i] = 1;
for (auto &v : adj[i]) {
if (!visited[v]) {
dep[v] = dep[i]+1;
dfs(v, dep, visited);
}
}
}
signed main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n;
cin >> n;
for (int i = 0; i < n-1; ++i) {
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
vector<int> dep(n+1, 0);
vector<bool> visited(n+1, 0);
dfs(1, dep, visited);
int maxDeepNode = 1;
for (int i = 1; i <= n; ++i) {
if (dep[i] > dep[maxDeepNode]) maxDeepNode = i;
}
fill(dep.begin(), dep.end(), 0);
fill(visited.begin(), visited.end(), 0);
dfs(maxDeepNode, dep, visited);
int diameter = 0;
for (auto &i : dep) diameter = max(i, diameter);
cout << diameter << endl;
return 0;
}
TIOJ 1213 (有邊權)
樹 DP
也叫做樹分治
樹有著非常好的分治結構
所以當我們利用樹做分治、DP
透過在每個節點上紀錄其子樹的答案
父節點便能夠透過DFS時,子節點回傳的資訊推出該點的資訊
我們就可以維護正確的答案ㄌ
下週要學的線段樹的原理就是利用樹 DP 喔
樹深度 & 樹高度
- 在每個點多紀錄深度資訊
- 剛剛樹直徑寫過了
int dep[maxn];
void dfs(int n, int fa, int d) {
dep[n] = d;
for (int v:adj[n]) {
if (v != fa) dfs(v, n, d+1);
}
}子樹大小
How to 解?
- DFS每個子節點
-
當節點為葉節點時,答案為1
-
否則,節點答案為其子節點大小總和+1
-
注意此題最後輸出答案時要-1,因為要去掉自己
直接看程式碼
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define endl '\n'
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int maxn = 2e5+5;
vector<int> adj[maxn];
int sz[maxn];
int dfs(int i, int fa) {
sz[i] = 1;
for (auto &v : adj[i]) {
if (v == fa) continue;
sz[i] += dfs(v, i);
}
return sz[i];
}
signed main(){_
int n;
cin >> n;
for (int i = 2; i <= n; ++i) {
int boss;
cin >> boss;
adj[i].pb(boss);
adj[boss].pb(i);
}
dfs(1, 0);
for (int i = 1; i <= n; ++i) cout << sz[i]-1 << " ";
cout << endl;
return 0;
}
More 題目
More 簡報
樹重心
LCA
最低共同祖先
LCA是什麼?
若點\(x\)是點\(y\)的祖先,那麼
\(x = y\)
or
\(x\)是\(y\)的父親的祖先
兩個點\(u, v\)的最低共同祖先(LCA)就是深度最大的點\(x\),使得\(x\)同時是\(u\)和\(v\)的祖先
如何求 LCA ?
1. 暴力DFS法
先預處理每一點的深度
然後每次詢問\((u, v)\)時
直接從\(u\)開始DFS,紀錄到\(v\)路徑上面深度最小的那個點
複雜度 O(v)
又慢又難寫
如何求 LCA ?
2. 比較好的暴力法
先預處理每一點的深度&父親
每次拿兩個點中較深的點走到他的父親,當兩個點第一次重合的時候就是LCA。
走的步數是兩點之間的距離,最差是 O(v)
int lca (int u, int v) {
if(depth[u] < depth[v]) {
swap(u, v); //讓u當深度較大ㄉ點
}
while(depth[u] != depth[v]) { //爬到一樣高
u = parent[v];
}
while(u != v) { //一起往上爬
u = parent[u];
v = parent[v];
}
return u;
}
要怎麼更快地往上走 ?
假設 代表共同祖先
LCA
對於每個點,紀錄他的\(1,2,4,⋯,2^k\)倍祖先。
倍增法:跳著走!
找到非共同祖先裡面深度最淺的點e
e的父親就是lca
How? 用sparse table
e
倍增法演算法
先紀錄每個點的深度以及 \(2^k\) 倍祖先
要詢問\(a\)跟\(b\)的LCA的時候:
- 把 \(a\) 跟 \(b\) 裡面較深的往上走到相同的深度
- 如果此時\(a=b\),LCA就是 \(a\)
- 讓\(k\)由大到小,如果 \(a\) 和 \(b\) 的 \(2^k\) 倍祖先不同的話就往上走
- 最後LCA就會是 \(a\) 的父親
why?
LCA
e
假設 e 和 u 的距離
用二進位表示為
\(000101_2\)
u
我們會依序檢查
\(2^5\) :\(100000_2\)
\(2^4\) : \(010000_2\)
\(2^3\) : \(001000_2\)
\(2^2\) : \(000100_2\)
x
x
x
v
這時候我們走到\(2^2\)祖先,你會發覺\(e, u\)距離縮短了,且剩下的距離一定小於\(2^2\)
也就是說,透過這個方法,我們一定有辦法讓\(e, u\) 距離為0
u
8
1
2
4
3
5
7
6
1
2
4
3
倍增法演算法
先紀錄每個點的深度以及 \(2^k\) 倍祖先
要詢問\(a\)跟\(b\)的LCA的時候:
- 把 \(a\) 跟 \(b\) 裡面較深的往上走到相同的深度
- 如果此時\(a=b\),LCA就是 \(a\)
- 讓\(k\)由大到小,如果 \(a\) 和 \(b\) 的 \(2^k\) 倍祖先不同的話就往上走
- 最後LCA就會是 \(a\) 的父親
why?
時間複雜度: \(O(n\log n)\) 預處理, \(O(\log n)\)詢問
所以到底要如何預處理?
倍增法預處理
如果我們令 \(p[i][j]\)
代表第 \(j\) 個節點的第 \(2^i\) 輩祖先
很酷的事情是
\(p[i][j] = p[\ i-1\ ][\ p[i-1][j]\ ]\)
我們就可以在\(O(1)\)的時間找到祖先
由於總共有\(O(\log d)\)個祖先
又有\(O(V)\)個點
預處理ㄉ時間複雜度 : \(O(V \log d) \in O(V \log V)\)
➜ 第 \(j\) 個節點的第 \(2^i\) 輩祖先為
第 \(j\) 個節點的第 \(2^{i-1}\) 輩祖先的第 \(2^{i-1}\)倍祖先
int dep[maxn];
int anc[18][maxn];
// anc[i][j] 代表 j 的 2^i 倍祖先
// 紀錄到每一點的 2^17 倍祖先 (大於1e5)
void dfs(int n, int fa, int d) {
anc[0][n] = fa; // 一倍祖先就是父親
dep[n] = d;
for (int v : adj[n]) {
if (v != fa) dfs(v, n, d+1);
}
}
void setupLCA() {
dep[0] = -1;
dfs(1, 0, 0);
for (int i = 1; i < 18; i++) {
for (int j = 1; j <= n; j++) {
anc[i][j] = anc[i-1][anc[i-1][j]];
}
}
}
int lca(int a, int b){
if (dep[a] < dep[b]) swap(a, b);
for (int i = 17;i >= 0;i--) {
if (dep[anc[i][a]] >= dep[b]) {
a = anc[i][a];
}
}
if (a == b) return a;
for (int i = 17;i >= 0;i--) {
if (anc[i][a] != anc[i][b]) {
a = anc[i][a];
b = anc[i][b];
}
}
return anc[0][a];
}
int main() {
// 省略輸入圖
setupLCA();
while (q--) {
int u, v;
cin >> u >> v;
cout << lca(u, v) << endl;
}
}來寫寫看
LCA的性質
樹壓平
我備課好累我決定繼續偷
更多來不及講的
樹論東東
結束啦
學弟妹記得準備學術考啦!