圖論[0]

Graph Theory[0]

INFOR 36th. @小海_夢想特急_夢城前

  • 定義 / 基本名詞

Index

  • 儲存方式
  • 遍歷 (traversal)

講師

  • 225 賴柏宇
  • 海之音、小海或其他類似的
  • 美術能力見底
  • 表達能力差，不懂要問
  • INFOR 36th 學術長
  • 這頁是偷來的
  • 不會圖論所以來當圖論講師
  • BrineTW 的簡報

Reference

  • 8e7 的簡報
  • FHVirus 的簡報
  • 劉澈的簡報
  • 資芽
  • 維基百科
  • 本次的講師很弱
  • 本次提供的範例 Code 可能有誤，請見諒
  • 為了提高可讀性，拆成很多函式以及回傳值處理，有時會導致常數較大，請自行修改
  • 表達能力很差，所以聽不懂 一定 一定 要問
  • 講師永遠不會放棄你 啊對 保有最終解釋權 人很ㄐㄅ不在此範圍
  • 簡報或我的觀念可能有誤，歡迎隨時糾正
  • 有些奇怪的連結是我推薦的歌.jpg (不是 Rickroll...)

聲明

定義/名詞

Glossary.

  • 名詞解釋：
    • 由各種線條、形狀、色彩等描繪成的形象或畫面。
    • 疆域。
    • 欲念。
  • 動詞解釋：
    • 繪畫、描繪。
    • 策劃、考慮。
    • 謀取、謀求。

何謂「圖」

  • 名詞解釋：
    • 由各種線條、形狀、色彩等描繪成的形象或畫面。
    • 疆域。
    • 欲念。
  • 動詞解釋：
    • 繪畫、描繪。
    • 策劃、考慮。
    • 謀取、謀求。

何謂「圖」

如果你不知道這是啥，這是教育部的解釋

A graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related".

Wikipedia

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

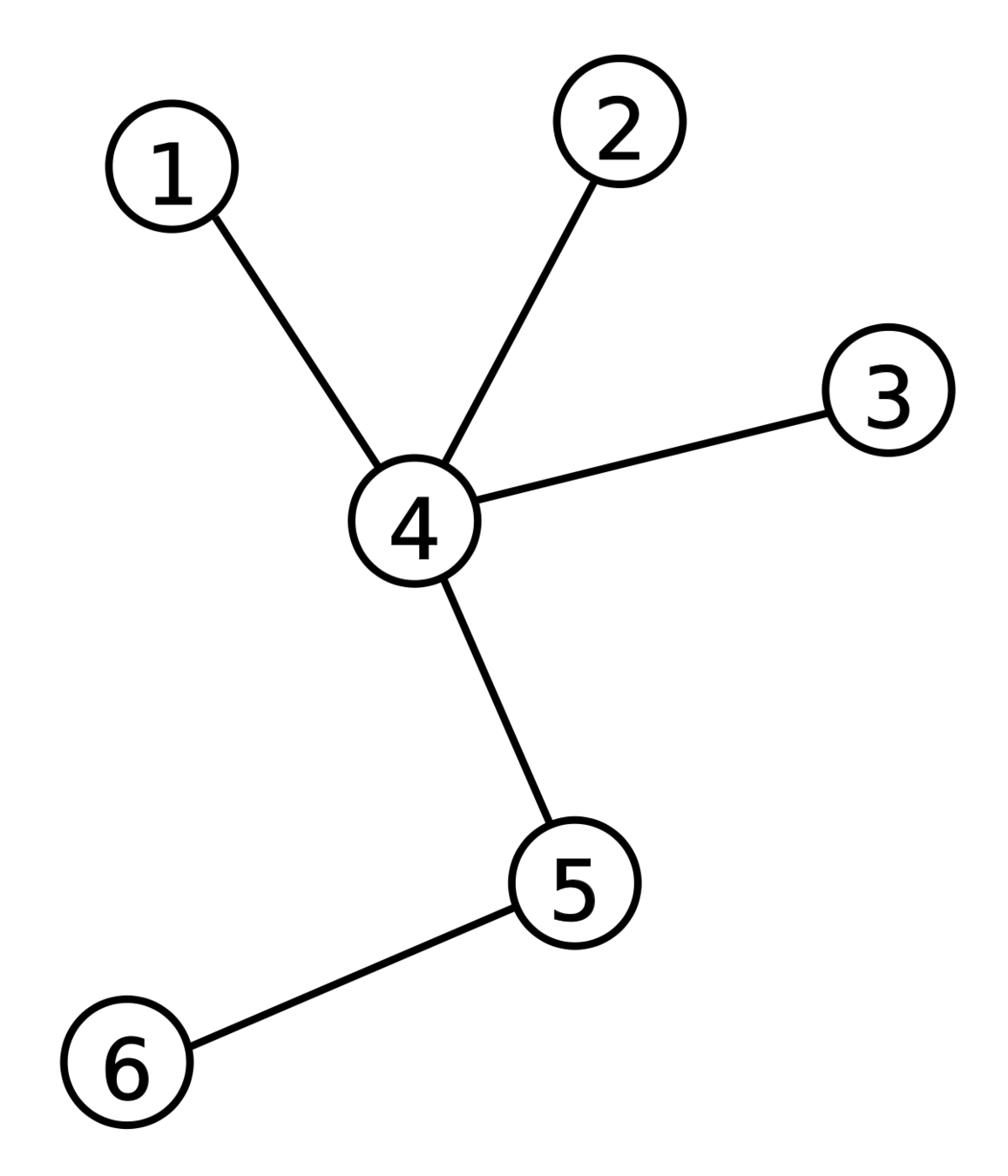
Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

：點

：邊

Definition

點集：點構成的集合，以     表示

V

Definition

邊集：邊構成的集合，以     表示

E

Definition

圖：點和邊構成的集合，以                  表示

G(V,E)

Edge (邊)

  • 可以用兩點             表示
  • 方向性 (direction)
    • 若為有向，以箭頭表示
  • 邊權 (weight)
  • 自環 (loop)
    • 自己指到自己
  • 重邊 (parallel edges)
    • 起終點相同的邊

Vertex (點)

  • 點權 (weight)
  • 度 (degree)
    • 無向圖：一個點接多少邊
    • 入度：指到自己邊的數量
    • 出度：指到它點邊的數量
  • 入度 & 出度為有向圖專屬
(u, v)
  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Path

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Trace

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Track

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Circuit

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Cycle

  • 簡單圖 (Simple Graph)：不存在重邊自環
  • 有向圖 (Directed Graph)：邊是有向的
    • 強連通 (SC)：所有點對都存在一條路徑
    • 弱連通 (WC)：要變成無向圖才全部連通
    • 有向無環圖(DAG)
  • 無向圖：邊是無向的
    • 連通圖：所有點對都存在一條路徑

一些分類

  • 完全圖：所有點對都有一條邊連著
  •  

一些分類

|E| = \frac {|V|(|V|-1)} {2}
  • 子圖：每條邊、每個點都存在於原圖中的圖
  •  

一些分類

for\ G'(V', E'):\ V'\subseteq V,\ E'\subseteq E
  • 補圖：點集相同，邊集是補集 (以完全圖的邊集為宇集)
  •  

一些分類

for\ G'(V', E'):\ V'= V,\ E' = E^c
  • 樹：不存在環的無向連通圖
  •  

一些分類

|E| = |V| - 1
  • 稀疏圖                                       ，例如樹
  • 稠密圖                                       ，例如完全圖

一些分類

|E| \leq |V| log |V|
|E| \geq |V| log |V|

TIOJ 1210 (Havel 定理)

一般做法                        或              ，但可以

O(n\ log\ n)
O(n^2log\ n)
O(n^2)

TIOJ 1032

NEOJ 410

CSES 1756

怪題思考題

儲存

Storage.

在開始前，先了解一下我的習慣...

#include <bits/stdc++.h>
using namespace std;
int n; // |V|
int m; // |E|
int u, v, vertex; // 某個點
int e, edge; // 某個邊
int w, weight; // 某個權重
int cur; // 通常是遞迴時現在在哪個點
int pre, prev; // 上一個點
int next, nxt; // 下一個點
vector<vector<type>> graph; // 圖
vector<int> neighbor; // 一個點附近的點
const int INF = 1e9 + 7;
  • 鄰接矩陣
  • 開一個                    的表記錄邊
  • 如果帶權就記錄權重
  • 有向邊？

Adjacency Matrix

|V|\times |V|
(u, v)
0
1
2
\begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix}
  • 鄰接矩陣
  • 開一個                    的表記錄邊
  • 如果帶權就記錄權重
  • 有向邊？

Adjacency Matrix

|V|\times |V|
(u, v)
0
1
2
\begin{bmatrix} 0 & 5 & 3 \\ 5 & 0 & 0 \\ 3 & 0 & 0 \end{bmatrix}
5
3
  • 鄰接矩陣
  • 開一個                    的表記錄邊
  • 如果帶權就記錄權重
  • 有向邊？令            記錄的是從    指向    就好啦

Adjacency Matrix

|V|\times |V|
(u, v)
0
1
2
\begin{bmatrix} 0 & 5 & 0 \\ 0 & 0 & 0 \\ 3 & 0 & 0 \end{bmatrix}
5
3
(u, v)
u
v
int n, m;
cin >> n >> m;
vector<vector<bool>> graph(n, vector<bool>(n, 0));
for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    graph[u][v] = 1;
    graph[v][u] = 1;
}
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 帶權？有向？

Adjacency List

u
v
0
1
2
0: \{1, 2\}
1: \{0\}
2: \{0\}
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 帶權？用 pair 把權重包在邊裡

Adjacency List

u
v
0
1
2
0: \{(1, 5), (2, 3)\}
1: \{(0, 5)\}
2: \{(0, 3)\}
5
3
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 有向應該不需要我解釋吧

Adjacency List

u
v
0
1
2
0: \{\}
1: \{(0, 5)\}
2: \{(0, 3)\}
5
3
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 有向應該不需要我解釋吧

Adjacency List

u
v
0
1
2
0: \{\}
1: \{(0, 5)\}
2: \{(0, 3)\}
5
3

空間複雜度？

int n, m;
cin >> n >> m;
vector<vector<int>> graph(n);
for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    graph[u].push_back(v);
    graph[v].push_back(u);
}

因為這東西比較常用，所以如果後面有 graph 應該都是指鄰接串列的存法

鄰接矩陣

  • 快速查看 u, v 間的邊
  • 浪費空間
  • 不好處理重邊
  • 處理稠密圖較有效率

鄰接串列

  • 不能直接查看 u, v 間的邊
  • 對於相鄰點的操作方便
  • 比較不浪費空間
  • 處理稀疏圖、稠密圖都很好

比較

方式 鄰接矩陣 鄰接串列
空間複雜度
存取特定邊
枚舉邊
O(|V|^2)
O(|V|+|E|)
O(1)
O(|E|)
O(|V|^2)
O(|V|+|E|)

同時儲存點和邊的資訊？

這裡有一個我滿喜歡的方法

reference: 張秉中學長的樹論簡報

struct Node {
    int weight; // 點的資訊
    struct Edge {
        int v;
        int weight; // 邊的資訊
    };
    vector<Edge> neighbor;
};
vector<Node> graph;

其他方法

比較少用到的東西

  • 每個格子都是一個點
  • 反正要用的時候會用就好了(?

網格座標(?)

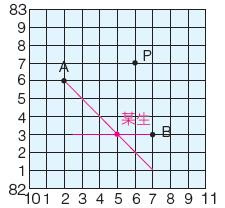
  • 就 把輸入進來的邊丟到一個 list 裡面

邊串列 Edge List

int n, m;
cin >> n >> m;
vector<pair<int, int>> edges;
for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    edges.push_back({u, v});
}

TIOJ 1807

TIOJ 1915

遍歷

Traversal.

Graph traversal refers to the process of visiting each node in a graph".

Wikipedia

「圖的遍歷代表以某種方式走過圖的每個點」

這次夠白話了吧

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1

等等 是不是哪裡怪怪的

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1

等等 是不是哪裡怪怪的

：那記錄上一個點是誰，然後不要往回走啊

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2

好像還有哪裡怪怪的欸

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2

改成記錄走過的點？

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3

2 號節點表示自己被排擠了

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3

要回溯看看之前的其他點，所以我們採用遞迴

  • 深度優先搜尋 / 遍歷
  • 對於每個點連到的所有點，如果還沒拜訪過就繼續 DFS
  • 記錄是否拜訪過哪個點
  • 樹可以不用記錄

DFS

vector<vector<int>> graph;
vector<bool> visited;

void dfs(int cur) {
    visited[cur] = true;
    for (int i = 0; i < graph[cur].size(); i++) {
        int nxt = graph[cur][i];
        if (!visited[nxt]) dfs(nxt);
    }
}

記得在進點時就要記錄 visited

不然你會兩個點一直來回跳

  • 啊 真的就是提供你一種方式走過所有連通的點
  • 可以處理相鄰節點的問題
  • 可以處理兩點連通的問題

DFS 能幹嘛

  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1
  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1
  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1
  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1

你會發現，距離越近的點淹得越快

  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1
  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1

如何知道下一輪要淹哪？

  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1

你可以在淹一輪後掃過整個點集

如果這個點有淹水且它的鄰居沒有淹就淹下去

  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1

你可以在淹一輪後掃過整個點集

如果這個點有淹水且它的鄰居沒有淹就淹下去

時間複雜度？

BFS

0
1
1
2
1
1

時間複雜度？

  • 總共要淹 k 次，其中 k 是點到最遠點的距離
  • 每次要檢查        個點，最壞情況
|V|
O(|V|^2)

BFS

0
1
1
2
1
1

時間複雜度？

  • 總共要淹 k 次，其中 k 是點到最遠點的距離
  • 每次要檢查        個點，最壞情況
|V|
O(|V|^2)

花太多時間決定下一輪淹哪了

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
Next: \{1, 2, 3, 4\}

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
Next: \{1, 2, 3, 4\}

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
Next: \{2, 3, 4, 2?\}

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
  • 在記錄符合條件的點時，就記錄 visited
Next: \{2, 3, 4, 2?\}

小觀察

  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
  • 在記錄符合條件的點時，就記錄 visited

時間複雜度？

每個點被經過一次 + 每條邊最多被處理兩次

O(|V|+|E|)

小觀察

  • 空間？
  • 你會發現，走過的點就不用記錄了
  • 使用一個 queue 記錄下一輪應該有哪些點，用完 pop 掉可以省一些空間
vector<vector<int>> graph;

void bfs(int origin) {
    queue<int> nexts;
    vector<bool> visited;
    while(!nexts.empty()) {
        int cur = nexts.front();
        nexts.pop();
        for (int i = 0; i < graph[cur].size(); i++) {
            int nxt = graph[cur][i];
            if (!visited[nxt]) {
                visited[nxt] = true;
                nexts.push(nxt);
            }
        }
    }
}

在 push 進 queue 時就要記得 visited!

小觀察：把 queue 換成 stack 就是在 dfs 了

但通常會用遞迴啦 好寫

  • 不帶權時可以找最短路
    • 記錄自己上個節點即可
    • 應該很輕鬆可以得到第一次碰到某節點時一定是最短路徑碰到的
    • 帶權時會發生什麼？
  • 某種方式跑過整個圖
  • 處理相鄰節點的問題

用途

  • 那這樣 DFS 聽起來很沒用欸
  • DFS 主要是好實作，碼短
  • 之後會用到

蛤

  • 在網格座標上 BFS、DFS 時找鄰近點都很方便...嗎？
  • 二維網格座標 (x+1, y+1), (x, y+1), (x-1, y+1)... 有 8 個鄰居
    • ：其實還行啊
    • ：如果是三維的呢

網格座標

const int dx[] = {1, 0, -1};
const int dy[] = {1, 0, -1};
void dfs(int cur_x, int cur_y, const vector<vector<int>> &graph) {
    vector<vector<bool>> visited(graph.size(), vector<bool> graph[0].size());
    for (int i: dx)
        for (int j: dy)
            if (!visited[cur_x + i][cur_y + j])
                visited[cur_x + i][cur_y + j] = true,
                dfs(cur_x + i, cur_y + j, graph);
}

把重複的部分換成迴圈

如果你只要上下左右就自己調整吧

TIOJ 1209

二分圖的課時會講更酷的做法

TIOJ 1085

TIOJ 1794

TIOJ 1794

iscoj 4534 (電研一四學術上機考 B3)

TIOJ 1142

ZJ g598 (APCS)

ZJ j124 (APCS)

CSES 1193

CSES 1669

TIOJ 1008

TIOJ 1025

TIOJ 1061

CSES 1678

補：2023 APCS 10月場 P3 / ZJ m372

但我懶得用 DFS 題解在後面 DSU

Made with Slides.com