圖論。

Graph Theory

INFOR 36th. @小海_夢想特急_夢城前

  • 定義 / 基本名詞
  • 分類
  • 儲存方式
  • 遍歷 (traversal)
  • 拓撲排序
  • 最短路
    • 全點源
    • 單點源
  • 倍增 LCA

Index

  • 併查集
  • (最小)生成樹
  • 連通性
    • 割點
    • 橋
  • 連通分量
    • BCC, BCC
    • SCC, WCC
  • 特殊分類
    • 二分圖
    • 水母圖
    • 仙人掌圖
  • 一些應用
    • 差分約束
    • 2 - SAT

Others

講師

  • 225 賴柏宇
  • 海之音、小海或其他類似的
  • 美術能力見底
  • 表達能力差，不懂要問
  • INFOR 36th 學術長
  • 這頁是偷來的
  • 不會圖論所以來當圖論講師
  • BrineTW 的簡報

Reference

  • 8e7 的簡報
  • FHVirus 的簡報
  • 劉澈的簡報
  • 資芽
  • 維基百科
  • 本次的講師很弱
  • 本次提供的範例 Code 可能有誤，請見諒
  • 為了提高可讀性，拆成很多函式以及回傳值處理，有時會導致常數較大，請自行修改
  • 表達能力很差，所以聽不懂 一定 一定 要問
  • 講師永遠不會放棄你 啊對 保有最終解釋權 人很ㄐㄅ不在此範圍
  • 簡報或我的觀念可能有誤，歡迎隨時糾正
  • 有些奇怪的連結是我推薦的歌.jpg (不是 Rickroll...)

聲明

定義/名詞

Glossary.

  • 名詞解釋：
    • 由各種線條、形狀、色彩等描繪成的形象或畫面。
    • 疆域。
    • 欲念。
  • 動詞解釋：
    • 繪畫、描繪。
    • 策劃、考慮。
    • 謀取、謀求。

何謂「圖」

  • 名詞解釋：
    • 由各種線條、形狀、色彩等描繪成的形象或畫面。
    • 疆域。
    • 欲念。
  • 動詞解釋：
    • 繪畫、描繪。
    • 策劃、考慮。
    • 謀取、謀求。

何謂「圖」

如果你不知道這是啥，這是教育部的解釋

A graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related".

Wikipedia

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

「一張圖是一種結構，描述了一個集合中成對物件之間的關聯性。」

結構兩字可以理解成資料結構，雖然它的本意更接近程式中的 object

  • 集合：一堆物件
  • 成對物件：兩個兩個一組的物件
  • 關聯性：兩個物件之間的關係

Definition

：點

：邊

Definition

點集：點構成的集合，以     表示

V

Definition

邊集：邊構成的集合，以     表示

E

Definition

圖：點和邊構成的集合，以                  表示

G(V,E)

Edge (邊)

  • 可以用兩點             表示
  • 方向性 (direction)
    • 若為有向，以箭頭表示
  • 邊權 (weight)
  • 自環 (loop)
    • 自己指到自己
  • 重邊 (parallel edges)
    • 起終點相同的邊

Vertex (點)

  • 點權 (weight)
  • 度 (degree)
    • 無向圖：一個點接多少邊
    • 入度：指到自己邊的數量
    • 出度：指到它點邊的數量
  • 入度 & 出度為有向圖專屬
(u, v)
  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Path

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Trace

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Track

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Circuit

  •  
  • 點、邊交錯構成的集合，其中邊要連到左右點
  • 行跡 (trace)
    • 經過的邊不重複
  • 簡單路徑 (track)
    • 經過的點不重複 (可以保證不經過重複邊)
  • 迴路 (circuit)
    • 起終點相同的路徑
    • 環 (cycle) : 只有起終點相同的路徑

Path (路徑)

P(v_0, e_1, v_1, e_2, v_2 ...)

Cycle

  • 簡單圖 (Simple Graph)：不存在重邊自環
  • 有向圖 (Directed Graph)：邊是有向的
    • 強連通 (SC)：所有點對都存在一條路徑
    • 弱連通 (WC)：要變成無向圖才全部連通
    • 有向無環圖(DAG)
  • 無向圖：邊是無向的
    • 連通圖：所有點對都存在一條路徑

一些分類

  • 完全圖：所有點對都有一條邊連著
  •  

一些分類

|E| = \frac {|V|(|V|-1)} {2}
  • 子圖：每條邊、每個點都存在於原圖中的圖
  •  

一些分類

for\ G'(V', E'):\ V'\subseteq V,\ E'\subseteq E
  • 補圖：點集相同，邊集是補集 (以完全圖的邊集為宇集)
  •  

一些分類

for\ G'(V', E'):\ V'= V,\ E' = E^c
  • 樹：不存在環的無向連通圖
  •  

一些分類

|E| = |V| - 1
  • 稀疏圖                                       ，例如樹
  • 稠密圖                                       ，例如完全圖

一些分類

|E| \leq |V| log |V|
|E| \geq |V| log |V|

TIOJ 1210 (Havel 定理)

一般做法                        或              ，但可以

O(n\ log\ n)
O(n^2log\ n)
O(n^2)

TIOJ 1032

NEOJ 410

CSES 1756

怪題思考題

儲存

Storage.

在開始前，先了解一下我的習慣...

#include <bits/stdc++.h>
using namespace std;
int n; // |V|
int m; // |E|
int u, v, vertex; // 某個點
int e, edge; // 某個邊
int w, weight; // 某個權重
int cur; // 通常是遞迴時現在在哪個點
int pre, prev; // 上一個點
int next, nxt; // 下一個點
vector<vector<type>> graph; // 圖
vector<int> neighbor; // 一個點附近的點
const int INF = 1e9 + 7;
  • 鄰接矩陣
  • 開一個                    的表記錄邊
  • 如果帶權就記錄權重
  • 有向邊？

Adjacency Matrix

|V|\times |V|
(u, v)
0
1
2
\begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix}
  • 鄰接矩陣
  • 開一個                    的表記錄邊
  • 如果帶權就記錄權重
  • 有向邊？

Adjacency Matrix

|V|\times |V|
(u, v)
0
1
2
\begin{bmatrix} 0 & 5 & 3 \\ 5 & 0 & 0 \\ 3 & 0 & 0 \end{bmatrix}
5
3
  • 鄰接矩陣
  • 開一個                    的表記錄邊
  • 如果帶權就記錄權重
  • 有向邊？令            記錄的是從    指向    就好啦

Adjacency Matrix

|V|\times |V|
(u, v)
0
1
2
\begin{bmatrix} 0 & 5 & 0 \\ 0 & 0 & 0 \\ 3 & 0 & 0 \end{bmatrix}
5
3
(u, v)
u
v
int n, m;
cin >> n >> m;
vector<vector<bool>> graph(n, vector<bool>(n, 0));
for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    graph[u][v] = 1;
    graph[v][u] = 1;
}
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 帶權？有向？

Adjacency List

u
v
0
1
2
0: \{1, 2\}
1: \{0\}
2: \{0\}
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 帶權？用 pair 把權重包在邊裡

Adjacency List

u
v
0
1
2
0: \{(1, 5), (2, 3)\}
1: \{(0, 5)\}
2: \{(0, 3)\}
5
3
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 有向應該不需要我解釋吧

Adjacency List

u
v
0
1
2
0: \{\}
1: \{(0, 5)\}
2: \{(0, 3)\}
5
3
  • 鄰接串列 但它和 linked list 是不同東西
  • 把所有     連到的點    存在一個 list 裡面
  • 有向應該不需要我解釋吧

Adjacency List

u
v
0
1
2
0: \{\}
1: \{(0, 5)\}
2: \{(0, 3)\}
5
3

空間複雜度？

int n, m;
cin >> n >> m;
vector<vector<int>> graph(n);
for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    graph[u].push_back(v);
    graph[v].push_back(u);
}

因為這東西比較常用，所以如果後面有 graph 應該都是指鄰接串列的存法

鄰接矩陣

  • 快速查看 u, v 間的邊
  • 浪費空間
  • 不好處理重邊
  • 處理稠密圖較有效率

鄰接串列

  • 不能直接查看 u, v 間的邊
  • 對於相鄰點的操作方便
  • 比較不浪費空間
  • 處理稀疏圖、稠密圖都很好

比較

方式 鄰接矩陣 鄰接串列
空間複雜度
存取特定邊
枚舉邊
O(|V|^2)
O(|V|+|E|)
O(1)
O(|E|)
O(|V|^2)
O(|V|+|E|)

同時儲存點和邊的資訊？

這裡有一個我滿喜歡的方法

reference: 張秉中學長的樹論簡報

struct Node {
    int weight; // 點的資訊
    struct Edge {
        int v;
        int weight; // 邊的資訊
    };
    vector<Edge> neighbor;
};
vector<Node> graph;

其他方法

比較少用到的東西

  • 每個格子都是一個點
  • 反正要用的時候會用就好了(?

網格座標(?)

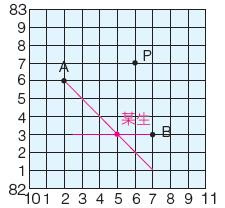
  • 就 把輸入進來的邊丟到一個 list 裡面

邊串列 Edge List

int n, m;
cin >> n >> m;
vector<pair<int, int>> edges;
for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    edges.push_back({u, v});
}
  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:

edge_id

  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1

edge_id

  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1

edge_id

  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1

edge_id

0
  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1

edge_id

0
  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1

edge_id

0
2
  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1

edge_id

0
2
  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1

edge_id

0
2
0
  • 概念和鄰接串列類似，所以一般用鄰接串列即可
  • 對於每個節點，我們儲存邊的 Linked list 尾端節點指標
  • 創建邊數個節點，每加一條邊就拿一個節點來用

(鏈式) 前向星

0
1
2
0:
1:
2:
1
0
2
0

扣，reference

struct Graph {
    struct Edge {
        int next;
        int v;
    } edges[max_m];
    int neighbor[max_n];
    int edge_id = 0;
    void add_edge(int u, int v) {
        edges[edge_id].v = v;
        edges[edge_id].next = neighbor[u];
        neighbor[u] = edge_id;
        edge_id++;
    }
};

TIOJ 1807

TIOJ 1915

遍歷

Traversal.

Graph traversal refers to the process of visiting each node in a graph".

Wikipedia

「圖的遍歷代表以某種方式走過圖的每個點」

這次夠白話了吧

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1

等等 是不是哪裡怪怪的

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？

DFS

0
1

等等 是不是哪裡怪怪的

：那記錄上一個點是誰，然後不要往回走啊

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2

好像還有哪裡怪怪的欸

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄上一個點是誰，不要走過去

DFS

0
1
2

改成記錄走過的點？

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3
  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3

2 號節點表示自己被排擠了

  • 深度優先搜尋 / 遍歷
  • 既然任何一種方式走過都可以，那我旁邊有一個點就走過去如何？
  • 記錄走過的點

DFS

0
1
2
3

要回溯看看之前的其他點，所以我們採用遞迴

  • 深度優先搜尋 / 遍歷
  • 對於每個點連到的所有點，如果還沒拜訪過就繼續 DFS
  • 記錄是否拜訪過哪個點
  • 樹可以不用記錄

DFS

void dfs(int cur, const vector<vector<int>> &graph) {
    static vector<bool> visited(graph.size(), false);
    visited[cur] = true;
    for (const int &nxt: graph[cur])
        if(!visited[nxt]) dfs(nxt, graph);
}

記得在進點時就要記錄 visited

不然你會兩個點一直來回跳

  • 啊 真的就是提供你一種方式走過所有連通的點
  • 可以處理相鄰節點的問題
  • 可以處理兩點連通的問題

DFS 能幹嘛

  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1
  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1
  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1
  • 淹水問題：淹水會怎麼淹？

BFS

0
1
1
2
1
1

你會發現，距離越近的點淹得越快

  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1
  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1

如何知道下一輪要淹哪？

  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1

你可以在淹一輪後掃過整個點集

如果這個點有淹水且它的鄰居沒有淹就淹下去

  • 淹水問題：越近的點越早淹到
  • 同樣要記錄淹過的點，原因同 DFS

BFS

0
1
1
2
1
1

你可以在淹一輪後掃過整個點集

如果這個點有淹水且它的鄰居沒有淹就淹下去

時間複雜度？

BFS

0
1
1
2
1
1

時間複雜度？

  • 總共要淹 k 次，其中 k 是點到最遠點的距離
  • 每次要檢查        個點，最壞情況
|V|
O(|V|^2)

BFS

0
1
1
2
1
1

時間複雜度？

  • 總共要淹 k 次，其中 k 是點到最遠點的距離
  • 每次要檢查        個點，最壞情況
|V|
O(|V|^2)

花太多時間決定下一輪淹哪了

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
Next: \{1, 2, 3, 4\}

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
Next: \{1, 2, 3, 4\}

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
Next: \{2, 3, 4, 2?\}

小觀察

0
1
4
5
2
3
  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
  • 在記錄符合條件的點時，就記錄 visited
Next: \{2, 3, 4, 2?\}

小觀察

  • 只有淹水範圍最外圍的鄰居會被淹到
  • 鄰居要是還沒淹過水的那些
  • 每做一輪就將符合條件的點記錄下來！
  • 在記錄符合條件的點時，就記錄 visited

時間複雜度？

每個點被經過一次 + 每條邊最多被處理兩次

O(|V|+|E|)

小觀察

  • 空間？
  • 你會發現，走過的點就不用記錄了
  • 使用一個 queue 記錄下一輪應該有哪些點，用完 pop 掉可以省一些空間
void bfs(int start, const vector<vector<int>> &graph) {
    queue<int> nexts;
    vector<int> visited(graph.size(), false);
    nexts.push(start), visited[start] = true;
    while(!nexts.empty()) {
        int cur = nexts.top();
        nexts.pop();
        for (const int &nxt: graph[cur]) {
            if(visited[nxt]) continue;
            visited[nxt] = true;
            nexts.push(nxt);
        }
    }
}

在 push 進 queue 時就要記得 visited!

小觀察：把 queue 換成 stack 就是在 dfs 了

但通常會用遞迴啦 好寫

  • 不帶權時可以找最短路
    • 記錄自己上個節點即可
    • 應該很輕鬆可以得到第一次碰到某節點時一定是最短路徑碰到的
    • 帶權時會發生什麼？
  • 某種方式跑過整個圖
  • 處理相鄰節點的問題

用途

  • 那這樣 DFS 聽起來很沒用欸
  • DFS 主要是好實作，碼短
  • 之後會用到

蛤

  • 在網格座標上 BFS、DFS 時找鄰近點都很方便...嗎？
  • 二維網格座標 (x+1, y+1), (x, y+1), (x-1, y+1)... 有 8 個鄰居
    • ：其實還行啊
    • ：如果是三維的呢

網格座標

const int dx[] = {1, 0, -1};
const int dy[] = {1, 0, -1};
void dfs(int cur_x, int cur_y, const vector<vector<int>> &graph) {
    vector<vector<bool>> visited(graph.size(), vector<bool> graph[0].size());
    for (int i: dx)
        for (int j: dy)
            if (!visited[cur_x + i][cur_y + j])
                visited[cur_x + i][cur_y + j] = true,
                dfs(cur_x + i, cur_y + j, graph);
}

把重複的部分換成迴圈

如果你只要上下左右就自己調整吧

TIOJ 1209

二分圖的課時會講更酷的做法

TIOJ 1085

TIOJ 1794

TIOJ 1794

iscoj 4534 (電研一四學術上機考 B3)

TIOJ 1142

ZJ g598 (APCS)

ZJ j124 (APCS)

CSES 1193

CSES 1669

TIOJ 1008

TIOJ 1025

TIOJ 1061

CSES 1678

補：2023 APCS 10月場 P3 / ZJ m372

但我懶得用 DFS 題解在後面 DSU

拓撲  排序

Topological Sort.

ㄆ

ㄨ

  • Topology
  • 「特定物件經過連續映射後不變性質的研究」
  • 較經典的例子像是「甜甜圈和馬克杯是同胚的」
  • 以比較視覺化的方式來說
    • 物體經過不包括黏合的變形後視為同個物體
  • 在圖論裡，類似地，我們不關心權重 (邊長)，只關心連接關係

拓撲

  • Topology
  • 「特定物件經過連續映射後不變性質的研究」
  • 較經典的例子像是「甜甜圈和馬克杯是同胚的」
  • 以比較視覺化的方式來說
    • 物體經過不包括黏合的變形後視為同個物體
  • 在圖論裡，類似地，我們不關心權重 (邊長)，只關心連接關係

拓撲

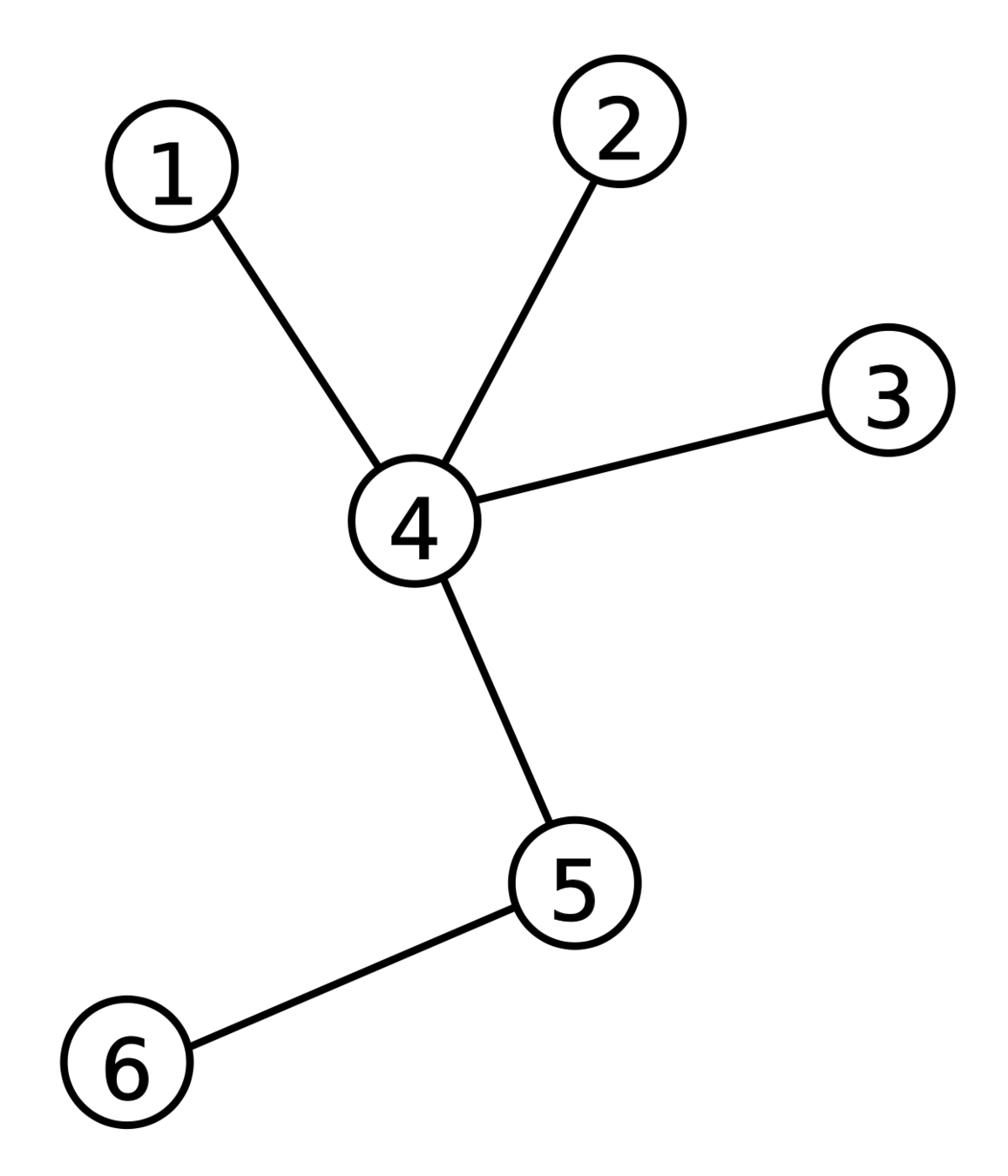
  • 你會發現在有向圖裡常存在一種狀況：
  • A 可以走到 B，但 B 不能走到 A
    • 以下圖舉例， 0 可以走到 2，但 2 無論如何都走不回 0
    • 1 可以走到 2，但 2 不能走到 1

有向圖的特性

0
1
2
  • 定義這樣的狀況叫 「 A 的輩分比 B 高」
  • 實際上應該沒有正式名稱
  • 如果對於一張圖的每個點對都符合這樣的關係，就可以做排序
  • 不一定是唯一的

有向圖的特性

1
2
0
  • 簡單的例外：存在環的時候不行 (顯然)
  • 只要無環都可行
    • 如果 A 能走到 B，B 不能走到 A
    • B 能走到 C ，C 不能走到 B
    • 如果 C 能走到 A 表示有環，所以 C 一定不能走到 A，因此這三點能被排序
    • 考慮更多點也會正確

唯一的例外

  • 對於一個排序後的點序列                                ，圖裡面每個有向邊              ，滿足
  • 每個有向邊都是往後面 (輩分較小) 指

形式化表述

\{p_1, p_2, ..., p_{|V|}\}
(p_i, p_j)
i < j
  • 我們排序完之後，在關心輩分較小的點時可以不用關心輩分大的點
  • 有時候在做事時，真的就得關心點的順序
    • 從起點一路推到終點
    • 從終點反推起點狀態
  • 很多時候，這東西和 DP 會扯上關係
    • 轉移時可以確保不會有前面的點的問題！
    • 等等講最短路就會遇到 (非常快)

為什麼要拓撲排序

  • 注意到排序中輩分最大的那個點一定不會有邊連到它，也就是入度為 0
  • 輩分比它低但最大的點 (也就是第二大的) 一定只會被比它大的點連到(也就是最大點)
    • 如果去除最大點的影響，第二大的入度一定是 0
    • 視為新的圖處理！

演算法概念

  1. 找到入度為 0 的點
  2. 把那個點還有相關的邊拔掉，更新入度
  3. 找到新的入度為 0 的點，放在原本的點後面
  • 重複執行以上流程，直到沒有入度為 0 的點
  • 如果這時還有點沒被拔掉，說明此圖有有向環！

執行流程

  • 類似 BFS ，你會發現如果暴力找點會跑很慢
  • 入度為 0 只會在被更新時發生！
  • 一樣用 queue 把那些入度為 0 的點推入！
  • 所以
    1. 計算所有點的入度
    2. 找到入度為 0 的點，推入 queue
    3. 取出 queue 的前端，放入排序結果
    4. 拔掉這個點，更新入度
      • 如果被拔掉後入度為 0，則推入 queue
    5. 重複直到 queue 為空

BFS 做法

BFS 做法

0
1
2
3
4

Queue: {}

Result: {}

BFS 做法

0
1
2
3
4

Queue: {0, 4}

Result: {}

BFS 做法

1
2
3
4

Queue: {4, 1}

Result: {0}

BFS 做法

1
2
3

Queue: {1}

Result: {0, 4}

BFS 做法

2
3

Queue: {2}

Result: {0, 4, 1}

BFS 做法

3

Queue: {3}

Result: {0, 4, 1, 2}

BFS 做法

Queue: {}

Result: {0, 4, 1, 2, 3}

vector<int> topological_sort(const vector<vector<int>> &graph) {
    vector<int> result;
    vector<int> indegree(graph.size(), 0);
    for (const auto &i : graph)
        for (const auto &j : i)
            indegree[j]++;
    queue<int> origin;
    for (int v = 0; v < graph.size(); v++)
        if (!indegree[v]) origin.push(v);
    while (!origin.empty()) {
        int cur = origin.front();
        result.push_back(cur);
        origin.pop();
        for (auto &neighbor : graph[cur])
            if (--indegree[neighbor] == 0) origin.push(neighbor);
    }
    return result;
}

                        扣

話說真的真的可以這樣寫欸

  • 如果序列結果     有                    ，依據之前的結論可知道此圖有環
  • 反之此圖無有向環，稱為有向無環圖 (DAG)

正確性

P
|P| < |V|
  • 有 BFS 做法當然有 DFS 做法
  • 會一種做法就好了，為什麼要學這個做法？
    • 時間戳記 (time stamp) 的概念以後會用到

DFS 做法

  • 在遍歷的過程中碰到點 / 離開點的時間順序

Time Stamp

struct Node {
    int in_time, out_time;
    bool visited = false;
    vector<int> neighbor;
};
void dfs(int cur, vector<Node> &graph) {
    static int time_stamp = 0;
    graph[cur].in_time = time_stamp++;
    graph[cur].visited = true;
    for (const auto &nxt : graph[cur].neighbor)
        if (!graph[nxt].visited) dfs(nxt, graph);
    graph[cur].out_time = time_stamp++;
}
  • 實際上在幹嘛

Time Stamp

0
(*, *)
1
(*, *)
2
(*, *)
4
(*, *)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, *)
1
(*, *)
2
(*, *)
4
(*, *)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, *)
1
(1, *)
2
(*, *)
4
(*, *)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, *)
1
(1, *)
2
(*, *)
4
(2, *)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, *)
1
(1, *)
2
(*, *)
4
(2, 3)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, *)
1
(1, 4)
2
(*, *)
4
(2, 3)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, *)
1
(1, 4)
2
(5, *)
4
(2, 3)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, *)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(*, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, *)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(*, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(10, *)
6
(*, *)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(10, *)
6
(11, *)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(10, *)
6
(11, 12)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(10, 13)
6
(11, 12)
  • 實際上在幹嘛

Time Stamp

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(10, 13)
6
(11, 12)
  • 值得觀察的是離開戳記
    • 如果 u 輩分比 v 大
      • 先到 u：u 的離開戳記較大
      • 先到 v：因為無法馬上到 u，u 的離開戳記較大
    • 如果有環
      • 注意到遇到「有進入戳記但無離開戳記」表示還沒離開但卻可以到
      • 這種情況下有環

DFS 做法

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(10, 13)
6
(11, 12)
  • 結論：離開戳記比較大則輩分較大！
  • 在 DFS 時一邊偵測是否有環，一邊在離開時記錄排序結果
  • 其實可以利用「是否是同一次 DFS」來判斷是否有環

DFS 做法

0
(0, 7)
1
(1, 4)
2
(5, 6)
4
(2, 3)
3
(8, 9)
5
(10, 13)
6
(11, 12)
vector<int> topological_sort(const vector<vector<int>> &graph) {
    vector<int> result;
    result.reserve(graph.size());
    vector<int> in_time(graph.size(), 0), out_time(graph.size(), 0);
    auto dfs = [&](int cur, auto &&dfs) -> bool {
        static int time_stamp = 0;
        in_time[cur] = ++time_stamp;
        for (const auto &nxt : graph[cur]) {
            if (!in_time[nxt]) {
                if (!dfs(nxt, dfs)) return false;
            }
            else if (!out_time[nxt]) {
                return false;
            }
        }
        result.push_back(cur);
        out_time[cur] = ++time_stamp;
        return true;
    };
    for (int origin = 0; origin < graph.size(); origin++)
        if (!in_time[origin])
            if (!dfs(origin, dfs)) return vector<int>(0);
    return result;
}

注意如果是用 vector 直接 push_back 排出來的結果是由輩分小到大

bool dfs(int cur, const vector<vector<int>> &graph, vector<int> &result, vector<int> &in_time, vector<int> &out_time) {
    static int time_stamp = 0;
    in_time[cur] = ++time_stamp;
    for (const auto &nxt : graph[cur]) {
        if (!in_time[nxt]) {
            if (!dfs(nxt, graph, result, in_time, out_time)) return false;
        } else if (!out_time[nxt])
            return false;
    }
    result.push_back(cur);
    out_time[cur] = ++time_stamp;
    return true;
}
vector<int> topological_sort(const vector<vector<int>> &graph) {
    vector<int> result;
    result.reserve(graph.size());
    vector<int> in_time(graph.size(), 0), out_time(graph.size(), 0);
    for (int origin = 0; origin < graph.size(); origin++)
        if (!in_time[origin])
            if (!dfs(origin, graph, result, in_time, out_time)) return vector<int>(0);
    return result;
}

給看不懂 lambda 函式的人

很多都是負責人丟給我的(

CSES 1681

CSES 1679

CSES 1680

TIOJ 1557

TIOJ 1092

NEOJ 165

TIOJ 2319 / 建中 2023 校內賽複試 PA

TIOJ 2254

最短路算法

Shortest Path.

  • 欸 非常直觀 最短路就是最短路
  • 你可以拿來算你家到學校的最短路啊 我不反對(
  • 主要分成幾種：
    • 單點源/全點對
    • 帶權/不帶權
    • 有負邊/無負邊
    • 有負環/無負環
  • 依照條件不同，有不同的演算法

最短路

  • 單點源：選定一個源點，看源點到其他點最短是多少
  • 就是 BFS
  • 如果是樹 DFS 就夠了，通常我們會叫它深度

單點源 + 不帶權

  • 單點源帶權最短路的基礎
  • 如果存在一個中繼邊              使得源點到     的距離      可以縮短（也就是                             ）就要更新
  • 叫鬆弛不叫繃緊的原因是因為採用了更多的邊（大概）

鬆弛 (relaxation)

e(u, v)
u
d_u
d_v + w_{e} < d_u
7122
O
v
u
2
d_u = 7122
  • 單點源帶權最短路的基礎
  • 如果存在一個中繼邊              使得源點到     的距離      可以縮短（也就是                             ）就要更新
  • 叫鬆弛不叫繃緊的原因是因為採用了更多的邊（大概）

鬆弛 (relaxation)

e(u, v)
u
d_u
d_v + w_{e} < d_u
7122
O
v
u
2
2
d_u = 7122
d_v + w_{uv} = 2 + 2< 7122
  • 單點源帶權最短路的基礎
  • 如果存在一個中繼邊              使得源點到     的距離      可以縮短（也就是                             ）就要更新
  • 叫鬆弛不叫繃緊的原因是因為採用了更多的邊（大概）

鬆弛 (relaxation)

e(u, v)
u
d_u
d_v + w_{e} < d_u
7122
O
v
u
2
2
d_u = 4
  • 沿用定義      指當前從源點到點    的最短距離
  • 暴力一點想想看
    • 一開始將源點到所有點的距離設成無限大
    • 一直跑過邊集，有得更新就更新
    • 沒得更新就結束
  • 時間複雜度？

Bellman-Ford

d_i
i
  • 不管怎麼說，在程式裡我們都不希望看到 while(true) 這種東西
  • 具體來說更新幾次後會是好的？
    • 不考慮負環，簡單路徑最多有                條邊
    • 更新                次可以確保所有邊都產生影響了
  • 時間複雜度
  • 有負環(權重加總為負的環)會卡死，可以一直卡在裡面不出來權重就會越來越小
  • 如果更新完                仍可以更新，表示存在負環

O(while(true))?

|V|-1
|V|-1
O(|V||E|)
|V|-1
  • 只有上一輪被鬆弛過的點會鬆弛到旁邊的點
    • 可以用 BFS 的想法，把有鬆弛到的點推進去 queue 裡面，具體來說：
    1. 取出一個點
    2. 用這個點鬆弛附近的點
    3. 把成功鬆弛的點放回去 queue
    • queue 空的時候就做完了
  • 因為要用到「附近的點」，所以得用鄰接串列

優化

  • 這作法叫 SPFA (Shortest Path Faster Algorithm)
  • 時間複雜度？
    •  
    • 這樣沒有變好啊？
    • 注意到對於隨機生成的圖可以做到
  • 注意，是對於「隨機生成」的圖，比賽要卡也是可以卡成
  • 因此，如果比賽的解可能會用到 SPFA ，則它的測資範圍應該要是 Bellman-Ford 可以過的

優化

O(|V||E|)
O(|V|+|E|)
O(|V||E|)
vector<int> Bellman_Ford(int origin, int n, const vector<vector<pair<int, int>>> &graph) {
    vector<int> d(graph.size(), INF); // 從源點到各個點的答案
    for (int i = 0; i < graph.size(); i++)
        for (int v = 0; v < graph.size(); v++)
            for (const pair<int, int> &edge: graph[v])
#define edge.second w
#define edge.first u
                if (d[v] + w < d[u]) d[u] = d[v] + w;
    return d;
}
vector<int> SPFA(int origin, const vector<vector<pair<int, int>>> &graph;) {
    vector<int> d(graph.size(), INF);
    vector<bool> inQueue(graph.size(), false);
    queue<int> nexts;
    nexts.push(origin);
    inQueue[origin] = true;
    while (!nexts.empty()) {
        int v = nexts.front();
        nexts.pop();
        inQueue[v] = false;
        for (const pair<int, int> &edge : graph[v]) {
#define w edge.second
#define u edge.first
            if (d[v] + w < d[u] && !inQueue[u]) {
                d[u] = d[v] + w;
                nexts.push(u);
                inQueue[u] = true;
            }
        }
    }
    return d;
}
  • 在日常生活中，兩點距離不為負比較正常吧
  • 如果不帶負權可以做哪些優化
    • 注意到如果      已經最小了，用    鬆弛別人得到      都會大等      ，
    • 並且，如果用比較大的                       來鬆弛       ，怎麼樣都不會鬆弛成功
  • 我們可以證明如果每次都選最小的點去鬆弛其他人會是好的！
  • 這樣每條邊只會被用到一次

不帶負權

d_u
u
d_v'
d_u
d_u + w = d_v' \geq d_u
d_v, d_v \geq d_u
d_u
  • 證明每次選擇當前距離最小的點 u 總是好的
    • 注意到如果用其他點鬆弛 u 並不會比較好，因為距離更長
    • 用 u 鬆弛其他人的距離也會更長，無法反過來鬆弛 u
    • u 是最短路，得證

證明(?

  • 剛剛講的東西如何實作？
  • 把 BFS 的 queue 換成 priority queue 就可以了
  • 在 priority queue 裡面記錄更新後的 d、點 v
  1. 將一個點取出並標記 visited
  2. 鬆弛附近的點 v，得到新的 d ，如果有鬆弛把 (d, v) 丟進 priority queue 裡面
  3. 以沒有被使用過的、距離最小的點繼續

Dijkstra

struct Edge {
    int v, w;
};
vector<int> Dijkstra(int origin, const vector<vector<Edge>> &graph) {
    vector<int> d(graph.size(), INF);
    vector<bool> visited(graph.size(), false);
    d[origin] = 0;
    priority_queue<Edge, vector<Edge>, 
        [](const Edge &a, const Edge &b) -> bool {
            return a.w > b.w;
        }
    > nexts;
    nexts.push({origin, 0});
    while (!nexts.empty()) {
        Edge cur = nexts.top();
        nexts.pop();
        if (visited[cur.v]) continue;
        visited[cur.v] = true;
        for (const Edge& e : graph[cur.v]) {
            if (cur.w + e.w >= d[e.v]) continue;
            d[e.v] = cur.w + e.w;
            nexts.push({e.v, d[e.v]});
        }
    }
    return d;
}
struct Edge {
    int v, w;
    friend bool operator<(const Edge& a, const Edge& b) {
        return a.w > b.w;
    }
};
vector<vector<Edge>> graph;
vector<int> Dijkstra(int origin) {
    vector<int> d(graph.size(), INF);
    vector<bool> visited(graph.size(), false);
    d[origin] = 0;
    priority_queue<Edge> nexts;
    nexts.push({origin, 0});
    while (!nexts.empty()) {
        Edge cur = nexts.top();
        nexts.pop();
        if (visited[cur.v]) continue;
        visited[cur.v] = true;
        for (const Edge& e : graph[cur.v]) {
            if (cur.w + e.w >= d[e.v]) continue;
            d[e.v] = cur.w + e.w;
            nexts.push({e.v, d[e.v]});
        }
    }
    return d;
}

吃點毒

  • 兩個部分
    • 選當前距離最小點
    • 修改點
  •  
  • 依據實作的不同，有不同的複雜度
    • 陣列暴力搜尋最小值：
    • binary heap:
    • 一些奇怪的堆：

時間複雜度

O(|V| + |E|^2)
O(|V| + |E|\ log\ |E|)
O(|V|\ log\ |V| + |E|)
O(|V|T_{getmin} + |E|T_{modify})
  • 怎麼鬆弛會是最好的？
  • 注意到以下情況

DAG 上最短路

7122
O
v
u
2
d_u = 7122
  • 怎麼鬆弛會是最好的？
  • 注意到以下情況

DAG 上最短路

7122
O
v
u
2
d_u = 7122
2
d_v + w_{uv} = 2 + 2< 7122
  • 怎麼鬆弛會是最好的？
  • 注意到以下情況

DAG 上最短路

7122
O
v
u
2
d_u = 4
2
  • 怎麼鬆弛會是最好的？
  • 注意到以下情況
    • 鬆弛同樣是具有方向性的！

DAG 上最短路

7122
O
v
u
2
d_u = 4
2
  • 鬆弛具有方向性，代表輩分較小的點不能鬆弛輩分大的點
  • 拓撲排序後由輩分大到小鬆弛，可以保證每條邊至多只用一次
  • 時間複雜度

DAG 上最短路

O(|V|+|E|)

單點源 Ver.

vector<int> DAG_shortest_path(int origin, const vector<vector<pair<int, int>>> &graph) {
    vector<int> sort_result = topological_sort(graph);
    vector<int> result(graph.size(), INF);
    result[origin] = 0;
    int origin_index = 0;
    while (sort_result[origin_index] != origin) origin_index++;
    for (int u = origin_index; u < graph.size(); u++)
        for (const auto &[v, w] : graph[sort_result[u]])
            result[v] = min(result[v], result[sort_result[u]] + w);
    return result;
}

單點源最短路算法比較

Bellman-Ford

處理負環

處理負權

帶環

時間複雜度

Dijkstra

處理負環

處理負權

帶環

時間複雜度

DAG 上最短路

處理負環

處理負權

帶環

時間複雜度

帶負權/負環時用

O(|V||E|)

一般情況最常用

僅 DAG 上可用

O(|E|\ log\ |E|)
O(|V|+|E|)
  • Floyd-Warshall
  • 開二維陣列記錄每個點對          之間的最短路
  • 不要懷疑，DP
    • 令                  是           用前    個點作中繼點的最短距離
    •  
  • 複雜度
  • 可以滾動

全點對最短路

dp[u][v][i+1] = min(dp[u][v][i], dp[u][i][i] + dp[i][v][i])
dp[u][v][i]
(u, v)
(u, v)
O(|V|^3)
i

一樣，處理不了負環

但是負權會是好的

vector<vector<int>> Floyd_Warshall(const vector<vector<pair<int, int>>> &graph) {
    vector<vector<int>> result(graph.size(), vector<int>(graph.size(), INF));
    for (int i = 0; i < graph.size(); i++) result[i][i] = 0;
    for (int u = 0; u < graph.size(); u++)
        for (const auto &[v, w] : graph[u])
            result[u][v] = w;
    for (int k = 0; k < graph.size(); k++)
        for (int u = 0; u < graph.size(); u++)
            for (int v = 0; v < graph.size(); v++)
                result[u][v] = min(result[u][v], result[u][k] + result[k][v]);
    return result;
}
  • 舉個題目當作例子：iscoj 4457
  • 題目問全點對最短路，但是
  • 用剛剛做法直接暴斃
  • 有沒有什麼方法可以壓過稀疏圖的測資？

稀疏圖上優化

|V|^3 = 8\times 10^9
|V| = 2000, |E| = 5000
  • 某天和 807 吃午餐時：
    • 啊對所有點跑過 Dijkstra 不就好了？
    • 複雜度
    • 還好這題只有正邊
  • 如果有負邊怎麼辦？

稀疏圖上優化

O(|V||E|\ log\ |E|) \approx 1.23 \times 10^8
  • 對每個點跑一次單點源最短路
  • 我們理所當然地，單點源最短路算法必須使用 Dijkstra，用 Bellman-Ford 不如去用 Floyd-Warshall
  • 如果可以把負權修正成正權就好了？

Johnson

  • How?
  • 如果我們對於每個點加上一個數 k，最後減掉 k * 路徑長？

修正邊權

0
1
2
4
-1
2
3
0
0
0

0 到 4 最短路：0->2->3->4  = 0

  • How?
  • 如果我們對於每個點加上一個數 k，最後減掉 k * 路徑長？

修正邊權

0
1
2
4
1
4
3
2
2
2

0 到 4 最短路：0->2->3->4  = 0

全部 +2

  • How?
  • 如果我們對於每個點加上一個數 k，最後減掉 k * 路徑長？

修正邊權

0
1
2
4
1
4
3
2
2
2

0 到 4 最短路：0->2->3->4  = 0

全部 +2

最短路：0->1->4 = 5

  • 如果按上述方法求最短路，求出來的已經不是原圖的最短路了！
  • 每條路徑總共加上的值不相同

修正邊權

0
1
2
4
1
4
3
2
2
2

0->1->4 總共被 +4

0->2->3->4 總共被 +6

  • 引入位能的觀念
  • 以重力位能為例
    • 每個點的絕對位能會和零位面有關
    • 位能差和路徑無關，只和位置有關
  • 為每個點定義一個位能，把一條路徑視為實際上在爬山 / 移動的過程
  • 其他能量 + 位能(固定) = 移動所需能量
  • 原路徑長 + 位能(固定) = 修正後路徑長

位能

  • 具體來說
    • 假設你去爬山
    • 重力場是均勻的
    • 同樣一條路徑，你會因為整座山突然向上平移而變累嗎？
      • 不會，因為高度差並沒有改變
  • 所以，爬山累不累只和路徑有關
  • 同理，圖上同樣的兩點，含位能路徑長只和原路徑長度有關

位能

  • 關於位能有趣的例子
    • 你考了 95 分，A 同學考了 80 分，B 同學考了 70 分
    • 今天老師宣布全部人 +5 分，你和 A, B 同學的分數差有變嗎？
  • 但這樣沒有說明到路徑的部分
  • @下一個圖論講師 幫我想想包含路徑的講法

位能

  • 如上所述，接著我們要知道如何訂定每個點的位能
  • 建立一個超級源點 O，向各點連一條權重為 0 的邊，接著求各點與源點的最短距離
  • 該點的絕對位能 = 源點到該點的距離，令 i 的位能 h(i)
  • 更新 w'(e(u, v)) = w(e(u, v)) + h(u) - h(v)

定每點位能

  • 首先，看看這樣做路徑長會發生什麼
    • 對於路徑                                         ，有權重和 w(P')

 

 

 

  • 也就是說，對於任意兩點要修正的值是固定的位能差
  • 所以，它對應到的會是原圖上的最短路

正確性

P'\{v_0, e'_1, v_1, e'_2 ...e'_n, v_n\}
= (w_1 + h_0 - h_1) + (w_2 + h_1 - h_2) + ...(w_n + h_n-1 - h_n)
= (w_1 + w_2 + ... w_n) + h_0 - h_n
= w(P) + h_0 - h_n
  • 接著要證明每條邊都 
  • 對於超級源點 O 來說，                                                        因為已經是最短路不能再鬆弛
  • 因此我們有修正後的邊權

正確性

d_v \leq d_u + w(u, v), h_v \leq w(u, v) + h_u
w'(u, v) = w(u, v) + h_u - h_v \geq 0
\geq 0
  • 證明它是正確的了
  • 如何實做？
    1. 為每個點定位能
      • 對超級源點 O 做 Bellman-Ford
    2. 修正邊權
    3. 對每一點做 Dijkstra
    4. 答案修正回來
  • 複雜度？

Johnson

O(|V||E|\ log\ |E|)
vector<vector<int>> Johnson(vector<vector<pair<int, int>>> graph) {
    vector<int> h(graph.size(), 0);
    for (int i = 0; i < graph.size(); i++)
        for (int u = 0; u < graph.size(); u++)
            for (const auto &[v, w] : graph[u])
                h[v] = min(h[v], h[u] + w);

    for (int u = 0; u < graph.size(); u++)
        for (auto &[v, w] : graph[u])
            w += h[u] - h[v];

    vector<vector<int>> result;
    for (int u = 0; u < graph.size(); u++) result[u] = Dijkstra(u, graph);

    for (int u = 0; u < graph.size(); u++)
        for (int v = 0; v < graph.size(); v++)
            result[u][v] -= h[u] - h[v];
    return result;
}

我好像沒看到有學長的簡報裡有這東西(?

會不會用上是個好問題

Floyd-Warshall

  • 適合稠密圖
  • 時間複雜度
  • 實作非常容易
  • 跑到最後才能確定負環

Johnson

  • 適合稀疏圖
  • 時間複雜度
  • 實作麻煩
  • 一開始就能確定負環
O(|V|^3)
O(|V||E|\ log\ |E|)

TIOJ 1034

TIOJ 1706

TIOJ 2208

TIOJ 1604

CSES 1671

CSES 1672

TIOJ 1641

TIOJ 1096

TIOJ 2283

NEOJ 391

NEOJ 431

TIOJ 2313 / 2023 建中校內賽初試 pE

建中複賽 '21 pC

CF 1887B

CSES 1196

CSES 1197

CSES 1673

CSES 1195

CSES 1202

洛谷 P1993 (ianwangorz)

CF 1815C

ABC077 D

OII '22 pB

最低共同祖先

Lowest Common Ancestor, LCA

  • 嘿對，我要來偷跑樹論了(?
  • 你知道為什麼要偷跑樹論嗎？
  • 你答對了！因為學長也偷跑 因為我們要講最短路

偷跑樹論

  • 來看看生物的 LCA (MRCA)
  • 最近的共同祖先

What is LCA?

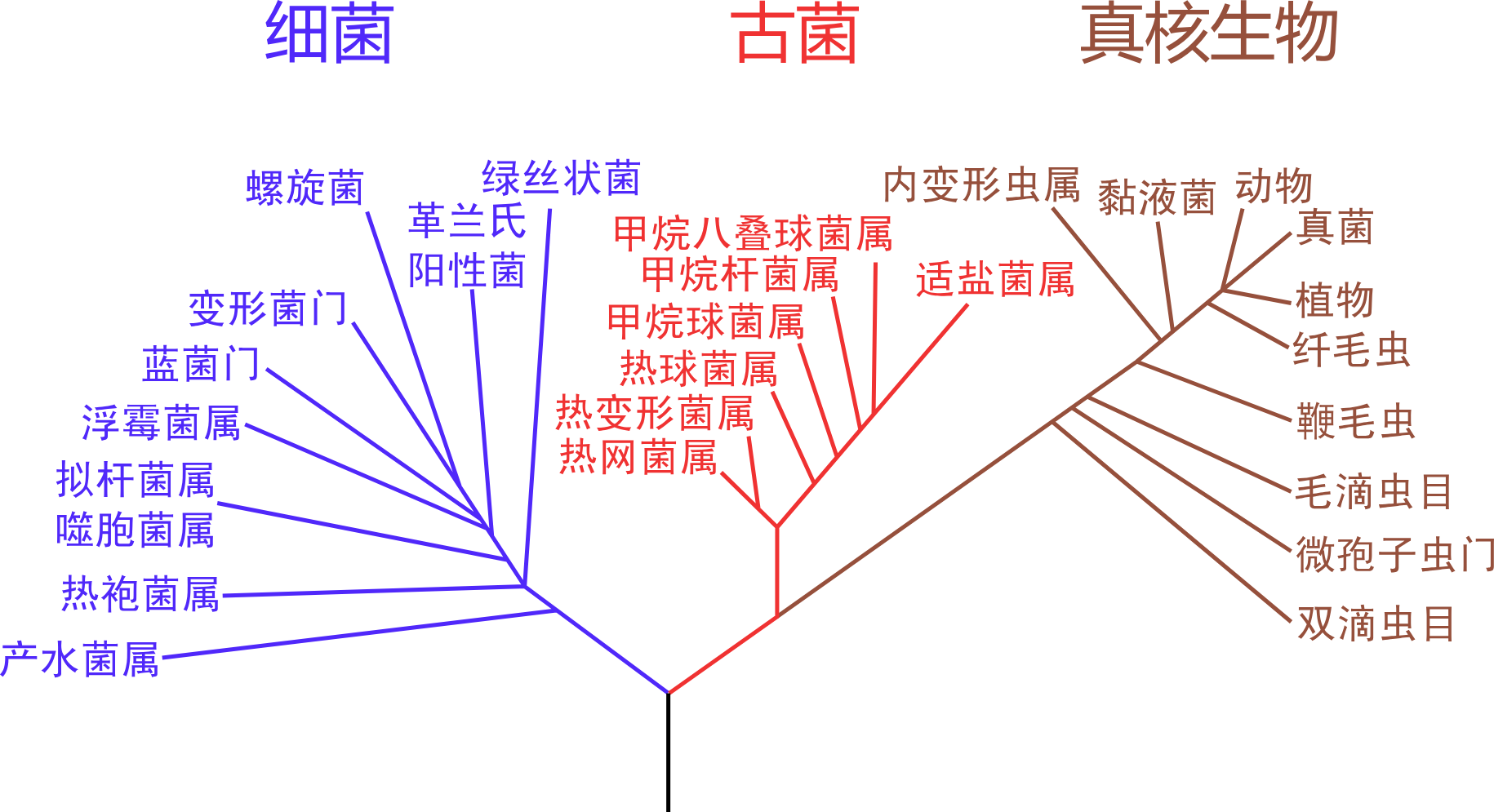
  • 資訊的 LCA
  • 兩點的共同祖先中，深度最低的
  • 深度：離根的距離

What is LCA?

0
1
2
3
4
5

depth = 0

depth = 1

depth = 2

  • 兩點的最短路徑中一定會經過 LCA
    • 拿來求最短路
    • 樹上其他問題

LCA 的用途

  • 最簡單的方式，先預處理每個點的爸爸是誰，然後往上爬爬看

如何求 LCA

0
1
2
3
4
5
  • 最簡單的方式，先預處理每個點的爸爸是誰，然後往上爬爬看

如何求 LCA

0
1
2
3
4
5
  • 最簡單的方式，先預處理每個點的爸爸是誰，然後往上爬爬看

如何求 LCA

0
1
2
3
4
5
  • 最簡單的方式，先預處理每個點的爸爸是誰，然後往上爬爬看
    • 但是深度不一樣時會出事

如何求 LCA

1
2
5
3
4
0
  • 最簡單的方式，先預處理每個點的爸爸是誰，然後往上爬爬看
    • 但是深度不一樣時會出事

如何求 LCA

1
2
5
3
4
0
  • 最簡單的方式，先預處理每個點的爸爸是誰，然後往上爬爬看
    • 但是深度不一樣時會出事

如何求 LCA

1
2
5
3
4
0
  • 最簡單的方式，先預處理每個點的爸爸是誰，然後往上爬爬看
    • 但是深度不一樣時會出事
  • 預處理深度
  • 先爬到相同深度再一起爬
  • 多次查詢時太慢了！

如何求 LCA

  • 你會發現，慢主要慢在爬的部分
    • 想辦法爬快點
    • 跨大步一點啊
  • 如果一次可以前進更多，就可以大幅改進速度！

跨大步點！

  • 假設           的深度相等且            的 LCA 是它們的第 n 代祖先
  • n 可以以二進位表示成 11101 之類的
  • 可以將 n 拆成 10000 + 1000 + 100 + 00 + 1
    • (u, v) 的 16 代祖先的 8 代祖先的 4 代祖先的 1 代祖先
  • 那麼，在每個節點記錄自己的 2 的冪次的祖先
    • 「建祖先表」

二進位

(u, v)
(u, v)
  • 當你看到一格要記錄和 2 的冪次相關的東西時會想到什麼
    • 稀疏表？
  • 不難發現，一個點的     代祖先的     代祖先是         代祖先
  • 可以用建稀疏表的方式建祖先表
    • 令 ancestor[i][v] 是點 v 的     代祖先
    • ancestor[i + 1][v] = ancestor[i][ancestor[i][v]]
  • 根的祖先設為根

建祖先表

2^i
2^i
2^{i+1}
2^i
namespace BinaryLifting {
    vec<vec<int>> ancestors;
    vec<int> depths;

    void dfs(int cur, int pre, int cur_depth, const vec<vec<int>> &tree) {
        depths[cur] = cur_depth;
        ancestors[0][cur] = pre;
        for (const int &nxt : tree[cur])
            if (nxt != pre)
                dfs(nxt, cur, cur_depth + 1, tree);
    }

    void build_ancestor_table(const vec<vec<int>> &tree) {
        depths.resize(tree.size());
        ancestors.resize(std::__lg(tree.size()) + 1);
        for (auto &_list : ancestors) _list.resize(tree.size());
        dfs(0, 0, 0, tree);

        for (int i = 0; i < ancestors.size() - 1; i++)
            for (int u = 0; u < tree.size(); u++)
                ancestors[i + 1][u] = ancestors[i][ancestors[i][u]];
    }
}
  • 現在我們有祖先表了，要怎麼查詢？
    • 對兩個人的 k 代祖先是不是共同祖先二分搜？
    • 二分搜應該會長怎樣？
  • 你會發現當在二分搜時，你是對 k 做二分搜
    • 爬的時候怎麼爬？
      • 把 k 拆成二進位爬？
      • 有必要嗎？

查詢

  • 可以發現其實因為我們把祖先表拆成二進位了，能用這點來做二分搜
  • 二分搜的過程中，區間大小會一直減半
    • 以 i 對應到目前區間大小    ，cur 作為當前點
    • 保持 cur 在 LCA 下面
    • 如果確定向上移動不會違反上點，就向上移動

查詢

0
1
2
3
4
2^i

是共祖

不是共祖

起點

右界

cur

mid

i = 2

  • 可以發現其實因為我們把祖先表拆成二進位了，能用這點來做二分搜
  • 二分搜的過程中，區間大小會一直減半
    • 以 i 對應到目前區間大小    ，cur 作為當前點
    • 保持 cur 在 LCA 下面
    • 按情況縮小區間

查詢

0
1
2
3
4
2^i

是共祖

不是共祖

起點

右界

cur

mid

i = 1

  • 可以發現其實因為我們把祖先表拆成二進位了，能用這點來做二分搜
  • 二分搜的過程中，區間大小會一直減半
    • 以 i 對應到目前區間大小    ，cur 作為當前點
    • 保持 cur 在 LCA 下面
    • 如果確定向上移動不會違反上點，就向上移動

查詢

0
1
2
3
4
2^i

是共祖

不是共祖

起點

右界

cur

mid

i = 1

  • 可以發現其實因為我們把祖先表拆成二進位了，能用這點來做二分搜
  • 二分搜的過程中，區間大小會一直減半
    • 以 i 對應到目前區間大小    ，cur 作為當前點
    • 保持 cur 在 LCA 下面
    • 如果確定向上移動不會違反上點，就向上移動

查詢

0
1
2
3
4
2^i

是共祖

不是共祖

起點

右界

cur

mid

i = 0 break

  • 你會發現從頭到尾沒用到右界
    • 那就別用吧

查詢

0
1
2
3
4

是共祖

不是共祖

起點

右界

cur

i = 0 break

  1. 預處理深度、父親表
  2. 建祖先表
  3. 對於兩點求 LCA
    1. 先爬到相同深度（拆成二進位爬）
    2. 依照剛剛講的方式二分搜
    3. 因為搜出來的結果不是共祖，要再向上移一格

倍增法流程

namespace BinaryLifting {
    int LCA(int u, int v) {
        if (depths[v] > depths[u]) std::swap(u, v);

        for (int diff = depths[u] - depths[v], i = 0; diff; diff >>= 1, i++)
            if (diff & 1)
                u = ancestors[i][u];

        if (u == v) return u;

        for (int i = ancestors.size() - 1; i >= 0; i--)
            if (ancestors[i][u] != ancestors[i][v])
                u = ancestors[i][u], v = ancestors[i][v];

        return ancestors[0][u];
    }
}
  • 我們記錄根到每個點的距離
  • 兩點最短路 = 根到 u + 根到 v - 2 * 根到 LCA(u, v)
    • 倍增法因為會經過兩點間的最短路，所以也可以趁機對路徑做事

樹上兩點最短路

  • 樹壓平
  • 樹鍊剖分
  • Tarjan's LCA

其他 LCA

CF 1843F2

CSES 1687

CSES 1688

CSES 1135

TOI 2021 初選 pD

CSES 1136

CSA Root LCA Queries

TIOJ 2172

思考練習：把RMQ轉化成LCA

併查集

Disjoint Set Union Algorithm, DSU

「我是你今晚的噩夢。」

「參加資讀就別想逃過我的魔爪。」

Tarjan   

– Robert Endre Tarjan,
沒有說過

「不少他發明的算法都以他的名字命名，以至於有時會讓人混淆幾種不同的算法。」

– 維基百科

Dis - 不, Joint - 共同, Set - 集合

"Dis" "joint" "set"

有交集

Dis - 不, Joint - 共同, Set - 集合

"Dis" "joint" "set"

不交集

簡單來說，各集合彼此之間沒有交集

  • 一個資料結構，專門處理這種集合的問題
  • 各集合沒有共同元素
    • 一個元素必定屬於其中一個集合
  • 有哪些性質你希望可以套用在這種資料結構上的？
  • 它應該支援哪些操作？

併查集

  • 一個標準的併查集，應該支援
    • 查詢
      • 查詢一個元素所在的集合，回傳一個集合的代表元素
    • 合併
      • 合併兩個集合
  • 其他可以支援的操作
    • 查詢目前有幾個集合
    • 每個集合有幾個元素

併查集

  • 話是這麼說沒錯，但為什麼不是在資結教？
    • 因為這和圖論關係大啊廢話
  • 如果我們將有邊連在一起的點視在同一個集合
    • 查詢：回傳一個點作為代表元素
    • 合併：加入一條邊
    • 可以查詢兩個點是否連通
      • 連通分量

圖論上

  • 令         為    所在集合的代表元素
  • 我們假設一開始有 n 個集合
  • 每個集合內都只有一個元素，即

實作

1
q(i)
i
q(i) = i
2
0
3
4
  • 令         為    所在集合的代表元素
  • 我們假設一開始有 n 個集合
  • 每個集合內都只有一個元素，即
    • 合併兩集合時要怎麼選擇代表元素？

實作

1
q(i)
i
q(i) = i
2
0
3
4
  • 令         為    所在集合的代表元素
  • 我們假設一開始有 n 個集合
  • 每個集合內都只有一個元素，即
    • 合併兩集合時要怎麼選擇代表元素？
    • 合併兩個點要怎麼選擇代表元素？

實作

1
q(i)
i
q(i) = i
2
0
3
4
  • 令         為    所在集合的代表元素
  • 我們假設一開始有 n 個集合
  • 每個集合內都只有一個元素，即
    • 合併兩個點要怎麼選擇代表元素？
    • 不如令                  ？

實作

1
q(i)
i
q(i) = i
2
0
3
4
q(v) = u
  • 令         為    所在集合的代表元素
  • 我們假設一開始有 n 個集合
  • 每個集合內都只有一個元素，即
    • 合併兩個點要怎麼選擇代表元素？
    • 不如令                  ？

實作

1
q(i)
i
q(i) = i
2
0
3
4
q(v) = u
q(1) = 0
  • 令         為    所在集合的代表元素
  • 我們假設一開始有 n 個集合
  • 每個集合內都只有一個元素，即
    • 合併兩個點要怎麼選擇代表元素？
    • 不如令                  ？

實作

1
q(i)
i
q(i) = i
2
0
3
4
q(v) = u
q(1) = 0
q(2) = 1
  • 令         為    所在集合的代表元素
  • 我們假設一開始有 n 個集合
  • 每個集合內都只有一個元素，即
    • 合併兩個點要怎麼選擇代表元素？
    • 不如令                  ？

實作

1
q(i)
i
q(i) = i
2
0
3
4
q(v) = u
q(1) = 0
q(2) = 1

啊啊爛了，1 和 2 回傳的代表元素不同

  • 令         是    指向它的代表元素的「過程」？
    • 什麼意思？
    • 如果目前的元素還指向其他點，就要繼續追查下去！
    • 這樣代表元素唯一嗎？

修改 q(i) 定義

1
q(i)
i
2
0
3
4
q(1) = 0
q(2) = 1

查詢

struct DSU {
    vector<int> master;
    DSU(int n) {
        master.resize(n);
        for (int i = 0; i < n; i++) master[i] = i;
    }
    int find(int i) {
        if (master[i] == i) return i;
        return find(master[i]);
    }
};
  • 如果有人特別麻煩，弄出了以下的東西：

一些奇怪例外

1
2
0
q(1) = 2
q(2) = 0
q(0) = 1
  • 如果有人特別麻煩，弄出了以下的東西：
  • 你可以照                    的想法走，一律把數字小接往數字大
  • 有必要嗎？
  • 如果在每次合併時就看看兩個點是否在同一集合就沒這問題了
  • 或者，利用源頭合併就沒問題了

一些奇怪例外

CSES 1756

1
2
0
q(1) = 2
q(2) = 0
q(0) = 1
struct DSU {
    void combine(int a, int b) {
        master[find(a)] = find(b);
    }
};

合併

看起來的樣子

0
1
2
4
3
1
3

看起來的樣子

0
1
2
4
3

Merge(2, 3)

1
  • 類似二元搜尋樹，這東西也會退化：
    • 查詢變成           了

問題

0
1
2
3
O(n)
  • 類似二元搜尋樹，這東西因為沒有環所以其實是很多棵樹(森林)
  • 所以如果能修正樹高，搜尋的複雜度就可以降低

修正樹高

0
1
2
3
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 1
q(3) = 2
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 1
q(3) = 2
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 1
q(3) = 2
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 1
q(3) = 2
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 1
q(3) = 2
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 1
q(3) = 2
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 0
q(3) = 2
  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 0
q(3) = 0

查詢完後有效降低樹高了！

  • 最簡單的想法：既然查詢同一條路徑會有同樣的答案，那每次查完就把整條路徑更新成答案

壓縮路徑

0
1
2
3
q(0) = 0
q(1) = 0
q(2) = 0
q(3) = 0

查詢完後有效降低樹高了！

但這樣單次查詢還是 O(n) 耶...

  • 不只看「單次」操作複雜度，而是操作好幾次後平均
    • 聚集法：T(n)/操作次數
    • 記帳法：Credit
    • 位能法：位能函數
  • 一般是考慮最壞情況
  • 併查集使用路徑壓縮後單次操作降為
  • 我不會證明

均攤分析

O(log_{(1+\frac {Q}{|V|})}|V|)
  • 啟發式算法：把奇怪的東西依照經驗用在一起，唬爛一下感覺複雜度不會爛就是了(?
  • 在不需要精確解的情況下，不需要那麼多時間空間的算法
  • 如果你覺得我講了和沒講一樣，恭喜你理解了它的精髓

啟發式合併

  • 我們想要讓樹的高度降低，其實可以從合併時下手
  • 怎麼合併是好的？

啟發式合併

樹高：根到最遠點路徑長

h_1
h_2
  • 我們想要讓樹的高度降低，其實可以從合併時下手
  • 怎麼合併是好的？

啟發式合併

樹高：根到最遠點路徑長

h_1
h_2
  • 我們想要讓樹的高度降低，其實可以從合併時下手
  • 怎麼合併是好的？

啟發式合併

樹高：根到最遠點路徑長

新樹高：

h_1
h_2
max(h_1, h_2 + 1)
  • 我們想要讓樹的高度降低，其實可以從合併時下手
  • 怎麼合併是好的？
  •                                ：讓      比      大，樹高就不會增加
  • 在樹根記錄那棵樹目前的高度
  • 複雜度？

啟發式合併

h_2
max(h_1, h_2 + 1)
h_2
h_1
h_1
  • 假設達到高度     最少要經過          次合併
  •  
  •  
  • 觀察前幾項，0, 1, 3, 7, 15, 31...
  •  
  • 樹高不超過                   ，因此查詢複雜度

複雜度分析

h
f(h)
f(h + 1) = 2f(h) + 1
f(1) = 0
f(h) = 2^h - 1,\ h = log(f(h) + 1) = log\ |V|
\lceil log(|V|) \rceil
O(log\ |V|)
  • 把兩種優化套在一起
  • 時間複雜度？
    •  
    • 我說過了，我不會證明
  • 什麼是
    • 阿克曼函數的反函數
      • 阿克曼函數：                      ，共 x 個 2
      • 反函數：                        ，也就是說，這東西很小

もっと速く

O(\alpha (|V|))
\alpha (|V|)
\Alpha (x) = 2^{2^{2^{...}}}
\alpha (\Alpha(x)) = x
struct DisjointSet {
    vector<int> master, depth;
    DisjointSet(int n) {
        master.resize(n);
        depth.resize(n, 0);
        for (int i = 0; i < n; i++) master[i] = i;
    }
    int find(int n) {
        if (n == master[n]) return n;
        return (master[n] = find(master[n]));
    }
    void combine(int a, int b) {
        a = find(a), b = find(b);
        if (a == b) return;
        if (depth[a] < depth[b]) swap(a, b);
        else if (depth[a] == depth[b]) depth[a]++;
        master[b] = a;
    }
};

綜合

APCS 2023 十月場 P3 / ZJ m372

參考題解

CSES 1676

CSES 2101

CSES 2133

CSES 1706

CF 1770D

BOI '22 D2B

USACO '22 Jan Gold pB

CF 1513D

建中複賽 2021 pA

建中初賽 2022 pC

最小生成樹

Minimum Spanning Tree, MST.

  • 考慮以下問題：
    • 有 n 個地點需要(有線)網路，其中可以連接 m 條可能的邊，每條邊有價格      ，求總價格最小的做法
  • 這個問題有哪些限制？
    • 這個問題的解是原圖的一個子圖，並且點集與原圖相等
    • n 個點都需要被至少一條邊連通
    • 顯然，在正常情況(              )下，它會是一棵樹
  • 解是唯一的嗎？

最小生成子圖

w_i
w_i > 0
  • 環性質
  • 對於圖上任一個環 C 中最大的邊 e 一定不在最小生成樹中
  • 反證法
    • 如果 e 在最小生成樹 T 中，刪除 e 將會使 T 分裂成兩個子樹
    • 必定存在 C 中另一邊 e' 使得兩個子樹連通
    • 兩子樹權重和不變，但 e 被換成更小的 e'
    • 新的生成樹 T' 權重和更小，矛盾

Cycle Property

  • 如果最大權不只一個？
    • MST 不是唯一的，最大權邊一定不在某個 MST 中

Cycle Property

0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
  • 如果在加入邊時，就偵測是否會形成環？
    • 在原圖無環的情況下，加入一條邊最多可能會形成幾個環？
    • 怎麼判斷加入的邊會不會形成環？
      • 利用剛剛學的併查集，看看兩個點是不是原本就連通！
    • 如何尋找環中最大的邊？

Kruskal

  • 我們不如保證加入的邊一定是最大的
    • 怎麼做？
    • 排序！
  • 依照邊權由小到大加入，如果會形成環就不採用這個邊
  • 正確性
    • 保證生成出的圖會是無環的 (樹)
    • 不採用的邊都是保證不在某個 MST 中的
    • 所以保證生成出的是某個 MST

Kruskal

  • 複雜度
    • 對邊排序：
    • 對每個邊使用併查集：
  • 總複雜度：

Kruskal

O(|E|\ log\ |E|)
O(|E|\ \alpha (|V|))
O(|E|\ log\ |E|)
0
1
2
3
4
5
0
1
2
3
4
5
1
0
1
2
3
4
5
1
2
0
1
2
3
4
5
1
2
3
0
1
2
3
4
5
1
2
3
4
0
1
2
3
4
5
1
2
3
4
5
0
1
2
3
4
5
1
2
3
4
5
6
0
1
2
3
4
5
1
2
3
4
5
6
7
0
1
2
3
4
5
1
2
3
4
5
6
7
8
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
namespace MST {
    struct DSU {
        vector<int> master, depth;
        DSU(int n) {
            master.resize(n);
            depth.resize(n, 0);
            for (int i = 0; i < n; i++) master[i] = i;
        }
        int find(int n) {
            return (n == master[n]) ? n : (master[n] = find(master[n]));
        }
        void combine(int a, int b) {
            a = find(a), b = find(b);
            if (a == b) return;
            if (depth[a] < depth[b]) swap(a, b);
            else if (depth[a] == depth[b]) depth[a]++;
            master[b] = a;
        }
    };

    vector<vector<pair<int, int>>> Kruskal(const vector<vector<pair<int, int>>> &graph) {
        DSU components(graph.size());
        vector<pair<int, pair<int, int>>> edges;  // {w, {u, v}}
        vector<vector<pair<int, int>>> result(graph.size());

        for (int u = 0; u < graph.size(); u++)
            for (const auto &[v, w] : graph[u])
                edges.push_back({w, {u, v}});

        sort(edges.begin(), edges.end());

        for (const auto &[w, e] : edges) {
#define u e.first
#define v e.second
            if (components.find(u) != components.find(v)) {
                components.combine(u, v);
                result[u].push_back({v, w}), result[v].push_back({u, w});
            }
        }
#undef u
#undef v
        return result;
    }
}

事實上如果原本圖就用邊串列存會方便很多

如果用鄰接串列存圖建議用下一個寫法

  • 割性質
  • 什麼是割？
    • 點集分為二子點集
  • 割集（也就是跨越兩個點集的邊的集合）中邊權最小的一定在 MST 裡
  • 反證法
    • left as an exercise for the reader

Cut Property

0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
  • 我們可以枚舉一個點集的子集，這樣割集是唯一的
    • 是沒錯，但聽起來就很爛
    • 有沒有什麼改良的方法？
  • 觀察小的割集長怎樣
    • 當其中一個點集 V' 只有一個點？
    • 連出去的最小邊一定沒問題

Prim's Algorithm

0
1
2
3
4
5
1
2
3
4
6
7
8
9
5
  • 接著我們要避免之後的割集考慮到這條邊
    • 那我們將這條邊連到的點加入 V' 吧
  • 這樣我們又有一個新的點集
    • 如此迭代就可以了
  • 要怎麼找割集？
    • 每次迭代都暴力找？
    • 老方法了，有新的邊都記錄下來
    • 每次都要求最小值
      • priority queue

Prim's Algorithm

0
1
2
3
4
5
1
2
3
4
6
7
8
9
5
  • 時間複雜度？
    • 剛剛那樣的實作是
    • 用其他堆可以

Prim's Algorithm

0
1
2
3
4
5
1
2
3
4
6
7
8
9
5
O(|E|\ log\ |E|)
O(|E| + |V|\ log\ |V|)
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
typedef pair<int, int> pii;
typedef pair<int, pii> pipii;
typedef vector<vector<pair<int, int>>> Graph;
Graph Prim(const Graph &graph) {
    // edge: {w, v}
    Graph result(graph.size());
    vector<bool> visited(graph.size(), false);
    priority_queue<pipii, vector<pipii>, greater<pipii>> nexts;
#define w first
#define u second.first
#define v second.second
    visited[0] = true;
    for (const auto &[nxt_w, nxt_v] : graph[0])
        nexts.push({nxt_w, {0, nxt_v}});
    while (!nexts.empty()) {
        auto cur_edge = nexts.top();
        nexts.pop();
        if (visited[cur_edge.v]) continue;
        visited[cur_edge.v] = true;
        result[cur_edge.u].push_back({cur_edge.w, cur_edge.v});
        result[cur_edge.v].push_back({cur_edge.w, cur_edge.u});
        for (const auto &[nxt_w, nxt_v] : graph[cur_edge.v])
            nexts.push({nxt_w, {cur_edge.v, nxt_v}});
    }
#undef u
#undef v
#undef w
    return result;
}

CSES 1675

TIOJ 1445 (次小生成樹)

TIOJ 1163

建中初賽 2020 pD

CF 160D (全部學完再回來看)

CF 891C

CF 609E

USACO '22 Feb Gold pC

連通性

Connectivity.

  • 剛剛用最小生成樹架出來的網路只要一條線斷了就沒了喔
  • 或者，只要一個點爛掉就什麼都沒了
  • 耐受性 / 連通強度？
    • 如果損失幾個據點，其他點仍能連通
    • 損失幾條邊，所有點仍能連通

繼續架網路

  • 剛剛用最小生成樹架出來的網路只要一條線斷了就沒了喔
  • 或者，只要一個點爛掉就什麼都沒了
  • 耐受性 / 連通強度？
    • 如果損失幾個據點，其他點仍能連通
      • 點連通度
    • 損失幾條邊，所有點仍能連通
      • 邊連通度

繼續架網路

  • 一般情況下，我們希望連通度 
  • 但某些情況下連通度 = 1
  • 每個點 / 邊被拔掉都會使此圖不連通嗎？
  • 我們希望有演算法能找出這些弱點

找出弱點

\geq 2
  • 割
    • 沿用前面的定義，將一個點集分割成多個不連通的子集
  • 割點：點使點集分割成多個不連通的子集
  • 又稱關節點
  • 如何求所有的割點？

割點 Cut Vertex

「我是你今晚的噩夢。」

「參加資讀就別想逃過我的魔爪。」

Tarjan   

– Robert Endre Tarjan,
沒有說過

「不少他發明的算法都以他的名字命名，以至於有時會讓人混淆幾種不同的算法。」

– 維基百科

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？

DFS Tree

  • 首先介紹一個討論連通度時強大的工具 - DFS Tree
  • 什麼是 DFS Tree？
  • 看出來了嗎？
  • DFS 的軌跡不會經過相同的點，無環是樹

為邊做分類

樹邊：DFS Tree 中的邊

返祖邊：剩下不是樹邊的邊

觀察性質

  • 看完邊後來看點和邊的關係
  • 割點在哪裡？

觀察性質

  • 看完邊後來看點和邊的關係
  • 割點在哪裡？

觀察性質

  • 思考「被拔除後會變成多個不連通塊」的性質
  • 不連通代表不能從一邊走到令一邊
  • 子樹只能透過它的根走到另一邊
    • 什麼情況下不會發生？
    • 返祖邊！
  • 如何尋找返祖邊？
  • 思考 DFS 的過程
    • 如果戳到的是新的點，一定是樹邊
    • 如果戳到的是重複的點，一定是返祖邊
  • 要怎麼利用返祖邊？

返祖邊

  • 什麼情況下返祖邊能發揮作用？
  • 只要子樹中的所有點都能走到圖的另一個部分，這個點就不是割點，否則它是割點

返祖邊

因為左邊沒有邊能不經過紅點到達右邊，所以它是割點

因為左右邊所有點都能不經過紅點到達彼此，所以它不是割點

以紅點為根的子樹中，左邊一定要經過紅點到達其他部分

所以紅點是割點

以紅點為根的子樹中所有點都可以不經由紅點連到其他部分，所以它不是割點

  • 如何利用以上性質？
  • 暴力？
    • 對於子樹中的每個點都確認一次是否連通？
    • 想太多，單點複雜度就
  • 我們可以考慮 樹 DP 記錄一些事情

實作

O(|V|^2+|V||E|)
  • 一條返祖邊可能會改變哪些點是割點的性質？
    • 較高者/深度較淺者到另一者間的點

再次觀察

  • 這些點在 DFS  Tree 上有什麼特性？
    • 出點一定在出較低點後，入點一定在較低點前
    • 換句話說，我們一定能在遞迴返回的時候更新到它們

再次觀察

  • 所以，有必要急著更新嗎？
  • 我們不如把子樹處理完再處理較高的點吧
  • 現在滿足怎樣的情況這點會變得不是割點？
    • 子樹能連到比自己時間戳還小的點
    • 那我們記錄子樹時間戳最小能連到哪吧
  • 子樹處理完後怎麼轉移回子樹的根節點
    • 對於根節點來說，從分支挑一個最小的就行了
    • 注意不能用親代的樹邊更新

Tarjan 割點算法

  • 剛剛講得好像很有道理，但有一個例外
    • 根節點
    • 這個點是我們選定的，所以好像很正常？
    • 怎麼判斷？再做一次 DFS 嗎？

例外

  • 不是割點的情況：所有分支都相連？
    • 在 DFS 的過程中，回到根時所有點都已經被拜訪過一次了
    • 所以它只會往下一次 / 只有一個子節點

Case: root

你會發現，你的 DFS 樹應該長這樣

而非這樣

  • DFS，對每點記錄 DFS 序 (dfn)
    • 對於每個子樹，記錄它能走到的最小 dfn (low)
      • 對於每條邊，更新自己的 low
    • 使用每個分支的答案更新自己的答案
  • 特判根節點的子節點數
  • 對於每個點 u，如果 low(u) < dfn(u)，則它不是割點
  • 複雜度同 DFS，

總結過程

O(|V|+|E|)
using Graph = vector<vector<int>>;

vector<bool> cut_vertex(const Graph &graph) {
    int n = graph.size();
    vector<int> dfn(n, 0), low(n, 0);
    vector<bool> result(n, false);
    int time = 0;

    auto dfs = [&](int cur, int pre, auto &&dfs) -> void {
        dfn[cur] = low[cur] = ++time;
        for (const int &nxt : graph[cur]) {
            if (nxt == pre) continue;

            if (dfn[nxt]) {
                low[cur] = min(low[cur], dfn[nxt]);
            }
            else {
                dfs(nxt, cur, dfs);
                if (low[nxt] > dfn[cur]) result[cur] = true;
                low[cur] = min(low[cur], dfn[nxt]);
            }
        }
    };

    int child_count = 0;
    for (const auto &child : graph[0]) {
        if (dfn[child]) continue;
        child_count++;
        dfs(child, 0, dfs);
    }
    if (child_count > 1) result[0] = true;

    return result;
}
  • 剛剛討論完被拔掉點會不連通的割點，現在我們想要被拔掉會不連通的邊
  • 這種邊我們叫橋
  • 聽起來就很像割點，有關係嗎？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？

Edge

  • 看不出來？
  • 弄成 DFST 的樣子？
  • 　　：割點、割邊
  • 　　：其他點、樹邊
  • 　　：返祖邊

Edge

  • 你會發現，它和割點具有的性質簡直一模一樣
  • 對，所以基本上照抄割點的就行了，還不用特判根節點
  • 一個小地方要改掉：low(u) > dfn(u) 才能保證它是橋，其中 u 是起點
  • 一樣注意在更新 low 的時候不能用它的親代更新

相似？

void bridge(int cur, int pre, const vector<vector<int>> &graph, vector<pair<int, int>> &result, vector<int> &dfn, vector<int> &low) {
    static int cur_dfn = 0;
    dfn[cur] = ++cur_dfn;
    low[cur] = dfn[cur];
    for (const auto &nxt : graph[cur]) {
        if (nxt == pre) continue;
        if (!dfn[nxt]) {
            bridge(nxt, cur, graph, result, dfn, low);
            low[cur] = min(low[cur], low[nxt]);
            if (low[nxt] > dfn[cur]) result.push_back({cur, nxt});
        }
        else {
            low[cur] = min(low[cur], dfn[nxt]);
        }
    }
}

如果不是簡單圖記得處理重邊

CSES 2076 (橋)

CSES 2077 (割點)

CSES 2177

TIOJ 1137

連通分量

Components.

  • Bridge Connected Components

小目錄

  • BiConnected Components / Block-Cut Tree
  • Strongly Connected Components
  • Weakly Connected Components
  • 一張圖可以互相連在一起的部分就叫連通分量
  • 如果不能再向外連更多點，稱為極大連通分量，一般都討論極大連通分量
  • 某些定義在有向圖上可能需要調整或有多種定義，所以先記得它是圖的某部分就行

連通分量

  • 就是一般的連通分量，用前面教的 DSU 就做完了，沒要求加邊也可以用 DFS

單連通分量

「我是你今晚的噩夢。」

「參加資讀就別想逃過我的魔爪。」

Tarjan   

– Robert Endre Tarjan,
沒有說過

「不少他發明的算法都以他的名字命名，以至於有時會讓人混淆幾種不同的算法。」

– 維基百科

  • Bridge Connected Components, BCC
  • 記得前面講的連通度嗎？
    • 連通度 > 1 時網路可抗破壞！
  • 我們不如把這些拔掉任一點都還是連通的子區域劃分在同一個連通分量！
  • 怎麼找？
    • 找到橋後將所有東西分開
    • 把連通分量的點們「縮起來」

邊雙連通分量

  • 這簡單，把橋標記起來之後，對每個點做一次 DFS
  • 遇到橋就不要走，剩下在同一次 DFS 戳到的點就把它標記在同一個連通分量裡

怎麼做

  • 你會發現縮完之後是沒有環的
    • 如果有環，上面任一邊都不是橋，表示一定會被縮在一起
  • 很多時候我們不喜歡環。如果把這張圖變成一棵樹 /森林就會好處理很多

用途？

  • BiConnected Components, BCC
  • 對，又是 BCC
  • 你知道該請出誰了吧

點雙連通分量

「我是你今晚的噩夢。」

「參加資讀就別想逃過我的魔爪。」

Tarjan   

– Robert Endre Tarjan,
沒有說過

「不少他發明的算法都以他的名字命名，以至於有時會讓人混淆幾種不同的算法。」

– 維基百科

  • 和剛剛邊雙連通分量很像，拔掉分量內的任一點都保持連通
  • 我們這次好像不能像邊雙連通分量一樣標記然後不走了欸
    • 為什麼？
    • 看圖
    • 這要怎麼縮？

點雙連通分量

0
1
2
3
4
  • 和剛剛邊雙連通分量很像，拔掉分量內的任一點都保持連通
  • 我們這次好像不能像邊雙連通分量一樣標記然後不走了欸
    • 為什麼？
    • 看圖
    • 這要怎麼縮？

點雙連通分量

2
234
012

「等等，那個 2 剛剛是不是出現了三次」

  • 是，又是一個學長不講的東西了
  • 簡單來說，既然依定義縮起來很麻煩，那就別縮
  • 不如我們把在同一個連通分量的點指向一個新節點，以後要操作都對新節點操作
  • 忽略原圖的邊
    • 圓點：原本圖上的點
    • 方點：代表一個點雙連通分量的點

圓方樹

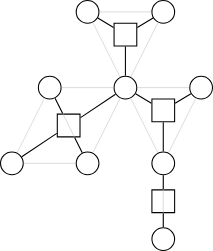
  • 首先它一定是一棵樹
  • 點數小於 2n，自己證，這很顯然
  • 如果原圖不連通，那新的圓方樹會是森林
  • 一個方點接到的圓點實際上就是一個 BCC

圓方樹的性質

  • 套用 Tarjan 割點算法再魔改下
  • 這裡把 low 的定義改成可以用連向親代的樹邊更新一次
  • 當 low[nxt] == dfn[cur] 時代表找到割點
    • 找到割點時，相關的 BCC 點應該在哪？
      • 在剛剛你經過的 DFS 路徑裡啊！
  • 我們用一個 Stack 維護 DFS 的路徑，如果找到一個割點就把還沒用過的、在割點底下的點縮進去
    • 割點以外的點只存在於一個 BCC
    • 割點不能被視為「用過」，因為它可能存在兩個內

建樹

←當你到這裡時，會發現 low[nxt] = dfn[cur]

cur

nxt

cur

nxt

這是剛剛經過的子樹

cur

nxt

將它連起來

cur

nxt

接著是來到這裡

cur

nxt

這是我們 BCC 還沒用過的點 / stack 還剩下的範圍

cur

nxt

建方點，連起來

cur

nxt

還有一個

cur

nxt

還有一個

完成圓方樹

vector<vector<int>> block_cut_tree(const vector<vector<int>> &graph) {
    int dfs_clock = 0;
    stack<int> path;
    vector<vector<int>> result;
    result.reserve(graph.size() * 2);
    vector<int> dfn(graph.size(), 0);
    vector<int> low(graph.size(), INF);

    auto dfs = [&](int cur, auto &&dfs) -> void {
        low[cur] = dfn[cur] = ++dfs_clock;
        path.push(cur);
        for (const auto &nxt : graph[cur]) {
            if (!dfn[nxt]) {
                dfs(nxt, dfs);
                low[cur] = min(low[cur], dfn[nxt]);
                if (low[nxt] == dfn[cur]) {	 // find cut vertex / BCC
                    result.push_back(vector<int>(0));
                    int square = result.size() - 1;
                    for(int v = -1; v != nxt; path.pop()) {
                        v = path.top();
                        result[v].push_back(square);
                        result[square].push_back(v);
                    }
                    result[square].push_back(cur);
                    result[cur].push_back(square);
                }
            }
            else {
                low[cur] = min(low[cur], dfn[nxt]);
            }
        }
    };

    dfs(0, dfs);
    return result;
}

其實邊雙連通也可以用 stack 喔

  • 這兩種方式都叫 BCC 都在縮點變樹，差別在哪
  • 邊雙連通分量是以「邊」為主體
  • 點雙連通分量是以「點」為主體
  • 具體來說，看題目想要你怎麼區分

差別

  • 終於要來講有向圖了
  • 前面提到圖有強連通、弱連通
  • 同理，有向圖也有強連通分量、弱連通分量
    • 強連通分量 (SCC)：對連通分量內每個 (u, v)，u 可以走到 v、v 也可以走到 u
    • 弱連通分量 (WCC)：對連通分量內每個 (u, v)，至少滿足 u 可以走到 v 或 v 可以走到 u
  • 注意弱連通分量的定義和弱連通圖不同

有向圖上的 CC

  • 不過有向圖反而有比較簡單的演算法(蛤
  • 我們可以不要再 Tarjan 了嗎
    • 不行。
    • 經過剛剛一番折磨，你應該知道為什麼這個演算法能被稱做「Tarjan 演算法」，它能應用的情況太多了

有向圖上

  • Strongly Connected Components
  • 裡面實際上就是一堆有向環
  • 引用拓撲排序說的：「這樣會沒辦法好好轉移」
  • 把環縮起來就沒事了
  • 縮起來後就是 DAG，你想拓撲排序或幹嘛都行

SCC

  • Strongly Connected Components
  • 裡面實際上就是一堆有向環
  • 引用拓撲排序說的：「這樣會沒辦法好好轉移」
  • 把環縮起來就沒事了
  • 縮起來後就是 DAG，你想拓撲排序或幹嘛都行

SCC

「我是你今晚的噩夢。」

「參加資讀就別想逃過我的魔爪。」

Tarjan   

– Robert Endre Tarjan,
沒有說過

「這傢伙讓我做簡報做到腦中風。」

– 海之音

  • 你會天真地以為 Tarjan 的那棵 DFS Tree 只能用在無向圖上嗎
  • 顯然否吧 他可是 Tarjan 欸
  • 所以在有向圖上會發生什麼事

拓展 DFS Tree

  • 在有向圖的情況下，會有新種類的邊產生
  • 樹邊 (tree edge)：戳到新點的邊
  • 返祖邊 (back edge)：從子孫連回祖先
  • 前向邊 (foward edge)：從祖先連向非兒子的子孫
  • 交錯邊 (cross edge)：連向非祖先、已經經過的點

更多分類

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

跑看看

返祖邊

樹邊

前向邊

交錯邊

樹 0 節點

樹 1 節點

樹 2 節點

  • 現在有更多邊的類型了，怎麼辦
  • 多判斷啊，不然你想幹嘛
  • 繼續引用前面割點 + stack 的想法
    • 如果沒戳過就繼續 DFS
    • 回點時看割點把 Stack 裡面的東西縮成 SCC
    • 不同的是，這次要把原本的點 pop 掉，因為 SCC 不會有重複
  • 如果把四種邊判斷完了就做完了

Tarjan's SCC

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

  • 遇到前向邊時會發生什麼？

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

  • 怎麼處理前向邊？
    • 不用處理啊
    • 如果今天底下還有一個子樹，那它因為已經被樹邊戳過了，沒差
    • 正常轉移就好了

前向邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

  • 返祖邊和交錯邊都是戳到時間戳較小的點
  • 但你會發現返祖邊可以縮點，但是交錯邊不見得能
  • 所以我們可能要判斷
    1. 這條邊是否是交錯邊
    2. 這條邊是否可以拿來被縮點

返祖邊 Vs. 交錯邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

  • 交錯邊具有什麼性質？
  • 可以對於指向的情況討論

判斷交錯邊

樹邊

樹 0 節點

返祖

前向

交錯

樹 1 節點

樹 2 節點

樹邊

子樹 0

返祖

前向

交錯

子樹 1

子樹 2

超級源點

Case 1: 指到的已經被分派 SCC

已經找到對應「割點」

樹邊

返祖

前向

交錯

分支 0

分支 1

子樹根

Case 2: 指到的還沒被分派 SCC

但之後會縮點

Case 3: 指到的還沒被分派 SCC

且之後不會縮點

  • Case 1: 指到的點已經被分派 SCC
    • 已經找到對應的分割點了，表示指到的點過不來，無法構成強連通分量
    • 對於 Case 1，保證是交錯邊
    • 並且，對於這種情況，不能用交錯邊更新

情況的分別

  • Case 2: 指到後會縮點
    • 對於這種情況，就算是交錯邊，用那條交錯邊更新也沒有差別，反正都會縮
  • Case 3: 指到後不會縮點
    • 真的有這種情況嗎？
    • 你想想，不會縮點表示下面一定是分割點嘛
    • 所以它已經被指派 SCC 了

情況的分別

  • 你仔細看就會發現我有要唬爛你的意思(

所以...交錯邊？

  • 所以我們對於交錯邊的結論是：如果指到的被分派 SCC 那就別用它更新
  • 否則使用它更新自己的 low 值
  • 記錄已分派 SCC 本身其實可以用 SCC 的編號來記錄，一舉兩得
    • 當找到新的 SCC 時，++scc_id, scc[...] = scc_id;
    • 否則 scc[i] 應設為 0

結論

  • DFS, 記錄每點的 dfn, low
    • 把自己加入 stack
    • 對於每個 u 附近的點 v
      • 如果 v 已經被分派 scc，continue
      • 如果 v 還沒被拜訪過，dfs(v)，更新自己的 low
      • 如果 v 被拜訪過，更新自己的 low
    • 判斷是否 dfn[u] = low[u]，是的話把目前 stack 在 u 以下的東西縮進 SCC，記錄編號

整體過程

vector<int> tarjan_SCC(const vector<vector<int>> &graph) {
    vector<int> scc(graph.size(), 0);
    vector<int> dfn(graph.size(), 0);
    vector<int> low(graph.size(), INF);
    stack<int> path;
    int dfs_clock = 0;
    int scc_id = 0;

    auto dfs = [&](int cur, auto &&dfs) -> void {
        low[cur] = dfn[cur] = ++dfs_clock;
        path.push(cur);

        for (const auto &nxt : graph[cur]) {
            if (scc[nxt]) continue;

            if (!dfn[nxt]) dfs(nxt, dfs), low[cur] = min(low[cur], low[nxt]);
            else low[cur] = min(low[cur], dfn[nxt]);
        }

        if (dfn[cur] == low[cur]) {
            ++scc_id;
            for (int v = -1; v != cur; path.pop()) {
                v = path.top();
                scc[v] = scc_id;
            }
        }
    };

    for (int v = 0; v < graph.size(); v++)
        if (!dfn[v]) dfs(v, dfs);

    return scc;
}
  • 另一個連通分量超人
  • 我的超人
  • 他想出了一個超好寫 SCC 的方法
    • 太神奇了，他不是 Tarjan 欸
    • 但這個方法常數比較大
    • 但他不是 Tarjan 欸
    • 他並沒有以此發表論文
    • 但他不是 Tarjan 欸

Kosaraju

  • 這個算法的核心在「反圖」
  • 點相同，所有邊相反的圖
  • 反圖具有什麼性質？
  • SCC 在反圖下具有什麼性質？

反圖

  • 這個算法的核心在「反圖」
  • 點相同，所有邊相反的圖
  • 反圖具有什麼性質？
  • SCC 在反圖下具有什麼性質？

反圖

  • SCC 在反圖下具有什麼性質？
    • SCC 在反圖下是點相同的
    • 因為在原圖 u 可以走到 v，v 可以走到 u，反圖上反過來 v 可以走到 u，u 可以走到 v

反圖

  • 在原圖上 DFS 如果有 u → v
  • 在反圖上只要確認 u → v
  • 這樣代表原圖上的 u → v，v -> u 都確認過了
  • 這聽起來感覺有一點像拓撲排序，拓撲排序在有向環有什麼性質？

怎麼利用？

  • 先把 SCC 當成一個群體來看
  • 拓撲排序出來會依照群體排序，原先輩分較大會被排在前面，輩分小的不能往輩分大的走
  • 今天反向圖會讓輩分順序反過來，會讓原先輩分大的不能走向輩分小的
  • 這時，我們將由反向後輩分小點的開始搜尋，可以發現走不到其他群體
  • 所以，這樣我們可以確定群體範圍

感性理解

原先 A > B > C

A 可以單向走到 B，B 可以單向走到 C

A

B

C

原先 A > B > C

反向後 A 走不到 B，B 走不到 C

這時如果在 A 裡面不管怎麼走都不會走到 B

B 可能會走到 A，但走不到 C

在走 B 前確認完 A 有哪些人，不要碰

A

B

C

  • 對原圖每點 DFS，確定拓撲排序 (時間戳)
  • 對反圖依照原拓撲排序大到小每點 DFS，點用過就「封鎖」，標記 visited
  • 就這樣，超好理解

算法流程

vector<int> KosarajuSCC(const vector<vector<int>> &graph) {
    vector<vector<int>> hparg(graph.size());
    for (int u = 0; u < graph.size(); u++)
        for (const auto &v : graph[u])
            hparg[v].push_back(u);

    vector<int> sort_result;
    sort_result.reserve(graph.size());
    vector<bool> visited(graph.size(), false);

    auto dfs = [&](int cur, auto &&dfs) -> void {
        visited[cur] = true;
        for (const auto &nxt : graph[cur])
            if (!visited[nxt]) dfs(nxt, dfs);
        sort_result.push_back(cur);
    };
    for (int v = 0; v < graph.size(); v++)
        if (!visited[v]) dfs(v, dfs);

    vector<int> scc(graph.size(), 0);
    int scc_id = 0;
    auto sfd = [&](int cur, auto &&sfd) -> void {
        scc[cur] = scc_id;
        for (const auto &nxt : hparg[cur])
            if (!scc[nxt]) sfd(nxt, sfd);
    };
    for (auto v_pt = scc.rbegin(); v_pt != scc.rend(); v_pt++)
        if (!scc[*v_pt]) ++scc_id, sfd(*v_pt, sfd);
}

會這麼長是因為建反圖等等的都在裡面

實際上算法本體不到 20 行

重點是他不是 Tarjan ，他很直觀

  • 我ly Weakly Connected Components, WCC
  • 老實說，這東西感覺不常用到，所以網路上資料也很少，我只講我會的做法
  • 對於任兩點至少存在一條單向路徑
  • 這和弱連通圖的定義有什麼不一樣？

弱連通分量

同色代表同個弱連通分量

  • 又來了，同一個點會出現在多個連通分量裡
  • 我們至少可以得出在同一個 SCC 裡面的點一定在同個 WCC 裡面
  • 既然如此，就先縮成 SCC
  • 縮出一棵樹之後怎麼辦？

又是一個難縮點...

  • 只要求單向連通，那它相當於是在剛剛縮出的樹上找一條存在的路徑
  • 只要找到每條最長路徑就找完了，對每棵樹做 DFS，用 stack 維護路徑內的點
  • 把路徑上的點都指向類似圓方樹的方點之類的
  • 但是！

路徑

  • 你會發現要處理的點會太多。
  • 光下面這張圖你就要處理 5*3 = 15 次點了喔
  • 也許可以用一些奇奇怪怪的方法維護 (樹鍊剖分 + 支援範圍修改的資結)
  • 通常題目不會需要用到...吧

太多了啊...

  • 一般來說，題目只會問點對是否在同個弱連通分量裡之類的
  • 因為圖有向，所以先定樹根 (找入度為 0 的點)
  • 我們可以搭配 LCA 之類的演算法確定一點是否是另一點的祖先，這樣就能確定是否在同條路徑上

因應要求

  • 看題目要求。(被扁)
  • 主要想法就是先把 SCC 做出來後找到樹根，之後看你想幹嘛再幹嘛

結論

TIOJ 1929

TIOJ 1868

TIOJ 1451

TIOJ 1149

TIOJ 1683

TIOJ 1744

NEOJ 179

NEOJ 737

NEOJ 738

NEOJ 739

TIOJ 2319 / 建中 2023 校內賽複試 PA

圖的特殊分類

Other Classes.

  • 之後會有一堂專門講二分圖的，這裡只講概念
  • 探討兩個獨立群體之間的關係
    • 男女關係
    • 勞資關係
    • ...
  • 同一個群組間不連邊

二分圖

  • 某次北市賽後出現的名詞，指只出現一個環的連通圖
  • 一個環旁邊都是樹
  • 邊數 = 點數
  • 拔一條環上的邊變樹
  • 繞環上一圈 DFS 之類的

水母圖

  • 一條邊最多只屬於一個環
  • 兩個環最多只有一個共點
  • 邊數 = 點數 + 環數 - 1
  • 通常用圓方樹解決

仙人掌圖

應用問題

System of Difference Constraints, 2-SAT

  • 說到底，圖論還是基於數學上發展出來的
  • 所以我們要拿圖來解決一些數學問題
    • 差分約束系統, System of Difference Constraints

數學

  • 我們有一堆變數
  • 以及一堆形如                           的不等式
  • 求符合條件的一組解

差分約束系統

x_1, x_2, x_3...
x_i - x_j \leq c_k
x_1, x_2, x_3...
x_{2}-x_{5}\leq 1 \\ x_{1}-x_{2}\leq 0 \\ x_{1}-x_{5}\leq -1 \\ x_{3}-x_{1}\leq 5 \\ x_{4}-x_{1}\leq 4 \\ x_{4}-x_{3}\leq -1 \\ x_{5}-x_{3}\leq -3 \\ x_{5}-x_{4}\leq -3
(x_1, x_2, x_3, x_4, x_5) = (0, 2, 5, 4, 1)
  • 你會發現                        移項過後                        長得很像鬆弛的式子
  • 事實上，我們在做的事剛好也是把     「縮」到不等式的範圍內
  • 所以，最短路算法又出現了
    • 令超級源點 O ，每個變量當做一個點
    • 對於每條不等式，連一條有向邊
    • 依照邊權正負決定要用什麼最短路
    • 對 O 跑完最短路後最短距就是一組解

鬆弛

x_i - x_j \leq c_k
x_i \leq x_j + c_k
d_u \leq d_v + w_{vu}
x_i
(x_j, x_i), w_{ji} = c_k

題目應該在最短路有混一點(

  • 資訊科學裡的經典問題：滿足性問題
  • 對於每個布林值                            以及它的反面                                 我們有一條式子必須滿足
  • 形式如
  • 其中 
  • 這樣的問題被稱為 k-SAT

k-SAT

x_1, x_2, x_3...x_n
\lnot x_1, \lnot x_2... \lnot x_n
(b_{11}\lor b_{12}...b_{1k}) \land (b_{21}\lor b_{22}...\lor b_{2k})... = true
b_i \in \{X, \lnot X\}
  • 讓我們從最簡單的情況看起
  • 它長成
  • 把所有變數設成 true就好了吧
  • 還要檢查 x 和 ~x 是否同時存在
    • 就這樣？
    • 對，沒了，就這樣
  • 蛤

k = 1

b_1 \land b_2 \land b_3... = true
  • 現在問題變複雜了
  • 它長成
  • 瞬間就變成不會解的樣子了

k = 2

(b_{11}\lor b_{12}) \land (b_{21}\lor b_{22})... = true
  • 如果                            且
    •                  才能滿足
    • 這就是一組約束條件
    • 想辦法轉化成圖論
  • 這時，因為「為了滿足                     必須有                」我們可以建一條邊
  • 同理為了滿足                    必須有                 ，建邊

觀察

(a\lor b) = true
b = true
\lnot a = true
\lnot a = true
b = true
\lnot a \rightarrow b
\lnot b = true
a = true
\lnot b \rightarrow a
a
b
\lnot a
\lnot b
(a\lor b)
(a\lor b) \land (c \lor d)
c
d
\lnot c
\lnot d
a
b
\lnot a
\lnot b
(a\lor b) \land (c \lor d) \land (b \lor \lnot c)
c
d
\lnot c
\lnot d
a
b
\lnot a
\lnot b
  • 什麼情況下無解
    • 矛盾的時候
    • 最直接的矛盾是什麼？
  •               聽起來非常顯然
  • 也就是說，當                 可行時無解
    • 雙向連通？
    • SCC

無解

a = \lnot a
a \leftrightarrow \lnot a
  • 撇除掉無解的情況，如果有解，要怎麼構造它？
  • 就...拓撲排序啊

構造解

題單待補

Thanks for your Listening！

有人要猜猜看總簡報頁數嗎

Made with Slides.com