[Imperial XAI Seminar] SHAP-XRT

SHAP-XRT

The Shapley Value Meets

Conditional Independence Testing

Beepul Bharti, Jacopo Teneggi, Yaniv Romano, Jeremias Sulam

Explainable AI Seminars @ Imperial

5/30/2024

Reproducibility
Practical Accuracy
Explainability
Fairness
Privacy

[M. E. Kaminski, 2019]

E.U.: “right to an explanation” of decisions made

on individuals by algorithms

F.D.A.: “interpretability of the model outputs”

Responsible ML

Explanations in ML

{f}\huge(

{f}\huge(

{\huge)} = \text{\texttt{sick}}

{\huge)} = \text{\texttt{sick}}

What parts of the image are important for this prediction?

What are the subsets of the input so that

{f}(x_S) \approx {f}(x) ?

{f}(x_S) \approx {f}(x) ?

S \subseteq [n]

S \subseteq [n]

Explanations in ML

Sensitivity or Gradient-based perturbations
Shapley coefficients
Variational formulations
Counterfactual & causal explanations

LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]

Shap [Lundberg & Lee, '17], ...

RDE [Macdonald et al, '19], ...

[Sani et al, 2020] [Singla et al '19],..

Shapley values

efficiency
nullity
symmetry

exponential complexity

Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.

Let be an - person cooperative game with characteristic function

G = ([n],f)

G = ([n],f)

n

n

f : \mathcal P([n]) \mapsto \mathbb R

f : \mathcal P([n]) \mapsto \mathbb R

How important is each player for the outcome of the game?

\displaystyle \phi_i = \sum_{S\subseteq [n]\setminus \{i\} } w_{S} \left[ f(S\cup \{i\}) - f(S) \right]

\displaystyle \phi_i = \sum_{S\subseteq [n]\setminus \{i\} } w_{S} \left[ f(S\cup \{i\}) - f(S) \right]

marginal contribution of player i with coalition S

Shap-Explanations

f(X) \approx \mathbb E[Y|X]

f(X) \approx \mathbb E[Y|X]

X \in \mathcal X \subset \mathbb R^n

X \in \mathcal X \subset \mathbb R^n

Y\in \mathcal Y = \{0,1\}

Y\in \mathcal Y = \{0,1\}

inputs

responses

f:\mathcal X \to \mathcal Y

f:\mathcal X \to \mathcal Y

\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline \text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}

\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline \text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}

predictor

x_S

x_S

x:

x:

x_{S^c}

x_{S^c}

\tilde{X}_S:

\tilde{X}_S:

Shap-Explanations

f(X) \approx \mathbb E[Y|X]

f(X) \approx \mathbb E[Y|X]

X \in \mathcal X \subset \mathbb R^n

X \in \mathcal X \subset \mathbb R^n

Y\in \mathcal Y = \{0,1\}

Y\in \mathcal Y = \{0,1\}

inputs

responses

f:\mathcal X \to \mathcal Y

f:\mathcal X \to \mathcal Y

\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline \text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}

\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline \text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}

predictor

x_S

x_S

x

x

\tilde{X}_S

\tilde{X}_S

Shap-Explanations

f(X) \approx \mathbb E[Y|X]

f(X) \approx \mathbb E[Y|X]

X \in \mathcal X \subset \mathbb R^n

X \in \mathcal X \subset \mathbb R^n

Y\in \mathcal Y = \{0,1\}

Y\in \mathcal Y = \{0,1\}

inputs

responses

f:\mathcal X \to \mathcal Y

f:\mathcal X \to \mathcal Y

\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline \text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}

\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline \text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}

predictor

\displaystyle \phi_i = \sum_{S\subseteq [n]\setminus \{i\}} w_S ~ \mathbb E \left[ f(\tilde X_{S\cup \{i\}}) - f(\tilde X_{S}) \right]

\displaystyle \phi_i = \sum_{S\subseteq [n]\setminus \{i\}} w_S ~ \mathbb E \left[ f(\tilde X_{S\cup \{i\}}) - f(\tilde X_{S}) \right]

What does it mean for a feature to receive a high Shapley Value?

Precise Notions of Importance

Formal Feature Importance

H_{0,i}:~ X_S \perp\!\!\!\perp Y | X_{[n]\setminus S}

H_{0,i}:~ X_S \perp\!\!\!\perp Y | X_{[n]\setminus S}

[Candes et al, 2018]

Do the features in $S$ contain any additional information about the label $Y$ that is not in the complement ${[n]\setminus S}$ ?

Precise Notions of Importance

Local Feature Importance

XRT: eXplanation Randomization Test

returns a valid p-value, $\hat{p}_{i,S}$ for the test above

\text{reject} ~\Rightarrow~ i=2 \text{: important}

\text{reject} ~\Rightarrow~ i=2 \text{: important}

\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal{D}_x

\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal{D}_x

H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})

H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})

Precise Notions of Importance

Local Feature Importance

\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal{D}_x

\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal{D}_x

H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})

H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})

\gamma_{i,S}

\gamma_{i,S}

\displaystyle \phi_{\color{red}i}(x) = \sum_{S\subseteq [n]\setminus \{{\color{red}i}\}} w_{S} ~ \mathbb E \left[ f(\tilde X_{S\cup \{{\color{red}i}\}}) - f(\tilde X_S) \right]

\displaystyle \phi_{\color{red}i}(x) = \sum_{S\subseteq [n]\setminus \{{\color{red}i}\}} w_{S} ~ \mathbb E \left[ f(\tilde X_{S\cup \{{\color{red}i}\}}) - f(\tilde X_S) \right]

Given the Shapley coefficient of any feature

Then

\mathbb{E}[\hat{p}_{i,S}]

\mathbb{E}[\hat{p}_{i,S}]

and the (expected) p-value obtained for , i.e.

H^0_{i,S}

H^0_{i,S}

Theorem 1:

\mathbb{E}[\hat{p}_{i,S}] \leq 1 - \gamma_{i,S}.

\mathbb{E}[\hat{p}_{i,S}] \leq 1 - \gamma_{i,S}.

i\in[n],

i\in[n],

Teneggi, Bharti, Romano, and S. "SHAP-XRT: The Shapley Value Meets Conditional Independence Testing." TMLR (2023).

What does the Shapley value test?

H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})

H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})

\displaystyle H^0_\text{global,{\color{red}i}} = \underset{{S\subseteq [n]\setminus \{{\color{red}i}\}}}{\Large\cap} H^0_{{\color{red}i},S}

\displaystyle H^0_\text{global,{\color{red}i}} = \underset{{S\subseteq [n]\setminus \{{\color{red}i}\}}}{\Large\cap} H^0_{{\color{red}i},S}

Given the Shapley value for the i-th feature, and

Theorem 2:

\displaystyle p_\text{global} = 2 \sum_{S \subseteq [n]\setminus i} w_{S} ~ \hat{p}_{i,S}

\displaystyle p_\text{global} = 2 \sum_{S \subseteq [n]\setminus i} w_{S} ~ \hat{p}_{i,S}

Then, under $\displaystyle H^0_\text{global}$ , $p_{\text{global}}$ is a valid p-value and

\mathbb{E}[p_\text{global}] \leq 2( 1-\phi_i(x))

\mathbb{E}[p_\text{global}] \leq 2( 1-\phi_i(x))

Full Spectrum of Tests

S

$\hat{p}_{4,S}$

$\hat{p}_{2,S}$

Testing Semantic Importance via Betting

Input features are not inherently

interpretable to users

So far

model

$\hat{y} = f(x)$

statistical importance of

$x_j$

input features $x_j$

$\rightarrow$

concepts $c_j$

Testing Semantic Importance via Betting

input features $x_j$

$\rightarrow$

concepts $c_j$

What are the important concepts for

the predictions of a model?

Global and local importance

Fixed predictor

Statistically-valid importance

Any set of concepts

Problem Setup

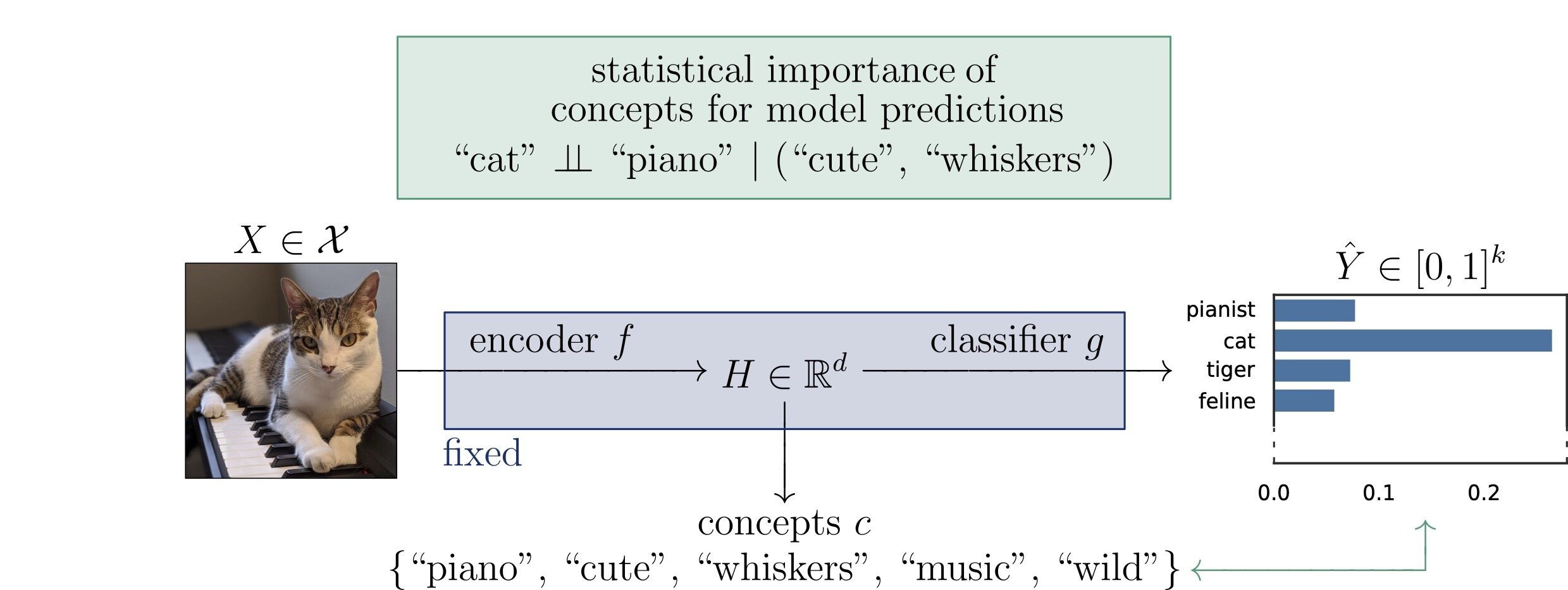
$x \in \mathcal{X}$

$f:~\mathcal{X} \to \mathbb{R}^d$

$g:~\mathbb{R}^d \to [0, 1]^k$

$c \in \mathbb{R}^{d \times m}$

input

encoder

classifier

concepts

$Z = c^{\top} H$

semantics

$\hat{Y} = g(f(X))$

predictions

$H = f(X)$

embeddings

Problem Setup

$x \in \mathcal{X}$

$f:~\mathcal{X} \to \mathbb{R}^d$

$g:~\mathbb{R}^d \to [0, 1]^k$

$c \in \mathbb{R}^{d \times m}$

input

encoder

classifier

concepts

$Z = c^{\top} H$

semantics

$\hat{Y} = g(f(X))$

predictions

$H = f(X)$

embeddings

FIXED

Defining Statistical Semantic Importance

For a concept $j \in [m] \coloneqq \{1, \dots, m\}$

type of dependence

marginal

over a population

global importance

$H^{\text{G}}_{0,j}:~\hat{Y} \perp \!\!\! \perp Z_j$

$Z_j$

$\hat{Y}$

Defining Statistical Semantic Importance

For a concept $j \in [m] \coloneqq \{1, \dots, m\}$

type of dependence

conditional

over a population

global conditional importance

$H^{\text{GC}}_{0,j}:~\hat{Y} \perp \!\!\! \perp Z_j \mid Z_{-j}$

$Z_j$

$\hat{Y}$

$Z_{-j}$

Defining Statistical Semantic Importance

For a concept $j \in [m] \coloneqq \{1, \dots, m\}$

type of dependence

conditional

for a specific input

semantic XRT

$H^{\text{LC}}_{0,j,S}:~g(\widetilde{H}_{S \cup \{j\}}) \overset{d}{=} g(\widetilde{H}_S),\quad\widetilde{H}_C \sim P_{H | Z_C = z_C}$

$z_j$

$\hat{Y}$

$z_S$

Testing by Betting

Null hypothesis $H_0$ , significance level $\alpha \in (0,1)$

Classical approach

collect data

analyze data

compute $p$ -value

$\rightarrow$

"Reject $H_0$ if $p \leq \alpha$ "

Sequential approach

Instantiate wealth process $K_0 = 1$ , $K_t = K_{t-1} \cdot (1 + v_t\kappa_t)$

"Reject $H_0$ when $K_t \geq 1/\alpha$ "

Testing by Betting

time

wealth

$1/\alpha$

under $H_0$

under $H_1$

rejection time $\tau$

Why Testing by Betting?

Data-efficient

Only use the data is needed to reject

Adaptive

The harder to reject, the longer the test

$\downarrow$

If concept $c$ rejects faster than $c'$

then it is more important

Induces a natural rank of importance

Technical Intuition: SKIT

All definitions of semantic importance are two-sample tests

$H_0:~P = \widetilde{P}$

(Podkopaev et. al, '23)

Global importance (SKIT)

$H^{\text{G}}_{0,j}$

$P_{\hat{Y} Z_j} = P_{\hat{Y}} \times P_{Z_j}$

$\iff$

$H^{\text{GC}}_{0,j}$

Global conditional importance (c-SKIT)

$\iff$

$P_{\hat{Y} Z_j Z_{-j}} = P_{\hat{Y} \widetilde{Z}_j, Z_{-j}},~\widetilde{Z}_j \sim P_{Z_j | Z_{-j}}$

$H^{\text{LC}}_{0,j,S}$

Local conditional importance (x-SKIT)

$\iff$

$P_{\hat{Y}_{S \cup \{j\}}} = P_{\hat{Y}_S}$

Technical Intuition: SKIT

All definitions of semantic importance are two-sample tests

$H_0:~P = \widetilde{P}$

(Podkopaev et. al, '23)

Global importance (SKIT)

$H^{\text{G}}_{0,j}$

$P_{\hat{Y} Z_j} = P_{\hat{Y}} \times P_{Z_j}$

$\iff$

$H^{\text{GC}}_{0,j}$

Global conditional importance (c-SKIT)

$\iff$

$P_{\hat{Y} Z_j Z_{-j}} = P_{\hat{Y} \widetilde{Z}_j, Z_{-j}},~\widetilde{Z}_j \sim P_{Z_j | Z_{-j}}$

$H^{\text{LC}}_{0,j,S}$

Local conditional importance (x-SKIT)

$\iff$

$P_{\hat{Y}_{S \cup \{j\}}} = P_{\hat{Y}_S}$

novel procedures

ImageNet Classification with CLIP

global importance

ImageNet Classification with CLIP

global conditional importance

ImageNet Classification with CLIP

local conditional importance

Thank You!

Jeremias Sulam

Jacopo Teneggi

Yaniv Romano

Beepul Bharti

SHAP-XRT

IBYDMT

SHAP-XRT

The Shapley Value Meets

Conditional Independence Testing

Reproducibility

Practical Accuracy

Explainability

Fairness

Privacy

Responsible ML

Explanations in ML

Explanations in ML

Sensitivity or Gradient-based perturbations

Shapley coefficients

Variational formulations

Counterfactual & causal explanations

LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]

Shap [Lundberg & Lee, '17], ...

RDE [Macdonald et al, '19], ...

[Sani et al, 2020] [Singla et al '19],..

Shapley values

marginal contribution of player i with coalition S

Shap-Explanations

Shap-Explanations

Shap-Explanations

Formal Feature Importance

Local Feature Importance

Local Feature Importance

Testing Semantic Importance via Betting

Testing Semantic Importance via Betting

Problem Setup

Problem Setup

Defining Statistical Semantic Importance

Defining Statistical Semantic Importance

Defining Statistical Semantic Importance

Testing by Betting

Testing by Betting

Why Testing by Betting?

Technical Intuition: SKIT

(Podkopaev et. al, '23)

Technical Intuition: SKIT

(Podkopaev et. al, '23)

ImageNet Classification with CLIP

ImageNet Classification with CLIP

ImageNet Classification with CLIP

Thank You!