

Aplicações de Lógicas não clássicas em programação
Aline Pêgas
Bacharel em matemática pura pela UNICAMP
Linux Ninja na ARKAN SYSTEM

slides.com/alinepegas/fuzzy

O que são lógicas não clássicas?
Existe mais de uma lógica?

Lógica Clássica
Lógica clássica é uma classe de lógicas formais. Cada sistema lógico nessa classe compartilha algumas propriedades:
- Lei do terceiro excluído: p ou ~p
- Dupla negação: p ≡ ~~p
- Lei da não contradição: ~(p e ~p)
- Princípio de explosão: {p, ~p} ⊢ q
Se algo é verdadeiro (p) e não verdadeiro (~p) ao mesmo tempo, é possível derivar qualquer conclusão (q). - Monotonicidade da implicação: p ⊢ q ⟶ p, s ⊢ q
- Idempotência da implicação: p,q,q ⊢ s ⟶ p,q ⊢ s
- Comutatividade da conjunção: a e b ≡ b e a
-
Dualidade de De Morgan: ~(p e q) ⟷ (~p) ou (~q)

p = Tudo o que está na internet é verdade
~p = Nem tudo o que está na internet é verdade
q = Unicórnios existem
p ou q - verdadeiro
~p ou q - verdadeiro
Portanto, unicórnios existem!


Lógicas Não-Clássicas
- Lógica multivalorada (fuzzy está aqui dentro)
- Lógica intuicionista
- Lógica modal
- Lógica paraconsistente (Newton da Costa - Curitibano)
- Lógica linear, de relevância e lógicas não-monotônicas
- Lógicas não-reflexivas
- Lógica de computabilidade
- Lógica deôntica

O Paradoxo de Russel

Se P é a propriedade de ser um peixe, então
o conjunto S de todos os peixes pode ser definido como S={x:P(x)}
Se w é um peixe chamado Wanda,
então w pertence à S
w ∊ S
Se φ(x) significa x ∈ x e R = {x: ~φ(x)}, então R é o conjunto cujos membros são os objetos que não são membros deles mesmos

O Paradoxo de Russel
Seja R = { x : x ∉ x}. Então, R ∈ R ⟺ R ∉ R
R é um membro dele mesmo? Se for, então deve satisfazer a condição de não ser membro dele mesmo, e portanto R ∉ R. Se não for, então não deve satisfazer a condição de não ser um membro dele mesmo, portanto R ∈ R.

R ∈ R ⋀ R ∉ R

Lógicas Multivaloradas
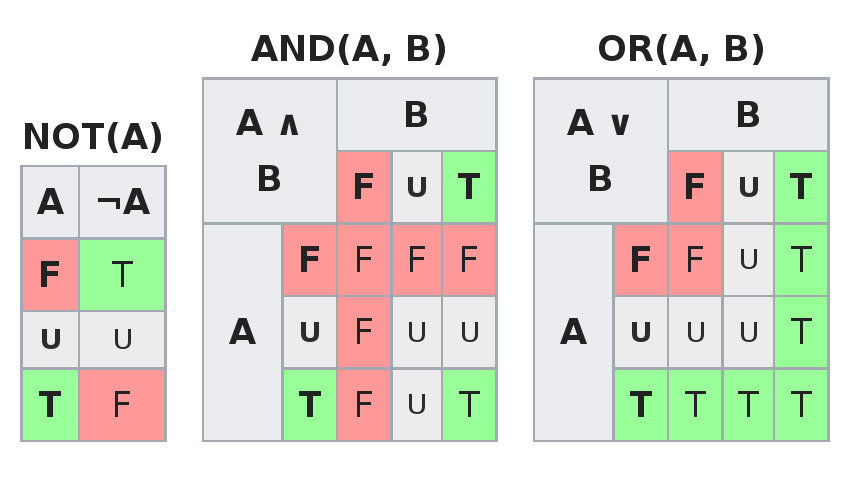
Lógica ternária
Três valores de verdade.
Por exemplo: verdadeiro, falso e incerto. Mas também pode ser 1, 0 e 1/2 ou laranja, maçã e banana.
Aplicação: SQL
NULL
TRUE FALSE UNKNOWN

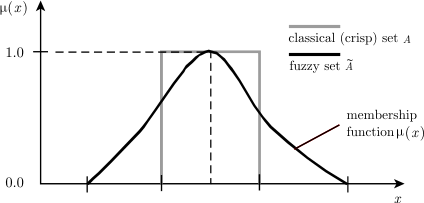
Lógica Fuzzy
- Foi feita para modelar o raciocínio lógico com afirmações vagas ou imprecisas, como "Brian é alto (pobre, bonito, jovem)"
- É vero-funcional, ou seja o valor de verdade (nesse caso grau de verdade) de uma afirmação como "Erik é alto e Terry é rico" é determinado pelo valor de verdade de suas componentes
- Veio da teoria de conjuntos fuzzy (Zadeh, 1965)
- Um conjunto fuzzy associa a seus elementos um grau de pertencimento (geralmente um número entre 0 e 1)
- A lógica fuzzy associa a proposições um grau de "verdade". Geralmente 0 = totalmente falso e 1 = totalmente verdadeiro
- É super legal

Lógica Fuzzy
Processo:
- Transformação das variáveis do problema em valores fuzzy, ou fuzzificação
- Aplicação dos operadores fuzzy
- Aplicação da implicação
- Combinação de todas as saídas fuzzy possíveis
- Transformação do resultado fuzzy em um resultado nítido, a defuzzificação.

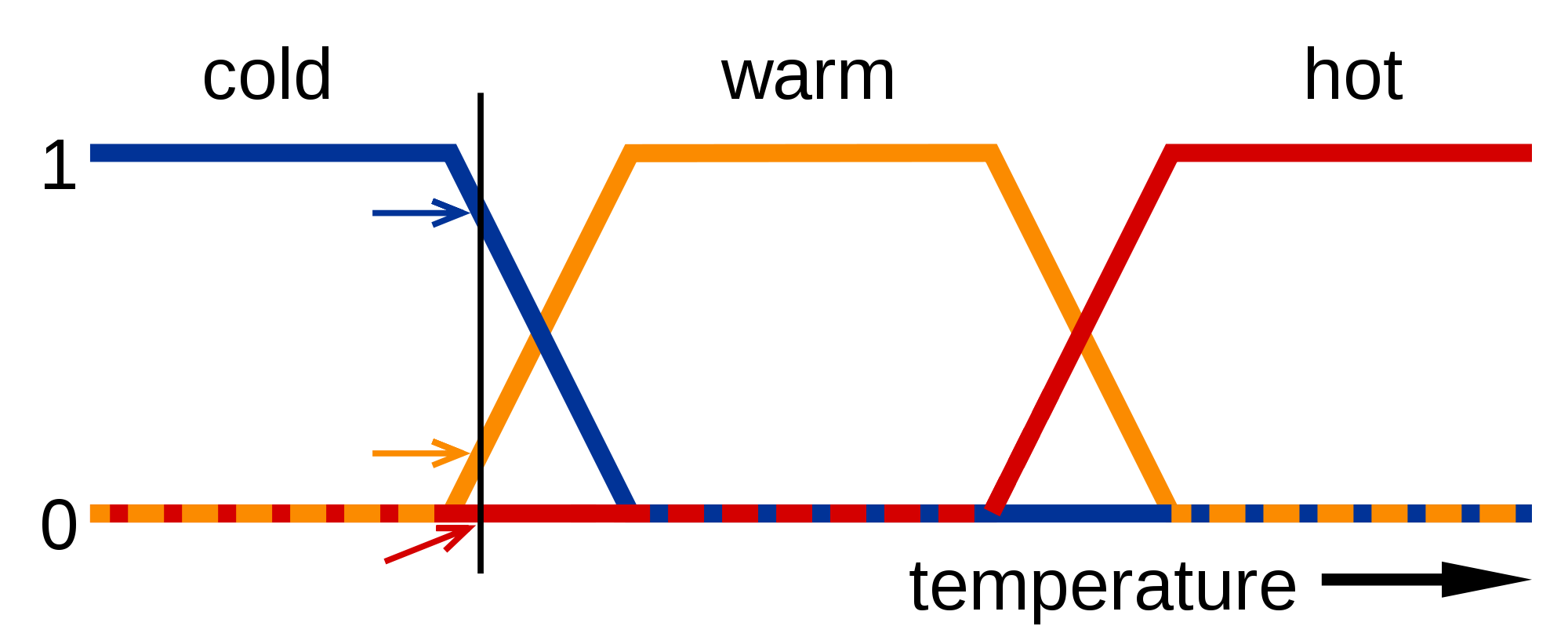


O problema da gorjeta
INPUT:
quality = Qualidade da comida
service = Qualidade do serviço
OUTPUT:
tip = porcentagem do valor da conta a ser adicionado como gorjeta

alto - médio - baixo

import numpy as np
import skfuzzy as fuzz
import matplotlib.pyplot as plt
# Generate universe variables
# * Quality and service on subjective ranges [0, 10]
# * Tip has a range of [0, 25] in units of percentage points
x_qual = np.arange(0, 11, 1)
x_serv = np.arange(0, 11, 1)
x_tip = np.arange(0, 26, 1)

numpy - Computação científica com Python
skfuzzy - Fuzzy logic toolbox
matplotlib - Python 2D plotting library
numpy.arange([start, ]stop, [step, ]dtype=None)

# Generate fuzzy membership functions
qual_lo = fuzz.trimf(x_qual, [0, 0, 5])
qual_md = fuzz.trimf(x_qual, [0, 5, 10])
qual_hi = fuzz.trimf(x_qual, [5, 10, 10])
serv_lo = fuzz.trimf(x_serv, [0, 0, 5])
serv_md = fuzz.trimf(x_serv, [0, 5, 10])
serv_hi = fuzz.trimf(x_serv, [5, 10, 10])
tip_lo = fuzz.trimf(x_tip, [0, 0, 13])
tip_md = fuzz.trimf(x_tip, [0, 13, 25])
tip_hi = fuzz.trimf(x_tip, [13, 25, 25])
Triangular membership function generator


# Visualize these universes and membership functions
fig, (ax0, ax1, ax2) = plt.subplots(nrows=3, figsize=(8, 9))
ax0.plot(x_qual, qual_lo, 'b', linewidth=1.5, label='Bad')
ax0.plot(x_qual, qual_md, 'g', linewidth=1.5, label='Decent')
ax0.plot(x_qual, qual_hi, 'r', linewidth=1.5, label='Great')
ax0.set_title('Food quality')
ax0.legend()
ax1.plot(x_serv, serv_lo, 'b', linewidth=1.5, label='Poor')
ax1.plot(x_serv, serv_md, 'g', linewidth=1.5, label='Acceptable')
ax1.plot(x_serv, serv_hi, 'r', linewidth=1.5, label='Amazing')
ax1.set_title('Service quality')
ax1.legend()
ax2.plot(x_tip, tip_lo, 'b', linewidth=1.5, label='Low')
ax2.plot(x_tip, tip_md, 'g', linewidth=1.5, label='Medium')
ax2.plot(x_tip, tip_hi, 'r', linewidth=1.5, label='High')
ax2.set_title('Tip amount')
ax2.legend()
# Turn off top/right axes
for ax in (ax0, ax1, ax2):
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
plt.tight_layout()

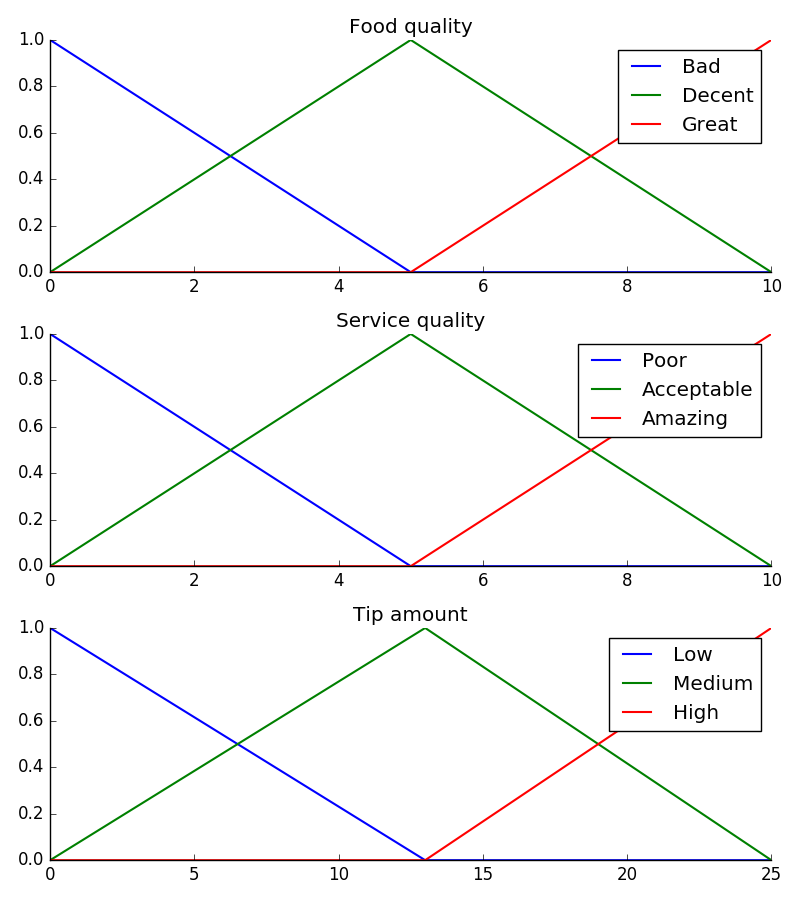



Regras fuzzy
Agora, para dar uma utilidade para os nossos triângulos, definimos uma relação fuzzy entre as variáveis de entrada e saída. No nosso exemplo vamos usar essas 3 regras:
- Se a comida estava ruim OU o serviço foi ruim, ENTÃO a gorjeta vai ser pequena
- Se o serviço foi aceitável, ENTÃO a gorjeta vai ser média
- Se a comida estava ótima OU o serviço foi maravilhoso, ENTÃO a gorjeta vai ser alta

# We need the activation of our fuzzy membership functions at
# these values.
# The exact values 6.5 and 9.8 do not exist on our universes...
# This is what fuzz.interp_membership exists for!
qual_level_lo = fuzz.interp_membership(x_qual, qual_lo, 6.5)
qual_level_md = fuzz.interp_membership(x_qual, qual_md, 6.5)
qual_level_hi = fuzz.interp_membership(x_qual, qual_hi, 6.5)
serv_level_lo = fuzz.interp_membership(x_serv, serv_lo, 9.8)
serv_level_md = fuzz.interp_membership(x_serv, serv_md, 9.8)
serv_level_hi = fuzz.interp_membership(x_serv, serv_hi, 9.8)
Qualidade da comida = 6.5
Qualidade do serviço = 9.8



# Now we take our rules and apply them.
# Rule 1 concerns bad food OR service.
# The OR operator means we take the maximum of these two.
active_rule1 = np.fmax(qual_level_lo, serv_level_lo)
# Now we apply this by clipping the top off the corresponding output
# membership function with `np.fmin`
tip_activation_lo = np.fmin(active_rule1, tip_lo)# removed entirely to 0
# For rule 2 we connect acceptable service to medium tipping
tip_activation_md = np.fmin(serv_level_md, tip_md)
# For rule 3 we connect high service OR high food with high tipping
active_rule3 = np.fmax(qual_level_hi, serv_level_hi)
tip_activation_hi = np.fmin(active_rule3, tip_hi)
tip0 = np.zeros_like(x_tip)

# Visualize this
fig, ax0 = plt.subplots(figsize=(8, 3))
ax0.fill_between(x_tip, tip0, tip_activation_lo, facecolor='b', alpha=0.7)
ax0.plot(x_tip, tip_lo, 'b', linewidth=0.5, linestyle='--', )
ax0.fill_between(x_tip, tip0, tip_activation_md, facecolor='g', alpha=0.7)
ax0.plot(x_tip, tip_md, 'g', linewidth=0.5, linestyle='--')
ax0.fill_between(x_tip, tip0, tip_activation_hi, facecolor='r', alpha=0.7)
ax0.plot(x_tip, tip_hi, 'r', linewidth=0.5, linestyle='--')
ax0.set_title('Output membership activity')
# Turn off top/right axes
for ax in (ax0,):
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
plt.tight_layout()


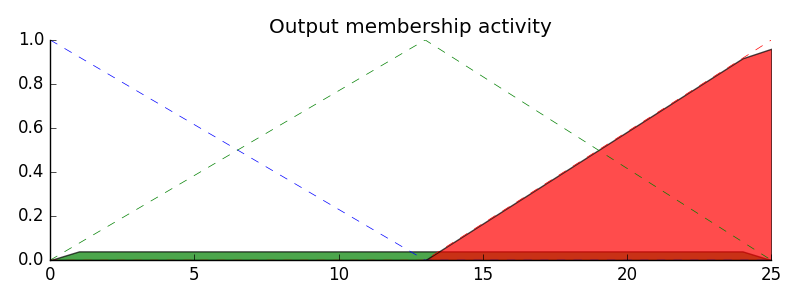




# Aggregate all three output membership functions together
aggregated = np.fmax(tip_activation_lo,
np.fmax(tip_activation_md, tip_activation_hi))
# Calculate defuzzified result
tip = fuzz.defuzz(x_tip, aggregated, 'centroid')
tip_activation = fuzz.interp_membership(x_tip, aggregated, tip) # for plot
Combinação das saídas fuzzy
Com a atividade de cada função pertencimento de saída conhecida, todas as funções de pertencimento de saída tem que ser combinadas. Geralmente isso e feito usando um operador de máximo.
Defuzzificação
Finalmente, para obter uma resposta prática, retornamos para a lógica crisp. Para o nosso exemplo, vamos usar o método do centróide.
O resultado é uma gorjeta de 20.2%.


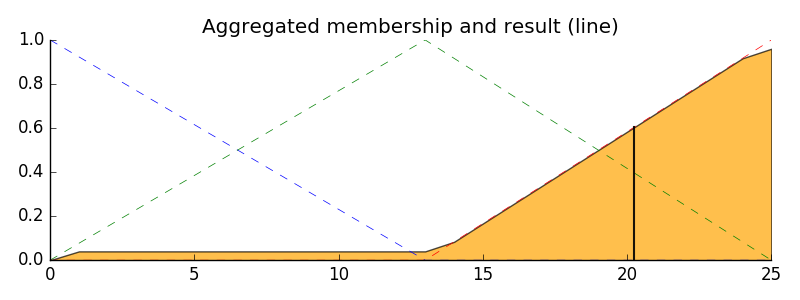
# Visualize this
fig, ax0 = plt.subplots(figsize=(8, 3))
ax0.plot(x_tip, tip_lo, 'b', linewidth=0.5, linestyle='--', )
ax0.plot(x_tip, tip_md, 'g', linewidth=0.5, linestyle='--')
ax0.plot(x_tip, tip_hi, 'r', linewidth=0.5, linestyle='--')
ax0.fill_between(x_tip, tip0, aggregated, facecolor='Orange', alpha=0.7)
ax0.plot([tip, tip], [0, tip_activation], 'k', linewidth=1.5, alpha=0.9)
ax0.set_title('Aggregated membership and result (line)')
# Turn off top/right axes
for ax in (ax0,):
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
plt.tight_layout()@alinepegas
Aplicações de Lógicas não Clássicas em Programação
By Aline Pêgas
Aplicações de Lógicas não Clássicas em Programação
Semana Acadêmica BSI 2017
- 1,398


