Verifiable Computing

In haskell

\(\color{#EC5f67}{\text{PRIVATE}} \)

\(\color{#6699CC}{\text{Public}} \)

Motivation

Efficiently verify the correctness of computations without executing them

Example

ALICE has query \( \color{#6699CC}u \)

BOB HAS private \( \color{#EC5f67} w \)

Alice wants to know

\color{#6699CC}{z} = \color{#6699CC}{f}(\color{#6699CC}{u},\color{#EC5F67}{w})
z=f(u,w)\color{#6699CC}{z} = \color{#6699CC}{f}(\color{#6699CC}{u},\color{#EC5F67}{w})

Desired

ALICE wants computation correctness 

Bob wants his secrets, \(\color{#EC5f67}{\text{secret}} \)

Example
USES

Pre Image

Prove you have a pre image to a hash function

Account Balance

Prove your account has enough monies for a transaction

Membership

Prove you are part of a group without revealing your identity

Sealed BID auction

Prove who won, without revealing any of the bids

GENERAL Approach

Put Computation in right
"FORM"​

evaluate "FORM" WITH  PRIVATE INPUTS
YieldING A PROof
THAT EACH part WAS executing according TO THE PRESHARED "form"

Mathematical

Wizardry
THAT FALLS OUT OF ALGEbraic
GEOMetry

BACKGROUND

pt 1

PARTIAL HOMOmophic ENCRyption

Performing a limited set of operations on CIPHER TEXT

HOMOmophic ENCRyption

GROUP HOMOMORPHISM

x,y \in G
x,y∈Gx,y \in G
f(xy) = f(x)f(y)
f(xy)=f(x)f(y)f(xy) = f(x)f(y)

For some cryptographic schemes this also works for encrypted values

HOMOmophic ENCRyption

Floor AREA of my shed?

Width: 7m

LENGTH: 3m

ENTER THE CLOUD

Width: \( \color{#EC5F67}7\)m

Shed FLOOR AREA SOLver™

PRIVACY

LENgTH: \( \color{#EC5F67}3\)m

RSA to the rescue

\text{Enc}(x \times y) = \text{Enc}(x) \times \text{Enc}(y)
Enc(x×y)=Enc(x)×Enc(y)\text{Enc}(x \times y) = \text{Enc}(x) \times \text{Enc}(y)
\begin{matrix} c_w & = & \color{#EC5F67}7^\color{#6699CC}{23} \mod \color{#6699CC}{143} \\ & = & 2 \\ c_l &= & \color{#EC5F67}3^\color{#6699CC}{23} \mod \color{#6699CC}{143} \\ &= & 126 \\ \end{matrix}
cw=723mod143=2cl=323mod143=126\begin{matrix} c_w & = & \color{#EC5F67}7^\color{#6699CC}{23} \mod \color{#6699CC}{143} \\ & = & 2 \\ c_l &= & \color{#EC5F67}3^\color{#6699CC}{23} \mod \color{#6699CC}{143} \\ &= & 126 \\ \end{matrix}
Public Key = ( \color{#6699CC}{23}, \color{#6699CC}{143})
PublicKey=(23,143)Public Key = ( \color{#6699CC}{23}, \color{#6699CC}{143})
Private Key = (\color{#EC5F67}{47}, \color{#6699CC}{143})
PrivateKey=(47,143)Private Key = (\color{#EC5F67}{47}, \color{#6699CC}{143})

GO CLOUD GO 

Shed FLOOR SIZE SOLver™

2 \times 126 = 252
2×126=2522 \times 126 = 252
\begin{matrix} \text{area} & = & 252^\color{#EC5F67}{47} \mod \color{#6699CC}{143} \\ & = & 21 \\ \end{matrix}
area=25247mod143=21\begin{matrix} \text{area} & = & 252^\color{#EC5F67}{47} \mod \color{#6699CC}{143} \\ & = & 21 \\ \end{matrix}

BACKGROUND

pt 2

Pairing Crypto

e :G_1 \times G_2 \to G_T
e:G1×G2→GTe :G_1 \times G_2 \to G_T

A relation between 2 group elements that gives an output, that has this algebraic relation to the inputs 

e(g^a,g^b) = e(g, g)^{ab}
e(ga,gb)=e(g,g)abe(g^a,g^b) = e(g, g)^{ab}

Text

more info

REAL WORLD PROCESS

Verifier generates circuit representation and shares

Prover evaluates the constraints

for the function homomorphically and obtains the output and witness 

Verifier verifies using pairing on the homomorphic output to verify the witness

SIMPLE

circuit
COmpiler

TASK

Prove you evaluated $$ m^2 + 36 - n $$

correctly with $$ m = 2, n = 3 $$

type Name = Text

data BinOp
  = BMul
  | BAdd
  | BSub

data Expr
  = Var Name
  | Lit Rational
  | BinOp BinOp Expr Expr

Code

instance Num Expr where
  (*) = BinOp BMul
  (+) = BinOp BAdd
  (-) = BinOp BSub
  fromInteger = Lit . fromInteger
  abs = notImplemented
  signum = notImplemented

task1 = (Var "m") * (Var "m") + 36 - (Var "n")

Code Cont.

m^2 + 36 - n
m2+36−nm^2 + 36 - n

STEp 1: FLATTEN

Convert \(m^2 + 36 - n \) so it only contains commands in the form

\begin{matrix} x &=& c \\ x &=& y \\ x &=& y \text{ op } z \end{matrix}
x=cx=yx=y op z\begin{matrix} x &=& c \\ x &=& y \\ x &=& y \text{ op } z \end{matrix}
\begin{matrix} b &=& m \times m \\ c &=& 36 \\ a &=& b + c \\ \text{result} &=& a - n \end{matrix}
b=m×mc=36a=b+cresult=a−n\begin{matrix} b &=& m \times m \\ c &=& 36 \\ a &=& b + c \\ \text{result} &=& a - n \end{matrix}

OUR EXAMPLE Flattened 

FORMS

Constraints

data Gate
  = GAdd
  | GSub
  | GMul deriving (Show)

data Constraint
  = CSet Name (Either Name Rational)
  | CBinOp {
      gate :: Gate
    , output :: Name
    , input1 :: Name
    , input2 :: Name
  } deriving (Show)
\begin{matrix} x &=& c \\ x &=& y \\ x &=& y \text{ op } z \end{matrix}
x=cx=yx=y op z\begin{matrix} x &=& c \\ x &=& y \\ x &=& y \text{ op } z \end{matrix}

data ConstraintSystem
  = ConstraintSystem {
      supply :: Int
    , cs :: [Constraint]
  } deriving (Show)

type Builder a = State ConstraintSystem a

runBuilder :: Builder a -> ConstraintSystem
runBuilder m = execState m initCS
 where
  initCS = ConstraintSystem { supply = 0, cs = []}

names :: [Text]
names = [1 ..] >>= flip replicateM ['a' .. 'z'] >>= return . toS

fresh :: Builder Name
fresh = do
  v <- gets supply
  modify $ \s -> s { supply = v + 1 }
  pure $ names `unsafeIndex` v

emit :: Constraint -> Builder ()
emit c = modify (\s -> s { cs = c : cs s })


compile :: Name -> Expr -> Builder ()
compile output expr = case expr of
  Var nm -> 
     emit $ CSet output (Left nm)

  Lit v -> 
     emit $ CSet output (Right v)

  BinOp op e1 e2 -> do
    input1 <- compile' e1
    input2 <- compile' e2
    let gop = case op of
                BMul -> GMul
                BAdd -> GAdd
                BSub -> GSub
    emit $ CBinOp gop output input1 input2


compile' :: Expr -> Builder Name
compile' (Var nm) = return nm
compile' e = do
  output <- fresh
  compile output e
  return output
> constraints task1
b = m * m
c = 36
a = b + c
result = a - n

And with the help of some pretty instances

\begin{matrix} b &=& m \times m \\ c &=& 36 \\ a &=& b + c \\ \text{result} &=& a - n \end{matrix}
b=m×mc=36a=b+cresult=a−n\begin{matrix} b &=& m \times m \\ c &=& 36 \\ a &=& b + c \\ \text{result} &=& a - n \end{matrix}

STEp 2: TO r1Cs

We can represent each one of our constraints
as a set of 3 polynomials

y = v \times w
y=v×wy = v \times w
(s \cdot v) \times (s \cdot w) - (s \cdot y) = 0
(s⋅v)×(s⋅w)−(s⋅y)=0(s \cdot v) \times (s \cdot w) - (s \cdot y) = 0

We are going to construct a clever polynomial that only is 0 on correct inputs

STEp 2: TO r1Cs

Each constraint can be represented as a relation between vectors.

 

\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& 0 & 1 & 0 & 0 & 0 & 0 & 0 &\\ w &=& 0 & 1 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 0 & 0 & 1 & 0 & \end{matrix}
one m n resulta b cv=0100000w=0100000y=0000010\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& 0 & 1 & 0 & 0 & 0 & 0 & 0 &\\ w &=& 0 & 1 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 0 & 0 & 1 & 0 & \end{matrix}
b = m \times m
b=m×mb = m \times m

R1CS


data R1C
  = R1C {
      v :: [Rational] 
    , w :: [Rational]
    , y :: [Rational] 
    } deriving (Show)

newtype R1CS = R1CS [R1C] deriving (Show)


uses :: Name -> [Rational]
uses var = fmap (bool 0 1 . (==var)) vars

toR1C :: Constraint -> R1C
toR1C c = case c of
  CBinOp GMul output input1 input2 -> R1C {
    v = uses input1
  , w = uses input2
  , y = uses output
  }

STEp 2: TO r1Cs

(cont.)

\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& -36 & 0 & 0 & 0 & 0 & 0 & 1 &\\ w &=& 1 & 0 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 0 & 0 & 0 & 0 & \end{matrix}
one m n resulta b cv=−36000001w=1000000y=0000000\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& -36 & 0 & 0 & 0 & 0 & 0 & 1 &\\ w &=& 1 & 0 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 0 & 0 & 0 & 0 & \end{matrix}
c = 36
c=36c = 36
uses :: Name -> [Rational]
uses var = fmap (bool 0 1 . (==var)) vars

toR1C :: Constraint -> R1C
toR1C c = case c of
  CBinOp GMul output input1 input2 -> R1C {
    v = uses input1
  , w = uses input2
  , y = uses output
  }

+  CSet output (Right value) -> R1C {
+    v = zipWith (+) 
+            (uses output) 
+            (fmap (bool 0 (-value) . (=="one")) vars)
+  , w = [1]
+  , y = [0]
+  }

STEp 2: TO r1Cs

(cont.)

\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& 0 & 0 & 0 & 0 & 0 & 1 & 1 &\\ w &=& 0 & 0 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 0 & 1 & 0 & 0 & \end{matrix}
one m n resulta b cv=0000011w=0000000y=0000100\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& 0 & 0 & 0 & 0 & 0 & 1 & 1 &\\ w &=& 0 & 0 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 0 & 1 & 0 & 0 & \end{matrix}
a = b + c
a=b+ca = b + c
s = \begin{bmatrix} 1, 2, 3, 37, 40, 36\end{bmatrix}
s=[1,2,3,37,40,36]s = \begin{bmatrix} 1, 2, 3, 37, 40, 36\end{bmatrix}
uses :: Name -> [Rational]
uses var = fmap (bool 0 1 . (==var)) vars

toR1C :: Constraint -> R1C
toR1C c = case c of
  CBinOp GMul output input1 input2 -> R1C {
    v = uses input1
  , w = uses input2
  , y = uses output
  }
  CSet output (Right value) -> R1C {
    v = zipWith (+) 
            (uses output) 
            (fmap (bool 0 (-value) . (=="one")) vars)
  , w = [1]
  , y = [0]
  }
+  CBinOp GAdd output input1 input2 -> R1C {
+    v = zipWith (+) (uses input1) (uses input2)
+  , w = [1]
+  , y = uses output
+  }

STEp 2: TO r1Cs

(cont.)

\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& 0 & 0 & -1 & 0 & 0 & 0 & 0 &\\ w &=& 1 & 0 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 1 & 0 & 0 & 0 & \end{matrix}
one m n resulta b cv=00−10000w=1000000y=0001000\begin{matrix} & &\text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ v &=& 0 & 0 & -1 & 0 & 0 & 0 & 0 &\\ w &=& 1 & 0 & 0 & 0 & 0 & 0 & 0 &\\ y &=& 0 & 0 & 0 & 1 & 0 & 0 & 0 & \end{matrix}
result = a - n
result=a−nresult = a - n 
...
  CSet output (Right value) -> R1C {
    v = zipWith (+) 
            (uses output) 
            (fmap (bool 0 (-value) . (=="one")) vars)
  , w = [1]
  , y = [0]
  }
  CBinOp GAdd output input1 input2 -> R1C {
    v = zipWith (+) (uses input1) (uses input2)
  , w = [1]
  , y = uses output
  }
+  CBinOp GSub output input1 input2 -> R1C {
+    v = zipWith (+) 
+            (uses input1) 
+            (fmap (bool 0 (-1) . (==input2)) vars)
+  , w = [1]
+  , y = uses output
+  }
> r1cs $ constraints task1
b = m * m
==================
v = [0,1,0,0,0,0,0]
w = [0,1,0,0,0,0,0]
y = [0,0,0,0,0,1,0]


c = 36
==================
v = [-36,0,0,0,0,0,1]
w = [1]
y = [0]


a = b + c
==================
v = [0,0,0,0,0,1,1]
w = [1]
y = [0,0,0,0,1,0,0]


result = a - n
==================
v = [0,0,-1,0,1,0,0]
w = [1]
y = [0,0,0,1,0,0,0]

STEp 3: WITNESS  ME

The witness is the assignment to all variables.
Execute the flattened commands and set the values as you go

Initial state ( with our inputs )

\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 0 & 2 & 3 & 0 & 0 & 0 & 0 \end{matrix}
one m n resulta b c0230000\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 0 & 2 & 3 & 0 & 0 & 0 & 0 \end{matrix}

Step 3.1

\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 0 & 0 & 4 & 0 \end{matrix}
one m n resulta b c1230040\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 0 & 0 & 4 & 0 \end{matrix}

Step 3.2

\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 0 & 0 & 4 & 36 \end{matrix}
one m n resulta b c12300436\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 0 & 0 & 4 & 36 \end{matrix}

Step 3.3

Step 3.4

b = m \times m
b=m×m b = m \times m
c = 36
c=36c = 36
a = b + c
a=b+ca = b + c
\text{result} = c - n
result=c−n \text{result} = c - n
\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 0 & 40 & 4 & 36 \end{matrix}
one m n resulta b c123040436\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 0 & 40 & 4 & 36 \end{matrix}
\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 37 & 40 & 4 & 36 \end{matrix}
one m n resulta b c1233740436\begin{matrix} \text{one} & \text{~m} & \text{~n} & \text{~result} & \text{a} & \text{~b} & \text{~c} \\ 1 & 2 & 3 & 37 & 40 & 4 & 36 \end{matrix}
satisfy ::  [Rational] -> R1C -> Bool
satisfy s (R1C v w y) = (sv * sw) - sy == 0
  where
    sv = dot s v
    sw = dot s w
    sy = dot s y
    dot a b = sum (zipWith (*) a b)
(s \cdot v) \times (s \cdot w) - (s \cdot y) = 0
(s⋅v)×(s⋅w)−(s⋅y)=0(s \cdot v) \times (s \cdot w) - (s \cdot y) = 0
> fmap (satisfy witness) (r1cs $ constraints task1)
[True,True,True,True]

Checking each gate INDIVIDUALLY?
No way jose

STEp 4: SUCCINCT

Lagrange interpolation

Given a set of points, give me a polynomial that passes through all of those points.
Thanks to this we can check

the witness in a single step

Boolean operations

...

data BinOp
  = BMul
  | BAdd
  | BSub
+ | BAnd
+ | BOr
+ | BXor

...
\begin{matrix} \text{AND}(a,b) &=& a \times b \\ \text{OR}(a,b) &=& a + b - ab \\ \text{XOR}(a,b) &=& (a-b)(a-b) \end{matrix}
AND(a,b)=a×bOR(a,b)=a+b−abXOR(a,b)=(a−b)(a−b)\begin{matrix} \text{AND}(a,b) &=& a \times b \\ \text{OR}(a,b) &=& a + b - ab \\ \text{XOR}(a,b) &=& (a-b)(a-b) \end{matrix}

Arithemitization

compile output expr = case expr of
...
  BinOp op e1 e2 -> do
    input1 <- compile' e1
    input2 <- compile' e2
    binOp op output input1 input2

binOp :: BinOp -> Name -> Name -> Name -> Builder ()
binOp BAnd out input1 input2 = binOp BMul out input1 input2
binOp BOr out input1 input2 = do
  tmp1 <- fresh
  tmp2 <- fresh
  binOp BMul tmp1 input1 input2
  binOp BAdd tmp2 input1 input2
  binOp BSub out tmp2 tmp1
binOp BXor out input1 input2 = do
  tmp1 <- fresh
  binOp BSub tmp1 input1 input2
  binOp BMul out tmp1 tmp1

binOp op output input1 input2 = emit $ CBinOp gate output input1 input2
  where
    gate =
      case op of
        BMul -> GMul
        BAdd -> GAdd
        BSub -> GSub

IMportant

WHAT we just did was a big simplification

IN the real world

All our arithmetic operations would be not be done with regular numbers.

IN the real world

Instead it'd be

elliptic curve elements

over a

finite field with a prime modulus. 

Elliptic curve ELEMENT

A \( (x, y) \) coordinate on a curve that looks like

y^2 = x^3 + ax + b
y2=x3+ax+by^2 = x^3 + ax + b
4a^3 + 27b^2 \neq 0
4a3+27b2≠04a^3 + 27b^2 \neq 0

... OVer a finite Field

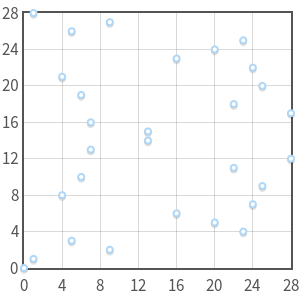
Instead of being a real curve, you have a set of discrete points.

( Barreto-Naehrig Curve: BN128 )

\frac{e( g^{v(s)}, g^{w(s)} )}{ e( g^{y(s)}, g) } \stackrel{?}{=} e( g^{h(s)}, g^{D(s)} )
e(gv(s),gw(s))e(gy(s),g)=?e(gh(s),gD(s))\frac{e( g^{v(s)}, g^{w(s)} )}{ e( g^{y(s)}, g) } \stackrel{?}{=} e( g^{h(s)}, g^{D(s)} )

The final verification step, relates the circuit output, the witness, and the circuit description, checked without having access the the private inputs.

It's computationally infeasible to construct a forged proof 

questions

github.com/adjoint-io

Verifiable Computing

By ..

Made with Slides.com

Verifiable Computing

  • 2,749

More from ..

  • Safer APIs with Ghosts of Departed Proofs
    ..
    5322
  • Linguistics
    ..
    2077
  • Mathematical Structure
    ..
    2049