Clustering with graphs:

Spectral clustering and Louvain's algorithm

France ROSE

Machine Learning Journal Club

February 28th, 2018

Outline

  • From data to graph

  • Spectral theory and clustering

  • When your graph is too large: Louvain's algorithm

  • Retrieving cell categories with graph clustering

Ressources

From data to graph

Data are already a graph

Data are not a graph yet

Ex: protein interactions

Similarity graph

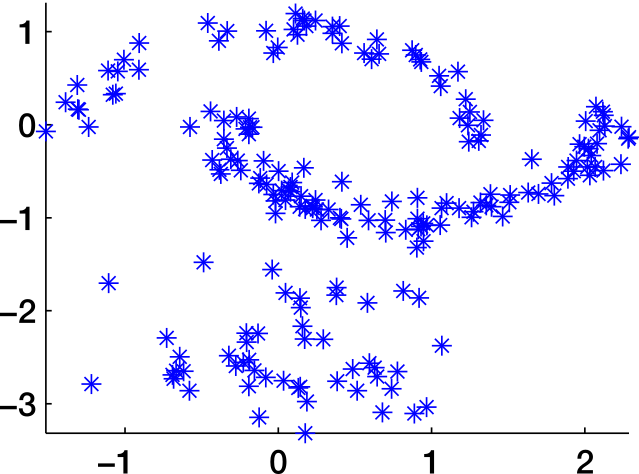
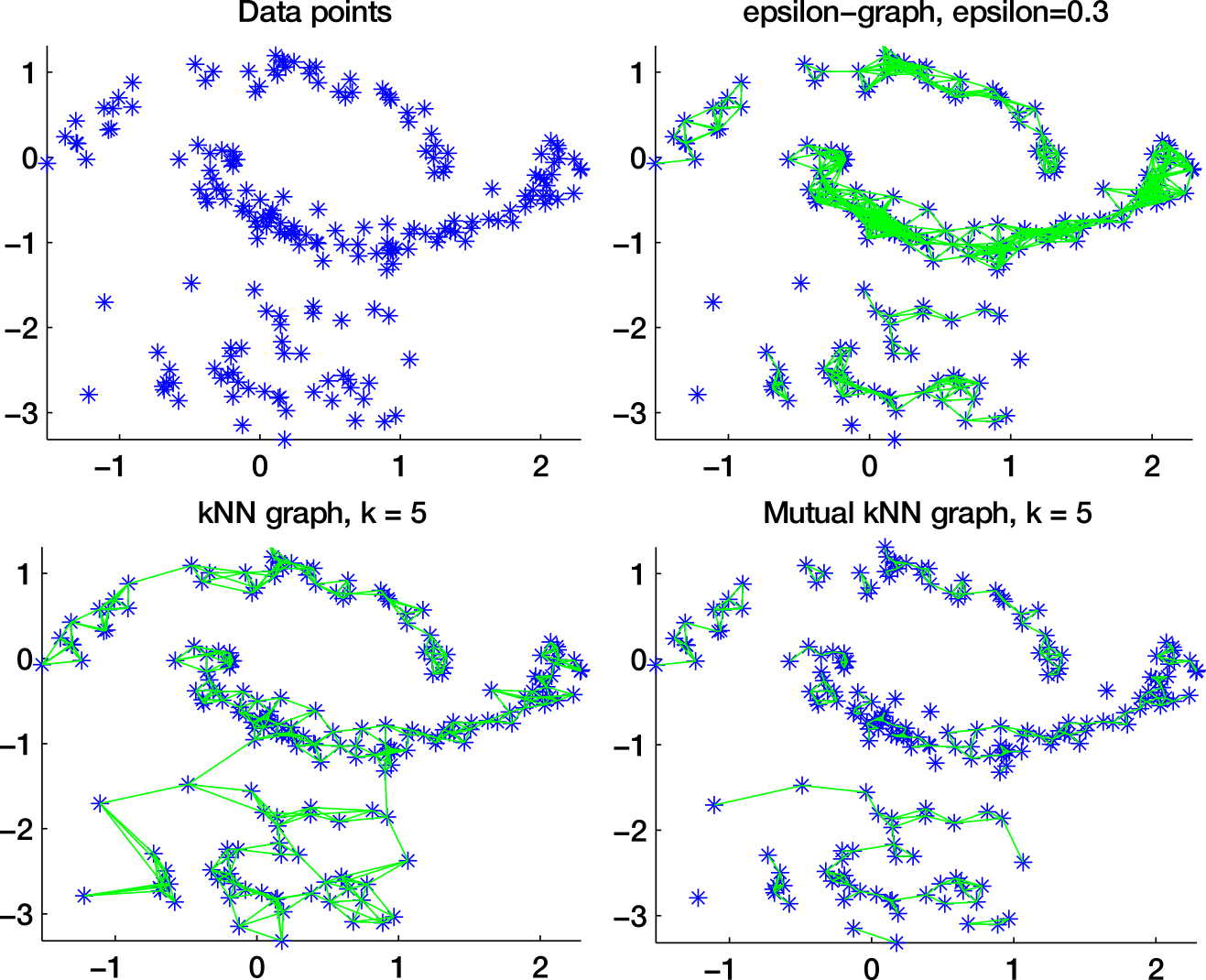
Similarity graphs

Distance function

-neighborhood graph

\epsilon

k-nearest neighbors graph

Compute

distances

RBF kernel

Euclidean, Mahalanobis, Manhattan...

\phi(x) = \phi ( || x || )
s(x_i,x_j) = exp\big( \frac{- ||x_i-x_j||^2}{2 \sigma^2} \big)

Spectral Theory

Spectrum: eigenvalues and eigenvectors

       Laplacian matrix       =   Degree matrix    -  Adjacency matrix

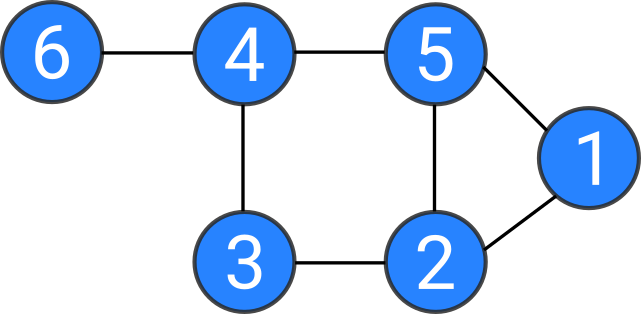
\begin{bmatrix} 2 & -1 & & & -1 & \\ -1 & 3 & -1 & & -1 & \\ & -1 & 2 & -1 & & \\ & & -1 & 3 & -1 & -1\\ -1 & -1 & & -1 & 3 \\ & & & & -1 &1 \end{bmatrix} = \begin{bmatrix} 2 & & & & & \\ & 3 & & & & \\ & & 2 & & & \\ & & & 3 & & \\ & & & & 3 \\ & & & & &1 \end{bmatrix} - \begin{bmatrix} 0 & 1 & & & 1 & \\ 1 & 0 & 1 & & 1 & \\ & 1 & 0 & 1 & & \\ & & 1 & 0 & 1 & 1 \\ 1 & 1 & & 1 &0 & \\ & & & 1 & &0 \end{bmatrix}

Laplacian matrix

L = \begin{bmatrix} 2 & -1 & & & -1 & \\ -1 & 3 & -1 & & -1 & \\ & -1 & 2 & -1 & & \\ & & -1 & 3 & -1 & -1\\ -1 & -1 & & -1 & 3 \\ & & & & -1 &1 \end{bmatrix}
  • L is symmetric and positive semi-definite
  • L has n non-negative, real-valued eigenvalues
  • The smallest eigenvalue of L is 0, with the corresponding eigenvector 1
0 \leq \lambda_1 \leq \lambda_2 \leq ... \leq \lambda_n
\forall f \in R^n, f'Lf = \frac{1}{2} \sum_{i,j =1}^{n} w_{i,j} (f_i - f_j)^2
\exists \lambda \in R, \exists v \in \mathbb R_{\ne 0}, Lv = \lambda v

Laplacian matrix

L\cdot v = \begin{bmatrix} 2 & -1 & & & -1 & \\ -1 & 3 & -1 & & -1 & \\ & -1 & 2 & -1 & & \\ & & -1 & 3 & -1 & -1\\ -1 & -1 & & -1 & 3 \\ & & & & -1 &1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 - 1 -1 \\ -1 +3 -1 -1 \\ -1 +2 -1 \\ -1 +3 -1 -1 \\ -1 -1 -1 +3 \\ -1 + 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}
  • The smallest eigenvalue of L is 0, with the corresponding eigenvector 1
\exists \lambda \in R, \exists v \in \mathbb R_{\ne 0}, Lv = \lambda v
\lambda v = 0 \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}

Intuition about spectral clustering

L = \begin{bmatrix} 2 & -1 & & & -1 & \\ -1 & 3 & -1 & & -1 & \\ & -1 & 2 & -1 & & \\ & & -1 & 3 & -1 & -1\\ -1 & -1 & & -1 & 3 \\ & & & & -1 &1 \\ &&&&&& 2 & -1 & & & -1 & \\ &&&&&& -1 & 3 & -1 & & -1 & \\ &&&&& & & -1 & 2 & -1 & & \\ &&&&& & & & -1 & 3 & -1 & -1\\ &&&&&&-1 & -1 & & -1 & 3 \\ &&&&&& & & & & -1 &1 \\ &&&&& &&&&&&& 2 & -1 & & & -1 & \\ &&&&& &&&&&&& -1 & 3 & -1 & & -1 & \\ &&&&& &&&&&&& & -1 & 2 & -1 & & \\ &&&&& &&&&&&& & & -1 & 3 & -1 & -1\\ &&&&& &&&&&&&-1 & -1 & & -1 & 3 \\ &&&&& &&&&&&& & & & & -1 &1 \end{bmatrix}
L = \begin{bmatrix} 2 & -1 & & & -1 & \\ -1 & 3 & -1 & & -1 & \\ & -1 & 2 & -1 & & \\ & & -1 & 3 & -1 & -1\\ -1 & -1 & & -1 & 3 \\ & & & & -1 &1 \\ &&&&&& 2 & -1 & & & -1 & \\ &&&&&& -1 & 3 & -1 & & -1 & \\ &&&&& & & -1 & 2 & -1 & & \\ &&&&& & & & -1 & 3 & -1 & -1\\ &&&&&&-1 & -1 & & -1 & 3 \\ &&&&&& & & & & -1 &1 \\ &&&&& &&&&&&& 2 & -1 & & & -1 & \\ &&&&& &&&&&&& -1 & 3 & -1 & & -1 & \\ &&&&& &&&&&&& & -1 & 2 & -1 & & \\ &&&&& &&&&&&& & & -1 & 3 & -1 & -1\\ &&&&& &&&&&&&-1 & -1 & & -1 & 3 \\ &&&&& &&&&&&& & & & & -1 &1 \end{bmatrix}

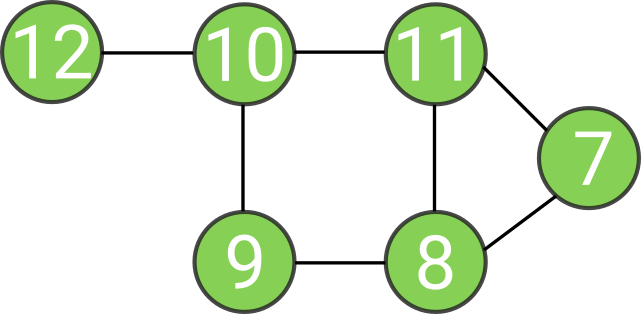
0 is now eigenvalue with 3 orthogonal vectors:

\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}
\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}

Intuition about spectral clustering

Count how many times 0 is eigenvalue

Matrix diagonalisation

L = P \Lambda P'
\Lambda = \begin{bmatrix} \lambda_1 \\ & \lambda_2 \\ & & \lambda_3 \\ & & & \ddots & \\ & & && \lambda_n \end{bmatrix} = \begin{bmatrix} 0 \\ & 0 \\ & & 0 \\ & & & \ddots & \\ & && & \lambda_n \end{bmatrix}
P = \begin{bmatrix} \\ \\ v_1 & v_2 & v_3 & ... & v_n \\ \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ \\ 0 & 1 & 0 & ... & v_n \\ \\ 0 & 0 & 1\\ \end{bmatrix}

Matrix diagonalization

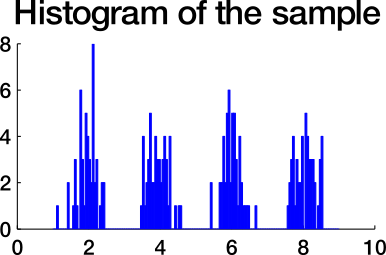
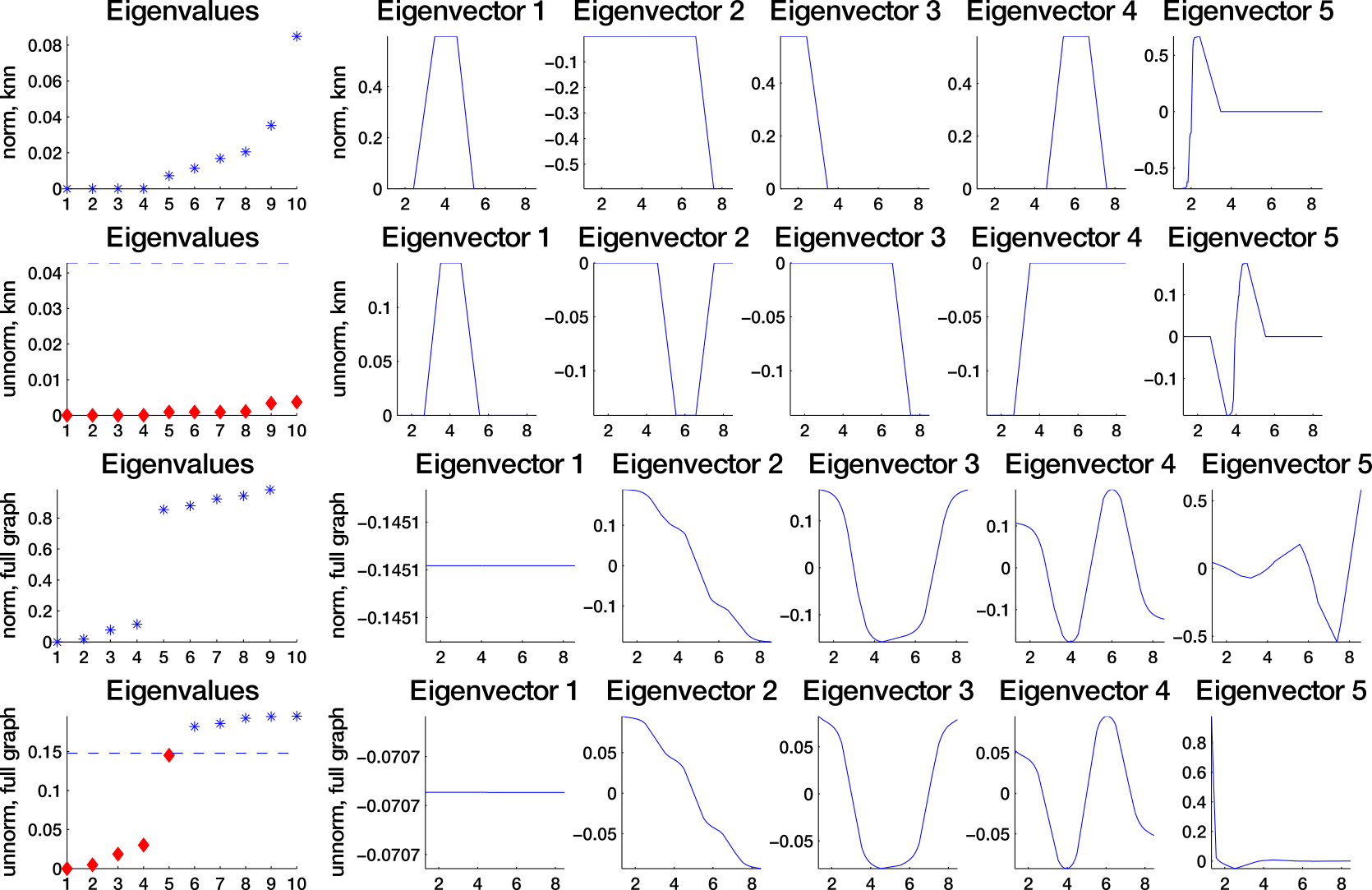
Which similarity graph?

fully connected graph (weighted)

Spectral clustering algorithm

How to choose k?

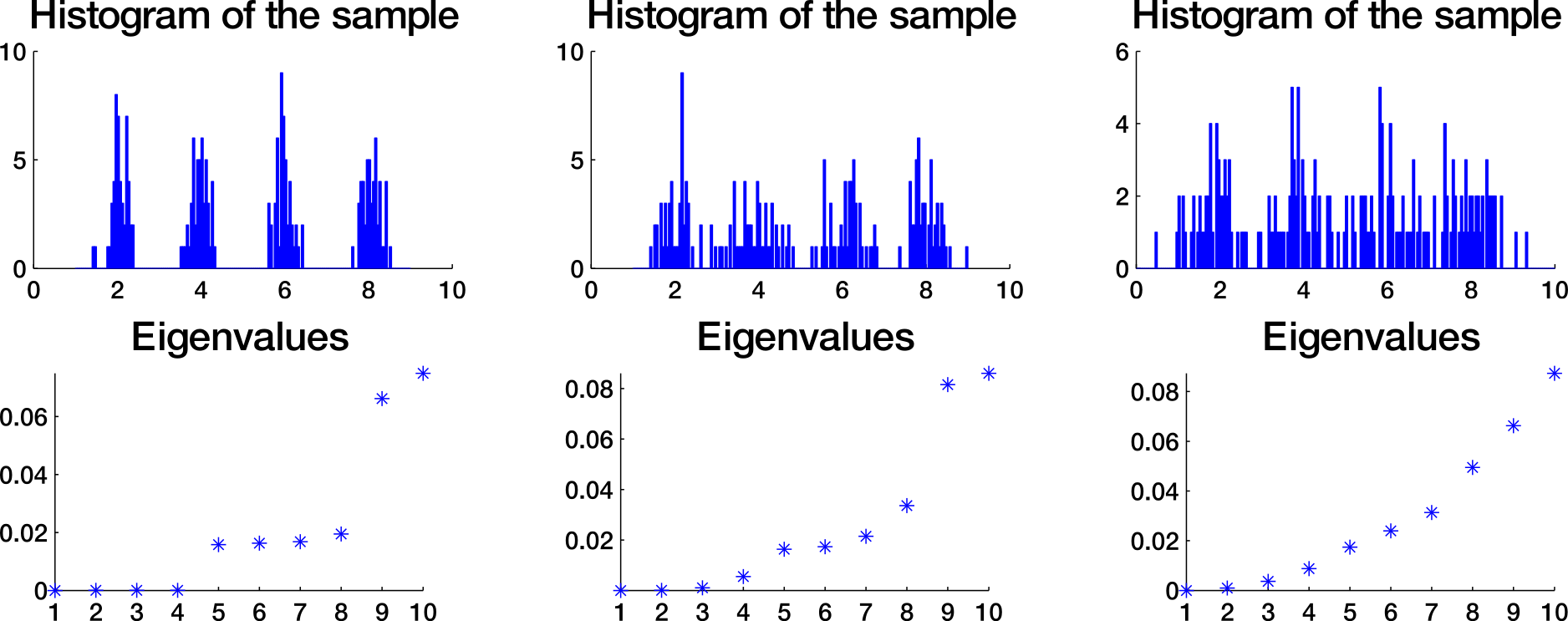
Eigengap heuristic

Spectral clustering algorithm

  • Method to choose the number of clusters (eigengap)
  • Based on strong theory
  • Doesn't assume a certain shape for the clusters
  • Problems when big matrices
  • Tricky to define your similarity graph

Louvain's algorithm

Looking for communities/groups:

- many links inside a group

- few links between groups

Modularity

Q = \frac{1}{2m} \sum_{v,w} \big[ A_{v,w} - \frac{d_v d_w}{2m} \big] \delta(c_v, c_w)

m: total number of edges

A: adjacency matrix

d: node degree

c: community membership

Optimize the modularity

Q = \frac{1}{2m} \sum_{v,w} \big[ A_{v,w} - \frac{d_v d_w}{2m} \big] \delta(c_v, c_w)

m: total number of edges

A: adjacency matrix

d: node degree

c: community membership

Actual edge presence between v and w

Expected edge presence knowing the degrees and the total number of edges

Only count if v and w are classified in the same community

Sum over all pairs of nodes

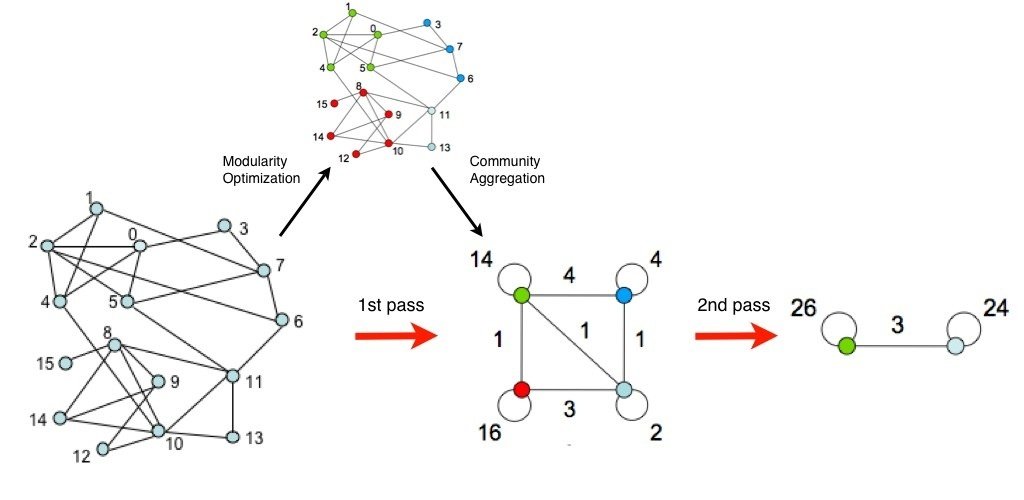
Louvain algorithm

Louvain algorithm

  • Good because you don't choose the number of clusters you want
  • Adapted to large graphs (www)
  • Heuristics: depends on the order you aggregate nodes
  • Tricky to define your similarity graph
  • Can have problems of reproducibility

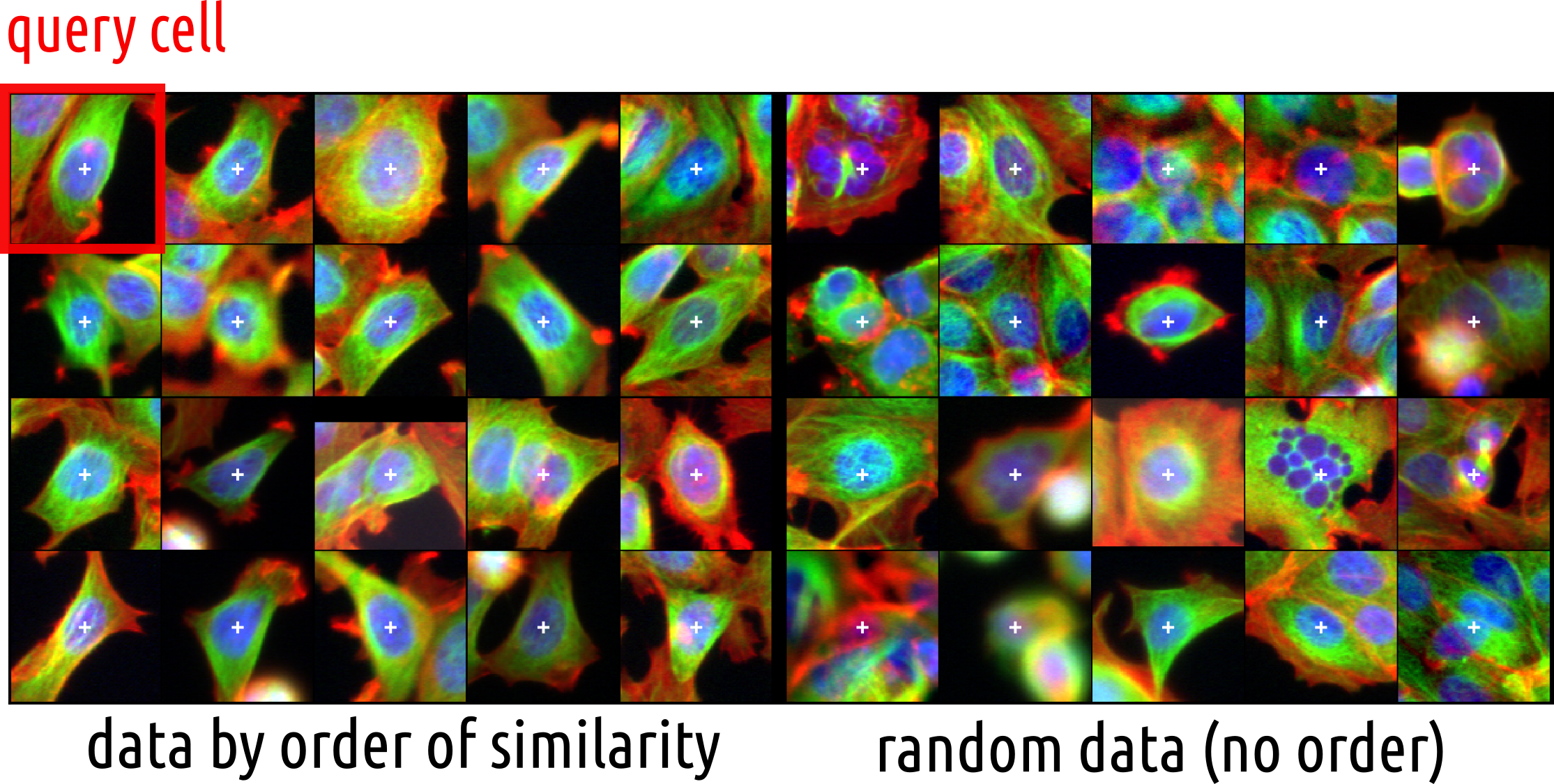
Using similarities between cells to cluster them

Clustering?

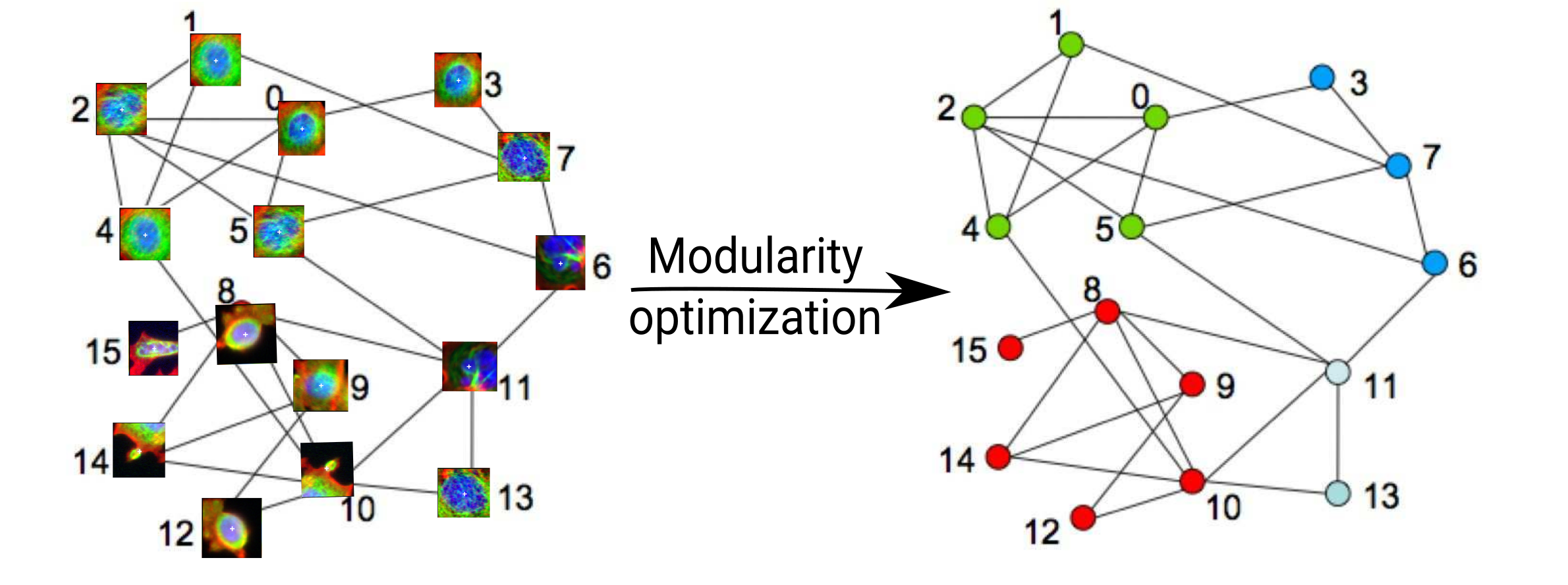
Applying Louvain algorithm

Cell categories

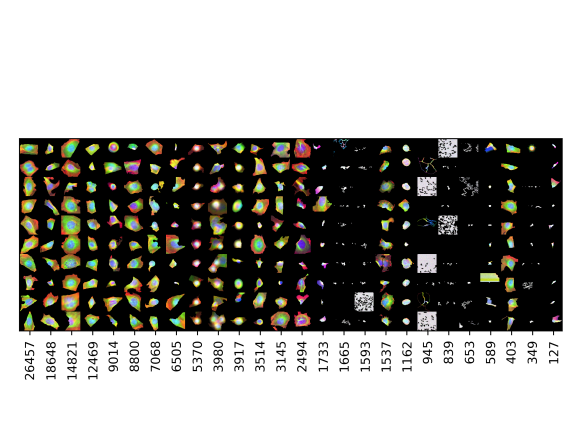
Cell categories

Number of cells

Examples of cells

Louvain algorithm

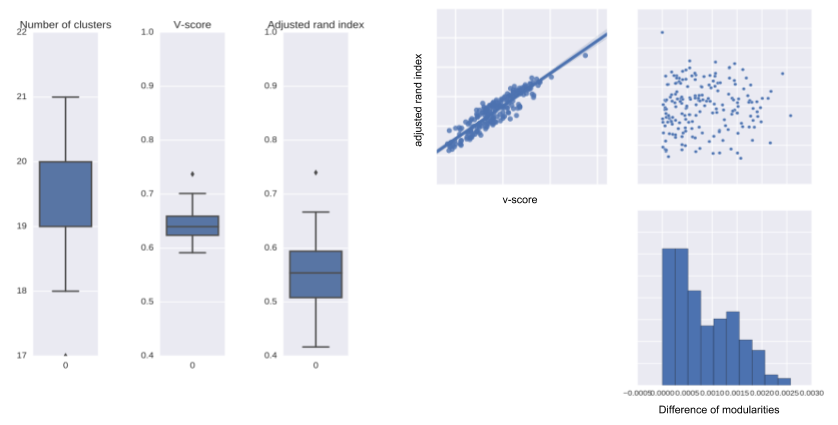
Take home message

  • Similarity graphs describe relationships between data points
  • Choosing a similarity measure can be tricky (high-dimension)
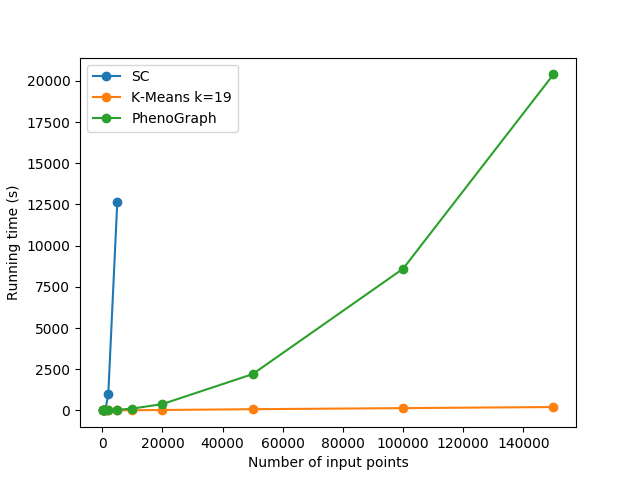
  • Spectral Clustering: good if not too large dataset (memory)
  • Louvain algorithm:  heuristic to find communities in large data  ! reproductibility !

Clustering with graphs:

By biocompibens

Private

Clustering with graphs:

More from biocompibens