Модальные типы для увеселения

и профита

Александр Грызлов

Statebox

Scaλa Russia 2019

Москва, 28/09/2019

план

инженерия доказательств

модальная логика

системы модальных типов

эффекты и линейные типы

продвинутые системы:

Granule и Blott

теория доказательств

лямбда-исчисление

финал

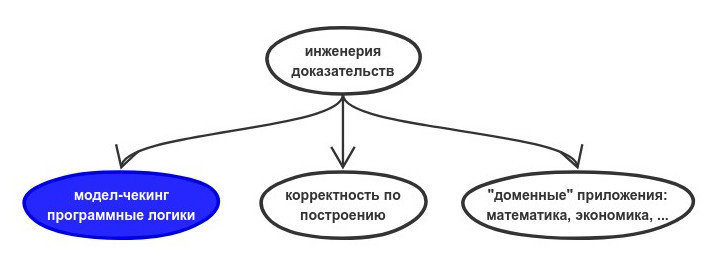
инженерия доказательств

пересечение software engineering и прикладной логики
хотим иметь доказанно "работающие" программы
условно 3 основные ветви:

верификация существующих программ или их моделей
написание корректных по построению программ
формализация математики/процессов/..

модели и верификация

проверка моделей (model checking)
автоматизируемо, "легковесно" но плохо масштабируется
SAT/SMT, темпоральная логика, методы оптимизации

программные логики а-ля Флойд-Хоар
сепарационная логика, динамическая логика
аннотирование переходов у фон Неймановского автомата

Карри-Говард

выше логика - некий отдельный от верифицируемой программы язык спецификаций
можем ли мы сделать логику частью программы?
да, используя соответствие Карри-Говарда:

типы ~ теоремы/высказывания в конструктивной логике
программы ~ доказательства в этой логике

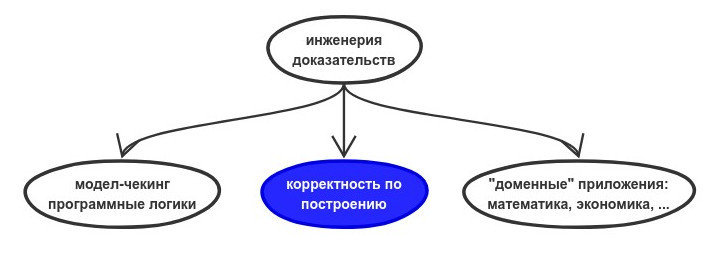
корректность по построению

"продвинутое" ФП
зависимые и refinement типы
в частности, верифицированные языки (т.е. интерпретаторы и компиляторы)
мы можем "погрузить" систему типов (т.е. логику) в индексы на типах зависимого хост-языка
компилятор следит за корректностью термов, т.е. соответствие типовой спецификации

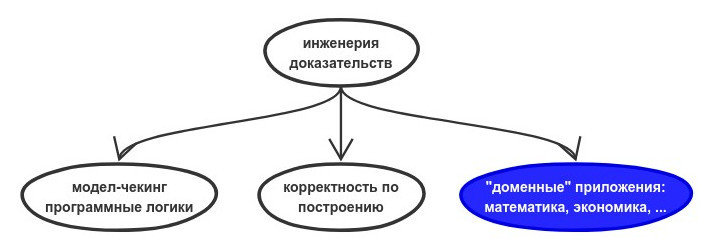
"доменная" ИД

использование корректных/логических инструментов для моделирования и формализации чего-то кроме программ:

математические доказательства
бизнес-процессы
...

модальные логики

модальность выражает "режим истинности"
происходит из философии и лингвистики (ср. модальные глаголы)
в современном виде придумана Льюисом (1920e, необходимость) и Гёделем (1930е, доказуемость)
ФП, как и логику, критикуют за разрыв с "реальным миром", модальности кодируют DSL внутри логики
модальные логики налагают дополнительные ограничения на использование переменных и формы контекстов

разновидности

алетическая (необходимо/возможно)
темпоральная (потом/всегда)

эпистемическая (известно)
деонтическая (обязательно/разрешено)
доксастическая (верим в)
динамическая (A обязательно после B)
доказательств
аксиологическая (хорошо/плохо)
пространственная
стрелочная

алетическая логика

две модальности:

◻ (необходимо) и ◊ (возможно)

грубо говоря, комонада и монада
аналоги кванторов ∀ и ∃
часто рассматривают только "необходимость"

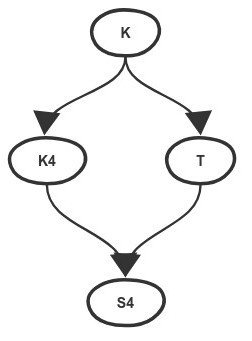
предпорядок систем (от аппликатива до комонады):

темпоральная логика

набор модальностей в зависимости от формулировки:

◯ - (будет верно) в следующий момент
◻ - всегда
◊ - (станет верным) в некоторый момент
A▹B - сначала будет верно А, затем B

применения модальной логики

благодаря разрешимости сильнее всего развита для модел чекеров (в основном темпоральная) и программных логик
TLA+, SPIN, NuSMV, CADP,...
Facebook Infer (сепарационная)
полезна для математики, будучи реализованной внутри пруф-ассистента
но как реализовать её конструктивно, т.е. в качестве системы типов?

конец 1 части

3 ветви инженерии доказательств:

модели и программная логика
корректность по построению
"доменные" доказательства

модальная логика:

алетическая
темпоральная

теория доказательств

ветвь математической логики
берет начало в 1920х, часть программы Гильберта:

закодировать математическое мышление как конечную механизированную систему
доказать непротиворечивость этой системы
ПРОФИТ

теория доказательств

мечтам не было суждено сбыться из-за теорем о неполноте Гёделя:
любая подобная система будет либо противоречивой, либо неполной
изучение формальных систем всё еще важно для программирования:

нормализация/устранение сечений (cut) как вычисление
- соответствует FP
поиск доказательства как вычисление
- соответствует LP

структурная теория доказательств

3 вида систем:

аксиоматические системы Гильберта (комбинаторы)
натуральная дедукция (лямбды)
исчисления секвенций (абстрактные машины)

(2 и 3 были изобретены Герхардом Генценом в 1930х)

секвенции & правила

доказательства строятся из применений правил

строительный блок правила называется секвенцией:

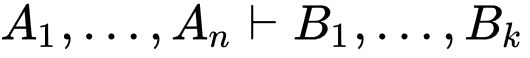
позволяет записывать классические логики
нас интересует только интуиционистское подмножество, т.е. секвенции с единственной формулой в правой части:

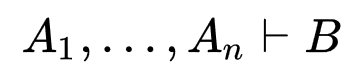
секвенции & правила

правила указывают как превратить набор секвенций в новую секвенцию:

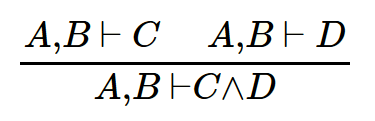
когда мы рассматриваем правила как шаги вычислений, они читаются снизу вверх
списки формул в левой части (так называемые контексты) обычно обозначают большими греческими буквами:

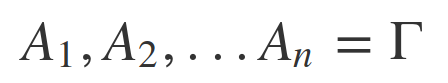
естественная дедукция

запишем правила минимальной логики высказываний:
у нас есть только набор примитивных формул (или даже только одна), переменные А, B, .. и импликация =>

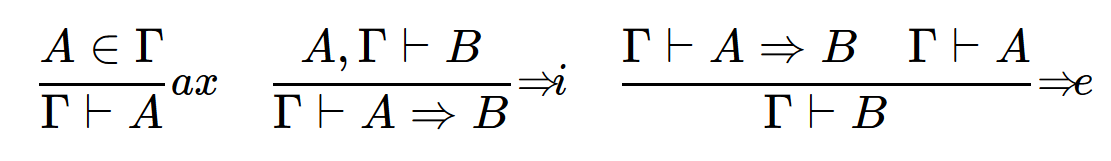
аксиома интродукция элиминация

Idris

практически Scala:

строгость
имплициты
отсутствие когерентности у интерфейсов (аналог тайпклассов)

но:

хаскелеобразный синтаксис
есть полноценные завтипы

унарные числа & списки

data List : Type -> Type where
  Nil  :                List a  -- aka `[]`
  (::) : a -> List a -> List a  -- aka `Cons`

data Nat : Type where
  Z : Nat
  S : Nat -> Nat

вхождение в список

стерев индексы, получим снова унарные числа

data Elem : a -> List a -> Type where
  Here  :              Elem x (x::xs)
  There : Elem x xs -> Elem x (y::xs)

--elem2Nat : {a : t} -> {g : List t} -> Elem a g -> Nat
elem2Nat : Elem a g -> Nat
elem2Nat  Here      = Z
elem2Nat (There el) = S (elem2Nat el)

конструктивное доказательство вхождения это номер элемента

минимальная логика это типизированная лямбда

открыто Вильямом Говардом в 1969

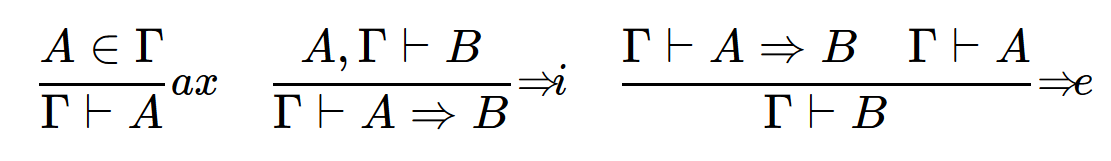
Var : 
 Elem a g ->
 Term g a

Lam :
 Term (a::g) b ->
 Term g (a~>b)

App : 
 Term g (a~>b) ->
 Term g a -> 
 Term g b

индексы деБрёйна

aka "глобально безымянное" представление

λx.x         ~ λ 0

λx.λy.y      ~ λ λ 0

λx.λy.x      ~ λ λ 1

λx.λy.(x y)  ~ λ λ (1 0)

λx.λy.λz.x   ~ λ λ λ 2

типизированная лямбда

infixr 5 ~>
data Ty = A | (~>) Ty Ty

data Term : List Ty -> Ty -> Type where
  Var : Elem a g                  -> Term g a 
  Lam : Term (a::g) b             -> Term g (a~>b)
  App : Term g (a~>b) -> Term g a -> Term g b
    
IdTy : Ty
IdTy = A ~> A

-- ((λx.x) (λx.x)) (λx.x)
Term1 : Term [] IdTy 
Term1 = App (App (Lam $ Var Here) (Lam $ Var Here)) (Lam $ Var Here)
  
-- (λx.x) ((λx.x) (λx.x))
Term2 : Term [] IdTy 
Term2 = App (Lam $ Var Here) (App (Lam $ Var Here) (Lam $ Var Here))

-- λx.x
Result : Term [] IdTy 
Result = Lam $ Var Here

конец 2 части

теория доказательств
естественная дедукция
списки и индексы
(просто типизированное) лямбда-исчисление

модальная теория доказательств

начнем с фрагмента алетической логики, т.е., единственной модальности ◻

диадические модальные типы

двухконтекстная интерпретация
разделим наши контексты/предпосылки на истинные и валидные:
A валидно, если ⋅⊢A
если A валидно, то Γ⊢A
отсюда мы можем вывести правила интродукции и элиминации для ◻-модальности (для системы К):

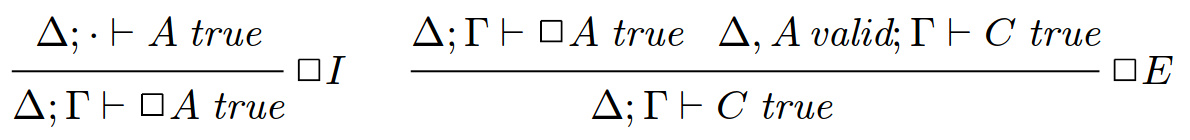
диадические модальные типы

infixr 5 ~>
data Ty = A | (~>) Ty Ty | Box Ty

data Term : List Ty -> List Ty -> Ty -> Type where
  Var    : Elem a g -> Term d g a
  Lam    : Term d (a::g) b -> Term d g (a~>b)
  App    : Term d g (a~>b) -> Term d g a -> Term d g b
  Shut   : Term [] d a -> Term d g (Box a)
  Letbox : Term d g (Box a) -> Term (a::d) g b -> Term d g b

axiomK : Term d g (Box (a ~> b) ~> Box a ~> Box b)
axiomK = Lam $ Lam $ Letbox (Var $ There Here)
           (Letbox (Var Here)
             (Shut $ App (Var $ There Here) (Var Here)))

диадические модальные типы (S4)

data Term : List Ty -> List Ty -> Ty -> Type where
  Var    : Elem a g -> Term d g a
  MVar   : Elem a d -> Term d g a
  Lam    : Term d (a::g) b -> Term d g (a~>b)
  App    : Term d g (a~>b) -> Term d g a -> Term d g b
  Shut   : Term d [] a -> Term d g (Box a)
  Letbox : Term d g (Box a) -> Term (a::d) g b -> Term d g b

axiomK : Term d g (Box (a ~> b) ~> Box a ~> Box b)
axiomK = Lam $ Lam $ Letbox (Var $ There Here)
           (Letbox (Var Here)
             (Shut $ App (MVar $ There Here) (MVar Here)))

-- aka `eval`
axiomT : Term d g (Box a ~> a)
axiomT = Lam $ Letbox (Var Here) (MVar Here)

axiom4 : Term d g (Box a ~> Box (Box a))
axiom4 = Lam $ Letbox (Var Here) (Shut $ Shut $ MVar Here)

модальные типы Фитча-Крипке

соответствует семантике возможных миров Крипке
мир это контекст
у нас есть текущий контекст и стек возможных
интродукция ◻ это выбор верхнего мира из стека
элиминация ◻ это сохранение текущего мира на стек

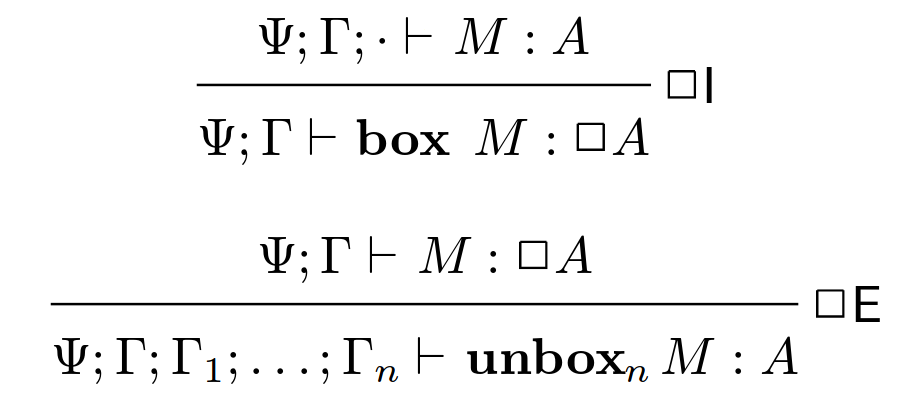
модальные типы Фитча-Крипке

в интерпретации Фитча вместо стека контекстов используется контекст с замка́ми:

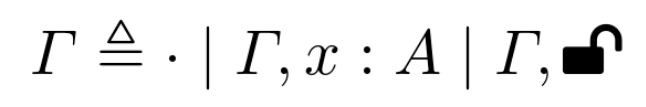
несложно показать что эта структура изоморфна непустому списку контекстов
замок соответствует границе соседних контекстов
формальное доказательство в репозитории

модальные типы Фитча-Крипке

data Term : List (List Ty) -> List Ty -> Ty -> Type where
  Var  : Elem a g -> Term ph g a
  Lam  : Term ph (a::g) b -> Term ph g (a~>b)
  App  : Term ph g (a~>b) -> Term ph g a -> Term ph g b
  Shut : Term (g::ph) [] a -> Term ph g (Box a)  -- ~quasiquote
  Open : Term ph g (Box a) -> Term (g::ph) d a   -- ~unquote0

axiomK : Term ph g (Box (a ~> b) ~> Box a ~> Box b)
axiomK = Lam $ Lam $ Shut $ App (Open $ Var $ There Here)
                                (Open $ Var Here)

модальные типы Фитча-Крипке (S4)

data Pref : a -> List a -> a -> List a -> Type where
  HereP  : Pref x xs x xs
  ThereP : Pref x xs y ys -> Pref x xs z (y::ys)

data Term : List (List Ty) -> List Ty -> Ty -> Type where
  Var  : Elem a g -> Term ph g a
  Lam  : Term ph (a::g) b -> Term ph g (a~>b)
  App  : Term ph g (a~>b) -> Term ph g a -> Term ph g b
  Shut : Term (g::ph) [] a -> Term ph g (Box a)             -- ~quasiquote
  Open : Pref g ph d ps -> Term ph g (Box a) -> Term ps d a -- ~unquoteN

axiomK : Term ph g (Box (a ~> b) ~> Box a ~> Box b)
axiomK = Lam $ Lam $ Shut $ App (Open (ThereP HereP) (Var $ There Here))
                                (Open (ThereP HereP) (Var Here))

axiomT : Term ph g (Box a ~> a)
axiomT = Lam $ Open HereP (Var Here)

axiom4 : Term ph g (Box a ~> Box (Box a))
axiom4 = Lam $ Shut $ Shut $ Open (ThereP $ ThereP HereP) (Var Here)

полярные модальности

можно пойти дальше и заметить, что обе интерпретации взаимосвязаны
возможно построить обобщенное исчисление
работает только для "алетикообразных" логик

классический пример полярных структур - положительные A⊕B и отрицательные A&B произведения (туплы)
одинаковая интродукция, но различная элиминация:

-- элиминация паттерн-матчингом
let (a, b) = a⊕b in foo a b

-- элиминация проекциями
let a = fst a&b in foo a
let b = snd a&b in bar b

полярные модальности

...
  Letbox : Term d g (Box a) -> Term (a::d) g b -> Term d g b

axiomK : Term d g (Box (a ~> b) ~> Box a ~> Box b)
axiomK = Lam $ Lam $ Letbox (Var $ There Here)
           (Letbox (Var Here)
             (Shut $ App (MVar $ There Here) (MVar Here)))

в диадической интерпретации мы "паттерн-матчим" содержимое коробки:

...
  Open : Pref g ph d ps -> Term ph g (Box a) -> Term ps d a

axiomK : Term ph g (Box (a ~> b) ~> Box a ~> Box b)
axiomK = Lam $ Lam $ Shut $ App (Open (ThereP HereP) (Var $ There Here))
                                (Open (ThereP HereP) (Var Here))

в Крипке-Фитча мы "проецируем" нужный контекст:

применения модальных типов

стейджинг/метапрограммирование
экспоненциал линейной логики
(ко)эффекты
темпоральная логика ~ FRP
распределенные вычисления (shared code)
ресурсный анализ
information-flow, гомоморфное шифрование

линейная лямбда

линейность ~ переменные можно использовать ровно 1 раз
диадическая интерпретация (линейный и интуиционистский контексты)
интуиционизм как модальность
исторически появилась до модальных

линейная лямбда

infixr 5 ~*
data Ty = A
        | (~*) Ty Ty
        | Bang Ty     -- !
        
data Split : List a -> List a -> List a -> Type where
  Nil   : Split [] [] []
  ConsR : Split xs ls rs -> Split (x::xs)     ls (x::rs)
  ConsL : Split xs ls rs -> Split (x::xs) (x::ls)    rs

data Term : List Ty -> List Ty -> Ty -> Type where
  Var     : Term [a] g a
  IVar    : Elem a g -> Term [] g a
  Lam     : Term (a::l) g b -> Term l g (a~*b)
  App     : Split l l1 l2 -> Term l1 g (a~*b) -> Term l2 g a -> Term l g b
  Lift    : Term [] g a -> Term [] g (Bang a)
  Letbang : Split l l1 l2 -> Term l1 g (Bang a) -> Term l2 (a::g) b -> Term l g b
  
ok : Term [] g (a ~* a)
ok = Lam Var

ok2 : Term [] g (a ~* Bang b ~* a)
ok2 = Lam $ Lam $ Letbang (ConsL $ ConsR Nil) Var Var

-- bad : Term [] [] (a ~* b ~* a)

метаязык Моджи и монады

хотим добавить в чистый язык эффекты
пометим их модальностью (примерно соответствует ◊, хотя полноценно кодируется обоими модальностями)
расщепляем сами суждения, а не контексты
для вычисления добавляем в язык примитивы соответствующих эффектов

метаязык Моджи и монады

infixr 5 ~>
data Ty = A
        | (~>) Ty Ty
        | M Ty       -- effect

mutual
  data Term : List Ty -> Ty -> Type where
    Var    : Elem a g -> Term g a
    Lam    : Term (a::g) b -> Term g (a~>b)
    App    : Term g (a~>b) -> Term g a -> Term g b
    Val    : PTerm g a -> Term g (M a)

  data PTerm : List Ty -> Ty -> Type where
    Wrap   : Term g a -> PTerm g a
    Letval : Term g (M a) -> PTerm (a::g) b -> PTerm g b

метаязык Моджи и монады

map : Term g ((a ~> b) ~> M a ~> M b)
map = Lam $ Lam $ Val $ Letval (Var Here)
                          (Wrap $ App (Var $ There $ There Here)
                                      (Var Here))

pure : Term g (a ~> M a)
pure = Lam $ Val $ Wrap $ Var Here

flatten : Term g (M (M a) ~> M a)
flatten = Lam $ Val $ Letval (Var Here)
                        (Letval (Var Here)
                           (Wrap $ Var Here))

flatMap : Term g ((a ~> M b) ~> M a ~> M b)
flatMap = Lam $ Lam $ Val $ Letval (Var Here)
                              (Letval (App (Var $ There $ There Here)
                                           (Var Here))
                                 (Wrap $ Var Here))

градуированные модальности

экспериментальный язык Granule
позволяет аннотировать линейность арифметическими выражениями
более тонкое управление ресурсами

-- You cannot have your cake and eat it...

-- impossible : Cake → (Happy, Cake)
-- impossible cake = (eat cake, have cake)

-- ...unless you have infinite cake

possible : Cake [∞] → (Happy, Cake [∞])
possible lotsOfCake =
  let [cake] = lotsOfCake in (eat cake, [have cake])

-- ...or to there is a more precise way

accurate : ∀ {n : Nat} . Cake [n+1] → (Happy, Cake [n])
accurate lotsOfCake =
  let [cake] = lotsOfCake in (eat cake, [have cake])

зависимые модальные типы

guarded рекурсия (семантический чекер тотальности)
модальность как расширенное метапрограммирование (Beluga/Cocon)
модальность как стирание (Bauer)
модальность как математические свойства (напр., дифференцируемость)

конец 3 части

диадические модальные типы
модальные типы Фитча-Крипке
поляризованные модальности
линейная лямбда
метаязык Моджи
градуированные модальности
зависимые модальные типы

ссылки (1)

ссылки (2)

ссылки (3)

финал

слайды:

https://slides.com/clayrat/modal-types

код:

https://github.com/sequents

https://github.com/clayrat/modal-types

вебинар:

https://www.youtube.com/channel/UC8reF8xuw05LOYLeWNRV0pg

патреон:

https://www.patreon.com/clayrat

Modal types for fun and profit

By Alex Gryzlov

Modal types for fun and profit

1,680

Модальные типы для увеселения

и профита

план

инженерия доказательств

модели и верификация

Карри-Говард

корректность по построению

"доменная" ИД

модальные логики

разновидности

алетическая логика

темпоральная логика

применения модальной логики

конец 1 части

теория доказательств

теория доказательств

структурная теория доказательств

секвенции & правила

секвенции & правила

естественная дедукция

Idris

унарные числа & списки

вхождение в список

минимальная логика это типизированная лямбда

индексы деБрёйна

типизированная лямбда

конец 2 части

модальная теория доказательств

диадические модальные типы

диадические модальные типы

диадические модальные типы (S4)

модальные типы Фитча-Крипке

модальные типы Фитча-Крипке

модальные типы Фитча-Крипке

модальные типы Фитча-Крипке (S4)

полярные модальности

полярные модальности

применения модальных типов

линейная лямбда

линейная лямбда

метаязык Моджи и монады

метаязык Моджи и монады

метаязык Моджи и монады

градуированные модальности

зависимые модальные типы

конец 3 части

ссылки (1)

ссылки (2)

ссылки (3)

финал

Modal types for fun and profit

More from Alex Gryzlov